Cálculo VectorialParte II INTERACTIVO
Juan Guillermo Rivera Berrío
Institución Universitaria Pascual Bravo
Elena E. Álvarez Saiz
Universidad de Cantabria


Fondo Editorial Pascual Bravo
Medellín2020
Título de la obra:
Cálculo Vectorial - Parte II
Interactivo
Autores:
Juan Guillermo Rivera Berrío
Elena Esperanza Álvarez Saiz
Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Obra derivada del libro Calculus Volume 3 de: Gilbert Strang (Massachusetts Institute of Technology) Edwin “Jed” Herman (University of Wisconsin-Stevens Point)
LICENCIA

Figura 4.1. Los estadounidenses usan (y pierden) millones de pelotas de golf al año, lo que mantiene a los fabricantes de pelotas de golf en el negocio. En este capítulo, estudiaremos un modelo de ganancias y aprenderemos métodos para calcular los niveles de producción óptimos para una empresa típica de fabricación de pelotas de golf. (crédito: modificación del trabajo de oatsy40, Flickr)
En las aplicaciones de las derivadas, estudiaste cómo determinar el máximo y el mínimo de una función de una variable durante un intervalo cerrado. Esta función puede representar la temperatura durante un intervalo de tiempo determinado, la posición de un automóvil en función del tiempo o la altitud de un avión a reacción mientras viaja de Medellín a Madrid.
En cada uno de estos ejemplos, la función tiene una variable independiente.
Supongamos, sin embargo, que tenemos una cantidad que depende de más de una variable. Por ejemplo, la temperatura puede depender de la ubicación y la hora del día, o el modelo de ganancias de una empresa puede depender de la cantidad de unidades vendidas y la cantidad de dinero gastado en publicidad. En este capítulo, nos fijamos en una empresa que produce pelotas de golf. Desarrollamos un modelo de ganancias y, bajo varias restricciones, encontramos que el nivel óptimo de producción y publicidad gastada determina el beneficio máximo posible. Dependiendo de la naturaleza de las restricciones, tanto el método de solución como la solución misma cambian.
Cuando se trata de una función de más de una variable independiente, surgen naturalmente varias preguntas. Por ejemplo, ¿cómo calculamos los límites de las funciones de más de una variable? La definición de derivada que usamos antes implicaba un límite. ¿La nueva definición de derivada también implica límites? ¿Se aplican las reglas de diferenciación en este contexto? ¿Podemos encontrar extremos relativos de funciones usando derivadas? Todas estas preguntas se responden en este capítulo.
En la parte I de este libro estudiamos los apartados:
En el cálculo de variable única, encontramos que una de las reglas de diferenciación más útiles es la regla de la cadena, que nos permite encontrar la derivada de la composición de dos funciones. Lo mismo es cierto para el cálculo multivariable, pero esta vez tenemos que lidiar con más de una forma de la regla de la cadena. En esta sección, estudiamos extensiones de la regla de la cadena y aprendemos cómo tomar derivadas de composiciones de funciones de más de una variable.
Recuerda que la regla de la cadena para la derivada de una composición de dos funciones se puede escribir en la forma
$$\frac{d}{dx}\big( f(g(x)\big) = f^{\prime}\big( g(x)\big)g^{\prime}(x)$$En esta ecuación, ambas $f(x)$ y $g(x)$son funciones de una variable. Ahora supongamos que $f$ es una función de dos variables y $g$ es una función de una variable, o quizás ambas son funciones de dos variables, o incluso más. ¿Cómo calcularíamos la derivada en estos casos? El siguiente teorema nos da la respuesta para el caso de una variable independiente.
La prueba de este teorema utiliza la definición de diferenciabilidad de una función de dos variables. Supongamos que $f$ es diferenciable en el punto $P(x_0, y_0)$, dónde $x_0=g(t_0)$ y $y_0=h(t_0)$ por un valor fijo de $t_0$. Queremos demostrar que $z=f(x(t),y(t))$ es diferenciable en $t=t_0$ y la ecuación 4.29 se mantiene en ese punto también.
Ya que $f$ es diferenciable en $P$, sabemos
$$\begin{aligned} z(t) &= f(x,y)\\ &= f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)\\ & + f_y(x_0,y_0)(y−y_0)+ E(x,y)\tag{$4.30$} \end{aligned}$$donde $\lim\limits_{(x, y) \to (x_0, y_0)}\frac{E(x, y)}{\sqrt{(x-x_0)^2+(y-y_0)^2}}=0$. Luego restamos $z_0=f(x_0, y_0)$ de ambos lados de esta ecuación:
A continuación, dividimos ambos lados por $t-t_0$
$$\begin{aligned} \frac{z(t)-z(t_0)}{t-t_0} &= f_x(x_0, y_0)\bigg(\frac{x(t)-x(t_0)}{t-t_0}\bigg) \\ &\quad + f_y(x_0, y_0)\bigg(\frac{y(t)-y(t_0)}{t-t_0}\bigg) + \frac{E\big(x(t) - y(t)\big)}{t-t_0} \end{aligned}$$Luego tomamos el límite cuando $t$ se acerca a $t_0$
$$\begin{aligned} \lim\limits_{t \to t_0}\frac{z(t)-z(t_0)}{t-t_0} &= f_x(x_0, y_0)\lim\limits_{t \to t_0}\bigg(\frac{x(t)-x(t_0)}{t-t_0}\bigg) \\ &\quad + f_y(x_0, y_0)\lim\limits_{t \to t_0}\bigg(\frac{y(t)-y(t_0)}{t-t_0}\bigg)\\ &\quad + \lim\limits_{t \to t_0}\frac{E\big(x(t) - y(t)\big)}{t-t_0} \end{aligned}$$El lado izquierdo de esta ecuación es igual a $\frac{dz}{dt}$, lo que lleva a
$$\frac{dz}{dt} = f_x(x_0, y_0)\frac{dx}{dt} + f_y(x_0, y_0)\frac{dy}{dt} + \lim\limits_{t \to t_0}\frac{E\big(x(t) - y(t)\big)}{t-t_0}$$El último término puede reescribirse como
$$\begin{aligned} \lim\limits_{t \to t_0}\frac{E\big(x(t) - y(t)\big)}{t-t_0} & = \lim\limits_{t \to t_0}\bigg(\frac{E(x, y)}{\sqrt{(x-x_0)^2+(y-y_0)^2}}\frac{\sqrt{(x-x_0)^2+(y-y_0)^2}}{t-t_0}\bigg)\\ &= \lim\limits_{t \to t_0}\bigg(\frac{E(x, y)}{\sqrt{(x-x_0)^2+(y-y_0)^2}}\bigg)\lim\limits_{t \to t_0}\bigg(\frac{\sqrt{(x-x_0)^2+(y-y_0)^2}}{t-t_0}\bigg) \end{aligned}$$Como $t$ se aproxima a $t_0$, $(x(t), y(t))$ se aproxima a $\big(x(t_0), y(t_0)\big)$, podemos reescribir el último producto como
$$\lim\limits_{(x, y) \to (x_0, y_0)}\bigg(\frac{E(x, y)}{\sqrt{(x-x_0)^2+(y-y_0)^2}}\bigg)\lim\limits_{(x, y) \to (x_0, y_0)}\bigg(\frac{\sqrt{(x-x_0)^2+(y-y_0)^2}}{t-t_0}\bigg)$$Como el primer límite es igual a cero, solo necesitamos mostrar que el segundo límite es finito:
$$\begin{aligned} \lim\limits_{(x, y) \to (x_0, y_0)}\bigg(\frac{\sqrt{(x-x_0)^2+(y-y_0)^2}}{t-t_0}\bigg) &= \lim\limits_{(x, y) \to (x_0, y_0)}\bigg(\sqrt{\frac{(x-x_0)^2+(y-y_0)^2}{(t-t_0)^2}}\bigg) \end{aligned}$$ $$= \sqrt{\bigg(\lim\limits_{(x, y) \to (x_0, y_0)}\bigg(\frac{x-x_0}{t-t_0}\bigg)\bigg)^2 + \bigg(\lim\limits_{(x, y) \to (x_0, y_0)}\bigg(\frac{y-y_0}{t-t_0}\bigg)\bigg)^2}$$Ya que $x(t)$ y $y(t)$ son ambas funciones diferenciables de $t$, existen ambos límites dentro del último radical. Por lo tanto, este valor es finito. Esto prueba la regla de la cadena en $t =t_0$; El resto del teorema se deriva de la suposición de que todas las funciones son diferenciables en todos sus dominios.
Un examen más detallado de la ecuación 4.29 revela un patrón interesante. El primer término en la ecuación es $\frac{\partial f}{\partial x}\cdot\frac{dx}{dt}$ y el segundo término es $\frac{\partial f}{\partial y}\cdot\frac{dy}{dt}$ . Recuerda que al multiplicar fracciones, se puede usar la cancelación. Si tratamos estas derivadas como fracciones, entonces cada producto se "simplifica" a algo parecido $\frac{\partial f}{dt}$. Las variables $x$ e $y$ que desaparecen en esta simplificación a menudo se denominan variables intermedias: son variables independientes para la función $f$, pero son variables dependientes para la variable $t$. Aparecen dos términos en el lado derecho de la fórmula, y $f$ es una función de dos variables. Este patrón también funciona con funciones de más de dos variables, como veremos más adelante en esta sección.
 |
Usando la regla de la cadena |
Calcula $dz/dt$ para cada una de las siguientes funciones:

En la siguiente escena interactiva, diseñada en GeoGebra, adaptada de la propuesta por Kristen Beck, se ilustra la regla de la cadena para una función de dos variables, correspondiente al ejercicio anterior.
A menudo es útil crear una representación visual de la ecuación 4.29 para la regla de la cadena. Esto se llama diagrama de árbol para la regla de la cadena para funciones de una variable y proporciona una forma de recordar la fórmula (Figura 4.34).
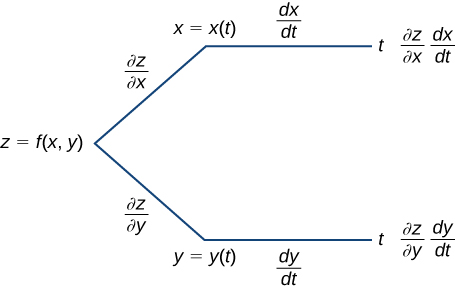
Figura 4.34. Diagrama de árbol para $\frac{dz}{dt} = \frac{\partial z}{\partial x}\cdot\frac{dx}{dt} + \frac{\partial z}{\partial y}\cdot\frac{dy}{dt}$
En este diagrama, la esquina más a la izquierda corresponde a $z=f(x, y)$. Ya que $f$ tiene dos variables independientes, hay dos líneas que provienen de esta esquina. La rama superior corresponde a la variable $x$ y la inferior a la variable $y$. Dado que cada una de estas variables depende de una variable $t$, una rama entonces viene de $x$ y otra de $y$. Por último, cada una de las ramas en el extremo derecho tiene una etiqueta que representa el camino recorrido para llegar a esa rama. Se llega a la rama superior siguiendo la rama $x$; por lo tanto, está etiquetado $(\partial z/ /\partial x)\times (dx/dt)$. La rama inferior es similar $(\partial z/ /\partial y)\times (dy/dt)$. Para obtener la fórmula para $dz/dt$, agrega todos los términos que aparecen en el lado derecho del diagrama. Esto nos da la ecuación 4.29. En la regla de la cadena para dos variables independientes, $z=f(x, y)$ es una función de $x$ e $y$, y ambas $x=g(u,v)$ y $y=h(u,v)$ son funciones de las variables independientes $u$ y $v$.
Podemos dibujar un diagrama de árbol para cada una de estas fórmulas, así:
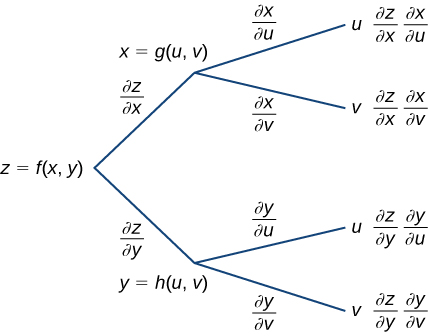
Figura 4.35. Diagrama de árbol para $\frac{\partial z}{\partial u} = \frac{\partial z}{\partial x}\cdot\frac{\partial x}{\partial u} + \frac{\partial z}{\partial y}\cdot\frac{\partial y}{\partial u}$ y $\frac{\partial z}{\partial v} = \frac{\partial z}{\partial x}\cdot\frac{\partial x}{\partial v} + \frac{\partial z}{\partial y}\cdot\frac{\partial y}{\partial v}$
Para deducir la fórmula para $\frac{\partial z}{\partial u}$, comienza desde el lado izquierdo del diagrama, luego sigue solo las ramas que terminan con $u$ y agrega los términos que aparecen al final de esas ramas. Para la fórmula para $\frac{\partial z}{\partial v}$, sigue solo las ramas que terminan con $v$ y agrega los términos que aparecen al final de esas ramas.
Hay una diferencia importante entre estos dos teoremas de la regla de la cadena. En la regla de la cadena para una variable independiente, el lado izquierdo de la fórmula para la derivada no es una derivada parcial, pero en la Regla de cadena para dos variable independientes sí lo es.
La razón es que, en la regla de cadena para una variable independiente, $z$ es en última instancia solo una función de $t$, mientras que en la regla de cadena para dos variables independientes, $z$ es una función de $u$ y $v$
 |
Usando la regla de la cadena para dos variables |
Calcule $\frac{\partial z}{\partial u}$ y $\frac{\partial z}{\partial v}$ usando las siguientes funciones: $$z = f(x, y) = 3x^2 − 2xy + y^2,\\ x = x(u, v) = 3u + 2v,\;\; y = y(u, v) = 4u − v$$

Ahora que hemos visto cómo extender la regla de la cadena original a las funciones de dos variables, es natural preguntar:
¿podemos extender La regla para más de dos variables? La respuesta es sí, como dice la regla generalizada de la cadena.
En el siguiente ejercicio calcularemos la derivada de una función de tres variables independientes en las que cada una de las tres variables dependen de otras dos variables.
 |
Usando la regla generalizada de la cadena |
Calcula $\frac{\partial w}{\partial u}$ y $\frac{\partial w}{\partial v}$ usando las siguientes funciones: $$w = f(x, y, z) = 3x^2 − 2xy + 4z^2\\ x = x(u, v) = e^usen v\\ y = y(u, v) = e^ucos v\\ z = z(u, v) = e^u$$

 |
Dibujando un diagrama de árbol |
Crea un diagrama de árbol para el caso cuando $$w = f (x, y, z),\; x = x (t, u, v),\; y = y (t, u, v),\; z = z (t, u, v)$$ y escribe las fórmulas para las tres derivadas parciales de $w$.

Recuerda que la diferenciación implícita proporciona un método para encontrar $dy/dx$ cuando $y$ se define implícitamente como una función de $x$. El método consiste en diferenciar ambos lados de la ecuación definiendo la función con respecto a $x$, luego resolviendo $dy/dx$. Las derivadas parciales proporcionan una alternativa a este método.
Considera la elipse definida por la ecuación $x^2 + 3y^2 + 4y - 4 = 0 $.
Esta ecuación define implícitamente $y$ como una función de $x$. Como tal, podemos encontrar la derivada $dy/dx$ usando el método de diferenciación implícita:
$$\begin{aligned} \frac{d}{dx}\big(x^2 + 3y^2 + 4y - 4\big) &= \frac{d}{dx}(0)\\ 2x + 6y\frac{dy}{dx} + 4\frac{dy}{dx} &= 0 \end{aligned}$$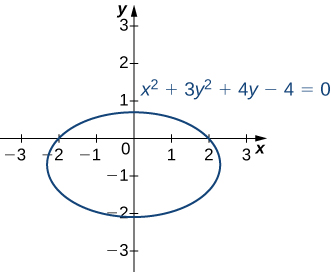
Figura 4.37. Gráfica de la elipse definida por $x^2 + 3y^2 + 4y - 4 = 0 $
También podemos definir una función $z = f (x, y)$ usando el lado izquierdo de la ecuación que define la elipse. Entonces $f (x, y) = x^2 + 3y^2 + 4y - 4$. La elipse $x^2 + 3y^2 + 4y - 4 = 0$ se puede describir con la ecuación $f (x, y) = 0$. Usando esta función y el siguiente teorema nos da un enfoque alternativo para el cálculo de $dy/dx$
La ecuación 4.34 es una consecuencia directa de la ecuación 4.31. En particular, si suponemos que $y$ se define implícitamente como una función de $x$ a través de la ecuación $f (x, y) = 0$, podemos aplicar la regla de la cadena para encontrar $dy/dx$:
$$\begin{aligned} \frac{d}{dx}f(x, y) &= \frac{d}{dx}(0)\\ \frac{\partial f}{\partial x}\cdot\frac{dx}{dx} + \frac{\partial f}{\partial y}\cdot\frac{dy}{dx} & = 0\\ \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y}\cdot\frac{dy}{dx} & = 0 \end{aligned}$$Resolver esta ecuación para $dy/dx$ da la ecuación 4.34. La ecuación 4.35 puede derivarse de manera similar.
Volvamos ahora al problema que comenzamos antes del teorema anterior. Usando la diferenciación implícita de una función de dos o más variables y la función $f (x, y) = x^2 + 3y^2 + 4y - 4$, obtenemos
$$\begin{aligned} \frac{\partial f}{\partial x} &=2x\\ \frac{\partial f}{\partial y} &= 6y+4 \end{aligned}$$Entonces por la ecuación 4.34 obtenemos
$$\frac{dy}{dx} = -\frac{\partial f/\partial x}{\partial f/\partial y} = -\frac{2x}{6y+4} = -\frac{x}{3y+2}$$que es el mismo resultado obtenido por el uso anterior de la diferenciación implícita.
 |
Diferenciación implícita por derivadas parciales |

La primera parte del ejercicio anterior, la hemos respresentado en la siguiente escena interactiva diseñada en GeoGebra:

 Para los siguientes ejercicios, usa la información provista para resolver el problema.
Para los siguientes ejercicios, usa la información provista para resolver el problema.
215. Sea $w (x, y, z) = xy cos z$, donde $x = t$, $y = t^2$ y $z = arcsen t$. Encuentra $\frac{dw}{dt}$ (Solución). 216. Sea $w (t, v) = e^{tv}$ donde $t = r + s$ y $v = rs$. Encuentra $\frac{\partial w}{\partial r}$ y $\frac{\partial w}{\partial s}$.
217. Si $w = 5x^2 + 2y^2, x = −3s + t$, y $y = s - 4t$, encuentra $\frac{\partial w}{\partial s}$ y $\frac{\partial w}{\partial t}$ (Solución). 218. Si $w = xy^2, x = 5 cos (2t)$ e $y = 5 sen (2t)$, encuentra $\frac{\partial w}{\partial t}$. 219. Si $f (x, y) = xy, x = r cos \theta$, y $y = r sen \theta$, encuentra $\frac{\partial f}{\partial r}$ y expresa la respuesta en términos de $r$ y $\theta$ (Solución). 220. Supón que $f (x, y) = x + y, u = e^xsen y, x = t^2$ e $y = \pi t$, donde $x = r cos \theta$ e $y = r sen \theta$. Encuentra $\frac{\partial f}{\partial \theta}$.
 Para los siguientes ejercicios, encuentra $\frac{df}{dt}$ usando la regla de la cadena y la sustitución directa
Para los siguientes ejercicios, encuentra $\frac{df}{dt}$ usando la regla de la cadena y la sustitución directa
227. Sea $w (x, y, z) = x^2 + y^2 + z^2, x = cos t, y = sen t$, y $z = e^t$. Expresa $w$ como una función de $t$ y encuentra $\frac{dw}{dt}$ directamente. Luego, encuentra $\frac{dw}{dt}$ usando la regla de la cadena (Solución).
228. Sea $z = x^2y$, donde $x = t^2$ e $y = t^3$. Encuentra $\frac{dz}{dt}$. 229. Sea $u = e^xsen y$, donde $x = t^2$ e $y = \pi t$. Encuentra $\frac{du}{dt}$ cuando $x = ln\; 2$ e $y = \frac{\pi}{4}$. (Solución).
 Para los siguientes ejercicios, encuentre $\frac{dy}{dx}$ usando derivadas parciales
Para los siguientes ejercicios, encuentre $\frac{dy}{dx}$ usando derivadas parciales
230. $sen(6x) + tan(8y) + 5 = 0$. 231. $x^3 + y^2x − 3 = 0$ (Solución). 232. $sen(x + y) + cos(x − y) = 4$. 233. $x^2 − 2xy + y^4 = 4$ (Solución). 234. $xe^y + ye^x − 2x^2y = 0$. 235. $x^{2/3} + y^{2/3} = a^{2/3}$ (Solución). 236. $x cos(xy) + y cos x = 2$. 237. $e^{xy}+ ye^y = 1$ (Solución). 238. $x^2y^3 + cos y = 0$ 239. Encuentra $\frac{dz}{dt}$ usando la regla de la cadena donde $z = 3x^2y^3, x = t^4$ e $y = t^2$ (Solución). 240. Sea $z = 3 cos x - sen(xy), x = \frac{1}{t}$, y $y = 3t$. Encuentra $\frac{dz}{dt}$ 241. Sea $z = e^{1 - xy}, x = t^{1/3}$ e $y = t^3.$ Encuentra $\frac{dz}{dt}$ (Solución). 242. Encuentra $\frac{dz}{dt}$ por la regla de la cadena donde $z = cosh^2 (xy), x = \frac12 t$ e $y = e^t$. 243. Sea $z = \frac{x}{y}, x = 2 cos u$, y $y = 3 sen v$. Encuentra $\frac{\partial z}{\partial u}$ y $\frac{\partial z}{\partial v}$ (Solución). 244. Sea $z = e^{x^2y}$, donde $x = uv$ e $y = \frac1v$. Encuentra $\frac{\partial z}{\partial u}$ y $\frac{\partial z}{\partial v}$. 245. Si $z = xye^{x/y}, x = r cos \theta$, e $y = r sen \theta$, encuentra $\frac{\partial z}{\partial r}$ y $\frac{\partial z}{\partial \theta}$ cuando $r = 2$ y $\theta = \frac{\pi}{6}$ (Solución). 246. Encuentra $\frac{\partial w}{\partial s}$ si $w = 4x + y^2 + z^3, x = e^{rs^2}, y = ln \big(\frac{r + s}{t}\big)$ y $z = rst^2$. 247. Si $w = sen (xyz), x = 1 - 3t, y = e^{1 - t}$, y $z = 4t$, encuentra $\frac{\partial w}{\partial t}$ (Solución).
 Para los siguientes ejercicios, usa esta información: Se dice que una función $f (x, y)$ es homogénea de grado $n$ si $f (tx, ty) = t^nf (x, y)$. Para todas las funciones homogéneas de grado $n$, la siguiente ecuación es verdadera:
$x\frac{\partial f}{\partial x} + y\frac{\partial f}{\partial y} = n f (x, y)$. Demuestra que la función dada es homogénea y verifica que $x\frac{\partial f}{\partial x} + y\frac{\partial f}{\partial y} = n f (x, y)$.
Para los siguientes ejercicios, usa esta información: Se dice que una función $f (x, y)$ es homogénea de grado $n$ si $f (tx, ty) = t^nf (x, y)$. Para todas las funciones homogéneas de grado $n$, la siguiente ecuación es verdadera:
$x\frac{\partial f}{\partial x} + y\frac{\partial f}{\partial y} = n f (x, y)$. Demuestra que la función dada es homogénea y verifica que $x\frac{\partial f}{\partial x} + y\frac{\partial f}{\partial y} = n f (x, y)$.
Encuentra la tasa de cambio del volumen de este tronco cuando $x = 10 pulg$., $y = 12 pulg.$ y $z = 18 pulg.$
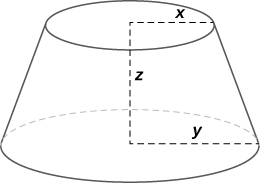
255. Una caja cerrada tiene la forma de un sólido rectangular con dimensiones $x, y$ y $z$ (las dimensiones están en pulgadas). Supongamos que cada dimensión está cambiando a razón de $0.5\;pulg./min$. Encuentra la tasa de cambio del área de superficie total de la caja cuando $x = 2 pulg.$, $y = 3 pulg.$ y $z = 1 pulg.$ (Solución). 256. La resistencia total en un circuito que tiene tres resistencias individuales representadas por $x, y$ y $z$ viene dada por la fórmula $R (x, y, z) = \frac{xyz}{yz + xz + xy}$. Supón que en un momento dado la resistencia $x$ es $100\Omega$, la resistencia $y$ es $200\Omega$ y la resistencia $z$ es $300\Omega$. Además, supón que la resistencia $x$ está cambiando a una velocidad de $2\Omega/min$, la resistencia $y$ está cambiando a una velocidad de $1\Omega/ min$, y la resistencia $z$ no cambia. Encuentra la tasa de cambio de la resistencia total en este circuito en este momento 257. La temperatura $T$ en un punto $(x, y)$ es $T (x, y)$ y se mide usando la escala Celsius. Una mosca se arrastra para que su posición después de $t$ segundos esté dada por $x = \sqrt{1 + t}$ e $y = 2 + \frac13 t$, donde $x$ e $y$ se miden en centímetros. La función de temperatura satisface $T_x(2, 3) = 4$ y $T_y (2, 3) = 3$.
¿Qué tan rápido aumenta la temperatura en la trayectoria de la mosca después de $3$ segundos? (Solución). 258. Las componentes $x$ e $y$ de un fluido que se mueve en dos dimensiones están dadas por las siguientes funciones: $u (x, y) = 2y$ y $v (x, y) = −2x$; $x \ge 0$; $y \ge 0$. La velocidad del fluido en el punto $(x, y)$ es $s(x, y) = \sqrt{u(x, y)^2 + v(x, y)^2}$. Encuentra $\frac{\partial s}{\partial x}$ y $\frac{\partial s}{\partial y}$ usando la regla de la cadena. 259. Sea $u = u (x, y, z)$, donde $x = x (w, t)$, $y = y (w, t)$, $z = z (w, t)$, $w = w (r, s)$ y $t = t (r, s)$. Usa un diagrama de árbol y la regla de la cadena para encontrar una expresión para $\frac{\partial u}{\partial r}$ (Solución).
En Derivadas parciales introdujimos la derivada parcial. Una función $z = f (x, y)$ tiene dos derivadas parciales: $\frac{\partial z}{\partial x}$ y $\frac{\partial z}{\partial y}$. Estas derivadas corresponden a cada una de las variables independientes y pueden interpretarse como tasas de cambio instantáneas (es decir, como pendientes de una línea tangente). Por ejemplo, $\frac{\partial z}{\partial x}$ representa la pendiente de una línea tangente que pasa a través de un punto dado en la superficie definida por $z = f (x, y)$, suponiendo que la línea tangente sea paralela al eje $x.$ Del mismo modo, $\frac{\partial z}{\partial y}$ representa la pendiente de la línea tangente paralela al eje $y$. Ahora consideramos la posibilidad de una línea tangente paralela a ninguno de los ejes.
Comenzamos con la gráfica de una superficie definida por la ecuación $z = f (x, y)$. Dado un punto $(a, b)$ en el dominio de $f$, elegimos una dirección para viajar desde ese punto.
Medimos la dirección usando un ángulo $\theta$, que se mide en sentido antihorario en el plano $x, y$, comenzando en cero desde el eje $x$ positivo (Figura 4.39). La distancia que recorremos es $h$ y la dirección en la que viajamos viene dada por el vector unitario $\bold{u} = (cos \theta)\bold{i} + (sen \theta)\bold{j}$. Por lo tanto, la coordenada $z$ del segundo punto en la gráfica viene dada por $z = f (a + h cos \theta, b + h sen \theta)$.

Figura 4.39. Encontrar la derivada direccional en un punto de la gráfica de $z = f (x, y)$. La pendiente de la flecha negra en el gráfico indica el valor de la derivada direccional en ese punto.
Podemos calcular la pendiente de la línea secante dividiendo la diferencia en los valores $z$ por la longitud del segmento de línea que conecta los dos puntos en el dominio. La longitud del segmento de línea es $h$. Por lo tanto, la pendiente de la línea secante es
$$m_{sec} = \frac{f(a + h cos \theta, b + h sen \theta) − f(a, b)}{h}$$Para encontrar la pendiente de la línea tangente en la misma dirección, tomamos el límite cuando $h$ se acerca a cero.
 |
Encontrar una derivada direccional desde la definición |
Sea $\theta = arccos (3/5)$. Encuentra la derivada direccional $D_\bold{u} f (x, y)$ de $f (x, y) = x^2 - xy + 3y^2$ en la dirección de $\bold{u} = (cos \theta)\bold{i} + (sen \theta)\bold{j}$. ¿Cuál es $D_u f (−1, 2)$?

La siguiente escena interactiva, diseñada por Elena Álvarez, muestra una interpretación geométrica de la derivada direccional, la cual tiene las siguientes características:
Otro enfoque para calcular una derivada direccional, como lo hace la escena anterior, implica derivadas parciales, como se describe en el siguiente teorema.
La ecuación 4.36 establece que la derivada direccional de $f$ en la dirección de $\bold{u} = cos \theta\bold{i} + sen \theta\bold{j}$ viene dada por
$$D_u f(a, b) = \lim\limits_{t \to 0}\frac{f(a + t cos \theta, b + t sen \theta) − f(a, b)}{t}$$Sea $x = a + t cos \theta$ e $y = b + t sen \theta$, y definamos $g (t) = f (x, y)$. Dado que $f_x$ y $f_y$ existen, podemos usar la regla de la cadena para funciones de dos variables para calcular $g^{\prime}(t)$:
$$\begin{aligned} g^{\prime}(t) &= \frac{\partial f}{\partial x}\frac{dx}{dt} + \frac{\partial f}{\partial y}\frac{dy}{dt}\\ &= f_x(x, y)cos \theta + f_y(x, y)sen \theta \end{aligned}$$Si $t = 0$, entonces $x = x_0$ e $y = y_0$, luego
$$g^{\prime}(0) = f_x(x_0, y_0)cos \theta + f_y(x_0, y_0)sen \theta.$$Por la definición de $g^{\prime}(t)$, también es cierto que
$$\begin{aligned} g^{\prime}(0) &= \lim\limits_{t \to 0}\frac{g(t)-g(0)}{t}\\ &= \lim\limits_{t \to 0}\frac{f(x_0 + t cos \theta, y_0 + t sen \theta) − f(x_0, y_0)}{t} \end{aligned}$$Por lo tanto, $D_\bold{u} f (x_0, y_0) = f_x (x, y) cos \theta + f_y (x, y) sen \theta$.
 |
Encontrar una derivada direccional: método alternativo |
Sea $\theta = arccos (3/5)$. Encuentra la derivada direccional $D_\bold{u} f (x, y)$ de $f (x, y) = x^2 - xy + 3y^2$ en la dirección de $\bold{u} = (cos \theta)\bold{i} + (sen \theta)\bold{j}$. ¿Cuál es $D_u f (−1, 2)$?

Si el vector que se da para la dirección de la derivada no es un vector unitario, entonces solo es necesario dividirlo por la norma del vector. Por ejemplo, si quisiéramos encontrar la derivada direccional de la función en el ejemplo anterior en la dirección del vector $\lang −5, 12\rang$, primero dividiríamos por su magnitud para obtener $\bold{u}$. Esto nos da $\bold{u} = \lang - (5/13), 12/13\rang$. Luego
$$\begin{aligned} D_\bold{u} f (x, y) &= \nabla f(x,y)\cdot\bold{u}\\ &= -\frac{5}{13}(2x-y)+\frac{12}{13}(-x+6y)\\ &= -\frac{22}{13}x + \frac{17}{13}y \end{aligned}$$El lado derecho de la ecuación 4.37 es igual a $f_x (x, y) cos \theta + f_y(x, y) sen \theta$, que puede escribirse como el producto escalar de dos vectores. Definamos el primer vector como $\nabla f (x, y) = f_x (x, y)\bold{i} + f_y (x, y)\bold{j}$ y el segundo vector como $\bold{u} = (cos \theta)\bold{i} + (sen \theta)\bold{j}$. Luego, el lado derecho de la ecuación se puede escribir como el producto escalar de estos dos vectores:
$$D_\bold{u} f(x, y) = \nabla f(x, y)\cdot\bold{u}\tag{$4.38$}$$El primer vector en la ecuación 4.38 tiene un nombre especial: el gradiente de la función $f$. El símbolo $\nabla$ se llama nabla.
 |
Encuentra el gradiente $\nabla f (x, y)$ de cada una de las siguientes funciones: |

El gradiente tiene algunas propiedades importantes. Ya hemos visto una fórmula que usa el gradiente: la fórmula para la derivada direccional. Recuerda de "El producto punto" que si el ángulo entre dos vectores $\bold{a}$ y $\bold{b}$ es $\phi$, entonces $\bold{a}\cdot\bold{b} = ||\bold{a}|| \text{ }||\bold{b}||cos \phi$. Por lo tanto, si el ángulo entre $\nabla f (x_0, y_0)$ y $\bold{u} = (cos \theta)\bold{i} + (sen θ)\bold{j}$ es $\phi$, tenemos
$$D_u f(x_0, y_0) = \nabla f(x_0, y_0)\cdot\bold{u} = ||\nabla f(x_0, y_0)||\text{ }||\bold{u}||cos \phi\\ = ||\nabla f(x_0, y_0) || cos \phi$$La $||\bold{u}||$ desaparece porque $\bold{u}$ es un vector unitario. Por lo tanto, la derivada direccional es igual a la magnitud del gradiente evaluado en $(x_0, y_0)$ multiplicado por $cos \phi$. Recuerda que $cos \phi$ varía de $−1$ a $1$. Si $\phi = 0$, entonces $cos \phi = 1$ y $\nabla f (x_0, y_0)$ y $\bold{u}$ apuntan en la misma dirección. Si $\phi = \pi$, entonces $cos \phi = −1$ y $\nabla f (x_0, y_0)$ y $\bold{u}$ apuntan en direcciones opuestas. En el primer caso, el valor de $D_\bold{u} f (x_0, y_0)$ se maximiza; en el segundo caso, el valor de $D_\bold{u} f (x_0, y_0)$ se minimiza. Si $\nabla f (x_0, y_0)=0$, entonces $D_\bold{u} f (x_0, y_0) = \nabla f (x_0, y_0)\cdot\bold{u} = 0$ para cualquier vector $\bold{u}$. Estos tres casos se resumen en el siguiente teorema
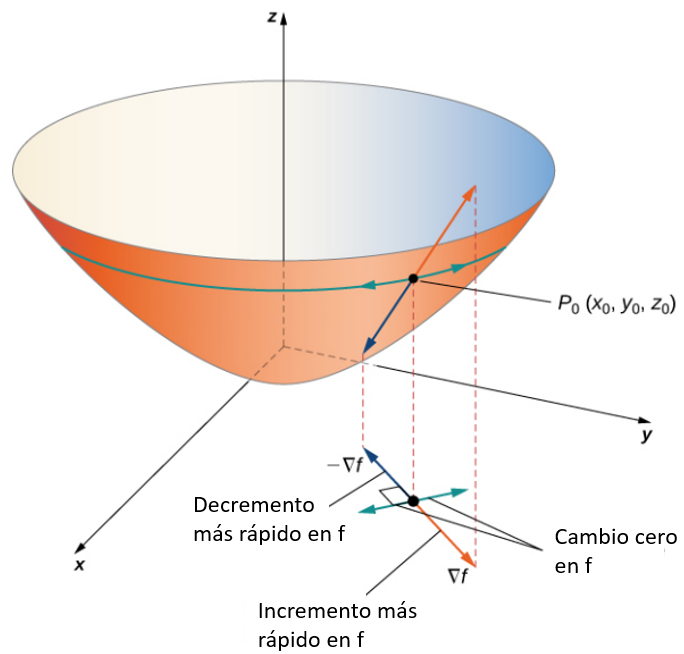
Figura 4.41. El gradiente indica los valores máximos y mínimos de la derivada direccional en un punto.
 |
Encontrar una derivada direccional máxima: |

La figura 4.43 muestra una parte de la gráfica de la función $f (x, y) = 3 + sen x sen y$. Dado un punto $(a, b)$ en el dominio de $f$, el valor máximo del gradiente en ese punto viene dado por $||\nabla f (a, b)||$. Esto sería igual a la velocidad de mayor ascenso si la superficie representara un mapa topográfico. Si fuéramos en la dirección opuesta, sería la tasa de mayor descenso.
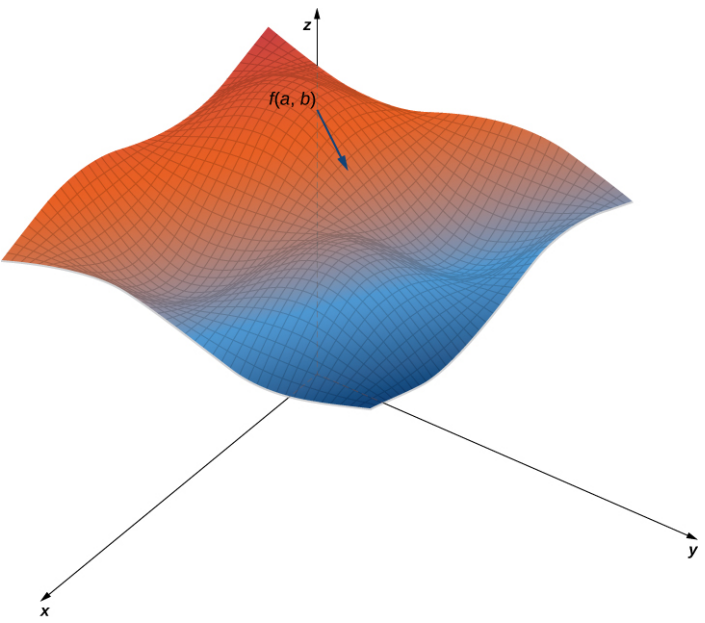
Figura 4.43. Una superficie típica en $\Reals^3$. Dado un punto en la superficie, la derivada direccional se puede calcular utilizando el gradiente.
En la siguiente escena interactiva, diseñada por Walerij Koschkin, hemos representado la función $f(x,y)=3x^2 − 4xy + 2y^2$ del ejercicio anterior. El punto $P$ es diferente, pues el valor de $z=54$, del ejercicio, se nos aleja demasiado en la gráfica. Puedes mover el punto y obervar el gradiente (flecha azul) y los valores de las derivada direccionales en ese punto.
Puedes hacer clic en el cuadrado de la esquina inferior derecha, para ver la escena en pantalla ampliada.
Cuando se usa un mapa topográfico, la pendiente más pronunciada siempre está en la dirección donde las líneas de contorno están más cercanas entre sí (ver figura 4.44). Esto es análogo al mapa de contorno de una función, suponiendo que las curvas de nivel se obtienen para valores igualmente espaciados en todo el rango de esa función.
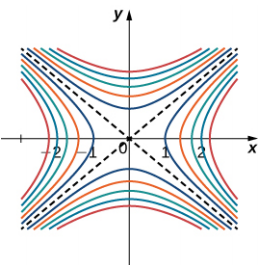
Figura 4.44. Mapa de contorno para la función $f (x, y) = x^2 - y^2$ usando valores de nivel entre $−5$ y $5$.
Recuerda que si una curva se define paramétricamente por el par de funciones $\big(x (t), y (t)\big)$, entonces el vector $x^{\prime}(t)\bold{i} + y^{\prime}(t)\bold{j}$ es tangente a la curva para cada valor de $t$ en el dominio. Ahora, supongamos que $z = f (x, y)$ es una función diferenciable de $x$ e $y$, y $(x_0, y_0)$ está en su dominio. Supongamos, además, que $x_0 = x (t_0)$ e $y_0 = y (t:0)$ para algún valor de $t$, y consideremos la curva de nivel $f (x, y) = k$. Definamos $g (t) = f \big(x (t), y (t)\big) $ y calculemos $g^{\prime}(t)$ en la curva de nivel. Por la regla de la cadena,
$$g^{\prime}(t) = f_x\big(x(t), y(t)\big)x^{\prime}(t) + f_y\big(x(t), y(t)\big)y′(t)$$Pero $g^{\prime}(t) = 0$ porque $g (t) = k$ para todo $t$. Por lo tanto, por un lado,
$$f_x\big(x(t), y(t)\big)x^{\prime}(t) + f_y\big(x(t), y(t)\big)y^{\prime}(t) = 0$$por otra parte,
Por lo tanto
$$\nabla f(x, y)\cdot\lang x^{\prime}(t), y^{\prime}(t)\rang = 0$$Por lo tanto, el producto escalar de estos vectores es igual a cero, lo que implica que son ortogonales. Sin embargo, el segundo vector es tangente a la curva de nivel, lo que implica que el gradiente debe ser normal a la curva de nivel, lo que da lugar al siguiente teorema.
Podemos usar este teorema para encontrar vectores tangentes y normales para las curvas de nivel de una función.
 |
Encontrar tangentes para curvas de nivel |

La siguiente escena interactiva, diseñada por Elena Álvarez, permite comprobar la propiedad que dice que el gradiente de una función f en un punto P es ortogonal a la curva de nivel que pasa por dicho punto.
En la escena, una vez introducida la función $z=f(x,y)$, se puede, o bien introducir las coordenadas de un punto $P(a,b)$, o bien el valor de $k$ que permite obtener la curva de nivel $f(x,y)=k$. En el primer caso, el valor de $k$ se obtiene como $k=f(a,b)$; en el segundo, el punto $P$ se puede mover únicamente por la curva $f(x,y)=k$.
La definición de un gradiente puede extenderse a funciones de más de dos variables.
Calcular el gradiente de una función en tres variables es muy similar a calcular el gradiente de una función en dos variables. Primero, calculamos las derivadas parciales $f_x, f_y$ y $f_z$, y luego usamos la ecuación 4.40.
 |
Encontrar gradientes en tres dimensiones |

La derivada direccional también se puede generalizar a funciones de tres variables. Para determinar una dirección en tres dimensiones, se necesita un vector con tres componentes. Este vector es un vector unitario, y los componentes del vector unitario se denominan cosenos direccionales. Dado un vector unitario tridimensional $\bold{u}$ en forma estándar (es decir, el punto inicial está en el origen), este vector forma tres ángulos diferentes con los ejes positivo $x, y$ y $z$. Llamemos a estos ángulos $\alpha, \beta$ y $\gamma$.
Luego, los cosenos direccionales están dados por $cos \alpha, cos \beta$ y $cos \gamma$. Estos son los componentes del vector unitario $\bold{u}$; como $\bold{u}$ es un vector unitario, es cierto que $cos^2 \alpha + cos^2 \beta + cos^2 \gamma = 1$.
Podemos calcular la derivada direccional de una función de tres variables usando el gradiente, lo que lleva a una fórmula análoga a la ecuación 4.38.
Los tres ángulos $\alpha, \beta$ y $\gamma$ determinan el vector unitario $\bold{u}$. En la práctica, podemos usar un vector arbitrario (no unitario), luego dividirlo por su magnitud para obtener un vector unitario en la dirección deseada.
 |
Encontrar una derivada direccional en tres dimensiones |


 Para los siguientes ejercicios, encuentra la derivada direccional utilizando solo la definición de límite.
Para los siguientes ejercicios, encuentra la derivada direccional utilizando solo la definición de límite.
260. $f(x, y) = 5 -2x^2 - \frac12y^2$ en el punto $P(3, 4)$ en la dirección de $\bold{u} = \big(cos\frac{\pi}{4}\big)\bold{i} + \big(sen\frac{\pi}{4}\big)\bold{j}$ 261. $f(x, y) = y^2cos(2x)$ en el punto $P\big(\frac{\pi}{3}, 2\big)$ en la dirección de $\bold{u} = \big(cos\frac{\pi}{4}\big)\bold{i} + \big(sen\frac{\pi}{4}\big)\bold{j}$ (Solución). 262. Encuentra la derivada direccional de $f (x, y) = y^2sen (2x)$ en el punto $P\big(\frac{\pi}{4}\big)$ en la dirección de $\bold{u} = 5\bold{i} +12\bold{j}$
 Para los siguientes ejercicios, encuentra la derivada direccional de la función en el punto $P$ en la dirección de $\bold{v}$.
Para los siguientes ejercicios, encuentra la derivada direccional de la función en el punto $P$ en la dirección de $\bold{v}$.
273. $f(x, y) = y^2 + xz, P(1, 2, 2), \bold{v} = \lang 2, −1, 2 \rang$ (Solución).
 Para los siguientes ejercicios, encuentra la derivada direccional de la función en la dirección del vector unitario $\bold{u} = cos \theta\bold{i} + sen \theta\bold{j}$.
Para los siguientes ejercicios, encuentra la derivada direccional de la función en la dirección del vector unitario $\bold{u} = cos \theta\bold{i} + sen \theta\bold{j}$.
274. $f(x, y) = x^2 + 2y^2, \theta = \frac{\pi}{6}$ 275. $f(x, y) = \frac{y}{x+2y}, \theta = -\frac{\pi}{4}$ (Solución). 276. $f(x, y) = cos(3x+y), \theta = \frac{\pi}{4}$ 277. $w(x, y) = ye^x, \theta = \frac{\pi}{3}$ (Solución). 278. $f(x, y) = x arctan(y), \theta = \frac{\pi}{2}$ 279. $f(x, y) = ln(x + 2y), \theta = \frac{\pi}{3}$ (Solución).
 Para los siguientes ejercicios, encuentra el gradiente.
Para los siguientes ejercicios, encuentra el gradiente.
280. Encuentra el gradiente de $f(x, y) =\frac{14-x^2-y^2}{3}$. Luego, halla el gradiente en el punto $P(1, 2)$ 281. Encuentra el gradiente de $f(x, y, z) = xy + yz + xz$ en el punto $P(1, 2, 3)$ (Solución). 282. Encuentra el gradiente de $f(x, y, z)$ en el punto $P$ en la dirección $\bold{u}$: $f(x, y, z) = ln(x^2 + 2y^2 + 3z^2), P(2, 1, 4), \bold{u} = \frac{-3}{13}\bold{i} - \frac{4}{13}\bold{j} - \frac{12}{13}\bold{k}$ 283. $f(x, y, z) = 4x^5y^2z^3, P(2, −1, 1), \bold{u} = \frac{1}{3}\bold{i} + \frac{2}{3}\bold{j} - \frac{2}{3}\bold{k}$ (Solución).
 Para los siguientes ejercicios, encuentra la derivada direccional de la función en el punto $P$ en la dirección de $Q$
Para los siguientes ejercicios, encuentra la derivada direccional de la función en el punto $P$ en la dirección de $Q$
284. $f(x, y) = x^2 + 3y^2, P(1, 1), Q(4, 5)$ 285. $f(x, y, z) = \frac{y}{x+z}, P(2, 1, −1), Q(−1, 2, 0)$ (Solución).
 Para los siguientes ejercicios, encuentra la derivada de la función en $P$ en la dirección de $\bold{u}$.
Para los siguientes ejercicios, encuentra la derivada de la función en $P$ en la dirección de $\bold{u}$.
286. $f(x, y) = −7x + 2y, P(2, −4), \bold{u} = 4\bold{i} − 3\bold{j}$ 287. $f(x, y) = ln(5x + 4y), P(3, 9), \bold{u} = 6\bold{i} + 8\bold{j}$ (Solución). 288. [T] Utiliza la tecnología para dibujar la curva de nivel de $f (x, y) = 4x - 2y + 3$ que pasa por $P (1, 2)$ y dibuja el vector gradiente en $P$. 289. [T] Utiliza la tecnología para dibujar la curva de nivel de $f (x, y) = x^2 + 4y^2$ que pasa a través de $P (−2, 0)$ y dibuja el vector de gradiente en $P$ (Solución).
 Para los siguientes ejercicios, encuentre el vector del gradiente en el punto indicado.
Para los siguientes ejercicios, encuentre el vector del gradiente en el punto indicado.
290. $f(x, y) = xy^2 − yx^2, P(−1, 1)$. 291. $f(x, y) = xe^y − ln(x), P(−3, 0)$ (Solución). 292. $f(x, y, z) = xy − ln(z), P(2, −2, 2)$. 293. $f(x, y, z) = x\sqrt{y^2+z^2}, P(−2, -1, -1)$ (Solución).
 Para los siguientes ejercicios, encuentra la derivada de la función.
Para los siguientes ejercicios, encuentra la derivada de la función.
294. $f (x, y) = x^2 + xy + y^2$ en el punto (−5, −4)$ en la dirección en que la función aumenta más rápidamente. 295. $f (x, y) = e^{xy}$ en el punto $(6, 7)$ en la dirección en que la función aumenta más rápidamente (Solución). 296. $f (x, y) = arctan (\frac{y}{x})$ en el punto $(−9, 9)$ en la dirección en que la función aumenta más rápidamente. 297. $f (x, y, z) = ln (xy + yz + zx)$ en el punto $(−9, −18, −27)$ en la dirección en que la función aumenta más rápidamente (Solución). 298. $f (x, y, z) = \frac{x}{y} + \frac{y}{z} + \frac{z}{x}$ en el punto $(5, −5, 5)$ en la dirección en que la función aumenta más rápidamente.
 Para los siguientes ejercicios, encuentra la tasa máxima de cambio de $f$ en el punto dado y la dirección en que ocurre.
Para los siguientes ejercicios, encuentra la tasa máxima de cambio de $f$ en el punto dado y la dirección en que ocurre.
299. $f(x, y) = xe^{−y}, (1, 0)$ (Solución). 300. $f (x, y) = \sqrt{x^2+2y}$ en el punto $(4, 10)$. 301. $ f(x, y) = cos(3x + 2y), \big(\frac{\pi}{6}, -\frac{\pi}{8}\big)$ (Solución).
 Para los siguientes ejercicios, encuentra las ecuaciones de
Para los siguientes ejercicios, encuentra las ecuaciones de
302. La curva de nivel $f (x, y, z) = 12$ para $f (x, y, z) = 4x^2 - 2y^2 + z^2$ en el punto $(2, 2, 2)$.
303. $f(x, y, z) = xy + yz + xz = 3$ en el punto $(1, 1, 1)$ (Solución). 304. $f(x, y, z) = xyz = 6$ en el punt $(1, 2, 3)$ 305. $f(x, y, z) = xe^{y}cosz - z = 1$ en el punto $(1, 0, 0)$ (Solución).
 Resuelve los siguientes problemas.
Resuelve los siguientes problemas.
306. La temperatura T en una esfera metálica es inversamente proporcional a la distancia desde el centro de la esfera (el origen: $(0, 0, 0)$). La temperatura en el punto $(1, 2, 2)$ es de $120 ^oC$.
307. El potencial eléctrico (voltaje) en una determinada región del espacio viene dado por la función $V (x, y, z) = 5x^2 - 3xy + xyz$.
308. Si el potencial eléctrico en un punto $(x, y)$ en el plano $xy$ es $V (x, y) = e^{−2x}cos (2y)$, entonces el vector de intensidad eléctrica en $(x, y$) es $\bold{E} = −\nabla V ( x, y)$.
309. En dos dimensiones, el movimiento de un fluido ideal se rige por un potencial de velocidad $\phi$. Las componentes de velocidad del fluido $\bold{u}$ en la dirección $x$ y $\bold{v}$ en la dirección $y$, están dadas por $\lang u, v\rang = \nabla \phi$. Encuentra los componentes de velocidad asociados con el potencial de velocidad $\phi (x, y) = sen \pi x sen 2\pi y$ (Solución).
Una de las aplicaciones más útiles para derivadas de una función de una variable es la determinación de valores máximos y/o mínimos. Esta aplicación también es importante para las funciones de dos o más variables, pero como hemos visto en secciones anteriores de este capítulo, la introducción de más variables independientes conduce a más resultados posibles para los cálculos. Las ideas principales de encontrar puntos críticos y usar pruebas derivadas siguen siendo válidas, pero aparecen nuevas aristas al evaluar los resultados.
Para las funciones de una sola variable, definimos los puntos críticos como los valores de la función cuando la derivada es igual a cero o no existe.
Para funciones de dos o más variables, el concepto es esencialmente el mismo, excepto por el hecho de que ahora estamos trabajando con derivadas parciales.
 |
Encontrar puntos críticos |
Encuentra los puntos críticos de cada una de las siguientes funciones:

El objetivo principal para determinar los puntos críticos es localizar máximos y mínimos relativos, como en el cálculo de variable única.
Cuando se trabaja con una función de una variable, la definición de un extremo local implica encontrar un intervalo alrededor del punto crítico de modo que el valor de la función sea mayor o menor que todos los demás valores de la función en ese intervalo. Cuando trabajamos con una función de dos o más variables, trabajamos con un disco abierto alrededor del punto.
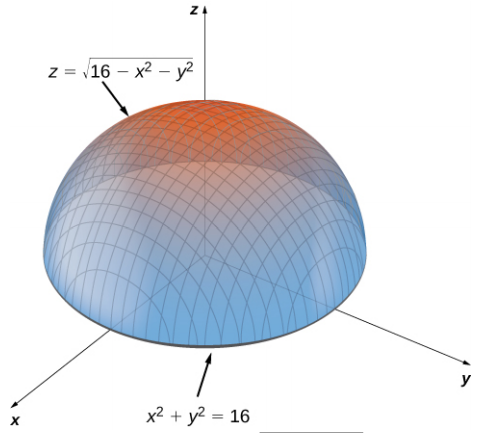
Figura 4.47. La gráfica de $z = \sqrt{16 - x^2 - y^2}$ tiene un valor máximo cuando $(x, y) = (0, 0)$. Alcanza su valor mínimo en el límite de su dominio, que es el círculo $x^2 + y^2 = 16$.
En el curso de cálculo diferencial, mostramos que los extremos de las funciones de una variable ocurren en puntos críticos. Lo mismo es cierto para funciones de más de una variable, como se indica en el siguiente teorema.
Considera la función $f (x) = x^3$. Esta función tiene un punto crítico en $x = 0$, ya que $f^{prime}(0) = 3 (0)^2 = 0$. Sin embargo, $f$ no tiene un valor extremo en $x = 0$. Por lo tanto, la existencia de un valor crítico en $x = x_0$ no garantiza un extremo local en $x = x_0$. Lo mismo es cierto para una función de dos o más variables. Una forma en que esto puede suceder es en un punto de silla. Un ejemplo de un punto de silla aparece en la siguiente figura interactiva.
Figura 4.48. Gráfico de la función $z = x^2 - y^2$. Este gráfico tiene un punto de silla en el origen.
En este gráfico, el origen es un punto de silla. Esto se debe a que las primeras derivadas parciales de $f (x, y) = x^2 - y^2$ son iguales a cero en este punto, pero no es un máximo ni un mínimo para la función. Además, la traza vertical correspondiente a $y = 0$ es $z = x^2$ (una parábola que se abre hacia arriba), pero la traza vertical correspondiente a $x = 0$ es $z = −y^2$ (una parábola que se abre hacia abajo). Por lo tanto, es tanto un máximo global para una traza como un mínimo global para otra.
La prueba de la segunda derivada para una función de una variable proporciona un método para determinar si un extremo se produce en un punto crítico de una función. Al extender este resultado a una función de dos variables, surge un problema relacionado con el hecho de que hay, de hecho, cuatro derivadas parciales de segundo orden diferentes, aunque la igualdad de los parciales mixtos reduce esto a tres.
La prueba de la segunda derivada para una función de dos variables, establecida en el siguiente teorema, usa un discriminante $D$ que reemplaza $f^{\prime\prime} (x_0)$ en la prueba de la segunda derivada para una función de una variable.
Para aplicar la prueba de la segunda derivada, es necesario que primero encontremos los puntos críticos de la función. Hay varios pasos involucrados en todo el procedimiento, que se describen en una la estrategia de resolución de problemas, que presentamos en la página siguiente.
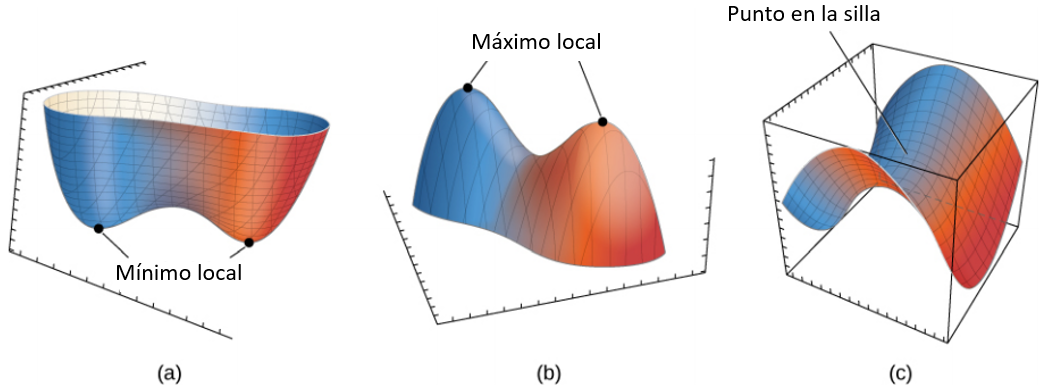
Figura 4.49. La prueba de la segunda derivada a menudo puede determinar si una función de dos variables tiene un mínimo local (a), un máximo local (b) o un punto de silla (c).
 |
Usando la prueba de la segunda derivada |
Encuentra los puntos críticos para cada una de las siguientes funciones, y usa la prueba de la segunda derivada para encontrar los extremos locales:

Al encontrar extremos globales de funciones de una variable en un intervalo cerrado, comenzamos verificando los valores críticos durante ese intervalo y luego evaluamos la función en los puntos finales del intervalo. Cuando se trabaja con una función de dos variables, el intervalo cerrado se reemplaza por un conjunto cerrado y acotado. Un conjunto está limitado si todos los puntos de ese conjunto pueden estar contenidos dentro de una bola (o disco) de radio finito. Primero, necesitamos encontrar los puntos críticos dentro del conjunto y calcular los valores críticos correspondientes. Entonces, es necesario encontrar el valor máximo y mínimo de la función en el límite del conjunto. Cuando tenemos todos estos valores, el valor de función más grande corresponde al máximo global y el valor de función más pequeño corresponde al mínimo absoluto.
Primero, sin embargo, debemos estar seguros de que tales valores existen. El siguiente teorema hace esto.
Ahora que sabemos que cualquier función continua $f$ definida en un conjunto cerrado y acotado alcanza sus valores extremos, necesitamos saber cómo encontrarlos.
La prueba de este teorema es una consecuencia directa del teorema del valor extremo y del teorema de Fermat. En particular, si cualquiera de los extremos no está ubicado en el límite de $D$, entonces está ubicado en un punto interior de $D$. Pero un punto interior $(x_0, y_0)$ de $D$ que es un extremo absoluto también es un extremo local; por lo tanto, $(x_0, y_0)$ es un punto crítico de $f$ según el teorema de Fermat. Por lo tanto, los únicos valores posibles para los extremos globales de $f$ en $D$ son los valores extremos de $f$ en el interior o límite de $D$.
Encontrar los valores máximos y mínimos de $f$ en el límite de $D$ puede ser un desafío. Si el límite es un rectángulo o un conjunto de líneas rectas, entonces es posible parametrizar los segmentos de línea y determinar los máximos en cada uno de estos segmentos, como se ver'a en el siguiente ejercicio. El mismo enfoque se puede utilizar para otras formas, como círculos y elipses. Si el límite del conjunto $D$ es una curva más complicada definida por una función $g (x, y) = c$ para alguna constante $c$, y existen las derivadas parciales de primer orden de $g$, entonces el método de multiplicadores de Lagrange puede resultar útil para determinar los extremos de $f$ en el límite. El método de multiplicadores de Lagrange lo veremos en el próximo apartado.
 |
Encontrar el extremo absoluto |
Usa la estrategia de resolución de problemas para encontrar los extremos absolutos de una función, para determinar los extremos absolutos de cada una de las siguientes funciones:

 |
Introducción del capítulo: pelotas de golf rentables |

Figura 4.56. (crédito: modificación del trabajo de oatsy40, Flickr)
La compañía Pro-T ha desarrollado un modelo de ganancias que depende del número $x$ de pelotas de golf vendidas por mes (medido en miles) y el número de horas por mes de publicidad y, según la función
$$z = f(x, y) = 48x + 96y − x^2 − 2xy − 9y^2$$, donde $z$ se mide en miles de dólares. El número máximo de pelotas de golf que se pueden producir y vender es de $50,000$, y el número máximo de horas de publicidad que se puede comprar es $25$. Encuentra los valores de $x$ e $y $que maximizan la ganancia, y encuentra la ganancia máxima.

 Para los siguientes ejercicios, encuentra los puntos críticos.
Para los siguientes ejercicios, encuentra los puntos críticos.
310. $f(x, y) = 1 + x^2 + y^2$ 311. $f(x, y) = (3x − 2)^2 + (y − 4)^2$ (Solución). 312. $f(x, y) = x^4 + y^4 − 16xy$ 313. $f(x, y) = 15x^3 − 3xy + 15y^3$ (Solución).
 Para los siguientes ejercicios, encuentra los puntos críticos de la función utilizando técnicas algebraicas (completando el cuadrado) o examinando la forma de la ecuación. Verifica sus resultados utilizando la prueba de derivadas parciales.
Para los siguientes ejercicios, encuentra los puntos críticos de la función utilizando técnicas algebraicas (completando el cuadrado) o examinando la forma de la ecuación. Verifica sus resultados utilizando la prueba de derivadas parciales.
314. $f(x, y) = \sqrt{x^2 + y^2} + 1$ 315. $f(x, y) = −x^2 − 5y^2 + 8x − 10y − 13$ (Solución). 316. $f(x, y) = x^2 + y^2 + 2x − 6y + 6$ 317. $f(x, y) = \sqrt{x^2 + y^2} + 1$ (Solución).
 Para los siguientes ejercicios, usa la prueba de la segunda derivada para identificar los puntos críticos y determinar si cada punto crítico es un punto máximo, mínimo, de silla o ninguno de estos.
Para los siguientes ejercicios, usa la prueba de la segunda derivada para identificar los puntos críticos y determinar si cada punto crítico es un punto máximo, mínimo, de silla o ninguno de estos.
318. $f(x, y) = −x^3 + 4xy − 2y^2 + 1$ 319. $f(x, y) = x^2y^2$ (Solución).
320. $f(x, y) = x^2 − 6x + y^2 + 4y − 8$ 321. $f(x, y) = 2xy + 3x + 4y$ (Solución). 322. $f(x, y) = 8xy(x + y) + 7$ 323. $f(x, y) = x^2 + 4xy + y^2$ (Solución). 324. $f(x, y) = x^3 + y^3 − 300x − 75y − 3$ 325. $f(x, y) = 9 − x^4y^4$ (Solución). 326. $f(x, y) = 7x^2y + 9xy^2$ 327. $f(x, y) = 3x^2 − 2xy + y^2 − 8y$ (Solución). 328. $f(x, y) = 3x^2 + 2xy + y^2$ 329. $f(x, y) = y^2 + xy + 3y + 2x + 3$ (Solución). 330. $f(x, y) = x^2 + xy + y^2 − 3x$ 331. $f(x, y) = x^2 + 2y^2 − x^2y$ (Solución). 332. $f(x, y) = x^2 + y − e^y$ 333. $f(x, y) = e^{−(x^2 + y^2 + 2x)}$ (Solución). 334. $f(x, y) = x^2 + xy + y^2 − x − y + 1$ 335. $f(x, y) = x^2 + 10xy + y^2$ (Solución). 336. $f(x, y) = −x^2 − 5y^2 + 10x − 30y − 62$ 337. $f(x, y) = 120x + 120y − xy − x^2 − y^2$ (Solución). 338. $f(x, y) = 2x^2 + 2xy + y^2 + 2x − 3$ 339. $f(x, y) = x^2 + x − 3xy + y^3 − 5$ (Solución). 340. $f(x, y) = 2xye^{−x^2 − y^2}$
 Para los siguientes ejercicios, determina los valores extremos y los puntos de silla. Usa un CAS para graficar la función.
Para los siguientes ejercicios, determina los valores extremos y los puntos de silla. Usa un CAS para graficar la función.
341. [T] $f(x, y) = ye^x − e^y$ (Solución). 342. [T] $f(x, y) = x sen(y)$
343. [T] $f(x, y) = sen(x)sin(y), x \isin (0, 2\pi), y \isin (0, 2\pi)$ (Solución).
 Encuentra los extremos absolutos de la función dada en el conjunto cerrado y acotado $R$.
Encuentra los extremos absolutos de la función dada en el conjunto cerrado y acotado $R$.
344. $f (x, y) = xy - x - 3y$; R es la región triangular con vértices $(0, 0), (0, 4)$ y $(5, 0)$.
345. Encuentra los valores máximos y mínimos absolutos de $f (x, y) = x^2 + y^2 - 2y + 1$ en la región $R = \big\lbrace (x, y) | x^2 + y^2 \le 4\big\rbrace$ (Solución). 346. $f(x, y) = x^3 − 3xy − y^3$ en $R = \lbrace (x, y): −2 \le x \le 2, −2 \le y \le 2\rbrace$. 347. $f(x, y) = \frac{-2y}{x^2+y^2+1}$ en $R = \lbrace (x, y): x^2 + y^2 \le 4\rbrace$ (Solución).
348. Encuentra tres números positivos cuya suma sea $27$, de modo que la suma de sus cuadrados sea lo más pequeña posible.
349. Encuentra los puntos en la superficie $x^2 − yz = 5$ que están más cerca del origen (Solución).
350. Encuentra el volumen máximo de una caja rectangular con tres caras en los planos de coordenadas y un vértice en la primera octante en el plano$ x + y + z = 1$.
351. La suma de la longitud y la circunferencia (perímetro de una sección transversal) de un paquete transportado por un servicio de entrega no puede exceder $108$ pulgadas. Encuentra las dimensiones del paquete rectangular de mayor volumen que se puede enviar (Solución).
352. Una caja de cartón sin tapa se fabricará con un volumen de $4\; pies^3$. Encuentra las dimensiones de la caja que requiere la menor cantidad de cartón.
353. Encuentra el punto en la superficie $f (x, y) = x^2 + y^2 + 10$ más cercano al plano $x + 2y - z = 0$. Identifica el punto en el plano (Solución).
354. Encuentra el punto en el plano $2x − y + 2z = 16$ que está más cerca del origen.
355. Una empresa fabrica dos tipos de calzado deportivo: calzado deportivo y cross-trainers. El ingreso total de $x$ unidades de calzado deportivo y unidades y de cross-trainers viene dado por $R (x, y) = −5x^2 - 8y^2 - 2xy + 42x + 102y$, donde $x$ e $y$ están en miles de unidades. Encuentra los valores de $x$ e $y$ para maximizar el ingreso total (Solución).
356. Una compañía de envío maneja cajas rectangulares siempre que la suma de la longitud, el ancho y la altura de la caja no exceda las $96$ pulgadas. Encuentra las dimensiones de la caja que cumple con esta condición y tiene el mayor volumen.
357. Halla el volumen máximo de una lata de refresco cilíndrico de modo que la suma de su altura y circunferencia sea de $120 cm$ (Solución).
La solución del ejercicio 343 nos muestra que hay un punto de silla en $(\pi, \pi)$, un máximo local en $\big(\frac{\pi}{2}, \frac{\pi}{2}\big)$ y en $\big(\frac{3\pi}{2}, \frac{3\pi}{2}\big)$, y un mínimo local $\big(\frac{\pi}{2}, \frac{3\pi}{2}\big)$ y $\big(\frac{3\pi}{2}, \frac{\pi}{2}\big)$
En la siguiente escena interactiva, puedes observar esos puntos de máxima y mínima, desplazando el deslizador. Igulamente, se muestran las curvas de nivel en la ventana derecha, las cuales se reducen a medida que nos aproximamos a los puntos locales de máxima y de mínima.
Si desplazas el deslizador al centro, observarás el punto de silla. Sólo se muestra la gráfica de la función en el dominio definido para $x \isin (0, 2\pi), y \isin (0, 2\pi)$. Haz clic en el cuadro inferior derecho para ver la escena en pantalla completa, luego presiona la tecla "esc", para regresar al libro.
Para este mismo ejercicio, presentamos otra escena interactiva, diseñada por Elena Álvarez en DescartesJS, que permite realizar un análisis de los puntos criticos de una función real de dos variables, $z=f(x,y)$.
Se permite practicar en su búsqueda con la función dada o la que el usuario desee. Para ello, se ofrece un camino en tres pasos y una justificación teórica de los mismos basada en el metodo del Hessiano. La escena tiene por objetivos: estudiar el concepto de punto crítico de una función de dos variables, practicar en la búsqueda de puntos críticos de funciones de dos variables y autoevaluarse en esta práctica.
¡Haz clic en la esquina superior derecha, para ampliar la escena!
Resolver problemas de optimización para funciones de dos o más variables puede ser similar a resolver dichos problemas en el cálculo de una sola variable. Sin embargo, las técnicas para lidiar con múltiples variables nos permiten resolver problemas de optimización más variados para los cuales necesitamos lidiar con condiciones o restricciones adicionales. En esta sección, examinamos uno de los métodos más comunes y útiles para resolver problemas de optimización con restricciones.
El último ejercicio del apartado anterior era una situación aplicada que implicaba maximizar una función de ganancias, sujeta a ciertas restricciones. En ese ejercicio, las restricciones involucraban un número máximo de pelotas de golf que podían ser producidas y vendidas en $1$ mes $(x)$, y un número máximo de horas publicitarias que se pueden comprar por mes $(y)$. Supongamos que estos se combinan en una restricción presupuestaria, como $20x+4y \le 216$,que tuvo en cuenta el costo de producir las pelotas de golf y la cantidad de horas publicitarias compradas por mes. El objetivo es, aún, maximizar las ganancias, pero ahora hay un tipo diferente de restricción en los valores de $x$ y $y$. Esta restricción, cuando se combina con la función de beneficio $f(x, y)=48x+96y-x^2-2xy-9y^2$,e s un ejemplo de un problema de optimización, y la función $f(x,y)$ se llama la función objetivo. Un gráfico de varias curvas de nivel de la función $f(x, y)$ es el siguiente:
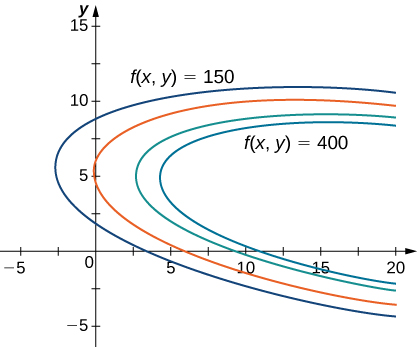
Figura 4.59. Gráfico de las curvas de nivel de la función $f (x, y) = 48x + 96y − x^2−2xy − 9y^2$ correspondientes a $c = 150,250,350$ y $400$.
En la figura 4.59, el valor $c$ representa diferentes niveles de beneficio (es decir, valores de la función $f$). Como el valor de $c$ aumenta, la curva se desplaza hacia la derecha. Dado que nuestro objetivo es maximizar las ganancias, queremos elegir una curva lo más a la derecha posible. Si no hubiera restricciones en la cantidad de pelotas de golf que la compañía podría producir, o la cantidad de unidades de publicidad disponibles, entonces podríamos producir tantas pelotas de golf como queramos y publicitar tanto como queramos, y no podría no ser un beneficio máximo para la empresa. Desafortunadamente, tenemos una restricción presupuestaria modelada por la desigualdad $20x+4y \le 216$. Para ver cómo esta restricción interactúa con la función de beneficio, la figura 4.60 muestra el gráfico de la línea $20x+4y=216$ superpuesto en el gráfico anterior.

Figura 4.60. Gráfico de curvas de nivel de la función $f (x, y) = 48x + 96y - x^2 - 2xy - 9y^2$ correspondiente a $c = 150, 250, 350$ y $395$. El gráfico rojo es la función de restricción.
Como se mencionó anteriormente, la ganancia máxima ocurre cuando la curva de nivel está lo más hacia la derecha posible. Sin embargo, el nivel de producción correspondiente a este beneficio máximo también debe satisfacer la restricción presupuestaria, por lo que el punto en el que se produce este beneficio también debe estar en (o a la izquierda de) la línea roja en la figura 4.60. La inspección de este gráfico revela que este punto existe donde la línea es tangente a la curva de nivel de $f$. Una prueba y error revela que este nivel de beneficio parece ser alrededor de $395$, cuando $x$ e $y$ son ambos menos de $5$. Volveremos a la solución de este problema más adelante en esta sección.
Desde un punto de vista teórico, en el punto donde la curva de beneficio es tangente a la línea de restricción, el gradiente de ambas funciones evaluadas en ese punto debe apuntar en la misma dirección (u opuesta).
Recuerda que el gradiente de una función de más de una variable es un vector. Si dos vectores apuntan en la misma dirección (u opuesta), entonces uno debe ser un múltiplo constante del otro. Esta idea es la base del método de multiplicadores de Lagrange.
Supón que se produce un extremo limitado en el punto $(x_0, y_0)$. Además, suponemos que la ecuación $g (x, y) = 0$ se puede parametrizar sin problemas como
$$x = x(s)\text{ y } y = y(s)$$donde $s$ es un parámetro de longitud de arco con punto de referencia $(x_0, y_0)$ en $s = 0$. Por lo tanto, la cantidad $z = f (x (s), y (s))$ tiene un máximo relativo o un mínimo relativo en $s = 0$, y esto implica que $\frac{dz}{ds} = 0$ en ese punto. De la regla de la cadena,
donde todas las derivadas se evalúan en $s = 0$. Sin embargo, el primer factor en el producto escalar es el gradiente de $f$, y el segundo factor es el vector unitario tangente $T (0)$ a la curva de restricción. Como el punto $(x_0, y_0)$ corresponde a $s = 0$, de esta ecuación se deduce que
$$\nabla f(x_0, y_0)\cdot T(0) = 0$$lo que implica que el gradiente es $0$ o es normal a la curva de restricción en un extremo relativo restringido. Sin embargo, la curva de restricción $g (x, y) = 0$ es una curva de nivel para la función $g (x, y)$ de modo que si $\nabla g (x_0, y_0) \cancel{=} 0$, entonces $\nabla g (x_0, y_0)$ es normal para esta curva en $(x_0, y_0)$. Se deduce, entonces, que hay algún escalar $\lambda$ tal que
$$\nabla f (x_0, y_0) = \lambda \nabla g (x_0, y_0)$$Para aplicar el Método de multiplicadores de Lagrange: una restricción a un problema de optimización similar al del fabricante de pelotas de golf, necesitamos una estrategia de resolución de problemas
 |
Usando multiplicadores de Lagrange |

Para este mismo ejercicio, presentamos otra escena interactiva de Elena Álvarez, que permite la práctica del cálculo de los extremos de una función real de dos variables condicionados a una restricción sobre el dominio, $g(x,y)=0$.
Después de repasar la definición de extremo condicionado se pasa a la escena en la que se pueden introducir tanto la función objeto de estudio, como la curva restricción.
Los objetivos de la escenas son: repasar la definiciones de extremos condicionados y multiplicadores de Lagrange; repasar el teorema de Lagrange y, practicar el cálculo, así como su representación, de los extremos condicionados de una función.
¡Haz clic en la esquina superior derecha de la escena, para ampliarl!
Volvamos ahora al problema planteado al comienzo de la sección.
 |
Pelotas de golf y multiplicadores de Lagrange |

En el caso de una función de optimización con tres variables y una función de restricción única, también es posible utilizar el método de multiplicadores de Lagrange para resolver un problema de optimización. Un ejemplo de una función de optimización con tres variables podría ser la función Cobb-Douglas en el ejemplo anterior: $f (x, y, z) = x^{0.2} y^{0.4} z^{0.4}$, donde $x$ representa el costo de la mano de obra, $y$ representa entrada de capital, y $z$ representa el costo de la publicidad. El método es el mismo que para el método con una función de dos variables; las ecuaciones a resolver son
$$\begin{aligned} \nabla f(x, y, z) &= \lambda \nabla g(x, y, z)\\ g (x, y, z) &= 0 \end{aligned}$$ |
Multiplicadores de Lagrange con una función de optimización de tres variables |

El método de los multiplicadores de Lagrange se puede aplicar a problemas con más de una restricción. En este caso la función de optimización $w$ es una función de tres variables:
$$ w = f(x, y, x)$$y está sujeto a dos restricciones:
$$g(x, y, z) = 0 \text{ y } h(x, y, z) = 0$$Hay dos multiplicadores de Lagrange, $\lambda_1$ y $\lambda_2$, y el sistema de ecuaciones se convierte en:
$$\begin{aligned} \nabla f(x_0, y_0, z_0) &= \lambda_1\nabla g(x_0, y_0, z_0) + \lambda_2 \nabla h(x_0, y_0, z_0)\\ g(x_0, y_0, z_0) &= 0\\ h(x_0, y_0, z_0) &= 0 \end{aligned}$$ |
Multiplicadores de Lagrange con una función de optimización de tres variables |


 Para los siguientes ejercicios, usa el método de multiplicadores de Lagrange para encontrar los valores máximos y mínimos de la función sujeta a las restricciones dadas.
Para los siguientes ejercicios, usa el método de multiplicadores de Lagrange para encontrar los valores máximos y mínimos de la función sujeta a las restricciones dadas.
358. $f(x, y) = x^2y;\; x^2 + 2y^2 = 6$ 359. $f(x, y, z) = xyz,\; x^2+ 2y^2 +3z^2$ (Solución). 360. $f(x, y) = xy;\; 4x^2 + 8y^2 = 16$ 361. $f(x, y) = 4x^3 + y^2;\; 2x^2 + y^2 = 1$ (Solución). 362. $f(x, y, z) = x^2 + y^2 + z^2,\; x^4 + y^4 + z^4 = 1$ 363. $f(x, y, z) = yz + xy, xy = 1,\; y^2 + z^2 = 1$ (Solución). 364. $f(x, y) = x^2 + y^2,\; (x − 1)^2 + 4y^2 = 4$ 365. $f(x, y) = 4xy,\; \frac{x^2}{9} + \frac{y^2}{16} = 1$ (Solución). 366. $f(x, y, z) = x + y + z,\;\frac1x + \frac1y + \frac1z = 1$ 367. $f(x, y, z) = x + 3y − z,\; x^2 + y^2 + z^2 = 4$ (Solución). 368. $f(x, y, z) = x^2 + y^2 + z^2,\; xyz = 4$
369. Minimiza $f (x, y) = x^2 + y^2$ en la hipérbola $xy = 1$ (Solución). 370. Minimiza $f(x, y) = xy$ en la elipse $b^2x^2 + a^2y^2 = a^2b^2$ 371. Maximiza $f(x, y, z) = 2x + 3y + 5z$ en la esfera $x^2+y^2+z^2=19$ (Solución). 372. Maximiza $f(x, y) = x^2-y^2;\; x \gt 0, y\gt 0;\; g(x,y) = y-x^2 = 0$ 373. La curva $x^3 - y^3 = 1$ es asintótica a la línea $y = x$. Encuentra los puntos en la curva $x^3 - y^3 = 1$ más alejado de la línea $y = x$ (Solución). 374. Maximiza $U(x, y) = 8x^{4/5}y^{1/5};\;4x+2y=12$ 375. Minimiza $f(x,y) = x^2+y^2,\; x+2y-5 = 0$ (Solución). 376. Maximiza $f(x, y) = \sqrt{6-x^2 - y^2};\;x+y-2=0$ 377. Minimiza $f(x,y) = x^2+y^2+z^2,\; x+y+z=1$ (Solución). 378. Minimiza $f(x, y) = x^2 - y^2$ sujeto a la restricción $x-2y+6=0$ 379. Minimiza $f(x,y) = x^2+y^2+z^2$ cuando $x+y+z=9$ y $x+2y+3z=20$ (Solución).
 Para el siguiente grupo de ejercicios, usa el método de multiplicadores de Lagrange para resolver los siguientes problemas aplicados.
Para el siguiente grupo de ejercicios, usa el método de multiplicadores de Lagrange para resolver los siguientes problemas aplicados.
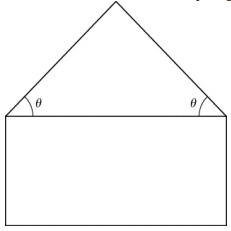
380. Un pentágono se forma colocando un triángulo isósceles en un rectángulo, como se muestra en el diagrama. Si el perímetro del pentágono es de $10\; pulgadas$, encuentra las longitudes de los lados del pentágono que maximizarán el área del pentágono.
381. Se debe hacer una caja rectangular sin una tapa (una caja sin topless) de $12\; pies^2$ de cartón. Encuentra el volumen máximo de tal caja (Solución).
382. Encuentra las distancias mínima y máxima entre la elipse $x^2 + xy + 2y^2 = 1$ y el origen.
383. Encuentra el punto en la superficie $x^2 - 2xy + y^2 - x + y = 0$ más cercano al punto $(1, 2, −3)$ (Solución).
384. Demuestra que, de todos los triángulos inscritos en un círculo de radio $R$ (ver diagrama), el triángulo equilátero tiene el perímetro más grande
385. Encuentra la distancia mínima desde el punto $(0, 1)$ a la parábola $x^2 = 4y$ (Solución). 386. Encuentra la distancia mínima desde la parábola $y = x^2$ al punto $(0, 3)$. 387. Encuentra la distancia mínima desde el plano $x + y + z = 1$ al punto $(2, 1, 1)$ (Solución). 388. Un contenedor grande en forma de sólido rectangular debe tener un volumen de $480\; m^3$. El fondo del contenedor cuesta $\$ 5/m^2$ para construir mientras que la parte superior y los costados cuestan $\$ 3/m^2$ para construir. Usa los multiplicadores de Lagrange para encontrar las dimensiones del contenedor de este tamaño que tiene el costo mínimo. 389. Encuentra el punto en la línea $y = 2x + 3$ que está más cerca del punto $(4, 2)$ (Solución). 390. Encuentra el punto en el plano $4x + 3y + z = 2$ que esté más cerca del punto $(1, −1, 1)$. 391. Encuentra el valor máximo de $f (x, y) = sen x sen y$, donde $x$ e $y$ denotan los ángulos agudos de un triángulo rectángulo. Dibuja los contornos de la función usando un CAS (Solución). 392. Un sólido rectangular está contenido dentro de un tetraedro con vértices en $(1, 0, 0), (0, 1, 0), (0, 0, 1)$ y el origen. La base de la caja tiene dimensiones $x, y$, y la altura de la caja es $z$. Si la suma de $x, y$ y $z$ es $1.0$, encuentra las dimensiones que maximicen el volumen del sólido rectangular. 393. [T] Al invertir $x$ unidades de trabajo y $y$ unidades de capital, un fabricante de relojes puede producir $P (x, y) = 50x^{0.4} y^{0.6}$ relojes. Encuentra la cantidad máxima de relojes que se pueden producir con un presupuesto de $\$ 20,000$ si la mano de obra cuesta $\$ 100 / unidad$ y el capital cuesta $\$ 200 / unidad$. Usa un CAS para dibujar un diagrama de contorno de la función (Solución).
En la siguiente escena interactiva, diseñada en GeoGebra por Vladimiro González Zelaya, se muestra la función $x^2+2y^2=2$ con la restricción $x^2+y^2=1$

Figura 5.1. La Ciudad de las Artes y las Ciencias en Valencia, España, tiene una estructura única a lo largo de un eje de solo dos kilómetros que anteriormente era el lecho del río Turia. L'Hemisfèric tiene un cine IMAX con tres sistemas de proyecciones digitales modernas en una pantalla cóncava de $900$ metros cuadrados. Se ha hecho un techo ovalado de más de $100$ metros de largo para que parezca un enorme ojo humano que cobra vida y se abre al mundo como el "Ojo de la Sabiduría" (crédito: modificación del trabajo de Javier Yaya Tur, Wikimedia Commons)
En este capítulo ampliamos el concepto de una integral definida de una sola variable a integrales dobles y triples de funciones de dos y tres variables, respectivamente. Examinamos aplicaciones que involucran integración para calcular volúmenes, masas y centroides de regiones más generales.
También veremos cómo el uso de otros sistemas de coordenadas (como coordenadas polares, cilíndricas y esféricas) simplifica el cálculo de integrales múltiples sobre algunos tipos de regiones y funciones. Como ejemplo, utilizaremos coordenadas polares para encontrar el volumen de estructuras como l'Hemisfèric.
En el capítulo anterior, discutimos el cálculo diferencial con múltiples variables independientes. Ahora examinamos el cálculo integral en múltiples dimensiones. Así como una derivada parcial nos permite diferenciar una función con respecto a una variable mientras se mantienen constantes las otras variables, veremos que una integral iterada nos permite integrar una función con respecto a una variable mientras se mantienen constantes las otras variables.
En este apartado investigamos las integrales dobles y mostramos cómo podemos usarlas para encontrar el volumen de un sólido sobre una región rectangular en el palno $xy$. Muchas de las propiedades de las integrales dobles son similares a las que ya hemos discutido para las integrales individuales.
Comenzamos considerando el espacio por encima de una región rectangular $R$. Considera una función continua $f(x, y) \ge 0$ de dos variables definidas en el rectángulo cerrado $R$:
$$R = [a, b] \times [c, d] = \lbrace (x, y) \isin \Reals^2 |a \le x \le b, c \le y \le d\rbrace$$aquí $[a,b]\times [c,d]$ denota el producto cartesiano de los dos intervalos cerrados $[a,b]$ y $[c,d]$. Consiste en pares rectangulares $(x,y)$ tal que $a\le x\le b$ y $c\le y\le d$. La gráfica de $f$ representa una superficie sobre el plano $xy$ con ecuación $z=f(x,y)$ dónde $z$ es la altura de la superficie en el punto $(x,y)$. Sea $S$ el sólido que yace arriba de $R$ y debajo de la gráfica de $f$ (Figura 5.2). La base del sólido es el rectángulo $R$ en el plano$xy$. Queremos encontrar el volumen $V$ del sólido $S$.
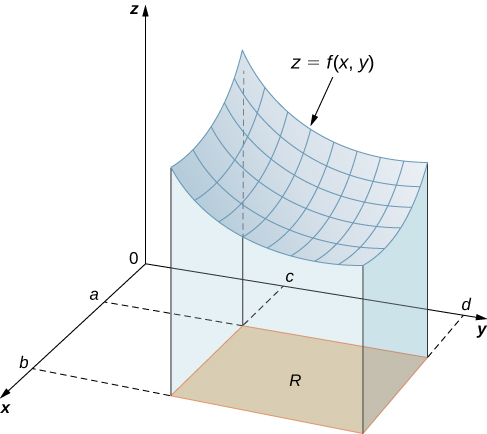
Figura 5.2. La gráfica de $f(x,y)$ sobre el rectángulo $R$ en el plano $xy$ es una superficie curva.
Dividimos la region $R$ en pequeños rectángulos $R_{ij}$, cada uno con area $\Delta A$ y con lados $\delta x$ y $\Delta y$ (Figura 5.3).
Hacemos esto dividiendo el intervalo $[a,b]$ dentro $m$ subintervalos y dividiendo el intervalo $[c,d]$ dentro $n$ subintervalos. Por lo tanto $\Delta x = \frac{b−a}{m}, \Delta y = \frac{d - c}{m}$, y $\Delta A = \Delta x\Delta y$.

Figura 5.3. El rectángulo $R$ se divide en pequeños rectángulos $R_{ij}$, cada uno con area $\Delta A$.
El volumen de una caja rectangular delgada arriba de $R_{ij}$ es $f(x_{ij}^*, y_{ij}^*)\Delta A$, dónde $(x_{ij}^*, y_{ij}^*)$ es un punto de muestra arbitrario en cada $R_{ij}$ como se muestra en la siguiente figura.
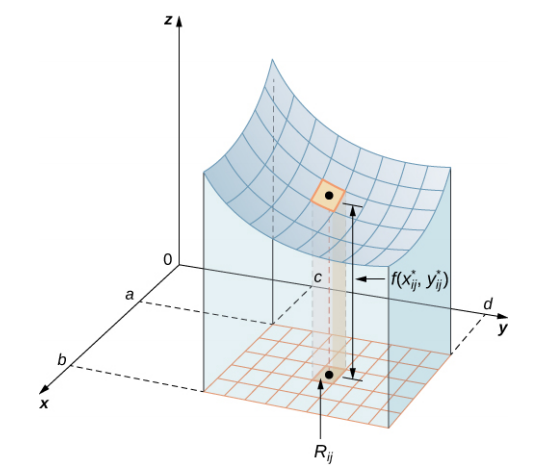
Figura 5.4. Una caja rectangular delgada arriba de $R_{ij}$ con altura $f(x_{ij}^*, y_{ij}^*)$.
Usando la misma idea para todos los subrectangulos, obtenemos un volumen aproximado del sólido $S$ como $V \approx \displaystyle\sum_{i=1}^m\sum_{j=1}^n f(x_{ij}^*, y_{ij}^*)\Delta A$. Esta suma se conoce como una suma doble de Riemann y se puede usar para aproximar el valor del volumen del sólido. Aquí la suma doble significa que para cada subrectangulo evaluamos la función en el punto elegido, multiplicamos por el área de cada rectángulo y luego sumamos todos los resultados.
Como hemos visto en el caso de una variable, se obtiene una mejor aproximación al volumen real si $m$ y $n$ se hacen más grandes.
$$V = \lim\limits_{m,n \to \infin}\sum_{i=1}^m\sum_{j=1}^n f(x_{ij}^*, y_{ij}^*)\Delta A$$O de otra forma
$$V = \lim\limits_{\Delta x,\Delta y \to \infin}\sum_{i=1}^m\sum_{j=1}^n f(x_{ij}^*, y_{ij}^*)\Delta A$$Ten en cuenta que la suma se aproxima a un límite en cualquiera de los casos y el límite es el volumen del sólido con la base $R$. Ahora estamos listos para definir la integral doble.
Si $f(x,y)\ge 0$, entonces el volumen $V$ del sólido $S$, que se encuentra arriba de $R$ en el plano $xy$ y debajo de la gráfica de $f$, es la doble integral de la función $f( x , y)$ sobre el rectángulo $R$. Si la función es alguna vez negativa, entonces la integral doble puede considerarse un volumen "con signo" de una manera similar a la forma en que definimos el área neta con signo en la integral definida de una función de un variable.
 |
Configuración de una integral doble y aproximación por sumas dobles |
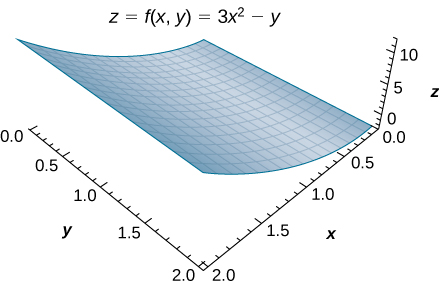
Figura 5.5. La función $z = f(x,y)$ graficada sobre la región rectangular $R=[0,2]\times [0,2]$.

Ten en cuenta que hemos desarrollado el concepto de integral doble usando una región rectangular $R$. Este concepto puede extenderse a cualquier región general. Sin embargo, cuando una región no es rectangular, los subrectángulos pueden no encajar perfectamente en $R$, particularmente si el área base es curva. Examinamos esta situación con más detalle en la siguiente sección, donde se estudian las regiones que no siempre son rectangulares y los subrentángulos no pueden encajar perfectamente en la región $R$. Además, las alturas pueden no ser exactas si la superficie $z= f( x , y)$ es curva. Sin embargo, los errores en los lados y la altura donde las piezas pueden no encajar perfectamente dentro del sólido $S$ se acercan a $0$ con $m$ y $n$ acercándose al infinito. Además, la doble integral de la función $z= f( x , y)$ existe siempre que la función $f$ no sea demasiado discontinua. Si la función es acotada y continua sobre $R$, excepto en un número finito de curvas suaves, entonces existe la integral doble y decimos que $f$ es integrable sobre $R$.
Ya que $\Delta A = \Delta x \Delta y = \Delta y\Delta x$, podemos expresar $\Delta A$ como $\Delta x\Delta y$ o $\Delta y\Delta x$. Esto significa que, cuando usamos coordenadas rectangulares, la integral doble sobre una región $R$ denotada por $\displaystyle\iint_R f(x,y)dA$ puede ser escrita como $\displaystyle\iint_r f(x, y)dxdy$ o $\displaystyle\iint_r f(x, y)dydx$. Ahora enumeremos algunas de las propiedades que pueden ser útiles para calcular integrales dobles.
Las propiedades de las integrales dobles son muy útiles al calcularlas o trabajar con ellas.
Enumeramos aquí seis propiedades de integrales dobles. Las propiedades $1$ y $2$ se conocen como la linealidad de la integral, la propiedad $3$ es la aditividad de la integral, la propiedad $4$ es la monotonicidad de la integral y la propiedad $5$ se usa para encontrar los límites de la integral. La propiedad $6$ se usa si $f(x , y)$ es un producto de dos funciones $g(x)$ y $h(y)$.
Estas propiedades se utilizan en la evaluación de integrales dobles, como veremos más adelante. Nos convertiremos en expertos en el uso de estas propiedades una vez que nos familiaricemos con las herramientas computacionales de las integrales dobles. Pero, antes de ir a ello, veamos una escena interactiva diseñada por Elena Álvarez, la cual permite modificar la función, los parámetros $m$ y $n$ que definen la partición y obtener el valor exacto de la integral doble para una función de dos variables así como una aproximación mediante sumas de Riemann.
Pulsando sobre el botón información, se ilustra a través de varios pasos el proceso de construcción de la integral doble. Puedes intentar resolver el ejercicio anterior, cambiando los parámetros.
En el siguiente vídeo, puedes observar cómo se interactúa con la escena.
Hasta ahora, hemos visto cómo configurar una integral doble y cómo obtener un valor aproximado para ella. También podemos imaginar que evaluar integrales dobles usando la definición puede ser un proceso muy largo si elegimos valores más grandes para $m$ y $n$. Por lo tanto, necesitamos una técnica práctica y conveniente para calcular integrales dobles. En otras palabras, necesitamos aprender cómo calcular integrales dobles sin emplear la definición que usa límites y sumas dobles.
La idea básica es que la evaluación se vuelve más fácil si podemos dividir una integral doble en integrales individuales al integrar primero con respecto a una variable y luego con respecto a la otra. La herramienta clave que necesitamos se llama integral iterada.
La notación $\displaystyle\int_a^b\bigg[\int_c^d f(x, y)dy\bigg]dx$ significa que integramos $f(x, y)$ con respecto a $y$ mientras mantenemos $x$ constante. Del mismo modo, la notación $\displaystyle\int_c^d\bigg[\int_a^b f(x, y)dx\bigg]dy$ significa que integramos $f(x, y)$ con respecto a $x$ mientras mantenemos $y$ constante. El hecho de que las integrales dobles se pueden dividir en integrales iteradas se expresa en el teorema de Fubini. Piensa en este teorema como una herramienta esencial para evaluar integrales dobles.
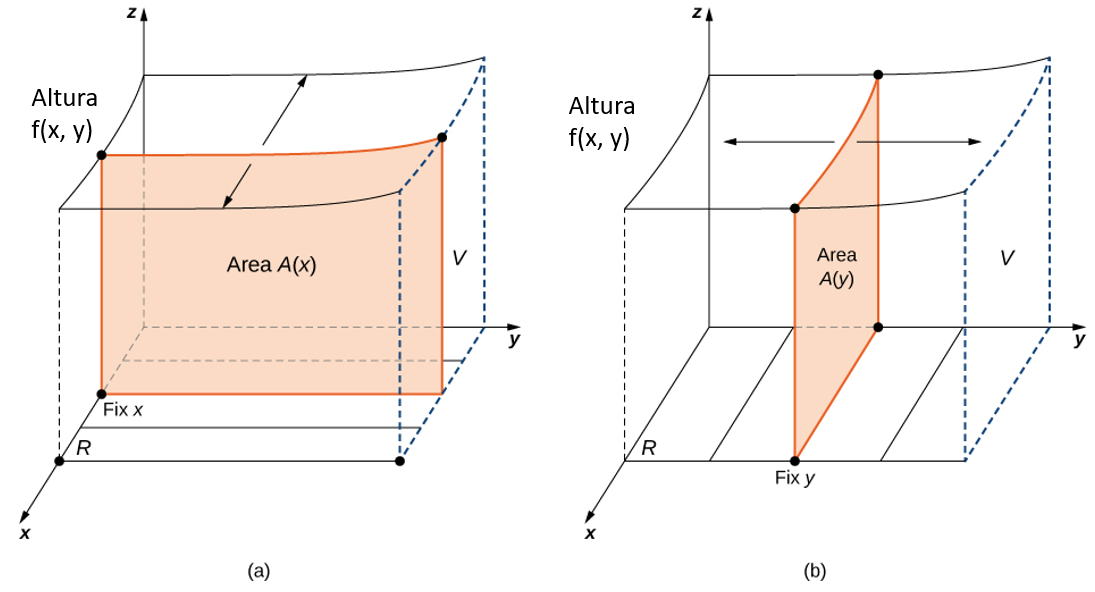
Figura 5.7. (a) Integrar primero con respecto a $y$ luego con respecto a $x$ para encontrar el área $A(x)$ y luego el volumen $V$; (b) integrando primero con respecto a $x$ y luego con respecto a $y$ para encontrar el área $A(y$) y luego el volumen $V$.
 |
Usando el teorema de Fubini |

La doble integración en este ejemplo es lo suficientemente simple como para usar el teorema de Fubini directamente, lo que nos permite convertir una integral doble en una integral iterada.
En consecuencia, ahora estamos listos para convertir todas las integrales dobles en integrales iteradas y demostrar cómo las propiedades enumeradas anteriormente pueden ayudarnos a evaluar integrales dobles cuando la función $f (x, y)$ es más compleja. Ten en cuenta que el orden de integración se puede cambiar.
 |
Ilustrando las propiedades i y ii |

 |
Ilustrando la propiedad v |

 |
Ilustrando la propiedad vi |

En la siguiente escena interactiva, diseñada en GeoGebra por Andreas Lindner, puedes interactuar con el ejercicio anterior, donde $f(x,y) = e^ycos x$
Como mencionamos anteriormente, cuando usamos coordenadas rectangulares, la integral doble sobre una región $R$ denotada por $\displaystyle\iint_Rf (x, y) dA$ puede escribirse como $\displaystyle\iint_Rf (x, y) dxdy$ o $\displaystyle\iint_Rf (x, y) dydx$. El siguiente ejercicio se muestra que los resultados son los mismos independientemente del orden de integración que elijamos.
 |
Evaluación de una integral iterada de dos maneras |

En el siguiente ejercicio, vemos que en realidad puede ser beneficioso cambiar el orden de integración para facilitar el cálculo. Volveremos a esta idea varias veces en este capítulo.
 |
Evaluación de una integral iterada de dos maneras |

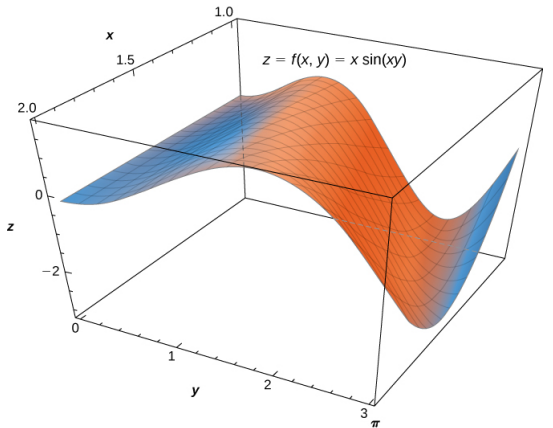
Figura 5.8. La función $z = f (x, y) = x sen (xy)$ sobre la región rectangular $R = [0, \pi] \times [1, 2]$.
Las integrales dobles son muy útiles para encontrar el área de una región delimitada por curvas de funciones. Describimos esta situación con más detalle en la siguiente sección. Sin embargo, si la región es de forma rectangular, podemos encontrar su área integrando la función constante $f (x, y) = 1$ sobre la región $R$.
Esta definición tiene sentido porque usar $f (x, y) = 1 $ y evaluar la integral lo convierten en un producto de largo y ancho. Veamos esta fórmula con un ejemplo y veamos cómo funciona.
 |
Encontrar el área usando una integral doble |

Ya hemos visto cómo se pueden usar integrales dobles para encontrar el volumen de un sólido limitado anteriormente por una función $f (x, y)$ sobre una región $R$ proporcionada $f (x, y) \ge 0$ para todos los $(x, y)$ en $R$. Aquí hay otro ejemplo para ilustrar este concepto.
 |
Volumen de un paraboloide elíptico |

Recuerda que definimos el valor promedio de una función de una variable en un intervalo $[a, b]$ como
$$f_{\text{prom}} = \frac{1}{b-a} \int_a^bf(x)dx$$De manera similar, podemos definir el valor promedio de una función de dos variables sobre una región $R$. La principal diferencia es que dividimos por un área en lugar del ancho de un intervalo.
 |
Cálculo de la precipitación pluvial promedio |

Figura 5.10. Efectos del huracán Karl, que arrojó $4-8$ pulgadas $(100-200 mm)$ de lluvia en algunas partes del suroeste de Wisconsin, el sur de Minnesota y el sureste de Dakota del Sur en un lapso de $300$ millas de este a oeste y $250$ millas de norte a sur.

 En los siguientes ejercicios, usa la regla del punto medio con $m = 4$ y $n = 2$ para estimar el volumen del sólido delimitado por la superficie $z = f (x, y)$, los planos verticales $x = 1, x = 2, y = 1$, y $y = 2$, y el plano horizontal $z = 0$.
En los siguientes ejercicios, usa la regla del punto medio con $m = 4$ y $n = 2$ para estimar el volumen del sólido delimitado por la superficie $z = f (x, y)$, los planos verticales $x = 1, x = 2, y = 1$, y $y = 2$, y el plano horizontal $z = 0$.
1. $f(x, y) = 4x + 2y + 8xy$ (Solución). 2. $f(x, y) = 16x^2 + \frac{y}{2}$
 En los siguientes ejercicios, calcula el volumen del sólido debajo de la superficie $z = f (x, y)$ y arriba de la región rectangular $R$ usando una suma de Riemann con $m = n = 2$, los puntos de muestra son las esquinas inferiores izquierdas de los subrectangulos de la partición.
En los siguientes ejercicios, calcula el volumen del sólido debajo de la superficie $z = f (x, y)$ y arriba de la región rectangular $R$ usando una suma de Riemann con $m = n = 2$, los puntos de muestra son las esquinas inferiores izquierdas de los subrectangulos de la partición.
3. $f(x, y) = sen x − cos y, R = [0, \pi] \times [0, \pi]$ (Solución).
4. $f(x, y) = cos x + cos y, R = [0, π] \times [0, \frac{\pi}{2}]$
5. Usa la regla del punto medio con $m = n = 2$ para estimar $\displaystyle\iint_Rf (x, y) dA$, donde los valores de la función $f$ en $R = [8, 10] \times [9, 11]$ se dan en la siguiente tabla (Solución).
6. Los valores de la función $f$ en el rectángulo $R = [0, 2] \times [7, 9]$ se dan en la siguiente tabla. Estima la integral doble $\iint_Rf (x, y) dA$ utilizando una suma de Riemann con $m = n = 2$. Selecciona los puntos de muestra para que sean las esquinas superiores derechas de los subcuadrados de $R$
7. En la siguiente tabla se muestra la profundidad de una piscina para niños de $4$ pies por $4$ pies, medida a intervalos de $1$ pie.
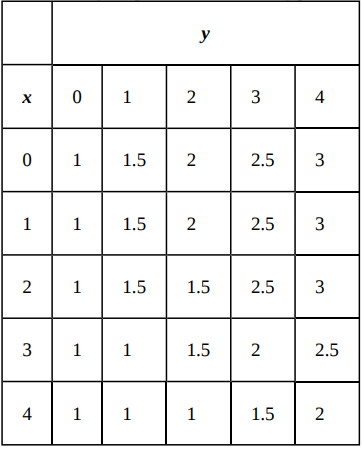
8. La siguiente tabla muestra la profundidad de un hoyo de $3$ pies por $3$ pies en el suelo, medido a intervalos de $1$ pie.
 9. Las curvas de nivel $f (x, y) = k$ de la función $f$ se dan en el siguiente gráfico, donde $k$ es una constante.
9. Las curvas de nivel $f (x, y) = k$ de la función $f$ se dan en el siguiente gráfico, donde $k$ es una constante.
10. Las curvas de nivel $f (x, y) = k$ de la función $f$ se dan en el siguiente gráfico, donde $k$ es una constante.
11. El sólido que se encuentra debajo de la superficie $z = \sqrt{4 - y^2}$ y encima de la región rectangular $R = [0, 2] \times [0, 2]$ se ilustra en el siguiente gráfico. Evalúa la integral doble $\iint_Rf (x, y) dA$, donde $f (x, y) = \sqrt{4 - y^2}$, encontrando el volumen del sólido correspondiente (Solución).
12. El sólido que se encuentra debajo del plano $z = y + 4$ y encima de la región rectangular $R = [0, 2] \times [0, 4]$ se ilustra en el siguiente gráfico. Evalúa la integral doble $\iint_Rf (x, y) dA$, donde $f (x, y) = y + 4$, encontrando el volumen del sólido correspondiente.
 En los siguientes ejercicios, calcula las integrales intercambiando el orden de integración.
En los siguientes ejercicios, calcula las integrales intercambiando el orden de integración.
13. $\displaystyle\int_{-1}^1\bigg(\int_{-2}^2(2x+3y+5)dx\bigg)dy$ (Solución). 14. $\displaystyle\int_{0}^2\bigg(\int_{0}^1(x+2e^y-3)dx\bigg)dy$ 15. $\displaystyle\int_{1}^{27}\bigg(\int_{1}^2(\sqrt[3]{x}+\sqrt[3]{y})dy\bigg)dx$ (Solución). 16. $\displaystyle\int_{1}^{16}\bigg(\int_{1}^8(\sqrt[4]{x}+2\sqrt[3]{y})dy\bigg)dx$ 17. $\displaystyle\int_{ln2}^{ln3}\bigg(\int_{0}^1(e^{x+y})dy\bigg)dx$ (Solución).
18. $\displaystyle\int_{0}^{2}\bigg(\int_{0}^1(3^{x+y})dy\bigg)dx$ 19. $\displaystyle\int_{1}^{6}\bigg(\int_{2}^9(\frac{\sqrt{y}}{x^2})dy\bigg)dx$ (Solución). 20. $\displaystyle\int_{1}^{9}\bigg(\int_{4}^2(\frac{\sqrt{x}}{y^2})dy\bigg)dx$
 En los siguientes ejercicios, calcula las integrales intercambiando el orden de integración.
En los siguientes ejercicios, calcula las integrales intercambiando el orden de integración.
21. $\displaystyle\int_{0}^{\pi}\int_{0}^{\pi /2}sen(2x)cos(3y)dydx$ (Solución). 22. $\displaystyle\int_{\pi /12}^{\pi /8}\int_{\pi /4}^{\pi /3}[cotx + tan(2y)]dxdy$ 23. $\displaystyle\int_{1}^{e}\int_{1}^{e}\frac1x sen(ln x) + \frac1y cos(lny)dxdy$ (Solución). 24. $\displaystyle\int_{1}^{e}\int_{1}^{e}\frac{sen(ln x)cos(lny)}{xy}dxdy$ 25. $\displaystyle\int_{1}^{2}\int_{1}^{2}\bigg(\frac{lny}{x} + \frac{x}{2y+1}\bigg)dydx$ (Solución). 26. $\displaystyle\int_{1}^{e}\int_{1}^{2}x^2 ln(x)dydx$ 27. $\displaystyle\int_{1}^{\sqrt{3}}\int_{1}^{2}y\;arctan\bigg(\frac1x\bigg)dydx$ (Solución). 28. $\displaystyle\int_{0}^{1}\int_{0}^{1/2}(arcsen\;x + arcsen\;y)dydx$ 29. $\displaystyle\int_{0}^{1}\int_{1}^{2}xe^{x+4y}dydx$ (Solución).
30. $\displaystyle\int_{1}^{2}\int_{0}^{1}xe^{x-y}dydx$ 31. $\displaystyle\int_{1}^{e}\int_{1}^{e}\bigg(\sqrt{lny}{\sqrt{y} + \frac{lnx}{\sqrt{x}}}\bigg)dydx$ (Solución). 32. $\displaystyle\int_{1}^{e}\int_{1}^{e}\big(\frac{xlny}{\sqrt{y}} + \frac{ylnx}{\sqrt{x}}\bigg)dydx$ 33. $\displaystyle\int_{0}^{1}\int_{1}^{2}\bigg(\frac{x}{x^2 + y^2}\bigg)dydx$ (Solución). 34. $\displaystyle\int_{0}^{1}\int_{1}^{2}\frac{y}{x+y^2}dydx$
 En los siguientes ejercicios, encuentra el valor promedio de la función sobre los rectángulos dados.
En los siguientes ejercicios, encuentra el valor promedio de la función sobre los rectángulos dados.
35. $f(x, y) = −x + 2y, R = [0, 1] \times [0, 1]$ (Solución). 36. $f(x, y) = x^4 + 2y^3, R = [1, 2] \times [2, 3]$
37. $f(x, y) = senh x + senh y, R = [0, 1] \times [0, 2]$ (Solución). 38. $f(x, y) = arctan(xy), R = [0, 1] \times [0, 1]$ 39. Sean $f$ y $g$ dos funciones continuas de modo que $0 \le m_1 \le f (x) \le M_1$ para cualquier $x \isin [a, b]$ y $0 \le m_2 \le g (y) \le M_2$ para cualquier $y \isin [c, d]$. Demuestra que la siguiente desigualdad es verdadera: $$m_1m_2(b-a(c-d) \le \int_a^b\int_c^d f(x)g(y)dydx \le M_1M_2(b-a)(c-d)$$
 En los siguientes ejercicios, usa la propiedad $v$. Obtén integrales dobles y la respuesta del ejercicio anterior para mostrar que las siguientes desigualdades son verdaderas
En los siguientes ejercicios, usa la propiedad $v$. Obtén integrales dobles y la respuesta del ejercicio anterior para mostrar que las siguientes desigualdades son verdaderas
40. $\frac{1}{e^2}\le \iint_R e^{-x^2-y^2}dA \le 1$, donde $R = [0, 1] \times [0, 1]$ 41. $\frac{\pi^2}{144}\le \iint_R sen\;xcos\;ydA \le \frac{\pi^2}{48}$, donde $R = [\frac{\pi}{6}, \frac{\pi}{3}] \times [\frac{\pi}{6}, \frac{\pi}{3}]$ 42. $0\le \iint_R e^{-y}cos\;xdA \le \frac{\pi}{2}$, donde $R = [0, \frac{\pi}{2}] \times [0, \frac{\pi}{2}]$ 43. $0\le \iint_R (ln\;x)(ln\;y)dA \le (e-1)^2$, donde $R = [1,e] \times [1,e]$ 44. Supongamos que $f$ y $g$ son dos funciones continuas tales que $0 \le m_1 \le f (x) \le M_1$ para cualquier $x \isin [a, b]$ y $0 \le m_2 \le g (y) \le M_2$ para cualquier $y \isin [c, d]$. Demuestra que la siguiente desigualdad es verdadera:
$(m_1+m_2)(b-a)(c-d) \le \int_a^b\int_c^d [f(x)+g(y)]dydx \le (M_1+M_2)(b-a)(c-d)$
 En los siguientes ejercicios, usa la propiedad $v$ de integrales dobles y la respuesta del ejercicio anterior para mostrar que las siguientes desigualdades son verdaderas.
En los siguientes ejercicios, usa la propiedad $v$ de integrales dobles y la respuesta del ejercicio anterior para mostrar que las siguientes desigualdades son verdaderas.
45. $\frac2e\le \iint_R \big(e^{-x^2} + e^{-y^2}\big)dA \le 2$, donde $R = [0,1] \times [0,1]$ 46. $\frac{\pi^2}{36}\le \iint_R (sen\;x + cos\;y)dA \le \frac{\pi^2\sqrt{3}}{36}$, donde $R = [\frac{\pi}{6}, \frac{\pi}{3}] \times [\frac{\pi}{6}, \frac{\pi}{3}]$
47. $\frac{\pi }{2}e^{-\pi /2}\le \iint_R \big(cos\;x + e^{-y}\big)dA \le \pi$, donde $R = [0,\frac{\pi}{2}] \times [0,\frac{\pi}{2}]$ 48. $\frac{1}{e}\le \iint_R \big(e^{-y} - ln\;x\big)dA \le 2$, donde $R = [0, 1] \times [0, 1]$
 En los siguientes ejercicios, la función $f$ se da en términos de integrales dobles.
En los siguientes ejercicios, la función $f$ se da en términos de integrales dobles.
49. [T] $f(x, y) = \int_0^y\int_0^x (xs + yt)ds\;dt$, donde $(x, y) \isin R = [0,1] \times [0,1]$ (Solución) 50. [T] $f(x, y) = \int_0^x\int_0^x [cos(s) + cos(t)]dt\;ds$, donde $(x, y) \isin R = [0, 3] \times [0, 3]$
51. Demuestra que si $f$ y $g$ son continuas en $[a, b]$ y $[c, d]$, respectivamente, entonces $$\int_a^b\int_c^d[(f(x)+ g(y)]dy\;dx = (d- c)\int_a^bf(x)dx\\ + \int_a^b\int_c^dg(y)dy\;dx = (b-a)\int_d^cg(y)dy + \int_c^d\int_a^bf(x)dx\;dy$$
52. Desmuestra que $$\int_a^b\int_c^d (yf(x) + xg(y))dydx =\\ \frac12(d^2 - c^2)\bigg(\int_a^b f(x)dx\bigg) + \frac12(b^2-a^2)\bigg(\int_c^d g(y)dy\bigg)$$
53. Considera la función $f(x, y) = e^{-x^2-y^2}$, donde $(x, y)\isin R = [-1, 1]\times [-1,1]$ (Solución)
54. [T] Considera la función $f (x, y) = sen \big(x^2\big)cos\big(y^2\big)$, donde $(x, y) \isin R = [−1, 1] \times [−1, 1]$.
 En los siguientes ejercicios, se dan las funciones $f_n$, donde $n \ge 1$ es un número natural.
En los siguientes ejercicios, se dan las funciones $f_n$, donde $n \ge 1$ es un número natural.
55. $f(x, y) = x^n + y^n + xy, (x, y) \isin R = [0, 1] \times [0, 1]$ (Solución) 56. $f(x, y) = \frac{1}{x^n} + \frac{1}{y^n}, (x, y) \isin R = [1, 2] \times [1, 2]$ 57. Demuestra que el valor promedio de una función $f$ en una región rectangular $R = [a, b] \times [c, d]$ es $f_{prom} \approx \frac{1}{mn}\sum_{i=1}^m\sum_{j=1}^nf\big(x_{ij}^*, y_{ij}^*\big)$, donde $\big(x_{ij}^*, y_{ij}^*\big)$ son los puntos de muestra de la partición de $R$, donde $1 \le i \le m$ y $1 \le j \le n$ 58. Usa la regla del punto medio con $m = n$ para mostrar que el valor promedio de una función $f$ en una región rectangular $R = [a, b] \times [c, d]$ se aproxima por $$f_{prom} \approx \frac{1}{n^2}\sum_{j=1}^nf\bigg(\frac12(x_{i-1} + x_i), \frac12(y_{j-1}, y_i)\bigg)$$
59. Un mapa de isotermas es un gráfico que conecta puntos que tienen la misma temperatura en un momento dado durante un período de tiempo determinado. Usa el ejercicio anterior y aplica la regla del punto medio con $m = n = 2$ para encontrar la temperatura promedio sobre la región dada en la siguiente figura (Solución)
En Integrales dobles sobre regiones rectangulares, estudiamos el concepto de integrales dobles y examinamos las herramientas necesarias para calcularlas. Aprendimos técnicas y propiedades para integrar funciones de dos variables sobre regiones rectangulares. También discutimos varias aplicaciones, como encontrar el volumen limitado anteriormente por una función sobre una región rectangular, encontrar el área por integración y calcular el valor promedio de una función de dos variables.
En esta sección consideramos integrales dobles de funciones definidas sobre una región $D$ general limitada en el plano.
La mayoría de los resultados anteriores también se mantienen en esta situación, pero algunas técnicas deben extenderse para cubrir este caso más general.
En la figura 5.12 se muestra un ejemplo de una región $D$ general limitada en un plano. Como $D$ está acotado en el plano, debe existir una región rectangular $R$ en el mismo plano que encierra la región $D$, es decir, existe una región rectangular $R$ tal que $D$ es un subconjunto de $R (D \sube R)$.
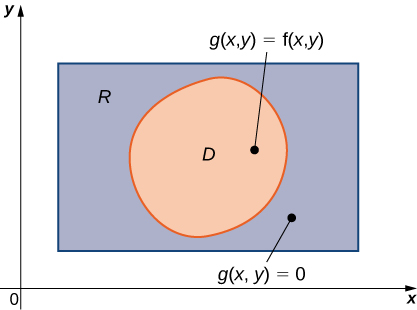
Figura 5.12. Para una región $D$ que es un subconjunto de $R$, podemos definir una función $g (x, y)$ para que sea igual a $f (x, y)$ en cada punto de $D$ y $0$ en cada punto de $R$ que no esté en $D$.
Supón que $z = f (x, y)$ se define en una región planar $D$ limitada general como en la figura 5.12. Para desarrollar integrales dobles de $f$ sobre $D$, ampliamos la definición de la función para incluir todos los puntos en la región rectangular $R$ y luego usamos los conceptos y herramientas de la sección anterior.
Pero, ¿cómo ampliamos la definición de $f$ para incluir todos los puntos en $R$? Hacemos esto definiendo una nueva función $g (x, y)$ en $R$ de la siguiente manera:
$$g(x, y) = \begin{cases} f(x, y) \text{ si } (x, y)\isin D\\ 0 \text{ si } (x, y)\isin R \text{ y } \cancel{\isin} D \end{cases}$$Ten en cuenta que podríamos tener algunas dificultades técnicas si el límite de $D$ es complicado. Por lo tanto, suponemos que el límite es una curva cerrada simple, suave y continua por partes. Además, dado que todos los resultados desarrollados en integrales dobles sobre regiones rectangulares utilizaron una función integrable $f (x, y)$, debemos tener cuidado con $g (x, y)$ y verificar que $g (x, y)$ sea una función integrable sobre la región rectangular $R$.
Esto sucede siempre que la región $D$ esté limitada por simples curvas cerradas. Por ahora nos concentraremos en las descripciones de las regiones en lugar de la función y ampliaremos nuestra teoría adecuadamente para la integración.
Consideramos dos tipos de regiones limitadas planas.
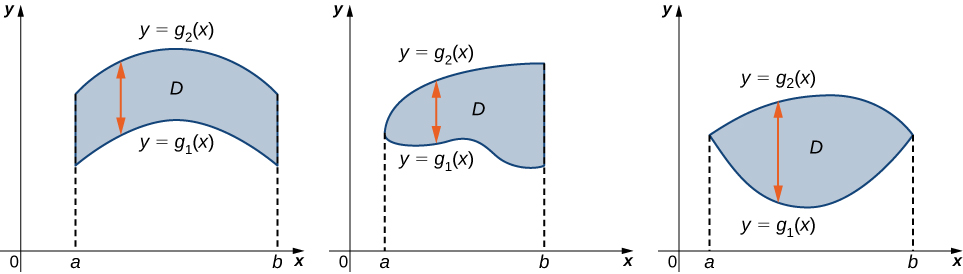
Figura 5.13. Una región de Tipo I se encuentra entre dos líneas verticales y las gráficas de dos funciones de $x$.

Figura 5.14. Una región de Tipo II se encuentra entre dos líneas horizontales y las gráficas de dos funciones de $y$.
 |
Describiendo una región como Tipo I y también como Tipo II |
Figura 5.15. La región D se puede describir como Tipo I o Tipo II.

Para desarrollar el concepto y las herramientas para la evaluación de una integral doble sobre una región general no rectangular, primero debemos entender la región y poder expresarla como Tipo I o Tipo II o una combinación de ambas. Sin comprender las regiones, no podremos decidir los límites de las integraciones en integrales dobles. Como primer paso, veamos el siguiente teorema
El lado derecho de esta ecuación es lo que hemos visto antes, por lo que este teorema es razonable porque $R$ es un rectángulo y $\iint_R g (x, y) dA$ se discutió en la sección anterior. Además, la igualdad funciona porque los valores de $g (x, y)$ son $0$ para cualquier punto $(x, y)$ que se encuentre fuera de $D$ y, por lo tanto, estos puntos no agregan nada a la integral. Sin embargo, es importante que el rectángulo $R$ contenga la región $D$.
De hecho, si la región $D$ está limitada por curvas suaves en un plano y podemos describirla como Tipo I o Tipo II o una combinación de ambas, entonces podemos usar el siguiente teorema y no tener que encontrar un rectángulo $R$ que contiene la región.
La integral en cada una de estas expresiones es una integral iterada, similar a las que hemos visto antes. Observa que, en la integral interna de la primera expresión, integramos $f (x, y)$ con $x$ siendo constante y los límites de integración son $g_1 (x)$ y $g_2 (x)$. En la integral interna en la segunda expresión, integramos $f (x, y)$ con $y $siendo constante y los límites de integración son $h_1 (y)$ y $h2 (y)$.
 |
Evaluación de una integral iterada sobre una región tipo I |

En el ejercicio anterior, podríamos haber observado la región de otra manera, como $D = \lbrace (x, y) | 0 \le y \le 1, 0 \le x \le 2y\rbrace$ (Figura 5.17).
Figura 5.17.
Esta es una región Tipo II y la integral se vería así
$$\iint_D x^2e^{xy}dA = \int_{y=0}^{y=1}\int_{x=0}^{x=2y}x^2e^{xy}dxdy$$Sin embargo, si integramos primero con respecto a $x$, esta integral es larga de calcular porque tenemos que usar la integración por partes dos veces.
 |
Evaluación de una integral iterada sobre una región tipo II |

Recordemos desde las integrales dobles sobre las regiones rectangulares las propiedades de las integrales dobles. Como hemos visto en los ejercicios aquí, todas estas propiedades también son válidas para una función definida en una región limitada no rectangular en un plano.
En particular, la propiedad 3 establece:
Si $R = S \cup T$ y $S \cap T = \empty$ excepto en sus límites, entonces
$$\iint_R f(x, y)dA = \iint_S f(x, y)dA + \iint_T f(x, y)dA$$Del mismo modo, tenemos la siguiente propiedad de integrales dobles sobre una región limitada no rectangular en un plano
Este teorema es particularmente útil para regiones no rectangulares porque nos permite dividir una región en una unión de regiones de Tipo I y Tipo II. Entonces podemos calcular la integral doble en cada pieza de una manera conveniente, como en el siguiente ejercicio.
 |
Descomposición de regiones |
Figura 5.19. Esta región se puede descomponer en una unión de tres regiones de Tipo I o Tipo II.

Como ya hemos visto, cuando evaluamos una integral iterada, a veces un orden de integración conduce a un cálculo que es significativamente más simple que el otro orden de integración. A veces, el orden de integración no importa, pero es importante aprender a reconocer cuándo un cambio en el orden simplificará nuestro trabajo.
Inicialmente, interactúa con la siguiente escena interactiva diseñada en GeoGebra por Kristen Beck, intercambiando el orden de integración:
A continuación, observa el siguiente ejercicio (puedes usar la escena anterior cambiando la función, pero en lugar de $e$, usa $2.7182$:
 |
Cambiando el orden de integración |

Ahora, observa este otro ejercicio:
 |
Evaluación de una integral iterada invirtiendo el orden de integración |

En la siguiente esecna interactiva diseñada por Elena Álvarez, se muestran ejemplos del cálculo de integrales dobles de funciones de dos variables definidas sobre dominios regulares, esto es, dominios que son verticalmente simples (barridos por franjas verticales) u horizontalmente simples (barridos por franjas horizontales). La función la hemos modificado, de acuerdo al ejercicio anterior.
Elegido el ejemplo, la escena permite representar las curvas que lo delimitan y describir el dominio como región horizontal o verticalmente simple.
Pulsando el botón Ver se muestra para cada ejemplo, la descripción del dominio según el tipo de franja elegida.
Pulsando sobre el botón Calcular se plantea la integral doble como integrales iteradas (los cálculos de las integrales se hacen a través de una comunicación entre DescartesJS y GeoGebra).
En el siguiente vídeo, puedes observar cómo se interactúa con la escena.
Podemos usar integrales dobles sobre regiones generales para calcular volúmenes, áreas y valores promedio.
Los métodos son los mismos que los de integrales dobles sobre regiones rectangulares, pero sin la restricción de una región rectangular, ahora podemos resolver una variedad más amplia de problemas.
 |
Encontrar el volumen de un tetraedro |

Encontrar el área de una región rectangular es fácil, pero encontrar el área de una región no rectangular no es tan fácil. Como hemos visto, podemos usar integrales dobles para encontrar un área rectangular. De hecho, esto es muy útil para encontrar el área de una región general no rectangular, como se indica en la siguiente definición.
Ya hemos visto cómo encontrar áreas en términos de integración única. Aquí estamos viendo otra forma de encontrar áreas mediante el uso de integrales dobles, que pueden ser muy útiles, como veremos en las secciones posteriores de este capítulo.
 |
Encontrar el área de una región |

También podemos usar una integral doble para encontrar el valor promedio de una función sobre una región general. La definición es una extensión directa de la fórmula anterior.

Figura 5.24. La región delimitada por $y = x^2$ e $y = 2x$.
 |
Encontrar un valor promedio |
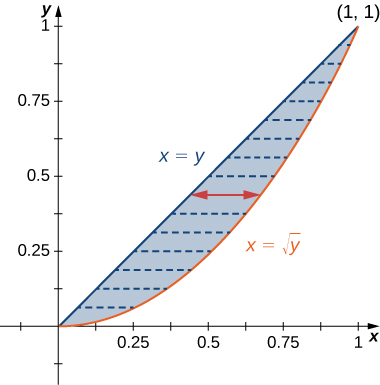
Figura 5.25. La región delimitada por $x = y$ y $x = \sqrt{y}$

Una integral doble impropia es una integral $iint_Df dA$ donde $D$ es una región ilimitada o $f$ es una función ilimitada. Por ejemplo, $D = \lbrace (x, y) || x - y | \ge 2\rbrace$ es una región ilimitada, y la función $f (x, y) = 1/(1 - x^2 - 2y^2$ sobre la elipse $x^2 + 3y^2 \le 1$ es una función ilimitada. Por lo tanto, las dos integrales siguientes son integrales impropias:
En esta sección, nos gustaría tratar con integrales impropias de funciones sobre rectángulos o regiones simples, de modo que $f$ solo tenga muchas discontinuidades finitas. No todas esas integrales impropias pueden ser evaluadas; sin embargo, una forma del teorema de Fubini se aplica a algunos tipos de integrales impropias.
Es muy importante tener en cuenta que requerimos que la función no sea negativa en $D$ para que el teorema funcione. Consideramos solo el caso en el que la función tiene muchas discontinuidades dentro de $D$.
 |
Evaluación de una integral doble impropia |

Como se mencionó anteriormente, también tenemos una integral impropia si la región de integración no tiene límites. Supongamos ahora que la función $f$ es continua en un rectángulo ilimitado $R$.
El siguiente ejercicio muestra cómo se puede usar este teorema en ciertos casos de integrales impropias.
 |
Evaluación de una integral doble impropia |

En algunas situaciones en la teoría de la probabilidad, podemos obtener información sobre un problema cuando podemos utilizar integrales dobles sobre regiones generales. Antes de repasar un ejercicio con una integral doble, necesitamos establecer algunas definiciones y familiarizarnos con algunas propiedades importantes.
 |
Aplicación a la probabilidad |

Otra aplicación importante en la probabilidad que puede involucrar integrales dobles impropias es el cálculo de los valores esperados. Primero definimos este concepto y luego mostramos un ejemplo de cálculo.
 |
Encontrar el valor esperado |


 En los siguientes ejercicios, especifique si la región es de Tipo I o Tipo II.
En los siguientes ejercicios, especifique si la región es de Tipo I o Tipo II.
60. La región $D$ delimitada por $y = x^3, y = x^3 + 1, x = 0$ y $x = 1$ como se muestra en la siguiente figura.
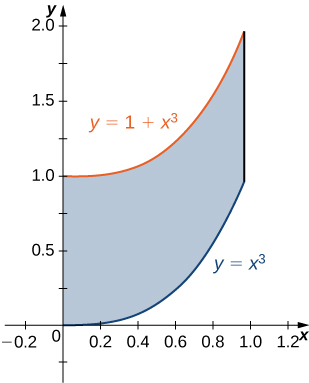
61. Encuentra el valor promedio de la función $f (x, y) = 3xy$ en la región graficada en el ejercicio anterior (Solución). 62. Encuentra el área de la región $D$ dada en el ejercicio anterior. 63. La región $D$ delimitada por $y = sen x, y = 1 + sen x, x = 0$ y $x = \frac{\pi}{2}$ como se muestra en la siguiente figura. (Solución).
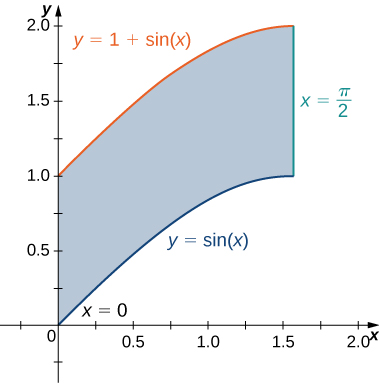
64. Encuentre el valor promedio de la función $f (x, y) = cos x$ en la región graficada en el ejercicio anterior.
65. Encuentre el área de la región $D$ dada en el ejercicio anterior (Solución).
66. La región $D$ delimitada por $x = y^2 - 1$ y $x = \sqrt{1 - y}$ como se muestra en la siguiente figura.
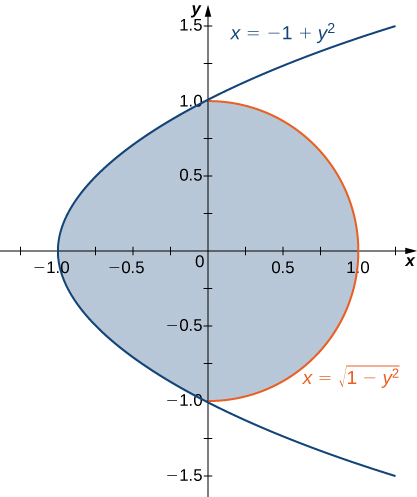 67. Encuentra el volumen del sólido debajo de la gráfica de la función $f (x, y) = xy + 1$ y arriba de la región en la figura del ejercicio anterior (Solución).
68. La región $D$ delimitada por $y = 0, x = −10 + y$ y $x = 10 - y$ como se muestra en la siguiente figura.
67. Encuentra el volumen del sólido debajo de la gráfica de la función $f (x, y) = xy + 1$ y arriba de la región en la figura del ejercicio anterior (Solución).
68. La región $D$ delimitada por $y = 0, x = −10 + y$ y $x = 10 - y$ como se muestra en la siguiente figura.
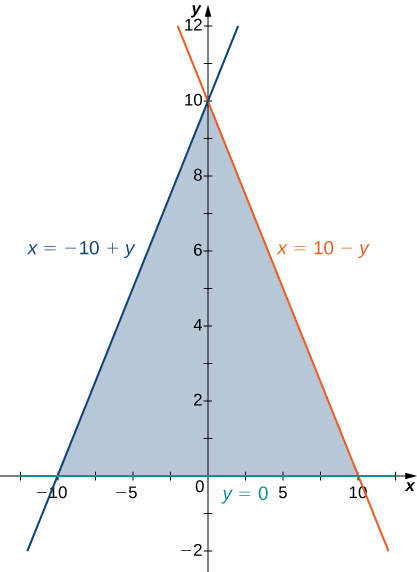
69. Encuentra el volumen del sólido debajo de la gráfica de la función $f (x, y) = x + y$ y arriba de la región en la figura del ejercicio anterior (Solución). 70. La región $D$ delimitada por $y = 0, x = y - 1, x = \frac{\pi}{2}$ como se muestra en la siguiente figura.
71. La región $D$ limitada por $y = 0$ e $y = x^2 - 1$ como dado en la siguiente figura (Solución).
 72. Sea $D$ la región limitada por las curvas de las ecuaciones $y = x, y = −x$ e $y = 2 - x^2$. Explica por qué $D$ no es de tipo I ni II
73. Sea $D$ la región limitada por las curvas de las ecuaciones $y = cos x$ e $y = 4 - x^2$ y el eje $x$. Explica por qué $D$ no es de tipo I ni II (Solución).
72. Sea $D$ la región limitada por las curvas de las ecuaciones $y = x, y = −x$ e $y = 2 - x^2$. Explica por qué $D$ no es de tipo I ni II
73. Sea $D$ la región limitada por las curvas de las ecuaciones $y = cos x$ e $y = 4 - x^2$ y el eje $x$. Explica por qué $D$ no es de tipo I ni II (Solución).
 En los siguientes ejercicios, evalúa la integral doble $\iint_Df (x, y) dA$ sobre la región $D$.
En los siguientes ejercicios, evalúa la integral doble $\iint_Df (x, y) dA$ sobre la región $D$.
74. $f(x, y) = 2x + 5y$ y $D = \lbrace (x, y)|0\le x \le 1, x^3\le y \le x^3+1\rbrace$ 75. $f(x, y) = 1$ y $D=\lbrace (x, y)|0\le x \le \frac{\pi}{2}, sen\;x\le y \le 1+sen\;x\rbrace$ (Solución). 76. $f(x, y) = 2$ y $D = \lbrace (x, y)|0\le y \le 1, y-1\le x \le arccos\;y\rbrace$
77. $f(x, y) = xy$ y $D=\lbrace (x, y)|-1\le y \le 1, y^2-1\le x \le \sqrt{1-y^2}\rbrace$ (Solución). 78. $f (x, y) = sen y$ y $D$ es la región triangular con vértices $(0, 0), (0, 3)$ y $(3, 0)$. 79. $f(x, y) = -x+1$ y $D$ es la región triangular con vértices $(0, 0), (0, 2)$, y $(2, 2)$ (Solución).
 Evalúa las integrales iteradas.
Evalúa las integrales iteradas.
80. $\displaystyle\int_0^1\int_{2x}^{3x}(x+y^2)dydx$. 81. $\displaystyle\int_0^1\int_{2\sqrt{x}}^{2\sqrt{x}+1}(xy+1)dydx$ (Solución). 82. $\displaystyle\int_e^{e^2}\int_{ln\;u}^{2}(v+ln\;u)dvdu$. 83. $\displaystyle\int_1^2\int_{-u^2-1}^{-u}(8uv)dvdu$ (Solución). 84. $\displaystyle\int_0^{1}\int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}}(2x+4x^3)dxdy$. 85. $\displaystyle\int_0^{1/2}\int_{-\sqrt{1-4y^2}}^{\sqrt{1-4y^2}}4dxdy$ (Solución). 86. Sea $D$ la región limitada por $y = 1 - x^2, y = 4 - x^2$, y los ejes $x$ e $y$
87. Sea $D$ la región limitada por $y = 1, y = x, y=ln\;x$, y el eje $x$
89. Sea $D$ la región limitada por $y = x^2, y = x+2$, y $y=-x$
90. La región $D$ limitada por $x = 0, y = x^5 + 1$, y $y = 3 - x^2$ se muestra en la siguiente figura. Encuentrael área $A (D)$ de la región $D$
91. La región $D$ delimitada por $y = cos x, y = 4 cos x$, y $x = \pm \frac{\pi}{3}$ se muestra en la siguiente figura. Encuentra el área $A (D)$ de la región $D$ (Solución).
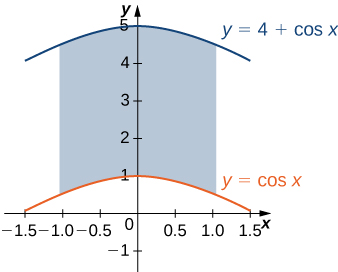
92. Encuentra el área $A (D)$ de la región $D = \lbrace (x, y) | y \ge 1 - x^2, y \le 4 - x^2, y \ge 0, x\ge 0\rbrace$.
93. Sea $D$ la región limitada por $y = 1, y = x, y = ln\; x$, y el eje $x$. Encuentra el área $A (D)$ de la región $D$ (Solución).
94. Encuentra el valor promedio de la función $f (x, y) = sen\; y$ en la región triangular con vértices $(0, 0), (0, 3)$ y $(3, 0)$.
95. Encuentra el valor promedio de la función $f (x, y) = −x + 1$ en la región triangular con vértices $(0, 0), (0, 2)$ y $(2, 2)$ (Solución).
 En los siguientes ejercicios, cambia el orden de integración y evalúa la integral.
En los siguientes ejercicios, cambia el orden de integración y evalúa la integral.
96. $\displaystyle\int_{-1}^{\pi /2}\int_{0}^{x+1}sen\;xdydx$ 97. $\displaystyle\int_{0}^{1}\int_{x-1}^{1-x}xdydx$ (Solución). 98. $\displaystyle\int_{-1}^{0}\int_{-\sqrt{y+1}}^{\sqrt{y+1}}sen\;y^2dxdy$ 99. $\displaystyle\int_{-1/2}^{1/2}\int_{-\sqrt{y^2+1}}^{\sqrt{y^2+1}}ydxdy$ (Solución).
100. La región $D$ se muestra en la siguiente figura. Evalúa la integral doble $\displaystyle\iint_D(x^2 + y)dA$ utilizando el orden más fácil de integración.
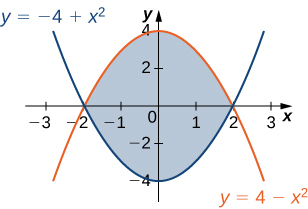
101. La región $D$ se da en la siguiente figura. Evalúa la integral doble $\displaystyle\iint_D(x^2 - y^2)dA$ utilizando el orden más fácil de integración (Solución).
102. Encuentra el volumen del sólido debajo de la superficie $z = 2x + y^2$ y por encima de la región delimitada por $y = x^5$ e $y = x$.
103. Encuentra el volumen del sólido debajo del plano $z = 3x + y$ y por encima de la región determinada por $y = x^7$ e $y = x$ (Solución).
104. Encuentra el volumen del sólido debajo del plano $z = x - y$ y por encima de la región delimitada por $x = tan\; y, x = −tan\; y$ y $x = 1$.
105. Encuentra el volumen del sólido debajo de la superficie $z = x^3$ y por encima de la región plana limitada por $x = sen\; y, x = −sen\; y$, y $x = 1$ (Solución).
106. Sea $g$ una función positiva, creciente y diferenciable en el intervalo $[a, b]$. Demuestra que el volumen del sólido debajo de la superficie $z = g^{\prime}(x)$ y por encima de la región limitada por $y = 0, y = g (x), x = a$, y $x = b $viene dado por $\frac12\big(g^2 (b) - g^2 (a)\big)$
107. Sea $g$ una función positiva, creciente y diferenciable en el intervalo $[a, b]$, y sea $k$ un número real positivo. Demuestra que el volumen del sólido debajo de la superficie $z = g^{\prime}(x)$ y por encima de la región limitada por $y = g (x), y = g (x) + k, x = a$, y $x = b$ viene dado por $k(g (b) - g (a))$.
108. Encuentra el volumen del sólido situado en el primer octante y determinado por los planos $z = 2, z = 0, x + y = 1, x = 0$ e $y = 0$. 109. Encuentra el volumen del sólido situado en el primer octante y delimitado por los planos $x + 2y = 1, x = 0, y = 0, z = 4$ y $z = 0$ (Solución). 110. Encuentra el volumen del sólido delimitado por los planos $x + y = 1, x - y = 1, x = 0, z = 0$ y $z = 10$. 111. Encuentra el volumen del sólido delimitado por los planos $x + y = 1, x - y = 1, x + y = −1, x - y = −1, z = 1$ y $z = 0$ (Solución).
112. Sean $S_1$ y $S_2$ los sólidos situados en el primer octante bajo los planos $x + y + z = 1$ y $x + y + 2z = 1$, respectivamente, y sea $S$ el sólido situado entre $S_1, S_2, x = 0$, y $y = 0$.
113. Sean $S_1$ y $S_2$ los sólidos situados en el primer octante bajo los planos $2x + 2y + z = 2$ y $x + y + z = 1$, respectivamente, y sea $S $el sólido situado entre $S_1, S_2, x = 0$, y $y = 0$.
114. Sean $S_1$ y $S_2$ los sólidos situados en el primer octante debajo del plano $x + y + z = 2$ y debajo de la esfera $x^2 + y^2 + z^2 = 4$, respectivamente. Si el volumen del sólido $S_2$ es $\frac{4\pi}{3}$, determina el volumen del sólido $S $situado entre $S_1$ y $S_2$ restando los volúmenes de estos sólidos.
115. Sean $S_1$ y $S_2$ los sólidos situados en el primer octante bajo el plano $x + y + z = 2$ y delimitados por el cilindro $x^2 + y^2 = 4$, respectivamente.
116. [T] La siguiente figura muestra la región $D$ delimitada por las curvas $y = sen\; x, x = 0$ e $y = x^4$. Usa una calculadora gráfica o CAS para encontrar las coordenadas $x$ de los puntos de intersección de las curvas y para determinar el área de la región $D$. Redondea tus respuestas a seis decimales.
117. [T] La región $D$ delimitada por las curvas $y = cos\; x, x = 0$ e $y = x^3$ se muestra en la siguiente figura. Usa una calculadora gráfica o CAS para encontrar las coordenadas $x$ de los puntos de intersección de las curvas y para determinar el área de la región $D$. Redondea tus respuestas a seis decimales (Solución).
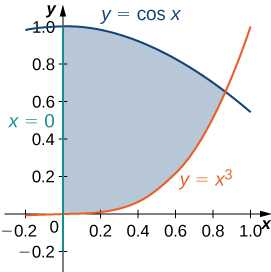
118. Supón que $(X, Y)$ es el resultado de un experimento que debe ocurrir en una región particular $S$ en el plano $xy$. En este contexto, la región $S$ se denomina espacio muestral del experimento y $X$ e $Y$ son variables aleatorias. Si $D$ es una región incluida en $S$, entonces la probabilidad de que $(X, Y)$ esté en $D$ se define como $P [(X, Y) \isin D] = \iint_Dp (x, y) dx dy$, donde $p (x, y)$ es la densidad de probabilidad conjunta del experimento. Aquí, $p (x, y)$ es una función no negativa para la cual $\iint_Sp (x, y) dx dy = 1$. Supón que un punto $(X, Y)$ se elige arbitrariamente en el cuadrado $[0, 3] \times [0, 3]$ con la densidad de probabilidad $$p(x, y) = \begin{cases} \frac19 &(x, y) \isin [0, 3] \times [0, 3] \\ 0 &\text{si no pertenece} \end{cases}$$ Encuentra la probabilidad de que el punto $(X, Y)$ esté dentro del cuadrado de la unidad e interpreta el resultado.
119. Considera $X$ e $Y$ dos variables aleatorias de densidades de probabilidad $p_1 (x)$ y $p_2 (x)$, respectivamente. Se dice que las variables aleatorias $X$ e $Y$ son independientes si su función de densidad conjunta está dada por$ p (x, y) = p_1 (x) p_2 (y)$. En un restaurante de autoservicio, los clientes pasan, en promedio, $3$ minutos haciendo sus pedidos y $5$ minutos adicionales pagando y recogiendo sus comidas. Supongamos que realiza el pedido y paga por/recoger la comida son dos eventos independientes $X$ e Y$. Si los tiempos de espera están modelados por las densidades de probabilidad exponencial $$p_1(x) = \begin{cases} \frac13e^{-x/3} & x\ge 0 \\ 0 &\text{otro caso} \end{cases}$$ y $$p_2(y) = \begin{cases} \frac15e^{-y/5} & y\ge 0 \\ 0 &\text{otro caso} \end{cases}$$ respectivamente, la probabilidad de que un cliente pase menos de $6$ minutos en la línea de autoservicio viene dada por $P [X + Y \le 6] = \iint_Dp (x, y) dx dy$, donde $D = \lbrace (x, y) | x \ge 0, y \ge 0, x + y \le 6\rbrace$. Encuentra $P [X + Y \le 6]$ e interpreta el resultado (Solución).
120. [T] El triángulo Reuleaux consiste en un triángulo equilátero y tres regiones, cada una de ellas delimitada por un lado del triángulo y un arco de un círculo de radio $s$ centrado en el vértice opuesto del triángulo. Demuestra que el área del triángulo Reuleaux en la siguiente figura de longitud lateral $s$ es $\frac{s^2}{2}(\pi - \sqrt{3})$.
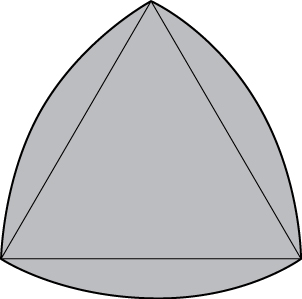
121. [T] Demuestra que el área de las lunas de Alhazen, los dos lunas azules en la siguiente figura, es el mismo que el área del triángulo rectángulo $ABC$. Los límites exteriores de las lunas son semicírculos de diámetros $AB$ y $AC$, respectivamente, y los límites interiores están formados por el círculo del triángulo $ABC$.
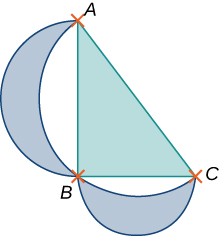
Las integrales dobles a veces son mucho más fáciles de evaluar si cambiamos las coordenadas rectangulares a coordenadas polares. Sin embargo, antes de describir cómo hacer este cambio, necesitamos establecer el concepto de una integral doble en una región rectangular polar.
Cuando definimos la integral doble para una función continua en coordenadas rectangulares, por ejemplo, $g$ sobre una región $R$ en el plano $xy$, dividimos $R$ en subreglangulos con lados paralelos a los ejes de coordenadas. Estos lados tienen valores $x$ constantes y/o valores $y$ constantes. En coordenadas polares, la forma con la que trabajamos es un rectángulo polar, cuyos lados tienen valores $r$ constantes y/o valores $\theta$ constantes. Esto significa que podemos describir un rectángulo polar como en la (Figura 5.28(a)), con $R = \lbrace (r, \theta) | a \le r \le b, \alpha \le \theta \le \beta\rbrace$.
En esta sección, buscamos integrar sobre rectángulos polares. Considera una función $f (r, \theta)$ sobre un rectángulo polar $R$. Dividimos el intervalo $[a, b]$ en $m$ subintervalos $[r_{i - 1}, r_i]$ de longitud $\Delta r = (b - a) / m$ y dividimos el intervalo $[\alpha, \beta]$ en $n$ subintervalos $[\theta_{i - 1}, \theta_i]$ de ancho $\Delta \theta = (\beta - \alpha) / n$. Esto significa que los círculos $r = r_i$ y los rayos $\theta = \theta_i$ para $1 \le i \le m$ y $1 \le j \le n$ dividen el rectángulo polar $R$ en subrectangulos polares más pequeños $R_{ij}$ (Figura 5.28(b)).

Figura 5.28. (a) Un rectángulo polar $R$ (b) dividido en subrectángulos $R_{ij}$. (c) Primer plano de un subrectangulo.
Como antes, necesitamos encontrar el área $\Delta A$ del subrectangulo polar $R_{ij}$ y el volumen “polar” de la caja delgada sobre $R_{ij}$. Recuerda que, en un círculo de radio $r$, la longitud $s$ de un arco subtendido por un ángulo central de $\theta$ radianes es $s = r\theta$. Observa que el rectángulo polar $R_{ij}$ se parece mucho a un trapezoide con lados paralelos $r_{i - 1}\Delta \theta$ y $r_i \Delta \theta$ y con un ancho $\Delta r$. Por tanto, el área del subrectangulo polar $R_{ij}$ es
$$\Delta A = \frac12 \Delta r(r_{i - 1}\Delta \theta + r_1\Delta \theta)$$Simplificando y dejando $r_{ij}^* = \frac12 (r_{i - 1} + r_i)$, tenemos $\Delta A = r_{ij}^*\Delta r\Delta \theta$. Por lo tanto, el volumen polar de la caja delgada sobre $R_{ij}$ se muestra en la figura 5.29.
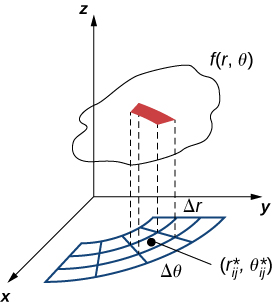
Figura 5.29. Hallando el volumen de la caja delgada sobre el rectángulo polar $R_{ij}$.
Usando la misma idea para todos los subrectangulos y sumando los volúmenes de las cajas rectangulares, obtenemos una suma doble de Riemann como
$$\sum_{i=1}^m\sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*)r_{ij}^*\Delta r\Delta\theta$$Como hemos visto antes, obtenemos una mejor aproximación al volumen polar del sólido por encima de la región $R$ cuando dejamos que $m$ y $n$ se hagan más grandes. Por lo tanto, definimos el volumen polar como el límite de la suma doble de Riemann
$$V = \lim\limits_{m,n \to \infin}\sum_{i=1}^m\sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*)r_{ij}^*\Delta r\Delta\theta$$Esto se convierte en la expresión de la integral doble.
Nuevamente, al igual que en las integrales dobles sobre regiones rectangulares, la integral doble sobre una región rectangular polar puede expresarse como una integral iterada en coordenadas polares. Por lo tanto,
$$\iint_Rf (r, \theta)dA = \iint_Rf(r, \theta)r dr d\theta = \int_{\theta = \alpha}^{\theta = \beta}\int_{r=a}^{r=b}f(r, \theta)r dr d\theta$$Observa que la expresión para $dA$ se reemplaza por $r dr d\theta$ cuando se trabaja en coordenadas polares. Otra forma de ver la integral doble polar es cambiar la integral doble en coordenadas rectangulares por sustitución. Cuando la función $f$ se da en términos de $x$ e $y$, usando $x = r cos \theta, y = r sen \theta$, y $dA = r dr d\theta$ la cambia a
$$\iint_Rf (x, y)dA = \iint_R f(r cos \theta, r sen \theta)r dr d\theta$$Ten en cuenta que todas las propiedades enumeradas en Integrales dobles sobre regiones rectangulares para la integral doble en coordenadas rectangulares también son válidas para la integral doble en coordenadas polares, por lo que podemos usarlas sin dudarlo.
 |
Dibujar una región polar |

Ahora que hemos esbozado una región polar, demostremos cómo evaluar una integral doble sobre esta región mediante el uso de coordenadas polares.
 |
Evaluación de una integral doble sobre una región polar |

 |
Evaluación de una integral doble mediante la conversión de coordenadas rectangulares |

 |
Evaluación de una integral doble mediante la conversión de coordenadas rectangulares |

Para evaluar la integral doble de una función continua mediante integrales iteradas sobre regiones polares generales, consideramos dos tipos de regiones, análogas a Tipo I y Tipo II como se discutió para coordenadas rectangulares en Integrales dobles sobre regiones generales.
Es más común escribir ecuaciones polares como $r = f (\theta)$ que $\theta = f (r)$, por lo que describimos una región polar general como $R = \lbrace (r, \theta) | \alpha \le \theta \le \beta, h_1 (\theta) \le r \le h_2 (\theta)$ (ver la siguiente figura).
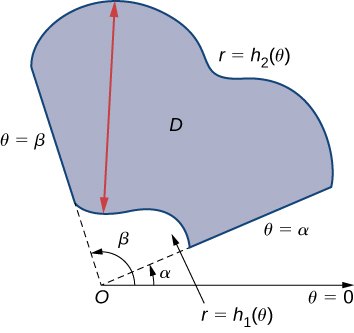
Figura 5.32. Una región polar general entre $\alpha \lt\theta\lt\beta$ y $h_1 (\theta) \lt r \lt h_2 (\theta)$.
 |
Evaluación de una integral doble sobre una región polar general |

Terminamos este apartado con una escena interactiva diseñada por Elena Álvarez. En esta escena se muestran ejemplos del cálculo de integrales dobles de funciones de dos variables definidas sobre dominios que pueden expresarse utilizando coordenadas polares (observa, inicialmente, el vídeo de cómo se puede interactuar).
Como en las coordenadas rectangulares, si un sólido $S$ está limitado por la superficie $z = f (r, \theta)$, así como por las superficies $r = a, r = b, \theta = \alpha$ y $\theta = \beta$, podemos encontrar el volumen $V$ de $S$ por doble integración, como
$$V = \iint_Rf(r, \theta)r dr d\theta = \int_{\theta = \alpha}^{\theta = \beta}\int_{r=a}^{r=b}f(r, \theta)r dr d\theta$$Si la base del sólido se puede describir como $D = \lbrace (r, \theta) | \alpha \le \theta \le \beta, h_1 (\theta) \le r\le h_2 (\theta)$, entonces la integral doble para el volumen se convierte en
Ilustramos esta idea con algunos ejercicios.
 |
Encontrar un volumen usando una integral doble |
Figura 5.34. El paraboloide $z = 1 - x^2 - y^2$

 |
Encontrar un volumen usando una integral doble |
Figura 5.35. Encontrar el volumen de un sólido con una tapa paraboloide y una base circular.

Observa en el siguiente ejercicio que la integración no siempre es fácil con coordenadas polares. La complejidad de la integración depende de la función y también de la región sobre la que necesitamos realizar la integración. Si la región tiene una expresión más natural en coordenadas polares o si $f$ tiene una antiderivada más simple en coordenadas polares, entonces el cambio en las coordenadas polares es apropiado; de lo contrario, usa coordenadas rectangulares.
 |
Encontrar un volumen usando una integral doble |

Para responder a la pregunta de cómo se encuentran las fórmulas para los volúmenes de diferentes sólidos estándar, como una esfera, un cono o un cilindro, queremos demostrar un ejemplo y encontrar el volumen de un cono arbitrario.
 |
Encontrar un volumen usando una integral doble |

Al igual que con las coordenadas rectangulares, también podemos usar coordenadas polares para encontrar áreas de ciertas regiones usando una integral doble. Como antes, necesitamos entender la región cuya área queremos calcular. Dibujar un gráfico e identificar la región puede ser útil para darte cuenta de los límites de la integración. En general, la fórmula del área en doble integración se verá como
$$\text{Área } A = \int_{\alpha}^{\beta}\int_{h1(\theta)}^{h2(\theta)}1rdrd\theta$$ |
Encontrar un área usando una integral doble en coordenadas polares |

 |
Encontrar el área entre dos curvas polares |

 |
Evaluación de una integral doble impropia en coordenadas polares |


 En los siguientes ejercicios, exprese la región $D$ en coordenadas polares.
En los siguientes ejercicios, exprese la región $D$ en coordenadas polares.
122. $D$ es la región del disco de radio $2$ centrada en el origen que se encuentra en el primer cuadrante. 123. $D$ es la región entre los círculos de radio $4$ y radio $5 $centrada en el origen que se encuentra en el segundo cuadrante (Solución). 124. $D$ es la región limitada por el eje $y$ y $x=\sqrt{1-y^2}$ 125. $D$ es la región limitada por el eje $x$ y $y=\sqrt{2-x^2}$ (Solución). 126. $D = \lbrace (x, y)|x^2 + y^2 \le 4x\rbrace$ 127. $D = \lbrace (x, y)|x^2 + y^2 \le 4y\rbrace$ (Solución).
 En los siguientes ejercicios, se muestra la gráfica de la región polar $D$. Expresa $D$ en coordenadas polares.
En los siguientes ejercicios, se muestra la gráfica de la región polar $D$. Expresa $D$ en coordenadas polares.
128.
 129. (Solución)
129. (Solución)
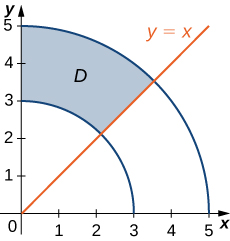 130.
130.
131. (Solución)
 132. En el siguiente gráfico, la región $D $está situada debajo de $y = x $y está limitada por $x = 1, x = 5$ e $y = 0$.
132. En el siguiente gráfico, la región $D $está situada debajo de $y = x $y está limitada por $x = 1, x = 5$ e $y = 0$.
 133. En el siguiente gráfico, la región $D$ está limitada por $y = x$ e $y = x^2$ (Solución)
133. En el siguiente gráfico, la región $D$ está limitada por $y = x$ e $y = x^2$ (Solución)
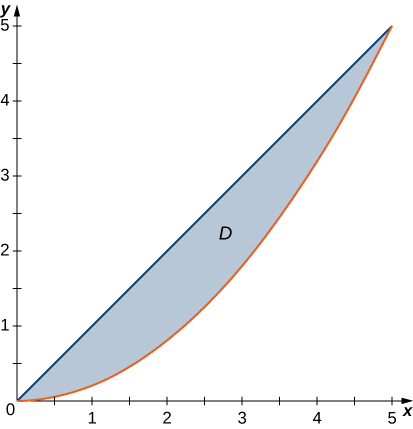
 En los siguientes ejercicios, evalúa la integral doble $\displaystyle\iint_Rf (x, y) dA$ sobre la región rectangular polar $D$.
En los siguientes ejercicios, evalúa la integral doble $\displaystyle\iint_Rf (x, y) dA$ sobre la región rectangular polar $D$.
134. $f(x, y) = x^2 + y^2, D = \lbrace (r, \theta)|3 \le r \le 5, 0 \le \theta \le 2\pi\rbrace$ 135. $f(x, y) = x+y, D = \lbrace (r, \theta)|3 \le r \le 5, 0 \le \theta \le 2\pi\rbrace$ (Solución) 136. $f(x, y) = x^2 + xy, D = \lbrace (r, \theta)|1 \le r \le 2, \pi \le \theta \le 2\pi\rbrace$ 137. $f(x, y) = x^4+y^4, D = \lbrace (r, \theta)|1 \le r \le 2, \frac{3\pi}{2} \le \theta \le 2\pi\rbrace$ (Solución) 138. $f(x, y) = x\sqrt[3]{x^2+y^2}, D = \lbrace (r, \theta)|0 \le r \le 1, \frac{\pi}{2} \le \theta \le \pi\rbrace$ 139. $f(x, y) = x^4+2x^2y^2+y^4$, $D = \lbrace (r, \theta)|3 \le r \le 4, \frac{\pi}{3} \le \theta \le \frac{2\pi}{3}\rbrace$ (Solución) 140. $f(x, y) = sen\bigg(arctan\frac{y}{x}\bigg)$, $D = \lbrace (r, \theta)|1 \le r \le 2, \frac{\pi}{6} \le \theta \le \frac{\pi}{3}\rbrace$
141. $f(x, y) = arctan\bigg(\frac{y}{x}\bigg), D = \lbrace (r, \theta)|2 \le r \le 3, \frac{\pi}{4} \le \theta \le \frac{\pi}{3}\rbrace$ (Solución) 142. $f(x, y) = \iint_De^{x^2+y^2}\bigg[1 + 2arctan\frac{y}{x}\bigg]dA$, $D = \lbrace (r, \theta)|1 \le r \le 2, \frac{\pi}{6} \le \theta \le \frac{\pi}{3}\rbrace$ 143. $f(x, y) = \iint_D\bigg(e^{x^2+y^2} + x^4+2x^2y^2+y^4\bigg)arctan\big(\frac{y}{x}\big)$, $D = \lbrace (r, \theta)|1 \le r \le 2, \frac{\pi}{4} \le \theta \le \frac{\pi}{3}\rbrace$ (Solución)
 En los siguientes ejercicios, las integrales se han convertido a coordenadas polares. Verifica que las identidades sean verdaderas y elige la forma más fácil de evaluar las integrales, en coordenadas rectangulares o polares.
En los siguientes ejercicios, las integrales se han convertido a coordenadas polares. Verifica que las identidades sean verdaderas y elige la forma más fácil de evaluar las integrales, en coordenadas rectangulares o polares.
144. $\displaystyle\int_1^2\int_0^x\big(x^2+y^2\big)dydx = \int_0^{\pi /4}\int_{sec\theta}^{2sec\theta}r^3drd\theta$ 145. $\displaystyle\int_2^3\int_0^x\frac{x}{\sqrt{x^2+y^2}}dydx = \int_0^{\pi /4}\int_{0}^{tan\theta sec\theta}rcos\theta drd\theta$ (Solución) 146. $\displaystyle\int_0^1\int_{x^2}^x\frac{1}{\sqrt{x^2+y^2}}dydx = \int_0^{\pi /4}\int_{0}^{tan\theta sec\theta}drd\theta$ 147. $\displaystyle\int_0^1\int_{x^2}^x\frac{y}{\sqrt{x^2+y^2}}dydx = \int_0^{\pi /4}\int_{0}^{tan\theta sec\theta}rsen\theta drd\theta$ (Solución)
 En los siguientes ejercicios, convierte las integrales a coordenadas polares y evalúalas.
En los siguientes ejercicios, convierte las integrales a coordenadas polares y evalúalas.
148. $\displaystyle\int_0^3 \int_0^{\sqrt{9-y^2}}\big(x^2+y^2\big)dxdy$ 149. $\displaystyle\int_0^2 \int_{-\sqrt{4-y^2}}^{\sqrt{4-y^2}}\big(x^2+y^2\big)^2dxdy$ (Solución) 150. $\displaystyle\int_0^1 \int_0^{\sqrt{1-x^2}}(x+y)dydx$ 151. $\displaystyle\int_0^4 \int_{-\sqrt{16-x^2}}^{\sqrt{16-x^2}}sen\big(x^2+y^2\big)^2dydx$ (Solución)
152. Evalúa la integral $\iint_Dr dA$ donde $D$ es la región limitada por el eje polar y la mitad superior del cardioide $r = 1 + cos \theta$.
153. Encuentra el área de la región $D$ limitada por el eje polar y la mitad superior del cardioide $r = 1 + cos \theta$ (Solución)
154. Evalúa la integral $\iint_Dr dA$, donde $D$ es la región delimitada por la parte de la rosa de cuatro hojas $r = sen 2\theta$ situada en el primer cuadrante (ver la siguiente figura).
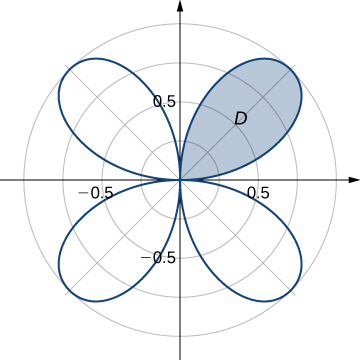
155. . Halla el área total de la región encerrada por la rosa de cuatro hojas $r = sen 2\theta (observa la figura del ejercicio anterior) (Solución)
156. Encuentra el área de la región $D$, que es la región delimitada por $y = \sqrt{4 - x^2}, x = \sqrt{3}, x = 2$ e $y = 0$.
157. Encuentra el área de la región $D$, que es la región dentro del disco $x^2 + y^2 \le 4$ y a la derecha de la línea $x = 1$ (Solución)
158. Determina el valor promedio de la función $f (x, y) = x^2 + y^2$ sobre la región $D$ limitada por la curva polar $r = cos 2\theta$, donde $−\frac{\pi}{4} \le \theta \le \frac{\pi}{4}$ (ver el siguiente gráfico).
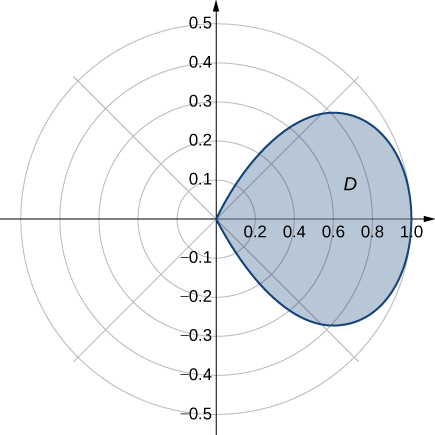
159. Determina el valor promedio de la función $f (x, y) = x^2 + y^2$ sobre la región $D$ limitada por la curva polar $r = 3 sen 2\theta$, donde $0 \le \theta \le \frac{\pi}{2}$ (ver el siguiente gráfico) (Solución)
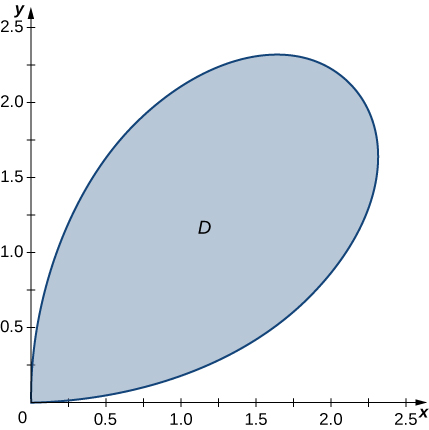
160. Encuentra el volumen del sólido situado en el primer octante y delimitado por el paraboloide $z = 1 - 4x^2 - 4y^2$ y los planos $x = 0, y = 0$ y $z = 0$.
161. Halla el volumen del sólido delimitado por el paraboloide $z = 2 - 9x^2 - 9y^2$ y el plano $z = 1$ (Solución)
162.
163.
 Para los dos ejercicios siguientes, considera un anillo esférico, que es una esfera con un orificio cilíndrico cortado de modo que el eje del cilindro pase por el centro de la esfera (consulte la siguiente figura).
Para los dos ejercicios siguientes, considera un anillo esférico, que es una esfera con un orificio cilíndrico cortado de modo que el eje del cilindro pase por el centro de la esfera (consulte la siguiente figura).

164. Si la esfera tiene radio $4$ y el cilindro tiene radio $2$, encuentra el volumen del anillo esférico. 165. Se perfora un agujero cilíndrico de $6\; cm$ de diámetro en una esfera de $5\; cm$ de radio tal que el eje del cilindro pasa por el centro de la esfera. Encuentra el volumen de el anillo esférico resultante (Solución)
166. Encuentra el volumen del sólido que se encuentra debajo del cono doble $z^2 = 4x^2 + 4y^2$, dentro del cilindro $x^2 + y^2 = x$, y sobre el plano $z = 0$. 167. Encuentra el volumen del sólido que se encuentra debajo del paraboloide $z = x^2 + y^2$, dentro del cilindro $x^2 + y^2 = x$, y por encima del plano $z = 0$ (Solución) 168. Encuentra el volumen del sólido que se encuentra debajo del plano $x + y + z = 10$ y por encima del disco $x^2 + y^2 = 4x$. 169. Encuentra el volumen del sólido que se encuentra debajo del plano $2x + y + 2z = 8$ y sobre el disco unitario $x^2 + y^2 = 1$ (Solución) 170. Una función radial $f$ es una función cuyo valor en cada punto depende únicamente de la distancia entre ese punto y el origen del sistema de coordenadas; es decir, $f (x, y) = g (r)$, donde $r = \sqrt{x^2 + y^2}$. Demuestra que si $f$ es una función radial continua, entonces $\iint_Df (x, y) dA = (\theta_2 - \theta_1)[G (R_2) - G (R_1)]$, donde $G^{\prime}(r) = rg (r)$ y $(x, y) \isin D = \lbrace (r, \theta) | R_1 \le r \le R_2, 0 \le \theta \le 2\pi\rbrace$, con $0 \le R_1 \lt R_2$ y $0 \le \theta_1 \lt\theta_2 \le 2\pi$. 171. Usa la información del ejercicio anterior para calcular la integral $\iint_D\big(x^2 + y^2\big)^3dA$, donde $D$ es el disco unitario (Solución) 172. Sea $f (x, y) = \frac{F^{\prime}(r)}{r}$ una función radial continua definida en la región anular $D = \lbrace (r, \theta) | R_1 \le r \le R_2, 0 \le \theta \le 2\pi\rbrace$, donde $r = \sqrt{x^2 + y^2}, 0 \lt R_1 \lt R_2$ y $F$ es una función diferenciable. Demuestra que $\iint_Df (x, y) dA = 2\pi [F (R_2) - F (R_1)]$. 173. Aplica el ejercicio anterior para calcular la integral $\iint_D\frac{e^{\sqrt{x^2 + y^2}}}{\sqrt{x^2 + y^2}} dx dy$, donde $D$ es la región anular entre los círculos de radios $1$ y $2$ situados en el tercer cuadrante (Solución)
174. Sea $f$ una función continua que se puede expresar en coordenadas polares en función de $\theta$ solamente; es decir, $f (x, y) = h (\theta)$, donde $(x, y) \isin D = \lbrace (r, \theta) | R_1 \le r \le R_2, \theta1 \le \theta \le \theta_2\rbrace$, con $0 \le R_1 \lt R_2 y 0 \le \theta_1 \lt \theta_2 ≤ 2\pi\rbrace$. Demuestra que $\iint_Df (x, y) dA = \frac12\big(R_2^2 - R_1^2\big)[H (\theta_2) - H (\theta_1)]$, donde $H$ es una antiderivada de $h$.
175. Aplica el ejercicio anterior para calcular la integral $\iint_D\frac{y^2}{x^2}dA$, donde $D = \big\lbrace (r, \theta) | 1 \le r \le 2, \frac{\pi}{6}\le \theta \le\frac{\pi}{3}\big\rbrace$ (Solución)
176. Sea $f$ una función continua que se puede expresar en coordenadas polares en función de $\theta$ solamente; es decir, $f (x, y) = g (r) h (\theta)$, donde $(x, y) \isin D = \lbrace(r, \theta) | R_1 \le r \le R_2, \theta1 \le \theta \le \theta2\rbrace$ con $0 \le R_1 \lt R_2$ y $0 \le \theta:1 \lt\theta:2 \le 2\pi$. Demuestra que $\iint_Df (x, y) dA = [G (R_2) - G (R_1)][ H (\theta_2) - H (\theta_1)]$, donde $G$ y $H$ son antiderivadas de $g$ y $h$, respectivamente.
177. Evalúa $\iint_Darctan \big(\frac{y}{x}\big)\sqrt{x^2 + y^2}dA$, donde $D = \big\lbrace (r, \theta) | 2 \le r \le 3, \frac{\pi}{4}\le \theta \le\frac{\pi}{3}\big\rbrace$ (Solución)
178. Un casquete esférico es la región de una esfera que se encuentra por encima o por debajo de un plano dado.
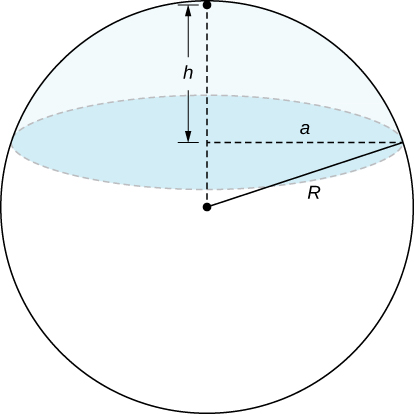
179. En estadística, la densidad conjunta de dos eventos independientes distribuidos normalmente con una media $\mu = 0$ y una distribución estándar $\sigma$ se define mediante $p (x, y) = \frac{1}{2π\sigma^2}e^{-\frac{x^2 + y^2}{2\sigma^2}}$. Considera $(X, Y)$, las coordenadas cartesianas de una bola en la posición de reposo después de que se soltó desde una posición en el eje $z$ hacia el plano $xy$.
Supón que las coordenadas de la pelota se distribuyen normalmente de forma independiente con una media $\mu = 0$ y una desviación estándar de $\sigma$ (en pies). La probabilidad de que la bola se detenga a no más de un pie del origen está dada por $P[X^2 + Y^2]\le a^2] = \iint_Dp (x, y) dy dx$, donde $D$ es el disco de radio $a$ centrado en el origen. Demuestra que $P[X^2 + Y^2\le a^2] = 1 − e^{− a^2 / 2\sigma^2}$.
180. La integral doble impropia $\int_{-\infin}^{\infin} \int_{-\infin}^{\infin}e^{-x^2+y^2 /2}dydx$ puede definirse como el valor límite de las integrales dobles $\iint_{D_a}e^{-x^2+y^2 /2}dA$ sobre discos $D_a$ de radios $a$ centrados en el origen, como a aumenta sin límite; es decir $$\int_{-\infin}^{\infin} \int_{-\infin}^{\infin}e^{-x^2+y^2 /2}dydx = \lim\limits_{a \to \infin}\iint_{D_a}e^{-x^2+y^2 /2}dA$$
En Integrales dobles sobre regiones rectangulares, discutimos la integral doble de una función $f (x, y)$ de dos variables sobre una región rectangular en el plano. En esta sección definimos la integral triple de una función $f (x, y, z)$ de tres variables sobre una caja sólida rectangular en el espacio, $\Reals^3$. Más adelante en esta sección ampliamos la definición a regiones más generales en $\Reals^3$.
Podemos definir una caja rectangular $B$ en $\Reals^3$ como $B = \lbrace (x, y, z) | a \le x \le b, c \le y \le d, e \le z \le f\rbrace$. Seguimos un procedimiento similar al que hicimos en Integrales dobles sobre regiones rectangulares. Dividimos el intervalo $[a, b]$ en $l$ subintervalos $[x_{i - 1}, x_i]$ de igual longitud $\displaystyle\Delta x = \frac{x_{i} - x_{i - 1}}{l}$, dividimos el intervalo $[c, d]$ en $m$ subintervalos $[y_{i - 1}, y_i]$ de igual longitud $\displaystyle\Delta y = \frac{y_{j} - y_{j - 1}}{m}$, y dividimos el intervalo $[e, f]$ en $n$ subintervalos $[z_{i - 1}, z_i]$ de igual longitud $\displaystyle\Delta z = \frac{z_k - z_{k - 1}}{n}$. Luego, la caja rectangular $B$ se subdivide en $lmn$ subcajas $B_{ijk} = [x_{i - 1}, x_i] \times [y_{i - 1}, y_i] \times [z_{i - 1}, z_i]$, como se muestra en la figura 5.40.
Para cada $i, j$ y $k$, considera un punto de muestra $(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)$ en cada subcaja $B^{ijk}$. Vemos que su volumen es $\Delta V = \Delta x\Delta y\Delta z$. Forma la suma triple de Riemann
$$\sum_{i=1}^l\sum_{j=1}^m\sum_{k=1}^n f(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\Delta x\Delta y\Delta z$$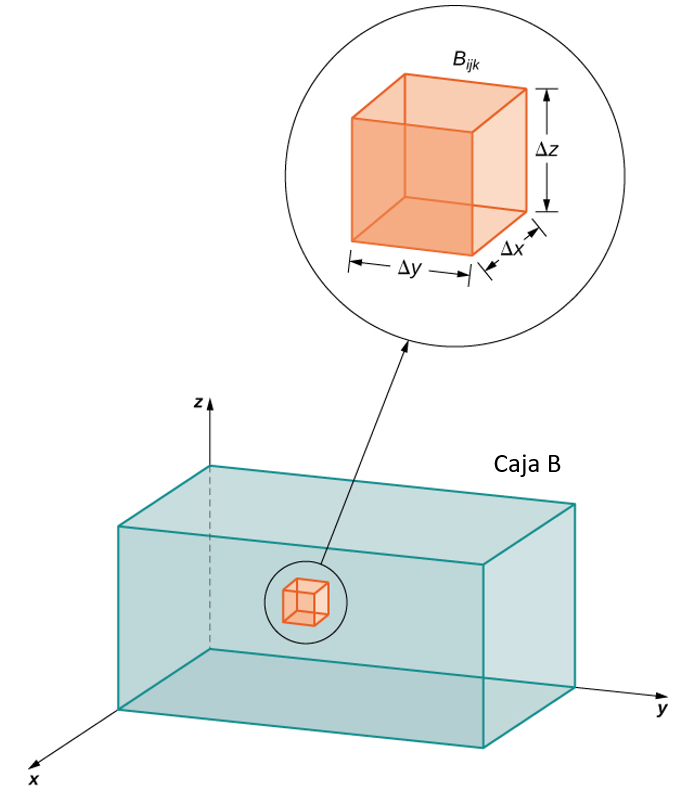
Figura 5.40. Una caja rectangular en $\Reals^3$ dividida en subcajas por planos paralelos a los planos de coordenadas.
Definimos la integral triple en términos del límite de una suma triple de Riemann, como hicimos para la integral doble en términos de una suma doble de Riemann.
Cuando existe la integral triple en $B$, se dice que la función $f (x, y, z)$ es integrable en $B$. Además, la integral triple existe si $f (x, y, z)$ es continua en $B$. Por lo tanto, usaremos funciones continuas para nuestros ejemplos. Sin embargo, la continuidad es suficiente pero no necesaria; en otras palabras, $f$ está limitada a $B$ y es continua excepto posiblemente en el límite de $B$.
El punto de muestra $(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)$ puede ser cualquier punto de la subcaja rectangular $B_{ijk}$ y todas las propiedades de una integral doble se aplican a una integral triple. Así como la integral doble tiene muchas aplicaciones prácticas, la integral triple también tiene muchas aplicaciones, que discutiremos en secciones posteriores. Ahora que hemos desarrollado el concepto de integral triple, necesitamos saber cómo calcularla. Al igual que en el caso de la integral doble, podemos tener una integral triple iterada y, en consecuencia, existe una versión de la misma de Fubini para integrales triples.
Para los números reales $a, b, c, d, e$ y $f$, la integral triple iterada se puede expresar en seis ordenamientos diferentes:
$\displaystyle\int_e^f\int_c^d\int_a^bf(x, y, z)dxdydz$$$\begin{aligned} &= \int_e^f(\int_c^d(\int_a^bf(x, y, z)dx)dy)dz = \int_c^d(\int_e^f(\int_a^bf(x, y, z)dx)dz)dy\\ &= \int_a^b(\int_e^f(\int_c^df(x, y, z)dy)dz)dx = \int_e^f(\int_a^b(\int_c^df(x, y, z)dy)dx)dz\\ &= \int_c^d(\int_a^b(\int_e^ff(x, y, z)dz)dx)dy = \int_a^b(\int_c^d(\int_e^ff(x, y, z)dz)dy)dx \end{aligned}$$
Para una caja rectangular, el orden de integración no hace ninguna diferencia significativa en el nivel de dificultad en el cálculo. Calculamos integrales triples usando el teorema de Fubini en lugar de usar la definición de suma de Riemann.
Seguimos el orden de integración de la misma manera que lo hicimos para las integrales dobles (es decir, de adentro hacia afuera).
 |
Evaluación de una integral triple |

 |
Evaluación de una integral triple |
Figura 5.41. Evaluando una integral triple sobre una caja rectangular dada.

Ahora expandimos la definición de integral triple para calcular una integral triple sobre una región acotada más general $E$ en $\Reals^3$. Las regiones delimitadas generales que consideraremos son de tres tipos. Primero, sea $D$ la región acotada que es una proyección de $E$ sobre el plano $xy$. Supón que la región $E$ en $\Reals^3$ tiene la forma
$$E = \lbrace (x, y, z)|(x, y) \isin D, u_1(x, y) \le z \le u_2(x, y)\rbrace$$Para dos funciones $z = u_1 (x, y)$ y $z = u_2 (x, y)$, tales que $u_1 (x, y) \le u_2(x, y)$ para todo $(x, y)$ en $D$ como se muestra en la siguiente figura.
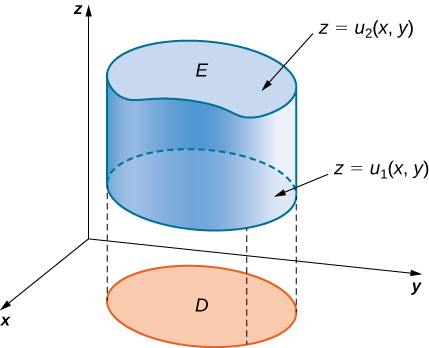
Figura 5.42. Podemos describir la región $E$ como el espacio entre $u_1 (x, y)$ y $u_2 (x, y)$ sobre la proyección $D$ de $E$ sobre el plano $xy$.
De manera similar, podemos considerar una región general limitada $D$ en el plano $xz$ y dos funciones $y = u_1 (x, z)$ e $y = u_2 (x, z)$ tales que $u_1 (x, z) \le u_2 (x, z)$ para todo $(x, z)$ en $D$. Entonces podemos describir la región sólida $E$ en $\Reals^3$ como
$$E = \lbrace (x, y, z)|(x, z) \isin D, u_1(x, z) \le y \le u_2(x, z)\rbrace$$donde $D$ es la proyección de $E$ sobre el plano $xz$ y la integral triple es
$$\iiint_Ef(x, y, z)dV = \iint_D\bigg[\int_{u_1(x, z)}^{u_2(x, z)} f(x,y,z)dy\bigg]dA$$Finalmente, si $D$ es una región limitada general en el plano $yz$ y tenemos dos funciones $x = u_1 (y, z)$ y $x = u_2 (y, z)$ tales que $u_1 (y, z) \le u_2 (y, z )$ para todo $(y, z)$ en $D$, entonces la región sólida $E$ en $\Reals^3$ se puede describir como
donde $D$ es la proyección de $E$ sobre el plano $yz$ y la integral triple es
$$\iiint_Ef(x, y, z)dV = \iint_D\bigg[\int_{u_1(y, z)}^{u_2(y, z)} f(x,y,z)dx\bigg]dA$$Observa que la región $D$ en cualquiera de los planos puede ser de Tipo I o Tipo II como se describe en Integrales dobles sobre regiones generales. Si $D$ en el plano $xy$ es de Tipo I (Figura 5.43), entonces
$$E = \lbrace (x, y, z)|a \le x \le b, g_1(x) \le y \le g_2(x), u_1(x, y) \le z \le u_2(x, y)\rbrace$$
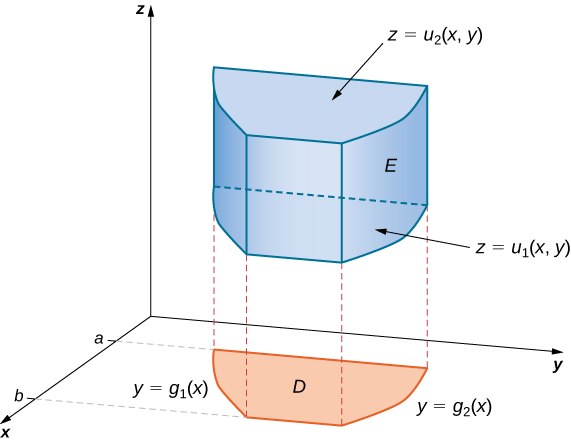
Figura 5.43. Una caja $E$ donde la proyección $D$ en el plano $xy$ es de Tipo I.
Entonces la integral triple se convierte en
Si $D$ en el plano $xy$ es de Tipo II (Figura 5.44), entonces
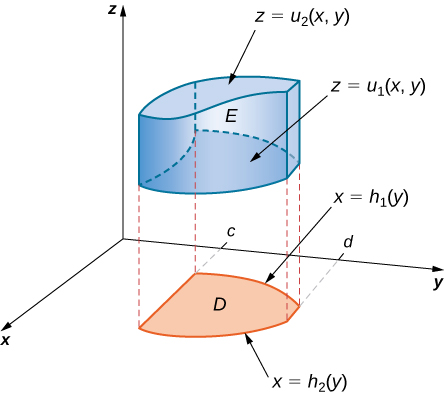
Figura 5.44. Una caja $E$ donde la proyección $D$ en el plano $xy$ es de Tipo II.
la integral triple se convierte en
$$\iiint_E f(x,y,z)dV = \int_c^d\int_{h_1(y)}^{h_2(y)}\int_{u_1(x,y)}^{u_2(x,y)}f(x,y,z)dzdxdz$$ |
Evaluación de una integral triple sobre una región acotada general |

Así como usamos la integral doble $\displaystyle\iint_D1dA$ para encontrar el área de una región general acotada $D$, podemos usar $\displaystyle\iiint_E1dV$ para encontrar el volumen de una región sólida general acotada $E$. El siguiente ejercicio ilustra el método.
 |
Encontrar un volumen mediante la evaluación de una integral triple |
Figura 5.46. Hallando el volumen de una pirámide de base cuadrada.

A continuación, interactúa con la siguiente escena interactiva diseñada en GeoGebra por Brian Abbott y Joseph Manthey, en la cual se describen los límites de integración y, además, pulsando los botones, la interpretación gráfica de los mismos.
Una segunda escena interactiva, diseñada también en GeoGebra, muestra la región de integración de una integral triple (de una función arbitraria) en coordenadas rectangulares (para mostrar una región que cubre un área grande sobre el plano $xy$, puede ser útil reducir la densidad primero y alejar la imagen si es necesario).
Haz clic sobre la siguiente imagen, para interactuar con la segunda escena:
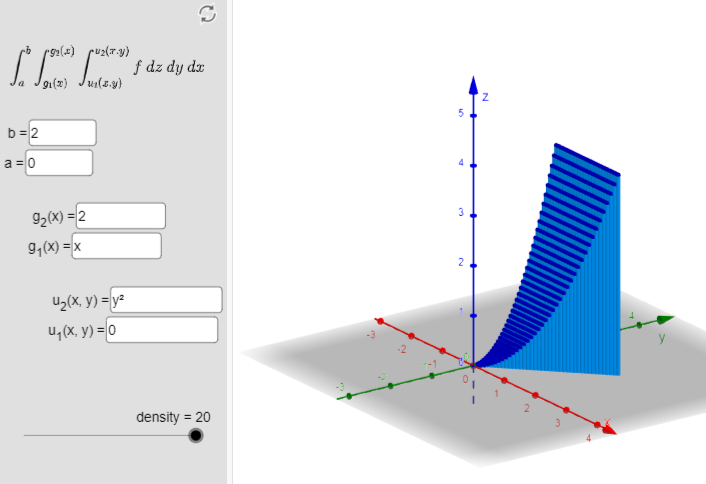
Como ya hemos visto en integrales dobles sobre regiones limitadas generales, el cambio del orden de integración se realiza con bastante frecuencia para simplificar el cálculo. Con una integral triple sobre una caja rectangular, el orden de integración no cambia el nivel de dificultad del cálculo. Sin embargo, con una integral triple sobre una región limitada general, la elección de un orden de integración apropiado puede simplificar bastante el cálculo. A veces, hacer el cambio a las coordenadas polares también puede ser muy útil. Demostramos en dos ejercicios aquí.
 |
Cambiando el orden de integración |

 |
Cambiando el orden de integración y los sistemas de coordenadas |
Figura 5.48. Integrando una integral triple sobre un paraboloide.

Recuerda que encontramos el valor promedio de una función de dos variables al evaluar la integral doble sobre una región en el plano y luego dividir por el área de la región.
De manera similar, podemos encontrar el valor promedio de una función en tres variables al evaluar la integral triple sobre una región sólida y luego dividir por el volumen del sólido.
 |
Encontrando una temperatura promedio |


 En los siguientes ejercicios, evalúa las integrales triples sobre la caja sólida rectangular $B$.
En los siguientes ejercicios, evalúa las integrales triples sobre la caja sólida rectangular $B$.
181. $\iint_B (2x+3y^2+4z^3)dV$, donde $B = \lbrace (x, y, z)|0 \le x \le 1, 0 \le y \le 2, 0 \le z \le 3\rbrace$ (Solución). 182. $\iint_B (xy+yz+xz)dV$, donde $B = \lbrace (x, y, z)|1 \le x \le 2, 0 \le y \le 2, 1 \le z \le 3\rbrace$ 183. $\iint_B (x cos y + z)dV$, donde $B = \lbrace (x, y, z)|0 \le x \le 1, 0 \le y \le \pi, -1 \le z \le 1\rbrace$ (Solución). 184. $\iint_B (z sen x + y^2)dV$, donde $B = \lbrace (x, y, z)|0 \le x \le \pi, 0 \le y \le 1, -1 \le z \le 2\rbrace$
 En los siguientes ejercicios, cambia el orden de integración integrando primero con respecto a $z$, luego $x$, luego $y$.
En los siguientes ejercicios, cambia el orden de integración integrando primero con respecto a $z$, luego $x$, luego $y$.
189. Sean $F, G$ y $H$ funciones continuas en $[a, b], [c, d]$ y $[e, f]$, respectivamente, donde $a, b, c, d, e$ y $f$ son números reales tales que $a \lt b , c \lt d$, y $e \lt f$. Demuestra que
$\int_a^b\int_c^d\int_e^f F(x)G(y)H(z)dzdydz = \big(\int_a^bF(x)dx\big)\big(\int_c^dG(y)dy\big) \big(\int_e^fH(z)dz\big)$.
190. Sean $F, G$ y $H$ funciones diferenciales en $[a, b], [c, d]$ y $[e, f]$, respectivamente, donde $a, b, c, d, e$ y $f$ son números reales tales que $a \lt b, c \lt d$ y $e \lt f$. demuestra que $\int_a^b\int_c^d\int_e^f F^{\prime}(x)G^{\prime}(y)H^{\prime}(z)dzdydz = [F(b) − F(a)][G(d) − G(c)][H(f) − H(e)]$
 En los siguientes ejercicios, evalúe las integrales triples sobre la región acotada
$$E = \lbrace (x, y, z)|a \le x \le b, h_1(x) \le y \le h_2(x), e \le z \le f\rbrace$$
En los siguientes ejercicios, evalúe las integrales triples sobre la región acotada
$$E = \lbrace (x, y, z)|a \le x \le b, h_1(x) \le y \le h_2(x), e \le z \le f\rbrace$$
191. $\iiint_E(2x+5y+7z)dV$, donde $E = \lbrace (x,y,z)|0 \le x \le 1, 0 \le y \le -x+1, 1 \le z \le 2\rbrace$ (Solución). 192. $\iiint_E(yln\;x + z)dV$, donde $E = \lbrace (x,y,z)|1 \le x \le e, 0 \le y \le ln\;x, 0 \le z \le 1\rbrace$ 193. $\iiint_E(sen\;x + sen\;y)dV$, donde $E = (x,y,z)|\lbrace 0 \le x \le \frac{\pi}{2}, -cos\;x \le y \le cos\;x, -1 \le z \le 1\rbrace$ (Solución). 194. $\iiint_E(xy+yz+xz)dV$, donde $E = (x,y,z)|\lbrace 0 \le x \le 1, -x^2 \le y \le x^2, 0 \le z \le 1\rbrace$
 En los siguientes ejercicios, evalúa las integrales triples sobre la región acotada $E$ indicada.
En los siguientes ejercicios, evalúa las integrales triples sobre la región acotada $E$ indicada.
195. $\iiint_E(x+2yz)dV$, donde $E = (x,y,z)|\lbrace 0 \le x \le 1, -0 \le y \le x, 0 \le z \le 5-x-y\rbrace$ (Solución). 196. $\iiint_E(x^3+y^3+z^3)dV$, donde $E = (x,y,z)|\lbrace 0 \le x \le 2, 0 \le y \le 2x, 0 \le z \le 4-x-y\rbrace$ 197. $\iiint_EydV$, donde $E = (x,y,z)|\lbrace -1 \le x \le 1, -\sqrt{1-x^2} \le y \le \sqrt{1-x^2}, 0 \le z \le 1-x^2-y^2\rbrace$ (Solución). 198. $\iiint_ExdV$, donde $E = (x,y,z)|\lbrace -2 \le x \le 2, -4\sqrt{4-x^2} \le y \le 4\sqrt{4-x^2}, 0 \le z \le 4-x^2-y^2\rbrace$
 En los siguientes ejercicios, evalúa las integrales triples sobre la región acotada $E$ de la forma
En los siguientes ejercicios, evalúa las integrales triples sobre la región acotada $E$ de la forma
199. $\iiint_Ex^2dV$, donde $E = (x,y,z)|\lbrace 1-y^2 \le x \le y^2-1, -1 \le y \le 1, 1 \le z \le 2\rbrace$ (Solución). 200. $\iiint_E(sen\;x + y)dV$, donde $E = (x,y,z)|\lbrace -y^4 \le x \le y^4, 0 \le y \le 2, 0 \le z \le 4\rbrace$ 201. $\iiint_E(x-yz)dV$, donde $E = (x,y,z)|\lbrace -y^6 \le x \le \sqrt{y}, 0 \le y \le x, -1 \le z \le 1\rbrace$ (Solución). 202. $\iiint_EzdV$, donde $E = (x,y,z)|\lbrace 2-2y \le x \le 2+\sqrt{y}, 0 \le y \le 1x, 2 \le z \le 3\rbrace$
 En los siguientes ejercicios, evalúe las integrales triples sobre la región acotada
$$E = \lbrace (x,y,z)|g_1(y) \le x \le g_2(y), c \le y \le d, u_1(x,y) \le z \le u_2(x,y)\rbrace$$
En los siguientes ejercicios, evalúe las integrales triples sobre la región acotada
$$E = \lbrace (x,y,z)|g_1(y) \le x \le g_2(y), c \le y \le d, u_1(x,y) \le z \le u_2(x,y)\rbrace$$
 En los siguientes ejercicios, evalúe las integrales triples sobre la región acotada
$$E = \lbrace (x,y,z)|(x,y) \isin D, u_1(x,y) \le z \le u_2(x,y)\rbrace$$
donde $D$ es la proyección de $E$ sobre el plano $xy$
En los siguientes ejercicios, evalúe las integrales triples sobre la región acotada
$$E = \lbrace (x,y,z)|(x,y) \isin D, u_1(x,y) \le z \le u_2(x,y)\rbrace$$
donde $D$ es la proyección de $E$ sobre el plano $xy$
207. $\iint_D\big(\int_1^2(x+z)dz\big)dA$, donde $D=\lbrace (x,y)|x^2+y^2\le 1\rbrace$ (Solución). 208. $\iint_D\big(\int_1^3x(z+1))dz\big)dA$, donde $D=\lbrace (x,y)|x^2-y^2\ge 1, x\le \sqrt{5}\rbrace$
209. $\iint_D\big(\int_0^{10-x-y}(x+2z)dz\big)dA$, donde $D=\lbrace (x,y)|y\ge 0, x\ge 0, x+y\le 10\rbrace$ (Solución). 210. $\iint_D\big(\int_0^{4x^2+4y^2}ydz\big)dA$, donde $D=\lbrace (x,y)|x^2+y^2\le 4, y\ge 1, x\ge 0\rbrace$
211. La $E$ sólida limitada por $y^2 + z^2 = 9, z = 0$ y $x = 5$ se muestra en la siguiente figura. Evalúa la integral $\iiint_Ez dV$ integrando primero con respecto a $z$, luego $y$, y luego $x$ (Solución)
212. La $E$ sólida limitada por $y = \sqrt{x}, x = 4, y = 0$ y $z = 1$ se da en la siguiente figura. Evalúa la integral $\iiint_Exyz dV$ integrando primero con respecto a $x$, luego $y$, y luego $z$
213. [T] El volumen de un sólido $E$ está dado por la integral $\int_{−2}^0\int_x^0\int_0^{x^2 + y^2}dz dy dx$. Usa un sistema de álgebra computarizado (CAS) para graficar $E$ y encontrar su volumen. Redondea tu respuesta a dos cifras decimales (Solución)
214. [T] El volumen de un sólido $E$ está dado por la integral $\int_{-1}^0\int_{-x^2}^0\int_0^{1 + \sqrt{x^2+y^2}}dz dy dx$. Usa un CAS para graficar $E$ y hallar su volumen $V$. Redondea tu respuesta a dos lugares decimales.
 En los siguientes ejercicios, usa dos permutaciones circulares de las variables $x, y$ y $z$ para escribir nuevas integrales cuyos valores sean iguales al valor de la integral original. Una permutación circular de $x, y$ y $z$ es la disposición de los números en uno de los siguientes órdenes: $y, z$, y $x$ o $z, x$ e $y$.
En los siguientes ejercicios, usa dos permutaciones circulares de las variables $x, y$ y $z$ para escribir nuevas integrales cuyos valores sean iguales al valor de la integral original. Una permutación circular de $x, y$ y $z$ es la disposición de los números en uno de los siguientes órdenes: $y, z$, y $x$ o $z, x$ e $y$.
215. $\displaystyle\int_0^1\int_1^3\int_2^4(x^2z^2+1)dxdydz$ (Solución) 216. $\displaystyle\int_1^3\int_0^1\int_0^{-x+1}(2x+5y+7z)dydxdz$ 217. $\displaystyle\int_0^1\int_{-y}^y\int_0^{1-x^4-y^4}ln\;z\;dzdxdy$. 218. $\displaystyle\int_{-1}^1\int_0^1\int_{-y}^{\sqrt{y}}(x+yz)dxdydz$ 219. Establece la integral que dé el volumen del sólido $E$ acotado por $y^2 = x^2 + z^2$ e $y = a^2$, donde $a \gt 0$ (Solución) 220. Establece la integral que dé el volumen del sólido $E$ acotado por $x = y^2 + z^2$ y $x = a^2$, donde $a \gt 0$. 221. Encuentra el valor promedio de la función $f (x, y, z) = x + y + z$ sobre el paralelepípedo determinado por $x = 0, x = 1, y = 0, y = 3, z = 0$ y $z = 5$ (Solución) 222. Encuentra el valor promedio de la función $f (x, y, z) = xyz$ sobre el sólido $E = [0, 1] \times [0, 1] \times [0, 1]$ situado en el primer octante. 223. Encuentra el volumen del sólido $E$ que se encuentra debajo del plano $x + y + z = 9$ y cuya proyección sobre el plano $xy$ está limitada por $x = \sqrt{y - 1}, x = 0$ y $x + y = 7$ (Solución) 224. Halla el volumen del sólido $E$ que se encuentra debajo del plano $2x + y + z = 8$ y cuya proyección sobre el plano $xy $está limitada por $x = sen^{− 1} y, y = 0$ y $x = \frac{\pi}{2}$. 225. Considera la pirámide con la base en el plano $xy$ de $[−2, 2] \times [−2, 2]$ y el vértice en el punto $(0, 0, 8)$
227. La $E$ sólida limitada por la esfera de la ecuación $x^2 + y^2 + z^2 = r^2$ con $r\gt 0$ y ubicada en el primer octante se representa en la siguiente figura
228. La $E$ sólida limitada por la ecuación $9x^2 + 4y^2 + z^2 = 1$ y ubicada en el primer octante se representa en la siguiente figura.
229. Encuentra el volumen del prisma con vértices $(0, 0, 0), (2, 0, 0), (2, 3, 0), (0, 3, 0), (0, 0, 1$ y $( 2, 0, 1)$ (Solución) 230. Encuentra el volumen del prisma con vértices $(0, 0, 0), (4, 0, 0), (4, 6, 0), (0, 6, 0), (0, 0, 1)$ y $( 4, 0, 1)$. 231. El sólido $E$ limitado por $z = 10 - 2x - y$ y situado en el primer octante se muestra en la siguiente figura. Encuentra el volumen del sólido (Solución)
232. La $E$ sólida limitada por $z = 1 - x^2$ y situada en el primer octante se da en la siguiente figura. Calcula el volumen del sólido.
233. La regla del punto medio para la integral triple $\iiint_Bf (x, y, z) dV$ sobre la caja sólida rectangular $B$ es una generalización de la regla del punto medio para integrales dobles. La región $B$ se divide en subcajas de igual tamaño y la integral se aproxima por la suma triple de Riemann $\sum_{i=1}^l\sum_{j=1}^m\sum_{k=1}^n = f(\bar{x}_i, \bar{y}_j, \bar{z}_k) \Delta V$, donde $(\bar{x}_i, \bar{y}_j, \bar{z}_k)$ es el centro de la caja $B_{ijk}$ y $\Delta V$ es el volumen de cada subcaja. Aplica la regla del punto medio para aproximar $\iiint_Bx^2dV$ sobre el sólido $B = \lbrace (x, y, z) | 0 \le x \le 1, 0 \le y \le 1, 0 \le z \le 1\rbrace$ usando una partición de ocho cubos de igual tamaño. Redondea tu respuesta a tres lugares decimales (Solución). 234. [T]
237. Demuestra que el volumen de una pirámide cuadrada recta de altura $h$ y longitud de lado $a$ es $v = \frac{ha^2}{3}$ usando integrales triples.
238. Demuestra que el volumen de un prisma hexagonal recto regular de longitud de borde $a$ es $\frac{3a^3\sqrt{3}}{2}$ mediante el uso de integrales triples.
239. Demuestra que el volumen de una pirámide hexagonal recta regular de longitud de borde $a$ es $\frac{a^3\sqrt{3}}{2}$, mediante el uso de integrales triples.
240. Si la densidad de carga en un punto arbitrario $(x, y, z)$ de un sólido $E$ está dada por la función $\rho (x, y, z)$, entonces la carga total dentro del sólido se define como la integral triple $\iiint_E\rho (x, y, z) dV$. Supón que la densidad de carga del sólido $E$ encerrado por los paraboloides $x = 5 - y^2 - z^2$ y $x = y^2 + z^2 - 5$ es igual a la distancia desde un punto arbitrario de $E$ al origen. Configura la integral que produce la carga total dentro del sólido $E$.
Anteriormente en este capítulo, mostramos cómo convertir una integral doble en coordenadas rectangulares en una integral doble en coordenadas polares para tratar de manera más conveniente problemas que involucran simetría circular. Una situación similar ocurre con las integrales triples, pero aquí necesitamos distinguir entre simetría cilíndrica y simetría esférica. En esta sección convertimos integrales triples en coordenadas rectangulares en una integral triple en coordenadas cilíndricas o esféricas.
Recordemos también el primer capítulo, que mostraba la ópera l’Hemisphèric en Valencia, España. Tiene cuatro secciones, una de las cuales es un teatro en una esfera (pelota) de cinco pisos de altura bajo un techo ovalado tan largo como un campo de fútbol. En el interior hay una pantalla IMAX que convierte la esfera en un planetario con un cielo lleno de 9000 twink.
Como hemos visto anteriormente, en el espacio bidimensional $\Reals^2$, un punto con coordenadas rectangulares $(x, y)$ se puede identificar con $(r, \theta)$ en coordenadas polares y viceversa, donde $x = r cos \theta, y = r sen \theta, r^2 = x^2 + y^2$ y $tan \theta = \frac{y}{x}$ son las relaciones entre las variables.
En el espacio tridimensional $\Reals^3$, un punto con coordenadas rectangulares $(x, y, z)$ se puede identificar con coordenadas cilíndricas $(r, \theta, z)$ y viceversa. Podemos usar estas mismas relaciones de conversión, agregando $z$ como la distancia vertical al punto desde el plano $xy $como se muestra en la siguiente figura.
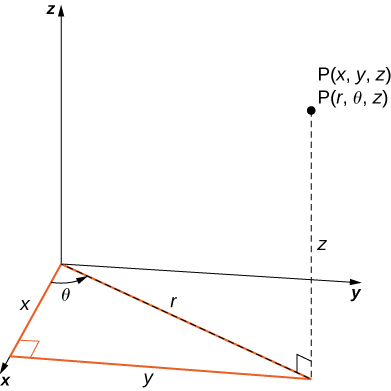
Figura 5.50. Las coordenadas cilíndricas son similares a las coordenadas polares con una coordenada $z$ vertical agregada.
Para convertir de coordenadas rectangulares a cilíndricas, usamos la conversión $x = r cos \theta$ e $y = r sen \theta$. Para convertir de coordenadas cilíndricas a rectangulares, usamos $r^2 = x^2 + y^2$ y $\theta = tan^{−1}\big(\frac{y}{x}\big)$. La coordenada $z$ sigue siendo la misma en ambos casos.
En el plano bidimensional con un sistema de coordenadas rectangular, cuando decimos $x = k$ (constante) nos referimos a una línea vertical ilimitada paralela al eje $y$ y cuando $y = l$ (constante) nos referimos a una línea horizontal ilimitada paralela al eje eje $x$.
Con el sistema de coordenadas polares, cuando decimos $r = c$ (constante), nos referimos a un círculo de radio $c$ unidades y cuando $\theta = \alpha$ (constante) nos referimos a un rayo infinito que forma un ángulo $\alpha$ con el eje $x$ positivo.
De manera similar, en un espacio tridimensional con coordenadas rectangulares $(x, y, z)$, las ecuaciones $x = k, y = l$, y $z = m$, donde $k, l$ y $m$ son constantes, representan planos ilimitados paralelos a los planos $yz, xz$ y $xy$, respectivamente. Con coordenadas cilíndricas $(r, \theta, z)$, por $r = c, \theta = \alpha$ y $z = m$, donde $c, \alpha$ y $m$ son constantes, nos referimos a un cilindro vertical ilimitado con el eje $z$ como eje radial; un plano que forma un ángulo constante $\alpha$ con el plano $xy$ y un plano horizontal ilimitado paralelo al plano $xy$, respectivamente. Esto significa que el cilindro circular $x^2 + y^2 = c2$ en coordenadas rectangulares se puede representar simplemente como $r = c$ en coordenadas cilíndricas.
Las integrales triples a menudo se pueden evaluar más fácilmente utilizando coordenadas cilíndricas en lugar de coordenadas rectangulares. Algunas ecuaciones comunes de superficies en coordenadas rectangulares junto con las ecuaciones correspondientes en coordenadas cilíndricas se enumeran en la siguiente tabla.
Estas ecuaciones serán útiles a medida que procedamos con la resolución de problemas utilizando integrales triples.

Como antes, partimos de la región acotada más simple $B$ en $\Reals^3$, para describir en coordenadas cilíndricas, en forma de caja cilíndrica, $B = \lbrace (r, \theta, z) | a \le r \le b, \alpha \le \theta \le \beta, c \le z \le d$ (Figura 5.51).
Supongamos que dividimos cada intervalo en $l, m$ y $n$ subdivisiones de modo que $\Delta r = \frac{b - a}{l}, \Delta \theta = \frac{\beta - \alpha}{m}$ y $\Delta z = \frac{d - c}{n}$. Entonces podemos enunciar la siguiente definición para una integral triple en coordenadas cilíndricas.
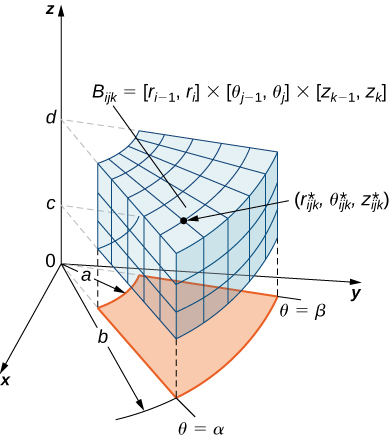
Figura 5.51. Una caja cilíndrica $B$ descrita en coordenadas cilíndricas.
Ten en cuenta que si $g (x, y, z)$ es la función en coordenadas rectangulares y la caja $B$ se expresa en coordenadas rectangulares, entonces la integral triple $\iiint_Bg (x, y, z) dV$ es igual a la integral triple $\iiint_Bg ( r cos \theta, r sen \theta, z) r dr d\theta dz$ y tenemos
$$\iiint_Bg (x, y, z) dV = \iiint_Bg ( r cos \theta, r sen \theta, z) r dr d\theta dz\\ = \iiint_B f(r,\theta, z)r dr d\theta dz \tag{$5.11$}$$Como se mencionó en la sección anterior, todas las propiedades de una integral doble funcionan bien en integrales triples, ya sea en coordenadas rectangulares o cilíndricas.
También son válidos para integrales iteradas. Para reiterar, en coordenadas cilíndricas, el teorema de Fubini toma la siguiente forma:
La integral iterada puede ser reemplazada de manera equivalente por cualquiera de las otras cinco integrales iteradas obtenidas integrando con respecto a las tres variables en otros órdenes. Los sistemas de coordenadas cilíndricas funcionan bien para sólidos que son simétricos alrededor de un eje, como cilindros y conos. Veamos algunos ejercicios antes de definir la integral triple en coordenadas cilíndricas en regiones cilíndricas generales.
 |
Evaluación de una integral triple sobre una caja cilíndrica |

Si la región cilíndrica sobre la que tenemos que integrarnos es un sólido general, miramos las proyecciones en los planos de coordenadas. Por tanto, la integral triple de una función continua $f (r, \theta, z)$ sobre una región sólida general $\lbrace E = (r, \theta, z) | (r, \theta) \isin D, u_1 (r, \theta) \le z \le u_2 ( r, \theta)$ en $\Reals^3$, donde $D$ es la proyección de $E$ sobre el plano $r\theta$, es
$$\iiint_E f(r, \theta, z)r dr d\theta dz = \iint_D\bigg[\int_{u_1(r,\theta)}^{u_2(r,\theta)}f(r, \theta, z)dz\bigg]r dz dr d\theta$$Existen fórmulas similares para proyecciones en los otros planos de coordenadas. Podemos usar coordenadas polares en esos planos si es necesario.
 |
Configuración de una integral triple en coordenadas cilíndricas sobre una región general |

Figura 5.52. Configuración de una integral triple en coordenadas cilíndricas sobre una región cilíndrica.
 |
Configuración de una triple integral de dos maneras |

Figura 5.53. Configuración de una integral triple en coordenadas cilíndricas sobre una región cónica.
 |
Encontrar un volumen con integrales triples de dos maneras |

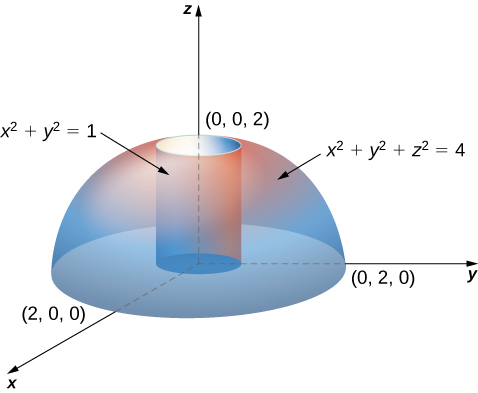
Figura 5.54. Encontrando un volumen cilíndrico con una integral triple en coordenadas cilíndricas.
Para las integrales triples en coordenadas cilíndricas, nuevamente recurrimos a las escenas interactivas diseñadas en GeoGebra por Brian Abbott y Joseph Manthey, en la cual se describen los límites de integración y, además, pulsando los botones, la interpretación gráfica de los mismos.
Una segunda escena interactiva, diseñada también en GeoGebra, muestra la región de integración para una integral triple (de una función $f$ arbitraria) en coordenadas cilíndricas (usa $t$ para $\theta$ cuando ingreses límites de integración).
Haz clic sobre la siguiente imagen, para interactuar con la segunda escena:
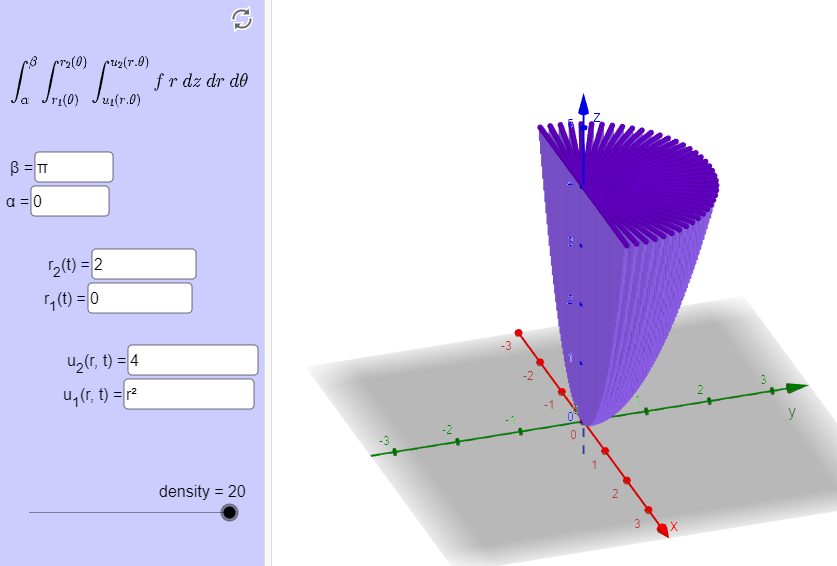
En el espacio tridimensional $\R^3$ en el sistema de coordenadas esféricas, especificamos un punto $P$ por su distancia $\rho$ desde el origen, el ángulo polar $\theta$ desde el eje $x$ positivo (igual que en el sistema de coordenadas cilíndricas) y el ángulo $\phi$ desde el eje $z$ positivo y la línea $OP$ (Figura 5.55). Observa que $\rho \ge 0$ y $0 \le \phi \le \pi$. Las coordenadas esféricas son útiles para integrales triples sobre regiones que son simétricas con respecto al origen.
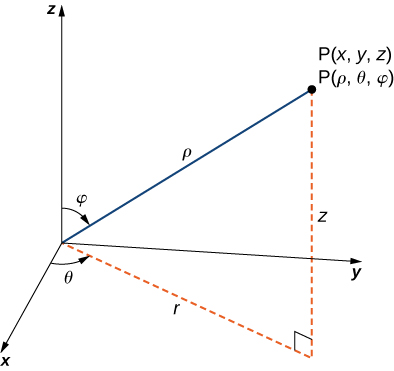
Figura 5.55. El sistema de coordenadas esféricas ubica puntos con dos ángulos y una distancia desde el origen.
Recuerda las relaciones que conectan coordenadas rectangulares con coordenadas esféricas. De coordenadas esféricas a coordenadas rectangulares:
$$x = \rho sen \phi cos \theta, y = \rho sen \phi sen \theta,\;\;\;\text{y}\;\;\;z = \rho cos \phi$$De coordenadas rectangulares a coordenadas esféricas:
$$\rho^2 = x^2 + y^2 + z^2, tan\theta =\frac{y}{x}, \phi = \bigg(\frac{z}{\sqrt{x^2+y^2+z^2}}\bigg)$$Otras relaciones que son importantes conocer para las conversiones son
Estas ecuaciones se utilizan para convertir de coordenadas esféricas a coordenadas cilíndricas | |
y
Estas ecuaciones se utilizan para convertir de coordenadas cilíndricas a coordenadas esféricas. | |
La siguiente figura muestra algunas regiones sólidas que son convenientes para expresar en coordenadas esféricas.
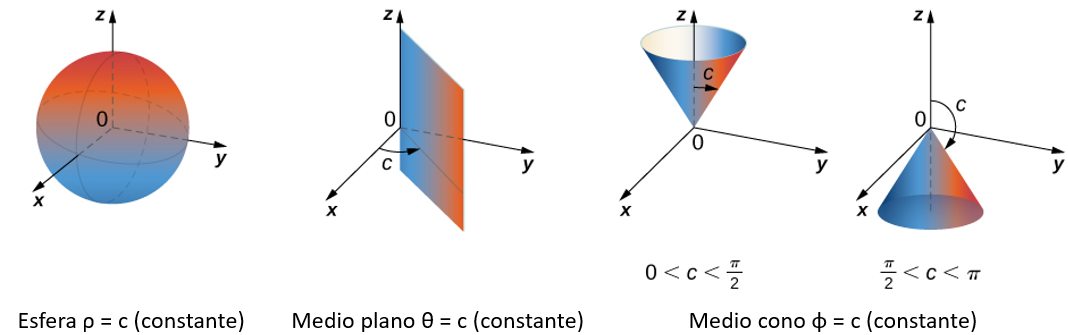
Figura 5.56. Las coordenadas esféricas son especialmente convenientes para trabajar con sólidos delimitados por este tipo de superficies (la letra $c$ indica una constante).
Ahora establecemos una integral triple en el sistema de coordenadas esféricas, como lo hicimos antes en el sistema de coordenadas cilíndricas.
Sea la función $f (\rho, \theta, \phi)$ continua en una caja esférica acotada, $B =\lbrace (\rho, \theta, \phi) | a \le \rho \le b, \alpha \le \theta \le \beta, \gamma \le \phi \le \psi\rbrace$.
Luego dividimos cada intervalo en subdivisiones $l, m$ y $n$ de manera que $\Delta \rho = \frac{b - a}{l}, \Delta \theta = \frac{\beta - \alpha}{m}, \Delta \phi = \frac{\psi - \gamma}{n}$.
Ahora podemos ilustrar el siguiente teorema para integrales triples en coordenadas esféricas con $(\rho_{ijk}^*, \theta_{ijk}^*, \phi_{ijk}^*)$ como cualquier punto muestral en la subcaja esférica $B_{ijk}$. Para el elemento de volumen de la subcaja $\Delta V$ en coordenadas esféricas, tenemos $\Delta V = (\Delta \rho)(\rho\Delta \phi)(\rho sen \phi\Delta \theta)$, como se muestra en la siguiente figura.
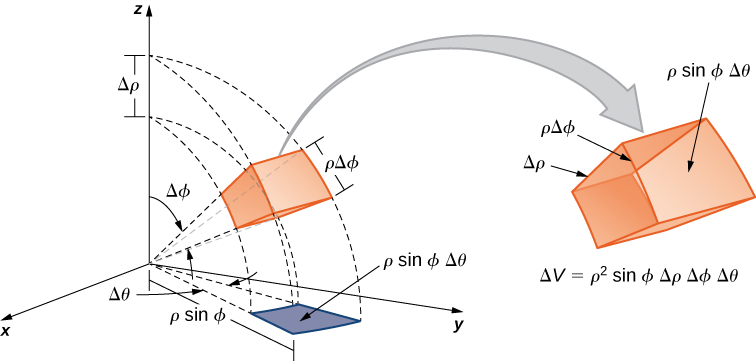
Figura 5.57. El elemento de volumen de una caja en coordenadas esféricas.
Al igual que con las otras integrales múltiples que hemos examinado, todas las propiedades funcionan de manera similar para una integral triple en el sistema de coordenadas esféricas, al igual que las integrales iteradas. El teorema de Fubini adopta la siguiente forma.
Como se indicó anteriormente, los sistemas de coordenadas esféricas funcionan bien para sólidos que son simétricos alrededor de un punto, como esferas y conos. Veamos algunos ejemplos antes de considerar integrales triples en coordenadas esféricas en regiones esféricas generales.
 |
Evaluando una integral triple en coordenadas esféricas |

El concepto de triple integración en coordenadas esféricas se puede extender a la integración sobre un sólido general, utilizando las proyecciones sobre los planos de coordenadas.
Ten en cuenta que $dV$ y $dA$ significan los incrementos en volumen y área, respectivamente. Las variables $V$ y $A$ se utilizan como variables de integración para expresar las integrales.
La integral triple de una función continua $f(\rho, \theta, \phi)$ sobre una región sólida general
$$E = \lbrace (\rho, \theta, \phi)|(\rho, \theta) \isin D, u_1(\rho, \theta) \le \phi \le u_2(\rho, \theta)\rbrace$$en $\Reals^3$, donde $D$ es la proyección de $E$ sobre el plano $\rho\theta$, es
$$\iiint_E f(\rho, \theta, \phi)dV = \iint_D\bigg[\int_{u_1(\rho, \theta)}^{u_2(\rho, \theta)}f(\rho, \theta, \phi)d\phi\bigg]dA$$En particular, si $D = \lbrace (\rho, \theta) | g_1(\theta) \le \rho \le g_2(\theta), \alpha \le \theta \le \beta \rbrace$, entonces tenemos
$$\iiint_E f(\rho, \theta, \phi)dV = \int_{\alpha}^{\beta}\int_{g_1(\theta)}^{g_2(\theta)}\int_{u_1(\rho, \theta)}^{u_2(\rho, \theta)}f(\rho, \theta, \phi)\rho^2 sen\phi d\phi d\rho d\theta$$Se producen fórmulas similares para las proyecciones sobre los otros planos de coordenadas.
 |
Evaluando una integral triple en coordenadas esféricas |
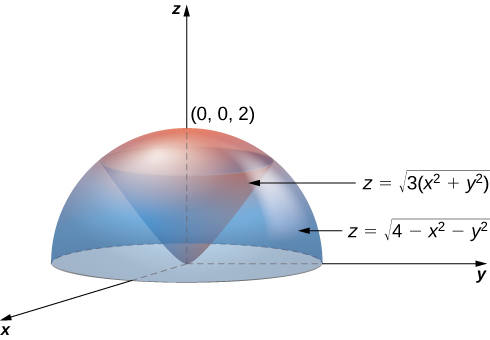
Figura 5.58. Región delimitada por debajo por un cono y por arriba por un hemisferio.

 |
Evaluando una integral triple en coordenadas esféricas |
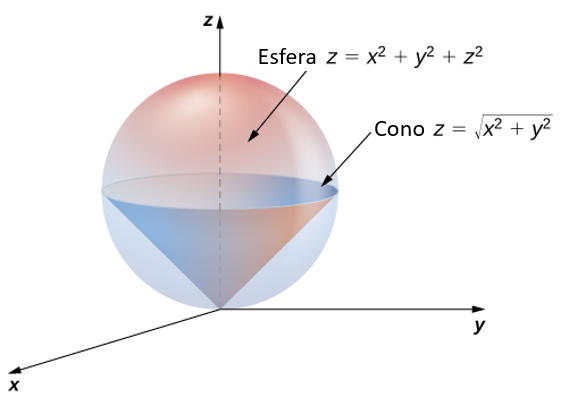
Figura 5.59. Región delimitada por debajo por un cono y por encima por una esfera.

Antes de finalizar esta sección, presentamos un par de ejemplos que pueden ilustrar la conversión de coordenadas rectangulares a coordenadas cilíndricas y de coordenadas rectangulares a coordenadas esféricas.
 |
Conversión de coordenadas rectangulares a coordenadas cilíndricas |

 |
Conversión de coordenadas rectangulares a coordenadas esféricas |

 |
Inicio del capítulo: Encontrar el volumen de l’Hemisphèric |


Figura 5.60. (crédito: modificación del trabajo de Javier Yaya Tur, Wikimedia Commons).
 |
Encontrando el volumen de un elipsoide |

 |
Hallando el volumen del espacio dentro de un elipsoide y fuera de una esfera |

Globos aerostáticos
Los globos aerostáticos son un pasatiempo relajante y pacífico que muchas personas disfrutan. Muchas reuniones de globos aerostáticos tienen lugar en todo el mundo, como la Fiesta Internacional de Globos Aerostáticos de Albuquerque. El evento de Albuquerque es el festival de globos aerostáticos más grande del mundo, con la participación de más de 500 globos cada año.
Figura 5.60. Los globos despegan en la Fiesta Internacional de Globos Aerostáticos de Albuquerque de 2001 (crédito: David Herrera, Flickr).
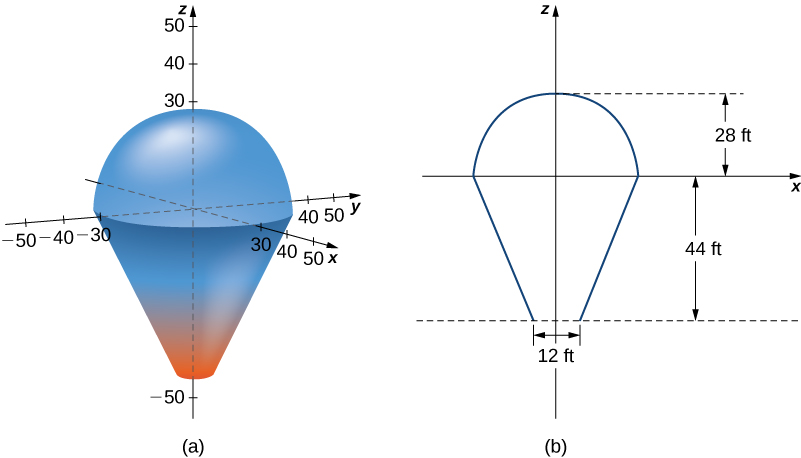
Figura 5.62. (a) Usa una media esfera para modelar la parte superior del globo y un tronco de cono para modelar la parte inferior del globo. (b) Una sección transversal del globo que muestra sus dimensiones.
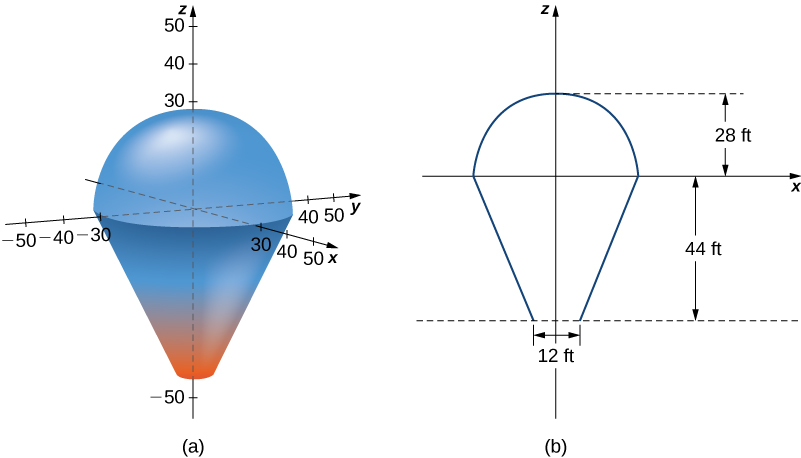
Figura 5.63. La activación del quemador calienta el aire en una columna de $20$ pies de altura y $12$ pies de ancho directamente sobre el quemador.
Para las integrales triples en coordenadas esféricas, presentamos dos escenas interactivas diseñadas en GeoGebra por Brian Abbott y Joseph Manthey y tdr. Esta última muestra la región de integración para una integral triple en coordenadas esféricas y permite, además, cambiar los límites de integración.
Haz clic sobre la siguiente imagen, para interactuar con la segunda escena:

 En los siguientes ejercicios, evalúa las integrales triples $\iiint_Ef (x, y, z) dV$ sobre el sólido $E$.
En los siguientes ejercicios, evalúa las integrales triples $\iiint_Ef (x, y, z) dV$ sobre el sólido $E$.
241. $f(x, y, z) = z, B = \lbrace (x, y, z)|x^2 + y^2 \le 9, x \ge 0, y \ge 0, 0 \le z \le 1\rbrace$ (Solución).
 242. $f(x, y, z) = xz^2, B = \lbrace (x, y, z)|x^2 + y^2 \le 16, x \ge 0, y \le 0, -1 \le z \le 1\rbrace$
243. $f(x, y, z) = z, B = \lbrace (x, y, z)|x^2 + y^2 \le 1, x \ge 0, x \ge y, -1 \le z \le 1\rbrace$ (Solución).
242. $f(x, y, z) = xz^2, B = \lbrace (x, y, z)|x^2 + y^2 \le 16, x \ge 0, y \le 0, -1 \le z \le 1\rbrace$
243. $f(x, y, z) = z, B = \lbrace (x, y, z)|x^2 + y^2 \le 1, x \ge 0, x \ge y, -1 \le z \le 1\rbrace$ (Solución).
244. $f(x, y, z) = xy, B = \lbrace (x, y, z)|x^2 + y^2 \le 4, x \ge 0, x \le y, 0 \le z \le 3\rbrace$ 245. $f(x, y, z) = e^{\sqrt{x^2+y^2}}, B = \lbrace (x, y, z)|1 \le x^2 + y^2 \le 4, y \le 0, x \le y\sqrt{3}, 2 \le z \le 3\rbrace$ (Solución). 246. $f(x, y, z) = \sqrt{x^2+y^2}, B = \lbrace (x, y, z)|1 \le x^2 + y^2 \le 9, y \le 0, 0 \le z \le 1\rbrace$
247.
 En los siguientes ejercicios, los límites del sólido $E$ se dan en coordenadas cilíndricas.
En los siguientes ejercicios, los límites del sólido $E$ se dan en coordenadas cilíndricas.
249. $E$ está delimitado por el cilindro circular recto $r = 4 sen \theta$, el plano $r\theta$ y la esfera $r^2 + z^2 = 16$ (Solución). 250. $E$ está limitado por el cilindro circular recto $r = cos \theta$, el plano $r\theta$ y la esfera $r^2 + z^2 = 9$. 251. $E$ está ubicado en el primer octante y está limitado por el paraboloide circular $z = 9 - 3r^2$, el cilindro $r = 3$ y el plano $r (cos \theta + sen \theta) = 20 - z$ (Solución). 252. $E$ está ubicado en el primer octante fuera del paraboloide circular $z = 10 - 2r^2$ y dentro del cilindro $r = 5$ y está limitado también por los planos $z = 20$ y $\theta = \frac{\pi}{4}$.
 En los siguientes ejercicios, se dan la función $f$ y la región $E$.
En los siguientes ejercicios, se dan la función $f$ y la región $E$.
253. $f(x,y,z) = \frac{1}{x+3}, E = \lbrace (x,y,z)|0 \le x^2+y^2 \le 9, x \ge 0, y \ge 0, 0 \le z \le x+3\rbrace$ (Solución). 254. $f(x,y,z) = x^2+y^2, E = \lbrace (x,y,z)|0 \le x^2+y^2 \le 4, y \ge 0, 0 \le z \le 3-x\rbrace$ 255. $f(x,y,z) = x, E = \lbrace (x,y,z)|1 \le y^2+z^2 \le 9, 0 \le x \le 1-y^2-z^2\rbrace$ (Solución). 256. $f(x,y,z) = y, E = \lbrace (x,y,z)|1 \le x^2+z^2 \le 9, 0 \le y \le 1-x^2-z^2\rbrace$
 En los siguientes ejercicios, encuentre el volumen del sólido $E$ cuyos límites se dan en coordenadas rectangulares.
En los siguientes ejercicios, encuentre el volumen del sólido $E$ cuyos límites se dan en coordenadas rectangulares.
257. $E$ está por encima del plano $xy$, dentro del cilindro $x^2 + y^2 = 1$ y por debajo del plano $z = 1$ (Solución). 258. $E$está debajo del plano $z = 1$ y dentro del paraboloide $z = x^2 + y^2$. 259. $E$ está limitado por el cono circular $z = \sqrt{x^2 + y^2}$ y $z = 1$ (Solución). 260. $E$ se encuentra por encima del plano $xy$, por debajo de $z = 1$, fuera del hiperboloide de una hoja $x^2 + y^2 - z^2 = 1$, y dentro del cilindro $x^2 + y^2 = 2$. 261. $E$ está ubicado dentro del cilindro $x^2 + y^2 = 1$ y entre los paraboloides circulares $z = 1 - x^2 - y^2$ y $z = x^2 + y^2$ (Solución). 262. $E$ está ubicado dentro de la esfera $x^2 + y^2 + z^2 = 1$, encima del plano $xy$ y dentro del cono circular $z = \sqrt{x^2 + y^2}$. 263. $E$ está ubicado fuera del cono circular $x^2 + y^2 = (z - 1)^2 $ y entre los planos $z = 0$ y $z = 2$ (Solución). 264. $E$ está ubicado fuera del cono circular $z = 1 - \sqrt{x^2 + y^2}$, sobre el plano $xy$, debajo del paraboloide circular y entre los planos $z = 0$ y $z = 2$. 265. [T] Usa un sistema de álgebra computarizado (CAS) para graficar el sólido cuyo volumen está dado por la integral iterada en coordenadas cilíndricas $\int_{-\pi/2}^{\pi/2}\int_0^1\int_{r^2}^{r}rdzdrd\theta$. Encuentra el volumen $V$ del sólido. Redondea tu respuesta a cuatro lugares decimales (Solución).
266. [T] Usa un CAS para graficar el sólido cuyo volumen está dado por la integral iterada en coordenadas cilíndricas $\displaystyle\int_0^{\pi/2}\int_0^1\int_{r^4}^{r}rdzdrd\theta$. Encuentra el volumen $V$ de la masa sólida, tu respuesta con cuatro decimales. 267. Convierte la integral $\displaystyle\int_0^1\int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}} \int_{x^2+y^2}^{\sqrt{x^2+y^2}} xzdzdxdy$ en una integral en coordenadas cilíndricas (Solución). 268. Convierte la integral $\displaystyle\int_0^2\int_0^x\int_0^1 (xy+z)dzdxdy$ en una integral en coordenadas cilíndricas.
 En los siguientes ejercicios, evalúa la triple integral $\iiint_B f(x,y,z)dV$ sobre le sólido $B$
En los siguientes ejercicios, evalúa la triple integral $\iiint_B f(x,y,z)dV$ sobre le sólido $B$
269. $f(x,y,z)=1, B=\lbrace (x,y,z)|x^2+y^2+z^2 \le 90, z \ge 0\rbrace$ (Solución).
 270. $f(x,y,z)=1-\sqrt{x^2+y^2+z^2}, B=\lbrace (x,y,z)|x^2+y^2+z^2 \le 9, y \ge 0,z \ge 0\rbrace$
270. $f(x,y,z)=1-\sqrt{x^2+y^2+z^2}, B=\lbrace (x,y,z)|x^2+y^2+z^2 \le 9, y \ge 0,z \ge 0\rbrace$
271. $f (x, y, z) = \sqrt{x^2 + y^2}$, $B$ está acotado arriba por la semiesfera $x^2 + y^2 + z^2 = 9$ con $z \ge 0$ y abajo por el cono $2z^2 = x^2 + y^2$ (Solución). 272. $f (x, y, z) = z$, $B$ está acotado arriba por la semiesfera $x^2 + y^2 + z^2 = 16$ con $z \ge 0$ y abajo por el cono $2z^2 = x^2 + y^2$. 273. Demuestra que si $F(\rho, \theta, \phi) = f (\rho) g (\theta) h (\phi)$ es una función continua en la caja esférica $B = \lbrace (\rho, \theta, \phi) | a \le \rho \le b, \alpha \le \theta \le \beta, \gamma \le \phi \le \psi\rbrace$, entonces, $$\iiint_B = \bigg(\int_a^b\rho^2f(\rho)dr\bigg)\bigg(\int_{\alpha}^{\beta}g(\theta)d(\theta)\bigg)\bigg(\int_{\gamma}^{\psi}h(\phi)sen\;\phi d\phi\bigg)$$ 274.
 En los siguientes ejercicios, se dan la función $f$ y la región $E$.
En los siguientes ejercicios, se dan la función $f$ y la región $E$.
276. $f(x,y,z) = z, E = \lbrace(x,y,z)| 0 \le x^2+y^2+z^2 \le 1, z \ge 0\rbrace$ 277. $f(x,y,z) = x + y, E = \lbrace(x,y,z)| 1 \le x^2+y^2+z^2 \le 2, z \ge 0, y \ge 0\rbrace$ (Solución). 278. $f(x,y,z) = z$, $E = \lbrace(x,y,z)| \sqrt{x^2+y^2} \le z \le \sqrt{1-x^2-y^2}, x \ge 0, y \ge0 \rbrace$. 279. $f(x,y,z) = x + y, E = \lbrace(x,y,z)| x^2+y^2+z^2-2z \le 0, \sqrt{x^2+y^2} \le z\rbrace$ (Solución).
 En los siguientes ejercicios, encuentra el volumen del sólido $E$ cuyos límites se dan en coordenadas rectangulares.
En los siguientes ejercicios, encuentra el volumen del sólido $E$ cuyos límites se dan en coordenadas rectangulares.
280. $E = \lbrace (x,y,z)|\sqrt{x^2+y^2} \le z \le \sqrt{16-x^2-y^2}, x \ge 0, y \ge 0\rbrace$ 281. $E = \lbrace (x,y,z)| x^2+y^2+z^2-2z \le 0, \sqrt{x^2+y^2} \le z\rbrace$ (Solución)
282. Utiliza coordenadas esféricas para encontrar el volumen del sólido situado fuera de la esfera $\rho = 1$ y dentro de la esfera $ρ = cos \phi$, con $\phi \isin \big[0, \frac{\pi}{2}\big]$. 283. Usa coordenadas esféricas para encontrar el volumen de la bola $\rho \le 3$ que está situada entre los conos $\phi = \frac{\pi}{4}$ y φ = $\phi = \frac{\pi}{3}$ (Solución). 284. Convertir la integral $\displaystyle\int_{-4}^4\int_{-\sqrt{16-y^2}}^{\sqrt{16-y^2}}\int_{-\sqrt{16-x^2-y^2}}^{\sqrt{16-x^2-y^2}} (x^2+y^2+z^2)dzdxdy$ en una integral en coordenadas esféricas. 285. Convertir la integral $\displaystyle\int_{0}^4\int_{0}^{\sqrt{16-y^2}}\int_{-\sqrt{16-x^2-y^2}}^{\sqrt{16-x^2-y^2}} (x^2+y^2+z^2)^2dzdxdy$ en una integral en coordenadas esféricas (Solución). 286. Convierte la integral $\displaystyle\int_{-2}^2\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}}\int_{\sqrt{x^2+y^2}}^{\sqrt{16-x^2-y^2}} dzdydx$ en una integral en coordenadas esféricas y evalúala. 287. [T] Usa un CAS para graficar el sólido cuyo volumen está dado por la integral iterada en coordenadas esféricas $\int_{\pi/2}^{\pi}\int{5\pi/6}^{\pi/6}\int_0^2\rho^2 sen\phi d\rho d\phi d\theta$. Encuentra el volumen $V$ del sólido. Redondea tu respuesta a tres lugares decimales (Solución). 288. [T] Usa un CAS para graficar el sólido cuyo volumen está dado por la integral iterada en coordenadas esféricas como $\int_0^{2\pi}\int_{3\pi/4}^{\pi/4}\int_0^1\rho^2 sen\phi d\rho d\phi d\theta$. Encuentra el volumen $V$ del sólido. Redondea tu respuesta a tres lugares decimales. 289. [T] Utiliza un CAS para evaluar la integral $\iiint_E(x^2 + y^2)dV$ donde $E$ se encuentra por encima del paraboloide $z = x^2 + y^2$ y por debajo del plano $z = 3y$ (Solución).
290. [T]
296. Utiliza el ejercicio anterior para encontrar la nube de carga total contenida en la esfera unitaria si la densidad de carga es $q (x, y, z) = 20 \sqrt{x^2 + y^2 + z^2} \frac{\mu C}{cm^3}$
Ya hemos discutido algunas aplicaciones de múltiples integrales, como encontrar áreas, volúmenes y el valor promedio de una función en una región acotada. En esta sección desarrollamos técnicas computacionales para encontrar el centro de masa y los momentos de inercia de varios tipos de objetos físicos, utilizando integrales dobles para una lámina (placa plana) e integrales triples para un objeto tridimensional con densidad variable.
Por lo general, se considera que la densidad es un número constante cuando la lámina o el objeto son homogéneos; es decir, el objeto tiene una densidad uniforme.
El centro de masa también se conoce como centro de gravedad si el objeto está en un campo gravitacional uniforme. Si el objeto tiene una densidad uniforme, el centro de masa es el centro geométrico del objeto, que se denomina centroide. La figura 5.64 muestra un punto $P$ como centro de masa de una lámina.
La lámina está perfectamente equilibrada alrededor de su centro de masa.
Figura 5.64. Una lámina está perfectamente equilibrada en un eje si el centro de masa de la lámina se encuentra en el eje.
Para encontrar las coordenadas del centro de masa $P (\bar{x}, \bar{y})$ de una lámina, necesitamos encontrar el momento $M_x$ de la lámina con respecto al eje $x$ y el momento $M_y$ con respecto al eje $y$. También necesitamos encontrar la masa $m$ de la lámina. Luego
$$\bar{x} = \frac{M_y}{m}\;\;\;\text{y}\;\;\;\bar{y} = \frac{M_x}{m}$$Consulta, en la siguiente unidad interactiva, cómo calcular el centro de masa de una lámina delgadaSi se asume que la densidad de la lámina es constante, el centro geométrico de dicha región se llama centroide, por lo que el centro de masa de la lámina depende únicamente de la forma de la región correspondiente en el plano; no depende de la densidad. En este caso, el centro de masa de la lámina corresponde al centroide de la región delineada en el plano..
Vamos a usar una idea similar aquí, excepto que en la lámina bidimensional usaremos una integral doble. Si permitimos una función de densidad constante, entonces $\bar{x} = \frac{M_y}{m}\;\;\;\text{y}\;\;\;\bar{y} = \frac{M_x}{m}$ dan el centroide de la lámina.
Supón que la lámina ocupa una región $R$ en el plano $xy$, y sea $\rho (x, y)$ su densidad (en unidades de masa por unidad de área) en cualquier punto $(x, y)$. Por lo tanto, $\rho (x, y) = \lim\limits_{\Delta A \to 0}\frac{\Delta m}{\Delta A}$, donde $\Delta m$ y $\Delta A$ son la masa y el área de un pequeño rectángulo que contiene el punto $(x, y)$ y el límite se toma cuando las dimensiones del rectángulo van hacia $0$ (ver figura 5.65).
Al igual que antes, dividimos la región $R$ en pequeños rectángulos $R_{ij}$ con área $\Delta A$ y elegimos $\big(x_{ij}^*, y_{ij}^*\big)$ como puntos de muestra.
Entonces la masa $m_{ij}$ de cada $R_{ij}$ es igual a $\rho\big(x_{ij}^*, y_{ij}^*\big)\Delta A$ (figura 5.66). Sean $k $y $l$ el número de subintervalos en $x$ e $y$, respectivamente. Además, ten en cuenta que es posible que la forma no siempre sea rectangular, pero el límite funciona de todos modos, como se vio en las secciones anteriores.
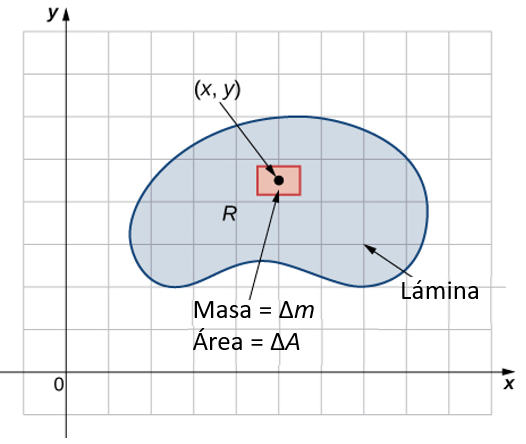
Figura 5.65. La densidad de una lámina en un punto es el límite de su masa por área en un pequeño rectángulo alrededor del punto cuando el área llega a cero.
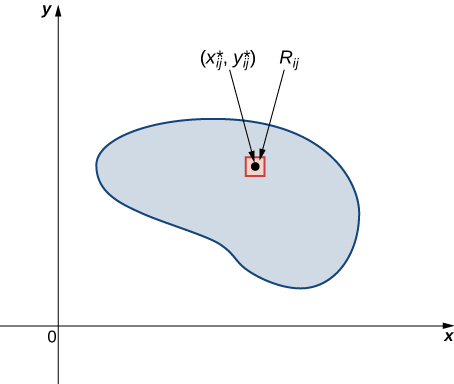
Figura 5.66. Subdivisión de la lámina en pequeños rectángulos Rij, cada uno con un punto de muestra $\big(x_{ij}^*, y_{ij}^*\big)$.
Por tanto, la masa de la lámina es
$$m = \lim\limits_{k, l \to \infin} \sum_{i=1}^k\sum_{j=1}^l m_{ij} = \lim\limits_{k, l \to \infin} \sum_{i=1}^k\sum_{j=1}^l \rho\big(x_{ij}^*, y_{ij}^*\big) \Delta A\\ = \iint_R \rho(x,y)dA \tag{$5.13$}$$Veamos ahora un ejemplo de cómo encontrar la masa total de una lámina triangular
 |
Hallando la masa total de una lámina |

Ahora que hemos establecido la expresión de masa, tenemos las herramientas que necesitamos para calcular momentos y centros de masa. El momento $M_x$ con respecto al eje $x$ para $R$ es el límite de las sumas de momentos de las regiones $R_{ij}$ con respecto al eje $x$.
Por lo tanto
$$M_x = \lim\limits_{k, l \to \infin} \sum_{i=1}^k\sum_{j=1}^l \big(y_{ij}^*\big)m_{ij} = \lim\limits_{k, l \to \infin} \sum_{i=1}^k\sum_{j=1}^l \big(y_{ij}^*\big)m_{ij}\big(y_{ij}^*\big)\rho\big(x_{ij}^*, y_{ij}^*\big)\Delta A\\ = \iint_R y\rho(x, y)dA \tag{$5.14$}$$
De manera similar, el momento $M_y$ respecto al eje $y$ para $R$ es el límite de las sumas de momentos de las regiones $R_{ij}$ respecto al eje $y$
Por lo tanto
$$M_y = \lim\limits_{k, l \to \infin} \sum_{i=1}^k\sum_{j=1}^l \big(x_{ij}^*\big)m_{ij} = \lim\limits_{k, l \to \infin} \sum_{i=1}^k\sum_{j=1}^l \big(x_{ij}^*\big)m_{ij}\big(y_{ij}^*\big)\rho\big(x_{ij}^*, y_{ij}^*\big)\Delta A\\ = \iint_R x\rho(x, y)dA \tag{$5.15$}$$
 |
Encontrando momentos |

Finalmente, estamos listos para reformular las expresiones del centro de masa en términos de integrales. Denotamos la coordenada $x$ del centro de masa por $\bar{x}$ y la coordenada $y$ por $\bar{y}$. Específicamente
$$\bar{x} = \frac{M_y}{m} = \frac{\iint_R x\rho(x, y)dA}{\iint_R \rho(x, y)dA}\;\;\text{y}\\ \bar{y} = \frac{M_x}{m} = \frac{\iint_R y\rho(x, y)dA}{\iint_R \rho(x, y)dA} \tag{$5.16$}$$ |
Encontrando el centro de masa |

Una vez más, de acuerdo con los comentarios al final del ejercicio anterior, tenemos expresiones para el centroide de una región en el plano:
$$x_c = \frac{M_y}{m} = \frac{\iint_R xdA}{\iint_R dA}\;\;\;\text{y}\;\;\;y_c = \frac{M_x}{m} = \frac{\iint_R ydA}{\iint_R dA}$$Debemos usar estas fórmulas y verificar el centroide de la región triangular $R$ a la que se hace referencia en los últimos tres ejercicios.
 |
Encontrando la masa, momentos y centro de masa |

Figura 5.68. Localizando el centro de masa de una lámina $R$ con densidad $\rho (x, y) = x + y$.
El momento de inercia de una partícula de masa $m$ alrededor de un eje es $mr^2$, donde $r$ es la distancia de la partícula al eje. Podemos ver en la figura 5.66 que el momento de inercia del subrectangulo $R_{ij}$ con respecto al eje $x$ es $(y_{ij}^*)^2\rho (x_{ij}^*, y_{ij}^*)\Delta A$. De manera similar, el momento de inercia del subrectangulo $R_{ij}$ alrededor del eje $y$ es $(x_{ij}^*)^2\rho (x_{ij}^*, y_{ij}^*) \Delta A$. El momento de inercia está relacionado con la rotación de la masa; específicamente, mide la tendencia de la masa a resistir un cambio en el movimiento de rotación alrededor de un eje.
El momento de inercia $I_x$ alrededor del eje $x$ para la región $R$ es el límite de la suma de momentos de inercia de las regiones $R_{ij}$ alrededor del eje $x$. Por lo tanto
$$\begin{aligned} I_x &= \lim\limits_{k, l \to \infin}\sum_{i=1}^k\sum_{j=1}^l\big(y_{ij}^*\big)^2 mi_{ij} = \lim\limits_{k, l \to \infin}\sum_{i=1}^k\sum_{j=1}^l \big(y_{ij}^*\big)^2\rho(x_{ij}^*, y_{ij}^*)\Delta A\\ &= \iint_R y^2 \rho(x,y)dA \end{aligned}$$De manera similar, el momento de inercia $I_y$ con respecto al eje $y$ para $R$ es el límite de la suma de momentos de inercia de las regiones $R_{ij}$ con respecto al eje $y$. Por lo tanto
$$\begin{aligned} I_y &= \lim\limits_{k, l \to \infin}\sum_{i=1}^k\sum_{j=1}^l\big(x_{ij}^*\big)^2 mi_{ij} = \lim\limits_{k, l \to \infin}\sum_{i=1}^k\sum_{j=1}^l \big(x_{ij}^*\big)^2\rho(x_{ij}^*, y_{ij}^*)\Delta A\\ &= \iint_R x^2 \rho(x,y)dA \end{aligned}$$A veces, necesitamos encontrar el momento de inercia de un objeto con respecto al origen, que se conoce como momento polar de inercia. Denotamos esto por $I_0$ y lo obtenemos sumando los momentos de inercia $I_x$ e $I_y$. Por lo tanto
$$I_0 = I_x + I_y = \iint_R\big(x^2+ y^2\big)\rho(x, y) dA$$Todas estas expresiones se pueden escribir en coordenadas polares sustituyendo $x = r cos \theta, y = r sen\theta$ y $dA = r dr d\theta$. Por ejemplo,
Antes de nuestro primer ejercicio, observa la siguiente escena interactiva del Proyecto Un_100, que describe cómo se calculan momentos de inercia con $\rho (x, y)$ constante en láminas delgadas o en secciones transversales de un elemento prismático:
 |
Encontrando los momentos de inercia para una lámina triangular |

Como se mencionó anteriormente, el momento de inercia de una partícula de masa $m$ alrededor de un eje es $mr^2$ donde $r$ es la distancia de la partícula al eje, también conocido como radio de giro.
Por lo tanto, los radios de giro con respecto al eje $x$, el eje $y$ y el origen son
$$R_x = \sqrt{\frac{I_x}{m}}, R_y = \sqrt{\frac{I_y}{m}}\;\;\;\text{y}\;\;\;R_0 = \sqrt{\frac{I_0}{m}}$$respectivamente.
En cada caso, el radio de giro nos dice a qué distancia (distancia perpendicular) del eje de rotación se puede concentrar la masa total de un objeto. Los momentos de un objeto son útiles para encontrar información sobre el equilibrio y el torque del objeto alrededor de un eje, pero los radios de giro se utilizan para describir la distribución de masa alrededor de su eje centroidal. Hay muchas aplicaciones en ingeniería y física. A veces es necesario encontrar el radio de giro, como en el siguiente ejemplo.
 |
Hallando el radio de giro de una lámina triangular |

Todas las expresiones de integrales dobles discutidas hasta ahora pueden modificarse para convertirse en integrales triples.
 |
Encontrando la masa de un sólido |

 |
Encontrando el centro de masa de un sólido |

Concluimos esta sección con un ejercicio de cómo encontrar momentos de inercia $I_x, I_y$ e $I_z$.
 |
Momentos de inercia de un sólido |


 En los siguientes ejercicios, la región $R$ ocupada por una lámina se muestra en un gráfico. Encuentra la masa de $R$ con la función de densidad $\rho$
En los siguientes ejercicios, la región $R$ ocupada por una lámina se muestra en un gráfico. Encuentra la masa de $R$ con la función de densidad $\rho$
297. $R$ es la región triangular con vértices $(0, 0), (0, 3) y (6, 0); \rho (x, y) = xy$ (Solución).
298. $R$ es la región triangular con vértices $(0, 0), (1, 1), (0, 5); \rho (x, y) = x + y$.
 299. $R$ es la región rectangular con vértices $(0, 0), (0, 3), (6, 3)$, y $(6, 0); \rho(x, y) = xy$ (Solución).
299. $R$ es la región rectangular con vértices $(0, 0), (0, 3), (6, 3)$, y $(6, 0); \rho(x, y) = xy$ (Solución).
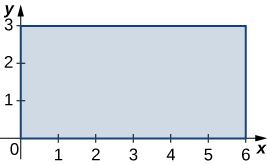
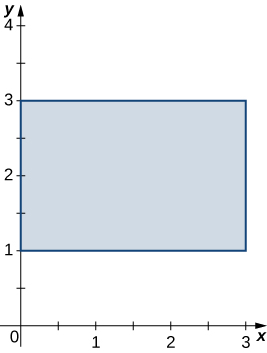
301. $R$ es la región trapezoidal determinada por las líneas $y = − \frac14x + \frac52, y= 0, y = 2$, y $x = 0; \rho(x, y) = 3xy$ (Solución).
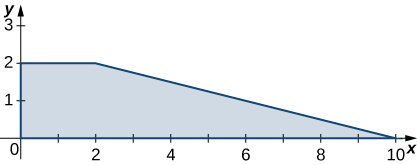 302. $R$ es la región trapezoidal determinada por las líneas $y = 0, y = 1, y = x$, y $y = −x + 3; \rho(x, y) = 2x + y$.
302. $R$ es la región trapezoidal determinada por las líneas $y = 0, y = 1, y = x$, y $y = −x + 3; \rho(x, y) = 2x + y$.
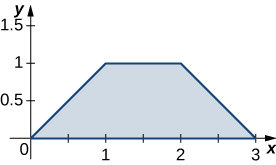
303. $R$ es el disco de radio $2$ centrado en $(1, 2); \rho (x, y) = x^2 + y^2 - 2x - 4y + 5$ (Solución).
 304. $R$ es el disco unitario; $\rho (x, y) = 3x^4 + 6x^2y^2 + 3y^4$.
304. $R$ es el disco unitario; $\rho (x, y) = 3x^4 + 6x^2y^2 + 3y^4$.
 305. $R$ es la región encerrada por la elipse $x^2 + 4y^2 = 1; \rho (x, y) = 1$ (Solución).
305. $R$ es la región encerrada por la elipse $x^2 + 4y^2 = 1; \rho (x, y) = 1$ (Solución).
306. $R = \lbrace (x, y)|9x^2 + y^2 \le 1, x \ge 0, y \ge 0\rbrace ;\rho(x, y) = 9x^2 + y^2$.
 307. $R$ es la región limitada por $y = x, y = −x, y = x + 2, y = −x + 2; \rho (x, y) = 1$ (Solución).
307. $R$ es la región limitada por $y = x, y = −x, y = x + 2, y = −x + 2; \rho (x, y) = 1$ (Solución).
308. $R$ es la región limitada por $y = \frac{1}{x}, y = \frac{2}{x}, y = 1$, y $y = 2; \rho(x, y) = 4(x + y)$.
 En los siguientes ejercicios, considera una lámina que ocupa la región $R$ y que tiene la función de densidad $\rho$ dada en el grupo de ejercicios anterior. Utiliza un sistema de álgebra computarizado (CAS) para responder las siguientes preguntas.
En los siguientes ejercicios, considera una lámina que ocupa la región $R$ y que tiene la función de densidad $\rho$ dada en el grupo de ejercicios anterior. Utiliza un sistema de álgebra computarizado (CAS) para responder las siguientes preguntas.
309. [T] $R$ es la región triangular con vértices $(0, 0), (0, 3)$ y $(6, 0); \rho (x, y) = xy$ (Solución). 310. [T] $R$ es la región triangular con vértices $(0, 0), (1, 1) y (0, 5); \rho (x, y) = x + y$. 311. [T] $R$ es la región rectangular con vértices $(0, 0), (0, 3), (6, 3) y (6, 0); \rho (x, y) = \sqrt{xy}$ (Solución). 312. [T] $R$ es la región rectangular con vértices $(0, 1), (0, 3), (3, 3) y (3, 1); \rho (x, y) = x^2y$. 313. [T] $R$ es la región trapezoidal determinada por las líneas $y = -\frac14x + \frac52, y = 0, y = 2$ y $x = 0; \rho (x, y) = 3xy$ (Solución). 314. [T] $R$ es la región trapezoidal determinada por las líneas $y = 0, y = 1, y = x$, y $y = −x + 3; \rho (x, y) = 2x + y$. 315. [[T] $R$ es el disco de radio $2$ centrado en $(1, 2); \rho (x, y) = x^2 + y^2 −2x - 4y + 5$ (Solución). 316. [T] $R$ es la unidad de disco; $\rho (x, y) = 3x^4 + 6x^2y^2 + 3y^4$. 317. [T] $R$ es la región encerrada por la elipse $x^2 + 4y^2 = 1; \rho (x, y) = 1$ (Solución). 318. [T] $R = \lbrace (x, y) | 9x^2 + y^2 \le 1, x \ge 0, y \ge 0\rbrace ; \rho (x, y) = \sqrt{9x^2 + y^2}$. 319. [T] $R$ es la región delimitada por $y = x, y = −x, y = x + 2$, y $y = −x + 2; \rho (x, y) = 1$ (Solución).
320. [T] $R$ es la región delimitada por $y = \frac{1}{x}, y = \frac{2}{x}, y = 1$ e $y = 2; \rho (x, y) = 4 (x + y)$.
 En los siguientes ejercicios, considera una lámina que ocupa la región $R$ y que tiene la función de densidad $\rho$ dada en los dos primeros grupos de ejercicios.
En los siguientes ejercicios, considera una lámina que ocupa la región $R$ y que tiene la función de densidad $\rho$ dada en los dos primeros grupos de ejercicios.
321. $R$ es la región triangular con vértices $(0, 0), (0, 3)$ y $(6, 0); \rho (x, y) = xy$ (Solución). 322. $R$ es la región triangular con vértices $(0, 0), (1, 1)$ y $(0, 5); \rho (x, y) = x + y$. 323. $R$ es la región rectangular con vértices $(0, 0), (0, 3), (6, 3)$ y $(6, 0); \rho (x, y) = \sqrt{xy}$ (Solución). 324. $R$ es la región rectangular con vértices $(0, 1), (0, 3), (3, 3)$ y $(3, 1); \rho (x, y) = x^2y$. 325. $R$ es la región trapezoidal determinada por las líneas $y = - \frac14x + \frac52, y = 0, y = 2 y x = 0; \rho (x, y) = 3xy$ (Solución). 326. $R$ es la región trapezoidal determinada por las líneas $y = 0, y = 1, y = x$, y $y = −x + 3; \rho (x, y) = 2x + y$. 327. $R$ es el disco de radio $2$ centrado en $(1, 2); \rho (x, y) = x^2 + y^2 - 2x −4y + 5$ (Solución). 328. $R$ es el disco unitario; $\rho (x, y) = 3x^4 + 6x^2y^2 + 3y^4$.
329. $R$ es la región encerrada por la elipse $x^2 + 4y^2 = 1; \rho (x, y) = 1$ (Solución). 330. $R = \lbrace (x, y) | 9x^2 + y^2 \le 1, x \ge 0, y \ge 0\rbrace; \rho (x, y) = \sqrt{9x^2 + y^2}$. 331. $R$ es la región delimitada por $y = x, y = −x, y = x + 2$, y $y = −x + 2; \rho (x, y) = 1$ (Solución). 332. $R $es la región limitada por $y = \frac{1}{x}, y = \frac{2}{x}, y = 1$ e $y = 2; \rho (x, y) = 4 (x + y)$.
333. Sea $Q$ el cubo unitario sólido. Encuentra la masa del sólido si su densidad $\rho$ es igual al cuadrado de la distancia de un punto arbitrario de $Q$ al plano $xy$ (Solución). 334. Sea $Q$ el hemisferio unitario sólido. Encuentra la masa del sólido si su densidad $\rho$ es proporcional a la distancia de un punto arbitrario de $Q$ al origen. 335. El sólido $Q$ de densidad constante $1$ está situado dentro de la esfera $x^2 + y^2 + z^2 = 16$ y fuera de la esfera $x^2 + y^2 + z^2 = 1$. Demuestra que el centro de masa del sólido no está ubicado dentro del sólido. 336. Halla la masa del sólido $Q = \lbrace (x, y, z) | 1 \le x^2 + z^2 \le 25, y \le 1 - x^2− z^2\rbrace$ cuya densidad es $\rho(x, y, z) = k$, donde $k \ge 0$. 337. [T] El sólido $Q = \lbrace (x, y, z) | x^2 + y^2 \le 9, 0 \le z \le 1, x \ge 0, y \ge 0\rbrace$ tiene una densidad igual a la distancia al plano $xy$. Utiliza un CAS para responder las siguientes preguntas.
338. Considera el sólido $Q = \lbrace (x, y, z) | 0 \le x \le 1, 0 \le y \le 2, 0 \le z \le 3\rbrace$ con la función de densidad $\rho (x, y, z) = x + y + 1$.
342. Sea $Q$ el sólido situado fuera de la esfera $x^2 + y^2 + z^2 = z$ y dentro del hemisferio superior $x^2 + y^2 + z^2 = R^2$, donde $R \gt 1$. Si la densidad del sólido es $\rho (x, y, z ) = \frac{1}{\sqrt{x^2 + y^2 + z^2}}$, encuentra $R$ tal que la masa del sólido sea $\frac{7\pi}{2}$. 343. La masa de un sólido $Q$ está dada por $\displaystyle\int_0^2\int_0^{\sqrt{4-x^2}}\int_{\sqrt{x^2+y^2}}^{\sqrt{16-x^2-y^2}} (x^2 + y^2 + z^2)^ndz dy dx$, donde $n$ es un número entero. Determina $n$ tal que la masa del sólido sea $(2 - \sqrt{2})\pi$ (Solución). 344. Sea $Q$ el sólido acotado por encima del cono $x^2 + y^2 = z^2$ y por debajo de la esfera $x^2 + y^2 + z^2 −4z = 0$. Su densidad es una constante $k \gt 0$. Encuentra $k$ tal que el centro de masa del sólido esté situado a $7$ unidades del origen. 345. El sólido $Q = \lbrace (x, y, z) | 0 \le x^2 + y^2 \le 16, x \ge 0, y \ge 0, 0 \le z \le x\rbrace$ tiene la densidad $\rho (x, y, z) = k$. Demuestra que el momento $M_{xy}$ con respecto al plano $xy$ es la mitad del momento $M_{yz}$ con respecto al plano $yz$. 346. El sólido $Q$ está limitado por el cilindro $x^2 + y^2 = a^2$, el paraboloide $b^2 - z = x^2 + y^2$, y el plano $xy$, donde $0 \lt a \lt b$. Encuentra la masa del sólido si su densidad está dada por $\rho (x, y, z) = \sqrt{x^2 + y^2}$. 347. Sea $Q$ un sólido de densidad constante $k$, donde $k \gt 0$, que se encuentra en el primer octante, dentro del cono circular $x^2 + y^2 = 9 (z - 1)^2$, y por encima del plano $z = 0$. Demuestra que el momento $M_{xy}$ con respecto al plano $xy$ es el mismo que el momento $M_{yz}$ con respecto al plano $xz$.
348. El sólido $Q $tiene la masa dada por la integral triple $\int_0^1\int_0^{\pi/2}\int_0^{r^2} (r^4 + r)dz d\theta dr$.
Encuentra el momento $M_{xy}$ del sólido alrededor del plano $xy$ si su densidad dada en coordenadas cilíndricas es $\rho (r, \theta, z) = \frac{d^2f}{dr^2} (r)$, donde $f$ es una función diferenciable con la primera y segunda derivadas continuas y diferenciables en $(0, a)$ (Solución). 352. Un sólido $Q$ tiene un volumen dado por $\iint_D\int_a^bdAdz$, donde $D$ es la proyección del sólido sobre el plano $xy$ y $a \lt b$ son números reales, y su densidad no depende de la variable $z$. Demuestra que su centro de masa se encuentra en el plano $z = \frac{a + b}{2}$. 353. Considera el sólido encerrado por el cilindro $x^2 + z^2 = a^2$ y los planos $y = b$ y $y = c$, donde $a \gt 0$ y $b \lt c$ son números reales. La densidad de $Q$ viene dada por $\rho (x, y, z) = f^{\prime}(y)$, donde $f$ es una función diferencial cuya derivada es continua en $(b, c)$. Demuestra que si $f (b) = f (c)$, entonces el momento de inercia sobre el plano $xz$ de $Q$ es nulo. 354. [T] La densidad media de un sólido $Q$ se define como $\rho_{prom} = \frac{1}{V (Q)}\iiint_Q \rho(x, y, z) dV = \frac{m}{V (Q)}$, donde $V (Q)$ y $m$ son el volumen y la masa de $Q$, respectivamente. Si la densidad de la bola unitaria centrada en el origen es $\rho (x, y, z) = e^{− x^2 - y^2 −z^2}$, usa un CAS para encontrar su densidad promedio. Redondea tu respuesta a tres lugares decimales. 355. Demuestra que los momentos de inercia $I_x, I_y$ e $I_z$ alrededor del plano $yz$, el plano $xz$ y el plano $xy$, respectivamente, de la bola unitaria centrada en el origen cuya densidad es $\rho (x, y, z) = e^{− x^2 − y^2 − z^2}$ son iguales. Redondea tu respuesta a dos cifras decimales (Solución).
Recuerda el método de integración por sustitución. Al evaluar una integral como $\displaystyle\int_2^3 x (x^2−4)^5dx$, sustituimos $u = g (x) = x^2 − 4$. Entonces $du = 2x dx$ o $x dx = \frac12du$ y los límites cambian a $u = g (2) = 2^2 - 4 = 0$ y $u = g (3) = 9 - 4 = 5$. Por lo tanto, la integral se convierte en $\displaystyle \int_0^5\frac12u^5du$ y esta integral es mucho más sencilla de evaluar. En otras palabras, al resolver problemas de integración, hacemos las sustituciones apropiadas para obtener una integral que se vuelve mucho más simple que la integral original.
También usamos esta idea cuando transformamos integrales dobles en coordenadas rectangulares en coordenadas polares y transformamos integrales triples en coordenadas rectangulares en coordenadas cilíndricas o esféricas para hacer los cálculos más simples. Más generalmente,
$$\int_a^b f(x=dx = \_c^d f(g(u))g^{\prime}(u)du$$Donde $x = g (u), dx = g^{\prime}(u) du$, y $u = c$ y $u = d$ satisfacen $c = g (a)$ y $d = g (b)$.
Un resultado similar ocurre en integrales dobles cuando sustituimos $x = f (r, \theta) = r cos \theta, y = g (r, \theta) = r sen \theta$, y $dA = dx dy = r dr dθ$. Entonces tenemos
$$\iint_R f(x,y)dA = \iint_S f(rcos\theta, rsen\theta)rdrd\theta$$donde el dominio $R$ se reemplaza por el dominio $S$ en coordenadas polares. Generalmente, la función que usamos para cambiar las variables para hacer la integración más simple se llama transformación o mapeo.
Una transformación plana $T$ es una función que transforma una región $G$ en un plano en una región $R$ en otro plano mediante un cambio de variables. Tanto $G$ como $R$ son subconjuntos de $R^2$. Por ejemplo, la figura 5.71 muestra una región $G$ en el plano $uv$ transformada en una región $R$ en el plano $xy$ por el cambio de variables $x = g (u, v)$ y $y = h (u, v)$, o algunas veces escribe $x = x (u, v)$ y $y = y (u, v)$. Normalmente asumiremos que cada una de estas funciones tiene primeras derivadas parciales continuas, lo que significa que $g_u, g_v, h_u$ y $h_v$ existen y también son continuas. La necesidad de este requisito se hará evidente pronto.
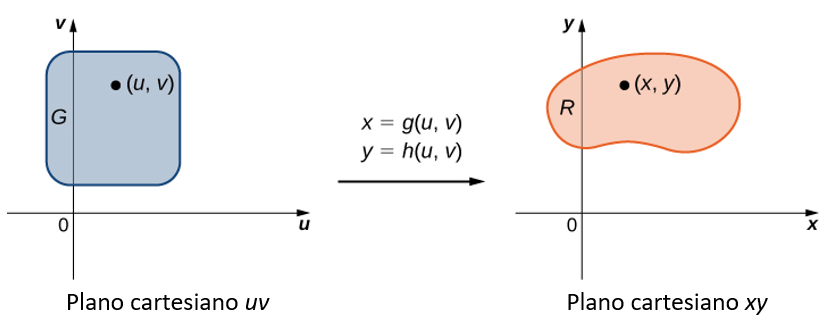
Figura 5.71. La transformación de una región $G$ en el plano $uv$ en una región $R$ en el plano $xy$.
Para mostrar que $T$ es una transformación uno a uno, asumimos $T (u_1, v_1) = T (u_2, v_2)$ y mostramos que, como consecuencia, obtenemos $(u_1, v_1) = (u_2, v_2)$. Si la transformación $T$ es uno a uno en el dominio $G$, entonces la inversa $T^{−1}$ existe con el dominio $R$ de manera que $T^{−1} \circ T$ y $T\circ T^{−1}$ son funciones de identidad.
La figura 5.71 muestra el mapeo $T (u, v) = (x, y)$ donde $x$ e $y$ están relacionados con $u$ y $v$ por las ecuaciones $x = g (u, v)$ e $y = h (u, v)$. La región $G$ es el dominio de $T$ y la región $R $es el rango de $T$, también conocida como la imagen de $G$ bajo la transformación $T$
 |
Determinando cómo funciona la transformación |

 |
Encontrando la imagen bajo $T$ |

Recuerda que mencionamos cerca del comienzo de esta sección que cada una de las funciones componentes debe tener primeras derivadas parciales continuas, lo que significa que $g_u, g_v, h_u$ y $h_v$ existen y también son continuas. Una transformación que tiene esta propiedad se llama transformación $C^1$ (aquí $C$ denota continua). Sea $T (u, v) = g (u, v), h (u, v)$, donde $x = g (u, v)$ y $y = h (u, v)$, una transformación $C^1$ uno a uno. Queremos ver cómo transforma una pequeña región rectangular $S$, $\Delta u$ unidades por $\Delta v$ unidades, en el plano $uv$ (ver la figura 5.74).
Como $x = g (u, v)$ y $y = h (u, v)$, tenemos el vector de posición $\bold{r} (u, v) = g (u, v)\bold{i} + h (u, v)\bold{j}$ de la imagen de el punto $(u, v)$. Supón que $(u_0, v_0)$ es la coordenada del punto en la esquina inferior izquierda que se asigna a $(x_0, y_0) = T (u_0, v_0)$.
La línea $v = v:0$ se asigna a la curva de la imagen con la función vectorial $r(u, v_0)$, y el vector tangente en $(x_0, y_0)$ a la curva de la imagen es
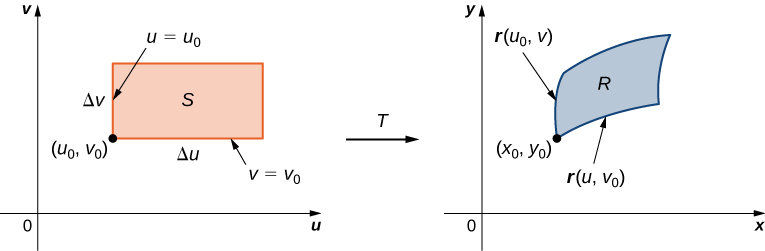
Figura 5.74. Un pequeño rectángulo $S$ en el plano $uv$ se transforma en una región $R$ en el plano $xy$.
$$\bold{r}_u = g_u(u_0, v_0)\bold{i} + h_u(u_0, v_0)\bold{j} = \frac{\partial x}{\partial u}\bold{i} + \frac{\partial y}{\partial u}\bold{j}$$De manera similar, la línea $u = u_0$ se asigna a la curva de la imagen con la función vectorial $r (u_0, v)$, y el vector tangente en $(x_0, y_0)$ a la curva de la imagen es
$$\bold{r}_v = g_v(u_0, v_0)\bold{i} + h_v(u_0, v_0)\bold{j} = \frac{\partial x}{\partial v}\bold{i} + \frac{\partial y}{\partial v}\bold{j}$$Ahora, observa que
$$\bold{r}_u = \lim\limits_{\Delta u \to 0} \frac{\bold{r}(u_0 + \Delta u, v_0)}{\Delta u}\;\;\rarr\;\;\bold{r}(u_0 + \Delta u, v_0) - \bold{r}(u_0, v_0) \approx \Delta u\bold{r}_u$$Similarmente,
$$\bold{r}_v = \lim\limits_{\Delta v \to 0} \frac{\bold{r}(u_0, v_0 + \Delta v)}{\Delta v}\;\;\rarr\;\;\bold{r}(u_0, v_0 + \Delta v) - \bold{r}(u_0, v_0) \approx \Delta v\bold{r}_v$$Esto nos permite estimar el área $\Delta A$ de la imagen $R$ encontrando el área del paralelogramo formado por los lados $\Delta v\bold{r}_v$ y $\Delta u\bold{r}_u$.
Al usar el producto cruz de estos dos vectores sumando el componente $\bold{k}$-ésimo como $0$, el área $\Delta A$ de la imagen $R $ es aproximadamente $|\Delta u\bold{r}_u \times \Delta v\bold{r}_v | = |\bold{r}_u \times \bold{r}_v |\Delta u\Delta v$. En forma determinante, el producto cruz es
$$\begin{vmatrix} \bold{i} & \bold{j} & \bold{k}\\ \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} & 0\\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} & 0 \end{vmatrix}= \begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u}\\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} \end{vmatrix}\bold{k}= \bigg(\frac{\partial x}{\partial u}\frac{\partial y}{\partial v} - \frac{\partial x}{\partial v}\frac{\partial y}{\partial u}\bigg)\bold{k}$$Ya que $|\bold{k}| = 1$, tenemos $\Delta A \approx |\bold{r}_u \times \bold{r}_v|\Delta u\Delta v = \big(\frac{\partial x}{\partial u}\frac{\partial y}{\partial v} - \frac{\partial x}{\partial v}\frac{\partial y}{\partial u}\big)\Delta u\Delta v$.
Usando la definición, tenemos
$$\Delta A \approx J(u,v)\Delta u\Delta v = \bigg|\frac{\partial(x,y)}{\partial(u, v)}\bigg|\Delta u\Delta v$$Ten en cuenta que el Jacobiano es frecuentemente denotado por la forma simple:
$$J(u,v) = \frac{\partial(x,y)}{\partial(u, v)}$$Ten en cuenta también que
$$\begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u}\\ \\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} \end{vmatrix} = \bigg(\frac{\partial x}{\partial u}\frac{\partial y}{\partial v} - \frac{\partial x}{\partial v}\frac{\partial y}{\partial u}\bigg) = \begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{vmatrix}$$De ahí la notación $J(u, v) = \frac{\partial(x,y)}{\partial(u, v)}$ sugiere que podemos escribir el determinante jacobiano con parciales de $x$ en la primera fila y parciales de $y$ en la segunda fila.
 |
Encontrando el Jacobiano |

 |
Encontrando el Jacobiano |

Ya hemos visto que, bajo el cambio de variables $T (u, v) = (x, y)$ donde $x = g (u, v)$ y $y = h (u, v)$, una pequeña región $\Delta A$ en el plano $xy$ está relacionado con el área formada por el producto $\Delta u\Delta v$ en el plano $uv$ por la aproximación
$$\Delta A \approx J(u,v)\Delta u\Delta v$$Ahora volvamos a la definición de integral doble por un momento:
$$\iint_R f(x,y)dA = \lim\limits_{m,n \to \infin}\sum_{i=1}^m\sum_{j=1}^n f(x_{ij}, y_{ij})\Delta A$$Con referencia a la figura 5.75, observa que dividimos la región $S$ en el plano $uv$ en pequeños subrectangulos $S_{ij}$ y dejamos que los subrectangulos $R_{ij}$ en el plano $xy$ sean las imágenes de $S_{ij}$ bajo la transformación $T (u, v) = (x, y)$.
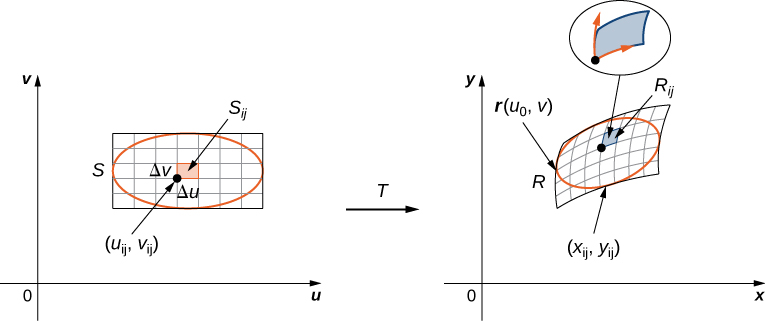
Figura 5.75. Los subrectangulos $S_{ij}$ en el plano $uv$ se transforman en subrectangulos $R_{ij}$ en el plano $xy$.
Entonces la integral doble se convierte en
$$\begin{aligned} \iint_R f(x,y)dA &= \lim\limits_{m,n \to \infin}\sum_{i=1}^m\sum_{j=1}^n f(x_{ij}, y_{ij})\Delta A\\ &= \lim\limits_{m,n \to \infin}\sum_{i=1}^m\sum_{j=1}^n f(g(u_{ij}, v_{ij}), h(u_{ij}, v_{ij}))|J(u_{ij}, v_{ij})|\Delta u\Delta v \end{aligned}$$
Observa que esta es exactamente la suma de Riemann para la integral doble
$$\iint_S f(g(u,v)), h(u,v))\bigg|\frac{\partial(x,y)}{\partial(u,v)}\bigg|dudv$$Con este teorema para integrales dobles, podemos cambiar las variables de $(x, y)$ a $(u, v)$ en una integral doble simplemente reemplazando
cuando usamos las sustituciones $x = g (u, v)$ y $y = h (u, v)$ y luego cambiamos los límites de integración en consecuencia, este cambio de variables a menudo simplifica mucho los cálculos.
Antes de realizar el primer ejercicio de este apartado, te invitamos a que explores la siguiente escena interactiva, diseñada por Elena Álvarez, en la que se muestra la interpretación geométrica del Jacobiano. Dada una transformación afin, el valor absoluto del jacobiano actúa como un factor de escala entre el área del rectángulo inicial y su transformado.
Observa que, en el caso de cualquier transformación, el jacobiano actúa como un factor de dilatación de las áreas a pequeña escala. Elegida la opción de Transformación Afín, se muestran distintos ejemplos en los que se observa la relación entre el área de una región y el área de la región transformada.
Para el caso de transformaciones no afines, la escena permite explorar el cambio a coordenadas polares.
Antes de interactuar con la escena, observa el vídeo que explica cómo hacerlo.
 |
Cambio de variables de coordenadas rectangulares a polares |

Observa en el siguiente ejercicio que la región sobre la que vamos a integrar puede sugerir una transformación adecuada para la integración. Ésta es una situación común e importante.
 |
Cambiando variables |


Figura 5.77. La región de integración para la integral dada.
Estamos listos para dar una estrategia de resolución de problemas para el cambio de variables.
En el siguiente ejercicio, encontraremos una sustitución que simplifica mucho el cálculo del integrando.
 |
Evaluando una integral |

El cambio de variables en integrales triples funciona exactamente de la misma manera. Las sustituciones de coordenadas cilíndricas y esféricas son casos especiales de este método, que demostramos aquí. Supón que $G$ es una región en el espacio $uvw$ y se asigna a $D$ en el espacio $xyz$ (Figura 5.80) mediante una transformación $C^1$ uno a uno $T (u, v, w) = (x, y, z)$ donde $x = g (u, v, w), y = h (u, v, w)$ y $z = k (u, v, w)$
Figura 5.80. Una región $G$ en el espacio $uvw$ mapeada a una región $D$ en el espacio $xyz$.
Entonces, cualquier función $F (x, y, z)$ definida en $D$ puede considerarse como otra función $H (u, v, w)$ que está definida en $G$:
$$F (x, y, z) = F(g (u, v, w), h (u, v, w), k (u, v, w)) = H (u, v, w)$$Ahora necesitamos definir el jacobiano para tres variables.
Con las transformaciones y el Jacobiano para tres variables, estamos listos para establecer el teorema que describe el cambio de variables para integrales triples.
Veamos ahora cómo los cambios en integrales triples para coordenadas cilíndricas y esféricas se ven afectados por este teorema. Esperamos obtener las mismas fórmulas que en las integrales triples en coordenadas cilíndricas y esféricas.
 |
Obtención de fórmulas en integrales triples para coordenadas cilíndricas y esféricas |

Probemos con otro ejercicio con una sustitución diferente.
 |
Evaluación de una integral triple con cambio de variables |


 En los siguientes ejercicios, la función $T: S \rarr R, T (u, v) = (x, y)$ en la región $S = \lbrace (u, v) | 0 \le u \le 1, 0 \le v \le 1\rbrace$ acotada por el cuadrado unitario está dada, donde $R \subset R^2$ es la imagen de $S$ debajo de $T$.
En los siguientes ejercicios, la función $T: S \rarr R, T (u, v) = (x, y)$ en la región $S = \lbrace (u, v) | 0 \le u \le 1, 0 \le v \le 1\rbrace$ acotada por el cuadrado unitario está dada, donde $R \subset R^2$ es la imagen de $S$ debajo de $T$.
356. $x = 2u, y = 3v$ 357. $x=\frac{u}{2}, y = \frac{v}{3}$ (Solución). 358. $x = u − v, y = u + v$ 359. $x = 2u − v, y = u + 2v$ (Solución). 360. $x = u ^2, y = v^2$ 361. $x = u^3, y = v^3$ (Solución).
 En los siguientes ejercicios, determina si las transformaciones $T: S \rarr R$ son uno a uno o no.
En los siguientes ejercicios, determina si las transformaciones $T: S \rarr R$ son uno a uno o no.
362. $x = u^2, y = v^2$, donde $S$ es el rectángulo de vértices $(−1, 0), (1, 0), (1, 1) y (−1, 1)$. 363. $x = u^4, y = u^2 + v$, donde $S$ es el triángulo de vértices $(−2, 0), (2, 0) y (0, 2)$ (Solución).
364. $x = 2u, y = 3v$, donde $S$ es el cuadrado de vértices $(−1, 1), (−1, −1), (1, −1) y (1, 1)$. 365. $T (u, v) = (2u - v, u)$, donde $S$ es el triángulo de vértices $(−1, 1), (−1, −1) y (1, −1)$ (Solución). 366. $x = u + v + w, y = u + v, z = w$, donde $S = R = R^3$. 367. $x = u^2 + v + w, y = u^2 + v, z = w$, donde $S = R = R^3$ (Solución).
 En los siguientes ejercicios, las transformaciones $T: S \rarr R$ son uno a uno. Encuentra sus transformaciones inversas relacionadas $T^{−1}: R \rarr S$.
En los siguientes ejercicios, las transformaciones $T: S \rarr R$ son uno a uno. Encuentra sus transformaciones inversas relacionadas $T^{−1}: R \rarr S$.
368. $x = 4u, y = 5v$, donde $S = R = R^2$. 369. $x = u + 2v, y = −u + v$, donde $S = R = R^2$ (Solución). 370. $x = e^{2u + v}, y = e^{u - v}$, donde $S = R^2$ y $R = \lbrace (x, y) | x \gt 0, y \gt 0\rbrace$ 371. $x = ln\; u, y = ln\; (uv)$, donde $S = \lbrace (u, v) | u\gt 0, v\gt 0\rbrace$ y $R = R^2$ (Solución). 372. $x = u + v + w, y = 3v, z = 2w$, donde $S = R = R^3$. 373. $x = u + v, y = v + w, z = u + w$, donde $S = R = R^3$ (Solución).
 En los siguientes ejercicios, la transformación $T: S \rarr R, T (u, v) = (x, y)$ y la región $R \subset R^2$ son dadas. Encuentra la región $S \subset R^2$.
En los siguientes ejercicios, la transformación $T: S \rarr R, T (u, v) = (x, y)$ y la región $R \subset R^2$ son dadas. Encuentra la región $S \subset R^2$.
374. $x = au, y = bv, R = \lbrace (x,y)|x^2+y^2 \le a^2b^2\rbrace$, donde $a,b \gt 0$. 375. $x = au, y = bv, R = \big\lbrace (x,y)\big|\frac{x^2}{a^2} + \frac{y^2}{b^2} \le 1\big\rbrace$, donde $a,b \gt 0$ (Solución). 376. $x=\frac{u}{a}, y=\frac{v}{b}, z=\frac{w}{c}, R = \lbrace (x,y)|x^2+y^2+z^2 \le 1\rbrace$, donde $a,b,c \gt 0$ 377. $x = au, y = bv, z = cw, R = \big\lbrace (x,y)\big|\frac{x^2}{a^2} - \frac{y^2}{b^2} - \frac{z^2}{c^2} \le 1, z \gt 0\big\rbrace$, donde $a,b,c \gt 0$ (Solución).
 En los siguientes ejercicios, encuentra la J jacobiana de la transformación.
En los siguientes ejercicios, encuentra la J jacobiana de la transformación.
378. $x = u + 2v, y = −u + v$. 379. $x = \frac{u^3}{2}, y = \frac{v}{u^2}$ (Solución). 380. $x = e^{2u - v}, y = e^{u + v}$. 381. $x = ue^v, y = e^{−v}$ (Solución). 382. $x = u cos (e^v), y = u sen (e^v)$ 383. $x = v sen\big(u^2\big), y = v cos\big(u^2\big)$ (Solución). 384. $x = u\; cosh\; v, y = u\; senh\; v, z = w$. 385. $x = v cosh\big(\frac{1}{u}\big), y = v senh\big(\frac{1}{u}\big), z = u + w^2$ (Solución). 386. $x = u + v, y = v + w, z = u$. 387. $x = u - v, y = u + v, z = u + v + w$ (Solución).
388. La región triangular $R$ con los vértices $(0, 0), (1, 1)$ y $(1, 2)$ se muestra en la siguiente figura.
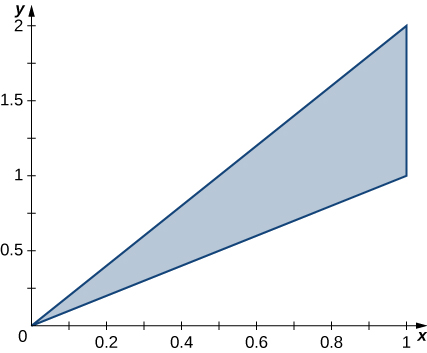
389. La región triangular $R$ con los vértices $(0, 0), (2, 0) y (1, 3)$ se muestra en la siguiente figura.
 En los siguientes ejercicios, usa la transformación $u = y - x, v = y$, para evaluar las integrales en el paralelogramo $R$ de vértices $(0, 0), (1, 0), (2, 1)$ y $(1, 1)$ que se muestra en la siguiente figura.
En los siguientes ejercicios, usa la transformación $u = y - x, v = y$, para evaluar las integrales en el paralelogramo $R$ de vértices $(0, 0), (1, 0), (2, 1)$ y $(1, 1)$ que se muestra en la siguiente figura.
390. $\displaystyle\iint_R(y-x)dA$.
391. $\displaystyle\iint_R(y^2-xy)dA$ (Solución)
 En los siguientes ejercicios, usa la transformación $y - x = u, x + y = v$ para evaluar las integrales en el cuadrado $R$ determinado por las líneas $y = x, y = −x + 2, y = x + 2$, y $y = −x$ se muestra en la siguiente figura
En los siguientes ejercicios, usa la transformación $y - x = u, x + y = v$ para evaluar las integrales en el cuadrado $R$ determinado por las líneas $y = x, y = −x + 2, y = x + 2$, y $y = −x$ se muestra en la siguiente figura
392. $\displaystyle\iint_R e^{x+y}dA$ 393. $\displaystyle\iint_R sen(x-y)dA$ (Solución)
 En los siguientes ejercicios, usa la transformación $x = u, 5y = v$ para evaluar las integrales en la región $R $limitada por la elipse $x^2 + 25y^2 = 1$ que se muestra en la siguiente figura.
En los siguientes ejercicios, usa la transformación $x = u, 5y = v$ para evaluar las integrales en la región $R $limitada por la elipse $x^2 + 25y^2 = 1$ que se muestra en la siguiente figura.
394. $\displaystyle\iint_R \sqrt{x^2 + 25y^2}dA$.
395. $\displaystyle\int_R (x^2 + 25y^2)^2dA $ (Solución)
 En los siguientes ejercicios, usa la transformación $u = x + y, v = x - y$ para evaluar las integrales en la región trapezoidal $R$ determinadas por los puntos $(1, 0), (2, 0), (0, 2)$, y $(0, 1)$ que se muestran en la siguiente figura.
En los siguientes ejercicios, usa la transformación $u = x + y, v = x - y$ para evaluar las integrales en la región trapezoidal $R$ determinadas por los puntos $(1, 0), (2, 0), (0, 2)$, y $(0, 1)$ que se muestran en la siguiente figura.
396. $\displaystyle\iint_R (x^2 − 2xy + y^2)e^{x+y}dA$.
397. $\displaystyle\iint_R (x^3 + 3x^2y + 3xy^2 + y^3)dA$ (Solución).
398. El sector del anillo circular $R$ delimitado por los círculos $4x^2 + 4y^2 = 1$ y $9x^2 + 9y^2 = 64$, la línea $x = y\sqrt{3}$ y el eje $y$ se muestran en la siguiente figura. Encuentra una transformación $T$ de una región rectangular $S$ en el plano $r\theta$ a la región $R$ en el plano $xy$.
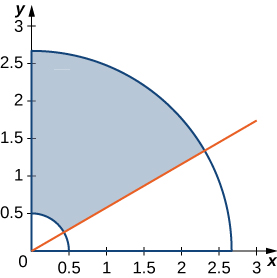
399. El sólido $R$ delimitado por el cilindro circular $x^2 + y^2 = 9$ y los planos $z = 0, z = 1, x = 0$ e $y = 0$ se muestra en la siguiente figura. Encuentra una transformación $T$ de una caja cilíndrica $S$ en el espacio $r\theta z$ al sólido $R$ en el espacio $xyz$ (Solución).
400. Demuestra que $\displaystyle\iint_R \bigg(\sqrt{\frac{y^2}{3} + \frac{x^2}{3}}\bigg)dA = 2\pi\sqrt{15}\int_0^1 f(\rho)\rho d\rho$, donde $f$ es una función continua en $[0, 1]$ y $R$ es la región limitada por la elipse $5x^2 + 3y^2 = 15$.
401. Demestra que $\displaystyle\iint_R f\big(\sqrt{16x^2+4y^2+z^2}\big)dV = \frac{\pi}{2}\int_0^1 f(\rho)\rho^2 d\rho$, donde $f$ es una función continua en $[0, 1]$ y $R$ es la región limitada por el elipsoide $16x^2 + 4y^2 + z^2 = 1$.
402. [T] Encuentra el área de la región delimitada por las curvas $xy = 1, xy = 3, y = 2x$ e $y = 3x$ usando la transformación $u = xy$ y $v = \frac{y}{x}$. Utiliza un sistema de álgebra computarizado (CAS) para graficar las curvas de los límites de la región $R$.
403. [T] Encuentra el área de la región limitada por las curvas $x^2y = 2, x^2y = 3, y = x$, y $y = 2x$ usando la transformación $u = x^2y $y $v = \frac{y}{x}$. Utiliza un CAS para graficar las curvas de los límites de la región $R$ (Solución).
404. Evalúa la integral triple $\displaystyle\int_0^1\int_1^2\int_z^{z+1} (y + 1)dx dy dz$ usando la transformación $u = x - z, v = 3y$ y $w = \frac{z}{2}$.
405. Evalúa la integral triple $\displaystyle\int_0^2\int_4^6\int_{3z}^{3z+2} (5 - 4y)dx dz dy$ usando la transformación $u = x - 3z, v = 4y$ y $w = z$ (Solución).
406. Una transformación T$: R^2 \rarr R^2, T (u, v) = (x, y)$ de la forma $x = au + bv, y = cu + dv$, donde $a, b, c$ y $d$ son números reales, se llama lineal. Demuestra que una transformación lineal para la cual $ad - bc \cancel{=} 0$ asigna paralelogramos a paralelogramos.
407. La transformación $T_{\theta}: R^2 \rarr R^2, T_{\theta} (u, v) = (x, y)$, donde $x = u cos \theta - v sen \theta, y = u sen \theta + v cos \theta$, se llama rotación de ángulo $\theta$. Demuestra que la transformación inversa de $T_{\theta}$ satisface $T_{\theta}^{-1} = T_{-\theta}$, donde $T_{-\theta}$ es la rotación del ángulo $-\theta$.
408. [T] Encuentra la región $S$ en el plano $uv$ cuya imagen a través de una rotación de ángulo $\frac{\pi}{4}$ es la región $R$ encerrada por la elipse $x^2 + 4y^2 = 1$. Usa un CAS para responder las siguientes preguntas.
409. [T] Las transformaciones $T_i: \Reals^2 \rarr \Reals^2, i = 1,…, 4$, definido por $T_1 (u, v) = (u, −v), T_2 (u, v) = (−u, v) , T_3 (u, v) = (−u, −v)$ y $T_4 (u, v) = (v, u)$ se denominan reflexiones sobre el eje $x$, el eje $y$, el origen y la recta $y = x$, respectivamente.
410. [T] La transformación $T_{k, 1, 1}: \Reals^3 \rarr \Reals^3, T_{k, 1, 1} (u, v, w) = (x, y, z)$ de la forma $x = ku, y = v, z = w$, donde $k \cancel{=} 1$ es un número real positivo, se llama estiramiento si $k\gt 1$ y compresión si $0 \lt k \lt 1$ en la dirección $x$. Usa un CAS para evaluar la integral $\iiint_S e^{-(4x^2 + 9y^2 + 25z^2)} dxdy dz$ en el sólido $S = \lbrace (x, y, z) | 4x^2 + 9y^2 + 25z^2 \le 1\rbrace$ considerando la compresión $T_{2, 3, 5} (u, v, w) = (x, y, z)$ definida por $x = \frac{u}{2}, y = \frac{v}{3} y z = \frac{w}{5}$. Redondea tu respuesta a cuatro lugares decimales.
411. [T] La transformación $T_{a, 0}: \Reals^2 \rarr \Reals^2, T_{a, 0} (u, v) = (u + av, v)$, donde $a \cancel{=} 0$ es un número real, se llama cortante en la dirección $x$ . La transformación, $T_{b, 0}: R^2 \rarr R^2, T_{o, b} (u, v) = (u, bu + v)$, donde $b \cancel{=} 0$ es un número real, se llama cortante en la dirección $y$.
412. Usa la transformación, $x = au, y = av, z = cw$ y coordenadas esféricas para mostrar que el volumen de una región delimitada por el esferoide $\frac{x^2 + y^2}{a^2} + \frac{z^2}{c^2} = 1$ es $\frac{4\pi a^2}{c^3}$.
413. Calcula el volumen de una pelota de fútbol cuya forma es un esferoide $\frac{x^2 + y^2}{a^2} + \frac{z^2}{c^2} = 1$ cuya longitud de punta a punta es de $11$ pulgadas y la circunferencia en el centro es de $22$ pulgadas. Redondea tu respuesta a dos cifras decimales (Solución).
414. [T] Los óvalos de Lamé (o superelipses) son curvas planas de ecuaciones $\big(\frac{x}{a}\big)^n + \big(\frac{y}{b}\big)^n = 1$, donde $a, b$ y $n$ son números reales positivos.
415. Los óvalos de [T] Lamé han sido utilizados constantemente por diseñadores y arquitectos. Por ejemplo, Gerald Robinson, un arquitecto canadiense, ha diseñado un estacionamiento en un centro comercial en Peterborough, Ontario, en forma de superelipse de la ecuación $\big(\frac{x}{a}\big)^n + \big(\frac{y}{b}\big)^n = 1$ con $\frac{a}{b} = \frac97$ y $n=e$. Usa un CAS para encontrar una aproximación del área del estacionamiento en el caso $a = 900$ yardas, $b = 700$ yardas y $n = 2.72$ yardas (Solución).
Para terminar este capítulo presentamos un escena interactiva de Juan Carlos Ponce Campuzano, en la cual se muestra la transformación parabólica $x = u^2- v^2$ y $y= 2v$. El Jacobiano establece una relación entre el área del cuadrado azul (izquierda) y el área de la región roja (derecha).
Arrastra el punto verde (a la izquierda) para cambiar la posición del cuadrado azul. Observa lo que le sucede a la región roja. También, puedes arrastrar el control deslizante, que determina el lado del cuadrado azul y observar lo que le sucede a la región roja

Figura 6.1. Los huracanes se forman a partir de vientos giratorios impulsados por temperaturas cálidas sobre el océano. Los meteorólogos pronostican el movimiento de los huracanes mediante el estudio de los campos vectoriales giratorios de la velocidad del viento. Se muestra el ciclón Catarina en el Océano Atlántico Sur en 2004, visto desde la Estación Espacial Internacional (crédito: modificación del trabajo de la NASA).
Los huracanes son grandes tormentas que pueden producir enormes daños a la vida y la propiedad, especialmente cuando llegan a tierra. Predecir dónde y cuándo atacarán y qué tan fuertes serán los vientos es de gran importancia para prepararse para la protección o la evacuación. Los científicos se basan en estudios de campos vectoriales rotacionales para sus pronósticos.
En este capítulo, aprenderemos a modelar nuevos tipos de integrales sobre campos como campos magnéticos, campos gravitacionales o campos de velocidad.
También aprenderemos a calcular el trabajo realizado en una partícula cargada que viaja a través de un campo magnético, el trabajo realizado en una partícula con masa que viaja a través de un campo gravitacional y el volumen por unidad de tiempo del agua que fluye a través de una red arrojada a un río.
Todas estas aplicaciones se basan en el concepto de campo vectorial, que exploramos en este capítulo. Los campos vectoriales tienen muchas aplicaciones porque se pueden usar para modelar campos reales como campos electromagnéticos o gravitacionales. Una comprensión profunda de la física o la ingeniería es imposible sin una comprensión de los campos vectoriales. Además, los campos vectoriales tienen propiedades matemáticas que merecen ser estudiadas por derecho propio. En particular, los campos vectoriales se pueden utilizar para desarrollar varias versiones de dimensiones superiores del Teorema Fundamental del Cálculo.
Los campos vectoriales son una herramienta importante para describir muchos conceptos físicos, como la gravitación y el electromagnetismo, que afectan el comportamiento de los objetos en una gran región de un plano o del espacio. También son útiles para hacer frente a comportamientos a gran escala, como tormentas atmosféricas o corrientes oceánicas de profundidad.
En esta sección, examinamos las definiciones básicas y los gráficos de los campos vectoriales para poder estudiarlos con más detalle en el resto de este capítulo.
¿Cómo podemos modelar la fuerza gravitacional ejercida por múltiples objetos astronómicos?
¿Cómo podemos modelar la velocidad de las partículas de agua en la superficie de un río? La figura 6.2 ofrece representaciones visuales de tales fenómenos.
La figura 6.2 (a) muestra un campo gravitacional ejercido por dos objetos astronómicos, como una estrella y un planeta o un planeta y una luna. En cualquier punto de la figura, el vector asociado con un punto da la fuerza gravitacional neta ejercida por los dos objetos sobre un objeto de unidad de masa. Los vectores de mayor magnitud en la figura son los vectores más cercanos al objeto más grande. El objeto más grande tiene mayor masa, por lo que ejerce una fuerza gravitacional de mayor magnitud que el objeto más pequeño.
La figura 6.2 (b) muestra la velocidad de un río en puntos de su superficie. El vector asociado con un punto dado en la superficie del río da la velocidad del agua en ese punto. Dado que los vectores a la izquierda de la figura son de magnitud pequeña, el agua fluye lentamente en esa parte de la superficie. A medida que el agua se mueve de izquierda a derecha, encuentra algunos rápidos alrededor de una roca. La velocidad del agua aumenta y se produce un remolino en parte de los rápidos.
Cada figura ilustra un ejemplo de un campo vectorial. Intuitivamente, un campo vectorial es un mapa de vectores. En esta sección, estudiaremos campos vectoriales en $\Reals^2$ y $\Reals^3$.
Figura 6.2. (a) El campo gravitacional ejercido por dos cuerpos astronómicos sobre un objeto pequeño. (b) El campo vectorial de velocidad del agua en la superficie de un río muestra las distintas velocidades del agua. El rojo indica que la magnitud del vector es mayor, por lo que el agua fluye más rápidamente; el azul indica una magnitud menor y una velocidad más lenta del flujo de agua.
Un campo vectorial en $\Reals^2$ se puede representar de dos formas equivalentes. La primera forma es usar un vector con componentes que sean funciones de dos variables:
$$\bold{F}(x, y) = \lang P(x, y), Q(x, y) \rang\tag{$6.1$}$$La segunda forma es usar los vectores unitarios estándar:
$$\bold{F}(x, y) = P(x, y)\bold{i} + Q(x, y)\bold{j} \rang\tag{$6.2$}$$Se dice que un campo vectorial es continuo si sus funciones componentes son continuas.
 |
Encontrando un vector asociado a un punto dado |

Ahora podemos representar un campo vectorial en términos de sus componentes de funciones o vectores unitarios, pero representarlo visualmente es más complejo porque el dominio de un campo vectorial está en $\Reals^2$, al igual que el rango. Por lo tanto, la “gráfica” de un campo vectorial en $\Reals^2$ vive en un espacio de cuatro dimensiones. Como no podemos representar visualmente el espacio de cuatro dimensiones, en su lugar dibujamos campos vectoriales en $\Reals^2$ en un plano. Para hacer esto, dibuja el vector asociado con un punto dado en el punto de un plano.
Por ejemplo, supón que el vector asociado con el punto $(4, −1)$ es $\lang 3, 1\rang$. Entonces, dibujaríamos el vector $\lang 3, 1\rang$ en el punto $(4, −1)$.
Deberíamos trazar suficientes vectores para ver la forma general, pero no tantos como para que el boceto se convierta en un desorden. Si tuviéramos que trazar el vector de imagen en cada punto de la región, llenaría la región completamente y sería inútil.
En su lugar, podemos elegir puntos en las intersecciones de las líneas de la cuadrícula y trazar una muestra de varios vectores de cada cuadrante de un sistema de coordenadas rectangular en $\Reals^2$.
Hay dos tipos de campos vectoriales en $\Reals^2$ en los que se centra este capítulo: campos radiales y campos rotacionales. Los campos radiales modelan ciertos campos gravitacionales y campos de fuentes de energía, y los campos rotacionales modelan el movimiento de un fluido en un vórtice. En un campo radial, todos los vectores apuntan directamente hacia o directamente lejos del origen. Además, la magnitud de cualquier vector depende solo de su distancia al origen. En un campo radial, el vector ubicado en el punto $(x, y)$ es perpendicular al círculo centrado en el origen que contiene el punto $(x, y)$, y todos los demás vectores de este círculo tienen la misma magnitud.
 |
Dibujando un campo vectorial radial |

En contraste con los campos radiales, en un campo rotacional, el vector en el punto $(x, y)$ es tangente (no perpendicular) a un círculo con radio $r = \sqrt{x^2 + y^2}$. En un campo rotacional estándar, todos los vectores apuntan en el sentido de las agujas del reloj o en el sentido contrario a las agujas del reloj, y la magnitud de un vector depende solo de su distancia desde el origen.
Los dos ejercicios siguientes son campos de rotación en el sentido de las agujas del reloj, y vemos por sus representaciones visuales que los vectores parecen girar alrededor del origen.
 |
Apertura de capítulo: Dibujar un campo vectorial rotacional |

Figura 6.4. (crédito: modificación de un trabajo de la NASA)
Dibuja el campo vectorial $\bold{F} (x, y) = \lang y, −x\rang$
 |
Dibujar un campo vectorial |

 |
Campo de velocidad de un fluido |

Hemos examinado campos vectoriales que contienen vectores de diversas magnitudes, pero así como tenemos vectores unitarios, también podemos tener un campo vectorial unitario. Un campo vectorial $\bold{F}$ es un campo vectorial unitario si la magnitud de cada vector en el campo es $1$. En un campo vectorial unitario, la única información relevante es la dirección de cada vector.
 |
Un campo vectorial unitario |

¿Por qué son importantes los campos vectoriales unitarios? Supongamos que estamos estudiando el flujo de un fluido y que solo nos importa la dirección en la que fluye el fluido en un punto dado. En este caso, la velocidad del fluido (que es la magnitud del vector de velocidad correspondiente) es irrelevante, porque lo único que nos importa es la dirección de cada vector. Por lo tanto, el campo vectorial unitario asociado con la velocidad es el campo que estudiaríamos. Si $\bold{F} = \lang P, Q, R\rang$ es un campo vectorial, entonces el campo vectorial unitario correspondiente es $\lang \frac{P}{||\bold{F}||}, \frac{Q}{||\bold{F}||}, \frac{R}{||\bold{F}||}\rang$. Observa que si $\bold{F} (x, y) = \lang y, −x\rang$, entonces la magnitud de $\bold{F}$ es $\sqrt{x^2 + y^2}$ y, por lo tanto, el campo vectorial unitario correspondiente es el campo $G$ del ejemplo anterior.
Si $\bold{F}$ es un campo vectorial, entonces el proceso de dividir $\bold{F}$ por su magnitud para formar el campo vectorial unitario $\bold{F} /|| \bold{F} ||$ se llama normalizar el campo $\bold{F}$.
Antes de continuar con el siguiente apartado, interactúa con la siguiente escena, diseñada por Juan Carlos Ponce Campuzano, en la cual puedes modificar los componentes vectoriales; por ejemplo, intenta hacerlo con $\bold{F} (x, y) = \frac{y}{x^2+y^2}\bold{i} + \frac{x}{x^2+y^2}\bold{j}$
Recuerda que expresiones como $\frac{y}{x^2+y^2}$, en GeoGebra, se escriben así:
y/sqrt(x^2+y^2)
Hemos visto varios ejemplos de campos vectoriales en $\Reals^2$; ahora dirijamos nuestra atención a los campos vectoriales en $\Reals^3$. Estos campos vectoriales se pueden usar para modelar campos gravitacionales o electromagnéticos, y también se pueden usar para modelar el flujo de fluidos o el flujo de calor en tres dimensiones.
Un campo vectorial bidimensional en realidad solo puede modelar el movimiento del agua en un segmento bidimensional de un río (como la superficie del río). Dado que un río fluye a través de tres dimensiones espaciales, para modelar el flujo de toda la profundidad del río, necesitamos un campo vectorial en tres dimensiones.
La dimensión adicional de un campo tridimensional puede hacer que los campos vectoriales en $\Reals^3$ sean más difíciles de visualizar, pero la idea es la misma. Para visualizar un campo vectorial en $\Reals^3$, traza suficientes vectores para mostrar la forma general. Podemos usar un método similar para visualizar un campo vectorial en $\Reals^2$ eligiendo puntos en cada octante.
Al igual que con los campos vectoriales en $\Reals^2$, podemos representar campos vectoriales en $\Reals^3$ con las funciones componentes. Simplemente necesitamos una función de componente adicional para la dimensión adicional. Escribimos ya sea
$$\bold{F}(x, y, z) = \lang P(x, y, z), Q(x, y, z), R(x, y, z)\rang \tag{$6.3$}$$o
$$\bold{F}(x, y, z) = P(x, y, z)\bold{i} + Q(x, y, z)\bold{j} + R(x, y, z)\bold{k} \tag{$6.4$}$$ |
Dibujar un campo vectorial en tres dimensiones |

En el siguiente ejercicio, exploraremos uno de los casos clásicos de un campo vectorial tridimensional: un campo gravitacional.
 |
Describiendo un campo vectorial gravitacional |

En esta sección, estudiaremos un tipo especial de campo vectorial llamado campo gradiente o campo conservativo. Estos campos vectoriales son extremadamente importantes en física porque se pueden usar para modelar sistemas físicos en los que se conserva la energía. Los campos gravitacionales y los campos eléctricos asociados con una carga estática son ejemplos de campos gradiente. Recuerda que si $f $es una función (escalar) de $x$ e $y$, entonces el gradiente de $f$ es
Podemos ver la forma en que está escrito el gradiente que $\nabla f$ es un campo vectorial en $\Reals^2$. De manera similar, si $f$ es una función de $x, y$ y $z$, entonces el gradiente de $f$ es
$$grad f = \nabla f = f_x(x, y,z)\bold{i} + f_y(x, y,z)\bold{j} + f_z(x, y,z)\bold{k}$$El gradiente de una función de tres variables es un campo vectorial en $\Reals^3$. Un campo gradiente es un campo vectorial que se puede escribir como el gradiente de una función, y tenemos la siguiente definición.
 |
Dibujar un campo vectorial gradiente |

Considera la función $f (x, y) = x^2y^2$ del ejercicio anterior. La figura 6.11 muestra las curvas de nivel de esta función superpuestas en el campo vectorial gradiente de la función.
Los vectores gradiente son perpendiculares a las curvas de nivel, y las magnitudes de los vectores se hacen más grandes a medida que las curvas de nivel se acercan, porque las curvas de nivel agrupadas de cerca indican que el gráfico es empinado y la magnitud del vector gradiente es el valor más grande de la derivada direccional. Por lo tanto, puedes ver la inclinación local de un gráfico investigando el campo gradiente de la función correspondiente.
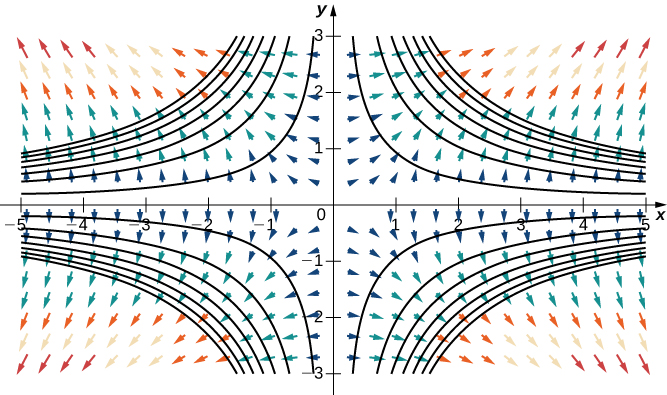
Figura 6.10. El campo gradiente de $f (x, y) = x^2y^2$ y varias curvas de nivel de $f$. Observa que a medida que las curvas de nivel se acercan, la magnitud de los vectores gradiente aumenta.
Interactúa con la siguiente escena, diseñada por Elena E. Álvarez Sáiz, en la cual se representa un campo gradiente. Observa que en el caso de un campo vectorial gradiente, en cada punto $P(x,y)$ el vector gradiente es ortogonal a la curva de nivel que pasa por dicho punto.
Se debe incluir la función escalar $f(x,y)$ y las coordenadas del campo gradiente, $M(x,y)$ y $N(x,y)$. En el caso de representar las curvas de nivel $f(x,y)=k$, se debe introducir el valor de $K$.
Cambia la función por la usada en los ejercicios anteriores: $x^2y^2$, donde $M(x,y) = 2xy^2$ y $N(x,y) = 2x^2y$.
Como aprendimos anteriormente, un campo vectorial $\bold{F}$ es un campo vectorial conservativo, o un campo gradiente si existe una función escalar $f$ tal que $\nabla f = \bold{F}$. En esta situación, $f$ se denomina función potencial para $\bold{F}$. Surgen campos vectoriales conservativos en muchas aplicaciones, particularmente en física. La razón por la que estos campos se denominan conservativos es que modelan fuerzas de sistemas físicos en los que se conserva la energía. Estudiaremos los campos vectoriales conservativos con más detalle más adelante en este capítulo.
Puedes notar que, en algunas aplicaciones, una función potencial $f$ para $\bold{F}$ se define en cambio como una función tal que $−\nabla f = \bold{F}$. Este es el caso de ciertos contextos en física; por ejemplo, observa el siguiente ejercicio.
 |
Verificación de una función potencial |

 |
Verificación de una función potencial |

Si $\bold{F}$ es un campo vectorial conservativo, entonces hay al menos una función potencial $f$ tal que $\nabla f = \bold{F}$. Pero, ¿podría haber más de una función potencial? Si es así, ¿existe alguna relación entre dos funciones potenciales para el mismo campo vectorial?
Antes de responder estas preguntas, recordemos algunos hechos del cálculo de una sola variable para guiar nuestra intuición. Recuerda que si $k (x)$ es una función integrable, entonces $k$ tiene infinitas antiderivadas. Además, si $F$ y $G$ son ambas antiderivadas de $k$, entonces $F$ y $G$ difieren solo por una constante. Es decir, hay un número $C$ tal que $F (x) = G (x) + C$.
Ahora sea $\bold{F}$ un campo vectorial conservativo y sean $f$ y $g$ funciones potenciales para $\bold{F}$. Dado que el gradiente es como una derivada, $\bold{F}$ siendo conservativo significa que $\bold{F}$ es "integrable" con las "antiderivadas" $f$ y $g$. Por lo tanto, si la analogía con el cálculo de una sola variable es válida, esperamos que haya alguna constante $C$ tal que $f (x) = g (x) + C$. El siguiente teorema dice que este es realmente el caso.
Para enunciar el siguiente teorema con precisión, debemos asumir que el dominio del campo vectorial está conectado y abierto. Estar conectado significa que si $P_1$ y $P_2$ son dos puntos cualesquiera en el dominio, entonces puede caminar de $P_1$ a $P_2$ a lo largo de un camino que permanece completamente dentro del dominio.
Dado que $f$ y $g$ son funciones potenciales para $\bold{F}$, entonces $\nabla f = f - g = \nabla f - \nabla g = \bold{F} - \bold{F} = 0$. Sea $h = f - g$, entonces tenemos $\nabla h = 0$. Nos gustaría demuestrar que $h$ es una función constante.
Supón que $h$ es una función de $x$ e $y$ (la lógica de esta demostración se extiende a cualquier número de variables independientes). Como $\nabla h = 0$, tenemos $h_x = 0$ e $h_y = 0$. La expresión $h_x = 0$ implica que $h$ es una función constante con respecto a $x$, es decir, $h (x, y) = k_1 (y)$ para alguna función $k_1$. De manera similar, $h_y = 0$ implica $h (x, y) = k_2 (x)$ para alguna función $k_2$. Por lo tanto, la función $h$ depende solo de $y$ y también depende solo de $x$. Por lo tanto, $h (x, y) = C$ para alguna constante $C $en el dominio conectado de $\bold{F}$. Observa que realmente necesitamos conectividad en este punto; si el dominio de $\bold{F}$ viene en dos piezas separadas, entonces $k$ podría ser una constante $C_1$ en una pieza pero podría ser una constante diferente $C_2$ en la otra pieza. Dado que $f - g = h = C$, tenemos que $f - g + C$, como se desea.
Los campos vectoriales conservativos también tienen una propiedad especial llamada propiedad parcial cruzada. Esta propiedad ayuda a probar si un campo vectorial dado es conservativo.
Como $\bold{F}$ es conservativa, hay una función $f (x, y)$ tal que $\nabla f = \bold{F}$. Por lo tanto, según la definición del gradiente, $f_x = P$ y $f_y = Q$. Según el teorema de Clairaut, $f_{xy} = f_{yx}$, Pero, $f_{xy} = P_y$ y $f_{yx} = Q_x$, y por tanto $P_y = Q_x$.
El teorema de Clairaut proporciona una prueba rápida de la propiedad parcial cruzada de los campos vectoriales conservativos en $\Reals^3$, tal como lo hizo para los campos vectoriales en $\Reals^2$.
La propiedad transversal de los campos vectoriales conservativos muestra que la mayoría de los campos vectoriales no son conservativos. La propiedad de parciales cruzados es difícil de satisfacer en general, por lo que la mayoría de los campos vectoriales no tendrán parciales cruzados iguales.
 |
Demostrar que un campo vectorial no es conservativo |

 |
Demostrar que un campo vectorial no es conservativo |

Concluimos esta sección con una advertencia: La propiedad de parciales cruzados de los campos vectoriales conservativos dice que si $\bold{F}$ es conservativo, $\bold{F}$ tiene la propiedad de parciales cruzados. El teorema no dice que, si $\bold{F}$ tiene la propiedad de parciales cruzados, entonces $\bold{F}$ es conservativo (el inverso de una implicación no es lógicamente equivalente a la implicación original).
En otras palabras, la propiedad entre parciales de los campos vectoriales conservativos solo puede ayudar a determinar que un campo no es conservativo; no le permite concluir que un campo vectorial sea conservativo. Por ejemplo, considera el campo vectorial $\bold{F} (x, y) = \big\lang x^2y, \frac{x^3}{3}\big\rang$. Este campo tiene la propiedad de parciales cruzados, por lo que es natural intentar usar la propiedad de parciales cruzados de los campos vectoriales conservativos para concluir que este campo vectorial es conservativo.
Sin embargo, esta es una mala aplicación del teorema. Más adelante aprenderemos cómo concluir que $\bold{F}$ es conservativo.

1. El dominio del campo vectorial $\bold{F} = \bold{F} (x, y)$ es un conjunto de puntos $(x, y)$ en un plano, y el rango de $\bold{F}$ es un conjunto de ¿qué en el plano? (Solución).
 Para los siguientes ejercicios, determine si la afirmación es verdadera o falsa.
Para los siguientes ejercicios, determine si la afirmación es verdadera o falsa.
2. El campo vectorial $\bold{F} = \big\lang 3x^2, 1\big\rang$ es un campo gradiente para $\phi_1 (x, y) = x^3 + y$ y $\phi_2 (x, y) = y + x^3 + 100$. 3. El campo vectorial $\bold{F} = \sqrt{\lang y, x\rang}{\sqrt{x^2+y^2}}$ es constante en la dirección y magnitud sobre un círculo unitario (Solución). 4. El campo vectorial $\bold{F} = = \sqrt{\lang y, x\rang}{\sqrt{x^2+y^2}}$ no es un campo radial ni rotacional.
 Para los siguientes ejercicios, describe cada campo vectorial dibujando algunos de sus vectores.
Para los siguientes ejercicios, describe cada campo vectorial dibujando algunos de sus vectores.
5. [T] $\bold{F}(x, y) = x\bold{i} + y\bold{j}$ (Solución). 6. [T] $\bold{F}(x, y) = −y\bold{i} + x\bold{j}$ 7. [T] $\bold{F}(x, y) = x\bold{i} − y\bold{j}$ (Solución). 8. [T] $\bold{F}(x, y) = \bold{i} + \bold{j}$ 9. [T] $\bold{F}(x, y) = 2x\bold{i} + 3y\bold{j}$ (Solución). 10. [T] $\bold{F}(x, y) = 3\bold{i} + x\bold{j}$
11. [T] $\bold{F}(x, y) = y\bold{i} + sin x\bold{j}$ (Solución). 12. [T] $\bold{F}(x, y,z) = x\bold{i} + y\bold{j} + z\bold{k}$ 13. [T] $\bold{F}(x, y,z) = 2x\bold{i} − 2y\bold{j} − 2z\bold{k}$ (Solución). 14. [T] $\bold{F}(x, y,z) = \frac{y}{z}\bold{i} − \frac{x}{z}\bold{j}$
 Para los siguientes ejercicios, encuentra el campo vectorial gradiente de cada función $f$.
Para los siguientes ejercicios, encuentra el campo vectorial gradiente de cada función $f$.
15. $f(x, y) = xsen\; y + cos\; y$ (Solución). 16. $f(x, y, z) = ze^{−xy}$ 17. $f(x, y, z) = x^2y + xy + y^2z$ (Solución). 18. $f(x, y) = x^2sen(5y)$ 19. $f(x, y) = ln\big(1 + x^2 + 2y^2\big)$ (Solución). 20. $f(x, y, z) = x cos\big(\frac{y}{z}\big)$ 21. ¿Cuál es el campo vectorial $\bold{F} (x, y)$ con un valor en $(x, y)$ que es de longitud unitaria y apunta hacia $(1, 0)$? (Solución).
 Para los siguientes ejercicios, escribe fórmulas para los campos vectoriales con las propiedades dadas.
Para los siguientes ejercicios, escribe fórmulas para los campos vectoriales con las propiedades dadas.
22. Todos los vectores son paralelos al eje $x$ y todos los vectores en una línea vertical tienen la misma magnitud. 23. Todos los vectores apuntan hacia el origen y tienen una longitud constante (Solución). 24. Todos los vectores son de longitud unitaria y son perpendiculares al vector de posición en ese punto.
25. Da una fórmula $\bold{F} (x, y) = M (x, y)\bold{i} + N (x, y)\bold{j}$ para el campo vectorial en un plano que tiene las propiedades de que $\bold{F} = 0$ en $(0, 0)$ y que en cualquier otro punto $(a, b)$, $\bold{F}$ es tangente al círculo $x^2 + y^2 = a^2 + b^2$ y apunta en el sentido de las agujas del reloj con magnitud $| \bold{F} | = \sqrt{a^2 + b^2}$ (Solución). 26. ¿Es el campo vectorial $\bold{F} (x, y) = P (x, y), Q (x, y) = (sin \;x + y)\bold{i} + (cos y + x)\bold{j}$ un campo gradiente? 27. Encuentra una fórmula para el campo vectorial $\bold{F} (x, y) = M (x, y)\bold{i} + N (x, y)\bold{j}$ dado el hecho de que para todos los puntos $(x, y)$, $\bold{F}$ apunta hacia el origen y $| \bold{F} | = \frac{10}{x^2 + y^2}$ (Solución).
 Para los siguientes ejercicios, supón que un campo eléctrico en el plano $xy$ causado por una línea infinita de carga a lo largo del eje $x$ es un campo gradiente con función potencial $V (x, y) = c\; ln\bigg(\frac{r_0}{\sqrt{x^2 + y^2}}\bigg)$, donde $c\gt 0$ es una constante y $r_0$ es una distancia de referencia en la que se supone que el potencial es cero.
Para los siguientes ejercicios, supón que un campo eléctrico en el plano $xy$ causado por una línea infinita de carga a lo largo del eje $x$ es un campo gradiente con función potencial $V (x, y) = c\; ln\bigg(\frac{r_0}{\sqrt{x^2 + y^2}}\bigg)$, donde $c\gt 0$ es una constante y $r_0$ es una distancia de referencia en la que se supone que el potencial es cero.
28. Encuentra las componentes del campo eléctrico en las direcciones $x$ e $y$, donde $\bold{E} (x, y) = −\nabla V (x, y)$. 29. Demuestra que el campo eléctrico en un punto del plano $xy$ se dirige hacia afuera desde el origen y tiene magnitud $\bold{E} = \frac{c}{r}$, donde $r = x^2 = y^2$ (Solución).
 Una línea de flujo (o línea de corriente) de un campo vectorial $\bold{F}$ es una curva $r (t)$ tal que $d\bold{r} / dt = \bold{F} (r (t))$. Si $\bold{F}$ representa el campo de velocidad de una partícula en movimiento, entonces las líneas de flujo son trayectorias tomadas por la partícula.
Una línea de flujo (o línea de corriente) de un campo vectorial $\bold{F}$ es una curva $r (t)$ tal que $d\bold{r} / dt = \bold{F} (r (t))$. Si $\bold{F}$ representa el campo de velocidad de una partícula en movimiento, entonces las líneas de flujo son trayectorias tomadas por la partícula.
Por lo tanto, las líneas de flujo son tangentes al campo vectorial. Para los siguientes ejercicios, demuestra que la curva $\bold{c} (t)$ dada es una línea de flujo del campo vectorial de velocidad dado $\bold{F} (x, y, z)$.
30. $\bold{c} (t) = \big(e^{2t}, ln | t |, \frac{1}{t}\big), t \cancel{=} 0; \bold{F} (x, y, z) = \lang 2x, z, −z^2\rang$. 31. $\bold{c} (t) = sen\; t, cos\; t, e^t; \bold{F} (x, y, z) = \lang y, −x, z\rang$ (Solución).
 Para los siguientes ejercicios, sea $\bold{F} = x\bold{i} + y\bold{j}, \bold{G} = −y\bold{i} + x\bold{j}$ y $\bold{H} = x\bold{i} - y\bold{j}$. Une $\bold{F}, \bold{G}$ y $\bold{H}$ con sus gráficas.
Para los siguientes ejercicios, sea $\bold{F} = x\bold{i} + y\bold{j}, \bold{G} = −y\bold{i} + x\bold{j}$ y $\bold{H} = x\bold{i} - y\bold{j}$. Une $\bold{F}, \bold{G}$ y $\bold{H}$ con sus gráficas.
32.
 33. (Solución).
33. (Solución).
34.
 Para los siguientes ejercicios, sea $\bold{F} = x\bold{i} + y\bold{j}, \bold{G} = −y\bold{i} + x\bold{j}$ y $\bold{H} = −x\bold{i} + y\bold{j}$. Haz coincidir los campos vectoriales con sus gráficos en (I) - (IV).
Para los siguientes ejercicios, sea $\bold{F} = x\bold{i} + y\bold{j}, \bold{G} = −y\bold{i} + x\bold{j}$ y $\bold{H} = −x\bold{i} + y\bold{j}$. Haz coincidir los campos vectoriales con sus gráficos en (I) - (IV).
35. (Solución).
Antes de iniciar el siguiente apartado, te compartimos la unidad interactiva "Campos vectoriales" del Proyecto Prometeo. Esta unidad fue diseñada por Alejandro Radillo Díaz, como introduccción a los campos vectoriales y a las herramientas usadas en su estudio, tales como el rotacional y la divergencia (que veremos más adelante). Se plantean dichas herramientas considerando elementos de volumen finitos (un disco que gira para el rotacional y una caja en la que entra o sale flujo para la divergencia). Con ello se pretende que el alumno tenga una noción física de cómo funcionan dichas herramientas y su asociación con la fórmula para rotacional y divergencia cuando dichos elementos de volumen se hacen infinitesimales. Finalmente se concluye con un resumen de lo aprendido y la relación formal con la definición de rotacional y divergencia en tres dimensiones, en los que profundizaremos en próximos apartados.
Estamos familiarizados con integrales de una sola variable de la forma $\displaystyle\int_a^bf (x) dx$, donde el dominio de integración es un intervalo $[a, b]$. Dicho intervalo se puede considerar como una curva en el plano $xy$, ya que el intervalo define un segmento de línea con puntos finales $(a, 0)$ y $(b, 0)$; en otras palabras, un segmento de línea ubicado en el eje $x$. Supón que queremos integrar sobre cualquier curva en el plano, no solo sobre un segmento de línea en el eje $x$. Tal tarea requiere un nuevo tipo de integral, llamada integral de línea.
Las integrales de línea tienen muchas aplicaciones en ingeniería y en física. También nos permiten hacer varias generalizaciones útiles del Teorema fundamental del cálculo. Y están estrechamente relacionadas con las propiedades de los campos vectoriales, como veremos.
Una integral de línea nos da la capacidad de integrar funciones multivariables y campos vectoriales sobre curvas arbitrarias en un plano o en el espacio. Hay dos tipos de integrales de línea: integrales de línea escalares e integrales de línea vectoriales. Las integrales de línea escalares son integrales de una función escalar sobre una curva en un plano o en el espacio.
Las integrales de línea vectoriales son integrales de un campo vectorial sobre una curva en un plano o en el espacio. Veamos primero las integrales de línea escalares.
Una integral de línea en un campo escalar, o integral de línea escalar, se define tal como se define una integral de variable única, excepto que para una integral de línea en un campo escalar, el integrando es una función de más de una variable y el dominio de integración es una curva en un plano o en el espacio, como opuesto a una curva en el eje $x$.
Para una integral de línea escalar, dejamos que $C$ sea una curva suave en un plano o en el espacio y sea $f$ una función con un dominio que incluya a $C$. Cortamos la curva en trozos pequeños. Para cada pieza, elegimos el punto $P$ en esa pieza y evaluamos $f$ en $P$ (podemos hacer esto porque todos los puntos en la curva están en el dominio de $f$). Multiplicamos $f (P)$ por la longitud del arco de la pieza $\Delta s$, agregamos el producto $f (P) \Delta s $ sobre todas las piezas y luego dejamos que la longitud del arco de las piezas se reduzca a cero tomando un límite. El resultado es la integral de línea escalar de la función sobre la curva.
Para una descripción formal de una integral de línea escalar, sea $C$ una curva suave en el espacio dada por la parametrización $\bold{r} (t) = \lang x (t), y (t), z (t)\rang$, $a \le t \le b$. Sea $f (x, y, z)$ una función con un dominio que incluye la curva $C$. Para definir la integral de línea de la función $f$ sobre $C$, comenzamos como comienzan la mayoría de las definiciones de una integral: cortamos la curva en trozos pequeños. Dividimos el intervalo de parámetros $[a, b]$ en $n$ subintervalos $[t_{i - l}, t_i]$ de igual ancho para $l \le i \le n$, donde $t_0 = a$ y $t_n = b$ (Figura 6.12). Dejamos que $t_i^*$ sea un valor en el i-ésimo intervalo $[t_{i - l}, t_i]$. Denotamos los puntos finales de $\bold{r} (t_0), \bold{r}(t_1),…, \bold{r} (t_n)$ por $P_0,…, P_n$. Los puntos $P_i$ dividen la curva $C$ en $n$ piezas $C_1, C_2,…, C_n$, con longitudes $\Delta s_1, \Delta s_2, … , \Delta s_n$, respectivamente.
Sea $P_i^*$ el punto final de $\bold{r} (t_i^*)$ para $1 \le i \le n$. Ahora, evaluamos la función $f$ en el punto $P_i^*$ para $1 \le i \le n$. Ten en cuenta que $P_i^*$ está en la pieza $C_1$ y, por lo tanto, $P_i^*$ está en el dominio de $f$. Multiplicamos $f\big(P_i^*\big)$ por la longitud $\Delta s_1$ de $C_1$, que da el área de la “hoja” con base $C_1$, y la altura $f\big(P_i^*\big)$. Esto es análogo a usar rectángulos para aproximar el área en una integral de una sola variable. Ahora, formamos la suma $\displaystyle\sum_{i=1}^n f\big(P_i^*\big)\Delta s_i$. Observa la similitud de esta suma con una suma de Riemann; de hecho, esta definición es una generalización de una suma de Riemann a curvas arbitrarias en el espacio. Al igual que con las sumas e integrales de Riemann de forma $\displaystyle\int_a^bg (x) dx$, definimos una integral dejando que el ancho de las piezas de la curva se reduzca a cero tomando un límite. El resultado es la integral de línea escalar de $f$ a lo largo de C.
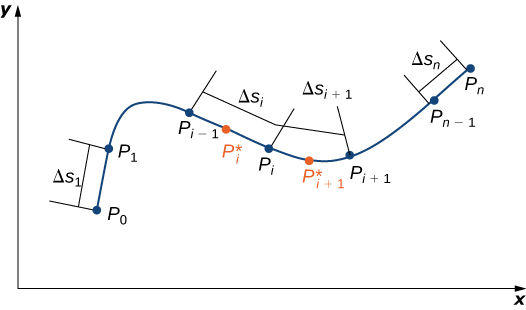
Figura 6.12. La curva $C$ se ha dividido en $n$ piezas y se ha elegido un punto dentro de cada pieza.
Es posible que hayas notado una diferencia entre esta definición de una integral de línea escalar y una integral de una sola variable. En esta definición, las longitudes de arco $\Delta s_1, \Delta s_2, … , \Delta s_n$ no son necesariamente iguales; en la definición de integral de una sola variable, la curva en el eje $x$ se divide en partes de igual longitud. Esta diferencia no tiene ningún efecto en el límite. A medida que reducimos las longitudes de arco a cero, sus valores se acercan lo suficiente como para que cualquier pequeña diferencia se vuelva irrelevante.
Si $f$ es una función continua en una curva suave $C$, entonces $\int_Cf ds$ siempre existe. Dado que $\int_Cf ds$ se define como un límite de las sumas de Riemann, la continuidad de $f$ es suficiente para garantizar la existencia del límite, así como la integral $\int_a^bg (x) dx$ existe si $g$ es continua sobre $[a, b]$.
Antes de ver cómo calcular una integral de línea, debemos examinar la geometría capturada por estas integrales. Supón que $f (x, y) \ge 0$ para todos los puntos $(x, y)$ en una curva plana suave $C$. Imagina tomar la curva $C$ y proyectarla "hacia arriba" a la superficie definida por $f (x, y)$, creando así una nueva curva $C^{\prime}$ que se encuentra en la gráfica de $f (x, y)$ (Figura 6.13). Ahora dejamos caer una “hoja” desde $C^{\prime}$ hasta el plano $xy$. El área de esta hoja es $\int_Cf (x, y) ds$ Si $f (x, y) \le 0$ para algunos puntos en $C$, entonces el valor de $\int_Cf (x, y) ds$ es el área por encima del plano $xy$ menos el área por debajo del plano $xy$ (observa la similitud con integrales de la forma $\int_a^bg (x) dx$).
Figura 6.13. El área de la hoja azul es $\int_Cf (x, y) ds$
A partir de esta geometría, podemos ver que la integral de línea $\displaystyle\int_Cf (x, y) ds$ no depende de la parametrización $\bold{r} (t)$ de $C$. Siempre que la curva sea recorrida exactamente una vez por la parametrización, el área de la hoja formada por la función y la curva es la misma. Este mismo tipo de argumento geométrico se puede ampliar para mostrar que la integral de línea de una función de tres variables sobre una curva en el espacio no depende de la parametrización de la curva.
 |
Hallando el valor de una integral de línea |

Observa que en una integral de línea escalar, la integración se realiza con respecto a la longitud del arco $s$, lo que puede hacer que una integral de línea escalar sea difícil de calcular. Para facilitar los cálculos, podemos traducir $\displaystyle\int_Cf ds$ a una integral con una variable de integración que es $t$.
Sea $\bold{r} (t) = \lang x (t), y (t), z (t)\rang$ para $a \le t \le b$ una parametrización de $C$. Dado que asumimos que $C$ es suave, $\bold{r^{\prime}} (t) = \lang x^{\prime} (t), y^{\prime} (t), z^{\prime} (t)\rang$ es continua para todo $t$ en $[a, b]$. En particular, $x^{\prime}(t), y ^{\prime} (t)$ y $z^{\prime}(t)$ existen para todo $t$ en $[a, b]$. Según la fórmula de la longitud del arco, tenemos
Si el ancho $\Delta t_i = t_i - t_{i - 1}$ es pequeño, entonces la función $\displaystyle\int_{t_{i-1}}^{t_i} ||\bold{r}^{\prime}||dt \approx ||\bold{r}^{\prime}t_i^*|| \Delta t_i, ||\bold{r}^{\prime}(t)||$ es casi constante en el intervalo $[t_{i - 1}, t_i]$. Por lo tanto,
$$\int_{t_{i-1}}^{t_i} ||\bold{r}^{\prime}||dt \approx ||\bold{r}^{\prime}\big(t_i^*\big)|| \Delta t_i$$y tenemos
$$\sum_{i=1}^nf\big(\bold{r}\big(t_i^*\big)\big)\Delta s_i = \sum_{i=1}^nf\big(\bold{r}\big(t_i^*\big)\big)||\bold{r}^{\prime}\big(t_i^*\big)|| \Delta t_i \tag{$6.6$}$$Ver figura Figura 6.15.
Figura 6.15. Si ampliamos la curva lo suficiente haciendo $\Delta t_i$ muy pequeño, entonces la parte correspondiente de la curva es aproximadamente lineal.
Observa que
$$\lim\limits_{n \to \infin} \sum_{i=1}^nf\big(\bold{r}\big(t_i^*\big)\big)||\bold{r}^{\prime}\big(t_i^*\big)|| \Delta t_i = \int_a^b f(\bold{r}(t)) ||\bold{r}^{\prime}||dt$$En otras palabras, a medida que los anchos de los intervalos $[t_{i −1}, t_i]$ se reducen a cero, la suma $\sum_{i=1}^nf\big(\bold{r}\big(t_i^*\big)\big)||\bold{r}^{\prime}\big(t_i^*\big)|| \Delta t_i$ converge a la integral $\int_a^bf (r (t)) || r^{\prime} (t)|| dt$. Por lo tanto, tenemos el siguiente teorema.
Aunque hemos etiquetado la ecuación 6.6 como una ecuación, se considera con mayor precisión una aproximación porque podemos demostrar que el lado izquierdo de la ecuación 6.6 se aproxima al lado derecho cuando $n \to\infin$. En otras palabras, dejar que el ancho de las piezas se reduzca a cero hace que la suma de la derecha se acerque arbitrariamente a la suma de la izquierda. Ya que
$$||\bold{r}^{\prime}|| = \sqrt{\big(x^{\prime}\big)^2 + \big(y^{\prime}\big)^2 + \big(z^{\prime}\big)^2}$$obtenemos el siguiente teorema, que usamos para calcular integrales de línea escalares.
Ten en cuenta que una consecuencia de este teorema es la ecuación $ds = ||\bold{r}^{\prime}(t)|| dt$. En otras palabras, el cambio en la longitud del arco puede verse como un cambio en el dominio $t$, escalado por la magnitud del vector $\bold{r}^{\prime}(t)$.
 |
Evaluando una integral de línea |

 |
Independencia de la parametrización |

Ahora que podemos evaluar integrales de línea, podemos usarlas para calcular la longitud del arco. Si $f (x, y, z) = 1$, entonces
$$\begin{aligned} \int_C f(x,y,z)ds &= \lim\limits_{n \to \infin}\sum_{i=1}^n f\big(t_i^*\big)\Delta s_i\\ &= \lim\limits_{n \to \infin}\sum_{i=1}^n \Delta s_i\\ &= \lim\limits_{n \to \infin} \text{ longitud}(C)\\ &= \text{ longitud}(C) \end{aligned}$$Por lo tanto, $\displaystyle\int_C1d$s es la longitud de arco de $C$.
 |
Calculando la longitud de arco |

En la siguiente escena interactiva, diseñada por Elena E. Álvarez Sáiz, se muestra la interpretación geométrica de la integral de línea de un campo escalar sobre una curva plana. El campo escalar a elegir puede venir dado por la tercera componente de una curva en el espacio que se proyecta sobre la curva plana o por el valor de una función de dos variables que es evaluable en los puntos de la curva plana.
El segundo tipo de integrales de línea son las integrales de línea vectoriales, o integrales de línea en un campo vectorial, en las que integramos a lo largo de una curva a través de un campo vectorial. Por ejemplo, sea
$$\bold{F} (x, y, z) = P (x, y, z)\bold{i} + Q (x, y, z)\bold{j} + R (x, y, z)\bold{k}$$un campo vectorial continuo en $Reals^3$ que representa una fuerza sobre una partícula, y sea $C$ una curva suave en $Reals^3$ contenida en el dominio de $\bold{F}$. ¿Cómo calcularíamos el trabajo realizado por $\bold{F}$ al mover una partícula a lo largo de $C$?
Para responder a esta pregunta, primero ten en cuenta que una partícula podría viajar en dos direcciones a lo largo de una curva: una dirección hacia adelante y una dirección hacia atrás. El trabajo realizado por el campo vectorial depende de la dirección en la que se mueve la partícula. Por lo tanto, debemos especificar una dirección a lo largo de la curva $C$; tal dirección especificada se llama orientación de una curva.
La dirección especificada es la dirección positiva a lo largo de $C$; la dirección opuesta es la dirección negativa a lo largo de $C$. Cuando a C se le ha dado una orientación, a $C$ se le llama curva orientada (Figura 6.16). El trabajo realizado en la partícula depende de la dirección a lo largo de la curva en la que se mueve la partícula.
Una curva cerrada es aquella para la que existe una parametrización $\bold{r} (t), a \le t \le b$, tal que $\bold{r} (a) = \bold{r} (b)$, y la curva se recorre exactamente una vez. En otras palabras, la parametrización es uno a uno en el dominio $(a, b)$.
Figura 6.16. (a) Una curva orientada entre dos puntos. (b) Una curva orientada cerrada
Sea $\bold{r} (t)$ una parametrización de $C$ para $a \le t \le b$ tal que la curva sea atravesada exactamente una vez por la partícula y la partícula se mueva en la dirección positiva a lo largo de $C$. Divide el intervalo de parámetros $[a, b]$ en $n$ subintervalos $[t_{i - 1}, t_i]$, $0 \le i \le n$, de igual ancho. Denota los puntos finales de $\bold{r} (t_0), \bold{r} (t_1), … , \bold{r} (t_n)$ por $P_0, …, P_n$. Los puntos $P_i$ dividen $C$ en $n$ piezas. Denota la longitud de la pieza de $P_{i − 1}$ a $P_i$ por $\Delta s_i$. Para cada $i$, elige un valor $t_i^*$ en el subintervalo $[t_{i - 1}, t_i]$.
Entonces, el punto final de $\bold{r} (t_i^*)$ es un punto en la pieza de $C$ entre $P_{i - 1}$ y $P_i$ (Figura 6.17). Si $\Delta s_i$ es pequeño, entonces a medida que la partícula se mueve de $P_{i - 1}$ a $P_i$ a lo largo de $C$, se mueve aproximadamente en la dirección de $\bold{T}(P_i)$, el vector tangente unitario en el punto final de $\bold{r} (t_i^*)$. Sea $P_i^*$ el punto final de $\bold{r} (t_i^*)$. Entonces, el trabajo realizado por el campo del vector de fuerza al mover la partícula de $P_{i −1}$ a $P_i$ es $\bold{F}\big(P_i^*\big)\cdot\big(\Delta s_i\bold{T}(P_i^*)\big)$, por lo que el trabajo total realizado a lo largo de $C$ es
$$\sum_{i=1}^n\bold{F}\big(P_i^*\big)\cdot\big(\Delta s_i \bold{T}\big(P_i^*\big)\big) = \sum_i^n \bold{F}\big(P_i^*\big)\cdot \bold{T}\big(P_i^*\big)\Delta s_i$$
Figura 6.17. La curva $C$ se divide en $n$ piezas y un punto dentro de cada pieza se elige. El producto escalar de cualquier vector tangente en la i-ésima pieza con el vector correspondiente $\bold{F}$ se aproxima por $\bold{F}\big(P_i^*\big)\cdot \bold{T}\big(P_i^*\big)$.
Al dejar que la longitud del arco de las piezas de $C$ se vuelva arbitrariamente pequeña tomando un límite como $n \to \infin$ nos da el trabajo realizado por el campo al mover la partícula a lo largo de $C$. Por lo tanto, el trabajo realizado por $\bold{F}$ al mover la partícula en la dirección positiva a lo largo de $C$ se define como
$$W = \int_C \bold{F}\cdot\bold{T}ds$$lo que nos da el concepto de integral de línea vectorial o, si se prefiere, integral de línea en un campo vectorial.
Con las integrales de línea escalar, ni la orientación ni la parametrización de la curva importan. Siempre que la curva sea atravesada exactamente una vez por la parametrización, el valor de la integral de línea no se modifica. Con integrales de línea vectorial, la orientación de la curva sí importa. Si pensamos en la integral de línea como trabajo de computación, entonces esto tiene sentido: si subes una montaña, entonces la fuerza gravitacional de la Tierra hace un trabajo negativo sobre ti. Si caminas por la montaña exactamente por el mismo camino, entonces la fuerza gravitacional de la Tierra hace un trabajo positivo en ti. En otras palabras, invertir la ruta cambia el valor del trabajo de negativo a positivo en este caso. Ten en cuenta que si $C$ es una curva orientada, entonces dejamos que $−C $represente la misma curva pero con orientación opuesta.
Al igual que con las integrales de línea escalares, es más fácil calcular una integral de línea vectorial si la expresamos en términos de la función de parametrización $\bold{r}$ y la variable $t$. Para traducir la integral $\int_C\bold{F}\cdot\bold{T}ds$ en términos de $t$, observa que el vector unitario tangente $\bold{T}$ a lo largo de $C$ está dado por $\bold{T} = \frac{\bold{r}^{\prime}(t)}{||\bold{r}^{\prime}(t) ||}$ (asumiendo $||\bold{r}^{\prime}(t) || \cancel{=} 0$).
Dado que $ds = ||\bold{r}^{\prime}(t) || dt$, como vimos al discutir las integrales de línea escalar, tenemos
$$\bold{F}\cdot\bold{T}ds = \bold{F}\big(\bold{r}(t)\big) \cdot \frac{\bold{r}^{\prime}(t)}{||\bold{r}^{\prime}(t) ||}||\bold{r}^{\prime}(t) ||dt = \bold{F}\big(\bold{r}(t)\big) \cdot \bold{r}^{\prime}(t)$$Por lo tanto, tenemos la siguiente fórmula para calcular integrales de líneas vectoriales:
$$\int_C\bold{F}\cdot\bold{T}ds = \int_a^b \bold{F}\big(\bold{r}(t)\big) \cdot \bold{r}^{\prime}(t)dt \tag{$6.9$}$$Debido a la ecuación 6.9, a menudo usamos la notación $\displaystyle\int_\bold{F} \cdot d\bold{r}$ para la integral de línea $\displaystyle\int_C\bold{F} \cdot \bold{T}ds$. Si $\bold{r} (t) = \lang x (t), y (t), z (t)\rang$, entonces $d\bold{r}$ denota el vector $\lang x^{\prime}(t), y ^{\prime} (t), z^{\prime} (t)\rang$.
 |
Evaluando una integral de línea vectorial |

 |
Orientación inversa |

Sea $C$ una curva orientada y $−C$ la misma curva pero con la orientación invertida. Luego, los dos ejercicios anteriores ilustran el siguiente hecho:
$$\int_C\bold{F} \cdot d\bold{r} = -\int_{-C}\bold{F} \cdot d\bold{r}$$Es decir, invertir la orientación de una curva cambia el signo de una integral de línea.
Otra notación estándar para la integral $\int_C\bold{F} \cdot d\bold{r}$ es $\int_C Pdx + Qdy + Rdz$. En esta notación, $P, Q$ y $R$ son funciones, y pensamos en $d\bold{r}$ como el vector $\lang dx, dy, dz\rang$. Para justificar esta convención, recuerda que $d\bold{r} = \bold{T}ds = \bold{r}^{\prime}(t) dt = \lang \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt}\rang dt$. Por lo tanto,
$$\int_C\bold{F} \cdot d\bold{r} = \lang P, Q, R \rang \cdot \lang dx, dy, dz \rang = Pdx + Qdy + Rdz$$Si $d\bold{r}\lang dx, dy, dz \rang$, entonces $\frac{d\bold{r}}{dt} = \lang \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt}\rang dt$. Por lo tanto
 |
Hallando el valor de una integral de la forma $\displaystyle\int_C Pdx + Qdy + Rdz$ |

Hemos aprendido a integrar curvas de orientación suave. Ahora, supón que $C$ es una curva orientada que no es suave, pero que puede escribirse como la unión de un número finito de curvas suaves. En este caso, decimos que $C$ es una curva suave a trozos. Para ser precisos, la curva $C$ es suave por partes si $C $se puede escribir como una unión de $n$ curvas suaves $C_1, C_2, …, C_n$ de manera que el punto final de $C_i$ es el punto de partida de $C_{i + 1}$ (Figura 6.19). Cuando las curvas $C_i$ satisfacen la condición de que el punto final de $C_i$ es el punto inicial de $C_{i + 1}$, escribimos su unión como $C_1 + C_2 + \cdots + C_n.$
El siguiente teorema resume varias propiedades clave de las integrales de líneas vectoriales.
Figura 6.19. La unión de $C_1, C_2, C_3$ es una curva suave a trozos.
Observa las similitudes entre estos elementos y las propiedades de las integrales de una sola variable. Las propiedades i. y ii. dicen que las integrales de línea son lineales, lo cual también es cierto para las integrales de una sola variable. La propiedad iii. dice que invertir la orientación de una curva cambia el signo de la integral. Si pensamos en la integral como el cálculo del trabajo realizado en una partícula que viaja a lo largo de $C$, entonces esto tiene sentido. Si la partícula se mueve hacia atrás en lugar de hacia adelante, entonces el valor del trabajo realizado tiene el signo opuesto. Esto es análogo a la ecuación $\int_a^b f(x)dx = -\int_b^a f(x)dx$. Finalmente, si $[a_1, a_2], [a_2, a_3],…, [a_{n − 1}, a_n]$ son intervalos, entonces
$$\int_{a_1}^{a_n} f(x)dx = \int_{a_1}^{a_2} f(x)dx + \int_{a_2}^{a_3} f(x)dx +\cdots + \int_{a_{n-1}}^{a_n} f(x)dx$$que es análogo a la propiedad iv.
 |
Usando las propiedades para calcular una integral de línea vectorial |
Figura 6.20. Rectángulo y campo vectorial

Para terminar este apartado, presentamos la siguiente escena interactiva, diseñada por Elena E. Álvarez Sáiz, en la cual se muestra cómo la integral de línea de un campo vectorial a lo largo de una curva, es la integral de línea de la componente tangencial del campo a la curva. Si $\bold{F}$ es un campo de fuerzas en el espacio, entonces una partícula que se mueva a lo largo de una curva mientras actúa sobre ella $\bold{F}$, realizará un trabajo $W$. Para calcular este trabajo se hace una partición de la curva $C$ y se calcula el trabajo parcial realizado por $\bold{F}$ para mover una partícula sobre un subarco cualquiera de la partición. El trabajo total será la suma de los trabajos sobre todos los subarcos considerados en $C$.
Las integrales de línea escalar tienen muchas aplicaciones. Se pueden usar para calcular la longitud o masa de un cable, el área de superficie de una hoja de una altura determinada o el potencial eléctrico de un cable cargado dada una densidad de carga lineal. Las integrales de línea vectoriales son extremadamente útiles en física. Se pueden usar para calcular el trabajo realizado en una partícula a medida que se mueve a través de un campo de fuerza, o el caudal de un fluido a través de una curva. Aquí, calculamos la masa de un cable usando una integral de línea escalar y el trabajo realizado por una fuerza usando una integral de línea vectorial.
Supón que un trozo de alambre está modelado por la curva $C$ en el espacio. La masa por unidad de longitud (la densidad lineal) del cable es una función continua $\rho (x, y, z)$. Podemos calcular la masa total del cable usando la integral de línea escalar $\int_C\rho (x, y, z) ds$.
La razón es que la masa es la densidad multiplicada por la longitud y, por lo tanto, la densidad de una pequeña pieza del cable se puede aproximar por $\rho x^*, y^*, z^* \Delta s$ para algún punto $(x^*, y^*, z^*)$ en la pieza. Al dejar que la longitud de las piezas se reduzca a cero con un límite, se obtiene la integral de línea $\int_C\rho (x, y, z) ds$.
 |
Calculando la masa de un cable |
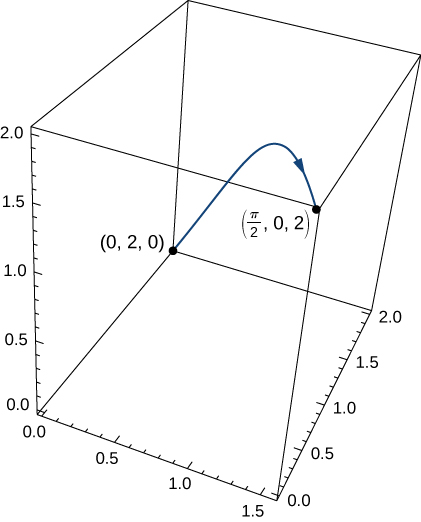
Figura 6.21. El cable parametrizado.

Cuando definimos por primera vez las integrales de línea vectorial, usamos el concepto de trabajo para motivar la definición. Por lo tanto, no es sorprendente que el cálculo del trabajo realizado por un campo vectorial que representa una fuerza sea un uso estándar de integrales de líneas vectoriales. Recuerda que si un objeto se mueve a lo largo de la curva $C$ en el campo de fuerza $\bold{F}$, entonces el trabajo requerido para mover el objeto está dado por $\int_C\bold{F}\cdot d\bold{r}$.
 |
Calculando el trabajo |

Cerramos esta sección discutiendo dos conceptos clave relacionados con las integrales de línea: flujo a través de una curva plana y circulación a lo largo de una curva plana. El flujo se utiliza en aplicaciones para calcular el flujo de un fluido a través de una curva, y el concepto de circulación es importante para caracterizar campos de gradientes conservativos en términos de integrales de línea. Ambos conceptos se utilizan mucho en el resto de este capítulo. La idea de flujo es especialmente importante para el teorema de Green, y en dimensiones superiores para el teorema de Stokes y el teorema de divergencia.
Sea $C$ una curva plana y sea $\bold{F}$ un campo vectorial en el plano. Imagina que $C$ es una membrana a través de la cual fluye el fluido, pero $C$ no impide el flujo del fluido. En otras palabras, $C$ es una membrana idealizada invisible para el fluido. Supón que $\bold{F}$ representa el campo de velocidad del fluido. ¿Cómo podríamos cuantificar la velocidad a la que el fluido atraviesa $C$?
Recuerda que la integral de línea de $\bold{F}$ a lo largo de $C$ es $\int_C\bold{F}\cdot\bold{T} ds$; en otras palabras, la integral de línea es el producto escalar del campo vectorial con el vector tangencial unitario con respecto a la longitud del arco. Si reemplazamos el vector tangencial unitario con el vector normal unitario $\bold{N} (t)$ y en su lugar calculamos la integral $\int_C\bold{F}\cdot\bold{N} ds$ y determinamos el flujo a través de $C$. Para ser precisos, la definición de la integral $\int_C\bold{F}\cdot\bold{N} ds$; es la misma que la integral $\int_C\bold{F}\cdot\bold{T} ds$;, excepto que la $\bold{T}$ en la suma de Riemann se reemplaza con $\bold{N}$. Por lo tanto, el flujo a través de C se define como
$$\int_C\bold{F}\cdot\bold{N} ds = \lim\limits_{n \to \infin}\sum_{i=1}^n \bold{F}\big(P_i^*\big)\cdot \bold{N}\big(P_i^*\big)\Delta s_i$$donde $\big(P_i^*\big)$ y $\Delta s_i$ se definen como lo fueron para la integral $\int_C\bold{F}\cdot\bold{T} ds$. Por lo tanto, una integral de flujo es una integral que es perpendicular a una integral de línea vectorial, porque $\bold{N}$ y $\bold{T}$ son vectores perpendiculares.
Si $\bold{F}$ es un campo de velocidad de un fluido y $C$ es una curva que representa una membrana, entonces el flujo de $\bold{F}$ a través de $C$ es la cantidad de fluido que fluye a través de $C$ por unidad de tiempo, o la tasa de flujo.
Más formalmente, sea $C$ una curva plana parametrizada por $\bold{r} (t) = \lang x (t), y (t)\rang, a \le t \le b$. Sea $\bold{n} (t) = \lang y^{\prime}(t), −x^{\prime} (t)\rang$ el vector que es normal a $C$ en el punto final de $\bold{r} (t)$ y apunta a la derecha a medida que recorremos $C$ en la dirección positiva (figura 6.23). Entonces, $\bold{N} (t) = \frac{\bold{n} (t)}{|| \bold{n} (t)||}$ es el vector normal unitario a $C$ en el punto final de $\bold{r} (t)$ que apunta a la derecha cuando atravesamos $C$.
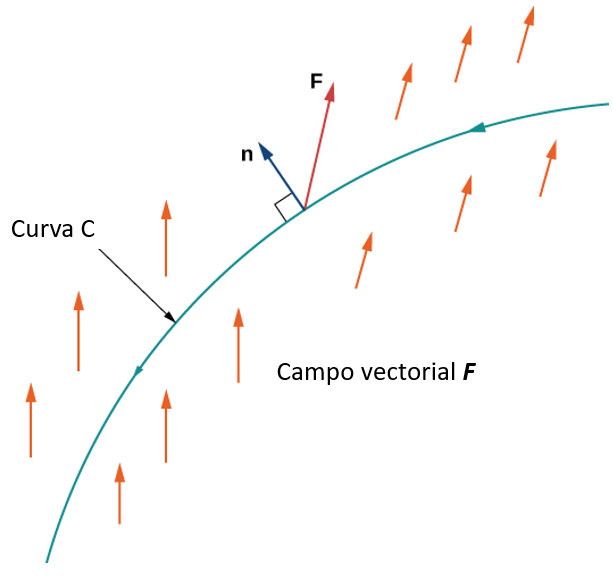
Figura 6.23. El flujo del campo vectorial $\bold{F}$ a través de la curva $C$ se calcula mediante una integral similar a una integral de línea vectorial.
Ahora damos una fórmula para calcular el flujo a través de una curva. Esta fórmula es análoga a la fórmula utilizada para calcular una integral de línea vectorial (ver Ecuación 6.9).
La demostración de la ecuación 6.11 es similar a la demostración de la ecuación 6.8. Antes de deducir la fórmula, ten en cuenta que $|| \bold{n} (t) || = || \lang y^{\prime} (t), −x^{\prime}(t)\rang || = \sqrt{y^{\prime}(t)^2 + x^{\prime}(t)^2} = ||\bold{r}^{\prime}(t )||$. Por lo tanto,
$$\begin{aligned} \int_C \bold{F}\cdot\bold{N} ds &= \int_C \bold{F}\cdot \frac{\bold{n}(t)}{||\bold{n}(t)||}ds\\ &= \int_a^b \bold{F}\cdot \frac{\bold{n}(t)}{||\bold{n}(t)||} ||\bold{r}^{\prime}(t)||dt\\ &= \int_a^b \bold{F}(\bold{r}(t)) \cdot \bold{n}(t)dt\end{aligned}$$ |
Flujo a través de una curva |

Figura 6.24. Un círculo unitario en el campo vectorial $\bold{F} = \lang 2x, 2y\rang$.

Sea $\bold{F} (x, y) = \lang P (x, y), Q (x, y)\rang$ un campo vectorial bidimensional. Recuerda que la integral $\int_C\bold{F}\cdot\bold{T}ds$ a veces se escribe como $\int_CPdx + Qdy$. De manera análoga, el flujo $\int_C\bold{F}\cdot\bold{N}ds$ a veces se escribe en la notación $\int_C − Qdx + Pdy$, porque el vector normal unitario $\bold{N}$ es perpendicular a la tangente unitaria $\bold{T}$. Al girar el vector $d\bold{r} = \lang dx, dy\rang$ $90^o$ se obtiene el vector $\lang dy, −dx\rang$.
Ahora que hemos definido el flujo, podemos centrar nuestra atención en la circulación. La integral de línea del campo vectorial $\bold{F}$ a lo largo de una curva cerrada orientada se llama circulación de $\bold{F}$ a lo largo de $C$. Las integrales de línea de circulación tienen su propia notación: $\oint_C\bold{F}\cdot\bold{T}ds$. El círculo en el símbolo integral denota que $C$ es "circular" porque no tiene puntos finales.
Para ver de dónde proviene el término circulación y qué mide, sea $\bold{v}$ el campo de velocidad de un fluido y sea $C$ una curva cerrada orientada. En un punto particular $P$, cuanto más cerca está la dirección de $\bold{v} (P)$ a la dirección de $\bold{T}(P)$, mayor es el valor del producto escalar $\bold{v} (P) \cdot \bold{T} (P)$. El valor máximo de $\bold{v} (P) \cdot \bold{T} (P)$ ocurre cuando los dos vectores apuntan exactamente en la misma dirección; el valor mínimo de $\bold{v} (P) \cdot \bold{T} (P)$ ocurre cuando los dos vectores apuntan en direcciones opuestas.
Así, el valor de la circulación $\oint_C\bold{v} \cdot \bold{T}ds$ mide la tendencia del fluido a moverse en la dirección de $C$
 |
Calculando la circulación |

En el ejercicio anterior, ¿qué pasaría si hubiéramos orientado el círculo unitario en el sentido de las agujas del reloj? Denotamos el círculo unitario orientado en sentido horario por $−C$. Luego
Observa que la circulación es negativa en este caso. La razón de esto es que la orientación de la curva fluye contra la dirección de $\bold{F}$.
 |
Calculando el trabajo |


39. ¿Verdadero o falso? La integral de línea $\int_Cf (x, y) ds$ es igual a una integral definida si $C$ es una curva suave definida en $[a, b]$ y si la función $f$ es continua en alguna región que contiene la curva $C$ (Solución).
40. ¿Verdadero o falso? Las funciones vectoriales $\bold{r}_1 = t\bold{i} + t^2\bold{j}, 0 \le t \le 1$ y $\bold{r}_2 = (1 - t)\bold{i} + (1 - t)^2\bold{j}, 0 \le t \le 1$, definen la misma curva orientada.
41. ¿Verdadero o falso? $\int_{− C} (Pdx + Qdy) = \int_C (Pdx −Qdy)$ (Solución).
42. ¿Verdadero o falso? Una curva suave $C$ por partes consta de un número finito de curvas suaves que se unen de un extremo a otro.
43. ¿Verdadero o falso? Si $C$ está dado por $x (t) = t, y (t) = t, 0 \le t \le 1$, entonces $\int_C xyds = \int_0^1 t^2dt$ (Solución).
 Para los siguientes ejercicios, usa un sistema de álgebra computarizado (CAS) para evaluar las integrales de línea sobre la ruta indicada
Para los siguientes ejercicios, usa un sistema de álgebra computarizado (CAS) para evaluar las integrales de línea sobre la ruta indicada
44. [T] $\int_C (x + y) ds$ $C: x = t, y = (1 - t), z = 0$ desde $(0, 1, 0)$ a $(1, 0, 0)$. 45. [T] $\int_C (x - y) ds C: \bold{r} (t) = 4t\bold{i} + 3t\bold{j}$ cuando $0 \le t \le 2$ (Solución). 46. [T] $\int_C (x^2 + y^2 + z^2) ds$ $C: \bold{r} (t) = sen\; t\bold{i} + cos\; t\bold{j} + 8t\bold{k}$ cuando $0 \le t \le \pi/2$ 47. [T] Evalúa $\int_Cxy^4ds$, donde $C$ es la mitad derecha del círculo $x^2 + y^2 = 16$ y se recorre en el sentido de las agujas del reloj (Solución). 48. [T] Evalúa $\int_C4x^3ds$, donde $C$ es el segmento de línea desde $(−2, −1)$ hasta $(1, 2)$.
 Para los siguientes ejercicios, encuentra el trabajo realizado.
Para los siguientes ejercicios, encuentra el trabajo realizado.
49. Encuentra el trabajo realizado por el campo vectorial $\bold{F} (x, y, z) = x\bold{i} + 3xy\bold{j} - (x + z)\bold{k}$ en una partícula que se mueve a lo largo de un segmento de línea que va desde $(1, 4, 2)$ hasta $(0, 5, 1)$ (Solución).
50. Encuentra el trabajo realizado por una persona que pesa $150\; lb$ caminando exactamente una revolución por una escalera circular en espiral de un radio de $3$ pies si la persona se eleva $10$ pies. 51. Encuentra el trabajo realizado por el campo de fuerza $\bold{F} (x, y, z) = - \frac12x\bold{i} −\frac12y\bold{j} + \frac14\bold{k}$ en una partícula a medida que se mueve a lo largo de la hélice $\bold{r} (t) = cos \;t\bold{i} + sen\; t\bold{j} + t\bold{k}$ desde el punto $(1, 0, 0)$ hasta el punto $(−1, 0, 3π)$ (Solución). 52. Encuentra el trabajo realizado por el campo vectorial $\bold{F} (x, y) = y\bold{i} + 2x\bold{j}$ al mover un objeto a lo largo de la trayectoria $C$, que une los puntos $(1, 0)$ y $(0, 1)$. 53. Encuentra el trabajo realizado por la fuerza $\bold{F} (x, y) = 2y\bold{i} + 3x\bold{j} + (x + y)\bold{k}$ al mover un objeto a lo largo de la curva $\bold{r} (t) = cos\; (t)\bold{i} + sen\; (t)\bold{j} + \frac16\bold{k}$, donde $0 \le t \le 2\pi$ (Solución). 54. Encuentra la masa de un alambre en la forma de un círculo de radio $2 $centrado en $(3, 4)$ con densidad de masa lineal $\rho (x, y) = y^2$.
 Para los siguientes ejercicios, evalúa las integrales de línea.
Para los siguientes ejercicios, evalúa las integrales de línea.
55. Evalúa $\int_C\bold{F}\cdot d\bold{r}$, donde $\bold{F} (x, y) = −1\bold{j}$, y $C$ es la parte de la gráfica de $y = \frac12x^3 - x$ desde $(2, 2)$ hasta $(−2, −2)$ (Solución). 56. Evalúa $\int_{\gamma}(x^2 + y^2 + z^2)^{−1}ds$, donde $\gamma$ es la hélice $x = cos\; t, y = sen\; t, z = t$ $(0 \le t \le T)$. 57. Evalúa $\int_Cyzdx + xzdy + xydz$ sobre el segmento de línea desde $(1, 1, 1)$ hasta $(3, 2, 0)$ (Solución). 58. Sea $C$ el segmento de recta desde el punto $(0, 1, 1)$ al punto $(2, 2, 3)$. Evaluar integral de línea $\int_Cyds$.
59. [T] Usa un sistema de álgebra de computadora para evaluar la integral de línea $\int_Cy^2dx + xdy$, donde $C$ es el arco de la parábola $x = 4 - y^2$ desde $(−5, −3)$ hasta $(0, 2)$ (Solución). 60. [T] Usa un CAS para evaluar la integral de línea $\int_C(x + 3y^2)dy$ sobre la trayectoria $C$ dada por $x = 2t, y = 10t$, donde $0 \le t \le 1$. 61. [T] Usa un CAS para evaluar la integral de línea $\int_Cxydx + ydy$ sobre la ruta $C$ dada por $x = 2t, y = 10t$, donde $0 \le t \le 1$ (Solución). 62. Evalúa la integral de línea $\int_C(2x - y)dx + (x + 3y)dy$, donde $C$ se encuentra a lo largo del eje $x$ desde $x = 0$ hasta $x = 5$. 63. [T] Usa un CAS para evaluar $\int_C\frac{y}{2x^2 - y^2}ds$, donde $C$ es $x = t, y = t, 1 \le t \le 5$ (Solución). 64. [T] Usa un CAS para evaluar $\int_Cxyds$, donde $C$ es $x = t^2, y = 4t, 0 \le t \le 1$.
 En los siguientes ejercicios, encuentra el trabajo realizado por el campo de fuerza $\bold{F}$ sobre un objeto que se mueve a lo largo de la trayectoria indicada.
En los siguientes ejercicios, encuentra el trabajo realizado por el campo de fuerza $\bold{F}$ sobre un objeto que se mueve a lo largo de la trayectoria indicada.
65. $\bold{F} (x, y) = −x\bold{i} - 2y\bold{j}$ $C: y = x^3$ desde $(0, 0)$ hasta $(2, 8)$ (Solución). 66. $\bold{F} (x, y) = 2x\bold{i} + y\bold{j}$ $C$: en sentido antihorario alrededor del triángulo con vértices $(0, 0), (1, 0)$ y $(1, 1)$. 67. $\bold{F} (x, y, z) = x\bold{i} + y\bold{j} - 5z\bold{k}$ $C: r (t) = 2 cos\; t\bold{i} + 2 sen\; t\bold{j} + t\bold{k}, 0 \le t \le 2\pi$ (Solución). 68. Sea $\bold{F}$ el campo vectorial $\bold{F} (x, y) = \big(y^2 + 2xe^y + 1\big)\bold{i} + \big(2xy + x^2e^y + 2y\big)\bold{j}$. Calcula el trabajo de la integral $\int_C\bold{F}\cdot d\bold{r}$, donde $C$ es la trayectoria $\bold{r} (t) = sen\; t\bold{i} + cos\; t\bold{j}, 0 \le t \le \frac{\pi}{2}$.
69. Calcula el trabajo realizado por la fuerza $\bold{F} (x, y, z) = 2x\bold{i} + 3y\bold{j} - z\bold{k}$ a lo largo de la trayectoria $\bold{r} (t) = t\bold{i} + t^2\bold{j} + t^3\bold{k}$, donde $0 \le t \le 1$ (Solución). 70. Evalúa $\int_C\bold{F}\cdot d\bold{r}$, donde $\bold{F} (x, y) = \frac{1}{x + y}\bold{i} + \frac{1}{x + y }\bold{j}$ y $C$ es el segmento del círculo unitario que va en sentido antihorario desde $(1, 0)$ hasta $(0, 1)$.
71. La fuerza $\bold{F} (x, y, z) = zy\bold{i} + x\bold{j} + z^2x\bold{k}$ actúa sobre una partícula que viaja desde el origen al punto $(1, 2, 3)$. Calcula el trabajo realizado si la partícula viaja:
72. Encuentra el trabajo realizado por el campo vectorial $\bold{F} (x, y, z) = x\bold{i} + 3xy\bold{j} - (x + z)\bold{k}$ en una partícula en movimiento a lo largo de un segmento de línea que va desde $(1, 4, 2)$ hasta $(0, 5, 1)$.
73. ¿Cuánto trabajo se requiere para mover un objeto en el campo vectorial $\bold{F} (x, y) = y\bold{i} + 3x\bold{j}$ a lo largo de la parte superior de la elipse $\frac{x^2}{4} + y^2 = 1$ desde $(2, 0)$ hasta $(−2, 0)$? (Solución).
74. Un campo vectorial está dado por $\bold{F} (x, y) = (2x + 3y)\bold{i} + (3x + 2y)\bold{j}$. Evalúa la integral de línea del campo alrededor de un círculo de radio unitario atravesado en el sentido de las agujas del reloj.
75. Evalúa la integral de línea de la función escalar $xy$ a lo largo de la trayectoria parabólica $y = x^2$ que conecta el origen con el punto $(1,1)$ (Solución).
76. Encuentra $\int_Cy^2dx + \big(xy - x^2\big)dy$ a lo largo de $C: y = 3x$ desde $(0, 0)$ hasta $(1, 3)$.
77. Encuentra $\int_Cy^2dx + \big(xy - x^2\big)dy$ a lo largo de $C: y^2 = 9x$ desde $(0, 0)$ hasta $(1, 3)$ (Solución).
 Para los siguientes ejercicios, usa un CAS para evaluar las integrales de línea dadas.
Para los siguientes ejercicios, usa un CAS para evaluar las integrales de línea dadas.
78. [T] Evalúa $\bold{F} (x, y, z) = x^2z\bold{i} + 6y\bold{j} + yz2^\bold{k}$, donde $C$ está representado por $\bold{r} (t) = t\bold{i} + t^2\bold{j} + ln\; t\bold{k}, 1 \le t \le 3$.
79. [T] Evalúa la integral de línea $\int_{\gamma}xe^yds$ donde, $\gamma$ es el arco de la curva $x = ey$ desde $(1, 0)$ hasta $(e, 1$) (Solución). 80. [T] Evalúa la integral $\int_{\gamma}xy^2ds$, donde $\gamma$ es un triángulo con vértices $(0, 1, 2), (1, 0, 3)$ y $(0, −1, 0)$. 81. [T] Evalúa la integral de línea $\int_{\gamma}\big(y^2 - xy\big)dx$, donde $\gamma$ es la curva $y = ln\; x$ desde $(1, 0)$ hacia $(e, 1)$ (Solución). 82. [T] Evalúa la integral de línea $\int_{\gamma}xy^4ds$, donde $\gamma$ es la mitad derecha del círculo $x^2 + y^2 = 16$. 83. [T] Evalúa $\int_C\bold{F}\cdot d\bold{r}$, donde $\bold{F} (x, y, z) = x^2y\bold{i} + (x - z)\bold{j} + xyz\bold{k}$ y $C: \bold{r} (t) = t\bold{i} + t^2\bold{j} + 2\bold{k}, 0 \le t \le 1$ (Solución). 84. Evalúa $\int_C\bold{F} \cdot d\bold{r}$, donde $\bold{F} (x, y) = 2x sen (y)\bold{i} + \big(x^2cos (y) - 3y^2\big)\bold{j}$ y $C$ es cualquier camino desde $(−1, 0)$ hasta $(5, 1)$. 85. Encuentra la integral de línea de $\bold{F} (x, y, z) = 12x^2\bold{i} - 5xy\bold{j} + xz\bold{k}$ sobre la ruta $C$ definida por $y = x^2, z = x^3$ desde el punto $(0, 0, 0)$ al punto $(2, 4, 8 )$ (Solución). 86. Encuentra la integral de línea de $\int_C\big(1 + x^2y\big)ds$, donde $C$ es la elipse $\bold{r} (t) = 2 cos\; t\bold{i} + 3 sen\; t\bold{j}$ de $0 \le t \le \pi$.
 Para los siguientes ejercicios, encuentre el flujo.
Para los siguientes ejercicios, encuentre el flujo.
87. Calcula el flujo de $\bold{F} = x^2\bold{i} + y\bold{j}$ a través de un segmento de línea desde $(0, 0)$ hasta $(1, 2)$ (Solución). 88. Sea $\bold{F} = 5\bold{i}$ y sea $C$ la curva $y = 0, 0 \le x \le 4$. Encuentra el flujo a través de $C$. 89. Sea $\bold{F} = 5\bold{j}$ y sea $C$ la curva $y = 0, 0 \le x \le 4$. Encuentra el flujo a través de $C$ (Solución).
90. Sea $\bold{F} = −y\bold{i} + x\bold{j}$ y sea $C: \bold{r} (t) = cos\; t\bold{i} + sen\; t\bold{j} (0 \le t \le 2\pi)$. Calcula el flujo a través de $C$. 91. Sea $\bold{F} = \big(x^2 + y^3\big)\bold{i} + (2xy)\bold{j}$. Calcula el flujo $\bold{F}$ orientado en sentido antihorario a través de la curva $C: x^2 + y^2 = 9$ (Solución).
92. Encuentra la integral de línea de $\int_Cz^2dx + ydy + 2ydz$, donde $C$ consta de dos partes: $C_1$ y $C_2$. $C_1$ es la intersección del cilindro $x^2 + y^2 = 16$ y el plano $z = 3$ desde $(0, 4, 3)$ hasta $(−4, 0, 3)$. $C_2$ es un segmento de línea desde $(−4, 0, 3)$ hasta $(0, 1, 5)$.
93. Un resorte está hecho de un alambre delgado retorcido en forma de hélice circular $x = 2 cos\; t, y = 2 sen\; t, z = t$. Encuentra la masa de dos vueltas del resorte si el alambre tiene una densidad de masa constante (Solución).
94. Un alambre delgado se dobla en forma de semicírculo de radio $a$. Si la densidad de masa lineal en el punto $P$ es directamente proporcional a su distancia desde la línea que pasa por los puntos extremos, calcula la masa del cable.
95. Un objeto se mueve en el campo de fuerza $\bold{F}(x, y, z) = y^2\bold{i} + 2 (x + 1) y\bold{j}$ en sentido antihorario desde el punto $(2, 0)$ a lo largo de la trayectoria elíptica $x^2 + 4y^2 = 4$ hasta $(-2, 0)$, y de regreso al punto $(2, 0)$ a lo largo del eje $x$. ¿Cuánto trabajo realiza el campo de fuerza sobre el objeto? (Solución).
96. Encuentra el trabajo realizado cuando un objeto se mueve en el campo de fuerza $\bold{F} (x, y, z) = 2x\bold{i} - (x + z)\bold{j} + (y - x)\bold{k}$ a lo largo de la trayectoria dada por $\bold{r} (t) = t^2\bold{i} + \big(t^2 - t\big)\bold{j} + 3\bold{k}, 0 \le t \le 1$.
97. Si un campo de fuerza inverso $\bold{F}$ está dado por $\bold{F} (x, y, z) = \frac{k}{||\bold{r}||^3}\bold{r}$, donde $k$ es una constante, encuentra el trabajo realizado por $\bold{F}$cuando su punto de aplicación se mueve a lo largo del eje $x$ desde $A (1, 0, 0)$ hacia $B (2, 0, 0)$ (Solución).
98. David y Sandra planean evaluar la integral de línea $\int_C\bold{F}\cdot d\bold{r}$ a lo largo de una trayectoria en el plano $xy$ desde $(0, 0)$ hasta $(1, 1)$. El campo de fuerza es $\bold{F} (x, y) = (x + 2y)\bold{i} + (−x + y^2)\bold{j}$. David elige la ruta que corre a lo largo del eje $x$ desde $(0,0)$ hasta $(1, 0)$ y luego corre a lo largo de la línea vertical $x = 1$ desde $(1, 0)$ hasta el punto final $(1, 1)$. Sandra elige el camino directo a lo largo de la línea diagonal $y = x$ desde $(0, 0)$ hasta $(1, 1)$. ¿De quién es la integral de línea más grande y en cuánto?
En este apartado, continuaremos el estudio de campos vectoriales conservativos. Examinaremos el Teorema fundamental para integrales de línea, que es una generalización útil del Teorema fundamental del cálculo para integrales de línea de campos vectoriales conservativos. También descubriremos cómo probar si un campo vectorial dado es conservativo y determinar cómo construir una función potencial para un campo vectorial que se sabe que es conservativo.
Antes de continuar nuestro estudio de campos vectoriales conservativos, necesitamos algunas definiciones geométricas. Todos los teoremas de las secciones siguientes se basan en la integración sobre ciertos tipos de curvas y regiones, por lo que aquí desarrollaremos las definiciones de esas curvas y regiones.
Primero definiremos dos tipos especiales de curvas: curvas cerradas y curvas simples. Como hemos aprendido, una curva cerrada es aquella que comienza y termina en el mismo punto. Una curva simple es aquella que no se cruza. Una curva que es a la vez cerrada y simple es una curva cerrada simple (figura 6.25).

Figura 6.25. Tipos de curvas que son simples o no simples y cerradas o no cerradas.
 |
Determinar si una curva es simple y cerrada |

Muchos de los teoremas de este capítulo relacionan una integral sobre una región con una integral sobre el límite de la región, donde el límite de la región es una curva cerrada simple o una unión de curvas cerradas simples. Para desarrollar estos teoremas, necesitamos dos definiciones geométricas para regiones: la de una región conectada y la de una región simplemente conectada. Una región conectada es aquella en la que hay una ruta en la región que conecta dos puntos cualesquiera que se encuentren dentro de esa región. Una región simplemente conectada es una región conectada que no tiene ningún agujero.
Estas dos nociones, junto con la noción de una curva cerrada simple, nos permiten formular varias generalizaciones del Teorema fundamental del cálculo más adelante en este capítulo. Estas dos definiciones son válidas para regiones en cualquier número de dimensiones, pero solo nos interesan las regiones en dos o tres dimensiones.
Todas las regiones simplemente conectadas están conectadas, pero no todas las regiones conectadas están simplemente conectadas (figura 6.27).
Ahora que entendemos algunas curvas y regiones básicas, generalicemos el Teorema fundamental del cálculo a integrales de línea.
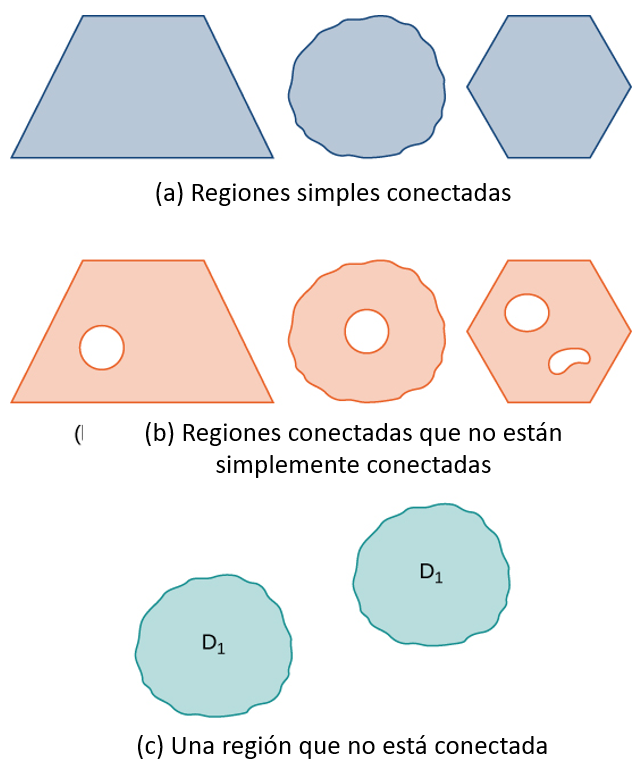
Figura 6.27. No todas las regiones conectadas están simplemente conectadas. (a) Las regiones simplemente conectadas no tienen agujeros. (b) Las regiones conectadas que no están simplemente conectadas pueden tener agujeros, pero aún puede encontrar una ruta en la región entre dos puntos cualesquiera. (c) Una región que no está conectada tiene algunos puntos que no pueden conectarse mediante una ruta en la región.
Recuerda que el Teorema fundamental del cálculo dice que si una función $f$ tiene una antiderivada $F$, entonces la integral de $f$ desde $a$ a $b$ depende solo de los valores de $F$ en $a$ y en $b$, es decir,
Si pensamos en el gradiente como una derivada, entonces el mismo teorema se aplica a las integrales de líneas vectoriales. Mostramos cómo funciona esto usando un ejercicio motivacional.
 |
Evaluación de una integral de línea y las antiderivadas de los puntos finales |

El siguiente teorema dice que, bajo ciertas condiciones, lo que sucedió en el ejercicio anterior es válido para cualquier campo gradiente. El mismo teorema es válido para integrales de línea vectoriales, que llamamos Teorema fundamental para integrales de línea.
De la ecuación 6.9
$$\int_C \nabla f\cdot d\bold{r} = \int_a^b \nabla f(\bold{r}(t))\cdot \bold{r}^{\prime}(t)dt$$Por la regla de la cadena
$$\frac{d}{dt}f(\bold{r}(t)) = \nabla f(\bold{r}(t))\cdot \bold{r}^{\prime}(t)$$Por lo tanto, según el Teorema Fundamental del Cálculo,
$$\begin{aligned} \int_C \nabla f\cdot d\bold{r} &= \int_a^b \nabla f(\bold{r}(t))\cdot \bold{r}^{\prime}(t)dt\\ &= \int_a^b \frac{d}{dt} (f(\bold{r}(t))dt\\ &= \bigg[f(\bold{r}(t))\bigg]_{t=a}^{t=b}\\ &= f(\bold{r}(b)) - f(\bold{r}(a)) \end{aligned}$$Sabemos que si $\bold{F}$ es un campo vectorial conservativo, existen funciones potenciales $f$ tales que $\nabla f = \bold{F}$. Por lo tanto, $\int_C\bold{F}\cdot d\bold{r} = \int_C\nabla f · d\bold{r} = f(\bold{r} (b) - f (\bold{r} (a))$.
En otras palabras, al igual que con el Teorema Fundamental del Cálculo, calcular la integral de línea $\int_C\bold{F}\cdot d\bold{r}$, donde $\bold{F}$ es conservativa, es un proceso de dos pasos: (1) encontrar una función potencial ("antiderivada") $f$ para $\bold{F}$ y (2) calcular el valor de $f$ en los puntos extremos de $C$ y calcular su diferencia $f(\bold{r} (b)) - f(\bold{r} (a))$. Sin embargo, ten en cuenta que hay una diferencia importante entre el Teorema Fundamental del Cálculo y el Teorema Fundamental para Integrales de Línea. Una función de una variable que es continua debe tener una antiderivada. Sin embargo, un campo vectorial, incluso si es continuo, no necesita tener una función potencial.
 |
Aplicando el Teorema Fundamental |

El ejercicio anterior ilustra una característica interesante del Teorema Fundamental de Integrales de Línea: nos permite calcular más fácilmente muchas integrales de línea vectoriales. Mientras tengamos una función potencial, calcular la integral de línea es solo una cuestión de evaluar la función potencial en los puntos finales y restar.
El Teorema Fundamental de las Integrales de Línea tiene dos consecuencias importantes. La primera consecuencia es que si $\bold{F}$ es conservativa y $C$ es una curva cerrada, entonces la circulación de $\bold{F}$ a lo largo de $C$ es cero, es decir, $\int_C\bold{F}\cdot d\bold{r} = 0$. Para ver por qué esto es cierto, sea $f$ una función potencial para $\bold{F}$. Dado que $C$ es una curva cerrada, el punto terminal $\bold{r} (b)$ de $C$ es el mismo que el punto inicial $\bold{r} (a)$ de $C$, es decir, $\bold{r} (a) = \bold{r} (b)$. Por lo tanto, según el Teorema Fundamental para Integrales de Línea,
$$\begin{aligned} \oint_C \bold{F}\cdot d\bold{r} &= \oint_C \nabla f\cdot d\bold{r}\\ &= f(\bold{r}(b)) -f(\bold{r}(a))\\ &= f(\bold{r}(b)) -f(\bold{r}(b))\\ &= 0 \end{aligned}$$Recuerda que la razón por la que un campo vectorial conservativo $\bold{F}$ se llama "conservativo" es porque tales campos vectoriales modelan fuerzas en las que se conserva energía. Hemos demostrado que la gravedad es un ejemplo de tal fuerza. Si pensamos en el campo vectorial $\bold{F}$ en la integral $\oint_C\bold{F}\cdot d\bold{r}$ como un campo gravitacional, entonces se sigue que la ecuación $\displaystyle\oint_C\bold{F}\cdot d\bold{r} = 0$. Si una partícula viaja a lo largo de un camino que comienza y termina en el mismo lugar, entonces el trabajo realizado por la gravedad sobre la partícula es cero.
La segunda consecuencia importante del Teorema Fundamental para Integrales de Línea es que las integrales de línea de los campos vectoriales conservativos son independientes de la ruta, es decir, dependen sólo de los puntos finales de la curva dada y no dependen de la ruta entre los puntos finales.
La segunda consecuencia se establece formalmente en el siguiente teorema.
Sea $D$ el dominio de $\bold{F}$ y sean $C_1$ y $C_2$ dos caminos en $D$ con los mismos puntos inicial y terminal (Figura 6.29). Llama al punto inicial $P_1$ y al punto terminal $P_2$. Dado que $\bold{F}$ es conservativa, existe una función potencial $f$ para $\bold{F}$. Según el Teorema Fundamental para Integrales de Línea,
$$\int_{C_1} \bold{F}\cdot d\bold{r} = f(P_2) - f(P_1) = \int_{C_2} \bold{F}\cdot d\bold{r}$$Por lo tanto, $\displaystyle\int_{C_1} \bold{F}\cdot d\bold{r} = \int_{C_2} \bold{F}\cdot d\bold{r}$ y $\bold{F}$ es independiente del camino.

Figura 6.29. El campo vectorial es conservador y, por tanto, independiente de la ruta.
Para visualizar lo que significa la independencia del camino, imagina a tres excursionistas subiendo desde el campamento base hasta la cima de una montaña. El excursionista 1 toma una ruta empinada directamente desde el campamento hasta la cima. El excursionista 2 toma una ruta sinuosa que no es empinada desde el campamento hasta la cima. El excursionista 3 comienza tomando la ruta empinada, pero a mitad de camino hacia la cima decide que es demasiado difícil para él. Por tanto, vuelve al campamento y toma el camino no empinado hasta la cima. Los tres excursionistas viajan por caminos en un campo gravitacional. Dado que la gravedad es una fuerza en la que se conserva la energía, el campo gravitacional es conservativo. Por independencia de camino, la cantidad total de trabajo realizado por gravedad sobre cada uno de los excursionistas es el mismo porque todos comenzaron en el mismo lugar y terminaron en el mismo lugar.
El trabajo realizado por los excursionistas incluye otros factores como la fricción y el movimiento muscular, por lo que la cantidad total de energía gastada por cada uno no es la misma, pero la energía neta gastada contra la gravedad es la misma para los tres excursionistas.
Hemos demostrado que si $\bold{F}$ es conservativa, entonces $\bold{F}$ es independiente de la trayectoria. Resulta que si el dominio de $\bold{F}$ está abierto y conectado, entonces lo contrario también es cierto. Es decir, si $\bold{F}$ es independiente de la trayectoria y el dominio de $\bold{F}$ está abierto y conectado, entonces $\bold{F}$ es conservativa. Por lo tanto, el conjunto de campos vectoriales conservativos en dominios abiertos y conectados es precisamente el conjunto de campos vectoriales independientes de la ruta.
Demostramos el teorema para campos vectoriales en $\Reals^2$. La prueba de campos vectoriales en $\Reals^3$ es similar. Para demostrar que $\bold{F} = \lang P, Q\rang$ es conservativo, debemos encontrar una función potencial $f$ para $\bold{F}$. Para ese fin, sea $X$ un punto fijo en D.
Para cualquier punto (x, y) en $D$, sea $C$ un camino de $X$ a $(x, y)$. Definamos $f (x, y)$ por $f (x, y) = \int_C\bold{F}\cdot d\bold{r}$ (ten en cuenta que esta definición de $f$ tiene sentido solo porque $\bold{F}$ es independiente de la ruta. Si F no fuera independiente de la ruta, entonces podría ser posible encontrar otra ruta $C^{\prime}$ de $X$ a $(x, y)$ tal que $\int_C\bold{F}\cdot d\bold{r} \cancel{=} \int_C\bold{F}\cdot d\bold{r}$, y en tal caso $f (x, y)$ no sería una función) Queremos demostrar que $f$ tiene la propiedad $\nabla f = \bold{F}$.
Dado que el dominio $D$ está abierto, es posible encontrar un disco centrado en $(x, y)$ tal que el disco esté contenido por completo dentro de $D$. Sea $(a, y)$ con $a \lt x$ un punto en ese disco. Sea $C$ un camino de $X$ a $(x, y)$ que consta de dos piezas: $C_1$ y $C_2$. La primera pieza, $C_1$, es cualquier camino de $C$ a $(a, y)$ que permanece dentro de $D$; $C_2$ es el segmento de línea horizontal desde $(a, y)$ a $(x, y)$ (Figura 6.30). Luego
$$f(x,y) = \int_{C_1} \bold{F}\cdot d\bold{r} + \int_{C_2} \bold{F}\cdot d\bold{r}$$La primera integral no depende de x, entonces
$$f_x = \frac{\partial}{\partial x}\int_{C_2} \bold{F}\cdot d\bold{r}$$Si parametrizamos $C_2$ por $\bold{r} (t) = \lang t, y\rang, a \le t \le x$, entonces
$$\begin{aligned} f_x &= \frac{\partial}{\partial x}\int_{C_2} \bold{F}\cdot d\bold{r}\\ &= \frac{\partial}{\partial x}\int_a^x \bold{F}(\bold{r}(t))\cdot \bold{r}^{\prime}(t)dt\\ \end{aligned}$$Según el Teorema Fundamental del Cálculo (parte 1),
$$f_x = \frac{\partial}{\partial x}\int_a^x P(t,y)dt = P(x,y$$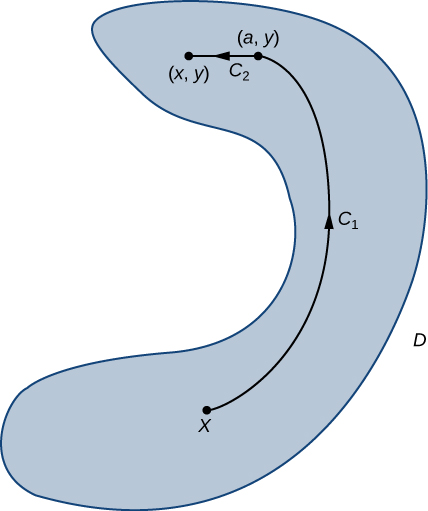
Figura 6.30. Aquí, $C_1$ es cualquier camino de $C$ a $(a, y)$ que permanece dentro de $D$, y $C_2$ es el segmento de línea horizontal desde $(a, y)$ a $(x, y)$.
Un argumento similar que usa un segmento de línea vertical en lugar de un segmento de línea horizontal muestra que $f_y = Q (x, y)$. Por lo tanto, $\nabla f = \bold{F}$ y $\bold{F}$ es conservativa.
Hemos pasado mucho tiempo discutiendo y probando la Independencia de la ruta de los campos conservativos y la Prueba de independencia de la ruta para los campos conservativos, pero podemos resumirlos simplemente: un campo vectorial $\bold{F}$ en un dominio abierto y conectado es conservativo si y solo si es independiente de la trayectoria. Es importante saber esto porque los campos vectoriales conservativos son extremadamente importantes en las aplicaciones, y estos teoremas nos brindan una forma diferente de ver lo que significa ser conservativo usando la independencia de la trayectoria.
 |
Demostrar que un campo vectorial no es conservativo |

Como hemos aprendido, el Teorema Fundamental para Integrales de Línea dice que si $\bold{F}$ es conservativo, entonces calcular $\int_C\bold{F}\cdot d\bold{r}$ tiene dos pasos: primero, encontrar una función potencial $f$ para $\bold{F}$ y, segundo, calcular $f (P_1) - f (P:0 )$, donde $P_1$ es el punto final de $C$ y $P_0$ es el punto de partida.
Para usar este teorema para un campo conservativo $F$, debemos poder encontrar una función potencial $f$ para $\bold{F}$. Por lo tanto, debemos responder la siguiente pregunta: Dado un campo vectorial conservativo $\bold{F}$, ¿cómo encontramos una función $f$ tal que $\nabla f = \bold{F}$? Antes de dar un método general para encontrar una función potencial, motivemos el método con un ejercicio.
 |
Encontrando una función potencial |

La lógica del ejercicio anterior se extiende a encontrar la función potencial para cualquier campo vectorial conservativo en $\Reals^2$. Por lo tanto, tenemos la siguiente estrategia de resolución de problemas para encontrar funciones potenciales:
Podemos adaptar esta estrategia para encontrar funciones potenciales para campos vectoriales en $\Reals^3$, como se muestra en el siguiente ejercicio.
 |
Encontrando una función potencial en $\Reals^3$ |

Podemos aplicar el proceso de encontrar una función potencial a una fuerza gravitacional. Recuerda que, si un objeto tiene masa unitaria y está ubicado en el origen, entonces la fuerza gravitacional en $\Reals^2$ que el objeto ejerce sobre otro objeto de masa unitaria en el punto $(x, y)$ viene dada por el campo vectorial
donde $G$ es la constante gravitacional universal. En el siguiente ejercicio, construimos una función potencial para $\bold{F}$, confirmando así lo que ya sabemos: que la gravedad es conservativa.
 |
Encontrando una función potencial |

Hasta ahora, hemos trabajado con campos vectoriales que sabemos que son conservativos, pero si no nos dicen que un campo vectorial es conservativo, debemos poder probar si es conservativo. Recuerda que, si $\bold{F}$ es conservativo, $\bold{F}$ tiene la propiedad de parciales cruzadas. Es decir, si $\bold{F} = \lang P, Q, R\rang$ es conservativo, entonces $P_y = Q_x, P_z = R_x$ y $Q_z = R_y$. Entonces, si $\bold{F}$ tiene la propiedad de parciales cruzadas, ¿es $\bold{F}$ conservativo? Si el dominio de $\bold{F}$ está abierto y simplemente conectado, entonces la respuesta es sí.
Aunque una demostración de este teorema está más allá del alcance del texto, podemos descubrir su poder con algunos ejemplos. Más adelante, veremos por qué es necesario que la región esté simplemente conectada.
Combinando este teorema con la propiedad de las parciales cruzadas, podemos determinar si un campo vectorial dado es conservativo:
La versión de este teorema en $\Reals^2$ también es cierta. Si $\bold{F} = \lang P, Q\rang$ es un campo vectorial en un dominio abierto, simplemente conectado en $\Reals^2$, entonces $\bold{F}$ es conservativo si y solo si $P_y = Q_x$.
 |
Determinando si un campo vectorial es conservativo |

 |
Determinando si un campo vectorial es conservativo |

Cuando se usa la propiedad de parciales cruzadas de campos conservativos, es importante recordar que un teorema es una herramienta y, como cualquier herramienta, solo se puede aplicar en las condiciones adecuadas. En el caso de la propiedad de parciales cruzadas de los campos conservadores, el teorema se puede aplicar solo si el dominio del campo vectorial está simplemente conectado.
Para ver qué puede salir mal al aplicar mal el teorema, considere el campo vectorial de:
$$\bold{F}(x,y) = \frac{y}{x^2+y^2}\bold{i} + \frac{-x}{x^2+y^2}\bold{j}$$Este campo vectorial satisface la propiedad de parciales cruzadas, ya que
$$\frac{\partial}{\partial y}\bigg(\frac{y}{x^2+y^2}\bigg) = \frac{(x^2+y^2) - y(2y)}{(x^2+y^2)^2} = \frac{x^2-y^2}{(x^2+y^2)^2}$$y
$$\frac{\partial}{\partial x} \bigg(\frac{-x}{x^2+y^2}\bigg) = \frac{-(x^2+y^2) + x(2x)}{(x^2+y^2)^2} = \frac{x^2-y^2}{(x^2+y^2)^2}$$Dado que $\bold{F}$ satisface la propiedad de las parciales cruzadas, podríamos estar tentados a concluir que $\bold{F}$ es conservativa. Sin embargo, $\bold{F}$ no es conservativa. Para ver esto, deja
$$\bold{r}(t) = \lang cos\;t, sen\;t \rang , 0 \le t \le \pi$$sea una parametrización de la mitad superior de un círculo unitario orientado en sentido antihorario (denotado como $C_1$) y deja
$$\bold{s}(t) = \lang cos\;t, -sen\;t \rang , 0 \le t \le \pi$$sea una parametrización de la mitad inferior de un círculo unitario orientado en sentido horario (denotado como $C_2$). Observa que $C_1$ y $C_2$ tienen el mismo punto inicial y final. Dado que $sen^2t + cos^2t = 1$,
$$\bold{F}(\bold{r}(t)) \cdot \bold{r}^{\prime} = \lang sen(t), -cos(t)\rang \cdot \lang -sen(t), cos(t)\rang = -1$$y
$$\begin{aligned} \bold{F}(\bold{s}(t)) \cdot \bold{s}^{\prime} &= \lang -sen(t), -cos(t)\rang \cdot \lang -sen(t), -cos(t)\rang\\ &= sen^2t + cos^2t\\ &=1 \end{aligned}$$Por lo tanto
$$\int_{C_1}\bold{F}\cdot d\bold{r} = \int_0^{\pi} -1dt = -\pi\;\;\text{ y }\;\;\int_{C_2}\bold{F}\cdot d\bold{r} = \int_0^{\pi} 1dt = \pi$$Luego, $C_1$ y $C_2$ tienen el mismo punto de inicio y final, pero $\int_{C_1}\bold{F}\cdot d\bold{r}\; \cancel{=} \int_{C_2}\bold{F}\cdot d\bold{r}$. Por tanto, $\bold{F}$ no es independiente de la trayectoria y $\bold{F}$ no es conservativa.
Para resumir: $\bold{F}$ satisface la propiedad de parciales cruzadas y, sin embargo, $\bold{F}$ no es conservativa. ¿Qué salió mal? ¿Contradice esto la propiedad de parciales cruzadas de los campos conservativos? El problema es que el dominio de $\bold{F}$ es todo $\Reals^2$ excepto el origen.
En otras palabras, el dominio de $\bold{F}$ tiene un agujero en el origen y, por lo tanto, el dominio no está simplemente conectado. Dado que el dominio no está simplemente conectado, la propiedad entre parciales de campos conservativos no se aplica a $\bold{F}$.
Cerramos esta sección mirando un ejercicio de la utilidad del Teorema Fundamental para Integrales de Línea. Ahora que podemos probar si un campo vectorial es conservativo, siempre podemos decidir si el Teorema Fundamental para Integrales de Línea se puede usar para calcular una integral de línea vectorial. Si se nos pide que calculemos una integral de la forma $\int_C\bold{F}\cdot d\bold{r}$, entonces nuestra primera pregunta debería ser: ¿$\bold{F}$ es conservativa? Si la respuesta es sí, entonces debemos encontrar una función potencial y usar el Teorema Fundamental para Integrales de Línea para calcular la integral. Si la respuesta es no, entonces el teorema no puede ayudarnos y tenemos que usar otros métodos, como usar la ecuación 6.9.
 |
Usando el Teorema Fundamental para Integrales de Línea |

 |
Trabajo realizado en una partícula |


99. ¿Verdadero o falso? Si el campo vectorial $\bold{F}$ es conservativo en la región abierta y conectada D, entonces las integrales de línea de $\bold{F}$ son independientes de la trayectoria de $D$, independientemente de la forma de $D$ (Solución).
100. ¿Verdadero o falso? La función $\bold{r} (t) = \bold{a} + t (\bold{b} - \bold{a})$, donde $0 \le t \le 1$, parametriza el segmento de línea recta de $\bold{a}$ a $\bold{b}$.
101. ¿Verdadero o falso? El campo vectorial $\bold{F} (x, y, z) = (y sen\;z)\bold{i} + (x sen\;z) \bold{j} + (xycos\;z) \bold{k}$ es conservativo (Solución).
102. ¿Verdadero o falso? El campo vectorial $\bold{F} (x, y, z) = y\bold{i} + (x + z) \bold{j} - y\bold{k}$ es conservativo.
103. Justifica el Teorema Fundamental de las Integrales de Línea para $\int_C\bold{F} \cdot d\bold{r}$ en el caso en que $\bold{F} (x, y) = (2x + 2y)\bold{i} + (2x + 2y)\bold{j}$ y $C$ es una porción del círculo de orientación positiva $x^2 + y^2 = 25$ desde $(5 , 0)$ hasta $(3,4)$ (Solución).
104. [T] Encuentra $\int_C\bold{F} \cdot dr$, donde $\bold{F} (x, y) = (ye^xy + cos\; x)\bold{i} + \big(xe^xy + \frac{1}{y^2 + 1}\big)\bold{j}$ y $C$ es una porción de la curva $y = sen\;x$ desde $x = 0$ hasta $x = \frac{\pi}{2}$.
105. [T] Evalúa la integral de línea $\int_C\bold{F}\cdot d\bold{r}$, donde $\bold{F} (x, y) = (e^xsen\;y - y)\bold{i} + (e^xcos\; y - x - 2)\bold{j}$, y $C $es la trayectoria dada por $\bold{r} (t) = \big[t^3sen\; \frac{\pi t}{2}\big] \bold{i} - \big[\frac{\pi}{2}cos\big(\frac{\pi t}{2} + \frac{\pi}{2}\big)\big] \bold{j}$ para $0 \le t \le 1$ (Solución).
 Para los siguientes ejercicios, determina si el campo vectorial es conservativo y, si lo es, encuentra la función potencial.
Para los siguientes ejercicios, determina si el campo vectorial es conservativo y, si lo es, encuentra la función potencial.
106. $\bold{F} (x, y) = 2xy^3\bold{i} + 3y^2x^2\bold{j}$. 107. $\bold{F} (x, y) = (−y + e^xsen\;y)\bold{i} + [(x + 2) e^xcos\; y]\bold{j}$ (Solución). 108. $\bold{F} (x, y) = \big(e^{2x}sen\;y\big)\bold{i} + \big[e^{2x}cos\; y\big]\bold{j}$ 109. $\bold{F} (x, y) = (6x + 5y) \bold{i} + (5x + 4y)\bold{j}$ (Solución). 110. $\bold{F} (x, y) = [2x cos (y) - y cos (x)] i + [−x^2sen (y) −sen (x)]\bold{j}$ 111. $\bold{F} (x, y) = [ye^x + sen (y)]\bold{i} + [e^x + x cos (y)]\bold{j}$ (Solución).
 Para los siguientes ejercicios, evalúa las integrales de línea usando el Teorema Fundamental de las Integrales de Línea.
Para los siguientes ejercicios, evalúa las integrales de línea usando el Teorema Fundamental de las Integrales de Línea.
112. $\oint_C (y\bold{i} + xj) \cdot d\bold{r}$, donde $C$ es cualquier trayectoria desde $(0, 0)$ hasta $(2, 4)$.
113. $\oint_C (2ydx + 2xdy)$, donde $C$ es el segmento de línea desde $(0, 0)$ hasta $(4, 4)$ (Solución). 114. [T] $\oint_C \big[arctan \frac{y}{x} − \frac{xy}{x^2 + y^2}\big] dx + \big[\frac{x^2}{x^2 + y^2} + e^{−y} (1 - y)\big]dy$, donde $C$ es cualquier curva suave desde $(1, 1)$ hasta $(−1 , 2)$. 115. Encuentra el campo vectorial conservativo para la función potencial $f (x, y) = 5x^2 + 3xy + 10y^2$ (Solución).
 Para los siguientes ejercicios, determina si el campo vectorial es conservativo y, de ser así, encuentra una función potencial.
Para los siguientes ejercicios, determina si el campo vectorial es conservativo y, de ser así, encuentra una función potencial.
116. $\bold{F} (x, y) = (12xy)\bold{i} + 6(x^2 + y^2)\bold{j}$ 117. $\bold{F} (x, y) = (e^xcos\; y)\bold{i} + 6(e^xsen\;y)\bold{j}$ (Solución). 118. $\bold{F} (x, y) = \big(2xye^{x^2y}\big)\bold{i} + 6\big(x^2e^{x^2y}\big)\bold{j}$. 119. $\bold{F} (x, y, z) = (ye^z)\bold{i} + (xe^z)\bold{j} + (xye^z)\bold{k}$ (Solución). 120. $\bold{F} (x, y, z) = (sen\;y)\bold{i} - (x cos \;y)\bold{j} + \bold{k}$ 121. $\bold{F} (x, y, z) = \big(\frac{1}{y}\big)\bold{i} + \big(\frac{x}{y^2}\bold{j} + (2z - 1)\bold{k}$ (Solución). 122. $\bold{F} (x, y, z) = 3z^2\bold{i} - cos\; y\bold{j} + 2xz\bold{k}$ 123. $\bold{F} (x, y, z) = (2xy)\bold{i} + (x^2 + 2yz)\bold{j} + y^2\bold{k}$ (Solución).
 Para los siguientes ejercicios, determina si el campo vectorial dado es conservativo y encuentra una función potencial.
Para los siguientes ejercicios, determina si el campo vectorial dado es conservativo y encuentra una función potencial.
124. $\bold{F} (x, y) = (e^xcos\; y)\bold{i} + 6(e^xsen\;y)\bold{j}$. 125. $\bold{F} (x, y) = \big(2xye^{x^2y}\big)\bold{i} + 6\big(x^2e^{x^2y}\big)\bold{j}$ (Solución).
 Para los siguientes ejercicios, evalúa la integral usando el Teorema Fundamental de las Integrales de Línea.
Para los siguientes ejercicios, evalúa la integral usando el Teorema Fundamental de las Integrales de Línea.
126. Evalúa $\int_C\nabla f \cdot d\bold{r}$, donde $f (x, y, z) = cos (\pi x) + sen (\pi y) - xyz$ y $C$ es cualquier trayectoria que comience en $(1,1/2, 2)$ y termine en $(2, 1, -1)$. 127. [T] Evalúa$\int_C\nabla f \cdot d\bold{r}$, donde $f (x, y) = xy + e^x$ y $C$ es una línea recta de $(0, 0)$ a $(2, 1)$ (Solución). 128. [T] Evalúa $\int_C\nabla f \cdot d\bold{r}$, donde $f (x, y) = x^2y - x$ y $C$ es cualquier trayectoria en un plano desde $(1, 2)$ hasta $(3, 2)$. 129. Evalúa $\int_C\nabla f \cdot d\bold{r}$, donde $f (x, y, z) = xyz^2 −yz$ y $C$ tiene el punto inicial $(1, 2)$ y el punto terminal $(3, 5)$ (Solución).
 Para los siguientes ejercicios, sea $\bold{F} (x, y) = 2xy^2\bold{i} + (2yx^2 + 2y)\bold{j}$ y $G (x, y) = (y + x)\bold{i} + (y - x) \bold{j}$, y sea $C_1$ la curva que consiste en el círculo de radio $2$, centrado en el origen y orientado en sentido antihorario, y $C_2$ ser la curva que consta de un segmento de línea desde $(0, 0)$ hasta $(1, 1)$ seguido de un segmento de línea desde $(1, 1)$ hasta $(3, 1 )$.
Para los siguientes ejercicios, sea $\bold{F} (x, y) = 2xy^2\bold{i} + (2yx^2 + 2y)\bold{j}$ y $G (x, y) = (y + x)\bold{i} + (y - x) \bold{j}$, y sea $C_1$ la curva que consiste en el círculo de radio $2$, centrado en el origen y orientado en sentido antihorario, y $C_2$ ser la curva que consta de un segmento de línea desde $(0, 0)$ hasta $(1, 1)$ seguido de un segmento de línea desde $(1, 1)$ hasta $(3, 1 )$.
130. Calcula la integral de línea de $\bold{F}$ sobre $C_1$. 131. Calcula la integral de línea de $\bold{G}$ sobre $C_1$ (Solución). 132. Calcula la integral de línea de $\bold{F}$ sobre $C_2$. 133. Calcula la integral de línea de $\bold{G}$ sobre $C_2$ (Solución).
134. [T] Sea $\bold{F} (x, y, z) = x^2\bold{i} + z sen (yz)\bold{j} + ysen (yz)\bold{k}$. Calcula $\oint_C\bold{F}\cdot d\bold{r}$, donde $C$ es un camino desde $A = (0,0, 1)$ hasta $B = (3, 1, 2)$.
135. [T] Encuentra la integral de línea $\oint_C\bold{F}\cdot d\bold{r}$ del campo vectorial $\bold{F} (x, y, z) = 3x^2z\bold{i} + z^2\bold{j} + (x^3 + 2yz)\bold{k}$ a lo largo de la curva $C$ parametrizada por $\bold{r} (t) = \big(\frac{ln\;t}{ln\; 2}\big)\bold{i} + t^{3/2}\bold{j} + tcos (\pi t), 1 \le t \le 4$ (Solución).
 Para los siguientes ejercicios, demuestra que los siguientes campos vectoriales son conservativos usando una computadora. Calcula $\int_C\bold{F}\cdot d\bold{r}$ para la curva dada.
Para los siguientes ejercicios, demuestra que los siguientes campos vectoriales son conservativos usando una computadora. Calcula $\int_C\bold{F}\cdot d\bold{r}$ para la curva dada.
136. $\bold{F} = (xy^2 + 3x^2y)\bold{i} + (x + y) x^2\bold{j}$; $C$ es la curva que consta de segmentos de línea desde $(1, 1)$ a $(0, 2)$ a $(3, 0)$. 137. $\bold{F} = \frac{2x}{y^2 + 1}\bold{i} − \frac{2y(x^2 + 1)}{(y^2 + 1)^2}\bold{j}$; $C$ está parametrizado por $x = t^3 - 1, y = t^6 - t, 0 \le t \le 1$ (Solución). 138. [T] $\bold{F} = \big[cos(xy^2) - xy^2sen(xy^2)\big]\bold{i} - 2x^2y sen(xy^2)\bold{j}$; $C$ es la curva $\big(e^t, e^t + 1\big), −1 \le t \le 0$.
139. La masa de la Tierra es de aproximadamente $6 \times 10^{27}\; g$ y la del Sol es $330.000$ veces mayor. La constante gravitacional es $6.7 \times 10^{−8}\; cm^3/s^2 \cdot g$. La distancia de la Tierra al Sol es de aproximadamente $1,5 \times 10^{12}\; cm$. Calcula, aproximadamente, el trabajo necesario para aumentar la distancia de la Tierra al Sol en $1\; cm$ (Solución).
140. [T] Sea $\bold{F} = (x, y, z) = (e^xsen\;y)\bold{i} + (e^xcos\: y)\bold{j} + z^2\bold{k}$. Evalúa la integral $\int_C\bold{F} \cdot d\bold{s}$, donde $\bold{c} (t) = \big(t, t^3, e^{\sqrt{t}}\big), 0 \le t \le 1$.
141. [T] Sea $\bold{c}: [1, 2] \to \Reals^2$ dado por $x = e^{t - 1}, y = sen\big(\frac{\pi}{t}\big)$. Usa una computadora para calcular la integral $\int_C\bold{F}\cdot d\bold{s} = \int_C2x cos\; ydx - x^2sen\;ydy$, donde $\bold{F} = (2x cos y)\bold{i} − (x^2sen\;y)\bold{j}$ (Solución).
142. [T] Usa un sistema de álgebra por computadora para encontrar la masa de un cable que se encuentra a lo largo de la curva $\bold{r} (t) = (t^2 - 1)\bold{j} + 2t\bold{k}, 0 \le t \le 1$, si la densidad es $\frac32t$.
143. Encuentra la circulación y el flujo del campo $\bold{F} = −y\bold{i} + x\bold{j}$ alrededor y a través de la trayectoria semicircular cerrada que consta de un arco semicircular $\bold{r}_1 (t) = (acos\;t)\bold{i} + (asen\;t)\bold{j}, 0 \le t \le \pi$, seguido de segmento de recta $\bold{r}_2 (t) = t\bold{i}, −a \le t \le a$ (Solución).
144. Calcula $\int_C cos\; x cos\; y dx - sen\;x sen\;y dy$, donde $\bold{c} (t) = \big(t, t^2\big), 0 \le t \le 1$.
145. Completa la prueba de independencia de trayectoria para campos conservativos mostrando que $f_y = Q (x, y)$.
En esta sección, examinaremos el teorema de Green, que es una extensión del Teorema Fundamental del Cálculo a dos dimensiones. El teorema de Green tiene dos formas: una forma de circulación y una forma de flujo, las cuales requieren que la región $D$ en la integral doble esté simplemente conectada. Sin embargo, ampliaremos el teorema de Green a regiones que no están simplemente conectadas.
En pocas palabras, el teorema de Green relaciona una integral de línea alrededor de una curva plana $C$ simplemente cerrada y una integral doble sobre la región encerrada por $C$.
El teorema es útil porque nos permite traducir integrales de línea difíciles en integrales dobles más simples o integrales dobles difíciles en integrales de línea más simples.
Recuerda que el Teorema Fundamental del Cálculo dice que
$$\int_a^b F^{\prime}(x)dx = F(b) - F(a)$$Como enunciado geométrico, esta ecuación dice que la integral sobre la región debajo de la gráfica de $F^{\prime} (x)$ y arriba del segmento de recta $[a, b]$ depende solo del valor de $F$ en los puntos extremos $a$ y $b$ de ese segmento. Dado que los números $a$ y $b$ son el límite del segmento de línea $[a, b]$, el teorema dice que podemos calcular la integral $\int_a^bF^{\prime}(x) dx$ con base en la información sobre el límite del segmento de línea $[a, b]$ (Figura 6.32). La misma idea es cierta del Teorema Fundamental para Integrales de Línea:
$$\int_C\nabla f\cdot d\bold{r} - f(\bold{r}(a))$$Cuando tenemos una función potencial (una "antiderivada"), podemos calcular la integral de línea basándonos únicamente en la información sobre el límite de la curva $C$.
El teorema de Green toma esta idea y la extiende al cálculo de integrales dobles. El teorema de Green dice que podemos calcular una integral doble sobre la región $D$ basándonos únicamente en la información sobre el límite de $D$.
El teorema de Green también dice que podemos calcular una integral de línea sobre una curva cerrada simple $C$ basada únicamente en la información sobre la región que $C$ encierra. En particular, el teorema de Green conecta una integral doble sobre la región $D$ con una integral de línea alrededor del límite de $D$.
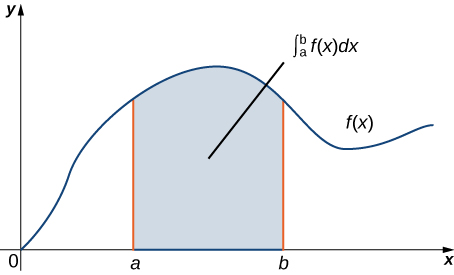
Figura 6.32. El Teorema Fundamental del Cálculo dice que la integral sobre el segmento de línea $[a, b]$ depende sólo de los valores de la antiderivada en los puntos finales de $[a, b]$.
La primera forma del teorema de Green que examinaremos es la forma de circulación. Esta forma del teorema relaciona la integral de línea vectorial sobre una curva plana simple cerrada $C$ con una integral doble sobre la región encerrada por $C$. Por lo tanto, la circulación de un campo vectorial a lo largo de una curva cerrada simple se puede transformar en una integral doble y viceversa.
Figura 6.33. La forma de circulación del teorema de Green relaciona una integral de línea sobre la curva $C$ con una integral doble sobre la región $D$.
Observa que el teorema de Green solo se puede usar para un campo vectorial bidimensional $\bold{F}$. Si $\bold{F}$ es un campo tridimensional, entonces el teorema de Green no se aplica. Ya que
$$\int_C Pdx + Qdy = \int_C \bold{F}\cdot \bold{T}ds,$$esta versión del teorema de Green a veces se denomina la forma tangencial del teorema de Green.
La prueba del teorema de Green es bastante técnica y está más allá del alcance de este texto. Aquí examinaremos una demostración del teorema en el caso especial de que $D$ es un rectángulo. Por ahora, observa que podemos confirmar rápidamente que el teorema es cierto para el caso especial en el que $\bold{F} = \lang P, Q\rang$ es conservativo. En este caso,
$$\oint_C Pdx + Qdy = 0$$porque la circulación es cero en campos vectoriales conservativos. Por la propiedad de parciales cruzadas de los campos conservativos, $\bold{F}$ satisface la condición de parciales cruzadas, por lo que $P_y = Q_x$. Por lo tanto,
$$\iint_D (Qx − Py)dA = \iint_D 0dA = \oint_C Pdx + Qdy,$$lo que confirma el teorema de Green en el caso de campos vectoriales conservativos.
Probemos ahora que la forma de circulación del teorema de Green es verdadera cuando la región $D$ es un rectángulo. Sea $D$ el rectángulo $[a, b] \times [c, d]$ orientado en sentido antihorario. Entonces, el límite $C$ de $D$ consta de cuatro partes lisas $C_1, C_2, C_3$ y $C_4$ (Figura 6.34). Parametrizamos cada lado de $D$ de la siguiente manera:
$$\begin{aligned} C_1: \bold{r}_1(t) &= \lang t, c \rang , a \le t\le b\\ C_2: \bold{r}_2(t) &= \lang b, t \rang , c \le t\le d\\ -C_3: \bold{r}_3(t) &= \lang t, d \rang , a \le t\le b\\ -C_4: \bold{r}_4(t) &= \lang a, t \rang , c \le t\le d \end{aligned}$$
Figura 6.34. El rectángulo $D$ está orientado en sentido antihorario.
Luego,
Por el Teorema Fundamental del Cálculo,
$$P(t,d) - P(t,c) = \int_c^d \frac{\partial}{\partial y} P(t,y)dy\\ \text{ y }\;\; Q(b, t) − Q(a, t) = \int_a^b \frac{\partial}{\partial x} Q(x, t)dx$$Por lo tanto,
$$-\int_a^b (P(t, d) − P(t, c))dt + \int_c^d (Q(b, t) − Q(a, t))dt\\ = -\int_a^b\int_c^d \frac{\partial}{\partial y} P(t, y)dydt + \int_c^d\int_a^b \frac{\partial}{\partial x} Q(x, t)dxdt$$Pero,
Por lo tanto, $\int_C \bold{F}\cdot d\bold{r} = \iint_D (Qx − Py)dA$ y hemos demostrado el teorema de Green en el caso de un rectángulo.
Para probar el teorema de Green sobre una región general $D$, podemos descomponer $D$ en muchos rectángulos diminutos y usar la prueba de que el teorema funciona sobre rectángulos. Sin embargo, los detalles son técnicos y están más allá del alcance de este texto.
 |
Aplicando el teorema de Green sobre un rectángulo |

 |
Aplicando el teorema de Green para calcular el trabajo |

En los dos ejercicios anteriores, la integral doble en el teorema de Green fue más fácil de calcular que la integral de línea, por lo que usamos el teorema para calcular la integral de línea. En el siguiente ejercicio, la integral doble es más difícil de calcular que la integral de línea, por lo que usamos el teorema de Green para transformar una integral doble en una integral de línea.
 |
Aplicando el teorema de Green sobre una elipse |
Figura 6.37. Elipse $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ denotada por $C$.

En el ejercicio anterior, usamos el campo vectorial $\bold{F} (x, y) = \lang P, Q\rang = \lang −\frac{y}{2},\frac{x}{2}\rang$ para encontrar el área de cualquier elipse. La lógica del ejercicio se puede ampliar para derivar una fórmula para el área de cualquier región $D$. Sea $D$ cualquier región con un límite que sea una simple curva cerrada $C$ orientada en sentido antihorario. Si $\bold{F} (x, y) = \lang P, Q\rang = \lang −\frac{y}{2},\frac{x}{2}\rang$, entonces $Q_x - P_y = 1$.
Por lo tanto, por la misma lógica que en el ejercicio anterior,
$$\text{área de } D = \iint_D dA = \frac12\oint_C −ydx + xdy \tag{$6.14$}$$Vale la pena señalar que si $\bold{F} (x, y) = \lang P, Q\rang$ es cualquier campo vectorial con $Q_x - P_y = 1$, entonces la lógica del párrafo anterior funciona. Entonces. La ecuación 6.14 no es la única ecuación que usa parciales mixtos de un campo vectorial para obtener el área de una región.
La forma de circulación del teorema de Green relaciona una integral doble sobre la región $D$ con la integral de línea $\int_C\bold{F}\cdot \bold{T}ds$, donde $C$ es el límite de $D$. La forma de flujo del teorema de Green relaciona una integral doble sobre la región $D$ con el flujo a través del límite $C$. El flujo de un fluido a través de una curva puede ser difícil de calcular utilizando la integral de la línea de flujo. Esta forma del teorema de Green nos permite transformar una integral de flujo difícil en una integral doble que a menudo es más fácil de calcular.
Debido a que esta forma del teorema de Green contiene el vector normal unitario $\bold{N}$, a veces se le llama la forma normal del teorema de Green.
Recuerda que $\oint_C\bold{F}\cdot \bold{N}ds = \oint_C − Qdx + Pdy$. Sea $M = −Q$ y $N = P$. Según la forma de circulación del teorema de Green,
$$\begin{aligned} \oint_C − Qdx + Pdy &= \oint_C Mdx + Ndy\\ &= \iint_D N_x - M_y dA\\ &= \iint_D P_x - (-Q)_ydA\\ &= \iint_D P_x + Q_y dA \end{aligned}$$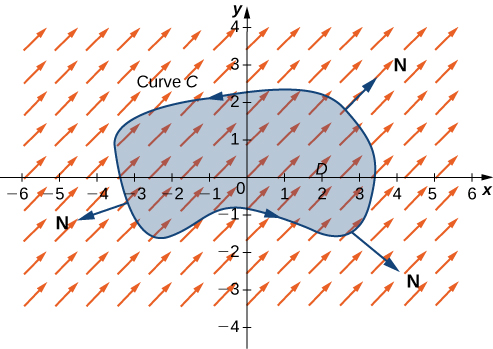
Figura 6.38. La forma de flujo del teorema de Green relaciona una integral doble sobre la región $D$ con el flujo a través de la curva $C$.
 |
Aplicando el teorema de Green para el flujo a través de un círculo |
Figura 6.39. La curva $C$ es un círculo de radio $r$ centrado en el origen

 |
Aplicando el teorema de Green para el flujo a través de un triángulo |
Figura 6.40. La curva $S$ es un triángulo con vértices $(0, 0), (1, 0)$ y $(0, 3)$ orientadosen el sentido de las agujas del reloj.

 |
Aplicando el teorema de Green para el flujo de agua a través de un rectángulo |
Figura 6.41. El agua fluye a través del rectángulo con vértices $(-1, -2), (1, -2), (1, 3)$ y $(-1, 3)$, orientados en sentido antihorario.

Recuerda que si el campo vectorial $\bold{F}$ es conservativo, $\bold{F}$ no funciona alrededor de curvas cerradas, es decir, la circulación de $\bold{F}$ alrededor de una curva cerrada es cero.
De hecho, si el dominio de $\bold{F}$ está simplemente conectado, entonces $\bold{F}$ es conservativo si y solo si la circulación de $\bold{F}$ alrededor de cualquier curva cerrada es cero. Si reemplazamos la "circulación de $\bold{F}$" con el "flujo de $\bold{F}$", obtenemos una definición de campo vectorial libre de la fuente. Las siguientes declaraciones son todas formas equivalentes de definir un campo libre de la fuente $\bold{F} = \lang P, Q\rang$ en un dominio simplemente conectado (observa las similitudes con las propiedades de los campos vectoriales conservativos):
En las siguientes escenas interactivas, diseñadas por Daniel Monsivais Velásquez, podrás: en la primera, verificar la propiedad 2, y en la segunda escena interactiva, una aplicación en la mecánica de fluidos.
Recuerda hacer clic en la esquina superior derecha, para interactuar con las escenas en una ventana ampliada.
 |
Encontrando una función de flujo |

Los campos vectoriales que son tanto conservativos como libres de fuentes son campos vectoriales importantes. Una característica importante de los campos vectoriales conservativos y libres de la fuente en un dominio simplemente conectado es que cualquier función potencial $f$ de dicho campo satisface la ecuación de Laplace $f_{xx} + f_{yy} = 0$. La ecuación de Laplace es fundamental en el campo de las ecuaciones diferenciales parciales porque modela tales fenómenos como potenciales gravitacionales y magnéticos en el espacio, y el potencial de velocidad de un fluido ideal. Una función que satisface la ecuación de Laplace se llama función armónica. Por lo tanto, cualquier función potencial de un campo vectorial conservativo y libre de la fuente es armónica.
Para ver que cualquier función potencial de un campo vectorial conservativo y libre de fuente en un dominio simplemente conectado es armónica, sea $f$ una función potencial del campo vectorial $\bold{F} = \lang P, Q\rang$. Entonces, $f_x = P$ y $f_y = Q$ porque $\nabla f = \bold{F}$. Por lo tanto, $f_{xx} = P_x$ y $f_{yy} = Q_y$. Como $\bold{F}$ no tiene fuente, $f_{xx} + f_{yy} = P_x + Q_y = 0$, y tenemos que $f$ es armónica.
 |
Satisfaciendo la ecuación de Laplace |

El teorema de Green, como se dijo, se aplica solo a las regiones que están simplemente conectadas, es decir, el teorema de Green, como se dijo hasta ahora, no puede manejar regiones con agujeros. Aquí, ampliamos el teorema de Green para que funcione en regiones con un número finito de agujeros (Figura 6.43).
Figura 6.43. El teorema de Green, como se establece, no se aplica a una región no simplemente conectada con tres agujeros como este.
Antes de discutir las extensiones del teorema de Green, necesitamos repasar alguna terminología con respecto al límite de una región. Sea $D$ una región y sea $C$ un componente del límite de $D$.
Decimos que $C$ está orientada positivamente si, mientras caminamos a lo largo de $C$ en la dirección de orientación, la región $D$ está siempre a nuestra izquierda. Por lo tanto, la orientación en sentido antihorario del límite de un disco es una orientación positiva, por ejemplo. La curva $C$ está orientada negativamente si, mientras caminamos por $C$ en la dirección de orientación, la región $D$ siempre está a nuestra derecha. La orientación en el sentido de las agujas del reloj del límite de un disco es una orientación negativa, por ejemplo.
Sea $D$ una región con un número finito de huecos (de modo que $D$ tenga un número finito de curvas de límite) y denota el límite de $D$ con $\partial D$ (Figura 6.44). Para extender el teorema de Green para que pueda manejar $D$, dividimos la región $D$ en dos regiones, $D_1$ y $D_2$ (con límites respectivos $\partial D_1$ y $\partial D_2$), de tal manera que $D = D_1 \cup D_2$ y ni $D_1$ ni $D_2$ tienen agujeros.
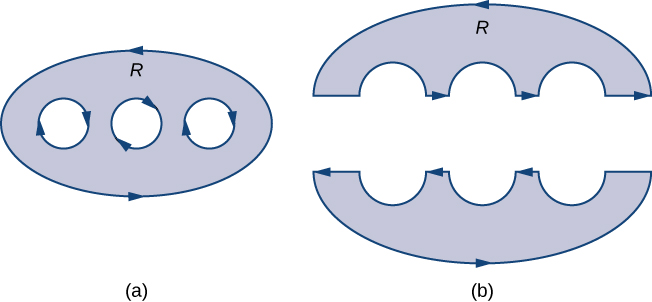
Figura 6.44. (a) La región $D$ con un límite orientado tiene tres agujeros. (b) La región $D$ dividida en dos regiones simplemente conectadas no tiene agujeros.
Supón que el límite de $D$ está orientado como en la figura, con los orificios internos con orientación negativa y el límite externo con orientación positiva. El límite de cada región simplemente conectada $D_1$ y $D_2$ está orientado positivamente. Si $\bold{F}$ es un campo vectorial definido en $D$, entonces el teorema de Green dice que
$$\begin{aligned} \oint_{\partial D} \bold{F}\cdot d\bold{r} &= \oint_{\partial D_1} \bold{F}\cdot d\bold{r} + \oint_{\partial D_2} \bold{F}\cdot d\bold{r}\\ &= \iint_{D_1} (Q_x - P_y) dA + \iint_{D_2} (Q_x - P_y) dA\\ &= \iint_D (Q_x - P_y)dA \end{aligned}$$Por lo tanto, el teorema de Green todavía funciona en una región con huecos.
Para ver cómo funciona esto en la práctica, considera el anillo $D$ en la figura 6.45 y supón que $\bold{F} = \lang P, Q\rang$ es un campo vectorial definido en este anillo. La región $D$ tiene un agujero, por lo que no está simplemente conectada. Orienta el círculo exterior del anillo en sentido contrario a las agujas del reloj y el círculo interior en el sentido de las agujas del reloj (Figura 6.45) de modo que, cuando dividimos la región en $D_1$ y $D_2$, podamos mantener la región a nuestra izquierda mientras caminamos por un camino que atraviesa el límite. Sea $D_1$ la mitad superior del anillo y $D_2$ la mitad inferior. Ninguna de estas regiones tiene agujeros, por lo que hemos dividido $D$ en dos regiones simplemente conectadas.
Etiquetamos cada parte de estos nuevos límites como $P_i$ para alguna $i$, como en la figura 6.45. Si comenzamos en $P$ y viajamos a lo largo del límite orientado, el primer segmento es $P_1$, luego $P_2, P_3$ y $P_4$.
Ahora hemos atravesado $D_1$ y regresado a $P$. Luego, comenzamos en $P$ nuevamente y atravesamos $D_2$. Dado que la primera parte del límite es la misma que $P_4$ en $D_1$, pero orientada en la dirección opuesta, la primera parte de $D_2$ es $−P_4$. A continuación, tenemos $P_5$, luego $−P_2$ y finalmente $P_6$.
Figura 6.45. Romper el anillo en dos regiones separadas nos da dos regiones simplemente conectadas. Las integrales de línea sobre los límites comunes se cancelan.
La figura 6.45 muestra un camino que atraviesa el límite de $D$. Observa que este camino atraviesa el límite de la región $D_1$, regresa al punto de partida y luego atraviesa el límite de la región $D_2$. Además, mientras caminamos por el sendero, la región siempre está a nuestra izquierda. Observa que este recorrido de las trayectorias $P_i$ cubre todo el límite de la región $D$. Si solo hubiéramos atravesado una porción del límite de $D$, entonces no podemos aplicar el teorema de Green a $D$. El límite de la mitad superior del anillo, por lo tanto, es $P_1 \cup P_2 \cup P_3 \cup P_4$ y el límite de la mitad inferior del anillo es $−P_4 \cup P_5 \cup - P_2 \cup P_6$. Entonces, el teorema de Green implica
Por lo tanto, llegamos a la ecuación que se encuentra en el teorema de Green, a saber
$$\oint_{\partial D} \bold{F}\cdot d\bold{r} = \iint_D (Q_x - P_y)dA$$La misma lógica implica que la forma de flujo del teorema de Green también se puede extender a una región con un número finito de agujeros:
$$\oint_C \bold{F}\cdot \bold{N} d\bold{s} = \iint_D (Q_x + P_y)dA$$ |
Usando el teorema de Green en una región con agujeros |
donde $D$ es el anillo dado por las desigualdades polares $1 \le \bold{r} \le 2, 0 \le \theta \le 2\pi$

 |
Usando la forma extendida del teorema de Green |

Medir el área desde un límite: el planímetro
Figura 6.47. Esta imagen de resonancia magnética del cerebro de un paciente muestra un tumor, que está resaltado en rojo (crédito: modificación del trabajo de Christaras A, Wikimedia Commons).
Imagina que eres un médico que acaba de recibir una imagen de resonancia magnética del cerebro de tu paciente. El cerebro tiene un tumor (Figura 6.47). ¿Qué tan grande es el tumor? Para ser precisos, ¿cuál es el área de la región roja? La sección transversal roja del tumor tiene una forma irregular y, por lo tanto, es poco probable que puedas encontrar un conjunto de ecuaciones o desigualdades para la región y luego poder calcular su área por medios convencionales.
Figura 6.48. a) Un planímetro rodante. El pivote permite que el brazo trazador gire. El rodillo en sí no gira; solo se mueve hacia adelante y hacia atrás. (b) Una vista interior de un planímetro rodante. Observa que la rueda no puede girar si el planímetro se mueve hacia adelante y hacia atrás con el brazo trazador perpendicular al rodillo.

Figura 6.49. Análisis matemático del movimiento del planímetro.

 Para los siguientes ejercicios, evalúa las integrales de línea aplicando el teorema de Green.
Para los siguientes ejercicios, evalúa las integrales de línea aplicando el teorema de Green.
146. $\int_C 2xydx + (x + y) dy$, donde $C$ es la trayectoria desde $(0, 0)$ hasta $(1, 1)$ a lo largo de la gráfica de $y = x^3$ y desde $(1,1)$ hasta $(0, 0)$ a lo largo de la gráfica de $y = x$ orientada en sentido antihorario. 147. $\int_C 2xydx + (x + y) dy$, donde $C$ es el límite de la región que se encuentra entre las gráficas de $y = 0$ y $y = 4 - x^2$ orientado en sentido antihorario (Solución). 148. $\int_C 2arctan\big(\frac{y}{x}\big)dx + ln\big(x^2 + y^2\big)dy$, donde $C$ se define por $x = 4 + 2 cos\;\theta, y = 4 sen\;\theta$ orientado en sentido antihorario. 149. $\int_C sen\; x cos\; ydx + (xy + cos\; x sen\; y) dy$, donde $C$ es el límite de la región que se encuentra entre las gráficas de $y = x$ y $y = \sqrt{x}$ orientadas en sentido antihorario (Solución).
150. $\int_C xydx + (x + y) dy$, donde $C$ es el límite de la región que se encuentra entre las gráficas de $x^2 + y^2 = 1$ y $x^2 + y^2 = 9$ orientada en sentido antihorario. 151. $\oint_C (−ydx + xdy)$, donde $C$ consiste en el segmento de recta $C_1$ desde $(−1, 0)$ hasta $(1, 0)$, seguido del arco semicircular $C_2$ desde $(1, 0)$ de regreso a $(1, 0 )$ (Solución)
 Para los siguientes ejercicios, usa el teorema de Green.
Para los siguientes ejercicios, usa el teorema de Green.
152. Sea $C$ la curva que consta de segmentos de línea desde $(0, 0)$ a $(1, 1)$ a $(0, 1)$ y de regreso a ($0, 0)$. Encuentra el valor de $\int_C xydx + \sqrt{y^2 + 1}dy$. 153. Evalúa la integral de línea $\int_C xe^{− 2x}dx + \big(x^4 + 2x^2y^2dy\big)$, donde $C$ es el límite de la región entre los círculos $x^2 + y^2 = 1$ y $x^2 + y^2 = 4$, y es una curva de orientación positiva (Solución) 154. Encuentra la circulación en sentido antihorario del campo $\bold{F} (x, y) = xy\bold{i} + y^2\bold{j}$ alrededor y sobre el límite de la región encerrada por las curvas $y = x^2$ e $y = x$ en el primer cuadrante y orientado en sentido antihorario
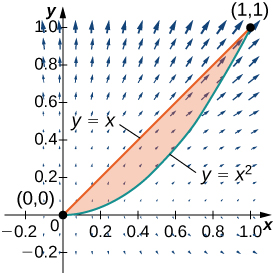
155. Evalúa $\oint_C y^3dx - x^3y^2dy$, donde $C$ es el círculo de radio $2$ de orientación positiva centrado en el origen (Solución). 156. Evalúa $\oint_C y^3dx - x^3dy$, donde $C$ incluye los dos círculos de radio $2$ y radio $1$ centrados en el origen, ambos con orientación positiva.
157. Calcula $\oint_C − x^2ydx + xy^2dy$, donde $C$ es un círculo de radio $2$ centrado en el origen y orientado en sentido antihorario (Solución).
158. Calcula la integral $\oint_C 2[y + x sen (y)] dx + \big[x^2cos (y) - 3y^2\big] dy$ a lo largo del triángulo $C$ con vértices $(0, 0), (1, 0)$ y $(1, 1)$, orientados en sentido antihorario, utilizando el teorema de Green. 159. Evalúa la integral $\oint_C\big(x^2 + y^2\big)dx + 2xydy$, donde $C$ es la curva que sigue a la parábola $y = x^2$ desde $(0, 0)$ $(2, 4)$, luego la recta de $(2, 4)$ a $(2,0)$, y finalmente la recta de $(2, 0)$ a $(0, 0)$ (Solución).
160. Evalúa la integral de línea $\oint_C (y - sen (y) cos (y)) dx + 2x sen^2 (y) dy$, donde $C$ se orienta en una trayectoria en sentido antihorario alrededor de la región limitada por $x = −1, x = 2, y = 4 - x^2$ y $y = x - 2$.
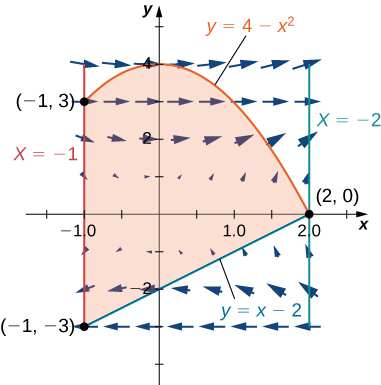
 Para los siguientes ejercicios, usa el teorema de Green para encontrar el área.
Para los siguientes ejercicios, usa el teorema de Green para encontrar el área.
161. Halla el área entre la elipse $\frac{x^2}{9} + \frac{y^2}{4} = 1$ y el círculo $x^2 + y^2 = 25$ (Solución). 162. Encuentra el área de la región encerrada por la ecuación paramétrica $p (\theta) = cos (\theta) - cos^2 (\theta)\bold{i} + sen (\theta) - cos (\theta) sen (\theta)\bold{j}$ para $0 \le \theta \le 2\pi$.
163. Halla el área de la región limitada por el hipocicloide $r (t) = cos^3 (t)\bold{i} + sen^3 (t)\bold{j}$. La curva está parametrizada por $t \isin [0, 2\pi]$ (Solución). 164. Halla el área de un pentágono con vértices $(0, 4), (4, 1), (3, 0), (−1, −1)$ y $(−2, 2)$. 165. Usa el teorema de Green para evaluar $\int_{C +} \big(y^2 + x^3\big)dx + x^4dy$, donde $C +$ es el perímetro del cuadrado $[0, 1] \times [0, 1]$ orientado en sentido antihorario (Solución).
166. Usa el teorema de Green para demostrar que el área de un disco con radio $a$ es $A = \pi a^2$. 167. Usa el teorema de Green para encontrar el área de un bucle de una rosa de cuatro hojas $r = 3 sen\; 2\theta$ (sugerencia: $xdy - ydx = \bold{r}^2d\theta$ ) (Solución). 168. Usa el teorema de Green para encontrar el área debajo de un arco de la cicloide dada por el plano paramétrico $x = t - sen \;t, y = 1 - cos\; t, t \le 0$. 169. Usa el teorema de Green para encontrar el área de la región encerrada por la curva (Solución).
$$\bold{r}(t) = t^2\bold{i} + \big(\frac{t^3}{3} - t\big)\bold{j}, -\sqrt{3} \le t\sqrt{3}$$
170. [T] Evalúa el teorema de Green usando un sistema de álgebra computarizada para evaluar la integral $\int_C xe^ydx + e^xdy$, donde $C$ es el círculo dado por $x^2 + y^2 = 4$ y está orientado en sentido antihorario. 171. Evalúa $\int_C \big(x^2y - 2xy + y^2\big)ds$, donde $C$ es el límite del cuadrado unitario $0 \le x \le 1, 0 \le y \le 1$, atravesado en sentido antihorario (Solución).
172. Evalúa $\int_C \frac{− (y + 2) dx + (x - 1) dy}{(x - 1)^2 + (y + 2)^2}$, donde $C$ es cualquier curva cerrada simple con un interior que no contiene el punto $(1 , −2)$ atravesado en sentido antihorario. 173. Evalúe $\int_C \frac{xdx + ydy}{x^2 + y^2}$, donde $C$ es cualquier curva cerrada simple, a trozos, suave, que encierra el origen, atravesada en sentido antihorario (Solución).
 Para los siguientes ejercicios, usa el teorema de Green para calcular el trabajo realizado por la fuerza $\bold{F}$ sobre una partícula que se mueve en sentido antihorario alrededor de la trayectoria cerrada $C$.
Para los siguientes ejercicios, usa el teorema de Green para calcular el trabajo realizado por la fuerza $\bold{F}$ sobre una partícula que se mueve en sentido antihorario alrededor de la trayectoria cerrada $C$.
174. $\bold{F} (x, y) = xy\bold{i} + (x + y)\bold{j}, C: x^2 + y^2 = 4$ 175. $\bold{F} (x, y) = \big(x^{3 / 2} - 3y\big)\bold{i} + (6x +5 y)\bold{j}$, $C$: límite de un triángulo con vértices $(0, 0), (5, 0)$ y $(0, 5)$ (Solución). 176. Evalúa $\int_C \big(2x^3 - y^3\big)dx + \big(x^3 + y^3\big)dy$, donde $C$ es un círculo unitario orientado en sentido antihorario. 177. Una partícula comienza en el punto $(−2, 0)$, se mueve a lo largo del eje $x$ hasta $(2, 0)$ y luego viaja a lo largo del semicírculo $y = \sqrt{4 - x^2}$ hasta el punto de partida. Utiliza el teorema de Green para encontrar el trabajo realizado en esta partícula por el campo de fuerza $\bold{F} (x, y) = x\bold{i} + \big(x^3 + 3xy^2\big)\bold{j}$ (Solución). 178. David y Sandra están patinando en un estanque sin fricción con el viento. David patina por dentro, recorriendo un círculo de radio $2$ en sentido antihorario. Sandra patina una vez alrededor de un círculo de radio $3$, también en sentido antihorario. Supón que la fuerza del viento en el punto $(x, y)$ es $\bold{F} (x, y) = \big(x^2y + 10y\big)\bold{i} + \big(x^3 + 2xy^2\big)\bold{j}$. Utiliza el teorema de Green para determinar quién hace más trabajo.
179. Usa el teorema de Green para encontrar el trabajo realizado por el campo de fuerza $\bold{F} (x, y) = (3y - 4x)\bold{i} + (4x - y)\bold{j}$ cuando un objeto se mueve una vez en sentido antihorario alrededor de la elipse $4x^2 + y^2 = 4$ (Solución). 180. Usa el teorema de Green para evaluar la integral de línea $\oint_C e^{2x}sen \;2ydx + e^{2x}cos\; 2ydy$, donde $C$ es la elipse $9 (x - 1)^2 + 4 (y - 3)^2 = 36$ orientada en sentido antihorario. 181. Evalúa la integral de línea $\oint_C y^2dx + x^2dy$, donde $C$ es el límite de un triángulo con vértices $(0, 0), (1, 1)$ y $(1, 0)$, con la orientación en sentido antihorario (Solución). 182. Usa el teorema de Green para evaluar la integral de línea $\int_C \bold{h}\cdot d\bold{r}$ si $\bold{h} (x, y) = e^y\bold{i}− sen\;\pi x\bold{j}$, donde $C$ es un triángulo con vértices $(1, 0), (0, 1)$ y $(−1, 0)$ desplazado en sentido antihorario. 183. Usa el teorema de Green para evaluar la integral de línea $\int_C \sqrt{1 + x^3}dx + 2xydy$ donde $C$ es un triángulo con vértices $(0, 0), (1, 0)$ y $(1, 3)$ orientado en el sentido de las agujas del reloj (Solución). 184. Usa el teorema de Green para evaluar la integral de línea $\int_C x^2ydx - xy^2dy$ donde $C$ es un círculo $x2^ + y^2 = 4$ orientado en sentido antihorario. 185. Usa el teorema de Green para evaluar la integral de línea $\int_C \big(3y - e^{sen\; x}\big)dx + \big(7x + \sqrt{y^4 + 1}\big)dy$ donde $C$ es el círculo $x^2 + y^2 = 9$ orientado en sentido antihorario (Solución). 186. Usa el teorema de Green para evaluar la integral de línea $\int_C (3x - 5y) dx + (x −6y) dy$, donde $C$ es elipse $\frac{x^2}{4} + y^2 = 1$ y está orientada en sentido antihorario.
187. Sea $C$ una curva triangular cerrada de $(0,0)$ a $(1, 0)$ a $(1, 1)$ y finalmente de vuelta a $(0, 0)$. Sea $\bold{F} (x, y) = 4y\bold{i} + 6x^2\bold{j}$. Usa el teorema de Green para evaluar $\oint_C\bold{F}\cdot d\bold{s}$ (Solución). 188. Usa el teorema de Green para evaluar la integral de línea $\oint_C ydx - xdy$, donde $C$ es el círculo $x^2 + y^2 = a^2$ orientado en el sentido de las agujas del reloj. 189. Usa el teorema de Green para evaluar la integral de línea $\oint_C (y + x) dx + (x + sin y) dy$, donde $C$ es cualquier curva cerrada simple y suave que une el origen consigo mismo orientada en sentido antihorario (Solución). 190. Usa el teorema de Green para evaluar la integral de línea $\oint_C \big(y - ln\big(x^2 + y^2\big)\big)dx + \big(2 arctan \frac{y}{x}\big)dy$, donde $C$ es el círculo de orientación positiva $(x - 2)^2 + (y - 3)^2 = 1$. 191. Usa el teorema de Green para evaluar $\oint_C xydx + x^3y^3dy$, donde $C$ es un triángulo con vértices $(0, 0), (1, 0)$ y $(1, 2)$ con orientación positiva (Solución). 192. Usa el teorema de Green para evaluar la integral de línea $\int_Csen\; ydx + x cos\; ydy$, donde $C$ es la elipse $x^2 + xy + y^2 = 1$ orientada en sentido antihorario.
193. Sea $\bold{F} (x, y) = \big(cos\big(x^5\big)\big) − \frac13y^3\bold{i} + \frac13x^3\bold{j}$. Encuentra la circulación en sentido antihorario $\oint_C \bold{F}\cdot d\bold{r}$, donde $C$ es una curva que consta del segmento de recta que une $(−2, 0)$ y $(−1, 0)$, el semicírculo $y = \sqrt{1 - x^2}$, el segmento de recta que une $(1, 0)$ y $(2, 0)$, y el semicírculo $y = \sqrt{4 - x^2}$ (Solución). 194. Usa el teorema de Green para evaluar la integral de línea $\int_C sen\;x^3dx + 2ye^{x^2}dy$, donde $C$ es una curva triangular cerrada que conecta los puntos $(0, 0), (2, 2)$ y $(0, 2)$ en sentido antihorario. 195. Sea $C$ el límite del cuadrado $0 \le x \le \pi, 0 \le y \le \pi$, atravesado en sentido antihorario. Usa el teorema de Green para encontrar $\int_C sen (x + y) dx + cos (x + y) dy$ (Solución). 196. Usa el teorema de Green para evaluar la integral de línea $\int_C \bold{F}\cdot d\bold{r}$, donde $\bold{F} (x, y) = \big(y^2 - x^2\big)\bold{i} + \big(x^2 + y^2\big)\bold{j}$, y $C$ es un triángulo acotado por $y = 0, x = 3$ y $y = x$, orientado en sentido antihorario. 197. Usa el teorema de Green para evaluar la integral $\int_C \bold{F}\cdot d\bold{r}$, donde $\bold{F} (x, y) = xy^2\bold{i} + x\bold{j}$, y $C$ es un círculo unitario orientado en sentido antihorario (Solución). 198. Usa el teorema de Green en un plano para evaluar la integral de línea $\oint_C\big(xy + y^2\big)dx + x2dy$, donde $C$ es una curva cerrada de una región delimitada por $y = x$ e $y = x^2$ orientada en sentido antihorario. 199. Calcula el flujo hacia afuera de $\bold{F} = −x\bold{i} + 2y\bold{j}$ sobre un cuadrado con esquinas $(\pm 1, \pm 1)$, donde la normal unitaria apunta hacia afuera y está orientada en la dirección contraria a las manecillas del reloj (Solución). 200. [T] Sea $C$ el círculo $x^2 + y^2 = 4$ orientado en sentido antihorario. Evalúe $\oint_C \big[\big(3y - e^{tan^{-1}x}\big)dx + \big(7x + \sqrt{y^4 + 1}dy\big]$ usando un sistema de álgebra informática.
201. Encuentra el flujo del campo $\bold{F} = −x\bold{i} + y\bold{j}$ a través de $x^2 + y^2 = 16$ orientado en la dirección contraria a las manecillas del reloj (Solución).
202. Sea $\bold{F} = \big(y^2 - x^2\big)\bold{i} + \big(x^2 + y^2\big)\bold{j}$, y sea $C$ un triángulo delimitado por $y = 0, x = 3$ e $y = x$ orientado en sentido antihorario. Encuentra el flujo hacia afuera de $\bold{F}$ a través de $C$.
203. [T] Sea $C$ el círculo unitario $x^2 + y^2 = 1$ atravesado una vez en sentido antihorario. Evalúa $\int_C \big[−y^3 + sen (xy) + xy cos (xy)\big] dx + \big[x^3 + x^2cos (xy)\big] dy$ usando un sistema de álgebra computarizada (Solución).
204. [T] Encuentra el flujo hacia afuera del campo vectorial $\bold{F} = xy^2\bold{i} + x^2y\bold{j}$ a través del límite del anillo $R = \lbrace (x, y): 1 \le x^2 + y^2 \le 4\rbrace = \lbrace (r, \theta): 1 \le r \le 2 , 0 \le \theta \le 2\pi \rbrace$ usando un sistema de álgebra por computadora.
205. Considera la región $R$ limitada por parábolas $y = x^2$ y $x = y^2$. Sea $C$ el límite de $R$ orientado en sentido antihorario. Utiliza el teorema de Green para evaluar $\oint_C \big(y + e^{\sqrt{x}}\big)dx + \big(2x + cos\big(y^2\big)\big)dy$ (Solución).
En este apartado, examinaremos dos operaciones importantes en un campo vectorial: divergencia y rotacional. Son importantes para el campo del cálculo por varias razones, incluido el uso del rotacional y la divergencia para desarrollar algunas versiones de dimensiones superiores del Teorema Fundamental del Cálculo. Además, el rotacional y la divergencia aparecen en las descripciones matemáticas de la mecánica de fluidos, el electromagnetismo y la teoría de la elasticidad, que son conceptos importantes en física e ingeniería. También podemos aplicar rotacional y divergencia a otros conceptos que ya exploramos. Por ejemplo, bajo ciertas condiciones, un campo vectorial es conservativo si y solo si su rotacional es cero.
Además de definir el rotacional y la divergencia, observaremos algunas interpretaciones físicas de ellos y demostraremos su relación con los campos vectoriales conservativos y libres de fuentes.
La divergencia es una operación en un campo vectorial que nos dice cómo se comporta el campo hacia o desde un punto. Localmente, la divergencia de un campo vectorial $\bold{F}$ en $\Reals^2$ o $\Reals^3$ en un punto particular $P$ es una medida de la "salida" del campo vectorial en $P$. Si $\bold{F}$ representa la velocidad de un fluido, entonces la divergencia de $\bold{F}$ en $P$ mide la tasa neta de cambio con respecto al tiempo de la cantidad de fluido que fluye desde $P$ (la tendencia del fluido a fluir "fuera" de $P$). En particular, si la cantidad de fluido que fluye hacia $P$ es la misma que la cantidad que sale, entonces la divergencia en $P$ es cero.
Observa la siguiente escena interactiva, la cual hace parte de la Unidad Interactiva "Campos Vectoriales", del Proyecto Prometeo, en la que se usa una caja en diferentes situaciones (tuberías, campo gravitacional, carga eléctrica, etc.), permitiendo analizar si entra más flujo que el que sale o viceversa:
La divergencia de un campo vectorial no es un campo vectorial, sino una función escalar. En términos del operador gradiente $\nabla = \big\lang \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}\big\rang$, la divergencia puede escribirse simbólicamente como el producto punto:
$$\text{div }\bold{F} = \nabla\cdot \bold{F}$$Ten en cuenta que esto es simplemente una notación útil, porque el producto escalar de un vector de operadores y un vector de funciones no está definido de manera significativa dada nuestra definición actual de producto escalar.
Si $\bold{F} = \lang P, Q\rang$ es un campo vectorial en $\Reals^2$, y tanto $P_x$ como $Q_y$ existen, entonces la divergencia de $\bold{F}$ se define de manera similar como
$$\text{div }\bold{F} = P_x + Q_y = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} = \nabla\cdot \bold{F}$$Para ilustrar este punto, considera los dos campos vectoriales de la figura 6.50. En cualquier punto en particular, la cantidad que fluye hacia adentro es la misma que la cantidad que fluye hacia afuera, por lo que en cada punto la "salida" del campo es cero.
Por lo tanto, esperamos que la divergencia de ambos campos sea cero, y este es el caso, ya que
$$div(\lang 1,2\rang) = \frac{\partial}{\partial x}(1) + \frac{\partial}{\partial y}(2) = 0$$y
$$div(\lang -y,x\rang) = \frac{\partial}{\partial x}(-y) + \frac{\partial}{\partial y}(x) = 0$$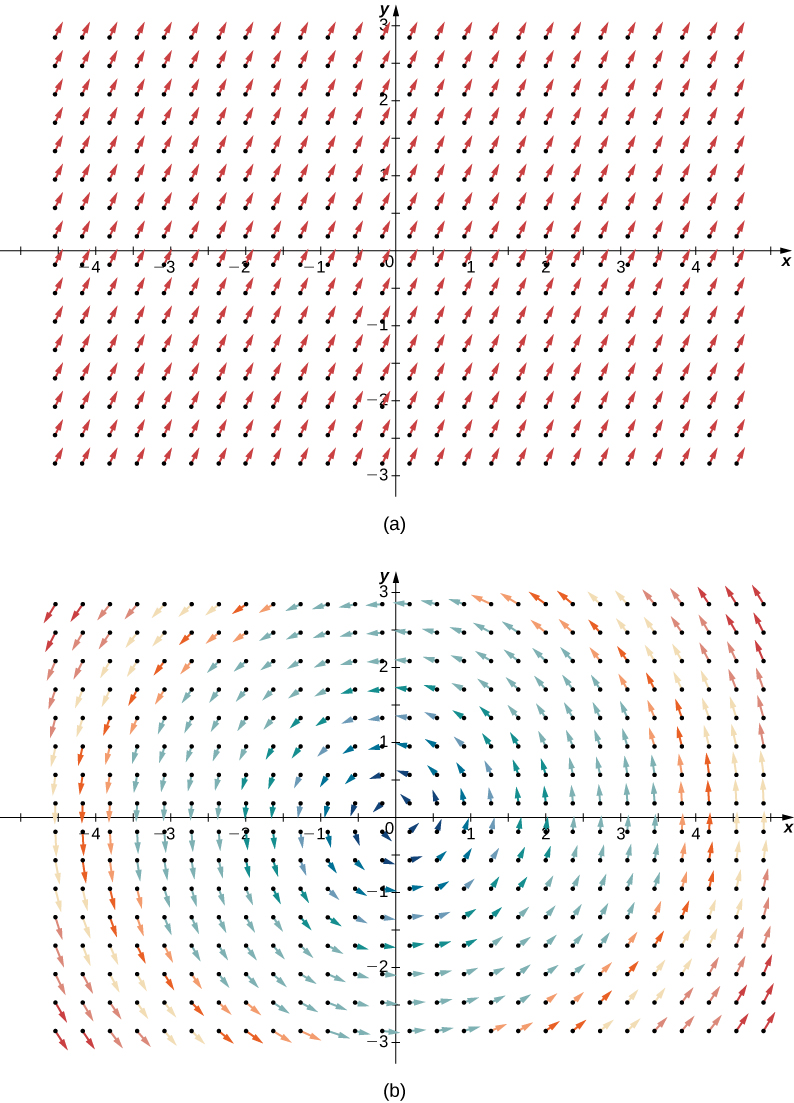
Figura 6.50. (a) El campo vectorial $\lang 1, 2\rang$ tiene divergencia cero. (b) El campo vectorial $\lang −y, x\rang$ también tiene divergencia cero.
Retornando a las escenas interactivas de la Unidad Interactiva "Campos Vectoriales", diseñadas por Alejandro Radillo Díaz, presentamos el siguiente modelo en el que puedes ingresar los campos vectoriales y verificar si es divergente o no. Para ello, desplaza la caja (azul) y verifica para cualquier punto. Por ejemplo, usa los campos vectoriales de la figura 6.50 para verificar la divergencia en cualquier punto.
Para cada caso, te sugerimos usar una escala menor; por ejemplo, usar los campos vectoriales $\lang 0.1, 0.2\rang$ y $\lang -y/5, x/5 \rang$, que para el análisis de divergencia surte el mismo efecto que los ejemplos originales de la figura 6.50.
Por el contrario, considera el campo vectorial radial $\bold{R} (x, y) = \lang −x, −y\rang$ en la figura 6.51. En cualquier punto dado, entra más fluido del que sale y, por lo tanto, la "extroversión" del campo es negativa.
Esperamos que la divergencia de este campo sea negativa, y este es el caso, ya que $div (\bold{R}) = \frac{\partial}{\partial x}(−x) + \frac{\partial}{\partial y}(−y) = −2$.
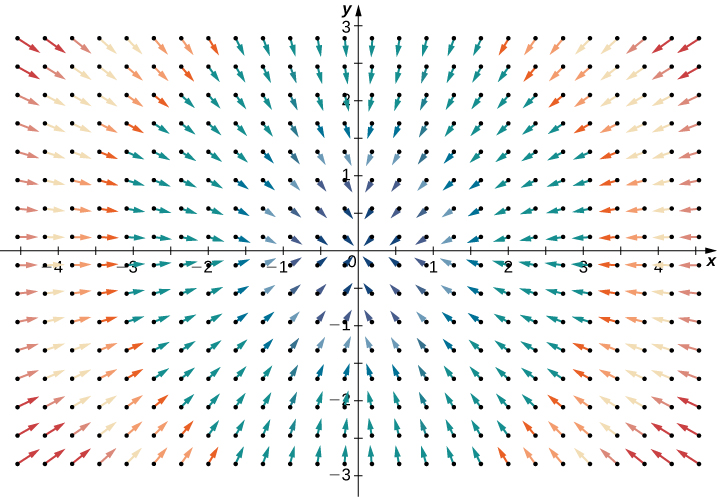
Figura 6.51. Este campo vectorial tiene divergencia negativa
Para tener una idea global de lo que nos dice la divergencia, supón que un campo vectorial en $\Reals^2$ representa la velocidad de un fluido. Imagínate tomando un círculo elástico (un círculo con una forma que puede ser cambiada por el campo vectorial) y soltándolo en un fluido. Si el círculo mantiene su área exacta a medida que fluye a través del fluido, entonces la divergencia es cero. Esto ocurriría para ambos campos vectoriales en la figura 6.50.
Por otro lado, si la forma del círculo se distorsiona de modo que su área se contrae o se expande, entonces la divergencia no es cero.
Imagina dejar caer tal círculo elástico en el campo vectorial radial de la figura 6.51 de modo que el centro del círculo aterrice en el punto $(3, 3)$. El círculo fluiría hacia el origen, y mientras lo hacía, el frente del círculo viajaría más lentamente que la parte posterior, causando que el círculo se "arrugara" y perdiera área. Así es como se puede ver una divergencia negativa (verifícalo en la escena interactiva).
 |
Calculando la divergencia en un punto |

Una aplicación de la divergencia ocurre en física, cuando se trabaja con campos magnéticos. Un campo magnético es un campo vectorial que modela la influencia de corrientes eléctricas y materiales magnéticos. Los físicos utilizan la divergencia en la ley de Gauss para el magnetismo, que establece que si $\bold{B}$ es un campo magnético, entonces $\nabla\cdot \bold{B} = 0;$ en otras palabras, la divergencia de un campo magnético es cero.
 |
Determinando si un campo es magnético |

Otra aplicación para la divergencia es detectar si un campo está libre de fuentes. Recuerda que un campo libre de la fuente es un campo vectorial que tiene una función de flujo; de manera equivalente, un campo libre de la fuente es un campo con un flujo que es cero a lo largo de cualquier curva cerrada. Los siguientes dos teoremas dicen que, bajo ciertas condiciones, los campos vectoriales sin fuente son precisamente los campos vectoriales con divergencia cero.
Como $\bold{F}$ no tiene fuente, hay una función $g (x, y)$ con $g_y = P$ y $−g_x = Q$. Por lo tanto, $\bold{F} = \lang g_y, −g_x\rang$ y $div\; \bold{F} = g_{yx} - g_{xy} = 0$ según el teorema de Clairaut.
Lo contrario de "Divergencia de un campo vectorial libre de fuente" es cierto en regiones simplemente conectadas, pero la prueba es demasiado técnica para incluirla aquí. Por lo tanto, tenemos el siguiente teorema, que puede probar si un campo vectorial en $\Reals^2$ está libre de fuentes.
 |
Determinando si un campo está libre de fuentes |

Recuerda que la forma de flujo del teorema de Green dice que
$$\oint_C \bold{F}\cdot \bold{N}ds = \iint_D (P_x + Q_y)dA$$donde $C$ es una curva cerrada simple y $D$ es la región encerrada por $C$. Dado que $P_x + Q_y = div\; \bold{F}$, el teorema de Green a veces se escribe como
$$\oint_C \bold{F}\cdot \bold{N}ds = \int_D div\;\bold{F}dA$$Por tanto, el teorema de Green se puede escribir en términos de divergencia. Si pensamos en la divergencia como una especie de derivada, entonces el teorema de Green dice que la "derivada" de $\bold{F}$ en una región se puede traducir en una integral de línea de $\bold{F}$ a lo largo del límite de la región. Esto es análogo al Teorema Fundamental del Cálculo, en el que la derivada de una función $f$ en un segmento de línea $[a, b]$ puede traducirse en un enunciado sobre $f$ en el límite de $[a, b]$. Usando la divergencia, podemos ver que el teorema de Green es un análogo dimensional superior del Teorema Fundamental del Cálculo.
Podemos utilizar todo lo que hemos aprendido en la aplicación de la divergencia. Sea $\bold{v}$ un campo vectorial que modela la velocidad de un fluido. Dado que la divergencia de $\bold{v}$ en el punto $\bold{P}$ mide la "salida" del fluido en $\bold{P}, div\; \bold{v} (\bold{P})\gt 0$ implica que sale más fluido de $\bold{P}$ que lo que entra. De manera similar, $div\; \bold{v} (\bold{P}) \lt 0$ implica que más fluido fluye hacia $\bold{P}$ que el que fluye hacia afuera, y $div\; \bold{v} (\bold{P}) = 0$ implica que fluye la misma cantidad de fluido que fluye hacia afuera.
 |
Determinando del flujo de un fluido |

Antes de continuar con el siguiente apartado, interactúa con la siguiente escena, diseñada por Antonio Di Muro, en la cual puedes modificar los campos vectoriales.
Los campos iniciales corresponde al ejercicio anterior, observa que al desplazar el punto $P$, la divergencia siempre será $-3$ (haz clic en el cuadro de la esquina inferior derecha, para ampliar la escena).
La segunda operación en un campo vectorial que examinamos es el rotacional, que mide la extensión de rotación del campo alrededor de un punto. Supón que $\bold{F}$ representa el campo de velocidad de un fluido. Entonces, el rotacional de $\bold{F}$ en el punto $P$ es un vector que mide la tendencia de las partículas cercanas a $P$ a rotar alrededor del eje que apunta en la dirección de este vector. La magnitud del vector rotacional en $P$ mide la rapidez con la que giran las partículas alrededor de este eje. En otras palabras, el rotacional en un punto es una medida del "giro" del campo vectorial en ese punto. Visualmente, imagina colocar una rueda de paletas en un fluido en $P$, con el eje de la rueda de paletas alineado con el vector rotacional (Figura 6.54). El rotacional mide la tendencia de la rueda de paletas a girar.
Figura 6.54. Para visualizar el rotacional en un punto, imagina colocar una pequeña rueda de paletas en el campo vectorial en un punto.
Considera los campos vectoriales de la figura 6.50. En la parte (a), el campo vectorial es constante y no hay espín en ningún punto. Por lo tanto, esperamos que la curvatura del campo sea cero, y este es el caso. La parte (b) muestra un campo rotacional, por lo que el campo tiene giro. En particular, si colocas una rueda de paletas en un campo en cualquier punto de modo que el eje de la rueda sea perpendicular a un plano, la rueda gira en sentido antihorario. Por lo tanto, esperamos que el rotacional del campo sea distinto de cero, y este es de hecho el caso (el rotacional es $2\bold{k}$).
Para ver qué rotacional mide globalmente, imagina que se dejas caer una hoja en el líquido. A medida que la hoja se mueve junto con el flujo de fluido, el rotacional mide la tendencia de la hoja a girar. Si el rotacional es cero, entonces la hoja no gira mientras se mueve a través del fluido.
Nuevamente, una escena interactiva de Alejandro Radillo Díaz nos describe el concepto de rotacional. Inicialmente, observarás un disco flotante que gira según las corrientes de agua justo debajo de él. Posteriormente se indica que el rotacional se aplica a cualquier campo, no necesariamente las corrientes de agua.
La definición de rotacional puede ser difícil de recordar. Para ayudar a recordar, usamos la notación $\nabla\times\bold{F}$ para representar un "determinante" que da la fórmula de rotacional:
$$\begin{vmatrix} \bold{i} & \bold{j} & \bold{k}\\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\ P & Q & R\\ \end{vmatrix}$$El determinante de esta matriz es
$$\begin{aligned} &\;\;\;\;\;\big(R_y - Q_z\big)\bold{i} - \big(Q_x - P_y\big)\bold{j} + \big(Q_x - P_y\big)\bold{k}\\ &= \big(R_y - Q_z\big)\bold{i} + \big(P_z - R_x\big)\bold{j} + \big(Q_x - P_y\big)\bold{k} = rot\;\bold{F} \end{aligned}$$Por lo tanto, esta matriz es una forma de ayudar a recordar la fórmula del rotacional. Sin embargo, ten en cuenta que la palabra determinante se usa de manera muy vaga. Un determinante no se define realmente en una matriz con entradas que son tres vectores, tres operadores y tres funciones.
Si $\bold{F} = \lang P, Q\rang$ es un campo vectorial en $\Reals^2$, entonces la curva de $\bold{F}$, por definición, es $$rot\;\bold{F} = \big(Q_x - P_y\big)\bold{k} = \bigg(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\bigg)\bold{k}$$
 |
Encontrando el rotacional de un campo vectorial tridimensional |

Compartimos una escena de GeoGebra, diseñada por Juan Carlos Ponce Campuzano, en la cual puedes incluir los campos vectoriales y calcular tanto la divergencia como el rotacional. Observa que los campos iniciales son los mismos del ejercicio anterior.
 |
Encontrando el rotacional de un campo vectorial bidimensional |

Observa que si $\bold{F} = \lang P, Q\rang$ es un campo vectorial en un plano, entonces $rot \bold{F}\cdot\bold{k} = (Q_x − P_y)\bold{k}\cdot\bold{k} = Q_x − P_y$. Por lo tanto, la forma de circulación del teorema de Green a veces se escribe como
donde $C$ es una curva cerrada simple y $D$ es la región encerrada por $C$. Por lo tanto, la forma de circulación del teorema de Green se puede escribir en términos del rotacional.
Si pensamos en el rotacional como una especie de derivada, entonces el teorema de Green dice que la "derivada" de $\bold{F}$ en una región puede traducirse en una integral de línea de $\bold{F}$ a lo largo del límite de la región. Esto es análogo al Teorema Fundamental del Cálculo, en el que la derivada de una función $f$ en el segmento de línea $[a, b]$ puede traducirse en un enunciado sobre $f$ en el límite de $[a, b]$. Usando el rotacional, podemos ver que la forma de circulación del teorema de Green es un análogo de dimensión superior del Teorema Fundamental del Cálculo.
Ahora podemos usar lo que hemos aprendido sobre el rotacional para mostrar que los campos gravitacionales no tienen "giro". Supón que hay un objeto en el origen con masa $m_1$ en el origen y un objeto con masa $m_2$. Recuerda que la fuerza gravitacional que el objeto $1$ ejerce sobre el objeto $2$ viene dada por el campo
$$\bold{F}(x,y,z) = -Gm_1m_2\big\lang \frac{x}{\big(x^2+y^2+z^2\big)^{3/2}}, \frac{y}{\big(x^2+y^2+z^2\big)^{3/2}}, \frac{z}{\big(x^2+y^2+z^2\big)^{3/2}}\big\rang$$ |
Determinando el giro de un campo gravitacional |

Ahora que entendemos los conceptos básicos de divergencia y rotacional, podemos discutir sus propiedades y establecer relaciones entre ellos y los campos vectoriales conservativos.
Si $\bold{F}$ es un campo vectorial en $\Reals^3$, entonces la curva de $\bold{F}$ también es un campo vectorial en $\Reals^3$. Por tanto, podemos tomar la divergencia de un rotacional. El siguiente teorema dice que el resultado siempre es cero. Este resultado es útil porque nos da una forma de demostrar que algunos campos vectoriales no son el rotacional de ningún otro campo. Para dar a este resultado una interpretación física, recuerda que la divergencia de un campo de velocidad $\bold{v}$ en el punto $P$ mide la tendencia del fluido correspondiente a fluir fuera de $P$. Dado que $div\; rot (\bold{v}) = 0$, la tasa neta de flujo en el campo vectorial $rot (\bold{v})$ en cualquier punto es cero. Tomar la curva del campo vectorial $\bold{F}$ elimina cualquier divergencia que estuviera presente en $\bold{F}$.
Por las definiciones de divergencia y rotacional, y por el teorema de Clairaut,
 |
Demostrando que un campo vectorial no es el rotacional de otro |

Con los dos teoremas siguientes, mostramos que si $\bold{F}$ es un campo vectorial conservativo, entonces su rotacional es cero, y si el dominio de $\bold{F}$ está simplemente conectado, lo contrario también es cierto. Esto nos da otra forma de probar si un campo vectorial es conservativo.
Dado que los campos vectoriales conservativos satisfacen la propiedad de las parciales cruzadas, todos las parciales cruzadas de $\bold{F}$ son iguales. Por lo tanto,
El mismo teorema es cierto para los campos vectoriales en un plano.
Dado que un campo vectorial conservativo es el gradiente de una función escalar, el teorema anterior dice que $rot\; \nabla (f) = 0$ para cualquier función escalar $f$. En términos de nuestra notación de rotación, $\nabla \times \nabla (f) = 0$. Esta ecuación tiene sentido porque el producto cruz de un vector consigo mismo es siempre el vector cero. A veces, la ecuación $\nabla \times \nabla (f) = 0$ se simplifica como $\nabla \times \nabla = 0$.
Como $rot\; \bold{F} = 0$, tenemos que $R_y = Q_z, P_z = R_x$ y $Q_x = P_y$. Por lo tanto, $\bold{F}$ satisface la propiedad de parciales cruzadas en un dominio simplemente conectado, y la propiedad de parciales cruzadas de campos conservativos implica que $\bold{F}$ es conservativo.
El mismo teorema también es cierto en un plano. Por lo tanto, si $\bold{F}$ es un campo vectorial en un plano o en el espacio y el dominio está simplemente conectado, entonces $\bold{F}$ es conservativo si y solo si $rot\; \bold{F} = 0$.
 |
Prueba de si un campo vectorial es conservador |

Hemos visto que el rotacional de un gradiente es cero. ¿Qué es la divergencia de un gradiente? Si $f$ es una función de dos variables, entonces $div\; (\nabla f) = \nabla\cdot (\nabla f) = f_{xx} + f_{yy}$. Abreviamos este "producto de doble punto" como $\nabla^2$. Este operador se llama operador de Laplace, y en esta notación la ecuación de Laplace se convierte en $\nabla^2 f = 0$. Por lo tanto, una función armónica es una función que se vuelve cero después de tomar la divergencia de un gradiente.
De manera similar, si $f$ es una función de tres variables, entonces
$$div \;(\nabla f) = \nabla \cdot (\nabla f) = f_{xx} + f_{yy} + f_{zz}$$Usando esta notación obtenemos la ecuación de Laplace para funciones armónicas de tres variables:
$$\nabla ^2 f = 0$$Las funciones armónicas surgen en muchas aplicaciones. Por ejemplo, la función potencial de un campo electrostático en una región del espacio que no tiene carga estática es armónica.
En la siguiente escena interactiva, diseñada por Lenore Horner, hemos ingresado el campo vectorial $\bold{F}$ del ejercicio anterior. Puedes mover el punto $A$ y observar que su rotacional es cero para cualquier punto $A$. Puedes cambiar las componentes de $\bold{F}$, para el análisis que desees. ¡Haz clic en el botón de la esquina inferior derecha para interactuar en pantalla completa!
 |
Analizando una función |


 Para los siguientes ejercicios, determina si la afirmación es verdadera o falsa.
Para los siguientes ejercicios, determina si la afirmación es verdadera o falsa.
206. Si las funciones de coordenadas de $\bold{F}: \Reals^3 \to \Reals^3$ tienen segundas derivadas parciales continuas, entonces $rot\; (div (\bold{F}))$ es igual a cero. 207. $\nabla\cdot (x\bold{i} + y\bold{j} + z\bold{k}) = 1$ (Solución). 208. Todos los campos vectoriales de la forma $\bold{F} (x, y, z) = f (x)\bold{i} + g (y)\bold{j} + h (z)\bold{k}$ son conservativos. 209. Si $rot\; \bold{F} = 0$, entonces $\bold{F}$ es conservativo (Solución). 210. Si $\bold{F}$ es un campo vectorial constante, $div\; \bold{F} = 0$. 211. Si $\bold{F}$ es un campo vectorial constante, entonces $rot\; \bold{F} = 0$ (Solución).
 Para los siguientes ejercicios, encuentre el rotacional de $\bold{F}$.
Para los siguientes ejercicios, encuentre el rotacional de $\bold{F}$.
212. $\bold{F} (x, y, z) = xy^2z^4\bold{i} + (2x^2y + z)\bold{j} + y^3z^2\bold{k}$ 213. $\bold{F} (x, y, z) = x^2z\bold{i} + y^2x\bold{j} + (y + 2z)\bold{k}$ (Solución). 214. $\bold{F} (x, y, z) = 3xyz^2\bold{i} + y^2sen\;z\bold{j} + xe^{2z}\bold{k}$ 215. $\bold{F} (x, y, z) = x^2yz\bold{i} + xy^2z\bold{j} + xyz^2\bold{k}$ (Solución). 216. $\bold{F} (x, y, z) = (x cos\; y)\bold{i} + xy^2\bold{j}$ 217. $\bold{F} (x, y, z) = (x - y)\bold{i} + (y - z)\bold{j} + (z - x)\bold{k}$ (Solución). 218. $\bold{F} (x, y, z) = xyz\bold{i} + x^2y^2z^2\bold{j} + y^2z^3\bold{k}$ 219. $\bold{F} (x, y, z) = xy\bold{i} + yz\bold{j} + xz\bold{k}$ (Solución). 220. $\bold{F} (x, y, z) = x^2\bold{i} + y^2\bold{j} + z^2\bold{k}$
221. $\bold{F} (x, y, z) = ax\bold{i} + by\bold{j} + c\bold{k}$ para las constantes $a, b, c$ (Solución).
 Para los siguientes ejercicios, encuentre la divergencia de $\bold{F}$.
Para los siguientes ejercicios, encuentre la divergencia de $\bold{F}$.
222. $\bold{F} (x, y, z) = x^2z\bold{i} + y^2x\bold{j} + (y + 2z)\bold{k}$ 223. $\bold{F} (x, y, z) = 3xyz^2\bold{i} + y^2sen\;z\bold{j} + xe^{2z}\bold{k}$ (Solución). 224. $\bold{F} (x, y) = (sen\;x)\bold{i} + (cos\; y)\bold{j}$ 225. $\bold{F} (x, y, z) = x^2\bold{i} + y^2\bold{j} + z^2\bold{k}$ (Solución). 226. $\bold{F} (x, y, z) = (x - y)\bold{i} + (y - z)\bold{j} + (z - x)\bold{k}$ 227. $\bold{F} (x, y) = \frac{x}{\sqrt{x^2 + y^2}}\bold{i} + \frac{y}{\sqrt{x^2 + y^2}}\bold{j}$ (Solución). 228. $\bold{F} (x, y) = x\bold{i} - y\bold{j}$ 229. $\bold{F} (x, y, z) = ax\bold{i} + by\bold{j} + c\bold{k}$ para las constantes $a, b, c$ (Solución). 230. $\bold{F} (x, y, z) = xyz\bold{i} + x^2y^2z^2\bold{j} + y^2z^3\bold{k}$ 231. $\bold{F} (x, y, z) = xy\bold{i} + yz\bold{j} + xz\bold{k}$ (Solución).
 Para los siguientes ejercicios, determine si cada uno de los funciones escalares dadas es armónica.
Para los siguientes ejercicios, determine si cada uno de los funciones escalares dadas es armónica.
232. $u (x, y, z) = e^{− x} (cos\; y - sen\;y)$ 233. $w (x, y, z) = \big(x^2 + y^2 + z^2\big)^{−1/2}$ (Solución). 234. Si $\bold{F} (x, y, z) = 2\bold{i} + 2x\bold{j} + 3y\bold{k}$ y $\bold{G} (x, y, z) = x\bold{i} - y\bold{j} + z\bold{k}$, encuentra $rot (\bold{F}\times \bold{G})$. 235. 235. Si $\bold{F} (x, y, z) = 2\bold{i} + 2x\bold{j} + 3y\bold{k}$ y $\bold{G} (x, y, z) = x\bold{i} - y\bold{j} + z\bold{k}$, encuentra $div (\bold{F}\times \bold{G})$ (Solución).
236. Encuentra $div\;\bold{F}$, dado que $\bold{F} = \nabla f$, donde $f (x, y, z) = xy^3z^2$.
237. Encuentra la divergencia de $\bold{F}$ para el campo vectorial $\bold{F} (x, y, z) = \big(y^2 + z^2\big) (x + y)\bold{i} + \big(z^2 + x^2\big) (y + z)\bold{j} + \big(x^2 + y^2\big) (z + x)\bold{k}$ (Solución). 238. Encuentra la divergencia de $\bold{F}$ para el campo vectorial $\bold{F} (x, y, z) = f_1 (y, z)\bold{i} + f_2 (x, z)\bold{j} + f_3 (x, y) k$ Para los siguientes ejercicios, usa $\bold{r} = | r |$ y $\bold{r} = (x, y, z)$.
Para los siguientes ejercicios, usa $\bold{r} = | r |$ y $\bold{r} = (x, y, z)$.
239. Halla el rotacional $rot\;\bold{r}$ (Solución). 240. Halla el rotacional $rot\;\frac{\bold{r}}{r}$. 241. Halla el rotacional $rot\;\frac{\bold{r}}{r^3}$ (Solución). 242. Sea $\bold{F} (x, y) = \frac{−y\bold{i} + xj}{x^2 + y^2}$, donde $\bold{F}$ se define en $\lbrace (x, y) \isin \Reals| (x, y) \;\cancel{=}\; (0, 0)\rbrace$. Encuentra el $rot \;\bold{F}$.
 Para los siguientes ejercicios, use un sistema de álgebra computarizada para encontrar la curva de los campos vectoriales dados.
Para los siguientes ejercicios, use un sistema de álgebra computarizada para encontrar la curva de los campos vectoriales dados.
243. [T] $\bold{F} (x, y, z) = arctan \big(\frac{x}{y}\big)\bold{i} + ln \sqrt{x^2 + y^2}\bold{j} + \bold{k}$ (Solución). 244. [T] $\bold{F} (x, y, z) = sen\; (x - y)\bold{i} + sen\; (y - z)\bold{j} + sen\; (z - x)\bold{k}$
 Para los siguientes ejercicios, encuentra la divergencia de $\bold{F}$ en el punto dado.
Para los siguientes ejercicios, encuentra la divergencia de $\bold{F}$ en el punto dado.
245. $\bold{F} (x, y, z) = \bold{i} + \bold{j} + \bold{k}$ en $(2, −1, 3)$ (Solución). 246. $\bold{F} (x, y, z) = xyz\bold{i} + y\bold{j} + z\bold{k}$ en $(1, 2, 3)$. 247. $\bold{F} (x, y, z) = e^{− xy}\bold{i} + e^{xz}\bold{j} + e^{yz}\bold{k}$ en $(3, 2, 0)$ (Solución). 248. $\bold{F} (x, y, z) = xyz\bold{i} + y\bold{j} + z\bold{k}$ en $(1, 2, 1)$. 249. $\bold{F} (x, y, z) = e^xsen\;y\bold{i} - e^xcos\; y\bold{j}$ en $(0, 0, 3)$ (Solución).
 Para los siguientes ejercicios, encuentra la rotación de $\bold{F}$ en el punto dado.
Para los siguientes ejercicios, encuentra la rotación de $\bold{F}$ en el punto dado.
250. $\bold{F} (x, y, z) = \bold{i} + \bold{j} + \bold{k}$ en $(2, −1, 3)$ 251. $\bold{F} (x, y, z) = xyz\bold{i} + y\bold{j} + x\bold{k}$ en $(1, 2, 3)$ (Solución). 252. $\bold{F} (x, y, z) = e^{− xy}\bold{i} + e^{xz}\bold{j} + e^{yz}\bold{k}$ en $(3, 2, 0)$ 253. $\bold{F} (x, y, z) = xyz\bold{i} + y\bold{j} + z\bold{k}$ en $(1, 2, 1)$ (Solución). 254. $\bold{F} (x, y, z) = e^xsen\;y\bold{i} - e^xcos \;y\bold{j}$ en $(0, 0, 3)$. 255. Sea $\bold{F} (x, y, z) = (3x^2y + az)\bold{i} + x^3\bold{j} + (3x + 3z^2)\bold{k}$. ¿Para qué valor de $a$ es $\bold{F}$ conservativo? (Solución). 256. Dado el campo vectorial $\bold{F} (x, y) = \frac{1}{x^2 + y^2} (−y, x)$ en el dominio $D = \frac{\Reals^2} {\lbrace (0, 0)\rbrace } = \lbrace (x, y) \isin\Reals^2 | (x, y)\;\cancel{=}\; (0 , 0)\rbrace$, ¿$\bold{F}$ es conservativo? 257. Dado el campo vectorial $\bold{F} (x, y) = \frac{1}{x^2 + y^2} (x, y)$ en el dominio $D = \frac{\Reals^2}{\lbrace (0, 0)\rbrace }$, ¿$\bold{F}$ es conservativo? (Solución). 258. Encuentra el trabajo realizado por el campo de fuerza $\bold{F} (x, y) = e^{− y}\bold{i} - xe^{− y}\bold{j}$ al mover un objeto de $P (0, 1)$ a $Q (2, 0)$. ¿Es el campo de fuerza conservativo? 259. Calcula la divergencia $\bold{F} = (senh\; x)\bold{i} + cosh\; y\bold{j} - xyz\bold{k}$ (Solución).
260. Calcula el rotacional $\bold{F} = (senh\; x)\bold{i} + cosh\; y\bold{j} - xyz\bold{k}$.
 Para los siguientes ejercicios, considera un cuerpo rígido que gira alrededor del eje $x$ en sentido antihorario con velocidad angular constante $\omega = \lang a, b, c\rang$. Si $P$ es un punto en el cuerpo ubicado en $\bold{r} = x\bold{i} + y\bold{j} + z\bold{k}$, la velocidad en $P$ está dada por el campo vectorial $\bold{F} = \omega\times\bold{r}$.
Para los siguientes ejercicios, considera un cuerpo rígido que gira alrededor del eje $x$ en sentido antihorario con velocidad angular constante $\omega = \lang a, b, c\rang$. Si $P$ es un punto en el cuerpo ubicado en $\bold{r} = x\bold{i} + y\bold{j} + z\bold{k}$, la velocidad en $P$ está dada por el campo vectorial $\bold{F} = \omega\times\bold{r}$.
261. Expresa $\bold{F}$ en términos de los vectores $\bold{i}, \bold{j}$ y $\bold{k}$ (Solución). 262. Encuentra $div\;\bold{F}$. 263. Halla $rot\;\bold{F}$ (Solución).
 En los siguientes ejercicios, supón que $\nabla\cdot \bold{F} = 0$ y $\nabla\cdot \bold{G} = 0$.
En los siguientes ejercicios, supón que $\nabla\cdot \bold{F} = 0$ y $\nabla\cdot \bold{G} = 0$.
264. ¿$\bold{F} + \bold{G}$ tiene necesariamente cero de divergencia? 265. ¿$\bold{F} \times\bold{G}$ tiene necesariamente cero de divergencia? (Solución)
 En los siguientes ejercicios, supón que un objeto sólido en $\Reals^3$ tiene una distribución de temperatura dada por $T (x, y, z)$. El campo del vector de flujo de calor en el objeto es $\bold{F} = −k\nabla T$, donde $k\gt 0$ es una propiedad del material. El vector de flujo de calor apunta en la dirección opuesta a la del gradiente, que es la dirección de mayor disminución de temperatura. La divergencia del vector de flujo de calor es $\nabla\cdot\bold{F} = −k\nabla\cdot \nabla T = −k\nabla^2 T$.
En los siguientes ejercicios, supón que un objeto sólido en $\Reals^3$ tiene una distribución de temperatura dada por $T (x, y, z)$. El campo del vector de flujo de calor en el objeto es $\bold{F} = −k\nabla T$, donde $k\gt 0$ es una propiedad del material. El vector de flujo de calor apunta en la dirección opuesta a la del gradiente, que es la dirección de mayor disminución de temperatura. La divergencia del vector de flujo de calor es $\nabla\cdot\bold{F} = −k\nabla\cdot \nabla T = −k\nabla^2 T$.
266. Calcula el campo vectorial de flujo de calor. 267. Calcula la divergencia (Solución).
268. [T] Considera el campo de velocidad de rotación $\bold{v} = \lang 0, 10z, −10y\rang$. Si se coloca una rueda de paletas en el plano $x + y + z = 1$ con su eje normal a este plano, usando un sistema de álgebra por computadora, calcula qué tan rápido gira la rueda de paletas en revoluciones por unidad de tiempo.
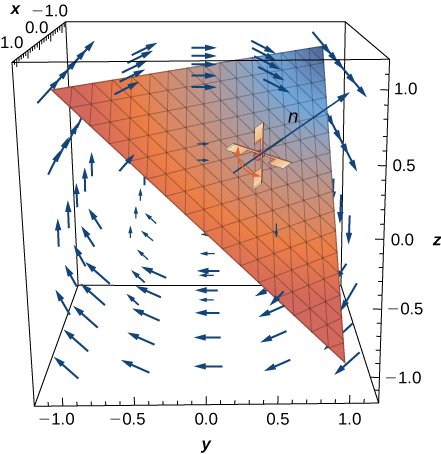
Hemos visto que una integral de línea es una integral sobre una trayectoria en un plano o en el espacio. Sin embargo, si deseamos integrar sobre una superficie (un objeto bidimensional) en lugar de una ruta (un objeto unidimensional) en el espacio, entonces necesitamos un nuevo tipo de integral que pueda manejar la integración sobre objetos en dimensiones superiores. Podemos extender el concepto de una integral de línea a una integral de superficie para permitirnos realizar esta integración.
Las integrales de superficie son importantes por las mismas razones que las integrales de línea. Tienen muchas aplicaciones para la física y la ingeniería, y nos permiten desarrollar versiones de dimensiones superiores del Teorema Fundamental del Cálculo. En particular, las integrales de superficie nos permiten generalizar el teorema de Green a dimensiones más altas y aparecen en algunos teoremas importantes que discutiremos en secciones posteriores.
Una integral de superficie es similar a una integral de línea, excepto que la integración se realiza sobre una superficie en lugar de una trayectoria. En este sentido, las integrales de superficie amplían nuestro estudio de integrales de línea. Al igual que con las integrales de línea, hay dos tipos de integrales de superficie: una integral de superficie de una función con valores escalares y una integral de superficie de un campo vectorial.
Sin embargo, antes de que podamos integrar sobre una superficie, debemos considerar la superficie en sí. Recuerda que para calcular una integral de línea escalar o vectorial sobre la curva $C$, primero necesitamos parametrizar $C$.
De manera similar, para calcular una integral de superficie sobre la superficie $S$, necesitamos parametrizar $S$. Es decir, necesitamos un concepto de trabajo de una superficie parametrizada (o una superficie paramétrica), de la misma forma que ya tenemos un concepto de curva paramétrica.
Una superficie parametrizada viene dada por una descripción de la forma
$$\bold{r} (u, v) = \lang x (u, v), y (u, v), z (u, v)\rang$$Observa que esta parametrización involucra dos parámetros, $u$ y $v$, porque una superficie es bidimensional y, por lo tanto, se necesitan dos variables para trazar la superficie. Los parámetros $u$ y $v$ varían en una región denominada dominio de parámetros, o parámetros espaciales, el conjunto de puntos en el plano $uv$ que pueden sustituirse en $\bold{r}$. Cada elección de $u$ y $v$ en el dominio del parámetro da un punto en la superficie, así como cada elección de un parámetro $t$ da un punto en una curva parametrizada. La superficie completa se crea haciendo todas las elecciones posibles de $u$ y $v$ sobre el dominio de parámetros.
 |
Parametrizando un cilindro |

Del ejercicio anterior se deduce que podemos parametrizar todos los cilindros de la forma $x^2 + y^2 = R^2$. Si $S$ es un cilindro dado por la ecuación $x^2 + y^2 = R^2$, entonces una parametrización de $S$ es $\bold{r} (u, v) = \lang R cos\; u, R sen\; u, v\rang, 0 \le u \lt 2\pi, −\infin \lt v \lt \infin$.
También podemos encontrar diferentes tipos de superficies dada su parametrización, o podemos encontrar una parametrización cuando se nos da una superficie.
 |
Describiendo una superficie |

 |
Encontrando una parametrización |

Hemos discutido las parametrizaciones de varias superficies, pero dos tipos importantes de superficies necesitan una discusión separada: esferas y gráficos de funciones de dos variables. Para parametrizar una esfera, es más fácil utilizar coordenadas esféricas. La esfera de radio $\rho$ centrada en el origen viene dada por la parametrización
$$\bold{r} (\phi, \theta) = \lang \rho cos \theta sin \phi, \rho sin \theta sin \phi, \rho cos\; \phi\rang, 0 \le \theta \le 2\pi, 0 \le \phi \le \pi$$La idea de esta parametrización es que a medida que $\phi$ se desplaza hacia abajo desde el eje $z$ positivo, se traza un círculo de radio $\rho sen\; \phi$ dejando que $\theta$ vaya de $0$ a $2\pi$. Para ver esto, fijemos $\phi$. Luego
$$\begin{aligned} x^2+y^2 &= (\rho cos\;\theta sen\;\phi)^2 + (\rho sen\;\theta sen\;\phi)^2\\ &= \rho^2 sen^2\phi(cos^2\theta + sen^2\theta)\\ &= \rho^2sen^2\phi\\ &= (\rho sen\;\phi)^2 \end{aligned}$$Esto da como resultado el círculo deseado (observa la siguiente figura).
Figura 6.61. La esfera de radio $\rho$ tiene parametrización $\bold{r} (\phi, \theta) = \lang \rho cos\; \theta sen\; \phi, \rho sen\; \theta sen\; \phi, \rho cos\; \phi\rang, 0 \le \theta \le 2\pi, 0 \le \phi \le \pi$.
Escena interactiva diseñada por Lenore Horner
Finalmente, para parametrizar la gráfica de una función de dos variables, primero dejamos que $z = f (x, y)$ sea una función de dos variables. La parametrización más simple de la gráfica de $f$ es $\bold{r} (x, y) = \lang x, y, f (x, y)\rang$, donde $x$ e $y$ varían en el dominio de $f$ (Figura 6.62). Por ejemplo, la gráfica de $f (x, y) = x^2y $ se puede parametrizar mediante $\bold{r} (x, y) = \lang x, y, x^2y\rang$, donde los parámetros $x$ e $y$ varían en el dominio de $f$. Si solo nos importa una parte de la gráfica de $f$ (digamos, la parte de la gráfica sobre el rectángulo $[1, 3] \times [2, 5]$), entonces podemos restringir el dominio del parámetro para dar esta parte de la superficie:
$$\bold{r} (x, y) = \lang x, y, x^2y\rang, 1 \le x \le 3, 2 \le y \le 5$$De manera similar, si $S$ es una superficie dada por la ecuación $x = g (y, z)$ o la ecuación $y = h (x, z)$, entonces una parametrización de $S$ es $\bold{r} (y, z) = \lang g (y, z), y, z\rang$ o $\bold{r} (x, z) = \lang x, h (x, z), z\rang$, respectivamente. Por ejemplo, la gráfica del paraboloide $2y = x^2 + z^2$ puede parametrizarse mediante $\bold{r} (x, z) = \lang x, \frac{x^2 + z^2}{2}, z\rang, 0 \le x \lt\infin, 0 \le z \lt\infin$. Observa que no es necesario que varíe todo el dominio de $y$ porque $x$ y $z$ son cuadrados.
Ahora generalicemos las nociones de suavidad y regularidad a una superficie paramétrica. Recuerda que la parametrización de la curva $\bold{r} (t), a \le t \le b$ es regular si $\bold{r}^{\prime} (t)\;\cancel{=}\; 0$ para todo $t$ en $[a, b]$. Para una curva, esta condición asegura que la imagen de $\bold{r}$ sea realmente una curva y no solo un punto. Por ejemplo, considere la parametrización de la curva $\bold{r} (t) = \lang 1, 2\rang, 0 \le t \le 5$. La imagen de esta parametrización es simplemente el punto $(1, 2)$, que no es una curva. Observa también que $\bold{r}^{\prime} (t) = 0$. El hecho de que la derivada sea cero indica que en realidad no estamos mirando una curva.
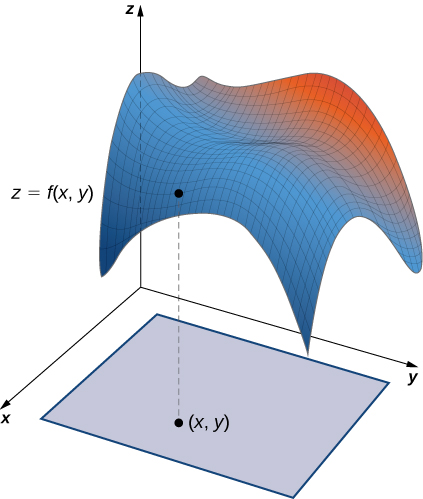
Figura 6.62. La parametrización más simple de la gráfica de una función es $\bold{r} (x, y) = \lang x, y, f (x, y)\rang$.
De manera análoga, nos gustaría una noción de regularidad para las superficies, de modo que una parametrización de superficies realmente traza una superficie. Para motivar la definición de regularidad de una parametrización de superficie, considera la parametrización
$$\bold{r} (u, v) = \lang 0, cos \;v, 1\rang, 0 \le u \le 1, 0 \le v \le \pi$$Aunque esta parametrización parece ser la parametrización de una superficie, observa que la imagen es en realidad una línea (Figura 6.63). ¿Cómo evitar parametrizaciones como ésta? ¿Parametrizaciones que no dan una superficie real?
Observa que $\bold{r}_u = \lang 0, 0, 0\rang$ y $\bold{r}_v = \lang 0, −sen\; v, 0\rang$, y el producto cruz correspondiente es cero. El análogo de la condición $\bold{r}^{\prime}(t) = 0$ es que $\bold{r}_u \times \bold{r}_v$ no es cero para el punto $(u, v)$ en el dominio del parámetro, que es una parametrización regular.
Figura 6.63. La imagen de la parametrización $\bold{r} (u, v) = \lang 0, cos\; v, 1\rang, 0 \le u \le 1, 0 \le v \le \pi$ es una línea.
Si la parametrización $\bold{r}$ es regular, entonces la imagen de $\bold{r}$ es un objeto bidimensional, como debería ser una superficie. A lo largo de este capítulo, se supone que las parametrizaciones $\bold{r} (u, v) = \lang x (u, v), y (u, v), z (u, v)\rang$ son regulares.
Recuerda que la parametrización de la curva $\bold{r} (t), a \le t \le b $es suave si $\bold{r}^{\prime} (t)$ es continua y $\bold{r}^{\prime} (t)\;\cancel{=}\; 0$ para todo $t$ en $[a, b]$. De manera informal, la parametrización de una curva es suave si la curva resultante no tiene esquinas pronunciadas. La definición de parametrización de una superficie lisa es similar. De manera informal, la parametrización de una superficie es suave si la superficie resultante no tiene esquinas afiladas.
Una parametrización de superficie $\bold{r} (u, v) = \lang x (u, v), y (u, v), z (u, v)\rang$ es suave si el vector $\bold{r}_u \times \bold{r}_v$ no es cero para cualquier elección de $u$ y $v$ en el dominio de parámetros.
Una superficie también puede ser lisa por partes si tiene caras lisas pero también tiene ubicaciones donde las derivadas direccionales no existen.
Nuestro objetivo es definir una integral de superficie y, como primer paso, hemos examinado cómo parametrizar una superficie. El segundo paso es definir el área de superficie de una superficie paramétrica. La notación necesaria para desarrollar esta definición se utiliza en el resto de este capítulo.
Sea $S$ una superficie con parametrización $\bold{r} (u, v) = \lang x (u, v), y (u, v), z (u, v)\rang$ sobre algún dominio de parámetros $D.$ Suponemos aquí y a lo largo de la superficie la parametrización $\bold{r} (u, v) = \lang x (u, v), y (u, v), z (u, v)\rang$ es continuamente diferenciable, es decir, cada función componente tiene derivadas parciales continuas. En aras de la simplicidad, supón que $D$ es un rectángulo (aunque el siguiente material puede extenderse para manejar dominios de parámetros no rectangulares). Divide el rectángulo $D$ en subrectangulos $D_{ij}$ con ancho horizontal $\Delta u$ y longitud vertical $\Delta v$. Supón que $i$ varía de $1$ a $m$ y $j$ varía de $1$ a $n$, de modo que $D$ se subdivide en $mn$ rectángulos. Esta división de $D$ en subrectangulos da una división correspondiente de la superficie $S$ en piezas $S_{ij}$. Elige el punto $P_{ij}$ en cada pieza $S_{ij}$. El punto $P_{ij}$ corresponde al punto $(u_i, v_j)$ en el dominio de los parámetros.
Ten en cuenta que podemos formar una cuadrícula con líneas paralelas al eje $u$ y el eje $v$ en el plano $uv$. Estas líneas de la cuadrícula corresponden a un conjunto de curvas de cuadrícula en la superficie $S$ que está parametrizada por $\bold{r} (u, v)$. Sin pérdida de generalidad, asumimos que $P_{ij}$ está ubicado en la esquina de dos curvas de la cuadrícula, como en la figura 6.65.
Si pensamos en $\bold{r}$ como un mapeo desde el plano $uv$ hasta $\Reals^3$, las curvas de la cuadrícula son la imagen de las líneas de la cuadrícula debajo de $\bold{r}$. Para ser precisos, considera las líneas de la cuadrícula que pasan por el punto $(u_i, v_j)$. Una línea está dada por $x = u_i, y = v$; el otro está dado por $x = u, y = v_j$. En la primera línea de la cuadrícula, el componente horizontal se mantiene constante, produciendo una línea vertical que pasa por $(u_i, v_j)$. En la segunda línea de la cuadrícula, el componente vertical se mantiene constante, produciendo una línea horizontal que pasa por $(u_i, v_j)$.
Las curvas de la cuadrícula correspondientes son $r (u_i, v)$ y $r (u, v_j)$, y estas curvas se intersecan en el punto $P_{ij}$.

Figura 6.65. Las líneas de la cuadrícula en un dominio de parámetro corresponden a curvas de la cuadrícula en una superficie.
Ahora considera los vectores que son tangentes a estas curvas de la cuadrícula. Para la curva de la cuadrícula $\bold{r} (u_i, v)$, el vector tangente en $P_{ij}$ es
$$\bold{t}_v(P_{ij}) = \bold{r}_v(u_i, v_j) = \lang x_v(u_i, v_j), y_v(u_i, v_j), z_v(u_i, v_j)\rang$$Para la curva de la cuadrícula $\bold{r} (u, v_j)$, el vector tangente en $P_{ij}$ es
Si el vector $\bold{N} = \bold{t}_u (P_{ij}) \times \bold{t}_v (P_{ij})$ existe y no es cero, entonces existe el plano tangente en $P_{ij}$ (Figura 6.66). Si la pieza $S_{ij}$ es lo suficientemente pequeña, entonces el plano tangente en el punto $P_{ij}$ es una buena aproximación de la pieza $S_{ij}$.
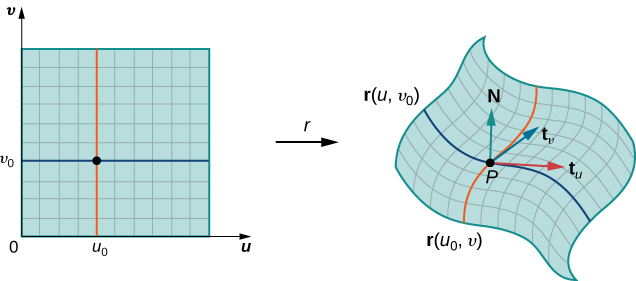
Figura 6.66. Si existe el producto cruz de los vectores $\bold{t}_u$ y $\bold{t}_v$, entonces hay un plano tangente.
El plano tangente en $P_{ij}$ contiene los vectores $\bold{t}u (P_{ij})$ y $\bold{t}_v (P_{ij})$ y, por lo tanto, el paralelogramo generado por $\bold{t}u (P_{ij})$ y $\bold{t}_v (P_{ij})$ está en el plano tangente. Dado que el rectángulo original en el plano $uv$ correspondiente a $S_{ij}$ tiene ancho $\Delta u$ y largo $\Delta v$, el paralelogramo que usamos para aproximar $S_{ij}$ es el paralelogramo generado por $\Delta u\bold{t}_u (P_{ij})$ y $\Delta v\bold{t}_v (P_{ij})$. En otras palabras, escalamos los vectores tangentes mediante las constantes $\Delta u$ y $\Delta v$ para que coincidan con la escala de la división original de rectángulos en el dominio de parámetros. Por lo tanto, el área del paralelogramo utilizada para aproximar el área de $S_ij$ es
$$\Delta S_{ij} \approx \big|\big| \big(\Delta u\bold{t}_u(P_{ij})\big) \times \big(\Delta v\bold{t}_v(P_{ij})\big)\big|\big| = \big|\big|\bold{t}_u(P_{ij})\times \bold{t}_v(P_{ij})\big|\big| \Delta u\Delta v$$La variación del punto $P_{ij}$ sobre todas las piezas $S_{ij}$ y la aproximación anterior conduce a la siguiente definición del área de superficie de una superficie paramétrica (Figura 6.66).
Figura 6.67. El paralelogramo generado por $\bold{t}_u$ y $\bold{t}_v$ se aproxima al trozo de superficie $S_{ij}$
 |
Calculando el área de la superficie |

 |
Calculando el área de la superficie |

Además de parametrizar superficies dadas por ecuaciones o formas geométricas estándar como conos y esferas, también podemos parametrizar superficies de revolución. Por tanto, podemos calcular el área de superficie de una superficie de revolución utilizando las mismas técnicas. Sea $y = f (x) \ge 0$ una función positiva de una sola variable en el dominio $a \le x \le b$ y sea $S$ la superficie obtenida al rotar $f$ sobre el eje $x$ (Figura 6.69). Sea $\theta$ el ángulo de rotación. Entonces, $S$ se puede parametrizar con los parámetros $x$ y $\theta$ mediante
$$\bold{r} (x, \theta) = \lang x, f (x) cos \;\theta, f (x) sen \;\theta\rang, a \le x \le b, 0 \le x \lt 2\pi$$
Figura 6.69. Podemos parametrizar una superficie de revolución por $\bold{r} (x, \theta) = \lang x, f (x) cos \;\theta, f (x) sen \;\theta\rang, a \le x \le b, 0 \le x \lt 2\pi$
 |
Calculando el área de la superficie |
Figura 6.70. Se puede utilizar una integral de superficie para calcular el área de superficie de este sólido de revolución.

Ahora que podemos parametrizar superficies y podemos calcular sus áreas de superficie, podemos definir integrales de superficie. Primero, veamos la integral de superficie de una función con valores escalares. De manera informal, la integral de superficie de una función con valores escalares es un análogo de una integral de línea escalar en una dimensión superior. El dominio de integración de una integral de línea escalar es una curva parametrizada (un objeto unidimensional); el dominio de integración de una integral de superficie escalar es una superficie parametrizada (un objeto bidimensional).
Por lo tanto, la definición de integral de superficie sigue muy de cerca la definición de integral de línea. Para las integrales de línea escalar, cortamos la curva de dominio en trozos pequeños, elegimos un punto en cada trozo, calculamos la función en ese punto y tomamos un límite de la suma de Riemann correspondiente. Para integrales de superficie escalar, cortamos la región del dominio (ya no es una curva) en trozos diminutos y procedemos de la misma manera.
Sea S una superficie lisa a trozos con parametrización $\bold{r} (u, v) = \lang x (u, v), y (u, v), z (u, v)\rang$〉 con dominio de parámetros $D$ y sea $f (x, y, z)$ una función con un dominio que contenga $S$. Por ahora, supón que el dominio de parámetros $D$ es un rectángulo, pero podemos extender la lógica básica de cómo procedemos a cualquier dominio de parámetros (la elección de un rectángulo es simplemente hacer la notación más manejable). Divide el rectángulo $D$ en subrectangulos $D_{ij}$ con ancho horizontal $\Delta u$ y longitud vertical $\Delta v$. Supón que $i$ varía de $1$ a $m$ y $j$ varía de $1$ a $n$, de modo que $D$ se subdivide en $mn$ rectángulos. Esta división de $D$ en subrectangulos da una división correspondiente de $S$ en piezas $S_{ij}$. Elige el punto $P_{ij}$ en cada pieza $S_{ij}$, evalúa $P_{ij}$ en $f$ y multiplica por el área $\Delta S_{ij}$ para formar la suma de Riemann
$$\sum_{i=1}^m\sum_{j=1}^n f(P_{ij})\Delta S_{ij}$$Para definir una integral de superficie de una función con valores escalares, dejamos que las áreas de las piezas de $S$ se reduzcan a cero tomando un límite
Antes de continuar, presentamos la siguiente escena interactiva, diseñada por Elena E. Álvarez Sáiz, se considera una superficie S dada por $z=(x,y)$ que está definida sobre un rectángulo $R=[0,a]\times [0,b]$, una partición de $R$ en $mn$ subrectángulos. Se considera el área de la superficie que se proyecta sobre cada uno de los subrectángulos y se aproxima por el área de un trozo de plano tangente a la superficie en un punto cualquiera del subrectángulo.
En la escena interactiva, calculando el límite de la suma de todas estas áreas cuando la norma de la partición tiende a cero, se podrá obtener el área de la superficie siempre que el límite exista y no dependa ni de la partición ni del punto elegido.
Nuevamente, observa las similitudes entre esta definición y la definición de una integral de línea escalar. En la definición de una integral de línea cortamos una curva en pedazos, evaluamos una función en un punto de cada pieza y dejamos que la longitud de las piezas se reduzca a cero tomando el límite de la suma de Riemann correspondiente. En la definición de integral de superficie, cortamos una superficie en pedazos, evaluamos una función en un punto de cada pieza y dejamos que el área de las piezas se reduzca a cero tomando el límite de la suma de Riemann correspondiente. Por lo tanto, una integral de superficie es similar a una integral de línea pero en una dimensión superior.
La definición de una integral de línea escalar puede extenderse a dominios de parámetros que no son rectángulos utilizando la misma lógica utilizada anteriormente. La idea básica es cortar el dominio del parámetro en trozos pequeños, elegir un punto de muestra en cada trozo, etc. La forma exacta de cada pieza en el dominio de la muestra se vuelve irrelevante a medida que las áreas de las piezas se reducen a cero.
Las integrales de superficie escalar son difíciles de calcular a partir de la definición, al igual que las integrales de línea escalar. Para desarrollar un método que facilite el cálculo de integrales de superficie, aproximamos las áreas de superficie $\Delta S_{ij}$ con pequeñas piezas de un plano tangente, tal como hicimos en la subsección anterior. Recuerda la definición de los vectores $\bold{t}_u$ y $\bold{t}_v$:
$$\bold{t}_u = \big\lang \frac{\partial x}{\partial u}, \frac{\partial y}{\partial u}, \frac{\partial z}{\partial u}\big\rang\;\;\text{y}\;\; \bold{t}_v = \big\lang \frac{\partial x}{\partial v}, \frac{\partial y}{\partial v}, \frac{\partial z}{\partial v}\big\rang$$Por el material que ya hemos estudiado, sabemos que
$$\Delta S_{ij} \approx ||\bold{t}_u (P_{ij}) \times \bold{t}_v(P_{ij})|| \Delta u \Delta v$$Por lo tanto,
$$\iint_S f(x,y,z)dS \approx \lim\limits_{m,n \to \infin} \sum_{i=1}^m\sum_{j=1}^n f(P_{ij}) ||\bold{t}_u (P_{ij}) \times \bold{t}_v(P_{ij})|| \Delta u \Delta v$$Esta aproximación se vuelve arbitrariamente cercana a $\lim\limits_{m,n \to \infin} \sum_{i=1}^m\sum_{j=1}^n f(P_{ij}) \Delta S_{ij}$ a medida que aumentamos el número de piezas $S_{ij}$ dejando que $m$ y $n$ vayan al infinito. Por lo tanto, tenemos la siguiente ecuación para calcular integrales de superficie escalar:
$$\iint_S f(x,y,z)dS = \iint_D f(\bold{r}(u,v)) ||\bold{t}_u \times \bold{t}_v||dA \tag{$6.19$}$$La ecuación 6.19 nos permite calcular una integral de superficie transformándola en una integral doble. Esta ecuación para integrales de superficie es análoga a la Ecuación para integrales de línea:
$$\iint_C f(x,y,z)ds = \int_a^b f(\bold{r}(t))||\bold{r}^{\prime}(t)||dt$$En este caso, el vector $\bold{t}_u \times \bold{t}_v$ es perpendicular a la superficie, mientras que el vector $\bold{r}^{\prime}(t)$ es tangente a la curva.
 |
Calculando una integral de superficie |

 |
Calculando la integral de superficie de un cilindro |

Figura 6.71. Función de integración $f (x, y, z) = x + y^2$ sobre un cilindro.

 |
Calculando la integral de superficie de una pieza de una esfera |
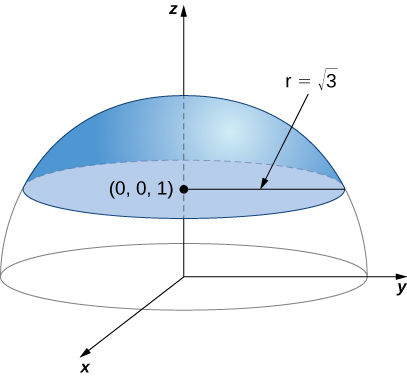
Figura 6.72. Calculando una integral de superficie sobre la superficie $S$.

Las integrales de superficie escalar tienen varias aplicaciones del mundo real. Recuerda que las integrales de línea escalar se pueden usar para calcular la masa de un cable dada su función de densidad.
De manera similar, podemos usar integrales de superficie escalar para calcular la masa de una hoja dada su función de densidad. Si una hoja delgada de metal tiene la forma de la superficie $S$ y la densidad de la hoja en el punto $(x, y, z)$ es $\rho (x, y, z)$, entonces la masa $m$ de la hoja es $m = \int_S\rho (x , y, z) dS$
 |
Calculando la masa de una hoja |

Recuerda que cuando definimos una integral de línea escalar, no tuvimos que preocuparnos por la orientación de la curva de integración.
Lo mismo ocurrió con las integrales de superficies escalares: no tuvimos que preocuparnos por una "orientación" de la superficie de integración.
Por otro lado, cuando definimos integrales de líneas vectoriales, la curva de integración necesitaba una orientación. Es decir, necesitábamos la noción de curva orientada para definir una integral de línea vectorial sin ambigüedad.
De manera similar, cuando definimos una integral de superficie de un campo vectorial, necesitamos la noción de una superficie orientada. A una superficie orientada se le da una orientación "hacia arriba" o "hacia abajo" o, en el caso de superficies tales como una esfera o cilindro, una orientación "hacia afuera" o "hacia adentro".
Sea $S$ una superficie lisa. Para cualquier punto $(x, y, z)$ en $S$, podemos identificar dos vectores normales unitarios $\bold{N}$ y $−\bold{N}$. Si es posible elegir un vector normal unitario $\bold{N}$ en cada punto $(x, y, z)$ de $S$ de modo que $\bold{N}$ varíe continuamente sobre $S$, entonces $S$ es "orientable". Tal elección de vector normal unitario en cada punto da la orientación de una superficie $S$. Si piensas que el campo normal describe el flujo de agua, entonces el lado de la superficie hacia el que fluye el agua es el lado "negativo" y el lado de la superficie por la que fluye el agua, en sentido contrario, es el lado "positivo". De manera informal, una elección de orientación le da a $S$ un lado "exterior" y un lado "interior" (o un lado "hacia arriba" y un lado "hacia abajo"), al igual que una elección de orientación de una curva da a la curva "hacia adelante" y direcciones "hacia atrás".
Las superficies cerradas, como las esferas, son orientables: si elegimos el vector normal hacia afuera en cada punto de la superficie de la esfera, entonces los vectores normales unitarios varían continuamente. Esto se llama orientación positiva de la superficie cerrada (Figura 6.74). También podríamos elegir el vector normal hacia adentro en cada punto para dar una orientación "hacia adentro", que es la orientación negativa de la superficie.
Una parte de la gráfica de cualquier función suave $z = f (x, y)$ también es orientable. Si elegimos el vector normal unitario que apunta "por encima" de la superficie en cada punto, entonces los vectores normales unitarios varían continuamente sobre la superficie.

Figura 6.74. Una esfera orientada con orientación positiva.
También podríamos elegir el vector normal unitario que apunta "debajo" de la superficie en cada punto. Para obtener dicha orientación, parametrizamos la gráfica de $f$ de la manera estándar: $\bold{r} (x, y) = \lang x, y, f (x, y)\rang$, donde $x$ e $y$ varían en el dominio de $f$. Entonces, $\bold{t}_x = \lang 1, 0, f_x\rang$ y $\bold{t}_y = \lang 0, 1, f_y\rang$, y por lo tanto el producto cruzado $\bold{t}_x \times \bold{t}_y$ (que es normal a la superficie en cualquier punto de la superficie) es $\lang −f_x, - f_y, 1\rang$. Dado que el componente $z$ de este vector es uno, el vector normal unitario correspondiente apunta "hacia arriba", y el lado hacia arriba de la superficie se elige como el lado "positivo".
Sea $S$ una superficie lisa orientable con parametrización $\bold{r} (u, v)$. Para cada punto $\bold{r} (a, b)$ de la superficie, los vectores $\bold{t}_u$ y $\bold{t}_v$ se encuentran en el plano tangente en ese punto. El vector $\bold{t}_u \times \bold{t}_v$ es normal al plano tangente en $\bold{r} (a, b)$ y, por lo tanto, es normal a $S$ en ese punto. Por tanto, la elección del vector normal unitario
$$\bold{N} = \frac{\bold{t}_u \times \bold{t}_v}{||\bold{t}_u \times \bold{t}_v||}$$da una orientación de la superficie $S$.
 |
Eligiendo una orientación |

Dado que cada curva tiene una dirección "hacia adelante" y "hacia atrás" (o, en el caso de una curva cerrada, una dirección hacia la derecha y hacia la izquierda), es posible dar una orientación a cualquier curva. Por tanto, es posible pensar en cada curva como una curva orientada. Sin embargo, este no es el caso de las superficies. Algunas superficies no se pueden orientar; tales superficies se denominan no orientables. Esencialmente, una superficie se puede orientar si la superficie tiene un lado "interior" y un lado "exterior", o un lado "hacia arriba" y un lado "hacia abajo". Algunas superficies están torcidas de tal manera que no existe una noción bien definida de un lado "interno" o "externo".
El ejemplo clásico de una superficie no orientable es la banda de Möbius.
Para crear una tira de Möbius, toma una tira rectangular de papel, dá una media vuelta a la hoja de papel y pega los extremos (Figura 6.76). Debido a la media torsión de la tira, la superficie no tiene un lado "exterior" ni un lado "interior". Si imaginas colocar un vector normal en un punto de la tira y hacer que el vector viaje alrededor de la banda, entonces (debido a la media torsión) el vector apunta en la dirección opuesta cuando vuelve a su posición original. Por lo tanto, la tira realmente solo tiene un lado.

Figura 6.76. La construcción de una tira de Möbius.
Dado que algunas superficies no son orientables, no es posible definir una integral de superficie vectorial en todas las superficies lisas por partes. Esto contrasta con las integrales de líneas vectoriales, que se pueden definir en cualquier curva suave por partes.
Con la idea de superficies orientables en su lugar, ahora estamos listos para definir una integral de superficie de un campo vectorial. La definición es análoga a la definición del flujo de un campo vectorial a lo largo de una curva plana. Recuerda que si $\bold{F}$ es un campo vectorial bidimensional y $C$ es una curva plana, entonces la definición del flujo de $\bold{F}$ a lo largo de $C$ implicó cortar $C$ en trozos pequeños, elegir un punto dentro de cada trozo y calcular $\bold{F} \cdot \bold{N}$ en el punto (donde $\bold{N}$ es el vector normal unitario en el punto). La definición de una integral de superficie de un campo vectorial procede de la misma manera, excepto que ahora cortamos la superficie $S$ en trozos pequeños, elegimos un punto en el trozo pequeño (bidimensional) y calculamos $\bold{F} \cdot \bold{N}$ en el punto.
Para colocar esta definición en un entorno del mundo real, sea $S$ una superficie orientada con un vector normal unitario $\bold{N}$. Sea $\bold{v}$ un campo de velocidad de un fluido que fluye a través de $S$, y supón que el fluido tiene densidad $\rho (x, y, z)$. Imagina que el fluido fluye a través de $S$, pero $S$ es completamente permeable, de modo que no obstaculiza el flujo de fluido (Figura 6.77). El flujo másico del fluido es la tasa de flujo másico por unidad de área. El flujo de masa se mide en masa por unidad de tiempo por unidad de área. ¿Cómo podríamos calcular el flujo de masa del fluido a través de $S$?

Figura 6.77. El fluido fluye a través de una superficie completamente permeable $S$.
La tasa de flujo, medida en masa por unidad de tiempo por unidad de área, es $\rho\bold{N}$.
Para calcular el flujo de masa a través de $S$, corta $S$ en trozos pequeños $S_{ij}$. Si $S_{ij}$ es lo suficientemente pequeño, entonces puede aproximarse mediante un plano tangente en algún punto $P$ en $S_{ij}$. Por lo tanto, el vector normal unitario en $P$ se puede usar para aproximar $\bold{N} (x, y, z)$ en toda la pieza $S_{ij}$, porque el vector normal a un plano no cambia cuando nos movemos a través del plano. La componente del vector $\rho\bold{v}$ en $P$ en la dirección de $\bold{N}$ es $\rho\bold{v}\cdot\bold{N}$ en $P$. Dado que $S_{ij}$ es pequeño, el producto escalar $\rho\bold{v}\cdot\bold{N}$ cambia muy poco a medida que variamos a través de $S_{ij}$, y por lo tanto $\rho\bold{v}\cdot\bold{N}$ puede tomarse como aproximadamente constante a través de $S_{ij}$. Para aproximar la masa de fluido por unidad de tiempo que fluye a través de $S_{ij}$ (y no solo localmente en el punto $P$), necesitamos multiplicar $(\rho\bold{v}\cdot\bold{N}) (P)$ por el área de $S_{ij}$. Por lo tanto, la masa de fluido por unidad de tiempo que fluye a través de $S_{ij}$ en la dirección de $\bold{N}$ se puede aproximar mediante $(\rho\bold{v}\cdot\bold{N}) \Delta S_{ij}$, donde $\bold{N}, \rho$ y $\bold{v}$ se evalúan en $P$ (Figura 6.78). Esto es análogo al flujo del campo vectorial bidimensional $\bold{F}$ a través de la curva plana $C$, en el que aproximamos el flujo a través de una pequeña parte de $C$ con la expresión $(\bold{F}\cdot\bold{N}) \Delta s$. Para aproximar el flujo de masa a través de $S$, forma la suma $\sum_{i=1}^m\sum_{j = 1}^n (\rho\bold{v}\cdot\bold{N}) \Delta S_{ij}$. A medida que las piezas $S_{ij}$ se hacen más pequeñas, la suma $\sum_{i=1}^m\sum_{j = 1}^n (\rho\bold{v}\cdot\bold{N}) \Delta S_{ij}$ se acerca arbitrariamente al flujo de masa. Por lo tanto, el flujo de masa es
$$\iint_S \rho\bold{v}\cdot\bold{N} dS = \lim\limits_{m,n \to \infin} \sum_{i=1}^m\sum_{j = 1}^n (\rho\bold{v}\cdot\bold{N}) \Delta S_{ij}$$Ésta es una integral de superficie de un campo vectorial. Dejando que el campo vectorial $\rho\bold{v}$ sea un campo vectorial arbitrario $\bold{F}$, se obtiene la siguiente definición.

Figura 6.78. La masa de fluido por unidad de tiempo que fluye a través de $S_{ij}$ en la dirección de $\bold{N}$ se puede aproximar mediante $(\rho\bold{v}\cdot\bold{N}) \Delta S_{ij}$.
Observa el paralelo entre esta definición y la definición de integral de línea vectorial $\int_C\bold{F}\cdot\bold{N}ds$. Una integral de superficie de un campo vectorial se define de manera similar a una integral de línea de flujo a través de una curva, excepto que el dominio de integración es una superficie (un objeto bidimensional) en lugar de una curva (un objeto unidimensional). La integral $\iint_S\bold{F}\cdot\bold{N}dS$ se denomina flujo de $\bold{F}$ a través de $S$, al igual que la integral $\int_C\bold{F}\cdot\bold{N}ds$ es el flujo de $\bold{F}$ a través de la curva $C$. Una integral de superficie sobre un campo vectorial también se llama integral de flujo.
Al igual que con las integrales de línea vectorial, la integral de superficie $\iint_S\bold{F}\cdot\bold{N}dS$ es más fácil de calcular después de que se haya parametrizado la superficie $S$. Sea $\bold{r} (u, v)$ una parametrización de $S$ con dominio de parámetro $D$. Entonces, el vector normal unitario viene dado por $\bold{N} = \frac{\bold{t}_u \times \bold{t}_v}{||\bold{t}_u \times \bold{t}_v||}$ y, de la ecuación 6.20, obtenemos:
$$\begin{aligned} \iint_S\bold{F}\cdot\bold{N}dS &= \iint_S\bold{F}\cdot \frac{\bold{t}_u \times \bold{t}_v}{||\bold{t}_u \times \bold{t}_v||}\\ &= \iint_D\big(\bold{F}(\bold{r}(u,v))\cdot \frac{\bold{t}_u \times \bold{t}_v}{||\bold{t}_u \times \bold{t}_v||}\big)||\bold{t}_u \times \bold{t}_v||dA\\ &= \iint_D\big(\bold{F}(\bold{r}(u,v))\cdot (\bold{t}_u \times \bold{t}_v)dA \end{aligned}$$Por lo tanto, para calcular una integral de superficie sobre un campo vectorial, podemos usar la ecuación
$$\iint_S\bold{F}\cdot\bold{N}dS = \iint_D\big(\bold{F}(\bold{r}(u,v))\cdot (\bold{t}_u \times \bold{t}_v)dA$$ |
Calculando una integral de superficie |

 |
Calculando la tasa de flujo másico |

En el ejercicio anterior, calculamos el flujo másico, que es la tasa de flujo másico por unidad de área. Si queremos encontrar el caudal (medido en volumen por tiempo), podemos usar la integral de flujo $\iint_S\bold{v}\cdot\bold{N}dS$, que omite la densidad. Dado que el caudal de un fluido se mide en volumen por unidad de tiempo, el caudal no tiene en cuenta la masa. Por lo tanto, tenemos la siguiente caracterización de la tasa de flujo de un fluido con velocidad $\bold{v}$ a través de una superficie $S$:
Para calcular el caudal del fluido del ejercicio anterior, simplemente eliminamos la constante de densidad, que da un caudal de $90\pi\; m^3 / seg$.
Tanto el flujo másico como el caudal son importantes en física e ingeniería. El flujo de masa mide cuánta masa fluye a través de una superficie; el caudal mide cuánto volumen de fluido fluye a través de una superficie.
Además de modelar el flujo de fluido, se pueden utilizar integrales de superficie para modelar el flujo de calor. Supón que la temperatura en el punto $(x, y, z)$ de un objeto es $T (x, y, z)$. Entonces, el flujo de calor es un campo vectorial proporcional al gradiente de temperatura negativo en el objeto. Para ser precisos, el flujo de calor se define como campo vectorial $\bold{F} = −k\nabla T$, donde la constante $k$ es la conductividad térmica de la sustancia a partir de la cual está hecho el objeto (esta constante se determina experimentalmente). La tasa de flujo de calor a través de la superficie $S$ en el objeto está dada por la integral de flujo
$$\iint_S\bold{F}\cdot d\bold{S} = \iint_S −k\nabla T \cdot d\bold{S}$$Terminamos este apartado con un último ejercicio y una escena interactiva de Elena E. Álvarez Sáiz, en la cual se considera: i) una superficie $S$ dada por $z=(x,y)$ que está definida sobre un rectángulo $R=[0,a]\times [0,b]$; ii) una partición de $R$ en $mn$ subrectángulos, y iii) un campo $\bold{F}$ definido en cada punto de la superficie $S$.
 |
Calculando el flujo de calor |


 Para los siguientes ejercicios, determina si las afirmaciones son verdaderas o falsas.
Para los siguientes ejercicios, determina si las afirmaciones son verdaderas o falsas.
269. Si la superficie $S$ está dada por $\lbrace (x, y, z): 0 \le x \le 1, 0 \le y \le 1, z = 10\rbrace$, entonces $\iint_Sf (x, y, z) dS = \int_0^1\int_0^1 f (x , y, 10) dxdy$ (Solución). 270. Si la superficie $S$ está dada por $\lbrace (x, y, z): 0 \le x \le 1, 0 \le y \le 1, z = x\rbrace$, entonces $\iint_Sf (x, y, z) dS = \int_0^1\int_0^1f (x, y , x) dxdy$ 271. Superficie $\bold{r} = \lang v cos\; u, v sen\; u, v^2\rang$, para $0 \le u \le \pi, 0 \le v \le 2$, es igual que la superficie $\bold{r} = \lang \sqrt{v} cos\; 2u, \sqrt{v} sen\; 2u, v\rang$, para $0 \le u \le \frac{\pi}{2}, 0 \le v \le 4$ (Solución). 272. Dada la parametrización estándar de una esfera, los vectores normales $\bold{t}_u \times \bold{t}_v$ son vectores normales hacia afuera.
 Para los siguientes ejercicios, busca descripciones paramétricas de las siguientes superficies.
Para los siguientes ejercicios, busca descripciones paramétricas de las siguientes superficies.
273. Plano $3x - 2y + z = 2$ (Solución). 274. Paraboloide $z = x^2 + y^2$, para $0 \le z \le 9$. 275. Plano $2x - 4y + 3z = 16$ (Solución). 276. El tronco del cono $z^2 = x^2 + y^2$, para $2 \le z \le 8$ 277. La porción del cilindro $x^2 + y^2 = 9$ en el primer octante, para $0 \le z \le 3$ (Solución).
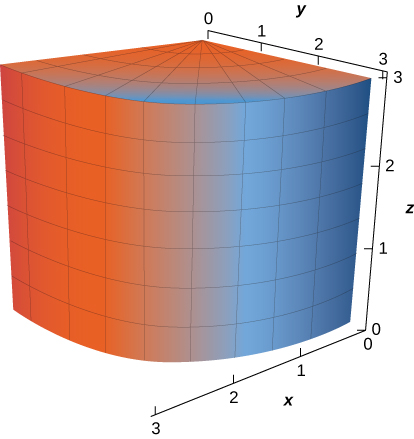
278. Un cono con radio de base $r$ y altura $h$, donde $r$ y $h$ son constantes positivas.
 Para los siguientes ejercicios, usa un sistema de álgebra computarizada para aproximar el área de las siguientes superficies usando una descripción paramétrica de la superficie.
Para los siguientes ejercicios, usa un sistema de álgebra computarizada para aproximar el área de las siguientes superficies usando una descripción paramétrica de la superficie.
279. [T] Medio cilindro $\lbrace (r, \theta, z): r = 4, 0 \le \theta \le \pi, 0 \le z \le 7\rbrace$ (Solución). 280. [T] Plano $z = 10 - x - y$ sobre el cuadrado $| x | \le 2, | y | \le 2$
 Para los siguientes ejercicios, sea $S$ el hemisferio $x^2 + y^2 + z^2 = 4$, con $z \ge 0$, y evalúa cada integral de superficie, en sentido antihorario.
Para los siguientes ejercicios, sea $S$ el hemisferio $x^2 + y^2 + z^2 = 4$, con $z \ge 0$, y evalúa cada integral de superficie, en sentido antihorario.
281. $\iint_SzdS$ (Solución). 282. $\iint_S (x - 2y) dS$ 283. $\iint_S\big(x^2 + y^2\big)zdS$ (Solución).
 Para los siguientes ejercicios, evalúa $\iint_S\bold{F}\cdot\bold{N}ds$ para el campo vectorial $\bold{F}$, donde $\bold{N}$ es un vector normal hacia afuera a la superficie $S$.
Para los siguientes ejercicios, evalúa $\iint_S\bold{F}\cdot\bold{N}ds$ para el campo vectorial $\bold{F}$, donde $\bold{N}$ es un vector normal hacia afuera a la superficie $S$.
284. $\bold{F} (x, y, z) = x\bold{i} + 2y\bold{j} - 3z\bold{k}$, y $S$ es la parte del plano $15x - 12y + 3z = 6$ que se encuentra por encima del cuadrado unitario $0 \le x \le 1, 0 \le y \le 1$. 285. $\bold{F} (x, y, z) = x\bold{i} + y\bold{j}$, y $S$ es el hemisferio $z = \sqrt{1 - x^2 - y^2}$ (Solución). 286. $\bold{F} (x, y, z) = x^2\bold{i} + y^2\bold{j} + z^2\bold{k}$, y $S$ es la parte del plano $z = y + 1$ que se encuentra dentro del cilindro $x^2 + y^2 = 1$.
 Para los siguientes ejercicios, calcula la masa de la lámina homogénea que tiene la forma de la superficie dada $S$. Redondea a cuatro decimales.
Para los siguientes ejercicios, calcula la masa de la lámina homogénea que tiene la forma de la superficie dada $S$. Redondea a cuatro decimales.
287. [T] $S$ es la superficie $z = 4 - x - 2y$, con $z \ge 0, x \ge 0, y \ge 0; \xi = x$ (Solución). 288. [T] $S$ es la superficie $z = x^2 + y^2$, con $z \le 1; \xi = z$. 289. [T] $S$ es la superficie $x^2 + y^2 + z^2 = 5$, con $z \ge 1; \xi = \theta^2$ (Solución). 290. Evalúa $\iint_S\big(y^2z\bold{i} + y^3\bold{j} + xz\bold{k}\big) \cdot d\bold{S}$, donde $S$ es la superficie del cubo $−1 \le x \le 1, −1 \le y \le 1$ y $0 \le z \le 2$. en sentido antihorario. 291. Evalúa la integral de superficie $\iint_SgdS$, donde $g (x, y, z) = xz + 2x^2 - 3xy$ y $S$ es la porción del plano $2x - 3y + z = 6$ que se encuentra sobre el cuadrado unitario $R: 0 \le x \le 1 , 0 \le y \le 1$ (Solución). 292. Evalúa $\iint_S (x + y + z) d\bold{S}$, donde $S$ es la superficie definida paramétricamente por $\bold{R} (u, v) = (2u + v)\bold{i} + (u - 2v)\bold{j} + (u + 3v)\bold{k}$ para $0 \le u \le 1$ y $0 \le v \le 2$.
293. [T] Evalúa $\iint_S (x - y^2 + z) d\bold{S}$, donde $S$ es la superficie definida por $\bold{R} (u, v) = u^2\bold{i} + v\bold{j} + u\bold{k}, 0 \le u \le 1, 0 \le v \le 1$ (Solución).
294. [T] Evaluar donde $S$ es la superficie definida por $\bold{R} (u, v) = u\bold{i} - u^2\bold{j} + v\bold{k}, 0 \le u ≤ 2, 0 \le v \le 1$, para $0 \le u \le 1, 0 \le v \le 2$. 295. Evalúa $\iint_S\big(x^2 + y^2\big)d\bold{S}$, donde $S$ es la superficie delimitada por encima del hemisferio $z = \sqrt{1 - x^2 - y^2}$, y por debajo del plano $z = 0$ (Solución). 296. Evalúa $\iint_S\big(x^2 + y^2 + z^2\big)d\bold{S}$, donde $S$ es la porción del plano $z = x + 1$ que se encuentra dentro del cilindro $x^2 + y^2 = 1$. 297. [T] Evalúa $\iint_Sx^2zdS$, donde $S$ es la porción del cono $z^2 = x^2 + y^2$ que se encuentra entre los planos $z = 1$ y $z = 4$ (Solución).
298. [T] Evalúa $\iint_S(xz / y)d\bold{S}$, donde $S$ es la porción del cilindro $x = y^2$ que se encuentra en el primer octante entre los planos $z = 0, z = 5, y = 1$ e $y = 4$.
299. [T] Evalúa $\iint_S (z + y) dS$, donde $S$ es la parte de la gráfica de $z = \sqrt{1 - x^2}$ en el primer octante entre el plano $xz$ y el plano $y = 3$ (Solución).
300. Evalúa $\iint_SxyzdS$ si $S$ es la parte del plano $z = x + y$ que se encuentra sobre la región triangular en el plano $xy$ con vértices $(0, 0, 0), (1, 0, 0)$ y $(0, 2, 0)$. 301. Encuentra la masa de una lámina de densidad $\xi (x, y, z) = z$ en la forma del hemisferio $z = \big(a^2 −x^2 - y^2\big)^{1/2}$ (Solución). 302. Calcula $\iint_S\bold{F}\cdot\bold{N}dS$, donde $\bold{F} (x, y, z) = x\bold{i} −5y\bold{j} + 4z\bold{k}$ y $\bold{N}$ es un vector normal hacia afuera de $S$, donde $S$ es la unión de dos cuadrados $S_1: x = 0, 0 \le y \le 1, 0 \le z \le 1$ y $S_2: z = 1, 0 \le x \le 1, 0 \le y \le 1$
303. Calcula $\iint_S\bold{F}\cdot\bold{N}dS$, donde $\bold{F} (x, y, z) = xy\bold{i} + z\bold{j} + (x + y) \bold{k}$ y $\bold{N}$ es un vector normal hacia afuera de $S$, donde $S$ es la región triangular cortada del plano $x + y + z = 1$ por los ejes de coordenadas positivos (Solución). 304. Calcula $\iint_S\bold{F}\cdot\bold{N}dS$, donde $\bold{F} (x, y, z) = 2yz\bold{i} + \big(tan^{-1}xz\big)\bold{j} + e^{xy}\bold{k}$ y $\bold{N}$ es un vector normal hacia afuera de $S$, donde $S$ es la superficie de la esfera $x^2 + y^2 + z^2 = 1$. 305. Calcule Calcula $\iint_S\bold{F}\cdot\bold{N}dS$, donde $\bold{F} (x, y, z) = xyz\bold{i} + xyz\bold{j} + xyz\bold{k}$ y $\bold{N}$ es un vector normal hacia afuera de $S$, donde $S$ es la superficie de las cinco caras del cubo unitario $0 \le x \le 1, 0 \le y \le 1, 0 \le z \le 1$ ausente $z = 0$ (Solución).
 Para los siguientes ejercicios, expresa la integral de superficie como una integral doble iterada usando una proyección en $S$ en el plano $yz$.
Para los siguientes ejercicios, expresa la integral de superficie como una integral doble iterada usando una proyección en $S$ en el plano $yz$.
306. $\iint_S xy^2z^3dS$; $S$ es la porción de primer octante del plano $2x + 3y + 4z = 12$. 307. $\iint_S\big(x^2 - 2y + z\big)dS$; $S$ es la parte de la gráfica de $4x + y = 8$ limitada por los planos de coordenadas y el plano $z = 6$ (Solución).
 Para los siguientes ejercicios, expresa la integral de superficie como una integral doble iterada usando una proyección en $S$ en el plano $xz$
Para los siguientes ejercicios, expresa la integral de superficie como una integral doble iterada usando una proyección en $S$ en el plano $xz$
308. $\iint_S xy^2z^3dS$; $S$ es la porción de primer octante del plano $2x + 3y + 4z = 12$.
309. $\iint_S\big(x^2 - 2y + z\big)dS$; $S$ es la parte de la gráfica de $4x + y = 8$ limitada por los planos de coordenadas y el plano $z = 6$ (Solución).
310. Evalúa la integral de superficie $\iint_S yzdS$, donde $S$ es la parte del primer octante del plano $x + y + z = \lambda$, donde $\lambda$ es una constante positiva.
311. Evalúa la integral de superficie $\iint_S\big(x^2z + y^2z\big)dS$, donde $S$ es el hemisferio $x^2 + y^2 + z^2 = a^2, z \ge 0$ (Solución).
312. Evalúa la integral de superficie $\iint_SzdA$, donde $S$ es la superficie $z = \sqrt{x^2 + y^2}, 0 \le z \le 2$.
313. Evalúa la integral de superficie $\iint_Sx^2yzdS$, donde $S$ es la parte del plano $z = 1 + 2x + 3y$ que se encuentra sobre el rectángulo $0 \le x \le 3$ y $0 \le y \le 2$ (Solución).
314. Evalúa la integral de superficie $\iint_SyzdS$, donde $S$ es el plano $x + y + z = 1$ que se encuentra en el primer octante.
315. Evalúa la integral de superficie $\iint_SyzdS$, donde $S$ es la parte del plano $z = y + 3$ que se encuentra dentro del cilindro $x^2 + y^2 = 1$ (Solución).
 Para los siguientes ejercicios, usa el razonamiento geométrico para evaluar las integrales de superficie dadas.
Para los siguientes ejercicios, usa el razonamiento geométrico para evaluar las integrales de superficie dadas.
316. $\iint_S\sqrt{x^2 + y^2 + z^2}dS$, donde $S$ es la superficie $x^2 + y^2 + z^2 = 4, z \ge 0$
317. $\iint_S (x\bold{i} + y\bold{j}) \cdot dS$, donde $S$ es la superficie $x^2 + y^2 = 4, 1 \le z \le 3$, orientada con vectores normales unitarios apuntando hacia afuera (Solución).
318. $\iint_S (z\bold{k}) \cdot d\bold{S}$, donde $S$ es el disco $x^2 + y^2 \le 9$ en el plano $z = 4$, orientado con vectores normales unitarios apuntando hacia arriba
319. Una lámina tiene la forma de una porción de esfera $x^2 + y^2 + z^2 = a^2$ que se encuentra dentro del cono $z = \sqrt{x^2 + y^2}$. Sea $S$ la concha esférica centrada en el origen con radio $a$, y sea $C$ el cono circular recto con un vértice en el origen y un eje de simetría que coincide con el eje $z$. Determina la masa de la lámina si $\delta (x, y, z) = x^2y^2z$ (Solución).
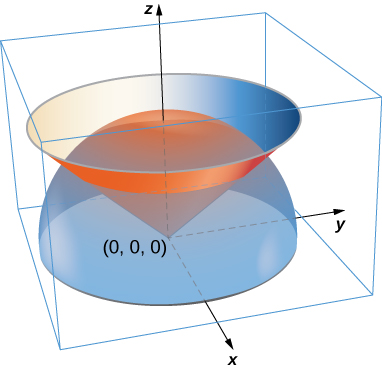
320. Una lámina tiene la forma de una porción de esfera $x^2 + y^2 + z^2 = a^2$ que se encuentra dentro del cono $z = \sqrt{x^2 + y^2}$. Sea $S$ la concha esférica centrada en el origen con radio $a$, y sea $C$ el cono circular recto con un vértice en el origen y un eje de simetría que coincide con el eje $z$. Supón que el ángulo del vértice del cono es $\phi_0$, con $0 \le \phi_0 \lt \pi/2$. Determina la masa de esa porción de la forma encerrada en la intersección de $S$ y $C$. Supón $\delta (x, y, z) = x^2y^2z$.
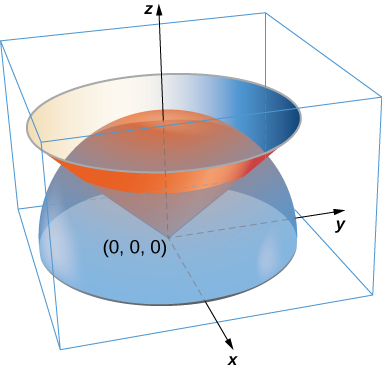
321. Un vaso de papel tiene la forma de un cono circular recto invertido de $6$ pulgadas de altura y un radio de $3$ pulgadas. Si el vaso está lleno de agua y pesa $62.5\; lb / pie^3$, calcula la fuerza total ejercida por el agua en el interior superficie de la taza (Solución).
 Para los siguientes ejercicios, el campo vectorial de flujo de calor para objetos conductores $\bold{F} = −k\nabla T$, donde $T (x, y, z)$ es la temperatura en el objeto y $k \gt 0$ es una constante que depende del material. Encuentra el flujo exterior de $\bold{F}$ a través de las siguientes superficies $S$ para las distribuciones de temperatura dadas y supón $k = 1$.
Para los siguientes ejercicios, el campo vectorial de flujo de calor para objetos conductores $\bold{F} = −k\nabla T$, donde $T (x, y, z)$ es la temperatura en el objeto y $k \gt 0$ es una constante que depende del material. Encuentra el flujo exterior de $\bold{F}$ a través de las siguientes superficies $S$ para las distribuciones de temperatura dadas y supón $k = 1$.
322. $T (x, y, z) = 100e^{− x - y}$; $S$ consta de las caras del cubo $| x | \le 1, | y | \le 1, | z | \le 1$.
323. $T (x, y, z) = −ln\big(x^2 + y^2 + z^2\big)$; $S$ es la esfera $x^2 + y^2 + z^2 = a^2$ (Solución).
 Para los siguientes ejercicios, considera los campos radiales $\bold{F} = \frac{\lang x, y, z\rang}{ \big(x^2 + y^2 + z^2\big)^{p/2}} = \frac{\bold{r}}{ | \bold{r} |^p}$, donde $p $es un número real. Sea $S$ formado por esferas $A$ y $B$ centradas en el origen con radios $0 \lt a \lt b$. El flujo total hacia afuera a través de $S$ consiste en el flujo hacia afuera a través de la esfera externa $B$ menos el flujo hacia $S$ a través de la esfera interna $A$.
Para los siguientes ejercicios, considera los campos radiales $\bold{F} = \frac{\lang x, y, z\rang}{ \big(x^2 + y^2 + z^2\big)^{p/2}} = \frac{\bold{r}}{ | \bold{r} |^p}$, donde $p $es un número real. Sea $S$ formado por esferas $A$ y $B$ centradas en el origen con radios $0 \lt a \lt b$. El flujo total hacia afuera a través de $S$ consiste en el flujo hacia afuera a través de la esfera externa $B$ menos el flujo hacia $S$ a través de la esfera interna $A$.
324. Encuentra el flujo total a través de $S$ con $p = 0$.
325. Demuestra que para $p = 3$ el flujo a través de $S$ es independiente de $a$ y $b$ (Solución).
En este apartado, estudiaremos el teorema de Stokes, una generalización de dimensiones superiores del teorema de Green. Este teorema, como el Teorema fundamental para Integrales de Línea y el teorema de Green, es una generalización del Teorema Fundamental del Cálculo a dimensiones superiores. El teorema de Stokes relaciona una integral de superficie vectorial sobre la superficie $S$ en el espacio con una integral de línea alrededor del límite de $S$. Por lo tanto, al igual que los teoremas anteriores, el teorema de Stokes se puede usar para reducir una integral sobre un objeto geométrico $S$ a una integral sobre el límite de $S$.
Además de permitirnos transformar entre integrales de línea e integrales de superficie, el teorema de Stokes conecta los conceptos de rotación y circulación. Además, el teorema tiene aplicaciones en mecánica de fluidos y en el electromagnetismo. Usamos el teorema de Stokes para deducir la ley de Faraday, un resultado importante que involucra campos eléctricos.
El teorema de Stokes dice que podemos calcular el flujo del rotacional $\bold{F}$ a través de la superficie $S$ conociendo información solo sobre los valores de $\bold{F}$ a lo largo del límite de $S$. A la inversa, podemos calcular la integral de línea del campo vectorial $\bold{F}$ a lo largo del límite de la superficie $S$ transformnado a una integral doble del rotacional de $\bold{F}$ sobre $S$.
Sea $S$ una superficie lisa orientada con un vector normal unitario $\bold{N}$. Además, supón que el límite de $S$ es una curva cerrada simple $C$.
La orientación de $S$ induce la orientación positiva de $C$ si, mientras camina en la dirección positiva alrededor de $C$ con su cabeza apuntando en la dirección de $\bold{N}$, la superficie siempre está a su izquierda. Con esta definición en su lugar, podemos enunciar el teorema de Stokes.
Supón que la superficie $S$ es una región plana en el plano $xy$ con orientación hacia arriba. Entonces, el vector normal unitario es $\bold{k}$ y la integral de superficie $\iint_S rot \bold{F}\cdot d\bold{S}$ es en realidad la integral doble $\iint_S rot \bold{F}\cdot \bold{k}dA$. En este caso especial, el teorema de Stokes da $\int_C\bold{F}\cdot d\bold{r} = \iint_S rot \bold{F}\cdot \bold{k}dA$. Sin embargo, esta es la forma de flujo del teorema de Green, que nos muestra que el teorema de Green es un caso especial del teorema de Stokes. El teorema de Green solo puede manejar superficies en un plano, pero el teorema de Stokes puede manejar superficies en un plano o en el espacio.
La prueba completa del teorema de Stokes está más allá del alcance de este texto.
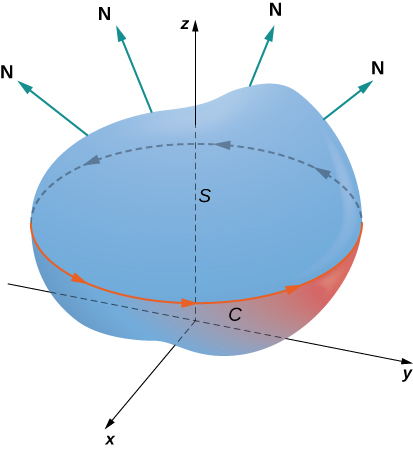
Figura 6.79. El teorema de Stokes relaciona la integral de flujo sobre la superficie con una integral de línea alrededor del límite de la superficie. Ten en cuenta que la orientación de la curva es positiva.
Observamos una explicación intuitiva de la verdad del teorema y luego vemos la prueba del teorema en el caso especial de que la superficie $S$ es una porción de una gráfica de una función, y $S$, el límite de $S$ y $\bold{F}$ son bastante mansos.
Primero, miramos una demostración informal del teorema. Esta demostración no es rigurosa, pero está destinada a dar una idea general de por qué el teorema es verdadero. Sea $S$ una superficie y sea $D$ una pequeña parte de la superficie para que $D$ no comparta ningún punto con el límite de S. Elegimos que $D$ sea lo suficientemente pequeño como para que pueda aproximarse mediante un cuadrado orientado $E$.
Sea $D$ tal que herede su orientación de $S$ y dé a $E$ la misma orientación. Este cuadrado tiene cuatro lados; denotados como $E_l, E_r, E_u$ y $E_d$ para los lados izquierdo, derecho, arriba y abajo, respectivamente. En el cuadrado, podemos usar la forma de flujo del teorema de Green:
$$\int_{E_l + E_d + E_r + E_u}\bold{F}\cdot d\bold{r} = \iint_E rot \bold{F}\cdot \bold{N}dS = \iint_E rot \bold{F}\cdot d\bold{S}$$Para aproximar el flujo sobre toda la superficie, agregamos los valores del flujo en los cuadrados pequeños que se aproximan a los pequeños pedazos de la superficie (Figura 6.80).
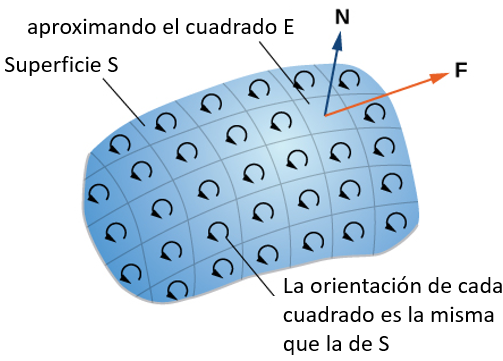
Figura 6.80. Pica la superficie en trozos pequeños. Las piezas deben ser lo suficientemente pequeñas como para que puedan aproximarse mediante un cuadrado.
Según el teorema de Green, el flujo a través de cada cuadrado aproximado es una integral de línea sobre su límite. Sea $F$ un cuadrado aproximado con una orientación heredada de $S$ y con un lado derecho $E_l$ (entonces $F$ está a la izquierda de $E$).
Sea $F_r$ el lado derecho de $F$; entonces, $E_l = −F_r$. En otras palabras, el lado derecho de $F$ es la misma curva que el lado izquierdo de $E$, simplemente orientado en la dirección opuesta. Por lo tanto,
$$\int_{E_l}\bold{F}\cdot d\bold{r} = −\int_{F_r}\bold{F}\cdot d\bold{r}$$A medida que sumamos todos los flujos sobre todos los cuadrados que se aproximan a la superficie $S$, las integrales de línea $int_{E_l}\bold{F}\cdot d\bold{r}$ y $\int_{F_r}\bold{F}\cdot d\bold{r}$ se cancelan entre sí. Lo mismo ocurre con las integrales de línea sobre los otros tres lados de $E$. Estas tres integrales de línea se cancelan con la integral de línea del lado inferior del cuadrado sobre $E$, la integral de línea sobre el lado izquierdo del cuadrado a la derecha de $E$, y la integral de línea sobre el lado superior del cuadrado debajo de $E$ (Figura 6.81).
Figura 6.81. (a) La integral de línea a lo largo de $E_l$ anula la integral de línea a lo largo de $F_r$ porque $E_l = −F_r$. (b) La integral de línea a lo largo de cualquiera de los lados de $E$ se cancela con la integral de línea a lo largo de un lado de un cuadrado aproximado adyacente
Después de que ocurra toda esta cancelación en todos los cuadrados aproximados, las únicas integrales de línea que sobreviven son las integrales de línea sobre los lados que se aproximan al límite de S. Por lo tanto, la suma de todos los flujos (que, según el teorema de Green, es la suma de todas las integrales de línea alrededor de los límites de los cuadrados aproximados) se puede aproximar mediante una integral de línea sobre el límite de $S$. En el límite, cuando las áreas de los cuadrados aproximados van a cero, esta aproximación se acerca arbitrariamente al flujo.
Veamos ahora una demostración rigurosa del teorema en el caso especial de que $S$ es la gráfica de la función $z = f (x, y)$, donde $x$ e $y$ varían en una región $D$ limitada y simplemente conectada de área finita (Figura 6.82).
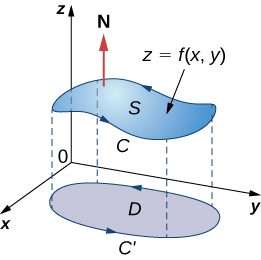
Figura 6.82. $D$ es la "sombra" o proyección de $S$ en el plano y $C^{\prime}$ es la proyección de $C$.
Además, supón que $f$ tiene derivadas parciales continuas de segundo orden. Sea $C$ el límite de $S$ y $C^{\prime}$ el límite de $D$.
Entonces, $D$ es la "sombra" de $S$ en el plano y $C^{\prime}$ es la "sombra" de $C$. Supón que $S$ está orientado hacia arriba. La orientación en sentido antihorario de $C$ es positiva, al igual que la orientación en sentido antihorario de $C^{\prime}$. Sea $\bold{F} (x, y, z) = \lang P, Q, R\rang$ un campo vectorial con funciones componentes que tienen derivadas parciales continuas.
Tomamos la parametrización estándar de $S: x = x, y = y, z = g (x, y)$. Los vectores tangentes son $\bold{t}_x = \lang 1, 0, g_x\rang$ y $\bold{t}_y = \lang 0, 1, g_y\rang$, y por lo tanto, $\bold{t}_x \cdot \bold{t}_y = \lang −g_x, −g_y, 1\rang$. Por la ecuación 6.19,
$$\iint_S rot \bold{F}\cdot d\bold{S} = \iint_D [−(R_y - Q_z)z_x −(P_z - R_x)z_y + (Q_x - P_y)] dA$$ donde todas las derivadas parciales se evalúan en $x, y, g (x, y)$, lo que hace que el integrando dependen de $x$ e $y$ solamente. Supón que $\lang x (t), y (t)\rang, a \le t \le b$ es una parametrización de $C^{\prime}$. Entonces, una parametrización de $C$ es $\lang x (t), y (t), gx (t), y (t)\rang, a \le t \le b$. Armados con estas parametrizaciones, la regla de la cadena y el teorema de Green, y teniendo en cuenta que $P, Q$ y $R$ son todas funciones de $x$ e $y$, podemos evaluar la integral de línea $\int_C\bold{F}\cdot d\bold{r}$: $$\begin{aligned} \int_C\bold{F}\cdot d\bold{r} &= \int_a^b (Px^{\prime}(t) + Qy^{\prime}(t) + Rz^{\prime}(t))dt\\ &= \int_a^b \bigg[Px^{\prime}(t) + Qy^{\prime}(t) + R\bigg(\frac{\partial z}{\partial x}\frac{\partial x}{\partial t} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial t}\bigg)\bigg]dt\\ &= \int_a^b \bigg[\bigg(P+R\frac{\partial z}{\partial x}\bigg)x^{\prime}(t) + \bigg(Q+R\frac{\partial z}{\partial y}\bigg)y^{\prime}(t)\bigg]dt\\ &= \int_{C^{\prime}} \bigg[\bigg(P+R\frac{\partial z}{\partial x}\bigg)dx + \bigg(Q+R\frac{\partial z}{\partial y}\bigg)dy\bigg]\\ \end{aligned}$$Según el teorema de Clairaut, $\frac{\partial^2 z}{\partial x\partial y} y = \frac{\partial^2 z}{\partial y\partial x}$. Por lo tanto, cuatro de los términos desaparecen de esta integral doble y nos quedamos con
$$\iint_D \big[−(R_y - Q_z\big)z_x − \big(P_z - R_x\big)z_y + \big(Q_x - P_y\big)\big] dA$$que es igual a $\iint_S rot \bold{F}\cdot d\bold{S}$.
Hemos demostrado que el teorema de Stokes es verdadero en el caso de una función con un dominio que es una región simplemente conectada de área finita. Podemos confirmar rápidamente este teorema para otro caso importante: cuando el campo vectorial $\bold{F}$ es conservativos. Si $\bold{F}$ es conservativo, el rotacional de $\bold{F}$ es cero, entonces $\iint_S rot \bold{F}\cdot d\bold{S} = 0$. Dado que el límite de $S$ es una curva cerrada, $\int_C\bold{F}\cdot d\bold{r}$ también es cero.
 |
Verificando el teorema de Stokes para un caso específico |
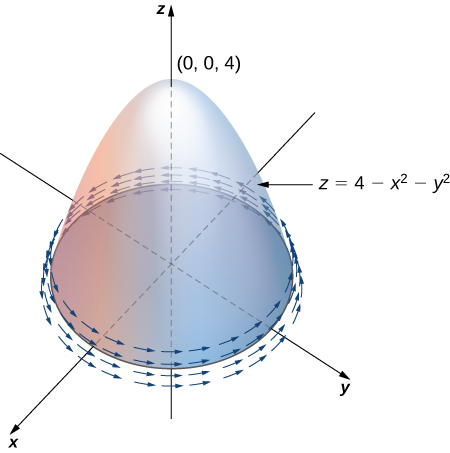
Figura 6.83. Verificación del teorema de Stokes para un hemisferio en un campo vectorial.

El teorema de Stokes se transforma entre la integral de flujo de la superficie $S$ a una integral de línea alrededor del límite de $S$. Por lo tanto, el teorema nos permite calcular integrales de superficie o integrales de línea que normalmente serían bastante difíciles al transformar la integral de línea en una integral de superficie o viceversa. Ahora estudiaremos algunos ejemplos de cada tipo de transformación.
 |
Calculando una integral de superficie |
Figura 6.84. Una superficie complicada en un campo vectorial

Una consecuencia asombrosa del teorema de Stokes es que si $S^{\prime}$ es cualquier otra superficie lisa con el límite $C$ y la misma orientación que $S$, entonces $\iint_S rot\;\bold{F}\cdot d\bold{S} = \int_C\bold{F}\cdot d\bold{r} = 0$ porque el teorema de Stokes dice que la integral de la superficie depende de la línea integral alrededor del límite solamente.
En el ejercicio anterior, calculamos una integral de superficie simplemente usando información sobre el límite de la superficie. En general, sean $S_1$ y $S_2$ superficies lisas con el mismo límite $C$ y la misma orientación. Según el teorema de Stokes,
$$\iint_{S_1} rot\;\bold{F}\cdot d\bold{S} = \int_C\bold{F}\cdot d\bold{r} = \iint_{S_2} rot\;\bold{F}\cdot d\bold{S} \tag{$6.23$}$$Por lo tanto, si $\iint_{S_1} rot\;\bold{F}\cdot d\bold{S}$ es difícil de calcular pero $\iint_{S_2} rot\;\bold{F}\cdot d\bold{S}$ es fácil de calcular, el teorema de Stokes nos permite calcular la integral de superficie más fácil. En el ejercicio anterior, podríamos haber calculado $\iint_{S} rot\;\bold{F}\cdot d\bold{S}$ calculando $\iint_{S^{\prime}} rot\;\bold{F}\cdot d\bold{S}$, donde $S^{\prime}$ es el disco encerrado por la curva límite $C$ (una superficie mucho más simple con la que trabajar).
La ecuación 6.23 muestra que las integrales de flujo de los campos vectoriales rotacionales son independientes de la superficie de la misma manera que las integrales de línea de los campos gradiente son independientes de la trayectoria. Recuerda que si $\bold{F}$ es un campo vectorial conservativo bidimensional definido en un dominio simplemente conectado, $f$ es una función potencial para $\bold{F}$, y $C$ es una curva en el dominio de $\bold{F}$, entonces $int_C\bold{F}\cdot d\bold{r}$ depende solo de los puntos finales de $C$ Por lo tanto, si $C^{\prime}$ es cualquier otra curva con el mismo punto inicial y final que $C$ (es decir, $C^{\prime}$ tiene la misma orientación que $C$), entonces $\int_C\bold{F}\cdot d\bold{r} = int_{C^{\prime}}\bold{F}\cdot d\bold{r}$.
En otras palabras, el valor de la integral depende únicamente del límite de la trayectoria; realmente no depende de la trayectoria en sí.
De manera análoga, supón que $S$ y $S^{\prime}$ son superficies con el mismo límite y la misma orientación, y supón que $\bold{G}$ es un campo vectorial tridimensional que se puede escribir como el rotacional de otro campo vectorial $\bold{F}$ (de modo que $\bold{F}$ es como un "campo potencial" de $\bold{G}$).
Por la ecuación 6.23,
$$\iint_S\bold{G}\cdot d\bold{S} = \iint_{S} rot\;\bold{F}\cdot d\bold{S} = \int_C\bold{F}\cdot d\bold{r} = \iint_{S^{\prime}} rot\;\bold{F}\cdot d\bold{S} = \iint_{S^{\prime}}\bold{G}\cdot d\bold{S}$$Por lo tanto, la integral de flujo de $\bold{G}$ no depende de la superficie, solo del límite de la superficie. Las integrales de flujo de campos vectoriales que se pueden escribir como el rotacional de un campo vectorial son independientes de la superficie de la misma manera que las integrales de línea de campos vectoriales que se pueden escribir como el gradiente de una función escalar son independientes de la trayectoria.
 |
Calculando una integral de línea |

Además de transformar entre integrales de línea e integrales de flujo, el teorema de Stokes se puede utilizar para justificar la interpretación física del rotacional que hemos aprendido. Aquí investigaremos la relación entre el rotacional y la circulación, y usaremos el teorema de Stokes para enunciar la ley de Faraday, una ley importante en electricidad y magnetismo que relaciona el rotacional de un campo eléctrico con la tasa de cambio de un campo magnético.
Recuerda que si $C$ es una curva cerrada y $\bold{F}$ es un campo vectorial definido en $C$, entonces la circulación de $\bold{F}$ alrededor de $C$ es integral de línea $\int_C\bold{F}\cdot d\bold{r}$. Si $\bold{F}$ representa el campo de velocidad de un fluido en el espacio, entonces la circulación mide la tendencia del fluido a moverse en la dirección de $C$.
Sea $\bold{F}$ un campo vectorial continuo y sea $D_r$ un pequeño disco de radio $r$ con centro $P_0$ (Figura 6.85). Si $D_r$ es lo suficientemente pequeño, entonces $(rot\;\bold{F}) (P) \approx (rot\;\bold{F}) (P_0)$ para todos los puntos $P$ en $D_r$ porque el rotacional es continuo. Sea $C_r$ el círculo límite de $D_r$. Por el teorema de Stokes,
$$\int_{C_r}\bold{F}\cdot d\bold{r} = \iint_{D_r} rot\;\bold{F}\cdot\bold{N}dS \approx \iint_{D_r} (rot\;\bold{F})(P_0)\cdot\bold{N}(P_0)dS$$La cantidad $(rot\;\bold{F})(P_0)\cdot\bold{N}(P_0)$ es constante, y por lo tanto
$$\iint_{D_r} (rot\;\bold{F})(P_0)\cdot\bold{N}(P_0)dS = \pi r^2\big[(rot\;\bold{F})(P_0)\cdot\bold{N}(P_0)\big]$$Así

Figura 6.85. El disco $D_r$ es un disco pequeño en un campo vectorial continuo.
y la aproximación se acerca arbitrariamente a medida que el radio se reduce a cero. Por tanto, el teorema de Stokes implica que
$$(rot\;\bold{F})(P_0)\cdot\bold{N}(P_0) = \lim\limits_{r \to 0^{+}} \frac{1}{\pi r^2}\int_{C_r} \bold{F}\cdot d\bold{r}$$Esta ecuación relaciona el rotacional de un campo vectorial con la circulación. Dado que el área del disco es $\pi r^2$, esta ecuación dice que podemos ver el rotacional (en el límite) como la circulación por unidad de área.
Recuerda que si $\bold{F}$ es el campo de velocidad de un fluido, entonces la circulación $\oint_{C_r}\bold{F}\cdot d\bold{r} = \oint_{C_r}\bold{F}\cdot\bold{T}ds$ es una medida de la tendencia del fluido a moverse alrededor de $C_r$. La razón de esto es que $\bold{F}\cdot\bold{T}$ es un componente de $\bold{F}$ en la dirección de $\bold{T}$ , y cuanto más cerca está la dirección de $\bold{F}$ de $\bold{T}$ , mayor es el valor de $\bold{F}\cdot\bold{T}$ (recuerda que si $\bold{a}$ y $\bold{b}$ son vectores y $\bold{b}$ es fijo, entonces el producto escalar $\bold{a}\cdot\bold{b}$ es máximo cuando a apunta en la misma dirección que $\bold{b}$).
Por lo tanto, si $\bold{F}$ es el campo de velocidad de un fluido, entonces el rotacional $\bold{F}\cdot\bold{N}$ es una medida de cómo el fluido gira alrededor del eje $\bold{N}$. El efecto del rotacional es mayor alrededor del eje que apunta en la dirección de $\bold{N}$, porque en este casa $rot\; \bold{F}\cdot\bold{N}$ es lo más grande posible.
Para ver este efecto de una manera más concreta, imagina colocar una pequeña rueda de paletas en el punto $P_0$ (Figura 6.86). La rueda de paletas alcanza su velocidad máxima cuando el eje de la rueda apunta en la dirección del rotacional $\bold{F}$. Esto justifica la interpretación del rotacional que hemos aprendido: el rotacional es una medida de la rotación en el campo vectorial alrededor del eje que apunta en la dirección del vector normal $\bold{N}$, y el teorema de Stokes justifica esta interpretación
Ahora que hemos aprendido sobre el teorema de Stokes, podemos discutir aplicaciones en el área del electromagnetismo. En particular, examinamos cómo podemos usar el teorema de Stokes para transformar entre dos formas equivalentes de la ley de Faraday. Antes de enunciar las dos formas de la ley de Faraday, necesitamos algunos antecedentes de terminología.
Figura 6.86. Para visualizar el rotacional en un punto, imagina colocar una pequeña rueda de paletas en ese punto del campo vectorial.
Sea $C$ una curva cerrada que modela un cable delgado. En el contexto de los campos eléctricos, el cable puede moverse con el tiempo, por lo que escribimos $C (t)$ para representar el cable. En un momento $t$ dado, la curva $C (t)$ puede ser diferente de la curva $C$ original debido al movimiento del alambre, pero asumimos que $C (t)$ es una curva cerrada para todos los tiempos $t$. Sea $D (t)$ una superficie con $C (t)$ como su límite y orienta $C (t)$ de modo que $D (t)$ tenga orientación positiva. Supón que $C (t)$ está en un campo magnético $\bold{B} (t)$ que también puede cambiar con el tiempo. En otras palabras, $\bold{B}$ tiene la forma
$$\bold{B}(x, y, z) = \lang P(x, y, z), Q(x, y, z), R(x, y, z)\rang$$donde $P, Q$ y $R$ pueden variar continuamente a lo largo del tiempo. Podemos producir corriente a lo largo del cable cambiando el campo $\bold{B} (t)$ (esto es una consecuencia de la ley de Ampere).
El flujo $\phi (t) = \iint_{D (t)} \bold{B} (t) \cdot d\bold{S}$ crea un campo eléctrico $\bold{E} (t)$ que funciona. La forma integral de la ley de Faraday establece que
$$\text{Trabajo } = \int_{C(t)} \bold{E}(t)\cdot d\bold{r} = -\frac{\partial \phi}{\partial t}$$En otras palabras, el trabajo realizado por $\bold{E}$ es la integral de línea alrededor del límite, que también es igual a la tasa de cambio del flujo con respecto al tiempo. La forma diferencial de la ley de Faraday establece que
$$rot\; \bold{E} = -\frac{\partial \bold{B}}{\partial t}$$Usando el teorema de Stokes, podemos demostrar que la forma diferencial de la ley de Faraday es una consecuencia de la forma integral. Por el teorema de Stokes, podemos convertir la integral de línea en la forma integral en integral de superficie
$$ -\frac{\partial \phi}{\partial t} = \int_{C(t)} \bold{E(t)}\cdot d\bold{r} = \iint_{D(t)} rot\; \bold{E}(t)\cdot d\bold{S}$$Dado que $\phi (t) = \iint_{D (t)}\bold{B} (t) \cdot s\bold{S}$, siempre que la integración de la superficie no varíe con el tiempo también tenemos
$$-\frac{\partial \phi}{\partial t} = \iint_{D(t)} -\frac{\partial \bold{B}}{\partial t}\cdot \bold{S}$$Por lo tanto
$$\iint_{D(t)} -\frac{\partial \bold{B}}{\partial t}\cdot \bold{S} = \iint_{D(t)} rot\;\bold{E}\cdot d\bold{S}$$Para derivar la forma diferencial de la ley de Faraday, nos gustaría concluir que $rot\;\bold{E} = -\frac{\partial \bold{B}}{\partial t}$. En general, la ecuación
$$\iint_{D(t)} -\frac{\partial \bold{B}}{\partial t}\cdot \bold{S} = \iint_{D(t)} rot\;\bold{E}\cdot d\bold{S}$$no es suficiente para concluir que $rot\;\bold{E} = -\frac{\partial \bold{B}}{\partial t}$. Los símbolos integrales no se "cancelan" simplemente, dejando la igualdad de los integrandos. Para ver por qué el símbolo integral no solo se cancela en general, considera las dos integrales de una sola variable $\int_0^1xdx$ y $\int_0^1f (x) dx$, donde
$$f(x) = \begin{cases} 1, & 0\le x \le 1/2 \\ 0, & 1/2 \le x \le 1 \end{cases}$$Ambas integrales son iguales a $\frac12$, por lo que $\int_0^1xdx = \int_0^1f (x) dx$. Sin embargo, $x\;\cancel{=}\; f (x)$. De manera análoga, con nuestra ecuación $\iint_{D(t)} -\frac{\partial \bold{B}}{\partial t}\cdot \bold{S} = \iint_{D(t)} rot\;\bold{E}\cdot d\bold{S}$, no podemos simplemente concluir que curl $\bold{E} = -\frac{\partial \bold{B}}{\partial t}$ solo porque sus integrales son iguales. Sin embargo, en nuestro contexto, la ecuación $\iint_{D(t)} -\frac{\partial \bold{B}}{\partial t}\cdot \bold{S} = \iint_{D(t)} rot\;\bold{E}\cdot d\bold{S}$ es verdadera para cualquier región, por pequeña que sea (esto contrasta con las integrales de una sola variable que acabamos de discutir ). Si $\bold{F}$ y $\bold{G}$ son campos vectoriales tridimensionales tales que $\iint_s\bold{F}\cdot d\bold{S} = \iint_s\bold{G}\cdot s\bold{S}$ para cualquier superficie $S$, entonces es posible mostrar que $\bold{F} = \bold{G}$ reduciendo el área de $S$ a cero tomando un límite (el menor es el área de $S$, más cercano es el valor de $\iint_s\bold{F}\cdot d\bold{S}$ al valor de $\bold{F}$ en un punto dentro de $S$). Por lo tanto, podemos hacer que el área $D (t)$ se reduzca a cero tomando un límite y obteniendo la forma diferencial de la ley de Faraday:
En el contexto de los campos eléctricos, la curvatura del campo eléctrico se puede interpretar como el negativo de la tasa de cambio del campo magnético correspondiente con respecto al tiempo.
 |
Usando la Ley de Faraday |

Para terminar este apartado, presentamos una escena interactiva del Teorema de Stokes, diseñada por Andreas Steiger. En este escena se representa el campo vectorial y la circulación calculada con el rotacional de las funciones vectoriales:
$$\begin{aligned} \bold{v}(x,y,z) &= \lang z,x,y\rang\\ \bold{v}(x,y,z) &= \lang -x^3-x+z, -y^3-2y+x, -z^3-2z+y \rang\\ \bold{v}(x,y,z) &= \lang -y,x,0\rang \end{aligned}$$Se puede seleccionar la representación gráfica del campo vectorial (global) o el rotacional (integral).
Observa que Steiger usa una notación deiferente a la que hemos estado trabajando, pero es fácil de interpretar.

 Para los siguientes ejercicios, sin usar el teorema de Stokes, calcula directamente tanto el flujo del rotacional $\bold{F}\cdot\bold{N}$ sobre la superficie dada como la integral de circulación alrededor de su límite, asumiendo que todos los límites están orientados en el sentido de las agujas del reloj, visto desde arriba.
Para los siguientes ejercicios, sin usar el teorema de Stokes, calcula directamente tanto el flujo del rotacional $\bold{F}\cdot\bold{N}$ sobre la superficie dada como la integral de circulación alrededor de su límite, asumiendo que todos los límites están orientados en el sentido de las agujas del reloj, visto desde arriba.
326. $\bold{F} (x, y, z) = y^2\bold{i} + z^2j + x^2k$; $S$ es la porción de primer octante del plano $x + y + z = 1$. 327. $\bold{F} (x, y, z) = z\bold{i} + x\bold{j} + y\bold{k}$; $S$ es el hemisferio $z = (a^2 - x^2 - y^2)^{1/2}$ (Solución). 328. $\bold{F} (x, y, z) = y^2\bold{i} + 2x\bold{j} + 5\bold{k}$; $S$ es el hemisferio $z = (4 - x^2 - y^2)^{1/2}$. 329. $\bold{F} (x, y, z) = z\bold{i} + 2x\bold{j} + 3y\bold{k}$; $S$ es el hemisferio superior $z = \sqrt{9 - x^2 - y^2}$ (Solución). 330. $\bold{F} (x, y, z) = (x + 2z)\bold{i} + (y - x)\bold{j} + (z - y)\bold{k}$; $S$ es una región triangular con vértices $(3, 0, 0), (0, 3 / 2, 0)$ y $(0,0, 3)$. 331. $\bold{F} (x, y, z) = 2y\bold{i} - 6zj + 3x\bold{k}$; $S$ es una porción del paraboloide $z = 4 - x^2 - y^2$ y está por encima del plano $xy$ (Solución).
 Para los siguientes ejercicios, usa el teorema de Stokes para evaluar $\iint_S (rot\; \bold{F}\cdot\bold{N}) dS$ para los campos vectoriales y la superficie.
Para los siguientes ejercicios, usa el teorema de Stokes para evaluar $\iint_S (rot\; \bold{F}\cdot\bold{N}) dS$ para los campos vectoriales y la superficie.
333. $\bold{F} (x, y, z) = xy\bold{i} + x^2\bold{j} + z^2\bold{k}$; y $C$ es la intersección del paraboloide $z = x^2 + y^2$ y el plano $z = y$, y usando el vector normal hacia afuera (Solución). 334. $\bold{F} (x, y, z) = 4y\bold{i} + z\bold{j} + 2y\bold{k}$ y $C$ es la intersección de la esfera $x^2 + y^2 + z^2 = 4$ con el plano $z = 0$, y usando el vector normal hacia afuera.
335. Usa el teorema de Stokes para evaluar $\int_C \big[2xy^2zdx + 2x^2yzdy + \big(x^2y^2 −2z\big)dz\big]$, donde $C$ es la curva dada por $x = cos\; t, y = sen\; t, z = sen\; t, 0 \le t \le 2\pi$, atravesada en la dirección de incremento de $t$ (Solución).
336. [T] Usa un sistema algebraico de computadora (CAS) y el teorema de Stokes para aproximar la integral de línea $\int_C(ydx + zdy + xdz)$, donde $C$ es la intersección del plano $x + y = 2$ y la superficie $x^2 + y^2 + z^2 = 2 (x + y)$, atravesado en sentido antihorario visto desde el origen.
337. [T] Usa un CAS y el teorema de Stokes para aproximar la integral de línea $\int_C (3ydx + 2zdy −5xdz)$, donde $C$ es la intersección del plano $xy$ y el hemisferio $z = \sqrt{1 - x^2 - y^2,}$ recorrido en sentido antihorario visto desde arriba; es decir, desde el eje $z$ positivo hacia el plano $xy$ (Solución).
338. [T] Usa un CAS y el teorema de Stokes para aproximar la integral de línea $\int_C [(1 + y)zdx + (1 + z) xdy + (1 + x) ydz$, donde $C$ es un triángulo con vértices $(1, 0, 0), (0, 1, 0)$ y $(0, 0, 1)$ orientados en sentido antihorario.
339. Usa el teorema de Stokes para evaluar $\iint_S rot\;\bold{F}\cdot d\bold{S}$, donde $\bold{F} (x, y, z) = e^{xy}cos\; z\bold{i} + x^2z\bold{j} + xy\bold{k}$, y $S$ es la mitad de la esfera $x = \sqrt{1 - y2 - z^2}$, orientada hacia el eje positivo $x$ (Solución).
340. [T] Usa un CAS y el teorema de Stokes para evaluar $\iint_S (rot\; \bold{F}\cdot\bold{N}) dS$, donde $\bold{F} (x, y, z) = x^2y\bold{i} + xy^2\bold{j} + z^3\bold{k}$ y $C$ es la curva de la intersección del plano $3x + 2y + z = 6$ y cilindro $x^2 + y^2 = 4$, orientados en el sentido de las agujas del reloj cuando se ven desde arriba.
341. [T] Usa un CAS y el teorema de Stokes para evaluar $\iint_S rot\; \bold{F} \cdot d\bold{S}$, donde $\bold{F} (x, y, z) = \big(sen (y + z) - yx^2 − \frac{y^3}{3}\big)\bold{i} + x cos (y + z)\bold{j} + cos(2y)\bold{k}$ y $S$ constan de la parte superior y los cuatro lados, pero no la parte inferior del cubo con vértices $(\pm 1, \pm 1, \pm 1)$, orientados hacia afuera (Solución).
342. [T] Usa un CAS y el teorema de Stokes para evaluar $\iint_S rot\; \bold{F} \cdot d\bold{S}$, donde $\bold{F} (x, y, z) = z^2\bold{i} - 3xy\bold{j} + x^3y^3\bold{k}$ y $S$ es la parte superior de $z = 5− x^2 - y^2$ arriba del plano $z = 1$, y $S$ está orientado hacia arriba.
343. Usa el teorema de Stokes para evaluar $\iint_S (rot\; \bold{F} \cdot\bold{N}) dS$, donde $\bold{F} (x, y, z) = z^2\bold{i} + y^2\bold{j} + x\bold{k}$ y $S$ es un triángulo con vértices $(1, 0, 0), (0 , 1, 0)$ y $(0, 0, 1)$ con orientación en sentido antihorario (Solución).
344. Usa el teorema de Stokes para evaluar la integral de línea $\int_C (zdx + xdy + ydz)$, donde $C$ es un triángulo con vértices $(3, 0, 0), (0, 0, 2)$ y $(0, 6, 0)$ atravesados en el orden dado.
345. Usa el teorema de Stokes para evaluar $\int_C\big(\frac12 y^2dx + zdy + xdz\big)$, donde $C$ es la curva de intersección del plano $x + z = 1$ y el elipsoide $x^2 + 2y^2 + z^2 = 1$, orientado en sentido horario desde el origen (Solución).
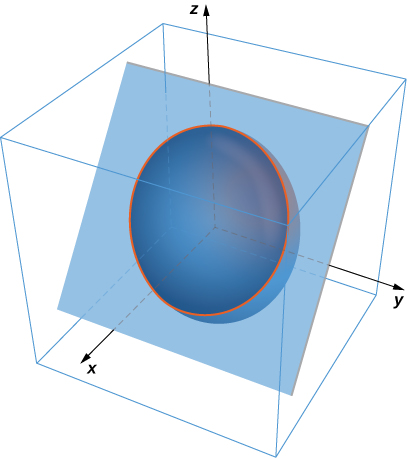
346. Usa el teorema de Stokes para evaluar $\iint_S (rot\; \bold{F} \cdot\bold{N}) dS$, donde $\bold{F} (x, y, z) = x\bold{i} + y^2\bold{j} + ze^{xy}\bold{k}$ y $S$ es la parte de la superficie $z = 1 - x^2− 2y^2$ con $z \ge 0$, orientado en sentido antihorario.
347. Usa el teorema de Stokes para el campo vectorial $\bold{F} (x, y, z) = z\bold{i} + 3x\bold{j} + 2z\bold{k}$ donde $S$ es la superficie $z = 1 - x^2 - 2y^2, z \ge 0$, $C$ es el círculo límite $x^2 + y^2 = 1$, y $S$ está orientado en la dirección $z$ positiva (Solución).
348. Usa el teorema de Stokes para el campo vectorial $\bold{F} (x, y, z) = - \frac32 y^2\bold{i} - 2xy\bold{j} + yz\bold{k}$, donde $S$ es la parte de la superficie del plano $x + y + z = 1$ contenida dentro del triángulo $C$ con vértices $(1 , 0, 0), (0, 1, 0)$ y $(0, 0, 1)$, recorridos en sentido antihorario como se ve desde arriba.
349. Se sabe que cierta trayectoria cerrada $C$ en el plano $2x + 2y + z = 1$ se proyecta sobre el círculo unitario $x^2 + y^2 = 1$ en el plano $xy$. Sea $c$ una constante y sea $\bold{R} (x, y, z) = x\bold{i} + y\bold{j} + z\bold{k}$. Usa el teorema de Stokes para evaluar $\int_C (c\bold{k}\times\bold{R}) \cdot dS$ (Solución).
350. Usa el teorema de Stokes y sea $C$ el límite de la superficie $z = x^2 + y^2$ con $0 \le x \le 2$ y $0 \le y \le 1$, orientado con la normal hacia arriba. Define $\bold{F} (x, y, z) = \big[sen (x^3) + xz\big]\bold{i} + (x −yz)\bold{j} + cos\big(z^4\big)\bold{k}$ y evalúa $\int_C\bold{F}\cdot d\bold{S}$.
351. Sea $S$ el hemisferio $x^2 + y^2 + z^2 = 4$ con $z \ge 0$, orientado hacia arriba. Sea $\bold{F} (x, y, z) = x^2e^{yz}\bold{i} + y^2e^{xz}\bold{j} + z^2e^{xy}\bold{k}$ un campo vectorial. Usa el teorema de Stokes para evaluar $\iint_S rot\; \bold{F} \cdot d\bold{S}$ (Solución).
352. Sea $\bold{F} (x, y, z) = xy\bold{i} + \big(ez^2 + y\bold)\bold{j} + (x + y)\bold{k}$ y sea $S$ la gráfica de la función $y = \frac{x^2}{9} + \frac{z^2}{9}− 1$ con $z \le 0$ orientada de modo que el vector normal $\bold{S}$ tenga un componente $y$ positivo. Usa el teorema de Stokes para calcular la integral $\iint_S rot \bold{F} \cdot d\bold{S}$.
353. Usa el teorema de Stokes para evaluar $\oint \bold{F}\cdot\bold{S}$, donde $\bold{F} (x, y, z) = y\bold{i} + z\bold{j} + x\bold{k}$ y $C$ es un triángulo con vértices $(0, 0, 0), (2, 0, 0)$ y $(0, -2, 2)$ orientado en sentido antihorario cuando se ve desde arriba (Solución).
354. Usa la integral de superficie en el teorema de Stokes para calcular la circulación del campo $\bold{F}$,$ \bold{F}(x, y, z) = x^2y^3\bold{i} + \bold{j} + z\bold{k}$ alrededor de $C$, que es la intersección del cilindro $x^2 + y^2 = 4$ y el hemisferio $x^2 + y^2 + z^2 = 16, z \ge 0$, orientado en sentido antihorario cuando se ve desde arriba.
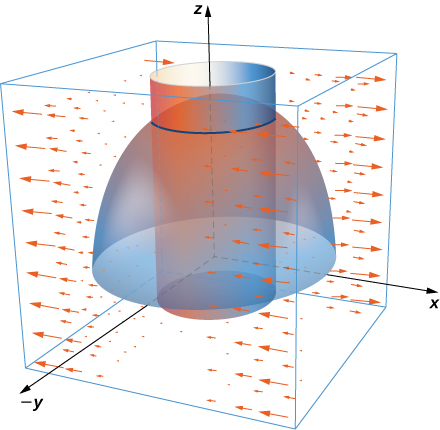
355. Usa el teorema de Stokes para calcular $\iint_S rot\; \bold{F}\cdot d\bold{S}$, donde $\bold{F} (x, y, z) = \bold{i} + xy^2\bold{j} + xy^2\bold{k}$ y $S$ es parte del plano $y + z = 2$ dentro del cilindro $x^2 + y^2 = 1$ y orientado en sentido anti-horario (Solución).
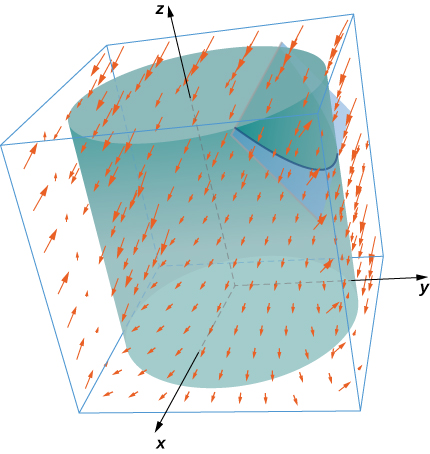
356. Usa el teorema de Stokes para evaluar $\iint_S rot\bold{F} \cdot d\bold{S}$, donde $\bold{F} (x, y, z) = −y^2\bold{i} + x\bold{j} + z^2\bold{k}$ y $S$ es la parte del plano $x + y + z = 1$ en el octante positivo y orientada en sentido antihorario $x \ge 0, y \ge 0, z \ge 0$.
357. Sea $\bold{F} (x, y, z) = xy\bold{i} + 2z\bold{j} - 2y\bold{k}$ y sea $C$ la intersección del plano $x + z = 5$ y el cilindro $x^2 + y^2 = 9$, que está orientado en sentido antihorario cuando se ve desde arriba. Calcula la integral de línea de $\bold{F}$ sobre $C$ usando el teorema de Stokes (Solución).
358. [T] Usa un CAS y sea $\bold{F} (x, y, z) = xy^2\bold{i} + (yz - x)\bold{j} + e^{yxz}\bold{k}$. Usa el teorema de Stokes para calcular la integral de superficie del rotacional de $\bold{F}$ sobre la superficie $S$ con orientación hacia adentro que consiste en el cubo $[0, 1] \times [0, 1] \times [0, 1]$ sin el lado derecho.
359. Sea $S$ el elipsoide $\frac{x^2}{4} + \frac{y^2}{9} + z^2 = 1$ orientado en sentido antihorario y sea $\bold{F}$ un campo vectorial con funciones componentes que tienen derivadas parciales continuas (Solución).
360. Sea $S$ la parte del paraboloide $z = 9 - x^2 - y^2$ con $z \ge 0$. Verifica el teorema de Stokes para el campo vectorial $\bold{F} (x, y, z) = 3z\bold{i} + 4x\bold{j} + 2y\bold{k}$.
361. [T] Usa un CAS y el teorema de Stokes para evaluar $\oint_C \bold{F} \cdot d\bold{S}$, si $\bold{F} (x, y, z) = (3z - sen\; x)\bold{i} + \big(x^2 + e^y\big)\bold{j} + \big(y^3 - cos\; z\big) \bold{k}$, donde $C$ es la curva dada por $x = cos\; t, y = sen\; t, z = 1; 0 \le t \le 2\pi$ (Solución).
362. [T] Usa un CAS y el teorema de Stokes para evaluar $\bold{F} (x, y, z) = 2y\bold{i} + e^z\bold{j} - arctan\; x\bold{k}$ con $S$ como una porción del paraboloide $z = 4 - x^2 - y^2$ cortado por el plano $xy$ orientado en sentido antihorario.
363. [T] Usa un CAS para evaluar $\iint_S rot\; (\bold{F}) \cdot d\bold{S}$, donde $\bold{F} (x, y, z) = 2z\bold{i} + 3x\bold{j} + 5y\bold{k}$ y $S$ es la superficie paramétrica $\bold{r} (r, \theta) = r cos\;\theta\bold{i} + rsen\;\theta\bold{j} + \big(4 - r^2\big)\bold{k}$; $(0 \le \theta \le 2\pi, 0 \le r \le 3)$ (Solución). 364. Sea $S$ el paraboloide $z = a\big(1 - x^2 - y^2\big)$, para $z \ge 0$, donde $a \gt 0$ es un número real. Sea $\bold{F} = \lang x - y, + z, z - x\rang$. ¿Para qué valor(es) de $a$ (si hay alguno) tiene $\iint_S (\nabla \times \bold{F})\cdot\bold{n}dS $su valor máximo?
 Para los siguientes ejercicios de aplicación, el objetivo es evaluar $A = \iint_S (\nabla\times \bold{F}) \cdot\bold{n}dS$, donde $\bold{F} = \lang xz, −xz, xy\rang$ y $S$ es la mitad superior del elipsoide $x^2 + y^2 + 8z^2 = 1$, donde $z\ge 0$.
Para los siguientes ejercicios de aplicación, el objetivo es evaluar $A = \iint_S (\nabla\times \bold{F}) \cdot\bold{n}dS$, donde $\bold{F} = \lang xz, −xz, xy\rang$ y $S$ es la mitad superior del elipsoide $x^2 + y^2 + 8z^2 = 1$, donde $z\ge 0$.
365. Evalúa una integral de superficie sobre una superficie más conveniente para encontrar el valor de $A$ (Solución). 366. Evalúa A usando una integral de línea.
367. Toma el paraboloide $z = x^2 + y^2$, para $0 \le z \le 4$, y córtalo con el plano $y = 0$. Sea $S$ la superficie que queda para $y \ge 0$, incluida la superficie plana en el plano $xz$. Sea $C$ el semicírculo y el segmento de recta que delimita el casquete de $S$ en el plano $z = 4$ con orientación en sentido antihorario. Sea $\bold{F} = \lang 2z + y, 2x + z, 2y + x\rang$. Evalúa $\iint_S (\nabla\times \bold{F})\cdot\bold{n}dS$ (Solución).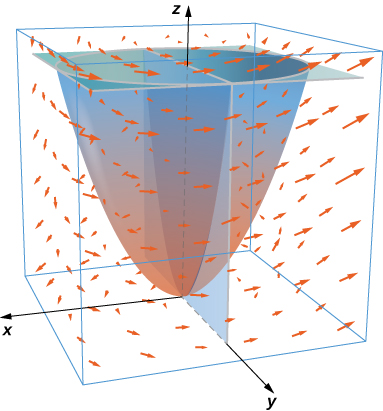
 Para los siguientes ejercicios, sea $S$ el disco encerrado por la curva $C: \bold{r}(t) = \lang cos\;\phi cos\; t, sen\;t, sen\;\phi cos\; t\rang$, para $0 \le t \le 2\pi$, donde $0 \le \phi \le \frac{\pi}{2}$ es un ángulo fijo.
Para los siguientes ejercicios, sea $S$ el disco encerrado por la curva $C: \bold{r}(t) = \lang cos\;\phi cos\; t, sen\;t, sen\;\phi cos\; t\rang$, para $0 \le t \le 2\pi$, donde $0 \le \phi \le \frac{\pi}{2}$ es un ángulo fijo.
368. ¿Cuál es la longitud de $C$ en términos de $\phi$? 369. ¿Cuál es la circulación de $C$ del campo vectorial $\bold{F} = \lang−y, −z, x\rang$ en función de $\phi$ (Solución). 370. ¿Para qué valor de $\phi$ es la circulación un máximo? 371. El círculo $C$ en el plano $x + y + z = 8$ tiene radio $4$ y centro $(2, 3, 3)$. Evalúa $\oint_C \bold{F}\cdot d\bold{r}$ para $\bold{F} = \lang 0, −z, 2y\rang$, donde $C$ tiene un sentido antihorario cuando se ve desde arriba (Solución). 372. El campo de velocidad $\bold{v} = \lang 0, 1 - x^2, 0\rang$, para $| x | \le 1$ y $| z | \le 1$, representa un flujo horizontal en la dirección $y$. Calcula el rotacional de $\bold{v}$ en una rotación en el sentido de las agujas del reloj. 373. Evalúa la integral $\iint_S (\nabla\times\bold{F})\cdot \bold{n}dS$, donde $\bold{F} = −xz\bold{i} + yz\bold{j} + xye^z\bold{k}$ y $S$ es el límite del paraboloide $z = 5 - x^2 - y^2$ sobre el plano $z = 3$, y $n$ puntos en la dirección $z$ positiva en $S$ (Solución).
 Para los siguientes ejercicios, usa el teorema de Stokes para encontrar la circulación de los siguientes campos vectoriales alrededor de cualquier curva cerrada simple $C$.
Para los siguientes ejercicios, usa el teorema de Stokes para encontrar la circulación de los siguientes campos vectoriales alrededor de cualquier curva cerrada simple $C$.
374. $\bold{F} = \nabla\big(x sen\; ye^z\big)$ 375. $\bold{F} = \big\lang y^2z^3, z^2xyz^3, 3xy^2z^2\big\rang$ (Solución).
Hemos examinado varias versiones del Teorema Fundamental del Cálculo en dimensiones superiores que relacionan la integral alrededor de un límite orientado de un dominio con una "derivada" de esa entidad en el dominio orientado. En este apartado plantearemos el teorema de la divergencia, que es el teorema final de este tipo que estudiaremos. El teorema de la divergencia tiene muchos usos en física; en particular, el teorema de la divergencia se utiliza en el campo de las ecuaciones diferenciales parciales para derivar ecuaciones que modelan el flujo de calor y la conservación de la masa. Usaremos el teorema para calcular integrales de flujo y aplicarlo a campos electrostáticos.
Antes de examinar el teorema de la divergencia, es útil comenzar con una descripción general de las versiones del Teorema Fundamental del Cálculo que hemos discutido:
El teorema de la divergencia sigue el patrón general de estos otros teoremas.
Si pensamos en la divergencia como una especie de derivada, entonces el Teorema de la Divergencia relaciona una integral triple de la derivada $div\;\bold{F}$ sobre un sólido con una integral de flujo de $\bold{F}$ sobre el límite del sólido. Más específicamente, el teorema de la divergencia relaciona una integral de flujo del campo vectorial $\bold{F}$ sobre una superficie cerrada $S$ con una integral triple de la divergencia de $\bold{F}$ sobre el sólido encerrado por $S$.
Recuerda que la forma de flujo del teorema de Green establece que $\iint_D div\;\bold{F}dA = \int_C \bold{F}\cdot\bold{N}ds$. Por tanto, el teorema de la divergencia es una versión del teorema de Green en una dimensión superior.
La prueba del teorema de la divergencia está más allá del alcance de este texto. Sin embargo, observamos una demostración informal que da una idea general de por qué el teorema es verdadero, pero no prueba el teorema con todo rigor. Esta explicación sigue la explicación informal dada de por qué el teorema de Stokes es verdadero.
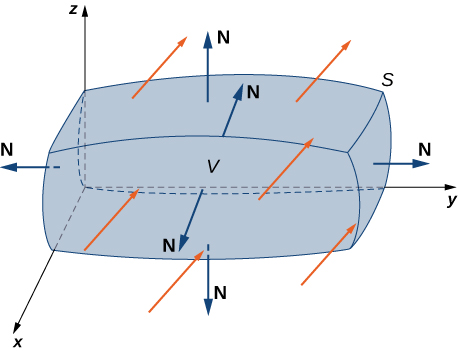
Figura 6.87. El teorema de la divergencia relaciona una integral de flujo a través de una superficie cerrada $S$ con una integral triple sobre un sólido $E$ encerrado por la superficie.
Sea $B$ una caja pequeña con lados paralelos a los planos de coordenadas dentro de $E$ (Figura 6.88). Deja que el centro de $B$ tenga coordenadas $(x, y, z)$ y supón que las longitudes de los bordes son $\Delta x, \Delta y$ y $\Delta z$ (figura 6.88 (b)). El vector normal que sale de la parte superior de la caja es $\bold{k}$ y el vector normal que sale de la parte inferior de la caja es $−\bold{k}$. El producto escalar de $\bold{F} = \lang P, Q, R\rang$ con $\bold{k}$ es $R$ y el producto escalar con $−\bold{k}$ es $−R$. El área de la parte superior de la caja (y la parte inferior de la caja) $\Delta S$ es $\Delta x\Delta y$.
Figura 6.88. (a) Una pequeña caja $B$ dentro de la superficie $E$ tiene lados paralelos a los planos de coordenadas. (b) La caja $B$ tiene longitudes laterales $\Delta x, \Delta y$ y $\Delta z$. (c) Si miramos la vista lateral de $B$, vemos que, dado que $(x, y, z)$ es el centro de la caja, para llegar a la parte superior de la caja debemos recorrer una distancia vertical de $\Delta z / 2$ desde $(x, y, z)$. De manera similar, para llegar al final de la caja debemos recorrer una distancia $\Delta z / 2 $ hacia abajo desde $(x, y, z)$.
El flujo que sale de la parte superior de la caja se puede aproximar mediante $R\big(x, y, z + \frac{\Delta z}{2}\big)\Delta x\Delta y$ (Figura 6.88(c)) y el flujo que sale de la parte inferior de la caja es $−R\big(x, y, z - \frac{\Delta z}{2}\big)\Delta x\Delta y$. Si denotamos la diferencia entre estos valores como $\Delta R$, entonces el flujo neto en la dirección vertical puede aproximarse por $\Delta R\Delta x\Delta y$. Sin embargo
$$\Delta R\Delta x\Delta y\bigg(\frac{\Delta R}{\Delta z}\bigg)\Delta x\Delta y\Delta z \approx \bigg(\frac{\partial R}{\partial z}\Delta V\bigg)$$Por lo tanto, el flujo neto en la dirección vertical se puede aproximar mediante $\big(\frac{\partial R}{\partial z}\Delta V\big)$. De forma similar, el flujo neto en la dirección $x$ se puede aproximar mediante $\big(\frac{\partial P}{\partial x}\Delta V\big)$ y el flujo neto en la dirección $y$ se puede aproximar mediante $\big(\frac{\partial Q}{\partial y}\Delta V\big)$.
Sumar los flujos en las tres direcciones da una aproximación del flujo total fuera de la caja:
$$\text{flujo total } = \bigg(\frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}\bigg)\Delta V = div\;\bold{F}\Delta V$$Esta aproximación se vuelve arbitrariamente cercana al valor del flujo total cuando el volumen de la caja se reduce a cero.
La suma de $div\;\bold{F}\Delta V$ sobre todas las cajas pequeñas que se aproximan a $E$ es aproximadamente $\iiint_E div\;\bold{F}dV$. Por otro lado, la suma de $div\;\bold{F}\Delta V$ sobre todas las cajas pequeñas que se aproximan a $E$ es la suma de los flujos sobre todas estas cajas. Al igual que en la demostración informal del teorema de Stokes, la adición de estos flujos sobre todas las casillas da como resultado la cancelación de muchos términos.
Si una caja aproximada comparte una cara con otra caja aproximada, entonces el flujo sobre una cara es el negativo del flujo sobre la cara compartida de la caja adyacente. Estas dos integrales se cancelan. Al sumar todos los flujos, las únicas integrales de flujo que sobreviven son las integrales sobre las caras que se aproximan al límite de $E$. A medida que los volúmenes de las cajas de aproximación se reducen a cero, esta aproximación se vuelve arbitrariamente cercana al flujo sobre $S$.
Antes de realizar nuestro primer ejercicio, practica con una escena interactiva, diseñada por el Grupo de Innovación Educativa MAMI de la Universidad Politécnica de Madrid, en la cual se observa el flujo a través de una superficie semiesférica. En la escena se presenta un campo constante (las flechas azules) y una semiesfera orientada en color gris, y se mide el flujo de ese campo sobre la semiesfera.
La posición de la semiesfera se puede mover arrastrando con el ratón el punto verde. Al cambiar la posición de la semiesfera el flujo cambia. Al aumentar el radio de la semiesfera el flujo aumenta (en valor absoluto). ¿Se puede colocar de alguna manera la semiesfera para que el flujo a través de ella sea nulo? Al marcar la casilla "Tapa" la semiesfera se cierra con un círculo en la parte inferior.
 |
Verificación del Teorema de la Divergencia |

Recuerda que la divergencia del campo continuo $\bold{F}$ en el punto $P$ es una medida de la "salida" del campo en $P$. Si $\bold{F}$ representa el campo de velocidad de un fluido, entonces la divergencia se puede considerar como la tasa por unidad de volumen del fluido que sale menos la tasa por unidad de volumen que entra.
El teorema de divergencia confirma esta interpretación. Para ver esto, sea $P$ un punto y sea $B_r$ una bola de radio pequeño $r$ centrada en $P$ (Figura 6.89). Sea $S_r$ la esfera límite de $B_r$. Dado que el radio es pequeño y $\bold{F}$ es continuo, $div\; \bold{F} (Q) \approx div\;\bold{F} (P)$ para todos los demás puntos $Q$ en la bola. Por lo tanto, el flujo a través de $S_r$ se puede aproximar usando el teorema de divergencia:
$$\iint_{S_r} \bold{F}\cdot d\bold{S} = \iiint_{B_r} div \; \bold{F}dV \approx \iiint_{B_r} div \; \bold{F}(P)dV$$Dado que $div \; \bold{F}(P)$ es una constante
$$\iiint_{B_r} div \; \bold{F}(P)dV = div\;\bold{F}(P)V(B_r)$$Por lo tanto, el flujo $\iint_{S_r} \bold{F}\cdot d\bold{S}$ se puede aproximar mediante $div\;\bold{F}(P) V (B_r)$. Esta aproximación mejora a medida que el radio se reduce a cero y, por lo tanto,
$$div\;\bold{F}(P) = \lim\limits_{r \to 0} \frac{1}{V(B_r)} \iint_{S_r} \bold{F}\cdot d\bold{S}$$Esta ecuación dice que la divergencia en $P$ es la tasa neta de flujo hacia afuera del fluido por unidad de volumen.
El teorema de la divergencia se genera entre la integral de flujo de la superficie cerrada $S$ y una integral triple sobre el sólido encerrado por $S$. Por lo tanto, el teorema nos permite calcular integrales de flujo o integrales triples que normalmente serían difíciles de calcular al transformar la integral de flujo a una integral triple y viceversa.
Figura 6.89. Bola $B_r$ de radio pequeño $r$ centrada en $P$.
 |
Aplicando el Teorema de la Divergencia |

 |
Aplicando el Teorema de la Divergencia |
Figura 6.90. Campo vectorial $\bold{v} = \big\lang -\frac{y}{2}, \frac{x}{2}, 0\big\rang$

El ejercicio anterior ilustra una consecuencia notable del teorema de la divergencia. Sea $S$ una superficie cerrada lisa por partes y sea $\bold{F}$ un campo vectorial definido en una región abierta que contiene la superficie encerrada por $S$. Si $\bold{F}$ tiene la forma $\bold{F} = \lang f (y, z), g (x, z), h (x, y)\rang$, entonces la divergencia de $\bold{F}$ es cero. Según el teorema de la divergencia, el flujo de $\bold{F}$ a través de $S$ también es cero. Esto hace que ciertas integrales de flujo sean increíblemente fáciles de calcular. Por ejemplo, supón que queremos calcular la integral de flujo $\iint_S\bold{F}\cdot d\bold{S}$ donde $S $es un cubo y
$$\bold{F} = \big\lang sen(y)e^{yz}, x^2z^2, cos(xy)e^{sen\;x}\big\rang$$Calcular la integral de flujo directamente sería difícil, si no imposible, usando técnicas que estudiamos previamente. Como mínimo, tendríamos que dividir la integral de flujo en seis integrales, una para cada cara del cubo. Pero, debido a que la divergencia de este campo es cero, el teorema de divergencia muestra inmediatamente que la integral de flujo es cero.
Ahora podemos usar el teorema de la divergencia para justificar la interpretación física de la divergencia que discutimos anteriormente. Recuerda que si $\bold{F}$ es un campo vectorial tridimensional continuo y $P$ es un punto en el dominio de $\bold{F}$, entonces la divergencia de $\bold{F}$ en $P$ es una medida de la "salida" de $\bold{F}$ en $P$. Si $\bold{F}$ representa el campo de velocidad de un fluido, entonces la divergencia de $\bold{F}$ en $P$ es una medida de la tasa de flujo neto fuera del punto $P$ (el flujo de fluido fuera de $P$ menos el flujo de fluido hacia $P$). Para ver cómo el teorema de la divergencia justifica esta interpretación, sea $B_r$ una bola de radio $r$ muy pequeño con centro $P$, y supón que $B_r$ está en el dominio de $\bold{F}$. Además, supón que $B_r$ tiene una orientación positiva hacia afuera. Dado que el radio de $B_r$ es pequeño y $\bold{F}$ es continuo, la divergencia de $\bold{F}$ es aproximadamente constante en $B_r$. Es decir, si $P^{\prime}$ es cualquier punto en $B_r$, entonces $div\; \bold{F} (P) \approx div\;\bold{F} (P^{\prime})$. Sea $S_r$ la esfera límite de $B_r$. Podemos aproximar el flujo a través de $S_r$ usando el teorema de divergencia de la siguiente manera:
$$\begin{aligned} \iint_{S_r} \bold{F}\cdot d\bold{S} &= \iiint_{B_r} div\;\bold{F} dV\\ &= \iiint_{B_r} div\;\bold{F}(P) dV\\ &= div\; \bold{F}(P)V(B_r) \end{aligned}$$A medida que reducimos el radio $r$ a cero mediante un límite, la cantidad $div\; \bold{F}(P)V(B_r)$ se acerca arbitrariamente al flujo. Por lo tanto,
$$div\; \bold{F}(P) = \lim\limits_{r \to 0} \frac{1}{V(B_r)}\iint_{S_r} \bold{F}\cdot d\bold{S}$$y podemos considerar la divergencia en $P$ como una medida de la tasa neta de flujo hacia afuera por unidad de volumen en $P$. Dado que "salida" es un término informal para la tasa neta de flujo hacia afuera por unidad de volumen, hemos justificado la interpretación física de la divergencia que discutimos anteriormente, y hemos utilizado el teorema de la divergencia para dar esta justificación.
El teorema de la divergencia tiene muchas aplicaciones en física e ingeniería. Nos permite escribir muchas leyes físicas tanto en una forma integral y una forma diferencial (de la misma manera que el teorema de Stokes nos permitió una forma integral y diferencial de la ley de Faraday). Las áreas de estudio como la dinámica de fluidos, el electromagnetismo y la mecánica cuántica tienen ecuaciones que describen la conservación de la masa, el momento o la energía, y el teorema de la divergencia nos permite dar estas ecuaciones tanto en forma integral como diferencial.
Una de las aplicaciones más comunes del teorema de la divergencia es en los campos electrostáticos. Un resultado importante en este tema es la ley de Gauss. Esta ley establece que si $S$ es una superficie cerrada en el campo electrostático $E$, entonces el flujo de $E$ a través de $S$ es la carga total encerrada por $S$ (dividida por una constante eléctrica).
Ahora usamos el teorema de la divergencia para justificar el caso especial de esta ley en el que el campo electrostático es generado por una carga puntual estacionaria en el origen.
Si $(x, y, z)$ es un punto en el espacio, entonces la distancia desde el punto hasta el origen es $r = \sqrt{x^2 + y^2 + z^2}$. Sea $\bold{F}_r$ el campo vectorial radial $\bold{F}_r = \frac{1}{r^2} \big\lang \frac{x}{r}, \frac{y}{r}, \frac{z}{r}\big\rang$. El vector en una posición dada en el espacio apunta en la dirección del vector radial unitario $\big\lang \frac{x}{r}, \frac{y}{r}, \frac{z}{r}\big\rang$ y se escala por la cantidad $1 / r^2$. Por lo tanto, la magnitud de un vector en un punto dado es inversamente proporcional al cuadrado de la distancia del vector al origen. Supóna que tenemos una carga estacionaria de $q$ culombios en el origen, que existe en el vacío. La carga genera un campo electrostático $E$ dado por
$$\bold{E} = \frac{q}{4\pi\epsilon_0}\bold{F}_r $$donde la aproximación $\epsilon_0 = 8.854 \times 10^{−12}\; farad (F) / m$ es una constante eléctrica (la constante $\epsilon_0$ es una medida de la resistencia que se encuentra al formar un campo eléctrico en el vacío). Observa que $E$ es un campo vectorial radial similar al campo gravitacional. La diferencia es que este campo apunta hacia afuera mientras que el campo gravitacional apunta hacia adentro. Porque
$$\bold{E} = \frac{q}{4\pi\epsilon_0} \bold{F}_r = \frac{q}{4\pi\epsilon_0}\bigg(\frac{1}{r^2}\big\lang \frac{x}{r}, \frac{y}{r}, \frac{z}{r}\big\rang\bigg)$$decimos que los campos electrostáticos obedecen a una ley del cuadrado inverso. Es decir, la fuerza electrostática en un punto dado es inversamente proporcional al cuadrado de la distancia desde la fuente de la carga (que en este caso está en el origen).
Dado este campo vectorial, mostramos que el flujo a través de la superficie cerrada $S$ es cero si la carga está fuera de $S$, y que el flujo es $q /\epsilon_0$ si la carga está dentro de $S$. En otras palabras, el flujo a través de $S$ es la carga dentro de la superficie dividida por la constante $\epsilon_0$. Este es un caso especial de la ley de Gauss, y aquí usamos el teorema de la divergencia para justificar este caso especial.
Para mostrar que el flujo a través de $S$ es la carga dentro de la superficie dividida por la constante $\epsilon_0$, necesitamos dos pasos intermedios. Primero mostramos que la divergencia de $\bold{F}_r$ es cero y luego mostramos que el flujo de $\bold{F}_r$ a través de cualquier superficie lisa $S$ es cero o $4\pi$. Entonces podemos justificar este caso especial de la ley de Gauss.
 |
La divergencia de $\bold{F}_r$ es cero |

Observa que dado que la divergencia de $\bold{F}_r$ es cero y $\bold{E}$ es $\bold{F}_r$ escalado por una constante, la divergencia del campo electrostático $\bold{E}$ también es cero (excepto en el origen).
En otras palabras, este teorema dice que el flujo de $\bold{F}_r$ a través de cualquier superficie $S$ cerrada lisa a trozos depende solo de si el origen está dentro de $S$.
Primero, supón que $S$ no incluye el origen. En este caso, el sólido encerrado por $S$ está en el dominio de $\bold{F}_r$, y dado que la divergencia de $\bold{F}_r$ es cero, podemos aplicar inmediatamente el teorema de la divergencia y encontrar que $\iint_S \bold{F}\cdot d\bold{S}$ es cero.
Ahora supón que $S$ abarca el origen. No podemos simplemente usar el teorema de la divergencia para calcular el flujo, porque el campo no está definido en el origen. Sea $S_a$ una esfera de radio $a$ dentro de $S $centrada en el origen. El campo vectorial normal hacia afuera en la esfera, en coordenadas esféricas, es
$$\bold{t}_{\phi} \times \bold{t}_{\theta} = \lang a^2cos\; \theta sen^2\phi, a^2sen\; \theta sen^2\phi, a^2sen\; \phi cos\; \phi \rang$$Por lo tanto, en la superficie de la esfera, el producto escalar $\bold{F}_r \cdot \bold{N}$ (en coordenadas esféricas) es
$$\begin{aligned} \bold{F}_r\cdot\bold{N} &= \bigg\lang \frac{sen\;\phi cos\;\theta}{a^2}, \frac{sen\;\phi sen\;\theta}{a^2}, \frac{cos\;\phi}{a^2}\bigg\rang \cdot \big\lang a^2cos\;\theta sen^2\phi, a^2sen\; \theta sen^2\phi,\\ &\;\;\;\;\;a^2sen\; \phi cos\; \phi\big\rang\\ &= sen\;\phi(\lang sen\; \phi cos\; \theta, sen \;\phi sen\; \theta, cos\; \phi \rang\cdot\lang sen\; \phi cos\; \theta, sen\; \phi sen\; \theta, cos\; \phi \rang\\ &= sen\;\phi \end{aligned}$$El flujo de $\bold{F}_r$ a través de $S_a$ es
$$\iint_{S_a} \bold{F}_r\cdot\bold{N}dS = \int_0^{2\pi}\int_0^{\pi} sen\;\phi d\phi d\theta = 4\pi$$Ahora, recuerda que nos interesa el flujo a través de $S$, no necesariamente el flujo a través de $S_a$. Para calcular el flujo a través de $S$, sea $E$ el sólido entre las superficies $S_a$ y $S$. Entonces, el límite de $E$ consiste en $S_a$ y $S$. Denota este límite con $S - S_a$ para indicar que $S$ está orientado hacia afuera pero ahora $S_a$ está orientado hacia adentro. Nos gustaría aplicar el teorema de la divergencia al sólido $E$. Observa que el teorema de la divergencia, como se indicó, no puede manejar un sólido como $E$ porque $E$ tiene un agujero.
Sin embargo, el teorema de la divergencia se puede extender para manejar sólidos con agujeros, al igual que el teorema de Green se puede extender para manejar regiones con agujeros. Esto nos permite usar el teorema de la divergencia de la siguiente manera.
$$\begin{aligned} \iint_{S-S_a} \bold{F}_r\cdot d\bold{S} &= \iint_{S} \bold{F}_r\cdot d\bold{S} - \iint_{S_a} \bold{F}_r\cdot d\bold{S}\\ &= \iiint_E div\; \bold{F}_rdV\\ \end{aligned}$$Por lo tanto
$$\iint_{S} \bold{F}_r\cdot d\bold{S} = \iint_{S_a} \bold{F}_r\cdot d\bold{S} = 4\pi$$y tenemos el resultado deseado. Ahora volvemos a calcular el flujo a través de una superficie lisa en el contexto del campo electrostático $\bold{E} = \frac{q}{4\pi\epsilon_0}\bold{F}_r$ de una carga puntual en el origen. Sea $S$ una superficie cerrada lisa a trozos que abarca el origen. Luego
$$\begin{aligned} \iint_S \bold{E}\cdot d\bold{S} &= \iint_S \frac{q}{4\pi\epsilon_0}\bold{F}_r\cdot d\bold{S}\\ &= \frac{q}{4\pi\epsilon_0} \iint_S \bold{F}_r\cdot d\bold{S}\\ &= \frac{q}{\epsilon_0} \end{aligned}$$Si $S$ no incluye el origen, entonces
$$\iint_S \bold{E}\cdot d\bold{S} = \frac{q}{4\pi\epsilon_0}\iint_S \bold{F}_r\cdot d\bold{S} = 0$$Por lo tanto, hemos justificado la afirmación que nos propusimos justificar: el flujo a través de la superficie cerrada $S $es cero si la carga está fuera de $S$, y el flujo es $q/\epsilon_0$ si la carga está dentro de $S$.
Este análisis solo funciona si hay una carga puntual única en el origen. En este caso, la ley de Gauss dice que el flujo de $\bold{E}$ a través de $S$ es la carga total encerrada por $S$.
La ley de Gauss puede extenderse para manejar múltiples sólidos cargados en el espacio, no solo una carga puntual en el origen. La lógica es similar al análisis anterior, pero más allá del alcance de este texto. En total generalidad, la ley de Gauss establece que si $S$ es una superficie cerrada lisa por partes y $Q $es la cantidad total de carga dentro de $S$, entonces el flujo de $E$ a través de $S$ es $Q / \epsilon_0$.
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, ajusta la magnitud de la carga y el radio de la superficie gaussiana a su alrededor. Observa cómo esto afecta el flujo total y la magnitud del campo eléctrico en la superficie gaussiana.
Las flechas representan la magnitud y dirección del campo eléctrico generado por la partícula. Puedes cambiar el radio de la superficie gaussiana y la carga. Puedes, también, rotar el cubo con clic sostenido.
 |
Usando la ley de Gauss |

Una última escena interactiva de PhET Simulaciones, mueve las cargas positivas y negativas alrededor del campo eléctrico.

 Para los siguientes ejercicios, usa un sistema algebraico computarizado (CAS) y el teorema de divergencia para evaluar la integral de superficie $\int_S\bold{F}\cdot \bold{n} ds$ para la elección dada de $\bold{F}$ y la superficie límite $S$. Para cada superficie cerrada, supón que $\bold{N}$ es el vector normal unitario externo.
Para los siguientes ejercicios, usa un sistema algebraico computarizado (CAS) y el teorema de divergencia para evaluar la integral de superficie $\int_S\bold{F}\cdot \bold{n} ds$ para la elección dada de $\bold{F}$ y la superficie límite $S$. Para cada superficie cerrada, supón que $\bold{N}$ es el vector normal unitario externo.
376. [T] $\bold{F} (x, y, z) = x\bold{i} + y\bold{j} + z\bold{k}$; $S$ es la superficie del cubo $0 \le x \le 1, 0 \le y \le 1, 0 \lt z \le 1$. 377. [T] $\bold{F} (x, y, z) = (cos\; yz)\bold{i} + e^{xz}\bold{j} + 3z^2\bold{k}$; $S$ es la superficie del hemisferio $z = \sqrt{4 - x^2 - y^2}$ junto con el disco $x^2 + y^2 ≤ 4$ en el plano $xy$ (Solución). 378. [T] $\bold{F} (x, y, z) = \big(x^2 + y^2 - z^2\big)\bold{i} + x^2y\bold{j} + 3z\bold{k}$; $S $es la superficie de las cinco caras del cubo unitario $0 \le x \le 1, 0 \le y \le 1, 0 \lt z ≤ 1$. 379. [T] $\bold{F} (x, y, z) = x\bold{i} + y\bold{j} + zk$; $S$ es la superficie del paraboloide $z = x^2 + y^2$ para $0 \le z \le 9$ (Solución). 380. [T] $\bold{F} (x, y, z) = x^2\bold{i} + y^2\bold{j} + z^2k$; $S$ es la superficie de la esfera $x^2 + y^2 + z^2 = 4$. 381. [T] $\bold{F} (x, y, z) = x\bold{i} + y\bold{j} + \big(z^2 - 1\big)\bold{k}$; Entonces $S$ es la superficie del sólido delimitado por el cilindro $x^2 + y^2 = 4$ y los planos $z = 0$ y $z = 1$ (Solución). 382. [T] $\bold{F} (x, y, z) = xy^2\bold{i} + yz^2\bold{j} + x^2z\bold{k}$; $S $es la superficie delimitada arriba por la esfera $\rho = 2$ y abajo por el cono $\phi = \frac{\pi}{4}$ en coordenadas esféricas (piensa en $S $como la superficie de un "cono de helado").
383. [T] $\bold{F} (x, y, z) = x^3\bold{i} + y^3\bold{j} + 3a^2z\bold{k}$ (constante $a \gt 0$); $S$ es la superficie delimitada por el cilindro $x^2 + y^2 = a^2$ y los planos $z = 0$ y $z = 1$ (Solución).
384. [T] La integral de superficie $\iint_S\bold{F}\cdot d\bold{S}$, donde $S$ es el sólido delimitado por el paraboloide $z = x^2 + y^2$ y el plano $z = 4$, y $\bold{F} (x, y, z) = \big(x + y^2z^2\big)\bold{i} + \big(y + z^2x^2\big)\bold{j} + \big(z + x^2y^2\big)\bold{k}$
385. Usa el teorema de la divergencia para calcular la integral de superficie $\iint_S\bold{F}\cdot d\bold{S}$, donde $\bold{F} (x, y, z) = \big(e^{y^2}\big)\bold{i} + \big(y + sen\big(z^2\big)\big)\bold{j} + (z - 1)\bold{k}$ y $S$ es el hemisferio superior $x^2 + y^2 + z^2 = 1, z \ge 0$, orientado hacia arriba (Solución).
386. Usa el teorema de la divergencia para calcular la integral de superficie $\iint_S\bold{F}\cdot d\bold{S}$, donde $\bold{F} (x, y, z) = x^4\bold{i} - x^3z^2\bold{j} + 4xy^2z\bold{k}$ y $S$ es la superficie limitada por el cilindro $x^2 + y^2 = 1$ y los planos $z = x + 2$ y $z = 0$.
387. Usa el teorema de la divergencia para calcular la integral de superficie $\iint_S\bold{F}\cdot d\bold{S}$ cuando $\bold{F}(x, y, z) = x^2z^3\bold{i} + 2xyz^3\bold{j} + xz^4\bold{k}$ y $S$ es la superficie de la caja con vértices $(\pm 1, \pm 2, \pm 3)$ (Solución).
388. Usa el teorema de la divergencia para calcular la integral de superficie $\iint_S\bold{F}\cdot d\bold{S}$ cuando $\bold{F} (x, y, z) = ztan^{−1}y^2\bold{i} + z^3 ln\big(x^2 + 1\big)\bold{j} + z\bold{k}$ y $S$ es parte del paraboloide $x^2 + y^2 + z = 2$ que se encuentra sobre el plano $z = 1$ y está orientado hacia arriba.
389. [T] Usa un CAS y el teorema de divergencia para calcular el flujo $\iint_S\bold{F}\cdot d\bold{S}$, donde $\bold{F} (x,y, z) = \big(x^3 + y^3\big)\bold{i} + \big(y^3 + z^3\big)\bold{j} + \big(z^3 + x^3\big)\bold{k}$ y $S$ es una esfera con centro $(0, 0)$ y radio $2$ (Solución).
390. Usa el teorema de la divergencia para calcular el valor de la integral de flujo $\iint_S\bold{F}\cdot d\bold{S}$, donde $\bold{F} (x, y, z) = \big(y^3 + 3x\big)\bold{i} + (xz + y)\bold{j} + \big[z + x^4cos\big(x^2y\big)\big]\bold{k}$ y $S$ es el área de la región limitada por $x^2 + y^2 = 1, x \ge 0, y \ge 0$ y $0 \le z \le 1$.
391. Usa el teorema de la divergencia para calcular la integral de flujo $\iint_S\bold{F}\cdot d\bold{S}$, donde $\bold{F} (x, y, z) = y\bold{j} - z\bold{k}$ y $S$ consiste en la unión del paraboloide $y = x^2 + z^2, 0 \le y \le 1$, y el disco $x^2 + z^2 \le 1, y = 1$, orientado hacia afuera. ¿Cuál es el flujo a través del paraboloide? (Solución).
392. Usa el teorema de divergencia para calcular la integral de flujo $\iint_S\bold{F}\cdot d\bold{S}$, donde $\bold{F} (x, y, z) = x\bold{i} + y\bold{j} + z^4\bold{k}$ y $S$ es una parte del cono $z = \sqrt{x^2 + y^2}$ debajo del plano superior $z = 1$, orientado hacia abajo.
393. Usa el teorema de la divergencia para calcular la integral de superficie $\iint_S\bold{F}\cdot d\bold{S}$ para $\bold{F} (x, y, z) = x^4\bold{i} - x^3z^2\bold{j} + 4xy^2z\bold{k}$, donde $S $es la superficie limitada por el cilindro $x^2 + y^2 = 1$ y los planos $z = x + 2$ y $z = 0$ (Solución).
394. Considera $\bold{F} (x, y, z) = x^2\bold{i} + xy\bold{j} + (z + 1)\bold{k}$. Sea $E$ el sólido encerrado por el paraboloide $z = 4 - x^2 - y^2$ y el plano $z = 0$ con vectores normales apuntando hacia afuera de $E$. Calcula el flujo de $\bold{F}$ a través de la frontera de $E$ usando el teorema de divergencia.
 Para los siguientes ejercicios, usa un CAS junto con el teorema de la divergencia para calcular el flujo neto hacia afuera para los campos a través de las superficies dadas $S$.
Para los siguientes ejercicios, usa un CAS junto con el teorema de la divergencia para calcular el flujo neto hacia afuera para los campos a través de las superficies dadas $S$.
395. [T] $\bold{F} = \lang x, −2y, 3z\rang$; $S$ es esfera $\lbrace (x, y, z): x^2 + y^2 + z^2 = 6\rbrace$ (Solución).
396. [T] $\bold{F} = \lang x, 2y, z\rang$; $S$ es el límite del tetraedro en el primer octante formado por el plano $x + y + z = 1$.
397. [T] $\bold{F} = \lang y - 2x, x^3 - y, y^2 - z\rang$; $S$ es la esfera $\lbrace (x, y, z): x^2 + y^2 + z^2 = 4\rbrace$ (Solución).
398. [T] $\bold{F} = \lang x, y, z\rang$; $S$ es la superficie del paraboloide $z = 4 - x^2 - y^2$, para $z \ge 0$, más su base en el plano $xy$.
 Para los siguientes ejercicios, usa un CAS y el teorema de la divergencia para calcular el flujo externo neto para los campos vectoriales a través del límite de las regiones dadas $D$.
Para los siguientes ejercicios, usa un CAS y el teorema de la divergencia para calcular el flujo externo neto para los campos vectoriales a través del límite de las regiones dadas $D$.
399. [T] $\bold{F} = \lang z - x, x - y, 2y - z\rang$; $D$ es la región entre las esferas de radio $2$ y $4$ centradas en el origen (Solución).
400. [T] $\bold{F} = \frac{\bold{r}}{|\bold{r}|} = \frac{\lang x, y, z\rang}{\sqrt{x^2 + y^2 + z^2}}$; $D$ es la región entre las esferas de radio $1$ y $2$ centradas en el origen.
401. [T] $\bold{F} = \lang x^2, −y^2, z^2\rang$; $D$ es la región del primer octante entre los planos $z = 4 - x - y$ y $z = 2 - x - y$ (Solución).
402. Sea $\bold{F} (x, y, z) = 2x\bold{i} - 3xy\bold{j} + xz^2\bold{k}$. Usa el teorema de la divergencia para calcular $\iint_S\bold{F}\cdot d\bold{S}$, donde $S$ es la superficie del cubo con esquinas en $(0, 0, 0), (1, 0, 0), (0, 1, 0), (1, 1, 0), (0, 0, 1), (1, 0, 1), (0 , 1, 1)$ y $(1, 1, 1)$, orientados hacia afuera.
403. Usa el teorema de la divergencia para encontrar el flujo hacia afuera del campo $\bold{F} (x, y, z) = \big(x^3 - 3y\big)\bold{i} + (2yz + 1)\bold{j} + xyz\bold{k}$ a través del cubo delimitado por los planos $x = \pm 1, y = \pm 1$ y $z = \pm 1$ (Solución).
404. Sea $\bold{F} (x, y, z) = 2x\bold{i} - 3y\bold{j} + 5z\bold{k}$ y sea $S$ el hemisferio $z = \sqrt{9 - x^2 − y^2}$ junto con el disco $x^2 + y^2 ≤ 9$ en el plano $xy$. Usa el teorema de la divergencia.
405. Evalúa $\iint_S\bold{F}\cdot \bold{N} dS$, donde $\bold{F} (x, y, z) = x^2\bold{i} + xy\bold{j} + x^3y^3\bold{k}$ y $S$ es la superficie que consta de todas las caras excepto el tetraedro delimitado por el plano $x + y + z = 1$ y los planos de coordenadas, con vector normal unidad exterior $\bold{N}$ (Solución).
406. Encuentra el flujo externo neto del campo $\bold{F} = \lang bz - cy, cx - az, ay - bx\rang$ a través de cualquier superficie cerrada lisa en $\bold{R}^3$, donde $a, b$ y $c$ son constantes.
407. Usa el teorema de divergencia para evaluar $\iint_S ||\bold{R}|| \bold{R} \cdot\bold{n}ds$, donde $\bold{R} (x, y, z) = x\bold{i} + y\bold{j} + z\bold{k}$ y $S$ es la esfera $x^2 + y^2 + z^2 = a^2$, con constante $a \gt 0$ (Solución).
408. Usa el teorema de la divergencia para evaluar $\iint_S\bold{F}\cdot d\bold{S}$, donde $\bold{F} (x, y, z) = y^2z\bold{i} + y^3\bold{j} + xz\bold{k}$ y $S$ es el límite del cubo definido por $−1 \le x \le 1, −1 \le y \le 1 y 0 \le z \le 2$.
409. Sea $R$ la región definida por $x^2 + y^2 + z^2 \le 1$. Usa el teorema de la divergencia para encontrar $\iiint_R z^2dV$ (Solución).
410. Sea $E$ el sólido limitado por el plano $xy$ y el paraboloide $z = 4 − x^2 - y^2$ de modo que $S$ es la superficie de la pieza del paraboloide junto con el disco en el plano $xy$ que forma su parte inferior. Si $\bold{F} (x, y, z) = \big(xz sen (yz) + x^3\big)\bold{i} + cos (yz)\bold{j} + \big(3zy^2 - e^{x^2 + y^2}\big)\bold{k}$, encuentre $\iint_S\bold{F}\cdot d\bold{S}$ usando el teorema de divergencia.
411. Sea $E$ el cubo unitario sólido con esquinas diagonalmente opuestas en el origen y $(1, 1, 1)$, y caras paralelas a los planos de coordenadas. Sea $S$ la superficie de $E$, orientada con la normal que apunta hacia afuera. Usa un CAS para encontrar $\iint_S\bold{F}\cdot d\bold{S}$ usando el teorema de divergencia si $\bold{F} (x, y, z) = 2xy\bold{i} + 3ye^z\bold{j} + x sen\; z\bold{k}$ (Solución).
412. Usa el teorema de la divergencia para calcular el flujo de $\bold{F} (x, y, z) = x^3\bold{i} + y^3\bold{j} + z^3\bold{k}$ a través de la esfera $x^2 + y^2 + z^2 = 1$.
413. Encuentra $\iint_S\bold{F}\cdot d\bold{S}$, donde $\bold{F} (x, y, z) = x\bold{i} + y\bold{j} + z\bold{k}$ y $S$ es la superficie orientada hacia afuera obtenida al eliminar el cubo $[1, 2] \times [1, 2] \times [1, 2 ]$ del cubo $[0, 2] \times [0, 2] \times [0, 2]$ (Solución).
414. Considera el campo vectorial radial $\bold{F} = \frac{\bold{r}}{ |\bold{r}|} = \frac{\lang x, y, z\rang}{\big(x^2 + y^2 + z^2\big)^{1/2}}$. Calcula la integral de superficie, donde $S$ es la superficie de una esfera de radio $a$ centrada en el origen.
415. Calcula el flujo de agua a través del cilindro parabólico $S: y = x^2$, desde $0 \le x \le 2, 0 \le z \le 3$, si el vector de velocidad es $\bold{F} (x, y, z) = 3z^2\bold{i} + 6\bold{j} + 6xz\bold{k}$ (Solución).
416. [T] Usa un CAS para encontrar el flujo del campo vectorial $\bold{F} (x, y, z) = z\bold{i} + z\bold{j} + \sqrt{x^2 + y^2}\bold{k}$ a través de la porción del hiperboloide $x^2 + y^2 = z^2 + 1$ entre los planos $z = 0$ y $z = \frac{\sqrt{3}}{3}$, orientado de manera que el vector normal unitario apunte hacia afuera desde el eje $z$.
417. [T] Usa un CAS para encontrar el flujo del campo vectorial $\bold{F} (x, y, z) = \big(e^y + x\big)\bold{i} + (3 cos (xz) - y)\bold{j} + z\bold{k}$ a través de la superficie $S$, donde $S$ está dado por $z^2 = 4x^2 + 4y^2$ desde $0 \le z \le 4$, orientado de manera que el vector normal unitario apunte hacia abajo (Solución).
418. [T] Usa un CAS para calcular $\iint_S\bold{F}\cdot d\bold{S}$, donde $\bold{F} (x, y, z) = x\bold{i} + y\bold{j} + 2z\bold{k}$ y $S$ es parte de la esfera $x^2 + y^2 + z^2 = 2$ con $0 \le z \le 1$.
419. Evalúa $\iint_S\bold{F}\cdot d\bold{S}$, donde $\bold{F} (x, y, z) = bxy^2\bold{i} + bx^2y\bold{j} + \big(x^2 + y^2\big)z^2\bold{k}$ y $S$ es una superficie cerrada que limita la región y que consta del sólido cilindro $x^2 + y^2 ≤ a^2$ y $0 \le z \le b$ (Solución).
420. [T] Usa un CAS para calcular el flujo de $\bold{F} (x, y, z) = \big(x^3 + y sen\; z\big)\bold{i} + \big(y^3 + z sen\; x\big)\bold{j} + 3z\bold{k}$ a través de la superficie $S$, donde $S$ es el límite del sólido delimitado por hemisferios $z = \sqrt{4 - x^2 - y^2}$ y $z = \sqrt{1 - x^2 - y^2}$, y el plano $z = 0$.
421. Usa el teorema de la divergencia para evaluar $\iint_S\bold{F}\cdot d\bold{S}$, donde $\bold{F} (x, y, z) = xy\bold{i} −\frac12y^2\bold{j} + z\bold{k}$ y $S$ es la superficie que consta de tres piezas: $z = 4 - 3x^2 - 3y^2, 1 \le z \le 4$ en la parte superior; $x^2 + y^2 = 1, 0 \le z \le 1$ en los lados; y en $z = 0$ en la parte inferior (Solución).
422. [T] Usa un CAS y el teorema de divergencia para evaluar $\iint_S\bold{F}\cdot d\bold{S}$, donde $\bold{F} (x, y, z) = (2x + y cos\; z)\bold{i} + \big(x^2 - y\big)\bold{j} + y^2z\bold{k}$ y $S$ es la esfera $x^2 + y^2 + z^2 = 4$ orientados hacia el exterior.
423. Usa el teorema de divergencia para evaluar $\iint_S\bold{F}\cdot d\bold{S}$, donde $\bold{F} (x, y, z) = x\bold{i} + yj + z\bold{k}$ y $S$ es el límite del sólido encerrado por el paraboloide $y = x^2 + z^2 - 2$, el cilindro $x^2 + z^2 = 1$, y el plano $x + y = 2$, y $S$ está orientado hacia afuera (Solución).
 Para los siguientes ejercicios, la ley de transferencia de calor de Fourier establece que el vector de flujo de calor $\bold{F}$ en un punto es proporcional al gradiente negativo de la temperatura; es decir, $\bold{F} = −k\nabla T$, lo que significa que la energía térmica fluye de regiones calientes a regiones frías.
Para los siguientes ejercicios, la ley de transferencia de calor de Fourier establece que el vector de flujo de calor $\bold{F}$ en un punto es proporcional al gradiente negativo de la temperatura; es decir, $\bold{F} = −k\nabla T$, lo que significa que la energía térmica fluye de regiones calientes a regiones frías.
La constante $k \gt 0$ se llama conductividad, que tiene unidades métricas de julios por metro por segundo-kelvin o vatios por metro-kelvin. Se da una función de temperatura para la región $D$. Usa el teorema de la divergencia para encontrar el flujo de calor neto hacia el exterior $\iint_S \bold{F}\cdot\bold{N}dS = −k \iint_S \nabla T \cdot\bold{N}dS$ a través del límite $S$ de $D$, donde $k = 1$.
424. $T (x, y, z) = 100 + x + 2y + z; D = \lbrace (x, y, z): 0 \le x \le 1, 0 \le y \le 1, 0 \le z \le 1\rbrace$ 425. $T (x, y, z) = 100 + e^{-z}; D = \lbrace (x, y, z): 0 \le x \le 1, 0 \le y \le 1, 0 \le z \le 1\rbrace$ (Solución). 426. $T (x, y, z) = 100e^{− x^2 - y^2 - z^2}$; $D$ es la esfera de radio $a$ centrada en el origen.