Solución

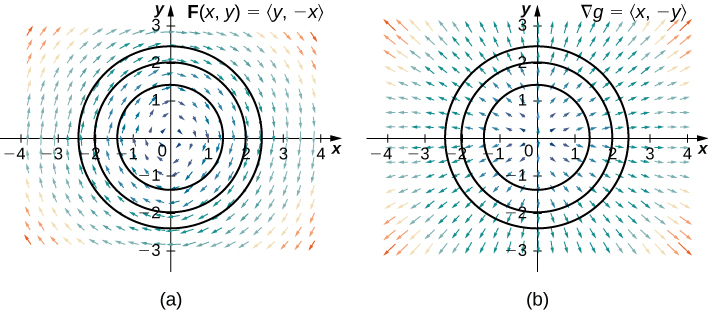
Ten en cuenta que el dominio de F\bold{F} es todo R2\Reals^2, que simplemente está conectado. Por lo tanto, para mostrar que F\bold{F} está libre de fuentes, podemos mostrar que cualquiera de los elementos del 11 al 44 de la lista anterior es verdadero. En este ejercicio, demostraremos que el elemento 44 es verdadero.

Sea P(x,y)=yP (x, y) = y y Q(x,y)=−xQ (x, y) = −x. Entonces Px+0=QyP_x + 0 = Q_y, y por lo tanto Px+Qy=0P_x + Q_y = 0. Por lo tanto, F\bold{F} es libre de fuentes.

Para encontrar una función de flujo para F\bold{F}, proceda de la misma manera que para encontrar una función potencial para un campo conservativo. Sea gg una función de flujo para F\bold{F}. Entonces gy=yg_y = y, lo que implica que

g(x,y)=y22+h(x)g(x,y) = \frac{y^2}{2} + h(x)

Dado que −gx=Q=−x−g_x = Q = −x, tenemos h′(x)=xh^{\prime}(x) = x. Por lo tanto,

h(x)=x22+Ch(x) = \frac{x^2}{2} + C

Dejando C=0C = 0 obtenemos un función de flujo

g(x,y)=x22+y22g(x,y) = \frac{x^2}{2} + \frac{y^2}{2}

Para confirmar que gg es una función de flujo para F\bold{F}, ten en cuenta que gy=y=Pg_y = y = P y −gx=−x=Q−g_x = −x = Q.

Observa que el campo vectorial de rotación libre de fuente F(x,y)=⟨y,−x⟩\bold{F} (x, y) = \lang y, −x\rang es perpendicular al campo vectorial radial conservativo ∇g=⟨x,y⟩\nabla g = \lang x, y\rang (ver la siguiente figura).

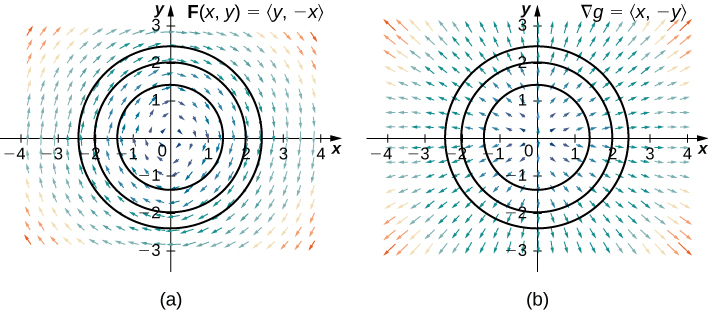
Figura 6.42. (a) En esta imagen, vemos las curvas de tres niveles de gg y el campo vectorial F\bold{F}. Observa que los vectores F\bold{F} en una curva de nivel dada son tangentes a la curva de nivel. (b) En esta imagen, vemos las curvas de tres niveles de gg y el campo vectorial ∇g\nabla g. Los vectores gradiente son perpendiculares a la curva de nivel correspondiente. Por lo tanto, F(a,b)⋅∇g(a,b)=0\bold{F} (a, b) \cdot \nabla g (a, b) = 0 para cualquier punto en el dominio de gg.