Solución

Usando la estrategia de resolución de problemas, el paso 1 implica encontrar los puntos críticos de $f$ en su dominio. Por lo tanto, primero calculamos $f_x (x, y)$ y $f_y (x, y)$ , luego las igualamos a cero:

f_x(x, y) = 48 − 2x − 2y

f_y(x, y) = 96 − 2x − 18y.

Al igualarlas a cero, se obtiene el sistema de ecuaciones.

\begin{aligned} 48 − 2x − 2y &= 0\\ 96 − 2x − 18y &= 0 \end{aligned}

La solución a este sistema es $x = 21$ e $y = 3$ . Por lo tanto $(21, 3)$ es un punto crítico de $f$ . Al calcular $f (21, 3)$ da $f (21, 3) = 48 (21) + 96 (3) - 21^2 - 2 (21) (3) - 9 (3)^2 = 648$ .
El dominio de esta función es $0 \le x \le 50$ y $0 \le y \le 25$ como se muestra en el siguiente gráfico.

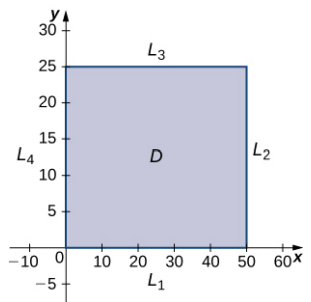
Figura 4.57. Gráfica del dominio de la función $f(x, y) = 48x + 96y − x^2 − 2xy − 9y^2$

$L_1$ es el segmento de línea que conecta $(0, 0)$ y $(50, 0)$ , y se puede parametrizar mediante las ecuaciones $x (t) = t, y (t) = 0$ para $0 \le t \le 50$ . Luego definimos $g ( t) = f \big(x (t), y (t)\big)$ :

\begin{aligned} g ( t) &= f \big(x (t), y (t)\big)\\ &= f(t, 0)\\ &= 48t + 96(0) − y^2 − 2(t)(0) − 9(0)^2\\ &= 48t − t^2 \end{aligned}

Al hacer $g^{\prime}(t) = 0$ produce el punto crítico $t = 24$ , que corresponde al punto $(24, 0)$ en el dominio de $f$ .

Al calcular $f (24, 0)$ da $576$ .

$L_2$ es el segmento de línea que conecta $(50, 0)$ y $(50, 25)$ , y puede ser parametrizado por las ecuaciones $x (t) = 50, y (t) = t$ para $0 \le t \le 25$ . Una vez más, definimos $g (t) = f \big(x (t), y (t)\big)$ :

\begin{aligned} g ( t) &= f \big(x (t), y (t)\big)\\ &= f(50, t)\\ &= 48(50) + 96t − 50^2 − 2(50)t − 9t^2\\ &= −9t^2 − 4t − 100 \end{aligned}

Esta función tiene un punto crítico en $t = - \frac29$ , que corresponde al punto $\bigg(50, −\frac29\bigg)$ . Este punto no está en el dominio de $f$ .

$L_3$ es el segmento de línea que conecta $(0, 25)$ y $(50, 25)$ , y se puede parametrizar mediante las ecuaciones $x (t) = t, y (t) = 25$ para $0 \le t \le 50$ . Definimos $g ( t) = f \big(x (t), y (t)\big)$ :

\begin{aligned} g ( t) &= f \big(x (t), y (t)\big)\\ &= f(t, 25)\\ &= 48t + 96(25) − t^2 − 2t(25) − 9(25^2)\\ &= −t^2 − 2t − 3225 \end{aligned}

Esta función tiene un punto crítico en $t = −1$ , que corresponde al punto $(−1, 25)$ , que no está en el dominio.

$L_4$ es el segmento de línea que conecta $(0, 0)$ a $(0, 25)$ , y se puede parametrizar mediante las ecuaciones $x (t) = 0, y (t) = t$ para $0 \le t \le 25$ . Definimos $g ( t) = f (x (t), y (t))$ :

\begin{aligned} g ( t) &= f \big(x (t), y (t)\big)\\ &= f(0, t)\\ &= 48(0) + 96t − (0)^2 − 2(0)t − 9t^2\\ &= 96t − t^2 \end{aligned}

Esta función tiene un punto crítico en $t = \frac{16}{3}$ , que corresponde al punto $\big(0, \frac{16}{3}\big)$ , que está en el límite del dominio. Calculando $f \big(0,\frac{16}{3}\big)$ da 256.

También necesitamos encontrar los valores de $f (x, y)$ en las esquinas de su dominio. Estas esquinas se encuentran en $(0, 0), (50, 0), (50, 25)$ y $(0, 25)$ :

\begin{aligned} f(0, 0) &= 48(0) + 96(0) − (0)^2 − 2(0)(0) − 9(0)^2 = 0\\ f(50, 0) &= 48(50) + 96(0) − (50)^2 − 2(50)(0) − 9(0)^2 = −100\\ f(50, 25) &= 48(50) + 96(25) − (50)^2 − 2(50)(25) − 9(25)^2 = −5825\\ f(0, 25) &= 48(0) + 96(25) − (0)^2 − 2(0)(25) − 9(25)^2 = −3225 \end{aligned}

El valor crítico máximo es $648$ , que ocurre en $(21, 3)$ . Por lo tanto, se obtiene una ganancia máxima de $\$ 648,000$ cuando se venden $21,000$ pelotas de golf y se compran $3$ horas de publicidad por mes como se muestra en la siguiente figura.

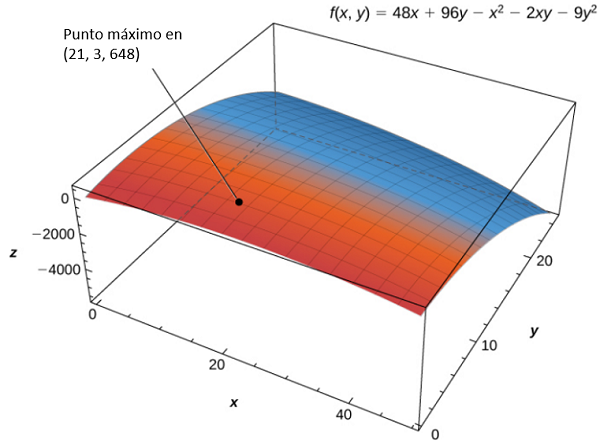
Figura 4.58. La función de beneficio $f (x, y)$ tiene un máximo en $(21, 3, 648)$ .