Solución
La mejor manera de hacer esto es dibujar la región E E E
E = { ( x , y , z ) ∣ 0 ≤ x ≤ 1 , 0 ≤ y ≤ x 2 , 0 ≤ z ≤ y } E = \lbrace (x, y, z)|0 \le x \le 1, 0 \le y \le x^2, 0 \le z \le y\rbrace E = {( x , y , z ) ∣0 ≤ x ≤ 1 , 0 ≤ y ≤ x 2 , 0 ≤ z ≤ y } y
∫ x = 0 x = 1 ∫ y = 0 y = x 2 ∫ z = 0 z = y 2 f ( x , y , z ) d z d y d x \int_{x=0}^{x=1}\int_{y=0}^{y=x^2}\int_{z=0}^{z=y^2} f(x,y,z)dzdydx ∫ x = 0 x = 1 ∫ y = 0 y = x 2 ∫ z = 0 z = y 2 f ( x , y , z ) d z d y d x Necesitamos expresar esta integral triple como
∫ y = c y = f ∫ z = v 1 ( y ) z = v 2 ( y ) ∫ x = u 1 ( y , z ) x = u 2 ( y , z ) f ( x , y , z ) = d x d z d y \int_{y=c}^{y=f}\int_{z=v_1(y)}^{z=v_2(y)}\int_{x=u_1(y,z)}^{x=u_2(y,z)} f(x,y,z)=dxdzdy ∫ y = c y = f ∫ z = v 1 ( y ) z = v 2 ( y ) ∫ x = u 1 ( y , z ) x = u 2 ( y , z ) f ( x , y , z ) = d x d z d y Conociendo la región E E E
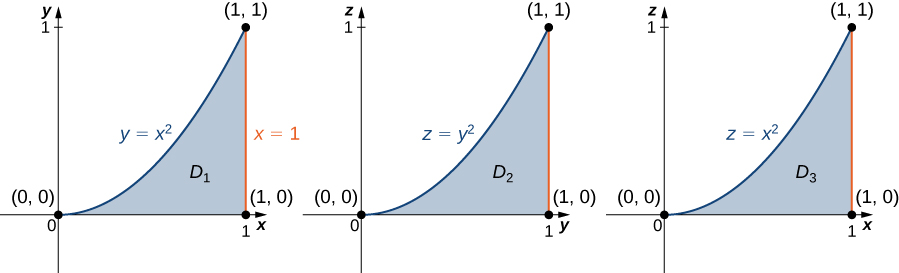
En el planox y xy x y D 1 = { ( x , y ) ∣ 0 ≤ x ≤ 1 , 0 ≤ y ≤ x 2 } = { ( x , y ) ∣ 0 ≤ y ≤ 1 , y ≤ x ≤ 1 } D_1 =\lbrace (x, y)|0 \le x \le 1, 0 \le y \le x^2\rbrace = \lbrace (x, y)|0 \le y \le 1, y \le x \le 1\rbrace D 1 = {( x , y ) ∣0 ≤ x ≤ 1 , 0 ≤ y ≤ x 2 } = {( x , y ) ∣0 ≤ y ≤ 1 , y ≤ x ≤ 1 } y z yz yz D 2 = { ( y , z ) ∣ 0 ≤ y ≤ 1 , 0 ≤ z ≤ y 2 } D_2 = \lbrace (y, z)|0 \le y \le 1, 0 \le z \le y^2\rbrace D 2 = {( y , z ) ∣0 ≤ y ≤ 1 , 0 ≤ z ≤ y 2 } x z xz x z D 3 = { ( x , z ) ∣ 0 ≤ x ≤ 1 , 0 ≤ z ≤ x 2 } D_3 = \lbrace (x, z)|0 \le x \le 1, 0 \le z \le x^2\rbrace D 3 = {( x , z ) ∣0 ≤ x ≤ 1 , 0 ≤ z ≤ x 2 }
Figura 5.47 . Las tres secciones transversales de E E E
Ahora podemos describir la misma región E E E { ( x , y , z ) ∣ 0 ≤ y ≤ 1 , 0 ≤ z ≤ y 2 , y ≤ x ≤ 1 } \lbrace (x, y, z) | 0 \le y \le 1, 0 \le z \le y^2, y \le x \le 1\rbrace {( x , y , z ) ∣0 ≤ y ≤ 1 , 0 ≤ z ≤ y 2 , y ≤ x ≤ 1 }
∫ y = c y = f ∫ z = v 1 ( y ) z = v 2 ( y ) ∫ x = u 1 ( y , z ) x = u 2 ( y , z ) f ( x , y , z ) = d x d z d y = ∫ y = 0 y = 1 ∫ z = 0 z = x 2 ∫ x = y x = 1 f ( x , y , z ) d x d z d y \int_{y=c}^{y=f}\int_{z=v_1(y)}^{z=v_2(y)}\int_{x=u_1(y,z)}^{x=u_2(y,z)} f(x,y,z)=dxdzdy = \int_{y=0}^{y=1}\int_{z=0}^{z=x^2}\int_{x=\sqrt{y}}^{x=1} f(x,y,z)dxdzdy ∫ y = c y = f ∫ z = v 1 ( y ) z = v 2 ( y ) ∫ x = u 1 ( y , z ) x = u 2 ( y , z ) f ( x , y , z ) = d x d z d y = ∫ y = 0 y = 1 ∫ z = 0 z = x 2 ∫ x = y x = 1 f ( x , y , z ) d x d z d y Ahora supóm que f ( x , y , z ) = x y z f (x, y, z) = xyz f ( x , y , z ) = x yz
∫ x = 0 x = 1 ∫ y = 0 y = x 2 ∫ z = 0 z = y 2 f ( x , y , z ) d z d y d x \displaystyle\int_{x=0}^{x=1}\int_{y=0}^{y=x^2}\int_{z=0}^{z=y^2} f(x,y,z)dzdydx ∫ x = 0 x = 1 ∫ y = 0 y = x 2 ∫ z = 0 z = y 2 f ( x , y , z ) d z d y d x
= ∫ x = 0 x = 1 ∫ y = 0 y = x 2 [ x y z 2 2 ∣ z = 0 z = y 2 ] d y d x = ∫ x = 0 x = 1 ∫ y = 0 y = x 2 ( x y 5 2 ) d y d x = ∫ x = 0 x = 1 [ x y 6 12 ∣ y = 0 y = x 2 ] d x = ∫ x = 0 x = 1 x 13 12 d x = 1 168 \begin{aligned}
&= \int_{x=0}^{x=1}\int_{y=0}^{y=x^2}\bigg[xy\frac{z^2}{2}\bigg|_{z=0}^{z=y^2}\bigg]dydx = \int_{x=0}^{x=1}\int_{y=0}^{y=x^2}\bigg(x\frac{y^5}{2}\bigg)dydx = \int_{x=0}^{x=1}\bigg[x\frac{y^6}{12}\bigg|_{y=0}^{y=x^2}\bigg]dx\\
&= \int_{x=0}^{x=1}\frac{x^{13}}{12}dx = \frac{1}{168}
\end{aligned} = ∫ x = 0 x = 1 ∫ y = 0 y = x 2 [ x y 2 z 2 ∣ ∣ z = 0 z = y 2 ] d y d x = ∫ x = 0 x = 1 ∫ y = 0 y = x 2 ( x 2 y 5 ) d y d x = ∫ x = 0 x = 1 [ x 12 y 6 ∣ ∣ y = 0 y = x 2 ] d x = ∫ x = 0 x = 1 12 x 13 d x = 168 1 ∫ y = 0 y = 1 ∫ z = 0 z = y 2 ∫ x = y x = 1 f ( x , y , z ) d x d z d y \displaystyle\int_{y=0}^{y=1}\int_{z=0}^{z=y^2}\int_{x=\sqrt{y}}^{x=1} f(x,y,z)dxdzdy ∫ y = 0 y = 1 ∫ z = 0 z = y 2 ∫ x = y x = 1 f ( x , y , z ) d x d z d y
= ∫ y = 0 y = 1 ∫ z = 0 z = y 2 ( y z 2 − y 2 z 2 ) d z d y = ∫ y = 0 y = 1 [ y z 2 4 − y 2 z 2 4 ∣ z = 0 z = y 2 ] = ∫ y = 0 y = 1 ( y 5 4 − y 6 4 ) d y = 1 168 \begin{aligned}
&= \int_{y=0}^{y=1}\int_{z=0}^{z=y^2}\bigg(\frac{yz}{2} - \frac{y^2z}{2}\bigg)dzdy = \int_{y=0}^{y=1}\bigg[\frac{yz^2}{4} - \frac{y^2z^2}{4}\bigg|_{z=0}^{z=y^2}\bigg]\\&=
\int_{y=0}^{y=1}\bigg(\frac{y^5}{4} - \frac{y^6}{4}\bigg)dy = \frac{1}{168}
\end{aligned} = ∫ y = 0 y = 1 ∫ z = 0 z = y 2 ( 2 yz − 2 y 2 z ) d z d y = ∫ y = 0 y = 1 [ 4 y z 2 − 4 y 2 z 2 ∣ ∣ z = 0 z = y 2 ] = ∫ y = 0 y = 1 ( 4 y 5 − 4 y 6 ) d y = 168 1 ¡Las respuestas coinciden!