Solución

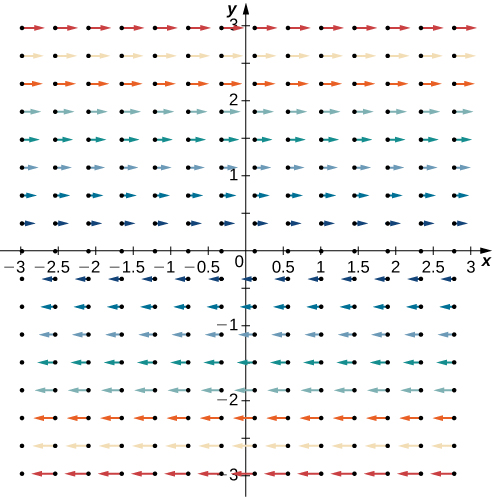
Observa que este campo vectorial consta de vectores que son todos paralelos. De hecho, cada vector del campo es paralelo al eje xx. Este hecho podría llevarnos a la conclusión de que el campo no tiene espín (giro) y que el rotacional es cero. Para probar esta teoría, ten en cuenta que

rot  F=(Qx−Py)k=−k  =  0rot\;\bold{F} = \big(Q_x - P_y\big)\bold{k} = -\bold{k}\;\cancel{=}\;0

Por lo tanto, este campo vectorial tiene giro. Para ver por qué, imagina que colocas una rueda de paletas en cualquier punto del primer cuadrante (ver la siguiente figura). Las mayores magnitudes de los vectores en la parte superior de la rueda hacen que la rueda gire.

La rueda gira en el sentido de las agujas del reloj (negativo), lo que hace que el coeficiente de rotación sea negativo

Figura 6.55. El campo vectorial F(x,y)=⟨y,0⟩\bold{F} (x, y) = \lang y, 0\rang consta de vectores que son todos paralelos.