Una vez que el objeto 1 está ubicado en el origen, la distancia entre los objetos viene dada por . El vector unitario del objeto 1 al objeto 2 es , y por lo tanto . Por lo tanto, el campo vectorial gravitacional ejercido por el objeto 1 sobre el objeto 2 es
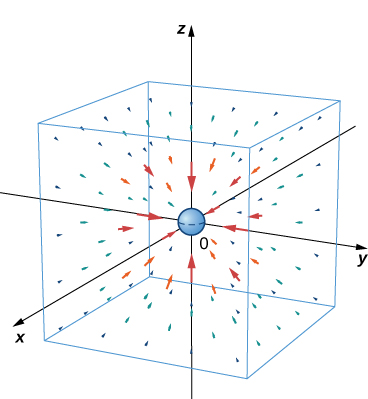
Este es un ejemplo de un campo vectorial radial en . La siguiente figura muestra cómo se ve este campo gravitacional para una gran masa en el origen. Ten en cuenta que las magnitudes de los vectores aumentan a medida que los vectores se acercan al origen.

Figura 6.8. Una representación visual del campo vectorial gravitacional para una gran masa en el origen.