Solución

Crea una tabla (observa la que sigue) usando una muestra representativa de puntos en un plano y sus vectores correspondientes. La figura 6.6 muestra el campo vectorial resultante

$(x,y)$	$\bold{F}(x,y)$	$(x,y)$	$\bold{F}(x,y)$	$(x,y)$	$\bold{F}(x,y)$
$(1,0)$	$\lang 0,1\rang$	$(2,0)$	$\lang 0,-2\rang$	$(1,1)$	$\lang -1,1\rang$
$(0,1)$	$\lang 1,0\rang$	$(0,2)$	$\lang 2,0\rang$	$(-1,1)$	$\lang 1,1\rang$
$(-1,0)$	$\lang 0,1\rang$	$(-2,0)$	$\lang 0,2\rang$	$(-1,-1)$	$\lang -1,1\rang$
$(0,-1)$	$\lang -1,0\rang$	$(0,-2)$	$\lang -2,0\rang$	$(1,-1)$	$\lang -1,-1\rang$

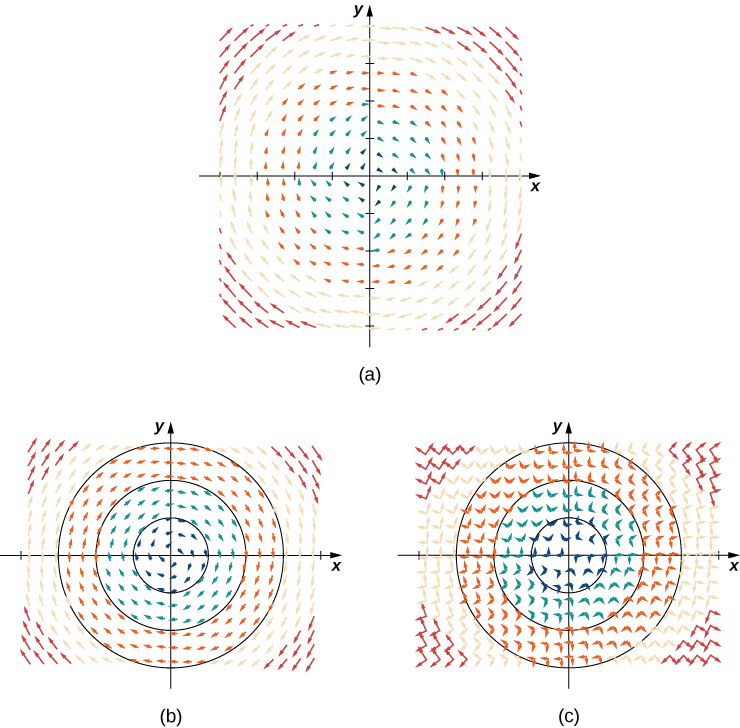
Figura 6.5. (a) Una representación visual del campo vectorial $\bold{F} (x, y) = \lang y, −x\rang$ . (b) Campo vectorial $\bold{F} (x, y) = \lang y, −x\rang$ con círculos centrados en el origen. (c) El vector $\bold{F} (a, b)$ es perpendicular al vector radial $\lang y, −x\rang$ en el punto $(a, b)$ .

Análisis

Observa que el vector $\bold{F} (a, b) = \lang b, −a\rang$ apunta en el sentido de las agujas del reloj y es perpendicular al vector radial $\lang a, b\rang$ . (podemos verificar esta afirmación calculando el producto escalar de los dos vectores: $\lang a, b\rang \cdot \lang -b, a\rang = −ab + ab = 0$ ). Además, el vector $\lang -b, a\rang$ tiene una longitud $r = \sqrt{a^2 + b^2}$ . Así, tenemos una descripción completa de este campo vectorial rotacional: el vector asociado con el punto $(a, b)$ es el vector con longitud $r$ tangente al círculo con radio $r$ , y apunta en el sentido de las agujas del reloj.

Los bocetos como el de la figura 6.6 se utilizan a menudo para analizar los principales sistemas de tormentas, incluidos los huracanes y ciclones. En el hemisferio norte, las tormentas giran en sentido antihorario; en el hemisferio sur, las tormentas giran en el sentido de las agujas del reloj (este es un efecto causado por la rotación de la Tierra sobre su eje y se llama Efecto Coriolis).