Solución

La siguiente figura muestra el tetraedro sólido EE y su proyección DD en el plano xyxy.

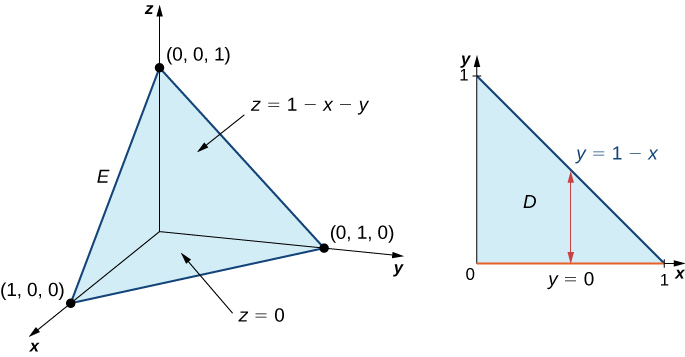
Figura 5.45. El sólido EE tiene una proyección DD en el plano xyxy del tipo I.

Podemos describir el tetraedro de región sólida como

E={(x,y,z)∣0≤x≤1,0≤y≤1−x,0≤z≤1−x−y}E = \lbrace (x, y, z)|0 \le x \le 1, 0 \le y \le 1 − x, 0 \le z \le 1 − x − y\rbrace

Entonces, la integral triples es

∭Ef(x,y,z)dV=∫x=0x=1∫y=0y=1−x∫z=0z=1−x−y(5x−3y)dzdydx\iiint_E f(x,y,z)dV = \int_{x=0}^{x=1}\int_{y=0}^{y=1-x}\int_{z=0}^{z=1-x-y}(5x − 3y)dz dy dx

Para simplificar el cálculo, primero evalemos la integral ∫z=0z=1−x−y(5x−3y)dz\displaystyle\int_{z=0}^{z=1-x-y}(5x − 3y)dz, obteniendo

∫z=0z=1−x−y(5x−3y)dz=(5x−3y)(1−x−y)\int_{z=0}^{z=1-x-y}(5x − 3y)dz =(5x-3y)(1-x-y)

Ahora evaluamos la integral ∫y=0y=1−x(5x−3y)(1−x−y)dy\displaystyle\int_{y=0}^{y=1-x}(5x-3y)(1-x-y)dy, resultando

∫y=0y=1−x(5x−3y)(1−x−y)dy=12(x−1)2(6x−1)\int_{y=0}^{y=1-x}(5x-3y)(1-x-y)dy = \frac12(x-1)^2(6x-1)

Finalmente, evaluamos

∫x=0x=112(x−1)2(6x−1)dx=112\int_{x=0}^{x=1}\frac12(x-1)^2(6x-1)dx = \frac{1}{12}