Solución

Usamos la Ecuación 6.9 para calcular ∫CF⋅dr\int_C\bold{F}\cdot d\bold{r}. La curva CC se puede parametrizar mediante r(t)=⟨2t,2t⟩,0≤t≤1\bold{r} (t) = \lang 2t, 2t\rang , 0 \le t \le 1. Entonces, F(r(t))=⟨4t,8t⟩\bold{F}(\bold{r} (t)) = \lang 4t, 8t\rang y r′(t)=⟨2,2⟩\bold{r}^{\prime}(t) = \lang 2, 2\rang, lo que implica que

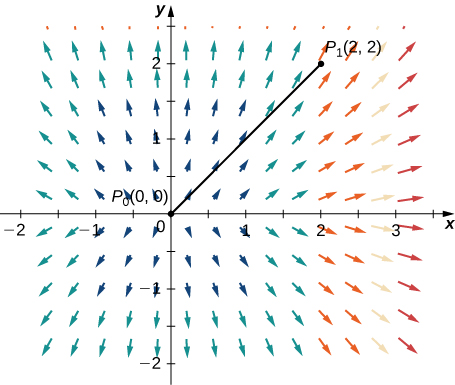
∫CF⋅dr=∫01⟨4t,8t⟩⋅⟨2,2⟩dt=∫01(8t+16t)dt=∫0124tdt=[12t2]01=12\begin{aligned} \int_C \bold{F}\cdot d\bold{r} &= \int_0^1 \lang 4t, 8t\rang \cdot \lang 2, 2\rang dt\\ &= \int_0^1 (8t + 16t)dt = \int_0^1 24t dt\\&= \bigg[12t^2\bigg]_0^1 = 12 \end{aligned}

Figura 6.28. El valor de la integral de línea ∫CF⋅dr\int_C\bold{F}\cdot d\bold{r} depende sólo en el valor de la función potencial de F\bold{F} en los puntos finales de la curva.

Observa que F=∇fF = \nabla f, donde f(x,y)=x2+2y2f (x, y) = x^2 + 2y^2. Si pensamos en el gradiente como una derivada, entonces ff es una "antiderivada" de F\bold{F}. En el caso de integrales de una sola variable, la integral de la derivada g′(x)g^{\prime}(x) es g(b)−g(a)g (b) - g (a), donde aa es el punto de inicio del intervalo de integración y bb es el punto final. Si las integrales de línea vectoriales funcionan como integrales de una sola variable, entonces esperaríamos que la integral F\bold{F} fuera f(P1)−f(P0)f\big(P_1\big) - f\big(P_0\big), donde P1P_1 es el punto final de la curva de integración y P0P_0 es el punto de inicio. Ten en cuenta que este es el caso de este ejercicio:

∫CF⋅dr=∫C∇f⋅dr=12\int_C \bold{F}\cdot d\bold{r} = \int_C \nabla f\cdot d\bold{r} = 12

y

f(2,2)−f(0,0)=4+8−0=12f(2, 2) − f(0, 0) = 4 + 8 − 0 = 12

En otras palabras, la integral de una "derivada" se puede calcular evaluando una "antiderivada" en los puntos finales de la curva y restando, al igual que para las integrales de una sola variable.