Solución

Podemos usar la Ecuación 6.9 para convertir la variable de integración de ss a tt. Entonces tenemos

F(r(t))=⟨−sen  t,cos  t⟩       y      r′(t)=⟨−sen  t,cos  t⟩\bold{F}\big(\bold{r}(t)\big) = \lang −sen\; t, cos\; t \rang\;\;\; \text{ y}\;\;\; \bold{r}^{\prime}(t) = \lang −sen \;t, cos\; t \rang

Por lo tanto,

∫CF⋅dr=∫0π⟨−sen  t,cos  t⟩⋅⟨−sen  t,cos  t⟩dt=∫0πsen2t+cos2tdt=∫0π1dt=π\begin{aligned} \int_C\bold{F}\cdot d\bold{r} &= \int_0^{\pi}\lang −sen\; t, cos\; t \rang \cdot \lang −sen \;t, cos\; t \rang dt\\ &= \int_0^{\pi}sen^2t + cos^2t dt\\ &= \int_0^{\pi} 1dt = \pi\end{aligned}

Observa la siguiente figura

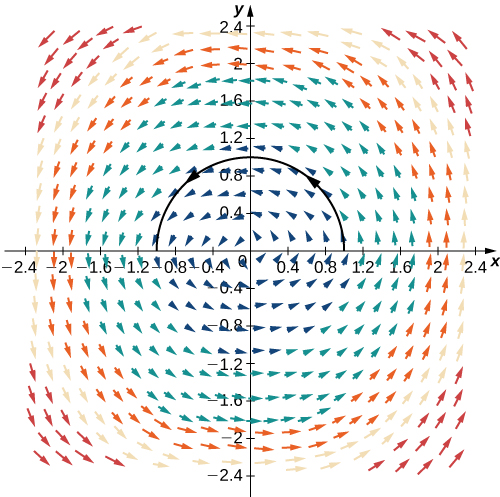
Figura 6.18. Esta figura muestra la curva r(t)=⟨cos  t,sen  t⟩,0≤t≤π\bold{r} (t) = \lang cos\; t, sen\; t\rang, 0 \le t \le \pi en el campo vectorial F=⟨−y,x⟩\bold{F} = \lang −y, x\rang.