Solución

Si F\bold{F} fuera magnético, entonces su divergencia sería cero. La divergencia de F\bold{F} es

∂∂x(x2y)+∂∂y(y−xy2)=2xy+1−2xy=1\frac{\partial}{\partial x}(x^2y) + \frac{\partial}{\partial y}(y-xy^2) = 2xy + 1 - 2xy = 1

y por lo tanto F\bold{F} no puede modelar un campo magnético (ver la siguiente figura)

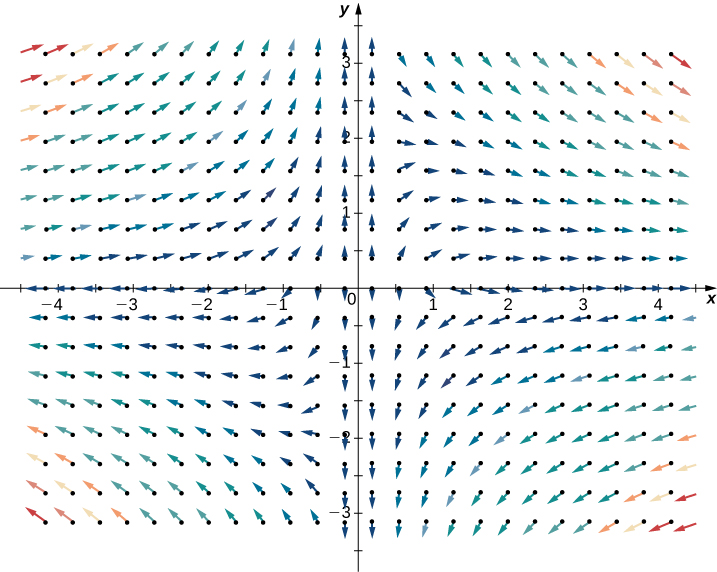
Figura 6.52. La divergencia del campo vectorial F(x,y)=⟨x2y,y−xy2⟩\bold{F} (x, y) = \lang x^2y, y −xy^2\rang es uno, por lo que no puede modelar un campo magnético.