Solución

Usamos la forma extendida del teorema de Green para mostrar que ∮CF⋅dr\oint_C\bold{F}\cdot d\bold{r} es 00 o $−2\po$; es decir, no importa cuán loca sea la curva CC, la integral de línea de F\bold{F} a lo largo de CC solo puede tener uno de dos valores posibles. Consideramos dos casos: el caso en el que CC abarca el origen y el caso en el que CC no abarca el origen.

Caso 1: CC no abarca el origen

En este caso, la región encerrada por CC está simplemente conectada porque el único agujero en el dominio de F\bold{F} está en el origen. Demostraremos en nuestra discusión de parciales cruzadas que F\bold{F} satisface la condición de parciales cruzadas. Si restringimos el dominio de F\bold{F} solo a CC y la región que encierra, entonces F\bold{F} con este dominio restringido ahora se define en un dominio simplemente conectado. Dado que F\bold{F} satisface la propiedad de parcial cruzada en su dominio restringido, el campo F\bold{F} es conservativo en esta región simplemente conectada y, por lo tanto, la circulación ∮CF⋅dr\oint_C\bold{F}\cdot d\bold{r} es cero.

Caso 2: CC incluye el origen

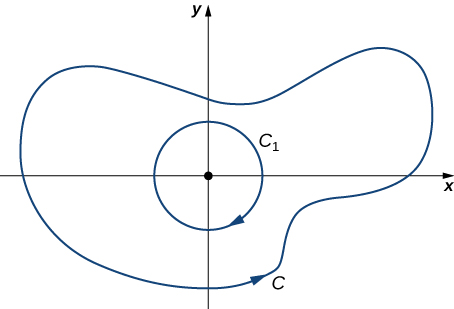
En este caso, la región encerrada por CC no está simplemente conectada porque esta región contiene un agujero en el origen. Sea C1C_1 un círculo de radio aa centrado en el origen de modo que C1C_1 esté completamente dentro de la región encerrada por CC (ver siguiente figura). Dá a C1C_1 una orientación en el sentido de las agujas del reloj.

Figura 6.46. Elige el círculo C1C_1 centrado en el origen que está contenido completamente dentro de CC.

Sea DD la región entre C1C_1 y CC, y C4C_4 está orientada en sentido antihorario. Según la versión extendida del teorema de Green

∫CF⋅dr+∫C1F⋅dr=∬D(Qx−Py)dA=∬D−y2−x2(x2+y2)2+y2−x2(x2+y2)2dA=0\begin{aligned} \int_C \bold{F}\cdot d\bold{r} + \int_{C_1} \bold{F}\cdot d\bold{r} &= \iint_D (Q_x - P_y)dA\\ &= \iint_D - \frac{y^2-x^2}{(x^2+y^2)^2}+ \frac{y^2-x^2}{(x^2+y^2)^2} dA\\ &= 0 \end{aligned}

y por lo tanto

∫CF⋅dr=−∫C1F⋅dr\int_C \bold{F}\cdot d\bold{r} = -\int_{C_1} \bold{F}\cdot d\bold{r}

Dado que C1C_1 es una curva específica, podemos evaluar intC1F⋅drint_{C_1} \bold{F}\cdot d\bold{r}, haciendo

x=acos  t,y=sen  t,0≤t≤2πx = acos\;t, y = sen\;t, 0 \le t \le 2\pi

una parametrización de C1C_1. Luego,

∫C1F⋅dr=∫02πF(r(t))⋅r′(t)dt=∫02π⟨−sen  ta,−cos  ta⟩⋅⟨−asen  t,−acos  t⟩dt=∫02π(sen2r+cos2t)dt=∫02πdt=2π\begin{aligned} \int_{C_1} \bold{F}\cdot d\bold{r} &= \int_0^{2\pi} \bold{F}(\bold{r}(t))\cdot \bold{r}^{\prime}(t)dt\\ &= \int_0^{2\pi} \big\lang -\frac{sen\;t}{a}, -\frac{cos\;t}{a}\big\rang \cdot \lang -asen\;t, -acos\;t\rang dt\\&= \int_0^{2\pi} (sen^2r + cos^2t) dt = \int_0^{2\pi} dt = 2\pi \end{aligned}

Por lo tanto ∫CF⋅ds=−2π\int_C \bold{F}\cdot ds = -2\pi