Solución

Para tener una idea de la forma de la superficie, primero trazamos algunos puntos. Dado que el dominio del parámetro es todo $\Reals^2$, podemos elegir cualquier valor para $u$ y $v$ y graficar el punto correspondiente. Si $u = v = 0$, entonces $\bold{r} (0, 0) = \lang 1, 0, 0\rang$, entonces el punto $(1, 0, 0)$ está en $S$. De manera similar, los puntos $\bold{r} (\pi, 2) = (−1, 0, 2)$ y $\bold{r} (\frac{\pi}{2}, 4) = (0, 1, 4)$ están en $S$.

Aunque trazar puntos puede darnos una idea de la forma de la superficie, normalmente necesitamos bastantes puntos para ver la forma. Dado que se necesita mucho tiempo para trazar docenas o cientos de puntos, usamos otra estrategia. Para visualizar $S$, visualizamos dos familias de curvas que se encuentran en $S$. En la primera familia de curvas mantenemos $u$ constante; en la segunda familia de curvas mantenemos $v$ constante. Esto nos permite construir un “esqueleto” de la superficie, obteniendo así una idea de su forma.

Primero, supón que $u$ es una constante $K$. Entonces la curva trazada por la parametrización es $\lang cos\; K, sen\; K, v\rang$, lo que da una línea vertical que pasa por el punto $(cos \;K, sen \;K, v)$ en el plano $xy$.

Ahora supón que $v$ es una constante $K$. Entonces la curva trazada por la parametrización es $\lang cos\; u, sen\; u, K\rang$, lo que da un círculo en el plano $z = K$ con radio $1$ y centro $(0, 0, K$).

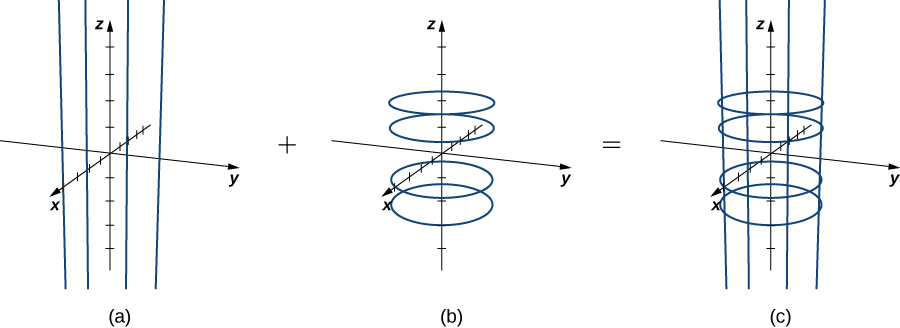
Si $u$ se mantiene constante, obtenemos líneas verticales; si $v$ se mantiene constante, obtenemos círculos de radio $1$ centrados alrededor de la línea vertical que pasa por el origen. Por tanto, la superficie trazada por la parametrización es el cilindro $x^2 + y^2 = 1$ (Observa la siguiente figura).

Figura 6.57. (a) Líneas $\lang cos\; K, sen \;K, v\rang$ para $K = 0, \frac{\pi}{2}, \pi$ y $\frac{3\pi}{2}$. (b) Círculos $\lang cos\; u, sen\; u, K\rang$ para $K = −2, −1, 1$ y $2$. (c) Las líneas y los círculos juntos. A medida que varían $u$ y $v$, describen un cilindro.

Observa que si $x = cos\; u$ y $y = sen \;u$, entonces $x^2 + y^2 = 1$, por lo que los puntos de $S$ se encuentran en el cilindro. A la inversa, cada punto del cilindro está contenido en algún círculo $\lang cos\; u, sen\; u, k\rang$ para algún $k$, y por lo tanto cada punto del cilindro está contenido en la superficie parametrizada (observa la figura).

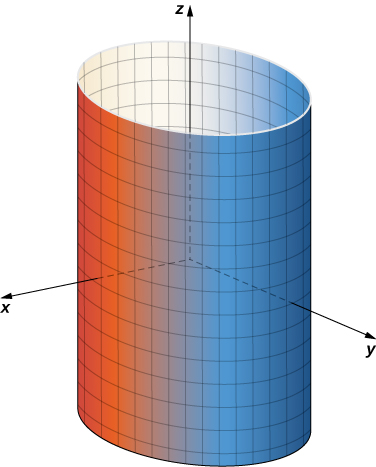
Figura 6.58. El cilindro $x^2 + y^2 = r^2$ tiene parametrización $\bold{r} (u, v) = \lang r cos\; u, r sen\; u, v\rang, 0 \le u \le 2\pi, -\infin \lt v \lt \infin$.

Análisi

Observa que si cambiamos el dominio del parámetro, podríamos obtener una superficie diferente. Por ejemplo, si restringimos el dominio a $0 \le u \le \pi, 0 \lt v \lt 6$, entonces la superficie sería un medio cilindro de altura $6$.