Solución

Sea CC el círculo y sea DD el disco encerrado por CC. El trabajo realizado en la partícula es

W=∮C(y+sen  x)dx+(ey−x)dyW = \oint_C (y + sen\; x)dx + (e^y − x)dy

Como en el ejercicio anterior, esta integral se puede calcular usando las herramientas que hemos aprendido, pero es más fácil usar la integral doble dada por el teorema de Green (ver la siguiente figura).

Deja F(x,y)=⟨P(x,y),Q(x,y)⟩=⟨y+sen  x,ey−x⟩\bold{F} (x, y) = \lang P (x, y), Q (x, y)\rang = \lang y + sen\; x, e^y - x\rang. Entonces, Qx=−1Q_x = −1 y Py=1P_y = 1. Por lo tanto, Qx−Py=−2Q_x - P_y = −2.

Según el teorema de Green,

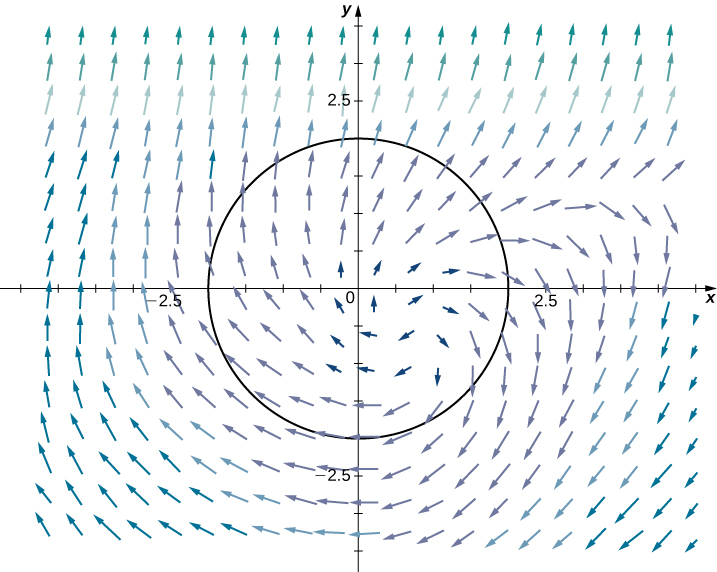
W=∮C(y+sen  x)dx+(ey−x)dy=∬D(Qx−Py)dA=∬D−2dA=−2(aˊrea(D))=−2π(22)=−8π\begin{aligned} W &= \oint_C (y + sen\; x)dx + (e^y − x)dy\\ &= \iint_D(Q_x - P_y)dA = \iint_D -2dA\\ &= −2(área(D)) = −2\pi(2^2) = −8\pi \end{aligned}

Figura 6.36. La integral de línea sobre el círculo límite se puede transformar en una integral doble sobre el disco encerrado por el círculo.