a. $T(u, v) = (g(u, v), h(u, v)), x = g(u, v) = u^3$ y $y = h(u, v) = v^3$. Las funciones $g$ y $h$ son continuas y diferenciables, y las derivadas parciales $g_u(u,v) = 3u^2, g_v(u,v) =0, h_u(u,v) = 0$ y $ h_v(u,v) = 3v^2$ son continuas en $S$.
b. $T(0, 0) = (0, 0), T(1, 0) = (1, 0), T(0, 1) = (0, 1)$, y $T(1, 1) = (1, 1)$.
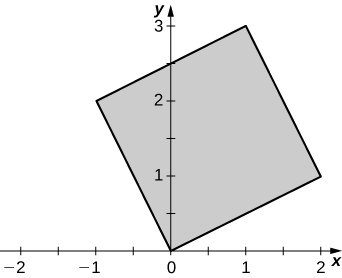
c. Es el cuadrado de vértices $s (0, 0), (2, 1), (1, 3)$, y $(−1, 2)$ en el plano $xy$. Ver la siguiente figura:
