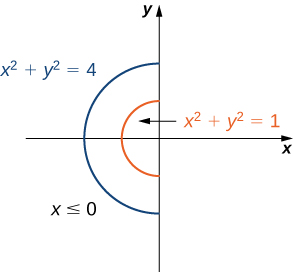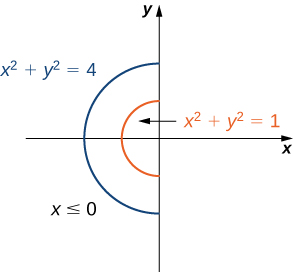Solución
Podemos ver que R R R R = { ( r , θ ) ∣ 1 ≤ r ≤ 2 , π 2 ≤ θ ≤ 3 π 2 } R = \bigg\lbrace \displaystyle(r, \theta) | 1 \le r \le 2, \frac{\pi}{2}\le \theta \le\frac{3\pi}{2}\bigg\rbrace R = { ( r , θ ) ∣1 ≤ r ≤ 2 , 2 π ≤ θ ≤ 2 3 π }
Figura 5.31 . La región anular de integración R R R
Por lo tanto, usando la conversión x = r c o s θ , y = r s e n θ x = r cos \theta, y = r sen \theta x = rcos θ , y = rse n θ d A = r d r d θ dA = r dr d\theta d A = r d r d θ
∬ R ( x + y ) d A = ∫ θ = π / 2 θ = 3 π / 2 ∫ r = 1 r = 2 ( r c o s θ + r s e n θ ) r d r d θ = ( ∫ r = 1 r = 2 r 2 d r ) ( ∫ θ = π / 2 θ = 3 π / 2 ( c o s θ + s e n θ ) d θ ) = [ r 3 3 ] 1 2 [ s e n θ − c o s θ ] ∣ θ = π / 2 θ = 3 π / 2 = − 14 3 \begin{aligned}
\iint_R (x + y) dA &= \int_{\theta=\pi /2}^{\theta = 3\pi /2}\int_{r=1}^{r=2}(r cos \theta + r sen \theta)r dr d\theta\\
&= \bigg(\int_{r=1}^{r=2}r^2dr\bigg)\bigg(\int_{\theta=\pi /2}^{\theta = 3\pi /2}(cos \theta + sen \theta)d\theta\bigg)\\
&= \bigg[\frac{r^3}{3}\bigg]_1^2\big[sen \theta − cos \theta\big]\bigg|_{\theta=\pi /2}^{\theta = 3\pi /2}\\
&= -\frac{14}{3}
\end{aligned} ∬ R ( x + y ) d A = ∫ θ = π /2 θ = 3 π /2 ∫ r = 1 r = 2 ( rcos θ + rse n θ ) r d r d θ = ( ∫ r = 1 r = 2 r 2 d r ) ( ∫ θ = π /2 θ = 3 π /2 ( cos θ + se n θ ) d θ ) = [ 3 r 3 ] 1 2 [ se n θ − cos θ ] ∣ ∣ θ = π /2 θ = 3 π /2 = − 3 14