Solución

Observa que si $u$ se mantiene constante, entonces la curva resultante es un círculo de radio $u$ en el plano $z = u$ . Por lo tanto, a medida que aumenta $u$ , aumenta el radio del círculo resultante. Si $v$ se mantiene constante, entonces la curva resultante es una parábola vertical. Por lo tanto, esperamos que la superficie sea un paraboloide elíptica. Para confirmar esto, observa que

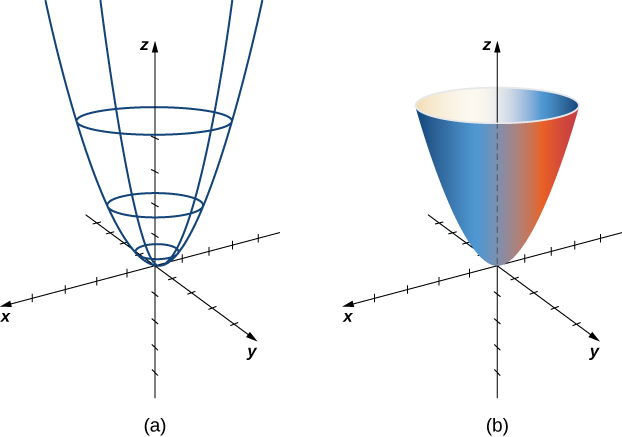
\begin{aligned} x^2+y^2 &= (ucos\;v)^2 + (usen\;v)^2\\ &= u^2cos^2v + u^2sen^2v\\ &= u^2\\ &= z \end{aligned}

Por lo tanto, la superficie es un paraboloide elíptico $x^2 + y^2 = z$ (ver la siguiente figura).

Figura 6.59. (a) Los círculos surgen de mantener $u$ constante; las parábolas verticales surgen de mantener constante $v$ . (b) Un paraboloide elíptico resulta de todas las opciones de $u$ y $v$ en el dominio de parámetros.