Solución
En primer lugar, dado que c o s θ = 3 / 5 cos \theta = 3/5 cos θ = 3/5 θ \theta θ
s e n θ = 1 − ( 3 5 ) 2 = 16 25 = 4 6 sen\theta = \sqrt{1-\bigg(\frac35\bigg)^2} = \sqrt{\frac{16}{25}} = \frac{4}{6} se n θ = 1 − ( 5 3 ) 2 = 25 16 = 6 4 Usando f ( x , y ) = x 2 − x y + 3 y 2 f (x, y) = x^2 - xy + 3y^2 f ( x , y ) = x 2 − x y + 3 y 2 f ( x + h c o s θ , y + h s e n θ ) f (x + h cos \theta, y + h sen \theta) f ( x + h cos θ , y + h se n θ ) f ( x + h c o s θ , y + h s e n θ ) = ( x + h c o s θ ) 2 − ( x + h c o s θ ) ( y + h s e n θ ) + 3 ( y + h s i n θ ) 2 = x 2 + 2 x h c o s θ + h 2 c o s 2 θ − x y − x h s e n θ − y h c o s θ − h 2 s e n θ c o s θ + 3 y 2 + 6 y h s e n θ + 3 h 2 s e n 2 θ = x 2 + 2 x h ( 3 5 ) + 9 h 2 25 − x y − 4 x h 5 − 3 y h 5 − 12 h 2 25 + 3 y 2 + 6 y h ( 4 5 ) + 3 h 2 ( 16 25 ) = x 2 − x y + 3 y 2 + 2 x h 5 + 9 h 2 5 + 21 y h 5 \begin{aligned}
f (x + h cos \theta, y + h sen \theta) &= (x + h cos \theta)^2 − (x + h cos \theta)(y + h sen \theta) + 3(y + h sin \theta)^2\\
&= x^2 + 2xh cos \theta + h^2cos^2\theta − xy − xh sen \theta − yh cos \theta\\
& −h^2sen \theta cos \theta + 3y^2 + 6yh sen \theta + 3h^2sen^2\theta\\
&= x^2 + 2xh\bigg(\frac35\bigg) + \frac{9h^2}{25} − xy − \frac{4xh}{5} − \frac{3yh}{5} − \frac{12h^2}{25} + 3y^2\\
& +6yh\bigg(\frac45\bigg) + 3h^2\bigg(\frac{16}{25}\bigg)\\
&= x^2 − xy + 3y^2 + \frac{2xh}{5} + \frac{9h^2}{5} + \frac{21yh}{5}
\end{aligned} f ( x + h cos θ , y + h se n θ ) = ( x + h cos θ ) 2 − ( x + h cos θ ) ( y + h se n θ ) + 3 ( y + h s in θ ) 2 = x 2 + 2 x h cos θ + h 2 co s 2 θ − x y − x h se n θ − y h cos θ − h 2 se n θ cos θ + 3 y 2 + 6 y h se n θ + 3 h 2 se n 2 θ = x 2 + 2 x h ( 5 3 ) + 25 9 h 2 − x y − 5 4 x h − 5 3 y h − 25 12 h 2 + 3 y 2 + 6 y h ( 5 4 ) + 3 h 2 ( 25 16 ) = x 2 − x y + 3 y 2 + 5 2 x h + 5 9 h 2 + 5 21 y h
Sustituimos esta expresión en la ecuación 4.36:
D u f ( a , b ) = lim h → 0 f ( a + h c o s θ , b + h s e n θ ) − f ( a , b ) h = lim h → 0 ( x 2 − x y + 3 y 2 + 2 x h 5 + 9 h 2 5 + 21 y h 5 ) − ( x 2 − x y + 3 y 2 ) h = lim h → 0 2 x h 5 + 9 h 2 5 + 21 y h 5 h = lim h → 0 2 x 5 + 9 h 5 + 21 y 5 = 2 x + 21 y 5 \begin{aligned}
D_\bold{u}f(a, b) &= \lim\limits_{h \to 0}\frac{f(a + h cos \theta, b + h sen \theta) − f(a, b)}{h}\\
&= \lim\limits_{h \to 0}\frac{\bigg(x^2 − xy + 3y^2 + \frac{2xh}{5} + \frac{9h^2}{5} + \frac{21yh}{5}\bigg)-\big(x^2- xy + 3y^2\big)}{h}\\
&= \lim\limits_{h \to 0}\frac{\frac{2xh}{5} + \frac{9h^2}{5} + \frac{21yh}{5}}{h}\\
&= \lim\limits_{h \to 0}\frac{2x}{5} + \frac{9h}{5} + \frac{21y}{5}\\
&= \frac{2x+21y}{5}
\end{aligned} D u f ( a , b ) = h → 0 lim h f ( a + h cos θ , b + h se n θ ) − f ( a , b ) = h → 0 lim h ( x 2 − x y + 3 y 2 + 5 2 x h + 5 9 h 2 + 5 21 y h ) − ( x 2 − x y + 3 y 2 ) = h → 0 lim h 5 2 x h + 5 9 h 2 + 5 21 y h = h → 0 lim 5 2 x + 5 9 h + 5 21 y = 5 2 x + 21 y Para calcular D u f ( − 1 , 2 ) D_\bold{u} f (−1, 2) D u f ( − 1 , 2 ) x = − 1 x = −1 x = − 1 y = 2 y = 2 y = 2
D u f ( − 1 , 2 ) = 2 ( − 1 ) + 21 ( 2 ) 5 = − 2 + 42 5 = 8 \begin{aligned}
D_\bold{u} f (−1, 2) &= \frac{2(−1) + 21(2)}{5}\\
&= \frac{-2+42}{5}\\
&= 8
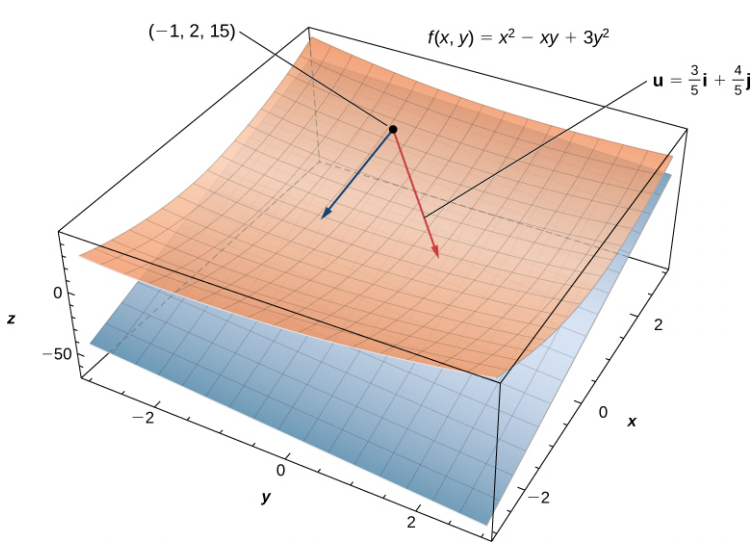
\end{aligned} D u f ( − 1 , 2 ) = 5 2 ( − 1 ) + 21 ( 2 ) = 5 − 2 + 42 = 8 Observa la siguiente figura:
Figura 4.40 . Encontrar la derivada direccional en una dirección dada u \bold{u} u ( − 1 , 2 , 15 ) (−1, 2, 15) ( − 1 , 2 , 15 )