Solución

La sección transversal horizontal del cono a la altura z=uz = u es el círculo x2+y2=u2x^2 + y^2 = u^2. Por lo tanto, un punto en el cono a la altura uu tiene coordenadas (ucos  v,usen  v,u)(u cos\; v, u sen\; v, u) para el ángulo vv. Por lo tanto, una parametrización del cono es r(u,v)=⟨ucos  v,usen  v,u⟩\bold{r} (u, v) = \lang u cos\; v, u sen\; v , u\rang. Dado que no estamos interesados en todo el cono, solo en la porción en o por encima del plano z=−2z = −2, el dominio del parámetro está dado por −2≤u<∞,0≤v<2π−2 \le u \lt\infin, 0 \le v \lt 2\pi (observa la figura).

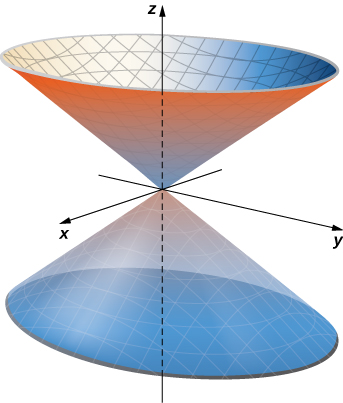
Figura 6.60. El cono x2+y2=z2x^2 + y^2 = z^2 tiene parametrización r(u,v)=⟨ucos  v,usen  v,u⟩,−∞<u<∞,0≤v≤2π\bold{r} (u, v) = \lang u cos\; v, u sen\; v, u\rang, −\infin \lt u \lt\infin, 0 \le v \le 2\pi.