Solución

Sigamos la estrategia de resolución de problemas:

1. La función de optimización es $f(x,y) = x^2 + 4y^2 − 2x + 8y$. Para determinar la función de restricción, primero debemos restar $7$ de ambos lados de la restricción. Esto da $x + 2y − 7 = 0$. La función de restricción es igual al lado izquierdo, entonces $g(x,y) = x + 2y − 7$. El problema nos pide que resolvamos el valor mínimo de $f$, sujeto a la restricción (ver el siguiente gráfico).
   

   

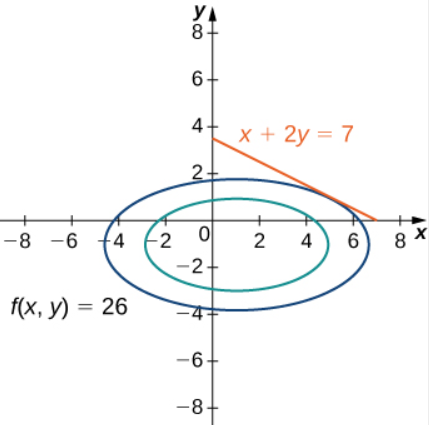
   Figura 4.61. Gráfico de curvas de nivel de la función $f(x,y) = x^2+4y^2−2x+8y$ correspondiente a $c= 10$ y $26$. El gráfico rojo es la función de restricción.

   
   
2. Luego debemos calcular los gradientes de $f$ y $g$:
   $$\begin{aligned} \nabla f(x, y) &= (2x - 2)\bold{i} + (8y + 8)\bold{j}\\ \nabla g(x, y) &= \bold{i} + 2\bold{j} \end{aligned}$$ La ecuación $\nabla f(x_0, y_0) = \lambda \nabla g(x_0, y_0)$ se convierte en
   $$(2x_0 - 2)\bold{i} + (8y_0 + 8)\bold{j} = \lambda(\bold{i} + 2\bold{j})$$ que puede reescribirse como
   $$(2x_0 - 2)\bold{i} + (8y_0 + 8)\bold{j} = \lambda\bold{i} + 2\lambda\bold{j}$$ A continuación, establecemos los coeficientes de $\bold{i}$ y $\bold{j}$ iguales entre sí:
   $$\begin{aligned} 2x_0 - 2 &= \lambda\\ 8y_0 + 8 &= 2\lambda \end{aligned}$$ La ecuacion $g(x_0, y_0) = 0$ se convierte $X_0 + 2y_0 - 7 = 0$. Por lo tanto, el sistema de ecuaciones que necesita ser resuelto es
   $$\begin{aligned} 2x_0 -2 &=\lambda\\ 8y_0 + 8 &= 2\lambda\\ x_0 + 2y_0 - 7 &=0 \end{aligned}$$
3. Este es un sistema lineal de tres ecuaciones en tres variables. Comenzamos resolviendo la segunda ecuación para $\lambda$ y sustituyéndolo en la primera ecuación. Esto da $\lambda = 4y_0 + 4$ , sustituyendo esto en la primera ecuación, obtenemos
   $$2x_0 - 2 = 4y_0 + 4$$ Resolviendo esta ecuación para $x_0$ da $X_0 = 2y_0 + 3$. Luego sustituimos esto en la tercera ecuación:
   $$\begin{aligned} (2y_0 + 3) + 2y_0 - &= 0\\ 4y_0 - &= 0\\ y_0 &= 1 \end{aligned}$$ Ya que $x_0= 2y_0 + 3$, entonces $x_0 = 5$.
4. A continuación, sustituimos $( 5 , 1 )$ dentro $f( x , y) = x^2+ 4y^2- 2 x + 8 y$, o sea $f( 5 , 1 ) = 5^2+ 4(1)^2 - 2(5) + 8(1) = 27$. Para garantizar que esto corresponde a un valor mínimo en la función de restricción, intentemos con otros valores, como las intersecciones de $g(x,y) = 0$, los cuales son $( 7 , 0 )$ y $( 0 , 3.5 )$ Obtenemos $f( 7 , 0 ) = 35$ y $f( 0 , 3.5 ) = 77$, según parece $f$ tiene un mínimo en $( 5 , 1 )$.