Solución

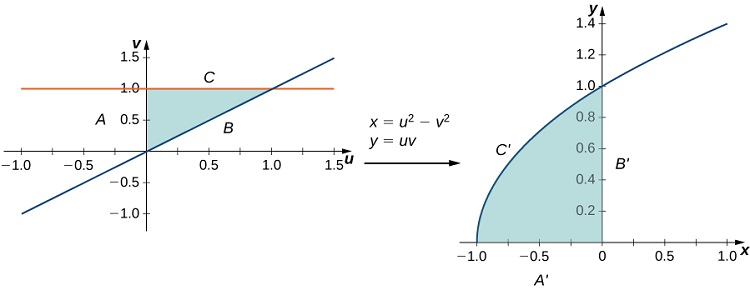
El triángulo y su imagen se muestran en la siguiente figura. Para entender cómo se transforman los lados del triángulo, llama al lado que une $(0, 0)$ y $(0, 1)$ el lado $A$, el lado que une $(0, 0)$ y $(1,1)$ el lado $B$, y el lado que une $(1, 1)$ y $(0, 1)$ el lado $C$.

Figura 5.73. Una región triangular en el plano $uv$ se transforma en una imagen en el plano $xy$.

Para el lado $A: u = 0, 0 \le v \le 1$ se transforma a $x = −v^2, y = 0$, entonces este es el lado $A^{\prime}$ que une $(−1, 0)$ y $(0, 0)$.

Para el lado $B: u = v, 0 \le u \le 1$ se transforma a $x = 0, y = u^2$ por lo que este es el lado $B^{\prime}$′ que une $(0, 0)$ y $(0, 1)$.

Para el lado $C: 0 \le u \le 1, v = 1$ se transforma a $x = u^2 - 1, y = u$(por lo tanto, $x = y^2 - 1$) por lo que este es el lado $C^{\prime}$ que hace la mitad superior del arco parabólico que une $(-1, 0)$ y $(0, 1)$.

Todos los puntos en toda la región del triángulo en el plano $uv$ están mapeados dentro de la región parabólica en el plano $xy$.