Aproximando el volumen con signo usando una suma de Riemann con m=n=2 tenemos ΔA=ΔxΔy=1×1=1. Además, los puntos de muestra son (1,1),(2,1),(1,2), y (2,2) como se muestra en la siguiente figura.
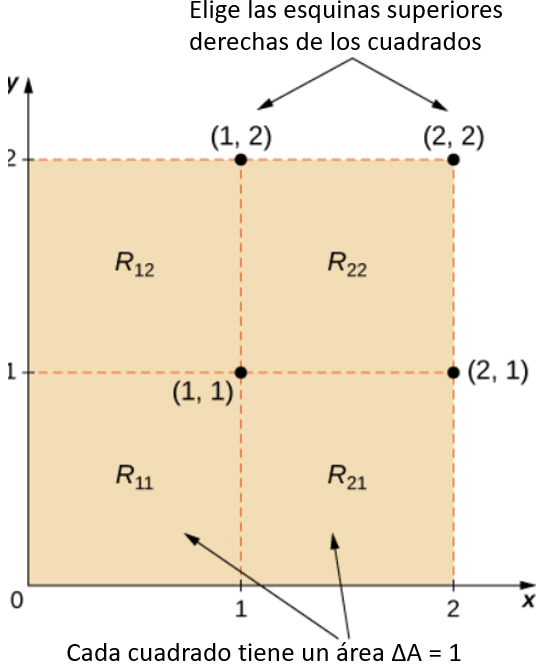
Figura 5.6. Subrectangulos para la región rectangular R=[0,2]×[0,2].
Por lo tanto,
V=i=1∑2j=1∑2f((xij∗,yij∗))ΔA=i=1∑2(f(xi1∗,yi1∗)+f(xi2∗,yi2∗))ΔA=f(x11∗,y11∗)ΔA+f(x12∗,y12∗)ΔA+f(x22∗,y22∗)ΔA=f(1,1)(1)+f(2,1)(1)+f(1,2)(1)+f(2,2)(1)=(3−1)(1)+(12−1)(1)+(3−2)(1)+(12−2)(1)=2+11+1+10=24
