Solución

La región QQ es un tetraedro (ver figura) que se encuentra con los ejes en los puntos (6,0,0),(0,3,0)y(0,0,2)(6, 0, 0), (0, 3, 0) y (0, 0, 2). Para encontrar los límites de integración, sea z=0z = 0 en el plano inclinado z=13(6−x−2y)z = \frac13(6 - x - 2y). Luego, para xx e yy, encuentra la proyección de QQ sobre el plano xyxy, que está limitado por los ejes y la línea x+2y=6x + 2y = 6. Por lo tanto, la masa es

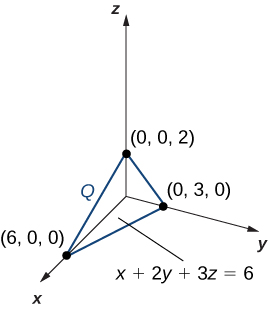
m=∭Qρ(x,y,z)dV=∫x=0x=6∫y=0y=1/2(6−x)∫z=0z=1/3(6−x−2y)x2yzdzdydx=10835≈3.086m = \iiint_Q \rho(x,y,z)dV = \int_{x=0}^{x=6}\int_{y=0}^{y=1/2(6-x)}\int_{z=0}^{z=1/3(6-x-2y)} x^2yzdzdydx = \frac{108}{35} \approx 3.086

Figura 5.70. Encontrando la masa de un sólido QQ