Solución

El integrando es f(x,y)=2f (x, y) = 2. La siguiente figura muestra la gráfica de f(x,y)=2f (x, y) = 2, la curva CC y la hoja formada por ellos. Observa que esta hoja tiene la misma área que un rectángulo con ancho π\pi y largo 22. Por lo tanto, ∫C2ds=2π\displaystyle\int_C2ds = 2\pi.

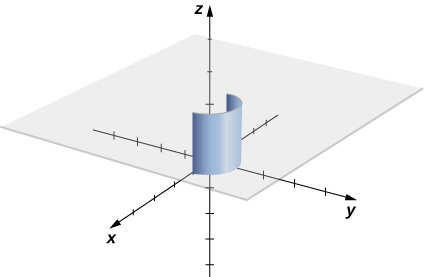
Figura 6.14. La hoja que está formada por la mitad superior del círculo unitario en un plano y la gráfica de f(x,y)=2f (x, y) = 2.

Para ver que ∫C2ds=2π\displaystyle\int_C2ds = 2\pi usando la definición de integral de línea, dejamos que r(t)\bold{r} (t) sea una parametrización de CC. Entonces, f(r(ti))=2f(\bold{r} (t_i)) = 2 para cualquier número tit_i en el dominio de r\bold{r}. Por lo tanto,

∫Cfds=lim⁡n→∞∑i=1nf(r(ti∗))Δsi=lim⁡n→∞∑i=1n2Δsi=2lim⁡n→∞∑i=1nΔsi=2(longitud de C)=2π\begin{aligned} \int_C fds &= \lim\limits_{n \to \infin}\sum_{i=1}^n f\big(\bold{r}(t_i^*)\big)\Delta s_i\\ &= \lim\limits_{n \to \infin}\sum_{i=1}^n 2\Delta s_i\\ &= 2\lim\limits_{n \to \infin}\sum_{i=1}^n \Delta s_i\\ &= 2(\text{longitud de }C)\\ &= 2\pi \end{aligned}