Solución

Coloca el origen en la esquina suroeste del mapa para que todos los valores puedan considerarse como del primer cuadrante y, por lo tanto, todos sean positivos. Ahora divide todo el mapa en seis rectángulos $(m = 2 \text{ y } n = 3)$ , como se muestra en la figura 5.11. Supón que $f (x, y)$ denota la lluvia de la tormenta en pulgadas en un punto aproximadamente $x$ millas al este del origen y $y$ millas al norte del origen. Supongamos que $R$ representa el área completa de $250 × 300 = 75000$ millas cuadradas. Entonces el área de cada subrectangulo es

\Delta A = \frac16(75000) = 12500

Supón que $(x_{ij}^*, y_{ij}^*)$ son aproximadamente los puntos medios de cada subrectangulo $R_{ij}$ . Observa la región codificada por colores en cada uno de estos puntos y calcula la lluvia. La precipitación en cada uno de estos puntos se puede estimar como:

En $(x_{11}, y_{11})$ la precipitación es $0.08$ .
En $(x_{12}, y_{12})$ la precipitación es $0.08$ .
En $(x_{13}, y_{13})$ la precipitación es $0.01$ .
En $(x_{21}, y_{21})$ la precipitación es $1.70$ .
En $(x_{22}, y_{22})$ la precipitación es $1.74$ .
En $(x_{23}, y_{23})$ la precipitación es $3.00$ .

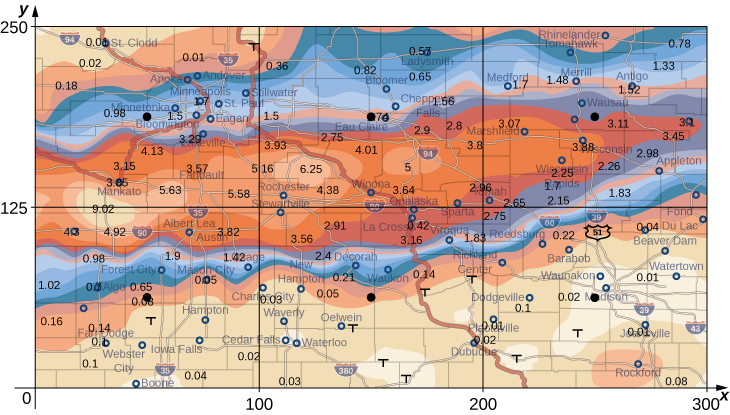
Figura 5.11. Tormenta de lluvia con ejes rectangulares y mostrando los puntos medios de cada subrectangulo.

Según nuestra definición, la precipitación pluvial promedio en toda el área durante esos dos días fue

\begin{aligned} f_{prom} &= \frac{1}{\text{Área R}}\iint_R f(x, y)dxdy = \frac{1}{75000}\iint_Rf(x, y)dxdy\\ &\cong \frac{1}{75000}\sum_{i=1}^3\sum_{j=1}^2 f(x_{ij}^*, y_{ij}^*)\Delta A\\ &\cong \frac{1}{75000}\big[f(x_{11}^*, y_{11}^*)\Delta A + f(x_{12}^*, y_{12}^*)\Delta A\\ &\text{ } \text{ }\text{ }\text{ }+ f(x_{13}^*, y_{13}^*)\Delta A + f(x_{22}^*, y_{22}^*)\Delta A + f(x_{23}^*, y_{23}^*)\Delta A\big]\\ &\cong \frac{1}{75000}[0.08 + 0.08 + 0.01 + 1.70 + 1.74 + 3.00]\Delta A\\ &\cong \frac{1}{75000}[0.08 + 0.08 + 0.01 + 1.70 + 1.74 + 3.00]12500\\ &\cong \frac{5}{30}[0.08 + 0.08 + 0.01 + 1.70 + 1.74 + 3.00]\\ &\cong 1.10 \end{aligned}

Del 22 al 23 de septiembre de 2010, esta área tuvo una precipitación pluvial promedio de aproximadamente $1.10$ pulgadas.