Solución

La región DD no es fácil de descomponer en ningún tipo; En realidad es una combinación de diferentes tipos. Entonces podemos escribirlo como una unión de tres regiones D1,D2D_1, D_2 y D3D_3 donde, D1={(x,y)∣−2≤x≤0,0≤y≤(x+2)2},D2=(x,y)∣0≤y≤4,0≤x≤(y−116y3)}D_1 = \lbrace (x, y) | - 2 \le x \le 0, 0 \le y \le (x + 2)^2\rbrace, D_2 = (x, y) | 0 \le y \le 4, 0 \le x \le \big(y − \frac{1}{16}y^3\big)\rbrace. Estas regiones se ilustran más claramente en la figura 5.20.

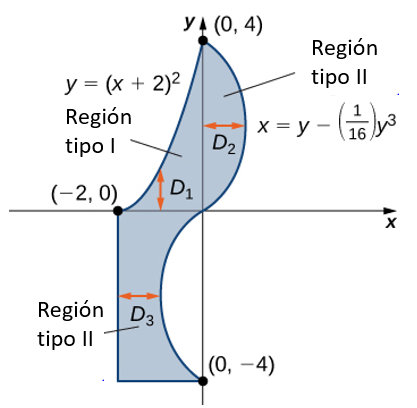
Figura 5.20. La división de la región en tres subregiones facilita la configuración de la integración.

Aquí D1D_1 es Tipo I y D2D_2 y D3D_3 son de Tipo II. Por lo tanto,

∬D(2x+5y)dA=∬D1(2x+5y)dA+∬D2(2x+5y)dA+∬D3(2x+5y)dA=∫x=−2x=0∫y=0y=(x+2)2(2x+5y)dydx+∫y=0y=4∫x=0x=y−(1/16)y3(2x+5y)dxdy        +∫y=−4y=0∫x=−2x=y−(1/16)y3(2x+5y)dxdy=∫x=−2x=0[12(2+x)2(20+24x+5x2]dx+∫y=0y=4[1256y6−716y4+6y2]dy        +∫y=−4y=0[1256y6−716y4+6y2+10y−4]dy=403+166435−169635=1304105\begin{aligned} \iint_D(2x+5y)dA &= \iint_{D_1}(2x+5y)dA + \iint_{D_2}(2x+5y)dA + \iint_{D_3}(2x+5y)dA\\ &= \int_{x=-2}^{x=0}\int_{y=0}^{y=(x+2)^2}(2x+5y)dydx + \int_{y=0}^{y=4}\int_{x=0}^{x=y-(1/16)y^3}(2x+5y)dxdy\\ &\;\;\;\;+ \int_{y=-4}^{y=0}\int_{x=-2}^{x=y-(1/16)y^3}(2x+5y)dxdy \\ &= \int_{x=-2}^{x=0}\bigg[\frac12(2+x)^2(20+24x+5x^2\bigg]dx + \int_{y=0}^{y=4}\bigg[\frac{1}{256}y^6 - \frac{7}{16}y^4 + 6y^2\bigg]dy\\ &\;\;\;\;+ \int_{y=-4}^{y=0}\bigg[\frac{1}{256}y^6 - \frac{7}{16}y^4 + 6y^2 + 10y - 4\bigg]dy\\ &= \frac{40}{3} + \frac{1664}{35} - \frac{1696}{35} = \frac{1304}{105} \end{aligned}