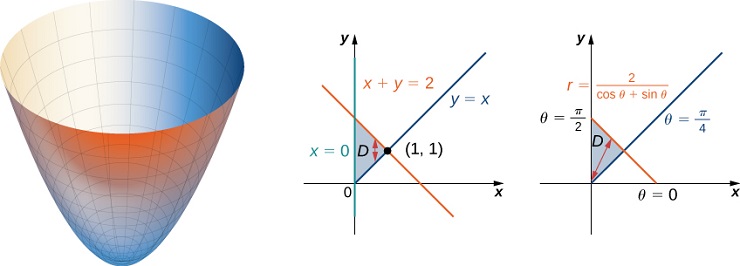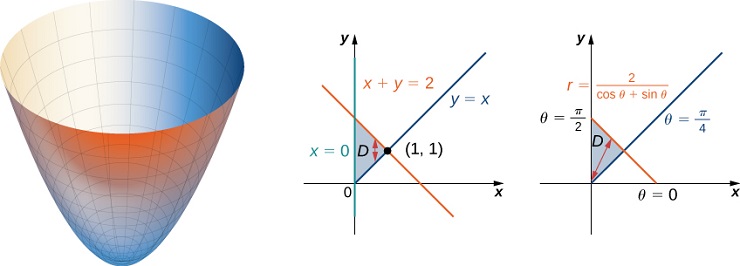Solución
Primero examina la región sobre la cual necesitamos establecer la integral doble y el paraboloide acompañante.
Figura 5.36 . Encontrar el volumen de un sólido debajo de un paraboloide y encima de un triángulo dado
La región D D D { ( x , y ) ∣ 0 ≤ x ≤ 1 , x ≤ y ≤ 2 − x } \lbrace (x, y) | 0 \le x \le 1, x \le y \le 2 - x\rbrace {( x , y ) ∣0 ≤ x ≤ 1 , x ≤ y ≤ 2 − x } y = x , x = 0 y = x, x = 0 y = x , x = 0 x + y = 2 x + y = 2 x + y = 2 x y xy x y r r r θ \theta θ θ = π / 4 , θ = π / 2 \theta = \pi / 4, \theta = \pi / 2 θ = π /4 , θ = π /2 r = 2 / ( c o s θ + s e n θ ) r = 2 / (cos \theta + sen \theta) r = 2/ ( cos θ + se n θ )
Graficando la región en el plano x y xy x y D = { ( r , θ ) ∣ π / 4 ≤ θ ≤ π / 2 , 0 ≤ r ≤ 2 / ( c o s θ + s e n θ ) } D = \lbrace (r, \theta) | \pi / 4 \le \theta \le\pi / 2, 0 \le r \le 2 / (cos \theta + sen \theta)\rbrace D = {( r , θ ) ∣ π /4 ≤ θ ≤ π /2 , 0 ≤ r ≤ 2/ ( cos θ + se n θ )} z = x 2 + y 2 = r 2 z = x^2 + y^2 = r^2 z = x 2 + y 2 = r 2
V = ∬ D f ( r , θ ) r d r d θ = ∫ θ = π / 4 θ = π / 2 ∫ r = 0 r = 2 / ( c o s θ + s e n θ ) r 2 r d r d θ = ∫ π / 4 π / 2 [ r 4 4 ] 0 2 / ( c o s θ + s e n θ ) = 1 4 ∫ π / 4 π / 2 ( 2 c o s θ + s e n θ ) d θ = 16 4 ∫ π / 4 π / 2 ( 1 c o s θ + s e n θ ) d θ = 4 ∫ π / 4 π / 2 ( 1 c o s θ + s e n θ ) d θ \begin{aligned}
V &= \iint_D f(r, \theta)r dr d\theta = \int_{\theta =\pi /4}^{\theta = \pi /2}\int_{r=0}^{r=2 / (cos \theta + sen \theta)}r^2rdrd\theta\\
&= \int_{\pi /4}^{ \pi /2}\bigg[\frac{r^4}{4}\bigg]_0^{2 / (cos \theta + sen \theta)} = \frac14\int_{\pi /4}^{ \pi /2}\bigg(\frac{2}{cos \theta + sen \theta}\bigg)d\theta\\
&= \frac{16}{4}\int_{\pi /4}^{ \pi /2}\bigg(\frac{1}{cos \theta + sen \theta}\bigg)d\theta = 4\int_{\pi /4}^{ \pi /2}\bigg(\frac{1}{cos \theta + sen \theta}\bigg)d\theta
\end{aligned} V = ∬ D f ( r , θ ) r d r d θ = ∫ θ = π /4 θ = π /2 ∫ r = 0 r = 2/ ( cos θ + se n θ ) r 2 r d r d θ = ∫ π /4 π /2 [ 4 r 4 ] 0 2/ ( cos θ + se n θ ) = 4 1 ∫ π /4 π /2 ( cos θ + se n θ 2 ) d θ = 4 16 ∫ π /4 π /2 ( cos θ + se n θ 1 ) d θ = 4 ∫ π /4 π /2 ( cos θ + se n θ 1 ) d θ Como puedes ver, esta integral es muy complicada. Entonces, podemos evaluar esta integral doble en coordenadas rectangulares como
V = ∫ 0 1 ∫ x 2 − x ( x 2 + y 2 ) d y d x V = \int_0^1\int_x^{2-x}(x^2+y^2)dydx V = ∫ 0 1 ∫ x 2 − x ( x 2 + y 2 ) d y d x Evaluando, obtenemos
∫ 0 1 ∫ x 2 − x ( x 2 + y 2 ) d y d x = ∫ 0 1 [ x 2 y + y 3 3 ] ∣ x 2 − x = ∫ 0 1 8 3 − 4 x + 4 x 2 − 8 x 3 3 d x = [ 8 x 3 − 2 x 2 + 4 x 3 3 − 2 x 4 3 ] ∣ 0 1 = 4 3 \begin{aligned}
\int_0^1\int_x^{2-x}(x^2+y^2)dydx &= \int_0^1\bigg[x^2y + \frac{y^3}{3}\bigg]\bigg|_x^{2-x}\\
&= \int_0^1 \frac83 -4x+4x^2 - \frac{8x^3}{3}dx\\
&= \bigg[\frac{8x}{3} - 2x^2 + \frac{4x^3}{3} - \frac{2x^4}{3}\bigg]\bigg|_0^1 = \frac43
\end{aligned} ∫ 0 1 ∫ x 2 − x ( x 2 + y 2 ) d y d x = ∫ 0 1 [ x 2 y + 3 y 3 ] ∣ ∣ x 2 − x = ∫ 0 1 3 8 − 4 x + 4 x 2 − 3 8 x 3 d x = [ 3 8 x − 2 x 2 + 3 4 x 3 − 3 2 x 4 ] ∣ ∣ 0 1 = 3 4