Solución

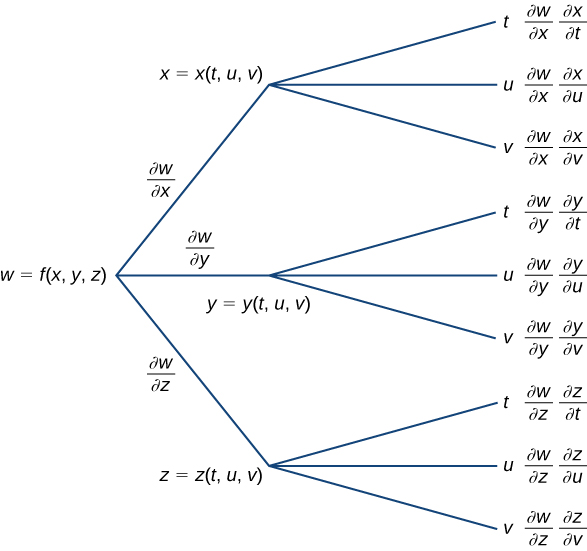
Comenzando desde la izquierda, la función ff tiene tres variables independientes: xx, yy y zz. Por lo tanto, tres ramas deben surgir del primer nodo. Cada una de estas tres ramas también tienen tres ramas, para cada una de las variables tt, uu y vv.

Figura 4.36. Diagrama de árbol para una función de tres variables, cada una de las cuales es una función de tres variables independientes.

Las tres fórmulas son:

∂w∂t=∂w∂x∂x∂t+∂w∂y∂y∂t+∂w∂z∂z∂t\frac{\partial w}{\partial t} = \frac{\partial w}{\partial x}\frac{\partial x}{\partial t} + \frac{\partial w}{\partial y}\frac{\partial y}{\partial t} + \frac{\partial w}{\partial z}\frac{\partial z}{\partial t} ∂w∂u=∂w∂x∂x∂u+∂w∂y∂y∂u+∂w∂z∂z∂u\frac{\partial w}{\partial u} = \frac{\partial w}{\partial x}\frac{\partial x}{\partial u} + \frac{\partial w}{\partial y}\frac{\partial y}{\partial u} + \frac{\partial w}{\partial z}\frac{\partial z}{\partial u} ∂w∂v=∂w∂x∂x∂v+∂w∂y∂y∂v+∂w∂z∂z∂v\frac{\partial w}{\partial v} = \frac{\partial w}{\partial x}\frac{\partial x}{\partial v} + \frac{\partial w}{\partial y}\frac{\partial y}{\partial v} + \frac{\partial w}{\partial z}\frac{\partial z}{\partial v}