Solución

Primero graficamos la región DD (Figura 5.26); entonces la expresamos de otra manera.

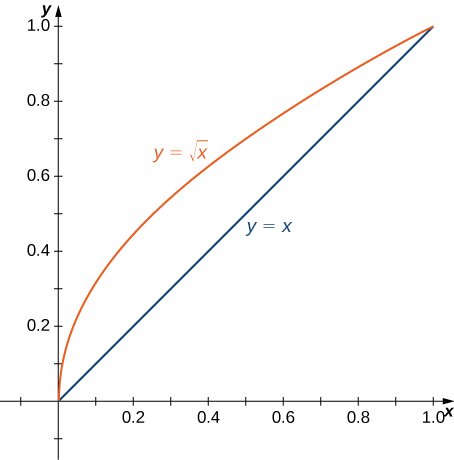
Figura 5.26. La función ff es continua en todos los puntos de la región DD excepto en (0,0)(0, 0).

La otra forma de expresar la misma región DD es

D={(x,y):0≤y≤1,y2≤x≤y}D = \lbrace (x, y): 0 \le y \le 1, y^2 \le x \le y\rbrace

Por lo tanto, podemos usar el teorema de Fubini para integrales impropias y evaluar la integral como

∫y=0y=1∫x=y2x=yeyydxdy\int_{y=0}^{y=1}\int_{x=y^2}^{x=y} \frac{e^y}{y}dxdy

Por lo tanto, tenemos

∫y=0y=1∫x=y2x=yeyydxdy=∫y=0y=1eyy∣x=y2x=ydy=∫y=0y=1eyy(y−y2)dy=∫01(ey−yey)dy=e−2\int_{y=0}^{y=1}\int_{x=y^2}^{x=y} \frac{e^y}{y}dxdy = \int_{y=0}^{y=1}\frac{e^y}{y}\bigg|_{x=y^2}^{x=y}dy = \int_{y=0}^{y=1}\frac{ey}{y}(y-y^2)dy = \int_0^1(ey - ye^y)dy = e - 2