Solución

Los tiempos de espera son modelados matemáticamente por funciones de densidad exponencial, siendo $m$ el tiempo de espera promedio, como

f(t) = \begin{cases} 0 &\text{si } t\lt 0 \\ \frac{1}{m}e^{-t/m} &\text{si } t\ge 0 \end{cases}

Si $X$ e $Y$ son variables aleatorias para "esperar una mesa" y "completar la comida", entonces las funciones de densidad de probabilidad son, respectivamente,

f_1(x) = \begin{cases} 0 &\text{si } x\lt 0 \\ \frac{1}{15}e^{-x/15} &\text{si } x\ge 0 \end{cases}

f_2(y) = \begin{cases} 0 &\text{si } y\lt 0 \\ \frac{1}{40}e^{-y/40} &\text{si } y\ge 0 \end{cases}

Claramente, los eventos son independientes y, por lo tanto, la función de densidad conjunta es el producto de las funciones individuales

f(x, y) = f_1(x)f_2(y) =\begin{cases} 0 &\text{si } x\lt 0 \;\;\text{o}\;\; y\le 0\\ \frac{1}{600}e^{-x/15}e^{-y/60} &\text{si } x, y\ge 0 \end{cases}

Queremos encontrar la probabilidad de que el tiempo combinado $X + Y$ sea inferior a $90$ minutos. En términos de geometría, significa que la región $D$ está en el primer cuadrante delimitado por la línea $x + y = 90$ (Figura 5.27).

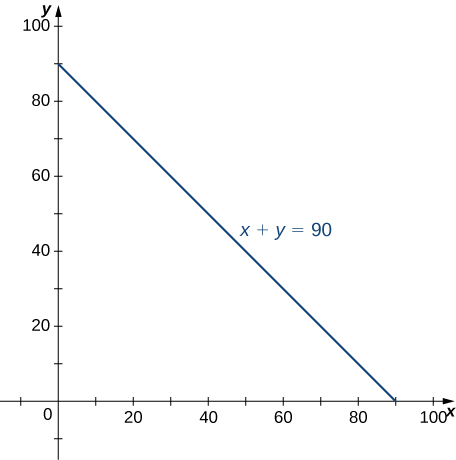
Figura 5.27. La región de integración para una función de densidad de probabilidad conjunta.

Por lo tanto, la probabilidad de que $(X, Y)$ esté en la región $D$ es

P(X + Y \le 90) = P((X, Y) \isin D) = \iint_Df(x, y)dA = \iint_D\frac{1}{600}e^{-x/15}e^{-y/40}dA

Como $x + y = 90$ es lo mismo que $y = 90 - x,$ tenemos una región de Tipo I, entonces

D = \lbrace(x, y):0\le x \le 90, 0 \le y \le 90-x\rbrace

\begin{aligned} P(X+ Y \le 90) &= \frac{1}{600}\int_{x=0}^{x=90}\int_{y=0}^{y=90-x}e^{-x/15}e^{-y/40}dxdy\\ &= \frac{1}{600}\int_{x=0}^{x=90}\int_{y=0}^{y=90-x} e^{-(x/15+y/40)}dxdy = 0.8328 \end{aligned}

Por lo tanto, existe una probabilidad del $83.2$ % de que un cliente pase menos de una hora y media en el restaurante.