Solución

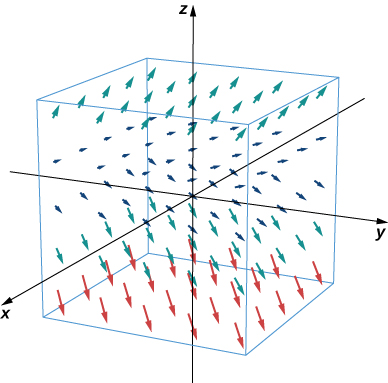
Para este campo vectorial, las componentes $x$ e $y$ son constantes, por lo que cada punto en $\Reals^3$ tiene un vector asociado con componentes $x$ e $y$ iguales a uno. Para visualizar $\bold{F}$, primero consideramos cómo se ve el campo en el plano $xy$. En el plano $xy, z = 0$. Por lo tanto, cada punto de la forma $(a, b, 0)$ tiene un vector $\lang 1, 1, 0\rang$ asociado. Para los puntos que no están en el plano $xy$, pero que están ligeramente por encima de él, el vector asociado tiene una componente $z$ pequeña pero positiva y, por lo tanto, el vector asociado apunta ligeramente hacia arriba. Para los puntos que están muy por encima del plano $xy$, la componente $z$ es grande, por lo que el vector es casi vertical. La siguiente figura muestra este campo vectorial.

Figura 6.7. Una representación visual del campo vectorial $\bold{F} (x, y, z) = \lang 1, 1, z\rang$.