Solución

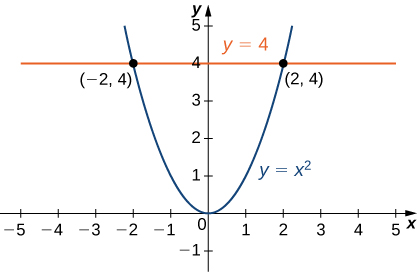
La proyección de la región sólida EE sobre el plano xyxy es la región acotada arriba por y=4y = 4 y abajo por la parábola y=x2y = x^2 como se muestra.

Figura 5.49. Sección transversal en el plano xyxy del paraboloide de la figura 5.48.

Por lo tanto, tenemos

E={(x,y,z)∣−2≤x≤2,x2≤y≤4,−y−x2≤z≤y−x2}E = \lbrace (x, y, z)| − 2 \le x \le 2, x^2 \le y \le 4, − \sqrt{y − x^2} ≤ z ≤ \sqrt{y − x^2}\rbrace

La integral triple se convierte en

∭Ex2+z2dV=∫x=−2x=2∫y=x2y=4∫z=−y−x2z=y−x2x2+z2dzdydz\iiint_E\sqrt{x^2+z^2}dV = \int_{x=-2}^{x=2}\int_{y=x^2}^{y=4}\int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}}\sqrt{x^2+z^2}dzdydz

Aquí el orden de integración cambia de ser primero con respecto a zz, luego yy, y luego xx a ser primero con respecto a yy, luego a zz, y luego a xx. Pronto quedará claro cómo este cambio puede ser beneficioso para la computación. Tenemos

∫x=−2x=2∫z=−y−x2z=y−x2x2+z2∫y=x2+z2y=4x2+z2dydzdx=∫x=−2x=2∫z=−y−x2z=y−x2x2+z2(4−x2−z2)x2+z2dzdx\int_{x=-2}^{x=2}\int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}}\sqrt{x^2+z^2}\int_{y=x^2+z^2}^{y=4}\sqrt{x^2+z^2}dydzdx \\= \int_{x=-2}^{x=2}\int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}}\sqrt{x^2+z^2}(4-x^2-z^2)\sqrt{x^2+z^2}dzdx

Ahora usa la sustitución polar x=rcosθ,z=rsenθx = r cos \theta, z = rsen \theta y dzdx=rdrdθdz dx = r dr d\theta en el plano xzxz. Esto es esencialmente lo mismo que cuando usamos coordenadas polares en el plano xyxy, excepto que reemplazamos yy por zz. En consecuencia, los límites de integración cambian y tenemos, al usar r2=x2+z2r^2 = x^2 + z^2,

∫x=−2x=2∫z=−y−x2z=y−x2x2+z2(4−x2−z2)x2+z2dzdx=∫θ=0θ=2π∫r=0r=2(4−r2)rdrdθ=∫02π[4r33−r55∣02]dθ=∫02π6415dθ=128π15\begin{aligned} \int_{x=-2}^{x=2}\int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}}\sqrt{x^2+z^2}(4-x^2-z^2)\sqrt{x^2+z^2}dzdx &= \int_{\theta=0}^{\theta=2\pi}\int_{r=0}^{r=2}(4-r^2)rdrd\theta\\ &= \int_{0}^{2\pi}\bigg[\frac{4r^3}{3} - \frac{r^5}{5}\bigg|_0^2\bigg]d\theta\\ &= \int_{0}^{2\pi}\frac{64}{15}d\theta = \frac{128\pi}{15} \end{aligned}