Solución

Un bosquejo de la región $R$ siempre es útil, como se muestra en la siguiente figura.

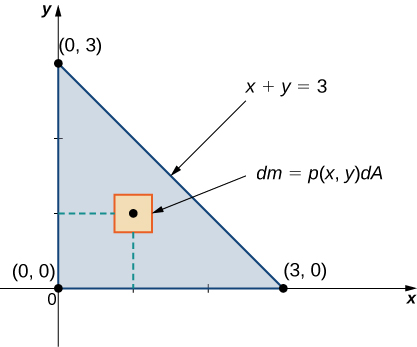
Figura 5.67. Una lámina en el plano $xy$ con densidad $\rho (x, y) = xy$

Usando la expresión desarrollada para masa, vemos que

\begin{aligned} m &= \iint_R dm = \iint_R \rho(x,y)dA = \int_{x=0}^{x=3}\int_{y=0}^{y=3-x} xydydx = \int_{x=0}^{x=3}\bigg[x\frac{y^2}{2}\bigg|_{y=0}^{y=3-x}\bigg]dx\\ &= \int_{x=0}^{x=3}\frac12x(3-x)^2dx = \bigg[\frac{9x^2}{4}- x^3 + \frac{x^4}{8}\bigg]\bigg|_{x=0}^{x=3}\\ &= \frac{27}{8} \end{aligned}

El cálculo es sencillo, dando la respuesta $m = \frac{27}{8}\;kg$ .