Cálculo
Volumen I
INTERACTIVO
Elena E. Álvarez Saiz
Universidad de Cantabria

Juan Guillermo Rivera Berrío
Institución Universitaria Pascual Bravo
Red Educativa Digital Descartes
Fondo Editorial RED Descartes

Córdoba (España)
2021
Título de la obra:
Cálculo - Volumen I
Interactivo
Autores:
Elena Esperanza Álvarez Saiz
Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Obra derivada del libro Calculus Volume 1 de:
Gilbert Strang (Massachusetts Institute of Technology)
Edwin “Jed” Herman (University of Wisconsin-Stevens Point)
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN Obra completa: 978-84-18834-18-9
ISBN Volumen I: 978-84-18834-19-6

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Este libro digital interactivo se ha diseñado con fundamento en la filosofía del Proyecto Descartes: "Trabajando altruistamente por la comunidad educativa de la aldea global", que sólo busca desarrollar contenidos educativos para el provecho de la comunidad académica, esperando únicamente como retribución el uso y difusión de estos contenidos. El contenido del libro, al igual que los objetos interactivos se han diseñado de forma que se puedan leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin. El libro se puede descargar para su uso en local sin dependencia de la red. Algunos de los objetos interactivos se han diseñado con el Editor DescartesJS.
El contenido del libro se basa en un recurso de OpenStax, organización sin fines de lucro de la Universidad de Rice, cuya misión, similar a la nuestra, es mejorar el acceso de los estudiantes a la educación. El libro corresponde al Volumen 1 de Cálculo, que cubre funciones elementales, límites, derivadas y sus aplicaciones e integración.

Figura 1.1. Una porción de la falla de San Andrés en California. Grandes fallas como esta aparecen en los terremotos más fuertes registrados. (crédito: modificación del trabajo por Robb Hannawacker, NPS)
En los últimos años, se han producido grandes terremotos en varios países del mundo. En enero de 2010, un terremoto de magnitud 7.3 golpeó Haití. Un terremoto de magnitud 9 sacudió el noreste de Japón en marzo de 2011. En abril de 2014, un terremoto de magnitud 8.2 sacudió la costa del norte de Chile. ¿Qué significan estos números? En particular, ¿cómo se compara un terremoto de magnitud 9 con un terremoto de magnitud 8.2? ¿o 7.3? Más adelante, en este capítulo, mostraremos cómo se utilizan las funciones logarítmicas para comparar la intensidad relativa de dos terremotos en función de la magnitud de cada uno de ellos (ver Ejemplo 1.39).
El cálculo es la matemática que describe los cambios en las funciones. En este capítulo, se revisarán todas las funciones necesarias para su estudio. Se definirán las funciones polinómicas, racionales, trigonométricas, exponenciales y logarítmicas. Se analizará cómo evaluar estas funciones y se mostrarán las propiedades de sus gráficas.
En este capítulo se proporcionarán también ejemplos de ecuaciones que involucran estas funciones y se ilustrarán técnicas algebraicas que se requieren para resolverlas. En resumen, este capítulo proporcionará la base para el estudio del material de los capítulos siguientes. Es por ello esencial, estar familiarizado con estos conceptos antes de proceder a la introducción formal del cálculo en el próximo capítulo.
En esta sección, se analizará la definición de una función y se examinarán varias formas de representarlas: a través de tablas, fórmulas y gráficas. Se estudiará cómo denotar una función y los términos relacionados con este concepto. También se definirá la composición de funciones y las propiedades de simetría. La mayor parte de este material posiblemente sea ya conocido, pero sirve como referencia útil para recordar algunas de las técnicas algebraicas que se requieren para trabajar con funciones.
Dados dos conjuntos $A$ y $B$, se puede definir una relación de $A$ a $B$ a partir de pares ordenados $(x, y)$, donde $x$ es un elemento de $A$ e $y$ es un elemento de $B$.
Una relación de $A$ a $B$ define un vínculo entre esos dos conjuntos. Una función es un tipo especial de relación en la que cada elemento del primer conjunto está relacionado con exactamente un elemento del segundo conjunto. El elemento del primer conjunto se llama entrada u origen. El elemento del segundo conjunto se denomina salida o imagen. Para cualquier función, cuando conocemos el origen, se determina la imagen, por lo que decimos que la imagen es una función del origen.
Por ejemplo, el área de un cuadrado está determinado por su longitud lateral, esto significa que el área (la salida o imagen) es una función de su longitud lateral (el origen). La velocidad de una pelota lanzada al aire puede describirse como una función de la cantidad de tiempo que la pelota está en el aire. El coste de enviar un paquete por correo es una función del peso del paquete. Como las funciones tienen muchos usos, es importante tener definiciones precisas y terminología adecuada para poder estudiarlas.
Por ejemplo, consideremos la función $f$, donde el dominio es el conjunto de todos los números reales y la regla consiste en obtener el cuadrado de cada número. Así, a la entrada $x = 3$ se le asigna la salida $3^2 = 9$.
Como cada número real no negativo tiene una raíz cuadrada de valor real, será un elemento del rango de esta función. Como no hay números reales con un cuadrado que sea negativo, los números reales negativos no formarán parte del rango o imagen. Concluimos por tanto que el rango es el conjunto de números reales no negativos.
Para una función general $f$ con dominio $D$, es frecuente utilizar $x$ para denotar la entrada y utilizamos $y$ para denotar la imagen o salida asociada a $x$. Al hacerlo, nos referimos a $x$ como la variable independiente e $y$ como la variable dependiente, ya que depende de $x$. Usando la notación de función, se escribirá $y = f (x)$, y esta expresión se leerá de la siguiente forma: "$y$ es igual a $f$ de $x$". Así, la función descrita anteriormente que eleva al cuadrado cada número, se escribirá $f (x) = x^2$.
El concepto de una función se puede visualizar utilizando la Figura 1.2, Figura 1.3 y la Figura 1.4.

Figura 1.2 Una función se puede visualizar como un dispositivo de entrada/salida.
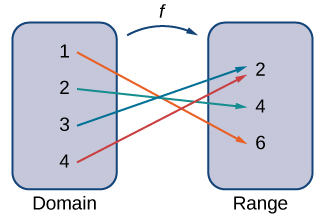
Figura 1.3 Una función asigna cada elemento del dominio exactamente un único elemento en el rango. Aunque a cada entrada se puede asignar una sola salida, es posible asignar a dos entradas diferentes la misma salida.

Figura 1.4 En este caso, la gráfica de la función $f$ tiene como dominio el conjunto $\{1,2,3\}$ y como rango $\{1,2\}$. La variable independiente es $x$ y la variable dependiente es $y$.
También se puede visualizar una función trazando puntos $(x, y)$ en el plano de coordenadas siendo $y = f (x)$. La gráfica de una función consiste en el conjunto de todos estos puntos.
Por ejemplo, consideremos la función $f$, donde el dominio es el conjunto $D = \{1,2,3\}$ y la regla es $f (x) = 3-x$. En la Figura 1.5, se da una representacion gráfica de esta función.
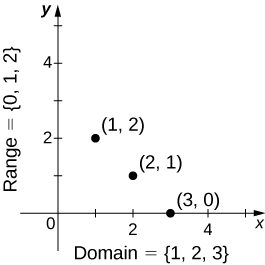
Figura 1.5 Gráfica de la función $f$ que viene dada por $f (x) = 3-x$ en el dominio $\{1,2,3\}$. La gráfica consta de los puntos $(x, f (x))$ para todos los $x$ en el dominio.
 En la siguiente escena interactiva traducida de la propuesta por J Mulholland, se ilustra cómo una función asigna para cada entrada una salida.
En la siguiente escena interactiva traducida de la propuesta por J Mulholland, se ilustra cómo una función asigna para cada entrada una salida.
Una vez elegida la función con el deslizador que se muestra en la parte superior izquierda, basta mover el punto rojo, la entrada, para ver el valor de la función en dicho punto, la salida.
Se debe observar que para cada ejemplo de función que se puede elegir, cada entrada tiene una única salida.
 En la siguiente escena interactiva se muestra el dominio y el rango de una función determinado por la expresión $f(x)$.
En la siguiente escena interactiva se muestra el dominio y el rango de una función determinado por la expresión $f(x)$.
Cada función tiene un dominio. Sin embargo, a veces una función viene dada por una expresión, como por ejemplo $f (x) = x^2$ sin especificar explícitamente cuál es. En este caso, se considerará que el dominio es el conjunto de todos los números reales $x$ para los cuales $f (x)$ es un número real. Dado que se puede obtener el cuadrado de cualquier número real se considerará, salvo que se indique otro conjunto, que el dominio de esta función es el conjunto de todos los números reales.
Si por ejemplo se considerara la función raíz cuadrada $f (x) = \sqrt{x}$, como solo se obtiene un valor real si $x$ es no negativo, su dominio será el conjunto de los números reales no negativos. Este conjunto se suele llamar su dominio natural.
Para las funciones $f (x) = x^2$ y $f (x) = \sqrt{x}$, los dominios son conjuntos formados por un número infinito de elementos no pudiendo por ello enumerar todos sus elementos.
A menudo, al describir un conjunto con un número infinito de elementos, es útil usar la notación de conjuntos o de intervalo. Cuando se usa la notación de conjuntos para describir un subconjunto de todos los números reales, denotado ${\R}$, se escribe $$\{x | x \text{ tiene alguna propiedad}\}$$
Esta expresión se lee como el conjunto de los números reales $x$ tal que $x$ tiene alguna propiedad. Por ejemplo, si estuviéramos interesados en el conjunto de números reales que son mayores que uno pero menores que cinco, podríamos denotar este conjunto escribiendo
$$\{ x|1 < x < 5\} $$A un conjunto como este, que contiene todos los números mayores que $a$ y menores que $b$, también se le puede denotar utilizando la notación de intervalo $(a, b)$. Por lo tanto,
$$(1,5) = \{ x | 1 < x < 5 \} $$Podemos usar una notación similar si queremos incluir uno de los puntos finales, pero no el otro. Para denotar el conjunto de números reales no negativos, podríamos usar la siguiente notación
$$\{x | 0 ≤ x\}$$El número más pequeño en este conjunto es cero, pero para este conjunto no existe un número que sea más grande que todos sus elementos. Usando notación de intervalo, usaríamos el símbolo $\infty$ que se refiere al infinito positivo, y escribiríamos el conjunto como $$[0, \infty) = \{x | 0 ≤ x\}$$
Es importante tener en cuenta que $\infty$ no es un número real. Aquí se usa simbólicamente para indicar que este conjunto incluye todos los números reales mayores o iguales que cero. Del mismo modo, si quisiéramos describir el conjunto de todos los números no positivos, podríamos escribir
$$(-\infty, 0] = \{x | x≤0\}$$La notación $-\infty$ se refiere al infinito negativo e indica que estamos incluyendo todos los números menores o iguales a cero, sin importar cuánto. El conjunto
$$( - \infty,\infty) = \{ x|x \in \R \} $$describiría al conjunto de todos los números reales.
Algunas funciones se definen usando diferentes expresiones para diferentes partes de su dominio. Estos tipos de funciones se conocen como funciones definidas por tramos o a trozos. Por ejemplo, supongamos que queremos definir una función $f$ con un dominio que es el conjunto de todos los números reales de modo que $f (x) = 3x + 1$ para $x\ge 2$ y $f (x) = x^2$ para $x <2$. Para expresar esta función se escribirá
$$f(x) = \begin{cases} 3x+1 & \text{si $x\ge 2$} \\ x^2 & \text{si $x \lt 2$} \end{cases} $$Al evaluar esta función para una entrada $x$, la ecuación a utilizar dependerá de si $x \ge 2$ o si $x < 2$.
Por ejemplo, como $5> 2$, utilizaremos el hecho de que $f (x) = 3x + 1$ para $x\ge 2$ y se tendrá que $f (5) = 3 \cdot 5 + 1 = 16$. Por otro lado, para $x =-1$, como $f (x) = x^2$ para $x ≤2$ se tendrá $f (-1) = 1.$
 |
1.1 Evaluando funciones |
Para la función $f(x)=3x^2+2x-1$, evaluar

 |
Cuestión 1.1 |
Para $f(x)=x^2-3x+5$, evaluar $f(1)$ y $f(a+h)$.
 |
1.2 Encontrando el dominio y rango |
Para cada una de las siguientes funciones, determinar el dominio y el rango

 |
Cuestión 1.2 |
Encontrar el dominio y rango de la función $$f(x)=\sqrt{4-2x}+5$$
 En la siguiente escena interactiva se obtiene el dominio y el rango de varias funciones. Esta escena está tomada del Proyecto EDAD y diseñada por la profesora María José García Cebrian.
En la siguiente escena interactiva se obtiene el dominio y el rango de varias funciones. Esta escena está tomada del Proyecto EDAD y diseñada por la profesora María José García Cebrian.
 En la siguiente escena interactiva se muestra cómo obtener el rango de algunas funciones.
En la siguiente escena interactiva se muestra cómo obtener el rango de algunas funciones.
Típicamente, una función se representa usando una o más de las siguientes herramientas:
Podemos identificar una función de cualquiera de las tres formas, pero también se pueden utilizar de forma conjunta. Por ejemplo, podemos trazar en un gráfico los valores de una tabla o crear una tabla a partir de una fórmula.
Tablas
Las funciones descritas usando una tabla de valores surgen con frecuencia en aplicaciones del mundo real.
Consideremos el siguiente ejemplo sencillo que consiste en obtener la temperatura en un día determinado en función de la hora del día, para ello se registra la temperatura cada hora durante un período de 24 horas a partir de la medianoche. La variable de entrada $x$ será el tiempo medido en horas después de la medianoche, y la variable de salida $y$ será la temperatura medida en grados Fahrenheit transcurridas $x$ horas después de la medianoche. Registramos nuestros datos en la Tabla 1.1.
Podemos ver en la tabla que la temperatura es una función del tiempo. Se observa que la temperatura disminuye, luego aumenta y finalmente vuelve a decrecer. Sin embargo, no podemos conocer el comportamiento de la función sin representar su gráfica.
| Horas después de medianoche | Temperatura (oF) | Horas después de medianoche | Temperatura |
| 1 | 58 | 12 | 84 |
| 2 | 54 | 13 | 85 |
| 3 | 52 | 15 | 83 |
| 4 | 52 | 16 | 82 |
| 5 | 55 | 17 | 80 |
| 6 | 60 | 18 | 77 |
| 7 | 64 | 19 | 74 |
| 8 | 72 | 20 | 69 |
| 9 | 75 | 21 | 65 |
| 10 | 78 | 22 | 60 |
| 11 | 80 | 23 | 58 |
Tabla 1.1 Temperatura en función de la hora del día
Gráfica
A partir de los puntos trazados en el gráfico de la Figura 1.6 obtenidos de la tabla 1.1, podemos visualizar la forma general del gráfico. A menudo es útil unir los puntos en el gráfico que representan los datos de la tabla. En este ejemplo, aunque no podemos llegar a una conclusión definitiva con respecto a la temperatura en un momento para el que no se registró la temperatura, dada la cantidad de puntos de datos recopilados y el patrón de estos puntos, es razonable sospechar que las temperaturas siguieron un comportamiento similar al que podemos ver en la Figura 1.7.
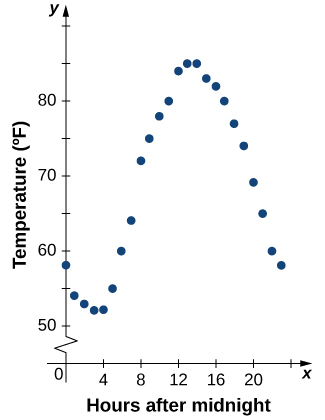
Figura 1.6 Gráfica correspondiente a los datos de la tabla 1.1 considerando la temperatura como función dependiente del tiempo-
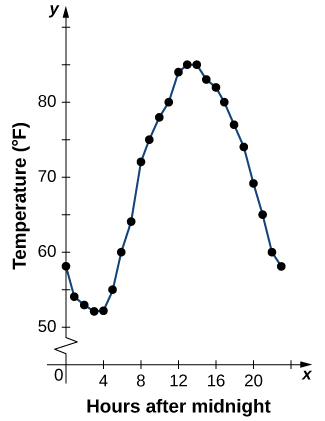
Figura 1.7 Uniendo los puntos de la figura 1.6 se muestra el patrón de los datos.
Fórmulas algebraicas
A veces no tenemos los valores de una función en forma de tabla, sino que los valores vienen dados en una fórmula explícita. Las fórmulas surgen en muchas aplicaciones. Por ejemplo, el área de un círculo de radio $r$ viene dada por la fórmula $$A (r) = \pi r^2.$$ Cuando un objeto se lanza hacia arriba desde el suelo con una velocidad inicial $v_0$ piesUn pie es una medida de longitud equivalente a 30,48 centímetros por segundo, su altura sobre el suelo desde el momento en que se arroja hasta que toca el suelo viene dada por la fórmula $$s (t) = - 16t^2 + v_0t$$ Cuando se invierten $P$ dólares en una cuenta a una tasa de interés anual $r$ compuesta continuamente, la cantidad de dinero después de $t$ años viene dada por la fórmula $$A (t) = Pe^{rt}$$
 En la siguiente escena, del libro Cálculo Diferencial Interactivo cuyo editor es Juan Gmo. Rivera, se muestra cómo evaluar una función en los puntos $x$ de valores $-2$, $-1$, $0$, $1$, $2$ cuando la función considerada es $f(x)$. Haciendo clic sobre cada número se mostrará el valor de la función en el punto correspondiente.
En la siguiente escena, del libro Cálculo Diferencial Interactivo cuyo editor es Juan Gmo. Rivera, se muestra cómo evaluar una función en los puntos $x$ de valores $-2$, $-1$, $0$, $1$, $2$ cuando la función considerada es $f(x)$. Haciendo clic sobre cada número se mostrará el valor de la función en el punto correspondiente.
Las fórmulas algebraicas son herramientas importantes para calcular valores de funciones. A menudo también representamos estas funciones visualmente en forma de gráfica.
Dada una fórmula algebraica para una función $f$, la gráfica de $f$ es el conjunto de puntos $(x, f (x))$, donde $x$ está en el dominio de $f$ y $f(x)$ está en el rango. Para graficar una función dada por una fórmula, es útil comenzar usando la fórmula para crear una tabla de entradas y salidas. Si el dominio de $f$ consiste en un número infinito de valores, no podemos enumerarlos todos, pero puede ser muy útil, para comenzar, dar valor a alguna de las entradas y obtener su imagen.
Al crear una tabla de entradas y salidas, generalmente verificamos si cero es una salida. Los valores de $x$ donde $f (x) = 0$ se llaman ceros de una función.
Por ejemplo, los ceros de $f (x) = x^2-4$ son $x = ± 2$. Los ceros determinan dónde la gráfica de $f$ corta al eje $X$, lo que da más información sobre ella. La gráfica puede no cortar nunca al eje $X$, o cortarlo múltiples veces, incluso infinitas veces.
Otro punto de interés, es la intersección con el eje $Y$. Cuando exista, vendrá dado por el punto $(0, f (0))$. Como una función tiene exactamente una única imagen para cada punto del dominio, el gráfico de una función puede tener, como máximo, una intersección con el eje $Y$.
De manera similar, para cualquier número real $c$,
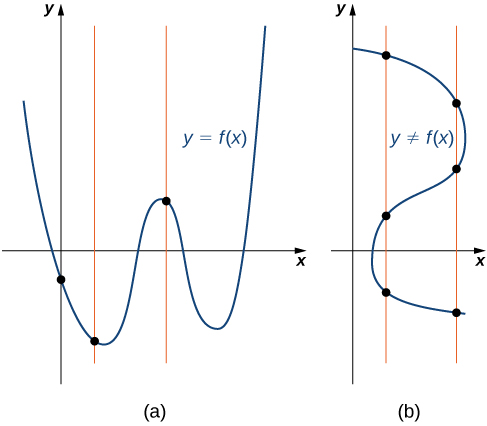
Figura 1.8 (a) El conjunto de puntos trazados representa el gráfico de una función porque cada línea vertical se cruza con el conjunto de puntos, como máximo, una vez. (b) El conjunto de puntos trazados no representa la gráfica de una función porque algunas rectas verticales se cruzan con el conjunto de puntos más de una vez.
 Practica lo anterior en la siguiente escena tomada del Proyecto EDAD diseñada por la profesora María José García Cebrian. Observa la gráfica de la función y haz clic en los botones "SI" o "NO", según el caso.
Practica lo anterior en la siguiente escena tomada del Proyecto EDAD diseñada por la profesora María José García Cebrian. Observa la gráfica de la función y haz clic en los botones "SI" o "NO", según el caso.
 |
1.3 Utilizando los ceros y las intersecciones con el eje $y$ |
Considera la función $f(x) =-4x+2$

 |
1.4 Utilizando los ceros y las intersecciones con el eje $Y$ |
Considera la función $f(x) = \sqrt {x + 3} + 1$

 |
Cuestión 1.3 |
Encuentra los ceros de $f(x)=x^3-5x^2+6x$.
 |
1.5 Encontrar la altura de un objeto en caída libre |
Si una pelota se cae desde una altura de 100 pies, su altura $s$ en el tiempo $t$ viene dada por la función $s (t) = - 16t^2 + 100$, donde $s$ se mide en pies y $t$ se mide en segundos. El dominio está restringido al intervalo $[0, c]$, donde $t = 0$ es el momento en que se cae la pelota y $t = c$ es el momento en que la pelota toca el suelo. Nota: 1 pie son 30,48 centímetros.

Para la función del ejemplo anterior y para la función $f (x) = - 4x + 2$ representada en la Figura 1.9, los valores de $f(x)$ se hacen más pequeños a medida que $x$ se hace más grande. Se dice que una función con esta propiedad es decreciente. Por otro lado, para la función $f (x) =\sqrt{ x + 3} + 1$ cuya gráfica se muestra en la Figura 1.10, los valores de $f (x)$ aumentan a medida que aumentan los valores de $x$. Se dice que una función con esta propiedad es creciente.
Sin embargo, es importante tener en cuenta que una función puede aumentar en algunos intervalos y disminuir en otros diferentes. Por ejemplo, usando la función de temperatura vista anteriormente en la Figura 1.6, observamos que la función está decreciendo en el intervalo $(0,4)$, aumenta en el intervalo $(4,14)$ y luego disminuye en el intervalo $(14,23)$.
Expresamos a continuación con más precisión la idea de que una función aumente o disminuya en un intervalo determinado.
Decimos que una función $f$ es creciente en el intervalo $I$ si para todo $x_1, x_2 \in I$, se cumple $f(x_1) \le f(x_2)$ cuando $x_1 <x_2$.
Decimos que $f$ es estrictamente creciente en el intervalo $I$ si para todo $x_1, x_2 \in I$, se cumple $f(x_1) <f (x_2)$ cuando $x_1 <x_2$.
Decimos que una función $f$ decrece en el intervalo $I$ si para todos $x_1, x_2 \in I$, se cumple $f (x_1) \ge f (x_2)$ cuando $x_1 <x_2$.
Decimos que una función $f$ es estrictamente decreciente en el intervalo $I$ si para todos $x_1, x_2 \in I$, se cumple $f (x_1)> f (x_2)$ cuando $x_1 <x_2$.
Por ejemplo,
Ahora que hemos revisado las características básicas de las funciones, vamos a analizar qué sucede cuando generamos nuevas
funciones combinando funciones mediante la aplicación de operaciones matemáticas básicas.
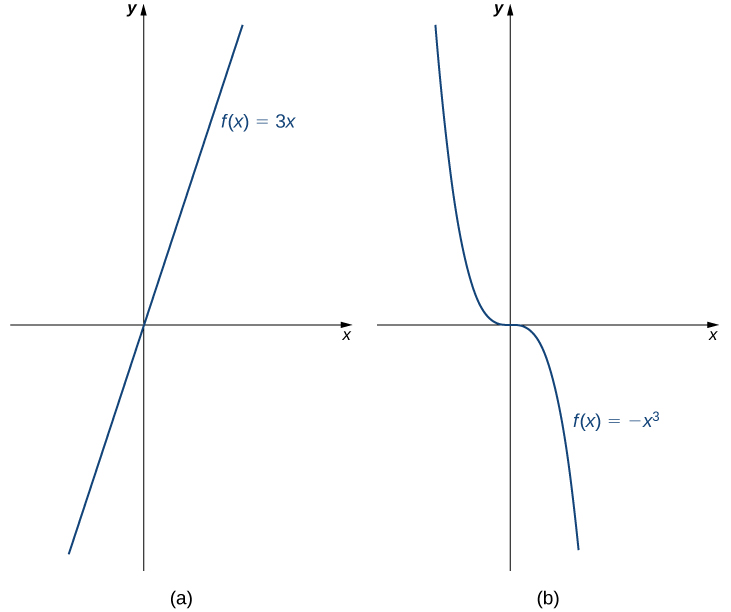
Figura 1.11 (a) La función $f(x) = 3x$ aumenta en el intervalo $(-\infty, \infty)$. (b) La función $f(x) =-x^3$ está disminuyendo en el intervalo $(-\infty, \infty)$.
Por ejemplo, si la función $C (x)$ describe el coste para una empresa de fabricar $x$ artículos y la función $R (x)$ describe los ingresos generados por la venta de $x$ artículos, entonces el beneficio de la fabricación y venta de $x$ elementos se define como $P (x) = R (x)-C (x)$. Usando la diferencia entre dos funciones, se ha creado una nueva función, veamos un ejemplo de cómo generar una nueva función componiendo dos funciones.
Por ejemplo, dadas las funciones $f (x) = x^2$ y $g (x) = 3x + 1$, la función $g$ compuesta con $f$, que se denota por $f\circ g$ se define de manera que $$(f\circ g) (x) = f (g (x)) = (g (x))^2 = (3x + 1)^2$$
Si se compone $f$ con $g$, es decir $g\circ f$, la función que se obtiene es $$(g \circ f) (x) = g (f (x)) = 3f (x) + 1 = 3x^2 + 1$$ Se debe observar que estas dos nuevas funciones, $f\circ g$ y $g\circ f$, son diferentes entre sí.
Vamos a analizar con más detalle la generación de funciones a partir de otras dadas.
Combinando funciones con operadores matemáticos
Para combinar funciones usando operadores matemáticos, simplemente aplicamos a las funciones el operador y simplificamos la expresión que se obtenga.
Así, dadas dos funciones $f$ y $g$, podemos definir las siguientes funciones nuevas:
 |
1.6 Combinando funciones usando operaciones matemáticas |
Dada la función $f(x)=2x-3$ y $g(x)=x^2-1$, encuentra para cada función su dominio.

 |
Cuestión 1.4 |
Para $f(x)=x^2+3$ y $g(x)=2x-5$, encuentra $(f/g)(x)$ y su dominio.
Función composición
Cuando componemos funciones, aplicamos una función a una función. Por ejemplo, supongamos que la temperatura $T$ en un día dado se describe como una función del tiempo $t$ medido en horas después de la medianoche, como en la Tabla 1.1.
Supongamos también que el coste $C$, para calentar o enfriar un edificio durante una hora, puede describirse como una función de la temperatura $T$. Combinando estas dos funciones, podemos describir el coste de calentar o enfriar un edificio como una función del tiempo mediante la evaluación de $C (T (t))$.
Hemos definido así una nueva función, denominada $C\circ T$, que se define de la siguiente manera: $(C\circ T) (t) = C (T (t))$ para todas las $t$ en el dominio de $T$ que cumplan que $T(t)$ es un punto del dominio de $C$.
Esta nueva función se denomina función compuesta . Notamos que dado que el coste es una función de la temperatura y la temperatura es una función del tiempo, tiene sentido definir esta nueva función $(C\circ T) (t)$, pero no tiene sentido considerar $(T\circ C) (t)$, porque la temperatura no es una función del coste.
Una función compuesta $g\circ f$ se puede ver en dos pasos. Primero, la función $f$ asigna cada entrada $x$ en el dominio de $f$ su imagen $f (x)$ en el rango de $f$. En segundo lugar, dado que el rango de $f$ es un subconjunto del dominio de $g$, el valor $f (x)$ es un elemento en el dominio de $g$ y, por lo tanto, se puede considerar $g (f (x))$ en el rango de $g$.
En la Figura 1.12>, se muestra una representacion visual de la composición de funciones.
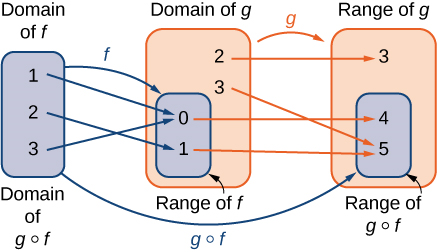
Figura 1.12 Para la composición $g\circ f$, tenemos $(g \circ f)(1)=4$,$(g\circ f)(2)=5$, y $(g\circ f)(3)=4$.
 En la siguiente escena interactiva diseñada en GeoGebra por Javier Cayetano, se muestra cómo componer distintas funciones.
En la siguiente escena interactiva diseñada en GeoGebra por Javier Cayetano, se muestra cómo componer distintas funciones.
 |
1.7 Composición de funciones definidas por fórmulas |
Consideramos las funciones $f(x)=x^2+1$ y $g(x)=1/x$

En el ejemplo 1.7, vemos que $(f\circ g)(x)\ne(g \circ f)(x)$. Esto nos indica que el orden en el que se componen las funciones, en general, es importante.
 |
Cuestión 1.5 |
Sea $f(x)=2-5x$, $g(x)=\sqrt{x}$, encuentra $(f \circ g)(x)$.
 |
1.8 Composición de funciones definidas por tablas |
Se consideran las funciones $f$ y $g$ de las tablas 1.4 y 1.5.

| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| f(x) | 0 | 4 | 2 | 4 | -2 | 0 | -2 | 4 |
Tabla 1.4
| x | -4 | -2 | 0 | 2 | 4 |
| g(x) | 1 | 0 | 3 | 0 | 5 |
Tabla 1.5
 |
1.9 Aplicación de la composición de funciones |
Una tienda está anunciando una venta del 20% de descuento en toda la mercancía. Carolina tiene un cupón que le da derecho a un 15% de descuento adicional en cualquier artículo, incluidos los productos en oferta.

 |
Cuestión 1.6 |
Si los artículos están en oferta con un 10% de descuento sobre su precio original y un cliente tiene un cupón con un 30% de descuento adicional, ¿cuál será el precio final de un artículo que originalmente cuesta $x$ dólares, después de aplicar el cupón al precio de oferta?
Las gráficas de ciertas funciones tienen propiedades de simetría que nos ayudan a comprender la función y la forma de su gráfica. Por ejemplo, consideremos la función $f (x) = x^4-2x^2-3$ que se muestra en la Figura 1.13a. Si tomamos la parte de la curva que se encuentra a la derecha del eje $Y$ y la volteamos sobre el eje $Y$, se sitúa exactamente encima de la curva a la izquierda del eje $Y$. En este caso, decimos que la función tiene simetría con respecto al eje $Y$.
Por otro lado, consideremos la función $f (x) = x^3-4x$ que se muestra en la Figura 1.13b. Si tomamos el gráfico y lo giramos 180° sobre el origen, el nuevo gráfico se verá exactamente igual. En este caso, decimos que la función tiene simetría con respecto al origen.

Figura 1.13 (a) Una gráfica que es simétrica respecto del eje $Y$ (b) Una imagen que es simétrica respecto del origen.
En la figura 1.13a, correspondiente a la función $$f (x) = x^4 - 2 x^2 - 3$$ el eje $X$ va de -3 a 4 y el eje $Y$ va de -4 a 5. Esta función disminuye hasta que llega al punto (-1, -4), que es el mínimo de la función. La gráfica aumenta hasta el punto (0,3), que es un máximo local. Luego, el gráfico disminuye hasta que llega al punto (1, -4), antes de volver a aumentar.
En la figura del apartado b), la función que se representa es $$f (x) = x^3 - 4 x$$ y su gráfica comienza en la intersección con $x$ en $(-2, 0)$ y aumenta hasta el punto aproximado de $(-1.2, 3.1)$.
Luego, la función disminuye, pasando por el origen, hasta que llega al punto aproximado de $(1.2, -3.1)$. Después, la función comienza a aumentar nuevamente y tiene otra intersección $x$ en $(2, 0)$.
Si se nos dan la gráfica de una función, es fácil ver si tiene uno de estos dos tipos de simetría. Pero sin una gráfica, ¿cómo podemos determinar algebraicamente si una función $f$ tiene simetría? Mirando la Figura 1.13 a nuevamente, vemos que dado que $f$ es simétrica con respecto al eje $Y$, si el punto $(x, y)$ está en la gráfica, el punto $(-x, y)$ también está. En otras palabras, $f (-x) = f (x)$. Si una función $f$ tiene esta propiedad, decimos que $f$ es una función par, esto es, que tiene simetría con respecto al eje $Y$. Por ejemplo, $f (x) = x^2$ es par porque
$$f(-x)=(-x)^2=x^2=f(x)$$Por el contrario, fijándonos en la Figura 1.13b, si una función $f$ es simétrica con respecto al origen, entonces siempre que el punto $(x, y)$ está en la gráfica, el punto $(-x, -y)$ también está en la gráfica. En otras palabras, $f (-x) = - f (x)$. Si $f$ tiene esta propiedad, decimos que $f$ es una función impar, que tiene simetría con respecto al origen. Por ejemplo, $f (x) = x^3$ es impar porque $$f (-x) = (- x)^3 = -x^3 = -f (x)$$
Si $f(x)=-f(-x)$ para todo $x$ en el dominio de $f$, entonces f es una función impar, este tipo de funciones son simétricas respecto al origen.
 |
1.10 Funciones pares e impares |

 |
Cuestión 1.7 |
Determina si $f(x)=4x^3-5x$ es par, impar o ni par ni impar.
Una función simétrica que surge con frecuencia es la función valor absoluto que se escribe $|x|$. Se define como $$f(x) = \begin{cases} -x & \text{si $x<0$} \\ x & \text{si $x \ge 0$} \end{cases} \tag{$1.2$} $$
Algunos estudiantes describen esta función diciendo que "hace que todo sea positivo".
Por la definición de la función valor absoluto, vemos que si $x <0$, entonces $| x | = -x> 0$, y si $x> 0$, entonces $| x | = x> 0$. Sin embargo, para $x = 0$, $| 0 | = 0$. Por lo tanto, es más exacto decir que para todas las entradas distintas de cero, la imagen es positiva, pero si $x = 0$, la imagen es cero, $| 0 | = 0$. Concluimos que el rango de la función valor absoluto es $$\{y | y \ge 0\}$$
En la figura 1.14, se muestra que la función valor absoluto es simétrica con respecto al eje $Y$ siendo, por lo tanto, una función par.
En la figura, el eje $X$ va de -3 a 3 y el eje $Y$ va de -4 a 4. La gráfica comienza en el punto $(-3, 3)$ y disminuye en línea recta hasta que llega al origen. Luego, la gráfica aumenta en línea recta hasta que llega al punto $(3, 3)$.
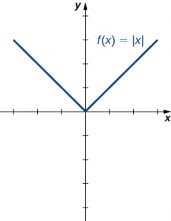
Figura 1.14 La gráfica de $f(x)=|x|$ es simétrica respecto del eje $Y$.
 |
1.11 Trabajando con la función valor absoluto |

 |
Cuestión 1.8 |
Dada $f(x)=|x+2|-4$, encuentra el dominio y el rango.
 1.2.5 Ejercicios
1.2.5 EjerciciosA continuación, encontrarás varios ejercicios para que confrontes lo aprendido. Lo ejercicios correspondientes a numerales impares, presentan la solución.
 Para los siguientes ejercicios, (a) determina el dominio y el rango de cada relación y (b) determina cuando la relación es una función.
Para los siguientes ejercicios, (a) determina el dominio y el rango de cada relación y (b) determina cuando la relación es una función.
1.
| $x$ | $y$ | $x$ | $y$ |
| -3 | 9 | 1 | 1 |
| -2 | 4 | 2 | 4 |
| -1 | 1 | 3 | 9 |
| 0 | 0 |
2.
| $x$ | $y$ | $x$ | $y$ |
| -3 | -2 | 1 | 1 |
| -2 | -8 | 2 | 8 |
| -1 | -1 | 3 | -2 |
| 0 | 0 |
3.
| $x$ | $y$ | $x$ | $y$ |
| 1 | -3 | 1 | 1 |
| 2 | -2 | 2 | 2 |
| 3 | -1 | 3 | 3 |
| 0 | 0 |
4.
| $x$ | $y$ | $x$ | $y$ |
| 1 | 3 | 5 | 1 |
| 2 | 1 | 6 | 1 |
| 3 | 1 | 7 | 1 |
| 4 | 1 |
5.
| $x$ | $y$ | $x$ | $y$ |
| 3 | 3 | 15 | 1 |
| 5 | 2 | 21 | 2 |
| 8 | 1 | 33 | 3 |
| 10 | 0 |
6.
| $x$ | $y$ | $x$ | $y$ |
| -7 | 11 | 1 | -2 |
| -2 | 5 | 3 | 4 |
| -2 | 1 | 6 | 11 |
| 0 | -1 |
 Para los siguientes ejercicios encuentra, si existen, los valores para cada función y da los resultados simplificados.
Para los siguientes ejercicios encuentra, si existen, los valores para cada función y da los resultados simplificados.
a. $f(0)$ b. $f(1)$ c. $f(3)$ d. $f(-x)$ e. $f(a)$ f. $f(a+h)$
7. $f(x)=\frac{2}{x}$ (Solución)
8. $f(x)=5x-2$
9. $f(x)=4x^2-3x+1$ (Solución)
10. $f(x)=|x-7|+8$
11. $f(x)=\sqrt{6x+5}$ (Solución)
12. $f(x)=\frac{x-2}{3x+7}$
13. $f(x)=9$ (Solución)
 Para los siguientes ejercicios, encuentra el dominio, rango, los ceros y la intersección con el eje $y$ de las funciones siguientes:
Para los siguientes ejercicios, encuentra el dominio, rango, los ceros y la intersección con el eje $y$ de las funciones siguientes:
14. $f(x)=\frac{x}{x^2-16}$
15. $f(x)=\sqrt{8x-1}$ (Solución)
16. $f(x)=\frac{3}{x^2+4}$
17. $f(x)=-1+\sqrt{x+2}$ (Solución)
18. $f(x)=\frac{1}{\sqrt{x-9}}$
19. $f(x)=\frac{3}{x-4}$ (Solución)
20. $f(x)=4|x+5|$
21. $f(x)=\sqrt{\frac{7}{x-5}}$ (Solución)
 Para los siguientes ejercicios, prepare una tabla para esbozar la gráfica de cada función utilizando los siguientes valores: $x=-3$, $-2$, $-1$, $0$, $1$, $2$, $3$.
Para los siguientes ejercicios, prepare una tabla para esbozar la gráfica de cada función utilizando los siguientes valores: $x=-3$, $-2$, $-1$, $0$, $1$, $2$, $3$.
22. $f(x)=x^2+1$
| $x$ | $y$ | $x$ | $y$ |
| -3 | 10 | 1 | 2 |
| -2 | 5 | 2 | 5 |
| -1 | 2 | 3 | 10 |
| 0 | 1 |
23. $f(x)=3x-6$
| $x$ | $y$ | $x$ | $y$ |
| -3 | -15 | 1 | -3 |
| -2 | -12 | 1 | -3 |
| -1 | -9 | 3 | 3 |
| 0 | -6 |
24. $f(x)=\frac{1}{2}x+1$
| $x$ | $y$ | $x$ | $y$ |
| -3 | $-\frac{1}{2}$ | 1 | $\frac{3}{2}$ |
| -2 | 0 | 2 | 2 |
| -1 | $\frac{1}{2}$ | 3 | $\frac{5}{2}$ |
| 0 | 1 |
25. $f(x)=2|x|$
| $x$ | $y$ | $x$ | $y$ |
| -3 | 6 | 1 | 2 |
| -2 | 4 | 2 | 4 |
| -1 | 2 | 3 | 6 |
| 0 | 0 |
26. $f(x)=-x^2$
| $x$ | $y$ | $x$ | $y$ |
| -3 | 9 | 1 | .1 |
| -2 | -4 | 2 | 4 |
| -1 | -1 | 3 | 9 |
| 0 | 0 |
27. $f(x)=x^3$
| $x$ | $y$ | $x$ | $y$ |
| -3 | 27 | 1 | 1 |
| -2 | -8 | 2 | 8 |
| -1 | -1 | 3 | 27 |
| 0 | 0 |
 En los siguientes ejercicios, utiliza el test de la recta vertical para determinar si cada gráfica representa a una función suponiendo que
En los siguientes ejercicios, utiliza el test de la recta vertical para determinar si cada gráfica representa a una función suponiendo que
cada gráfica continúa en ambos extremos extendiéndose más allá de la cuadrícula dada. En el caso de que la gráfica represente a una función, determina para cada gráfico:
28.
29.
 En los siguientes ejercicios, para cada par de funciones, encuentra a. $f+g$ b. $f-g$ c. $f\dot g$ d. $f/g$. Determina el dominio de estas funciones.
En los siguientes ejercicios, para cada par de funciones, encuentra a. $f+g$ b. $f-g$ c. $f\dot g$ d. $f/g$. Determina el dominio de estas funciones.
36. $f(x)=3x+4$, $g(x)=x-2$
37. $f(x)=x-8$, $g(x)=5x^2$ (Solución)
38. $f(x)=3x^2+4x+1$, $g(x)=x+1$
39. $f(x)=9-x^2$, $g(x)=x^2-2x-3$ (Solución)
40. $f(x)=\sqrt{x}$, $g(x)=x-2$
41. $f(x)=6+\frac{1}{x}$, $g(x)=\frac{1}{x}$ (Solución)
 En los siguientes ejercicios, para cada par de funciones, encuentra a. $\left( {f \circ g} \right)\left( x \right)$ b. $\left( {g \circ f} \right)\left( x \right)$ Simplifica los resultados y encuentra el dominio de cada una de las funciones obtenidas.
En los siguientes ejercicios, para cada par de funciones, encuentra a. $\left( {f \circ g} \right)\left( x \right)$ b. $\left( {g \circ f} \right)\left( x \right)$ Simplifica los resultados y encuentra el dominio de cada una de las funciones obtenidas.
42. $f(x)=3x$, $g(x)=x+5$
43. $f(x)=x+4$, $g(x)=4x-1$ (Solución)
44. $f(x)=2x+4$, $g(x)=x^2-2$
45. $f(x)=x^2+7$, $g(x)=x^2-3$ (Solución)
46. $f(x)=\sqrt{x}$, $g(x)=x+9$
47. $f\left( x \right) = {3 \over {2x + 1}}$, $g(x)=\frac{2} {x}$ (Solución)
48. $f\left( x \right) = \left| {x + 1} \right|$, $g(x)=x^2+x-4$
49. La tabla siguiente contiene los ganadores de la NBA desde los años 2001 a 2012.
| Año | Ganador |
| 2001 | LA Lakers |
| 2002 | LA Lakers |
| 2003 | San Antonio Spurs |
| 2004 | Detroit Pistons |
| 2005 | San Antonio Spurs |
| 2006 | Miami Heat |
| 2007 | San Antonio Spurs |
| 2008 | Boston Celtics |
| 2009 | LA Lakers |
| 2010 | LA Lakers |
| 2011 | Dallas Mavericks |
| 2012 | Miami Heat |
50. [T] El área $A$ de un cuadrado depende de la longitud del lado $s$.
51. [T] El volumen de un cubo depende de la longitud del lado $s$.
52. [T]Una empresa de alquiler de coches alquila coches por una tarifa fija de 20 dólares y un cargo por hora de 10.25 dólares. Por tanto, el total del coste C de alquilar un automóvil es una función de las horas $t$ que el automóvil esté alquilado más la tarifa plana.
53. [T] Un vehículo tiene un tanque de 20 galones y con esto recorre 15 millas por galón. El número de millas N que se pueden conducir depende de la cantidad de gas $x$ en el tanque.
54. [T] El volumen $V$ de una esfera depende de la longitud de su radio como $V = (4/3) πr^3$. Dado que la la Tierra no es una esfera perfecta, podemos usar el radio medio al medir desde el centro a su superficie. El radio medio es el promedio de la distancia desde el centro físico a la superficie, basada en una gran cantidad de muestras. Encuentra el volumen de la Tierra con radio medio $6,371 × 10^6 m$.
55. [T] Cierta bacteria crece en cultivo en forma de región circular. El radio del círculo, medido en centímetros, está dado por $r (t) = 6 −\frac{5}{t^2+1}$, donde $t$ es el tiempo medido en horas desde que la bacteria se puso en el cultivo con un círculo de radio 1 cm.
56. [T] Un turista estadounidense visita París y debe convertir dólares estadounidenses a euros usando la función $E (x) = 0,79x$, donde $x$ es la cantidad de dólares estadounidenses y $E (x)$ es el número equivalente a euros. Desde la conversión las tarifas fluctúan, cuando el turista regresa a los Estados Unidos dos semanas después, la conversión de euros a dólares estadounidenses es $D (x) = 1.245x$, donde $x$ es el número de euros y $D (x)$ es el número equivalente de dólares estadounidenses.
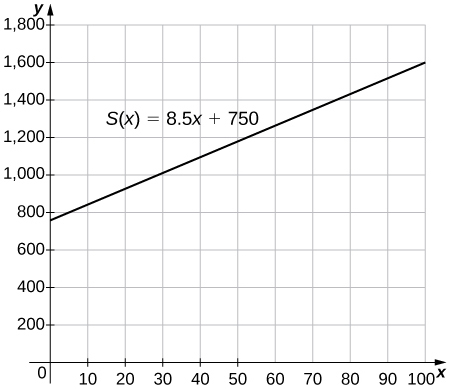
57. [T] El gerente de una tienda de patinetes paga a sus trabajadores un salario mensual $S$ de 750 dólares más una comisión de 8,5 dólares por cada patinete que vendan.
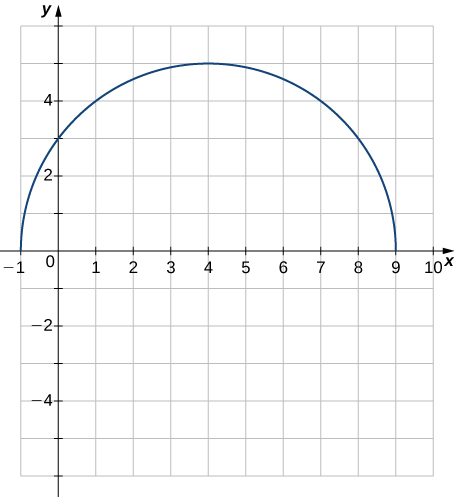
58. [T] Usa una calculadora gráfica para representar el semicírculo $y = 25 - (x - 4)^2$. Luego, utiliza la función que permita encontrar el valor de las intersecciones en los ejes $x$ e $y$
Objetivos de aprendizaje
Una vez estudiadas las características generales de las funciones, examinaremos en este momento algunas tipos específicos de funciones.
Comenzamos revisando las propiedades básicas de las funciones lineales y cuadráticas, y luego generalizaremos incluyendo polinomios de mayor grado. Combinando la función raíz con polinomios, podemos definir funciones algebraicas generales y se distinguirán de las funciones trascendentes que examinaremos más adelante en este capítulo.
Esta sección terminará mostrando ejemplos de funciones definidas por tramos o a trozos y se verá cómo obtener una función cuya gráfica resulta de desplazar, estirar o reflejar una función dada
El tipo de función a considerar más sencilla es una función lineal. Las funciones lineales son de la forma $f(x)=ax+b$, dónde $a$ y $b$ son constantes. En la Figura 1.15, vemos ejemplos de funciones lineales cuando $a$ es positiva, negativa y cero. Hay que tener en cuenta que
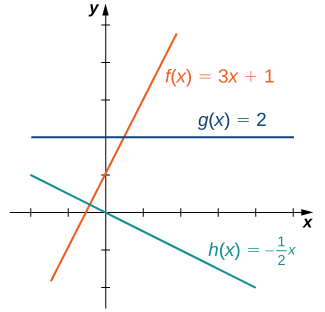
Figura 1.15 Estas funciones lineales aumentan o disminuyen en $(-\infty, \infty)$ y una de las funciones es una recta horizontal.
Como sugiere la Figura 1.15, la gráfica de cualquier función lineal es una recta. Una de las características distintivas de una recta es su pendiente.
La pendiente es el cambio en $y$ por cada cambio de unidad en $x$. La pendiente mide tanto la inclinación como la dirección de la recta. Si la pendiente es positiva, la recta apunta hacia arriba cuando se mueve de izquierda a derecha. Si la pendiente es negativa, la recta apunta hacia abajo cuando se mueve de izquierda a derecha. Si la pendiente es cero, la recta es horizontal.
Para calcular la pendiente de una recta, necesitamos determinar la razón del cambio en $y$ versus el cambio en $x$. Para hacerlo, elegimos dos puntos cualesquiera $(x_1,y_1)$ y $(x_2,y_2)$ en la recta y se calcula $$\frac{y_2-y_1}{x_2-x_1}$$
En la Figura 1.16, se muestra que esta relación es independiente de los puntos elegidos.
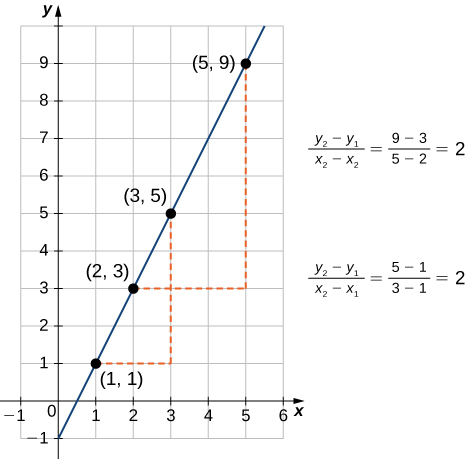
Figura 1.16 Para cualquier función lineal, la pendiente $(y_2-y_1)/(x_2-x_1)$ es independiente de la elección de puntos $(x_1,y_1)$ y $(x_2,y_2)$ de la recta.
Ahora examinaremos la relación entre la pendiente y la expresión de una función lineal dada por la fórmula $f(x) =ax+b$. Como se discutió anteriormente, sabemos que la gráfica de una función lineal es una recta. Podemos usar nuestra definición de pendiente para calcular la pendiente de dicha recta.
Como se muestra, podemos determinar la pendiente calculando $$\frac{y_2-y_1}{x_2-x_1}$$ por cualquier punto $(x_1,y_1)$ y $(x_2,y_2)$ en la recta. Consideramos la función $f$ en $x= 0$ y vemos que $(0,b)$ es un punto en la recta y evaluando en $x= 1$, se tiene que que $(1,a+b)$ es también un punto en esta recta. Por lo tanto, la pendiente de la recta será $$m = {{\left( {a + b} \right) - b} \over {1 - 0}} = a$$
 En la siguiente escena, elegida la opción "Recta", se puede mover el punto azul por la recta y observar que la pendiente no depende del punto elegido. Por otro lado, seleccionando la opción "dos puntos", la ecuación que pasa por los dos puntos que se consideren de la forma $y=ax+b$, tiene como valor $a$ el de la pendiente de la recta.
En la siguiente escena, elegida la opción "Recta", se puede mover el punto azul por la recta y observar que la pendiente no depende del punto elegido. Por otro lado, seleccionando la opción "dos puntos", la ecuación que pasa por los dos puntos que se consideren de la forma $y=ax+b$, tiene como valor $a$ el de la pendiente de la recta.
Hemos demostrado que el coeficiente $a$ de la función lineal es la pendiente de la recta. Además, vemos que esta recta corta al eje $Y$ en el punto $(0,b)$. Dado que a menudo usamos el símbolo $m$ para denotar la pendiente de una recta, podemos escribir $$f(x)=mx+b$$
como ecuación pendiente-ordenada en el origen de una función lineal.
A veces es conveniente expresar una función lineal de forma diferente. Por ejemplo, supongamos que la gráfica de una función lineal pasa por el punto $(x_1,y_1)$ y la pendiente de la recta es $m$. Desde cualquier otro punto $(x,f(x))$ en el gráfico de $f$ se debe satisfacer la ecuación $$m=\frac {f(x)-y_1} {x-x_1}$$
esta función lineal se puede expresar escribiendo $$f(x)-y_1=m(x-x_1)$$
Llamamos a esta expresión la ecuación punto-pendiente de la función lineal.
Dado que cada recta no vertical es la gráfica de una función lineal, estas rectas se pueden describir mediante las ecuaciones pendiente-ordenada en el origen o punto-pendiente. Sin embargo, cuando la recta es vertical, al no representar la gráfica de una función, no se puede expresar con estas ecuaciones. En cambio, una recta vertical se describe con la ecuación $x=k$ para alguna constante $k$.
Por esta razón, usamos la notación $$Ax+By=C,$$ dónde $A$, $B$ son ambos no nulos, para denotar la forma general de una recta.
Consideremos una recta que pasa por el punto $(x_1,y_1)$ y con pendiente $m$. La ecuacion $$y-y_1=m(x-x_1) \tag{$1.4$}$$ es la ecuación punto-pendiente para esa recta.
Consideremos una recta con pendiente $m$ siendo $(0,b)$ el punto de intersección con el eje $Y$. La ecuacion $$y=mx+b \tag{$1.5$}$$ es la forma pendiente-ordenada en el origen de la recta.
La forma general de una recta viene dada por la ecuación $$Ax+By=C \tag{$1.6$}$$ dónde $A$ y $B$ no son ambos nulos. Esta forma es más general porque admite las rectas verticales, $x=k$.
 En la siguiente escena, se muestra cómo a partir de dos puntos dados se pueden determinar las distintas ecuaciones de la recta.
En la siguiente escena, se muestra cómo a partir de dos puntos dados se pueden determinar las distintas ecuaciones de la recta.
 |
1.12 Encontrar la pendiente y las ecuaciones de las rectas |
Consideremos la recta que pasa por los puntos $(11, -4)$ y $(-4,5)$, como se muestra en la Figura 1.17.

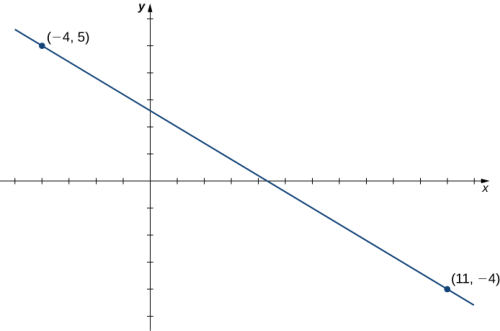
Figura 1.17 Ecuación de una función lineal que pasa por dos puntos dados.
 |
1.13 Una función lineal |

Una función lineal es un tipo especial de una clase más general: las funciones polinómicas. Una función polinómica es cualquier función que se pueda escribir de la forma siguiente $$f\left( x \right) = {a_n}{x^n} + {a_{n - 1}}{x^{n - 1}} + ... + {a_1}x + {a_0} \tag{$1.7$}$$ para algún entero $n \ge 0$ y constantes $a_n$, $a_{n-1}$, … , $a_0$, dónde $a_n \ne 0$. En el caso de que $n= 0$, se permitirá que $a_0= 0$ y en este caso la función $f(x) = 0$ recibe el nombre de función cero o nula. El valor $n$ se llama grado del polinomio; el coeficiente $a_n$ se llama coeficiente director.
Observamos que una función lineal de la forma $f(x) =mx+b$ es un polinomio de grado 1 en el caso de que $m\ne 0$ y de grado 0 si $m= 0$.
Un polinomio de grado 0 también se llama función constante. Una función polinomial de grado 2 se llama función cuadrática. En particular, una función cuadrática tiene la forma $$f\left( x \right) = a{x^2} + bx + c$$ dónde $a \ne 0$. Una función polinómica de grado 3 se llama función cúbica $$f\left( x \right) = a{x^3} + bx^2 + cx +d$$
Algunas funciones polinomiales son funciones potenciales. Una función potencial es cualquier función de la forma $f(x)=ax^b$, dónde $a$ y $b$ son números reales. El exponente en una función potencial puede ser cualquier número real, pero aquí consideramos el caso en el que el exponente es un número entero positivo dejando para más adelante otros casos.
 En la siguiente escena interactiva puedes observar las gráficas de las funciones $f(x)=ax^b$ para distintos valores de $a$ y $b$.
En la siguiente escena interactiva puedes observar las gráficas de las funciones $f(x)=ax^b$ para distintos valores de $a$ y $b$.
Si el exponente es un número entero positivo, entonces $f(x)=ax^n$ un polinomio.
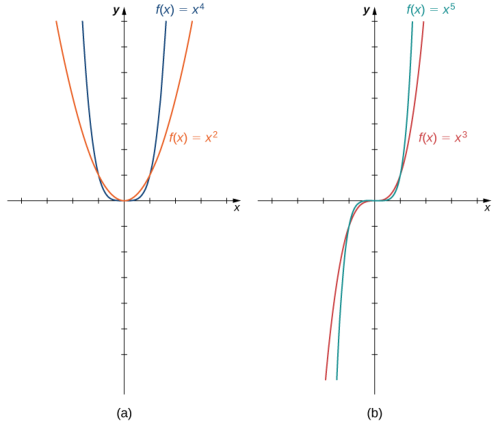
Figura 1.18 (a) Para cualquier número $n$ entero par, la función $f(x)=ax^n$ es par. (b) Para cualquier $n$ entero impar, la función $f(x)=ax^n$ es impar.
Comportamiento en el infinito
Para determinar el comportamiento de una función $f$ a medida que las puntos $x$ del dominio se acercan al infinito, se deben analizar los valores $f(x)$. Para algunas funciones, $f(x)$ se acerca a un número finito, por ejemplo, para la función $$f(x) = 2 + \frac{1}{x}$$ ya que los valores de $1 /x$ se acercan cada vez más a cero para valores de $x$ que se hacen cada más y más grandes. Para esta función, decimos que "f(x) se acerca a dos cuando $x$ tiende a infinito", y escribimos $f\left( x \right) \to 2$ cuando $x \to \infty$.
La recta $y= 2$ es una asíntota horizontal para la función $$f(x) = 2 + \frac{1}{x}$$ porque la gráfica de la función se aproxima a $y=2$ cuando $x$ se hace todo lo grande que se quiera.
Para otras funciones, los valores de $f(x)$ puede que no se acerquen a un número finito, sino que van creciendo indefinidamente para todos los valores de $x$ a medida que crecen lo que se quiera. En ese caso, decimos que "$f(x)$ tiende al infinito cuando $x$ tiende al infinito", y escribimos $f(x) \to \infty $ cuando $x \to \infty$.
Por ejemplo, para la función $$f(x) = 3x^2$$
los valores $f(x)$ se hacen cada vez más grandes cuando los valores $x$ se consideran cada vez más y más grandes. Podemos concluir que la función $f(x) = 3x^2$ tiende al infinito cuando $x$ tiende al infinito, y escribimos $3x^2 \to \infty$ cuando $x \to \infty$.
El comportamiento cuando $x \to -\infty$ y el significado de $f(x) \to -\infty$ cuando $x\to \infty$ o $x \to -\infty$ se puede definir de manera similar.
Podemos describir lo que sucede con los valores de $f(x)$ cuando $x \to \infty$ y cuando $x\to -\infty$ como el comportamiento en el límite de la función.
Para comprender el comportamiento en el límite de las funciones polinómicas, podemos centrarnos en funciones cuadráticas y cúbicas. El comportamiento de los polinomios de grado superior se puede analizar de forma similar.
Consideremos una función cuadrática $$f\left( x \right) = a{x^2} + bx + c$$
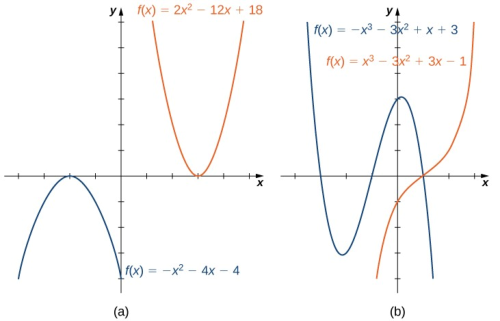
Figura 1.19 (a) Para una función cuadrática, si el coeficiente principal es $a> 0$,la parábola se abre hacia arriba. Si $a\lt 0$,la parábola se abre hacia abajo. (b) Para una función cúbica, si el coeficiente director $a$ verifica $a>0$, los valores $f(x) \to \infty$ cuando $x\to \infty$ y los valores $f(x) \to -\infty$ cuando $x\to -\infty$. Si el coeficiente principal $a <0$, la situación sería la contraria.
Ahora consideremos una función cúbica $$f\left( x \right) = a{x^3} + b{x^2} + cx + d$$
Como podemos ver en ambos gráficos, el término principal del polinomio determina el comportamiento en el infinito. (Ver Figura 1.19 (b)).
Ceros de funciones polinómicas
Otra característica de la gráfica de una función polinómica es los puntos de corte con el eje $X$. Para determinar estos puntos necesitamos resolver en $x$ la ecuación $f(x) = 0$.
En el caso de la función lineal $f(x) =mx+b$, la intersección se obtiene resolviendo la ecuación $mx+b= 0$. En este caso, vemos que el punto de corte con eje $X$ está dado por $(-b/m, 0)$.
En el caso de una función cuadrática, encontrar la intersección con el eje $X$ requiere encontrar los ceros de una ecuación cuadrática: $ax^2+bx+c= 0$, o lo que es lo mismo, factorizar el polinomio $ax^2+bx+c= 0$ y encontrar sus ceros. Cuando no es sencillo encontrar estos ceros, se puede utilizar la fórmula cuadrática.
Consideremos la ecuación cuadrática $$a{x^2} + bx + c = 0 \text{\,\, \, dónde $a\ne 0$}$$
Las soluciones de esta ecuación están dadas por la fórmula cuadrática $$x = {{ - b \pm \sqrt {{b^2} - 4ac} } \over {2a}}$$
 En la siguiente escena se muestra la representación de una función cuadrática y los puntos de corte con el eje de las $x$ o sus ceros.
En la siguiente escena se muestra la representación de una función cuadrática y los puntos de corte con el eje de las $x$ o sus ceros.
En el caso de polinomios de mayor grado, puede ser más complicado determinar dónde la gráfica corta al eje $X$. En algunos casos, es posible encontrar el punto factorizando el polinomio para encontrar sus ceros. En otros casos, es imposible calcular los valores exactos de las intersecciones con el eje $X$. Sin embargo, como veremos más adelante, en situaciones como estas, podemos utilizar herramientas analíticas para aproximar, con bastante precisión, dónde se localizan las intersecciones.
Aquí nos centraremos en los gráficos de polinomios para los cuales podemos calcular sus ceros explícitamente.
 |
1.14 Representar funciones polinomiales |
Para cada función $f$,

 |
Cuestión 1.10 |
Considera la función cuadrática $f(x) = 3x^2-6x+2$. Encuentra los ceros de $f$. ¿La parábola se abre hacia arriba o hacia abajo?
Modelos matemáticos
Para describir una gran variedad de situaciones del mundo real se pueden utilizar modelos matemáticos. Un modelo matemático es un método para simular situaciones de la vida real con ecuaciones matemáticas. Los físicos, ingenieros, economistas y otros investigadores desarrollan modelos combinando la observación con datos cuantitativos para desarrollar ecuaciones, funciones, gráficos y otras herramientas matemáticas con las que describir con precisión el comportamiento de varios sistemas. Los modelos son útiles porque ayudan a predecir resultados futuros. Algunos ejemplos de modelos matemáticos incluyen el estudio de la dinámica de la población, las investigaciones de los patrones climáticos y las predicciones de las ventas de productos.
Como ejemplo, consideremos un modelo matemático que una empresa podría usar para describir sus ingresos por la venta de un determinado artículo. La cantidad de ingresos $R$ que una empresa recibe por la venta de $n$ artículos vendidos a un precio de $p$ dólares por artículo, se describe mediante la ecuación $R=pn$. La empresa está interesada en conocer cómo cambian las ventas a medida que varía el precio del artículo. Supongamos que los datos de la Tabla 1.6 se corresponde con el número de unidades que vende una empresa en función del precio por artículo.
| $p$ | 6 | 8 | 10 | 12 | 14 |
| $n$ | 19.4 | 18.5 | 16.2 | 13.8 | 12.2 |
Tabla 1.6 Número de unidades vendidas $n$ (en miles) en función del precio por unidad $p$ (en dólares)
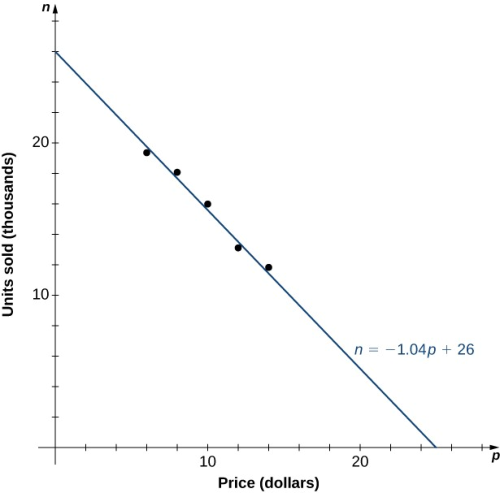
Figura 1.20 Los datos recopilados para el número de artículos vendidos en función del precio son aproximadamente lineales. Usamos la función lineal $n= -1.04p+26$ para estimar esta función.
En la Figura 1.20, vemos en la gráfica el número de unidades vendidas (en miles) en función del precio (en dólares).
Observamos a partir de la forma del gráfico que el número de unidades vendidas probablemente sea una función lineal del precio por artículo, y los datos pueden aproximarse mediante la función lineal $n= -1.04p+26$ para $0 \le p \le 25$ dónde $n$ es el número de unidades vendidas en miles. Usando esta función lineal, los ingresos (en miles de dólares) se pueden estimar mediante la función cuadrática $$R(p) =p\cdot(-1.04p+26) = - 1.04p^2+26p$$ para $0 \le p \le 25$.
En el Ejemplo 1.15, utilizaremos esta función cuadrática para predecir la cantidad de ingresos que recibe la empresa según el precio que cobra por artículo. Debemos tener en cuenta que no podemos concluir definitivamente el número real de unidades vendidas para cualquier valor de $p$. Sin embargo, dados los otros valores de datos y el gráfico que se muestra, parece razonable que la cantidad de unidades vendidas (en miles) considerando que el precio cobrado es $p$ dólares, pueden estar cerca de los valores predichos por la función lineal $n= -1.04p+26$.
 |
1.15 Maximizar los ingresos |
Una empresa está interesada en predecir la cantidad de ingresos que recibirá según el precio que cobre por un artículo en particular. Usando los datos de la tabla 1.6, la empresa llega a la siguiente función cuadrática para modelar los ingresos $R$ (en miles de dólares) en función del precio por artículo $p$:

Si se admiten cocientes, potencias fraccionarias de funciones polinomiales, se pueden construir nuevas funciones. Una función algebraica es aquella que involucra sumas, diferencias, productos, cocientes, potencias y radicales. Dentro de las funciones algebraicas dos tipos especiales de funciones son funciones racionales y las funciones radicales.
Así como los números racionales son cocientes de números enteros, las funciones racionales son cocientes de polinomios. En particular, una función racional es cualquier función de la forma $$f(x) =\frac{p(x)} {q(x)}$$ dónde $p(x)$ y $q(x)$ son polinomios.
Por ejemplo, $$f(x) = \frac{3x-1} {5x+ 2} \,\,\,\, y \,\,\,\, g(x) =\frac{4} {x^2+1}$$ son funciones racionales.
Una función radical es una función potencial de la forma $$f(x) =x^{1/n}$$ dónde $n$ un número entero positivo mayor que uno. Por ejemplo, $f(x) =x^{1/2}=\sqrt{x}$ es la función raíz cuadrada y $g(x) = x^{1/3} = \sqrt[3]{x}$ es la función de raíz cúbica. Al permitir composiciones de funciones radicales y funciones racionales, podemos crear otras funciones algebraicas. Por ejemplo,$f(x) = \sqrt{4-x}$ es una función algebraica.
 |
1.16 Encontrar el dominio y el rango de funciones algebraicas |
Para cada una de las siguientes funciones, encontrar el dominio y el rango.

 |
Cuestión 1.11 |
Encuentra el dominio y el rango de la función $$f(x) = \frac {5x+2} {2x-1}$$
Las funciones radicales de la forma $f(x) =x^{1/n}$ tienen características específicas dependiendo de si $n$ es par o impar. Para todos los enteros pares $n \ge 2$, el dominio de $f(x) =x^{1/n}$ es el intervalo $[0, \infty)$. Para todos los enteros impares $n \ge 1$, el dominio de $f(x) =x^{1/n}$ es el conjunto de todos los números reales.
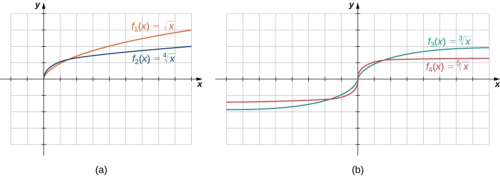
Figura 1.21 (a) Si $n$ es par, el dominio de $f(x) =x^{1/n}$ es $[0, \infty)$. (b) Si $n$ es impar, el dominio de $f(x) =x^{1/n}$ es $(-\infty, \infty)$ y la función es impar.
Ya que $x^{1/n}=(-x)^{1/n}$ para $n$ entero impar, $f(x) =x^{1/n}$ es una función impar si $n$ es impar. Vea las gráficas de funciones radical para diferentes valores de $n$ en Figura 1.21.
 En la siguiente escena interactiva se puede representar la función $y=a x^{1/n}$ para distintos valores de $a$ y $n$. Puede observarse el dominio y su gráfica en el caso de que $n$ sea par o impar.
En la siguiente escena interactiva se puede representar la función $y=a x^{1/n}$ para distintos valores de $a$ y $n$. Puede observarse el dominio y su gráfica en el caso de que $n$ sea par o impar.
 |
1.17 Encontrar dominios para funciones algebraicas |

 |
Cuestión 1.12 |
Encuentra el dominio para cada una de las siguientes funciones: $f(x)) = \frac {5-2x} {x^2+2}$ y $g(x) = \sqrt{5x-1}$
Hasta ahora, hemos analizado las funciones algebraicas. Algunas funciones, sin embargo, no se pueden describir mediante operaciones algebraicas básicas.
Estas funciones se conocen como funciones trascendentes porque se dice que "trascienden" o van más allá del álgebra.
Las funciones transcendentes más comunes son las funciones trigonométricas, exponenciales y logarítmicas.
Una función trigonométrica relaciona las razones de dos lados de un triángulo rectángulo. Estas funciones son $sen(x)$, $cos(x)$, $tg(x)$, $cot(x)$, $sec(x)$ y $csc(x)$. Analizaremos estas funciones trigonométricas más adelante en el capítulo 4.
Una función exponencial es una función de la forma $f(x)=b^x$, donde la base $b>0$,$b\ne 1$.
Una función logarítmica es una función de la forma $f(x) = {\log _b}x$ para alguna constante $b> 0$,$b\ne 1$, dónde ${\log _b}x=y$ si y solo si $b^y=x$. Tambien estudiaremos las funciones exponenciales y logarítmicas más adelante en este capítulo.
 En la siguiente escena interactiva se representan las funciones trascendentes anteriores.
En la siguiente escena interactiva se representan las funciones trascendentes anteriores.
 |
1.18 Clasificación de funciones algebraicas y tracendentes |
Clasifica cada una de las siguientes funciones indicando si son algebraicas o trascendentes.

 |
Cuestión 1.13 |
¿Es $f(x)=x/2$ una función algebraica o trascendente?
A veces, una función se define mediante diferentes fórmulas en diferentes partes de su dominio. Una función con esta propiedad se conoce como función definida por tramos o a trozos. La función valor absoluto es un ejemplo de este tipo de funciones porque la fórmula cambia dependiendo del signo de $x$: $$f(x) = \begin{cases} -x & \text{si $x\lt 0$} \\ x & \text{si $x \geq 0$} \end{cases}$$
Otras funciones definidas a trozos pueden representarse mediante fórmulas completamente diferentes, dependiendo de la parte del dominio que se considere.
Para representar una función definida a trozos, graficamos cada parte de la función en su dominio respectivo, en el mismo sistema de coordenadas. Si la fórmula de una función es diferente para los valores de $x$ mayores o menores que $a$, debemos prestar especial atención a lo que sucede en $x=a$ cuando dibujemos la gráfica de la función. A veces, el gráfico debe incluir un círculo abierto o cerrado para indicar el valor de la función en $x=a$. Examinamos esto en el siguiente ejemplo.
 |
1.19 Obtener la gráfica de una función definida a trozos |
Dibujar la gráfica de la siguiente función: $$f(x) = \begin{cases} x+3 & \text{si $x\lt 1$} \\ (x-2)^2 & \text{si $x \ge 2$} \end{cases}$$

 |
1.20 Tarifas de estacionamiento descritas por una función definida a trozos |
En una gran ciudad, a los conductores se les cobran tarifas variables por estacionarse en un aparcamiento.
Se les cobra 10 dólares por la primera hora o fracción y 2 dólares adicionales por cada hora o fracción hasta un máximo de 30 dólares por día.
El garaje de estacionamiento está abierto desde las 6 de la mañana hasta las 12 de la noche.

 |
Cuestión 1.15 |
El coste de enviar una carta por correo es una función del peso de la carta. Suponga que el costo de enviar una carta por correo es 49 centavos por la primera onza y 21 centavos por cada onza adicional.
Escribe una función definida a trozos que describa el coste $C$ en función del peso $x$ para valores mayores que 0 y cumpliendo $x ≤ 3$, dónde $C$ se mide en centavos y $x$ se mide en onzas.
Nota: Una onza es una medida de peso que equivale a 28,70 gramos
 En la siguiente escena del Proyecto Descartes, cuyo autor es Miguel Ángel Cabezón, se puede practicar la representación gráfica de funciones definidas en varios trozos de recta o funciones polinómicas de primer grado. También se presta atención a algunas de sus propiedades, dominio, crecimiento o decrecimiento, recorrido, etc.
En la siguiente escena del Proyecto Descartes, cuyo autor es Miguel Ángel Cabezón, se puede practicar la representación gráfica de funciones definidas en varios trozos de recta o funciones polinómicas de primer grado. También se presta atención a algunas de sus propiedades, dominio, crecimiento o decrecimiento, recorrido, etc.
Hemos visto varios casos en los que sumando, restado o multiplicado funciones más simples se han construido nuevas funciones. En el ejemplo anterior, por ejemplo, se aplicó la función $y=x^2$ al resultado de restar 2 a la variable $x$ obteniendo la función $f(x) = (x-2)^2$. Esta resta representa un cambio de la función $y=x^2$ trasladándola dos unidades a la derecha. Un desplazamiento, horizontal o vertical, es un tipo de transformación de una función. Otras transformaciones permiten realizar escalas horizontales y verticales y reflexiones sobre los ejes.
Cuando sumamos o restamos la misma constante a cada imagen $y$ de una función dada, se produce un desplazamiento vertical de dicha función. Para $c> 0$, la gráfica de
Por ejemplo, la gráfica de la función $f(x) =x^3+4$ es la gráfica de $y=x^3$ desplazada verticalmente hacia arriba 4 unidades; la gráfica de la función $f(x) =x^3-4$ es la gráfica de $y=x^3$ desplazada hacia abajo 4 unidades (Figura 1.23).

Figura 1.23 (a) Para $c> 0$, la gráfica de $y=f(x)+c$ es un desplazamiento vertical hacia arriba $c$ unidades de la gráfica de $y=f(x)$. (b) Para $c>0$, la gráfica de $y=f(x)-c$ es un desplazamiento vertical hacia abajo $c$ unidades de la gráfica de $y=f(x)$.
Para producir un desplazamiento horizontal de una función, hay que sumar o restar la misma constante a cada punto $x$ del domino. Para $c> 0$, la gráfica de
¿Por qué el gráfico se desplaza hacia la izquierda al sumar una constante y hacia la derecha al restar una constante? Para responder a esta pregunta, veamos un ejemplo.
Consideremos la función $f(x) =|x+3 |$ y evalúemos esta función en $x-3$. Ya que $f(x-3) = |x|$ y $x-3$ es menor que $x$, la gráfica de $f(x) = |x+3 |$ es la gráfica de $y= |x|$ desplazada a la izquierda 3 unidades. De manera similar, la gráfica de $f(x) = |x-3 |$ es la gráfica de $y= |x|$ desplazado a la derecha 3 unidades (Figura 1.24).
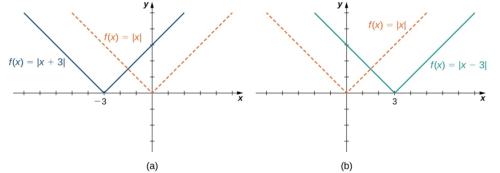
Figura 1.24 (a) Para $c> 0$, la gráfica de $y=f(x+c)$ es un desplazamiento horizontal a la izquierda $c$ unidades de la gráfica de $y=f(x)$. (b) Para $c> 0$, la gráfica de $y=f(x-c)$ es un desplazamiento horizontal a la derecha $c$ unidades de la gráfica de $y=f(x)$.
Se produce una escala vertical de un gráfico si multiplicamos todas las imágenes $y$ de una función por la misma constante positiva. Para $c> 0$, la gráfica de la función $cf(x)$ es la gráfica de $f(x)$ escalada verticalmente por un factor $c$.
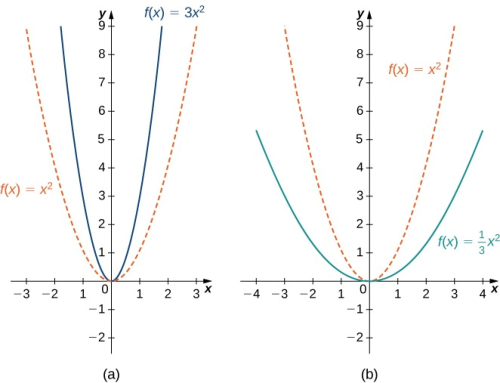
Figura 1.25 (a) Si $c> 1$, la gráfica de $y=cf(x)$ es un tramo vertical de la gráfica de $y=f(x)$. (b) Si $0 < c <1$, la gráfica de $y=cf(x)$ es una compresión vertical del gráfico de $y=f(x)$.
El escalado horizontal de una función ocurre si multiplicamos las entradas $x$ por la misma constante positiva. Para $c> 0$, la gráfica de la función $f(cx)$ es la gráfica de $f(x)$ escalada horizontalmente por un factor $c$.

Figura 1.26 (a) Si $c> 1$, la gráfica de $y=f(cx)$ es una compresión horizontal del gráfico de $y=f(x)$. (b) Si $0 < c < 1$, la gráfica de $y=f(cx)$ es un estiramiento horizontal de la gráfica de $y=f(x)$.
Hemos explorado lo que sucede con la gráfica de una función $f$ cuando multiplicamos $f$ por una constante $c> 0$ para obtener una nueva función $cf(x)$. También hemos discutido qué sucede con la gráfica de una función $f$ cuando multiplicamos la variable independiente $x$ por $c> 0$ para obtener una nueva función $f(cx)$. Sin embargo, no hemos abordado lo que sucede con la gráfica de la función si la constante $c$ es negativa.
Si tenemos una constante $c < 0$, podemos escribir $c$ como un número positivo multiplicado por $-1$; pero, ¿qué tipo de transformación obtenemos cuando multiplicamos la función o su argumento por $-1$? Cuando multiplicamos todas las imágenes por $-1$, tenemos una reflexión sobre el eje $X$. Cuando multiplicamos todas las entradas por $-1$, tenemos una reflexión sobre el eje $y$. Por ejemplo, la gráfica de $f(x) = - (x^3+1)$ es la gráfica de $y= (x^3+1)$ reflejada sobre el eje $X$. La gráfica de $f(x) = (-x)^3+1$ es la gráfica de $y=x^3+1$ reflejada sobre el eje $Y$ (Figura 1.27).
Si la gráfica de una función consta de más de una transformación de otra gráfica, es importante transformar la gráfica en el orden correcto. Dada una función $f(x)$, la gráfica de la función transformada $y=cf(a(x+b))+d$ se puede obtener de la gráfica de $y=f(x)$ realizando las transformaciones en el siguiente orden.

Figura 1.27 (a) La gráfica de $y= -f(x) es la gráfica de y=f(x)$ reflejada sobre el eje $X$. (b) La gráfica de $y=f(-x)$ es la gráfica de $y=f(x)$ reflejada sobre el $y$.
 Puedes practicar con la escena interactiva siguiente para ver cómo actúan las distintas transformaciones sobre las gráficas de las funciones.
Puedes practicar con la escena interactiva siguiente para ver cómo actúan las distintas transformaciones sobre las gráficas de las funciones.
A continuación, se resume en las siguiente tabla las diferentes transformaciones y sus efectos en la gráfica de una función.
| Transformación de $f$ ($c >0$) |
Efecto de la gráfica de $f$ |
| $f(x)+c$ | Desplazamiento vertical hacia arriba $c$ unidades |
| $f(x)-c$ | Desplazamiento vertical hacia abajo $c$ unidades |
| $f(x+c)$ | Desplazamiento horizontal hacia la derecha $c$ unidades |
| $f(x)-c$ | Desplazamiento horizontal hacia la izquierda $c$ unidades |
| $cf(x)$ | Escala vertical si $c > 1$ Compresión vertical si $0 < c < 1$ |
| $f(cx)$ | Escala horizontal si $0 < c < 1$ Compresión vertical si $c > 1$ |
| $-f(x)$ | Reflexión sobre el eje $x$ |
| $f(-x)$ | Reflexión sobre el eje $y$ |
Tabla 1.7 Transformación de funciones
 |
1.21 Transformando funciones |
Para cada una de las siguientes funciones, trazar un gráfico utilizando una secuencia de transformaciones de una función conocida.

 |
Cuestión 1.16 |
Describir cómo la función $f(x) = - (x+1)^2-4$ se puede representar usando el gráfico de $y=x^2$ y una secuencia de transformaciones.
 1.3.8 Ejercicios
1.3.8 Ejercicios Para los siguientes ejercicios, y para cada par de puntos,
Para los siguientes ejercicios, y para cada par de puntos,
a. encuentra la pendiente de la recta que pasa por dichos puntos
b. indica si la recta es creciente, decreciente, horizontal o vertical.
59. $(-2,4)$ y $(1,1)$ (Solución)
60. $(-1,4)$ y $(3,-1)$
61. $(3,5)$ y $(-1,2)$ (Solución)
62. $(6,4)$ y $(4,-3)$
63. $(2,3)$ y $(5,7)$ (Solución)
64. $(1,9)$ y $(-8,5)$
65. $(2,4)$ y $(1,4)$ (Solución)
66. $(1,4)$ y $(1,0)$
 Para los siguientes ejercicios, escribe la ecuación de una recta cumpliendo las condiciones dadas.
Para los siguientes ejercicios, escribe la ecuación de una recta cumpliendo las condiciones dadas.
67. pendiente $=-6$ y pasa por el punto $(1,3)$ (Solución)
68. pendiente $=3$ y pasa por el punto $(-3,2)$
69. pendiente $=1/3$ y pasa por el punto $(0,4)$ (Solución)
70. pendiente $=2/5$ la interseccón con el eje x $=8$
71. pasa por los puntos $(2,1)$ y $(-2,1)$ (Solución)
72. pasa por los puntos $(-3,7)$ y $(1,2)$
73. intersección con el eje x $=5$ e intersección con el eje $y$ $=-3$ (Solución)
74. intersección con el eje x $=-6$ e intersección con el eje $y$ $=9$
 Para los siguientes ejercicios y para cada ecuación, obtener
Para los siguientes ejercicios y para cada ecuación, obtener
a. el valor de la pendiente $m$ y la intersección con el eje $y$ si la hubiera
b. la gráfica de la recta.
75. $y=2x-3$ (Solución)
76. $y=-\frac{1}{7}x+1$
77. $f(x)=-6$ (Solución)
78. $f(x)=-5x+4$
79. $4y+24=0$ (Solución)
80. $8x-4$
81. $3x+3y=6$ (Solución)
82. $6x-5y+15=0$
 Para los siguientes ejercicios y para cada polinomio, determina
Para los siguientes ejercicios y para cada polinomio, determina
a. el grado
b. los ceros si los hubiera
c. las intersecciones con el eje $y$ si las hubiera
d. el comportamiento de la gráfica utilizando el coeficiente director
e. si el polinonomio es impar, par o ninguna de las dos cosas.
83. $f(x)=2x^2-3x-5$ (Solución)
84. $f(x)=-3x^2+6x$
85. $f(x)=\frac{1}{2}x^2-1$ (Solución)
86. $f(x)=x^3+3x^2-x-3$
87. $f(x)=3x-x^3$ (Solución)
 Para los siguientes ejercicios, utiliza la gráfica de la función $f(x)=x^2$ para representar cada transformada $g$.
Para los siguientes ejercicios, utiliza la gráfica de la función $f(x)=x^2$ para representar cada transformada $g$.
88. $g(x)=x^2-1$
89. $g(x)=(x+3)^2+1$ (Solución)
 Para los siguientes ejercicios, utiliza la gráfica de la función $f(x)=\sqrt{x}$ para representar cada transformada $g$.
Para los siguientes ejercicios, utiliza la gráfica de la función $f(x)=\sqrt{x}$ para representar cada transformada $g$.
90. $g(x)=\sqrt{x+2}$
91. $g(x)=-\sqrt{x}-1$ (Solución)
 Para los siguientes ejercicios, utiliza la gráfica de la función $f(x)$ para representar cada transformada $g$.
Para los siguientes ejercicios, utiliza la gráfica de la función $f(x)$ para representar cada transformada $g$.
92. $g(x)=f(x)+1$
93. $g(x)=f(x-1)+2$ (Solución)
 Para los siguientes ejercicios, utiliza la gráfica de la función $f(x)$ para representar cada transformada $g$ y para cada función definida a trozos,
Para los siguientes ejercicios, utiliza la gráfica de la función $f(x)$ para representar cada transformada $g$ y para cada función definida a trozos,
a. Evalúa la función en los valores dados.
b. Haz un bosquejo de la gráfica.
94. $$f(x) = \begin{cases} 4x+3 & \text{si $x \le 0$} \\ -x+1 & \text{si $x > 0$} \end{cases} $$ $$f(-3); f(0); f(2)$$
95. $$f(x) = \begin{cases} x^2-3 & \text{si $x < 0$} \\ 4x-3 & \text{si $x \ge 0$} \end{cases} $$
$f(-4); f(0); f(2)$ (Solución)
96. $$h(x) = \begin{cases} x+1 & \text{si $x \le 5$} \\ 4 & \text{si $x > 5$} \end{cases} $$ $$h(0); h(\pi); h(5)$$
97. $$g(x) = \begin{cases} \frac{3}{x-2} & \text{si $x \neq 2$} \\ 4 & \text{si $x =2$} \end{cases} $$
$g(0); g(-4); g(2)$ (Solución)
 Para los siguientes ejercicios,determina si la afirmación es cierta o falsa. Explica por qué.
Para los siguientes ejercicios,determina si la afirmación es cierta o falsa. Explica por qué.
98. $f(x)=\frac{4x+1}{7x-2}$ es una función trascendente.
99. $g(x)=\sqrt{3}{x}$ es una función impar. (Solución)
100. Una función logarítmica es una función algebraica
101. Una función de la forma $f(x)=x^b$, donde $b$ es un valor real constante, es una función exponencial. (Solución)
102. El dominio de un función raiz par es el conjutno de todos los números reales.
103. [T] Una empresa compra algunos equipos informáticos por 20,500 dólaresa. Al final de un período de 3 años, el valor del equipo ha disminuido linealmente a 12,300 dólares.
104. [T] El número total de compras online durante las vacaciones de Navidad ha aumentado drásticamente durante los últimos 5 años. En 2012 ($t = 0$), las ventas navideñas totales en línea fueron de 42,3 mil millones de dólares, mientras que en 2013 fueron 48.1 mil millones de dólares.
105. [T] Una panadería familiar hace cupcakes y los vende en festivales locales al aire libre. Para un festival de música, hay un coste fijo de 125 dólares para montar un puesto de magdalenas. El propietario estima que cuesta 0,75 euros para hacer cada cupcake.
El propietario está interesado en determinar el coste total $C$ como función del número de cupcakes hechos.
106. [T] Se espera que una casa comprada por 250,000 dólares valga el doble de su precio de compra en 18 años.
107. [T] Se compró un automóvil por 26,000 dólares. El valor del automóvil se deprecia en 1500 dólares por año.
108. [T] Un condominio en una zona exclusiva de la ciudad fue comprado por 432,000 dólares. En 35 años vale 60,500 dólares. Calcula la tasa de depreciación.
109. [T] El costo total $C$ (en miles de dólares) para producir un determinado artículo es modelizado por la función $C (x) = 10,50x + 28,500$, donde $x$ es el número de elementos producido. Determina el coste de producir 175 artículos. (Solución)
110. [T] Una profesora le pide a su clase que informe de la cantidad del tiempo que dedicaron a escribir dos tareas. La mayoría de los estudiantes informa que les lleva unos 45 minutos escribir una tarea de cuatro páginas y alrededor de 1,5 horas para escribir una tarea de 9 páginas.
111. [T] La producción de energía nuclear de las plantas de Estados Unidos (como porcentaje de la capacidad total) se pueden modelizar por la función $P (t) = 1.8576t + 68.052$, donde $t$ es el tiempo en años y $t = 0$ corresponde a principios de 2000. Utiliza el modelo para predecir el porcentaje de producción en 2015. (Solución)
112. [T] La oficina de admisiones de una universidad pública estima que el $65\% $ de los estudiantes que solicitaron admisión a la clase de 2019 realmente se inscribirá.
Objetivos de aprendizaje
Las funciones trigonométricas se utilizan para modelizar muchos fenómenos, incluidas ondas sonoras, vibraciones de cuerdas, corriente eléctrica alterna y el movimiento de péndulos. De hecho, casi cualquier movimiento repetitivo o cíclico puede modelizarse mediante alguna combinación de funciones trigonométricas. En esta sección, definimos las seis funciones trigonométricas básicas y observamos algunas de las principales identidades que involucran estas funciones.
Para usar funciones trigonométricas, primero debemos entender cómo medir los ángulos. Aunque podemos usar radianes y grados, los radianes son una medida más natural porque están relacionados directamente con el círculo unitario, un círculo con radio 1.
La medida en radianes de un ángulo se define de la siguiente manera. Dado un ángulo $\theta$, sea $s$ la longitud del arco correspondiente en el círculo unidad (Figura 1.30). Decimos que el ángulo correspondiente al arco de longitud 1 tiene medida en 1 radián.

Figura 1.30 La medida en radianes de un ángulo $\theta$ está asociado a un arco $s$ con esa longitud en el círculo unitario.
Dado que un ángulo de $360°$ corresponde a la circunferencia de un círculo, o un arco de longitud $2\pi$ en la circunferencia unidad, llegamos a la conclusión de que un ángulo con una medida en grados de $360°$ tiene una medida en radianes de $2\pi$. Del mismo modo, vemos que $180°$ es equivalente a $\pi$ radianes. En la Tabla 1.8 se muestra la relación entre grados y valores en radianes.
 En la siguiente escena se puede practicar la conversión entre grados y radianes.
En la siguiente escena se puede practicar la conversión entre grados y radianes.
| Grados | Radianes | Grados | Radianes |
| 0 | 0 | 120 | $2\pi/3$ |
| 30 | $\pi/6$ | 135 | $3\pi/4$ |
| 45 | $\pi/4$ | 150 | $5\pi/6$ |
| 60 | $\pi/3$ | 180 | $\pi$ |
| 90 | $\pi/2$ |
Tabla 1.8 Ángulos comunes expresados en grados y radianes
 |
1.22 Conversión entre radianes y grados |

 |
Cuestión 1.17 |
Expresa $210°$ usando radianes. Expresa $11\pi/6$ rad usando grados.
Las funciones trigonométricas nos permiten utilizar medidas de ángulos, en radianes o grados, para encontrar las coordenadas de un punto en cualquier círculo, no solo en un círculo unidad, o para encontrar un ángulo dado un punto en un círculo. También definen la relación entre los lados y ángulos de un triángulo.
Para definir las funciones trigonométricas, primero consideremos el círculo unidad centrado en el origen y un punto $P(x,y)$ en el círculo unidad. Sea $\theta$ el ángulo con un lado inicial que se encuentra a lo largo del eje positivo $X$ y con un lado terminal que es el segmento de línea $OP$. Se dice que un ángulo en esta posición está en la posición estándar (Figura 1.31).
Podemos entonces definir los valores de las seis funciones trigonométricas para $\theta$ en términos de las coordenadas $x$ e $y$.
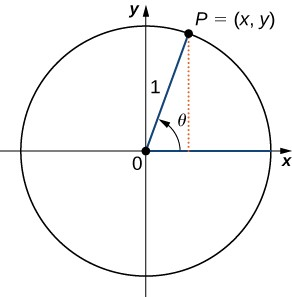
Figura 1.31 El ángulo $\theta$ está en posición estándar. Los valores de las funciones trigonométricas para $\theta$ se definen en términos de las coordenadas $x$ e $y$.
Sea $P(x,y)$ un punto en el círculo unidad centrado en el origen $O$. Sea $\theta$ el ángulo con un lado inicial a lo largo del eje positivo $X$ y un lado terminal dado por el segmento $OP$.
Las funciones trigonométricas se definen entonces como
$$sen(\theta)=y\,\,\,\,\,\,csc(\theta)=\frac{1}{y}$$ $$cos(\theta)=x\,\,\,\,\,\,sec(\theta)=\frac{1}{x}$$Si $x= 0$, $sec(\theta)$ y $tg(\theta)$ no están definidas. Si $y= 0$, $cot(\theta)$ y $csc(\theta)$ no están definidas.
Podemos ver que para un punto $P(x,y)$ en un círculo de radio $r$ con un ángulo correspondiente $\theta$, las coordenadas $x$ e $y$
satisfacen
$$cos(\theta)=\frac{x}{r} \,\,\,\,\,\,\,\,\,\,x=rcos(\theta)$$
$$sin(\theta)=\frac{y}{r} \,\,\,\,\,\,\,\,\,\,y=rsen(\theta)$$
Los valores de las otras funciones trigonométricas se pueden expresar en términos de $x$, $y$ y r
(Figura 1.32).
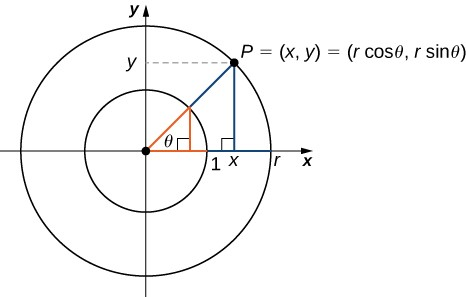
Figura 1.32 Para un punto $P(x,y)$ en un círculo de radio $r$, las coordenadas $x$ e $y$ satisfacen $x=rcos(\theta)$ , $y=rsen(\theta)$.
La tabla 1.9 muestra los valores del seno y coseno en los ángulos principales del primer cuadrante, a partir ellos, se pueden determinar los de los ángulos de los otros cuadrantes. El resto de las funciones trigonométricas se calculan fácilmente a partir de los valores del $sen(\theta)$ y $cos(\theta)$.
| $\theta$ | $sen(\theta)$ | $cos(\theta)$ |
| 0 | 0 | 1 |
| $\frac{\pi}{6}$ | $\frac{1}{2}$ | $\frac{\sqrt{3}}{6}$ |
| $\frac{\pi}{4}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{2}}{2}$ |
| $\frac{\pi}{3}$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{1}}{2}$ |
| $\frac{\pi}{2}$ | $1$ | $0$ |
Tabla 1.9 $sen$ y $cos$ en ángulos principales del primer cuadrante
 En la siguiente escena se muestra cómo obtener las razones trigonométricas elementales. Esta escena está tomada del Proyecto EDAD y diseñada por la profesora María José García Cebrian
En la siguiente escena se muestra cómo obtener las razones trigonométricas elementales. Esta escena está tomada del Proyecto EDAD y diseñada por la profesora María José García Cebrian
 |
1.23 Evaluación de funciones trigonométricas |
Evalúa cada una de las siguientes expresiones.

 |
Cuestión 1.18 |
Evalua $cos(\frac{3\pi}{4})$ y $sen(\frac{-\pi}{6})$.
Como se mencionó anteriormente, las razones de las longitudes de los lados de un triángulo rectángulo se pueden expresar en términos de las funciones trigonométricas evaluadas en cualquiera de los ángulos agudos del triángulo. Sea $\theta$ uno de los ángulos agudos. Sea $A$ la longitud del cateto adyacente, $O$ la longitud del cateto opuesta, y $H$ la longitud de la hipotenusa. Inscribiendo el triángulo en un círculo de radio $H$, como se muestra en la Figura 1.33, vemos que $A$, $H$, y $O$ satisfacen las siguientes relaciones : $$sen(\theta)=\frac{0}{A}\,\,\,\,\,\,csc(\theta)=\frac{H}{O}$$
$$cos(\theta)=\frac{A}{H}\,\,\,\,\,\,sec(\theta)=\frac{H}{A}$$ $$tg(\theta)=\frac{O}{A}\,\,\,\,\,\,cot(\theta)=\frac{A}{O}$$

Figura 1.33 Al inscribir un triángulo rectángulo en un círculo, podemos expresar las razones de las longitudes de los lados en términos de las funciones trigonométricas evaluadas en $\theta$.
 |
1.24 Construyendo una rampa de madera |
Se construirá una rampa de madera con un extremo en el suelo y el otro en la parte superior de una pequeña escalera. Si la parte superior de la escalera está a 4 pies del suelo y el ángulo entre el suelo y la rampa debe ser $10°$, ¿Cuánta longitud debe tener la rampa?

 |
Cuestión 1.19 |
Un pintor de casas quiere inclinarse 20 pies de escalera contra una casa. Si el ángulo entre la base de la escalera y el suelo debe ser 60°, ¿A qué distancia de la casa debe colocar la base de la escalera?
Una identidad trigonométrica es una ecuación que involucra funciones trigonométricas que es verdadera para todos los ángulos $\theta$ para lo cual se definen las funciones. Podemos usar las identidades para ayudarnos a resolver o simplificar ecuaciones. Las principales identidades trigonométricas se enumeran a continuación.
Identidades recíprocas $$tg(\theta)=\frac{sen(\theta)}{cos(\theta)}\,\,\,\,\,\,cot(\theta)=\frac{cos(\theta)}{sen(\theta)}$$ $$csc(\theta)=\frac{1}{sen(\theta)}\,\,\,\,\,\,sec(\theta)=\frac{1}{cos(\theta)}$$
Identidades pitagóricas $$sen^2(\theta)+cos^2(\theta)=1\,\,\,\,\,\,1+tg^2(\theta)=sec^2(\theta)$$ $$1+cot^2(\theta)=csc^2(\theta)$$
Fórmulas de suma y resta $$sen(\alpha \pm \beta) = sen\alpha \cdot cos\beta \pm cos\alpha \cdot sen\beta$$ $$cos(\alpha \pm \beta) = cos\alpha \cdot cos\beta \mp sen\alpha \cdot sen\beta$$
Fórmulas de doble ángulo $$sen (2\theta) = 2 sen(\theta) \cdot cos(\theta)$$ $$cos (2\theta) = 2cos^2(\theta)-1 = 1-2sen^2(\theta)= cos^2\theta-sen^2\theta$$
 |
1.25 Resolver ecuaciones trigonométricas |
Para cada una de las siguientes ecuaciones, utiliza una identidad trigonométrica para encontrar todas las soluciones.

 |
Cuestión 1.20 |
Encuentra todas las soluciones de la ecuación $cos (2\theta) = sen\theta$.
 |
1.26 Demostrando una identidad trigonométrica |
Demuestra la identidad trigonométrica $1 + tg^2\theta= sec^2\theta$.

 |
Cuestión 1.21 |
Demuestra la identidad trigonométrica $1 + ctg^2\theta= csc^2\theta$.
 En la siguiente escena se muestra cómo demostrar alguna de las identidades fundamentales. Esta escena está tomada del Proyecto EDAD y diseñada por la profesora María José García Cebrian
En la siguiente escena se muestra cómo demostrar alguna de las identidades fundamentales. Esta escena está tomada del Proyecto EDAD y diseñada por la profesora María José García Cebrian
Hemos visto que a medida que nos movemos alrededor del círculo unidad, los valores de las funciones trigonométricas se repiten. Podemos ver este patrón en las gráficas de las funciones. Sea $P(x,y)$ un punto en el círculo unidad y sea $\theta$ el ángulo correspondiente. Como el ángulo $\theta$ y $\theta+2\pi $corresponden al mismo punto $P$, los valores de las funciones trigonométricas en $\theta$ y en $\theta+2\pi$ coinciden. En consecuencia, las funciones trigonométricas son funciones periódicas.
El período de una función $f$ se define como el valor positivo más pequeño $p$ tal que $f(x+p) =f(x)$ para todos los valores $x$ en el dominio de $f$. Las funciones seno, coseno, secante y cosecante tienen un período de $2\pi$. Dado que las funciones tangente y cotangente se repiten en un intervalo de longitud $\pi$, su período es $\pi$ (Figura 1.34).
Al igual que con las funciones algebraicas, podemos aplicar transformaciones a funciones trigonométricas. En particular, consideremos la siguiente función: $$f(x) =Asen(B(x-\alpha)) +C \tag{$1.10$}$$
En la Figura 1.35, la constante $\alpha$ provoca un desplazamiento horizontal o de fase. El factor $B$ cambia el período. Esta función seno transformada tendrá un período $2\pi/ |B|$. El factor $A$ da como resultado un estiramiento vertical por un factor de $|A|$. Decimos $|A|$ es la "amplitud de F." La constante $C$ provoca un desplazamiento vertical.
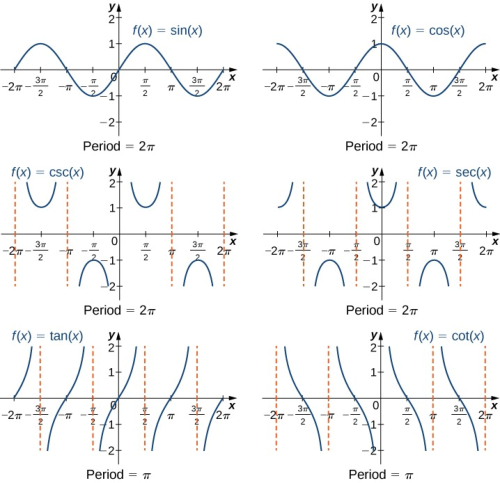
Figura 1.34 Las seis funciones trigonométricas son periódicas.
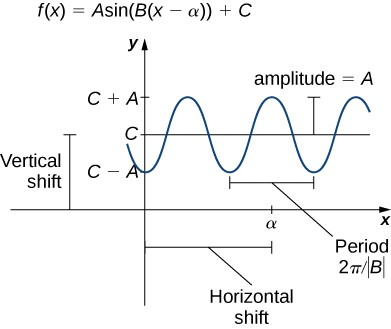
Figura 1.35 Una gráfica de una función seno general.
Se debe notar en la Figura 1.34 que la gráfica de $y= cosx$ es la gráfica de $y= senx$ desplazada a la izquierda $\pi/ 2$ unidades. Por tanto, podemos escribir $$cosx= sen (x+\pi/ 2)$$
De manera similar, podemos ver la gráfica de $y= senx$ como la de $y= cosx$ desplazada a la derecha $\pi/ 2 $ unidades, ya que $$senx= cos \left(x-\frac{\pi}{2}\right)$$
Una curva sinusoidal desplazada surge naturalmente al representar el número de horas de luz del día en una ubicación determinada en función del día del año. Por ejemplo, suponga que una ciudad informa que el 21 de junio es el día más largo del año con 15,7 horas y el 21 de diciembre es el día más corto del año con 8.3 horas. Se puede demostrar que la función $$h(t) = 3,7 sen\left(\frac{2\pi}{365} (t-80.5)\right)+12$$ es un modelo para el número de horas de luz del día $h$ en función del día del año $t$ (Figura 1.36).
Figura 1.36 Las horas de luz diurna en función del día del año pueden modelizarse mediante una curva sinusoidal desplazada.
 En la siguiente escena se muestra cuál es el periodo, la amplitud y la fase en una función cosenoidal.
En la siguiente escena se muestra cuál es el periodo, la amplitud y la fase en una función cosenoidal.
 |
1.27 Dibujar el gráfico de una curva sinusoidal transformada |
Dibuja la gráfica de $f(x) = 3 sen(2(x-\frac{\pi}{4}))+1$.

 |
Cuestión 1.22 |
Describe la relación entre la gráfica de $f(x) = 3 sen (4x) -5$ y la gráfica de $y= sen(x)$.
 1.4.5 Ejercicios
1.4.5 Ejercicios Para los siguientes ejercicios, convierte cada ángulo en grado en radianes. Escribe las respuestas como un múltiplo de $\pi$
Para los siguientes ejercicios, convierte cada ángulo en grado en radianes. Escribe las respuestas como un múltiplo de $\pi$
113. $240º$ (Solución)
114. $15º$
115. $-60º$ (Solución)
116. $-225º$
117. $330º$ (Solución)
 Para los siguientes ejercicios, convierte cada ángulo en radianes en grados.
Para los siguientes ejercicios, convierte cada ángulo en radianes en grados.
118. $\pi/2 rad$
119. $\frac{7\pi}{6} rad$ (Solución)
120. $\frac{11\pi}{2}rad$
121. $-3\pi rad$ (Solución)
122. $\frac{5\pi}{12} rad$
 Evalúa los siguientes valores.
Evalúa los siguientes valores.
123. $cos(\frac{4\pi}{3})$ (Solución)
124. $tg(\frac{19\pi}{4})$
125. $sen(\frac{-3\pi}{4})$ (Solución)
126. $sec(\frac{\pi}{6})$
127. $sen(\frac{\pi}{12})$ (Solución)
128. $cos(\frac{5\pi}{12})$
 Para los siguientes ejercicios, consideramos el triángulo rectángulo ABC con un ángulo recto en C.
Para los siguientes ejercicios, consideramos el triángulo rectángulo ABC con un ángulo recto en C.
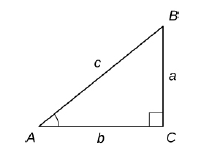
129. $a=4$, $c=7$ (Solución)
130. $a=21$, $c=29$
131. $a=85.3$, $b=125.4$ (Solución)
132. $b=40$, $c=41$
133. $a=84$, $b=13$ (Solución)
134. $b=28$, $c=35$
 Para los siguientes ejercicios, $P$ es un punto en el círculo unitario.
Para los siguientes ejercicios, $P$ es un punto en el círculo unitario.
a. Encuentra el valor (exacto) de las coordenadas faltantes de cada punto
b. encontrar los valores de las seis funciones trigonométricas para
el ángulo $\theta$ con un lado terminal que pasa por el punto
$P$. Racionalizar denominadores.
135. $P(\frac{7}{25},y)$, $y > 0$ (Solución)
136. $P(\frac{-15}{17},y)$, $y < 0$
137. $P(x,\frac{\sqrt{7}}{3})$, $x < 0$ (Solución)
138. $P(x,-\frac{\sqrt{15}}{4})$, $x > 0$
 Para los siguientes ejercicios, simplifica cada expresión escribiendo primero en términos de senos y cosenos. La respuesta final no debe quedar únicamente en senos y cosenos.
Para los siguientes ejercicios, simplifica cada expresión escribiendo primero en términos de senos y cosenos. La respuesta final no debe quedar únicamente en senos y cosenos.
139. $tan^2(x)+sen(x)\,\,csc(x)$ (Solución)
140. $sec(x) sen(x) cot(x)$
141. $\frac{tan^x}{sec^x}$ (Solución)
142. $sec(x) -cos(x)$
143. $(1+tg\theta)^2-2tg\theta$ (Solución)
144. $sen(x)(cscx-senx)$
145. $\frac{cost}{sent}+\frac{sent}{1+cost}$ (Solución)
146. $\frac{1+tg^2x}{1+cot^2x}$
 Para los siguientes ejercicios, verifica que cada ecuación es una identidad.
Para los siguientes ejercicios, verifica que cada ecuación es una identidad.
147. $\frac{tg\theta cot\theta}{csc\theta}=sen\theta$
148. $\frac{sec^2\theta}{tg\theta}=sec\theta csc\theta$
149. $\frac{sen(t)}{csc(t)}+\frac{cos(t)}{sect}=1$
150. $\frac{sen(x)}{cos(x)+1}+\frac{cos(x)-1}{senx}=0$
151. $cot\alpha+tan\alpha=sec\alpha csc\alpha$
152. $sen^2\alpha+tan^2\alpha+cos^2\alpha=sec^\alpha$
153. $\frac{1}{1-sen\alpha}+\frac{1}{1+sen\alpha}=2sec^2 \alpha$
154. $\frac{tan\theta-cot\theta}{sen\theta cos\theta}=sec^2\theta-csc^2\theta$
 Para los siguientes ejercicios, resolver las ecuaciones trigonométricas en el intervalo $0 \leq \theta <2\pi$.
Para los siguientes ejercicios, resolver las ecuaciones trigonométricas en el intervalo $0 \leq \theta <2\pi$.
155. $2sen\theta -1=0$ (Solución)
156. $1+cos\theta=\frac{1}{2}$
157. $2tan^2 \theta=2$ (Solución)
158. $4 sen^2\theta-2=0$
159. $\sqrt{3} cot\theta +1=0$ (Solución)
160. $3sec\theta-2\sqrt{3}=0$
161. $2cos\theta sen\theta=sen\theta$ (Solución)
162. $csc^2\theta+2csc\theta+1=0$
 En los siguientes ejercicios, cada gráfico corresponde a una función de la forma $y=Asen(Bx)$ o $y=cos(Bx)$, donde $B>0$. Escribe la expresión de la función correspondiente a la gráfica.
En los siguientes ejercicios, cada gráfico corresponde a una función de la forma $y=Asen(Bx)$ o $y=cos(Bx)$, donde $B>0$. Escribe la expresión de la función correspondiente a la gráfica.
(Solución)
166. 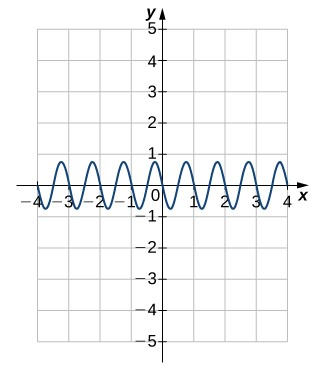
 En los siguientes ejercicios, encuentra
En los siguientes ejercicios, encuentra
167. $y=sen\left(x-\pi/4\right)$ (Solución)
168. $y=3cos\left(2x+3\right)$
169. $y=\frac{-1}{2}sen\left(\frac{1}{4}x\right)$ (Solución)
170. $y=2cos\left(x-\pi/3\right)$
171. $y=-3sen\left(\pi x+2 \right)$ (Solución)
172. $y=4cos\left(2x-\pi/2\right)$
173. [T] El diámetro de una rueda que gira por el suelo. es de 40 pulg. Si la rueda gira en un ángulo de 120°, ¿cuántas pulgadas se mueve? Aproximarlo al valro entero más cercano. (Solución)
174. [T] Encuentra la longitud del arco interceptado por un ángulo central $\theta$ en un círculo de radio $r$. Redondea a la centésima más cercana.
175. [T] Cuando un punto $P$ se mueve alrededor de un círculo, la medida del ángulo central recorrido cambia. La rapidez de cambio de este ángulo se llama velocidad angular, $\omega$, y viene dada por $\omega = \theta / t$, donde $\theta$ está en radianes y $t$ es el tiempo. Encuentra la velocidad angular para los datos siguientes redondeando a la milésima más cercana.
176. [T] Se necesita un total de $250.000$ $m^2$ de terreno para construir una planta de energía nuclear. Supongamos que se decide que el área en que se va a construir la central eléctrica debe ser circular.
177. [T] El área de un triángulo isósceles con lados iguales de longitud x es $12 x^2 sen\theta$, donde $\theta$ es el ángulo formado por los dos lados. Encuentra el área de un triángulo isósceles con lados iguales de 8 pulgadas de longitud y ángulo $\theta = \frac{5\pi} {12}$ rad. (Solución)
178. [T] Una partícula viaja en una trayectoria circular a una velocidad angular constante $\omega$. La velocidad angular está modelada por el función $\omega = 9 | cos \left(\pi t - \pi / 12\right) |$. Determina la velocidad angular en $t = 9$ seg.
179. [T] Una corriente alterna para enchufes en una casa tiene voltaje dado por la función $V (t) = 150cos368t$, donde $V$ es el voltaje en voltios en el tiempo $t$ en segundos.
180. [T] La cantidad de horas de luz diurna en el noreste de una ciudad está modelada por la función $N (t) = 12 + 3sin\left[\frac{2 \pi}{365}\left(t-79\right)\right]$ donde $t$ es el número de días después del 1 de enero.
Objetivos de aprendizaje
Una función inversa de una función invierte la operación realizada por esta función. En esta sección, definimos formalmente una función inversa y establecemos las condiciones necesarias para que exista una función inversa. Examinamos cómo encontrar una función inversa y estudiamos la relación entre la gráfica de una función y la de su inversa. Finalmente aplicaremos estas ideas para definir y discutir las propiedades de las funciones trigonométricas inversas.
Vamos a comenzar con un ejemplo. Se considera una función $f$ dada por $y = f(x)$, a menudo nos interesa encontrar para cada valor $y$ en la imagen qué valor o valores $x$ tienen asignado dicho valor $y$ por la aplicación $f$ .
Por ejemplo, consideremos la función $f (x) = x^3 + 4$. Para cualquier punto en la imagen $y = x^3 + 4$, podemos resolver esta ecuación para encontrar el valor x $x$, operando será $x = \sqrt[3]{y - 4}$. Esta ecuación define a $x$ como una función de $y$. Denotando esta función como $f^{-1}$, se escribirá $x =f^{-1}(y)=\sqrt[3]{y - 4}$. Para cada $x$ $$f^{-1}(f(x)) = f^{-1}(x^3 + 4)= x$$ Así, esta nueva función, $f^{-1}$, "deshace" lo que la función original $f$ "hizo". Una función con esta propiedad se llama función inversa de la función original.
Dada una función $f$ con dominio $D$ y rango $R$, su función inversa (si existe) es la función $f^{-1}$ cuyo dominio es $R$ y el rango es $D$ tal que $f^{-1}(y)=x$ si y solo si $f(x)=y$.
Es decir, para una función $f$ y su inversa $f^{-1}$ se cumple $$f^{-1}(f(x))=x \,\,\,\,\,\text{para todo x en D}$$ $$f(f^{-1}(y))=y \,\,\,\,\,\text{para todo y en R}$$
La función $f^{-1}$ se lee como "función inversa de $f$". Aquí el $-1$ no se usa como exponente y $$f^{-1}(x) \neq \frac{1}{f (x)}$$
La Figura 1.37, muestra la relación entre el dominio y rango de $f$ y el dominio y rango de $f^{-1}$.

Figura 1.37 Dada una función $f$ y su inversa $f^{-1}$, $f^{-1}(y) = x$ si y solo si $f(x) = y$. El rango de $f$ se convierte en el dominio de $f^{-1}$ y el dominio de $f$ se convierte en el rango de$f^{-1}$.
Recuerda que una función tiene exactamente una imagen para cada punto del dominio. Por lo tanto, para definir una función inversa, necesitamos asignar a cada entrada a exactamente una imagen. Por ejemplo, intentemos encontrar la función inversa para $f (x) = x^2$. Resolviendo la ecuación $y = x^2$ para $x$, llegamos a la ecuación $x = ± \sqrt{y}$. Esta ecuación no describe $x$ como una función de $y$ porque hay dos soluciones para esta ecuación a partir de cualquier valor $y> 0$. El problema de tratar de encontrar una función inversa para $f (x) = x^2$ es que hay dos valores que tienen la misma imagen cumpliendo $y>0$. La función $f (x) = x^3 + 4$ analizada anteriormente no tenía este problema. Para esa función, cada punto del origen se asigna a una imagen diferente. Una función que envía cada entrada a una imagen diferente se llama función uno-uno o función inyectiva.
Una función f es uno-uno si $f(x_1)\neq f(x_2)$ cuando $x_1\neq x_2$
Una forma de determinar si una función es uno-uno es analizando su gráfica. Como hemos dicho, si una función es uno-uno, no se pueden enviar dos puntos del c a una misma imagen.
Por lo tanto, si trazamos una línea horizontal en cualquier lugar del plano $XY$, no puede cortar a la gráfica más de una vez. Observamos que esta prueba de la recta horizontal es diferente de la prueba de la recta vertical. La prueba de la recta vertical permite determinar si una gráfica corresponde a una función. La prueba de la recta horizontal determina si una función es uno-uno (Figura 1.38).
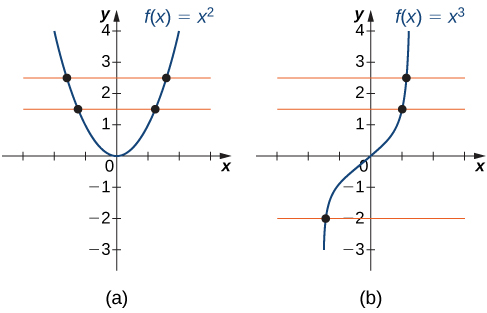
Figura 1.38 a) La función $f(x) = x^2$ no es uno a uno porque falla la prueba de la línea horizontal. (b) La función $f (x) = x^3$ es uno a uno porque pasa la prueba de la línea horizontal.
Una función $f$ es uno-uno o inyectiva si y solo si cada recta horizontal corta la gráfica de $f$ a lo sumo una vez.
 |
1.28 Determinar si una funión es uno-uno |
Para cada una de las siguientes funciones, utilizar el test de la recta horizontal para dterminar si la función es uno-uno

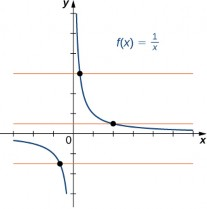
 |
Cuestión 1.23 |
¿Es la función $f$, cuya gráfica se muestra a continuación, una función uno-uno?
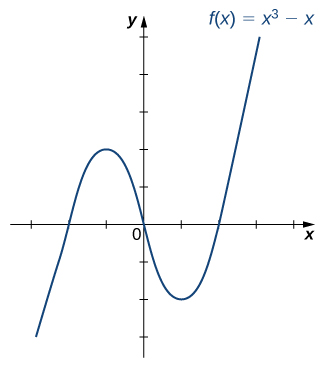
Nosotros ahora podemos considerar funciones uno a uno y mostrar cómo encontrar sus inversas. Recuerda que una función mapea elementos del dominio $f$ con elementos del rango de $f$. La función inversa mapea cada elemento del rango de $f$ de nuevo a su elemento correspondiente del dominio de $f$. Para encontrar la función inversa de una función uno-uno $f$, dada cualquier $y$ en el rango de $f$, necesitamos determinar qué $x$ en el dominio de $f$ satisface $f (x) = y$. Dado que $f es uno a uno$, existe exactamente uno de esos valores $x$. Podemos encontrar ese valor $x$ resolviendo la ecuación $f (x) = y$ para $x$.
Al hacerlo, podemos escribir $x$ como una función de $y$ donde el dominio de esta función es el rango de $f$ y el rango de esta nueva función es el dominio de $f$. En consecuencia, esta función es la inversa de $f$, y escribimos $x = f^{-1}(y)$. Dado que normalmente usamos la variable $x$ para denotar la variable independiente e $y$ para denotar la variable dependiente, a menudo intercambiamos los roles de $x$ e $y$, y escribimos $y = f^{-1} (x)$. Representando la función inversa de esta manera veremos su utilidad más adelante cuando graficamos una función $f$ y su inversa $f^{-1}$ en los mismos ejes.
 |
1.29 Encontrando la función inversa |
Encuentra la inversa de la función $f (x) = 3x - 4$. Indica el dominio y el rango de esta función y comprueba que se cumple $f^{-1}( f(x)) = x$.

 |
Cuestión 1.24 |
Encuentra la inversa de la función $f(x) =\frac {3x}{x-2}$. Indica el dominio y el rango de esta función.
Graficar funciones inversas
Consideremos la relación entre la gráfica de una función $f$ y la gráfica de su inversa. Consideremos la gráfica de $f$ que se muestra en la Figura 1.39 y consideremos también un punto $(a,b)$ en el gráfico. Si $b= f(a)$, entonces $f^{ -1} (b) = a$. Por lo tanto, cuando representemos $f^{-1}$, el punto $(b, a)$ está en el gráfico. Como resultado, la gráfica de $f^{-1}$ es un reflejo de la gráfica de $f$ sobre la recta $y =x$.
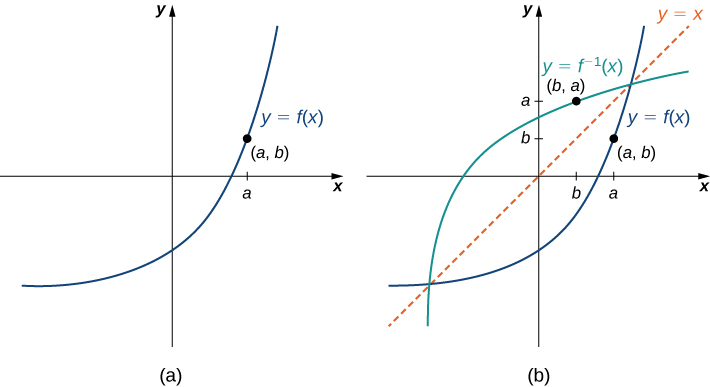
Figura 1.39 a) La gráfica de esta función $f$ muestra el punto $(a,b)$ en el gráfico de $f$ . (b) Dado que $(a,b)$ está en la gráfica de $f$ , el punto $(b,a)$ está en la gráfica de $f^{-1}$. La gráfica de $f^{-1}$ es un reflejo de la gráfica de $f$ sobre la recta $y =x$
 |
1.30 Representando gráficas de funciones inversas |
Para la gráfica de $f$ en la siguiente imagen, dibuje una gráfica de $f^{-1}$ trazando la recta $y = x$ y usando simetría. Identifique el dominio y el rango de $f^{-1}$.

 |
Cuestión 1.25 |
Dibuja la gráfica de $f(x) = 2x+ 3$ y la gráfica de su inversa usando la propiedad de simetría de las funciones inversas.
 En la siguiente escena interactiva puedes arrastrar el punto sobre la función y ver cómo se va representando la gráfica de la función inversa
En la siguiente escena interactiva puedes arrastrar el punto sobre la función y ver cómo se va representando la gráfica de la función inversa
Restricción de dominios
Como hemos visto, $f (x) = x^2$ no tiene función inversa porque no es uno-uno. Sin embargo, podemos elegir un subconjunto del dominio de $f$ tal que la función sea uno-uno. Este subconjunto se denomina dominio restringido.
Al restringir el dominio de $f$, podemos definir una nueva función $g$ tal que el dominio de $g$ es el dominio restringido de $f$ y $g (x) = f (x)$ para todo $x$ en el dominio de $g$. Entonces podemos definir una función inversa para $g $en ese dominio.
Por ejemplo, dado que $f (x) = x^2$ es uno-uno en el intervalo $[0, \infty)$, podemos definir una nueva función $g$ tal que el dominio de $g$ es $[0, \infty)$ y $g (x) = x^2$ para todo $x$ en su dominio. Como $g$ es una función uno-uno, tiene una función inversa, dada por la fórmula $g^{-1}(x) = x$.
Por otro lado, la función $f (x) = x^2$ también es uno-uno en el dominio $(-\infty, 0]$. Por lo tanto, podemos definir una nueva función $h$ tal que su dominio es y $h(x)=x^2$ para todos los valores de $x$ en el dominio de $h$. De esta manera, la función $h$ es uno-uno y tendrá inversa que vendrá dada por $h^{-1}(x)=-\sqrt{x}$ (Figura 1.40).
Figura 1.40 (a) Para $g(x) = x^2$ restringido a $[0, \infty)$, se tiene $g^{-1} (x) = x$. (b) Para $h(x) = x^2$ restringido para a$(\infty, 0]$, se tendrá $h^{-1} (x) =- x$.
 |
1.31 Restricción del dominio |
Consideremos la función $f(x) = (x + 1)^2$.

 |
Cuestión 1.26 |
Consideremos $f(x) = \frac{1}{x^2}$ restringido al dominio $(-\infty, 0)$. Comprueba que $f$ es uno-uno en este dominio. Determina también el dominio y el rango de la inversa de $f$ y encuentra una fórmula para $f^{-1}$.
Las seis funciones trigonométricas básicas vistas en apartados anteriores son periódicas y, por lo tanto, no son uno-uno. Sin embargo, si restringimos el dominio de una función trigonométrica a un intervalo en el que es uno-uno, podemos definir su función inversa.
Consideremos la función seno (Figura 1.34). La función seno es uno-uno en un número infinito de intervalos, pero la convención estándar es restringir el dominio al intervalo $[-\frac{\pi}{2},\frac{\pi}{2}]$. Al hacerlo, definimos la función inversa del seno en el dominio $[-1, 1]$ tal que para cualquier $x$ en este intervalo, la función inversa del seno nos dice qué ángulo $\theta$ en el intervalo $[-\frac{\pi}{2},\frac{\pi}{2}]$ satisface $sen \theta = x$.
De forma similar, podemos restringir los dominios de las otras funciones trigonométricas para definir funciones trigonométricas inversas, que son funciones que determina qué ángulo en un cierto intervalo tiene un valor trigonométrico específico.
La función inversa del seno, denotada por $sen^{-1}$ o $arcsen$, y la función inversa del coseno, denotada por $cos^{-1}$ o $arcos$, están definidas en el dominio $$D=\{x / -1 \leq x \leq 1\}$$ de la forma $$sen^{-1}(x)=y \,\,\,\,\,\,\, \text{si y solo si}\,\,\,\,\,sen(y)=x\,\,\,\,\,\, -\frac{\pi}{2} \leq y \leq \frac{\pi}{2}$$
La función inversa de la tangente, denotada por $tan^{-1}$ o $arctg$, y la función inversa de la cotangente, denotada por $cot^{-1}$ o $arcot$, están definidas en el dominio $$D=\{x / \infty < x < \infty \}$$ de la forma $$tan^{-1}(x)=y \,\,\,\,\,\,\, \text{si y solo si}\,\,\,\,\,tan(y)=x\,\,\,\,\,\, -\frac{\pi}{2} < y < \frac{\pi}{2}$$ $$cot^{-1}(x)=y \,\,\,\,\,\,\, \text{si y solo si}\,\,\,\,\,cot(y)=x\,\,\,\,\,\, 0 < y < \pi$$
La función inversa de la cosecante, denotada por $csc^{-1}$ o $arccsc$, y la función inversa de la secante, denotada por $sec^{-1}$ o $arsec$, están definidas en el dominio $$D=\{x / |x| \geq 1\}$$ de la forma $$csc^{-1}(x)=y \,\,\,\,\,\,\, \text{si y solo si}\,\,\,\,\,csc(y)=x\,\,\,\,\,\, -\frac{\pi}{2} \leq y \leq \frac{\pi}{2},\,\,\,y \neq 0$$ $$sec^{-1}(x)=y \,\,\,\,\,\,\, \text{si y solo si}\,\,\,\,\,sec(y)=x\,\,\,\,\,\, 0 \leq y \leq \pi, \,\,\,y \neq \pi/2$$
Para representar las funciones trigonométricas inversas, utilizamos las gráficas de las funciones trigonométricas restringidas a los dominios definidos anteriormente y reflejamos las gráficas sobre la recta $y = x$ (Figura 1.41).
Figura 1.41 La gráfica de cada una de las funciones trigonométricas inversas es un reflejo sobre la recta $y = x$ de la función trigonométrica restringida correspondiente.
 En la siguiente escena realizada en Geogebra por Ana Garcia puedes ver cómo las gráficas de las funciones trigonómetricas inversas son el reflejo respecto de la recta $y=x$ de la función original.
En la siguiente escena realizada en Geogebra por Ana Garcia puedes ver cómo las gráficas de las funciones trigonómetricas inversas son el reflejo respecto de la recta $y=x$ de la función original.
 En la siguiente escena interactiva puedes practicar representando las principales funciones transcendentes y sus inversas.
En la siguiente escena interactiva puedes practicar representando las principales funciones transcendentes y sus inversas.
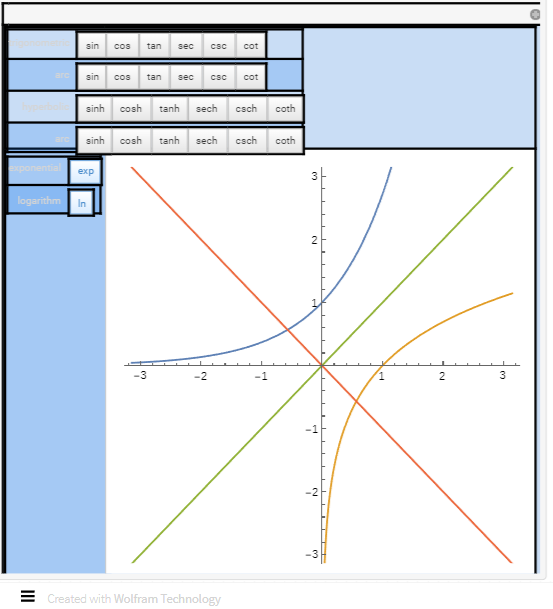
Al evaluar una función trigonométrica inversa, la salida es un ángulo. Por ejemplo, para evaluar $cos^{-1}( \frac{1}{2})$ necesitamos encontrar un ángulo $\theta$ tal que $cos \theta = \frac{1}{2}$.
Claramente, muchos ángulos tienen esta propiedad. Sin embargo, dada la definición de $cos^{-1}$, necesitamos el ángulo $\theta$ que no solo resuelve esta ecuación, sino que también se encuentra en el intervalo $[0, \pi]$. Concluimos que $cos^{-1}(\frac{1}{2}) = \frac{\pi}{3}$
Ahora consideramos una composición de una función trigonométrica y su inversa. Por ejemplo, las dos expresiones siguientes $sen(sen^{-1}(\frac{\sqrt{2}}{2}))$ y $sen^{-1}(sen(\pi))$. Para la primera expresión, lo simplificamos de la siguiente manera: $$sen(sen^{-1}(\frac{\sqrt{2}}{2}))=sen(\frac{\pi}{4})=\frac{\sqrt{2}}{2}$$ Para la segunda expresión, se tiene $$sen^{-1}(sen(\pi))=sen^{-1}(0)=0$$
Si pensamos que la función inversa “deshace” lo que "hace" la función original, entonces, ¿por qué no se cumple $sen^{-1}(sen(\pi))=sen^{-1}(0)=\pi$? Recordando nuestra definición de funciones inversas, una función $f$ y su inversa $f^{-1}$ satisfacen las condiciones $f(f^{-1}(y)) = y$ para todos $y$ en el dominio de $f^{-1}$ y $f^{ -1}(f(x))) = x$ para todos los puntos $x$ en el dominio $f$, ¿qué pasa entonces? El problema es que la función inversa del seno, $sen^{-1}$ está restringida al dominio $[-\frac{\pi}{2},\frac{\pi}{2}]$. Por lo tanto, para $x$ en este intervalo es cierto que $$sen^{-1}(sen(x))=x$$
Sin embargo, para valores de $x$ fuera de este intervalo, la ecuación no tiene que cumplirse aunque esté definido para todos los números reales $x$ el valor de $sen^{-1}(sen(x))$.
¿Qué ocurre para $sen(sen^{-1}(y))$? ¿Ocurre lo mismo? La respuesta es no. Dado que el dominio de $sen^{-1}$ es el intervalo $[-1, 1]$, concluimos que $sen (sen^{-1} (y) = y$ si $ -1 \leq y \leq 1$ y la expresión no está definida para otros valores de $y$. En resumen, $$sen(sen^{-1}(y))=y \,\,\,\,si \,\,\,\, -1 \leq y \leq 1$$ $$sen^{-1}(sen(x))=x \,\,\,\,si \,\,\,\, -\frac{\pi}{2} \leq x \leq \frac{\pi}{2}$$
De manera similar, para la función coseno, se tendrá $$cos(cos^{-1}(y))=y \,\,\,\,si \,\,\,\, -11 \leq y \leq 1$$ $$cos^{-1}(cos(x))=x \,\,\,\,si \,\,\,\, 0\leq x \leq \pi$$ De forma análoga se pueden obtener las mismas propiedades para el resto de funciones y sus inversas.
 |
1.32 Evaluación de expresiones que involucran funciones trigonométricas inversas |
Evalúa cada una de las siguientes expresiones.

En muchas áreas de la ciencia, la ingeniería y las matemáticas, es útil conocer el valor máximo que puede obtener una función, incluso si no conocemos su valor exacto en un instante dado. Por ejemplo, si tenemos una función que describe la resistencia de una viga de techo, querríamos saber el peso máximo que la viga puede soportar sin romperse. Si tenemos una función que describe la velocidad de un tren, querríamos saber su velocidad máxima antes de que salte de los rieles. El diseño seguro a menudo depende de conocer los valores máximos.
Este proyecto describe un ejemplo simple de una función con un valor máximo que depende de dos coeficientes de ecuación. Veremos que los valores máximos pueden depender de varios factores además de la variable independiente $x$.
| $A$ | 0 | 1 | 1 | 1 | 2 | 2 | 3 | 4 |
| $B$ | 1 | 0 | 1 | 2 | 1 | 2 | 4 | 3 |
| $A$ | $\sqrt{3}$ | 1 | 12 | 5 | ||||
| $B$ | 1 | $\sqrt{3}$ | 5 | 12 |
Tabla 1.11 Valores de $2^x$ para obtener una lista de números racionales aproximados $2^{\sqrt{2}}$
 1.5.4 Ejercicios
1.5.4 Ejercicios Para los siguientes ejercicios, usa la prueba de la línea horizontal para determinar si cada uno de los gráficos dados es uno-uno.
Para los siguientes ejercicios, usa la prueba de la línea horizontal para determinar si cada uno de los gráficos dados es uno-uno.
183.
 (Solución)
(Solución)
184.
188.
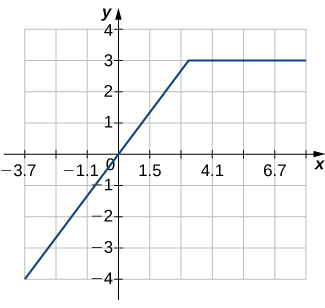
 Para los siguientes ejercicios, a. encontrar la función inversa, y b. encuentra el dominio y rango de la función inversa.
Para los siguientes ejercicios, a. encontrar la función inversa, y b. encuentra el dominio y rango de la función inversa.
189. $f(x)=x^2-4,\,\,\,x \ge 0$ (Solución)
190. $f(x)=\sqrt{3}{x-4}$
191. $f(x)=x^3+1$ (Solución)
192. $f(x)=(x-1)^2,\,\,x\le 1$
193. $f(x)=\sqrt{x-1}$ (Solución)
194. $f(x)=\frac{1}{x+2}$
 Para los siguientes ejercicios, usa la gráfica de $f$ para bosquejar la gráfica de su función inversa.
Para los siguientes ejercicios, usa la gráfica de $f$ para bosquejar la gráfica de su función inversa.
198.
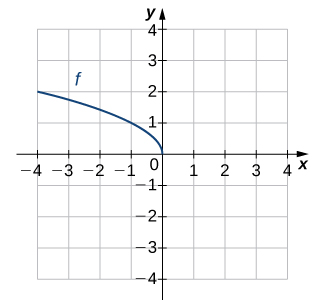
 Para los siguientes ejercicios, usa la composición para determinar qué pares de funciones son inversas.
Para los siguientes ejercicios, usa la composición para determinar qué pares de funciones son inversas.
199. $f(x)=8x$, $g(x)=x/8$ (Solución)
200. $f(x)=8x+3$, $g(x)=\frac{x-3}{8}$
201. $f(x)=5x-7$, $g(x)=\frac{x+5}{7}$ (Solución)
202. $f(x)=\frac{2}{3}x+2$, $g(x)=\frac{3}{2}x+3$
203. $f(x)=\frac{1}{x-1}$,$x \ne 1$, $g(x)=\frac{1}{x}+1$, $x\neq 0$ (Solución)
204. $f(x)=x^3+1$, $g(x)=(x-1)^{1/3}$
205. $f(x)=x^2+2x+1$, $x \ge 1$, $g(x)=-1+\sqrt{x}$, $x \ge 0$ (Solución)
206. $f(x)=\sqrt{4-x^2}$, $0 \le x \le 2$, $g(x)=\sqrt{4-x^2}$, $0 \le x \le 2$
 Para los siguientes ejercicios, evalúe las funciones. Dar el valor exacto.
Para los siguientes ejercicios, evalúe las funciones. Dar el valor exacto.
207. $tan^{-1}\left(\frac{\sqrt{3}}{3}\right)$ (Solución)
208. $cos^{-1}\left(-\frac{\sqrt{2}}{2}\right)$
209. $cot^{-1}\left(1 \right)$ (Solución)
210. $sen^{-1}\left(-1 \right)$
211. $cs^{-1}\left(\frac{\sqrt{3}}{2} \right)$ (Solución)
212. $cos^{-1}\left(tan^{-1} \left(\sqrt{3} \right) \right)$
213. $sen^{-1}\left(cos^{-1} \left(\frac{\sqrt{2}}{2} \right) \right)$ (Solución)
214. $tan^{-1}\left(tan^{-1} \left(\frac{\pi}{6} \right) \right)$
215. $tan^{-1}\left(tan^{-1} \left(\frac{\pi}{6} \right) \right)$ (Solución)
216. La función $C = T (F) = (5/9) (F − 32)$ convierte grados Fahrenheit a grados Celsius.
217. [T] La velocidad $V$ (en centímetros por segundo) de la sangre en una arteria a una distancia $x$ cm del centro de la arteria se puede modelar mediante la función $V = f (x) = 500 (0.04 − x^2)$ para $0≤x≤0.2$.
218. [T] Una función que convierte las tallas de los vestidos en los Estados Unidos a las de Europa viene dada por $D (x) = 2x + 24$.
219. [T] El costo de eliminar una toxina de un lago está modelado por la función $C(p) = 75p/ (85−p)$,donde $C$ es el costo (en miles de dólares) y $p$ es la cantidad de toxina en un lago pequeño (medido en partes por mil millones [ppb]). Este modelo es válido solo cuando la cantidad de toxina es inferior a 85 ppb.
220. [T] Un coche de carreras acelera a una velocidad dada por $v(t) =\frac{25}{4}t+54$, donde $v$ es la velocidad (en pies por segundo) en el tiempo $t$.
221. [T] El número de Mach de un avión $M$ es la relación entre su velocidad y la velocidad del sonido. Cuando un avión vuela a una altitud constante, su ángulo de Mach viene dado por $μ = 2sin^{− 1}(\frac{1}{M})$. Encuentra el ángulo de Mach (al grado más cercano) para los siguientes números de Mach.
 (Solución)
(Solución)
222. [T] Usando $μ = 2sin^{− 1} (\frac{1}{M})$, encuentra el número de Mach $M$ para los siguientes ángulos.
223. [T] La temperatura promedio (en grados Celsius) de una ciudad en el norte de los Estados Unidos se puede modelar mediante la función $T(x) = 5 + 18 sen\left[\frac{\pi}{6} (x−4.6)\right]$, donde $x$ es el tiempo en meses y $x = 1.00$ corresponde al 1 de enero. Determina el mes y el día en que la temperatura promedio es de 21°C. (Solución)
224. [T] La profundidad (en pies) del agua en un muelle cambia con la subida y bajada de las mareas. Está modelado por la función $D(t) = 5 sen\left(\frac{\pi}{6}t-\frac{7\pi}{6}\right)+8$,donde $t$ es el número de horas después de la medianoche. Determine la primera vez después de la medianoche cuando la profundidad es de 11.75 pies.
225. [T] Un objeto que se mueve en un movimiento armónico simple es modelado por la función $s(t) = - 6cos\left(\frac{\pi t}{2} \right)$,donde $s$ se mide en pulgadas y $t$ se mide en segundos. Determine la primera vez que la distancia recorrida es de 4.5 pulg. (Solución)
226. [T] Una galería de arte local tiene un retrato de 3 pies de altura que se cuelga a 2.5 pies por encima del nivel de los ojos de una persona promedio. El ángulo de visión $\theta$ se puede modelar mediante la función $\theta= tan^{−1}\frac{5.5}{x}−tan^{−1}\frac{2.5}{x}$,donde $x$ es la distancia (en pies) del retrato. Encuentra el ángulo de visión cuando una persona está a 4 pies del retrato.
227. [T] Usa una calculadora para evaluar $tan^{− 1} (tan (2.1))$ y $cos^{− 1} (cos (2.1))$. Explique ambos resultados. (Solución)
228. [T] Usa una calculadora para evaluar $sin (sin^{− 1} (−2))$ y $tan (tan^{− 1} (−2))$. Explique ambos resultados.
Objetivos de aprendizaje
En esta sección examinaremos las funciones exponenciales y logarítmicas y, utilizando las propiedades de estas funciones, se resolverán ecuaciones con términos exponenciales o logarítmicos. Analizaremos el significado y la importancia del número $e$ y definiremos también las funciones hiperbólicas e hiperbólicas inversas, que se definen a partir de combinaciones de funciones exponenciales y logarítmicas. En el capítulo de aplicaciones de las integrales se presentarán definiciones alternativas de las funciones exponenciales y logarítmicas viendo que tienen las mismas propiedades independientemente de cómo se definan.
Las funciones exponenciales surgen en muchas aplicaciones. Un ejemplo común es el crecimiento de la población.
Por ejemplo, si una población comienza con $P_0$ individuos y luego crece a una tasa anual de 2%, su población después de 1 año será $$P(1) =P_0+0.02P_0=P_0(1 + 0.02) =1.02 P_0.$$ Su población después de 2 años será $$P(2) =P(1)+0.02P(1)=1.02 \cdot P(1) =(1.02)^2 P_0.$$ En general, su población después $t$ años es $$P(t) =P_0(1.02)^t$$ que es una función exponencial. De manera más general, cualquier función de la forma $f(x) =b^x$, dónde $b> 0$, $b \neq 1$, es una función exponencial con base $b$ y exponente $x$. Las funciones exponenciales tienen bases constantes y exponentes variables. Debes tener en cuenta que una función de la forma $f(x) =x^b$ para alguna constante $b$ no es una función exponencial sino una función potencial.
Para ver la diferencia entre una función exponencial y una función potencial, compararemos las funciones $y=x^2$ e $y= 2^x$. En la tabla 1.10, vemos que ambos $2^x$ y $x^2$ se acercan al infinito cuando $x \to \infty$. Sin embargo, $2^x$ se vuelve más grande que $x^2$ y crece más rápidamente a medida que $x \to \infty$. En la dirección opuesta, cuando $x \to -\infty$, $x^2 \to \infty$, mientras $2^x \to 0$. La recta $y= 0$ es una asíntota horizontal para $y= 2^x$.
| $x$ | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| $x^2$ | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
| $2^x$ | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
Tabla 1.10 Valores de $x^2$ y $2^x$
En la Figura 1.43 representamos ambas curvas $y=x^2$ e $y= 2^x$ para mostrar en qué se diferencian las gráficas.
Figura 1.43. Ambas curvas $2^x$ y $x^2$ se acercan al infinito cuando $x \to \infty$, pero $2^x$ crece más rápidamente que $x^2$. Cuando $x \to -\infty$, $x^2 \to \infty$, mientras que $2^x \to 0$.
Evaluar funciones exponenciales
Recordemos en primer lugar las propiedades de los exponentes:
Sin embargo, ¿cómo se define $b^x$ si $x$ es un numero irracional? Por ejemplo, ¿qué entendemos por $2^{\sqrt{2}}$? Esta es una pregunta demasiado compleja para que podamos responderla completamente en este momento; sin embargo, podemos hacer una aproximación.
En la tabla 1.11, enumeramos algunos números racionales que se acercan $\sqrt{2}$, y también los valores de $2^x$ para cada número racional $x$. Afirmamos que si elegimos números racionales $x$ acercándose cada vez más a $\sqrt{2}$, los valores de $2^x$ se acercan más y más a algún número $L$. Definimos ese número $L$ como el valor de $2^{\sqrt{2}}$.
| $x$ | 1.4 | 1.41 | 1.414 | 1.4142 | 1.41421 | 1.414213 |
| $2^x$ | 2.639 | 2.65737 | 2.66475 | 2.665119 | 2.665138 | 2.665143 |
Tabla 1.11Valores de $2^x$ para obtener una lista de números racionales aproximados $2^{\sqrt{2}}$
 |
1.33 Crecimiento de bacterias |
Supongamos que se sabe que una población particular de bacterias duplica su tamaño cada 4 horas. Si un cultivo comienza con 1000 bacterias, el número de bacterias después 4 horas es $n(4) = 1000\cdot 2$. El número de bacterias después de 8 horas es $n(8) =n(4)\cdot 2 = 1000\cdot 2^2$. En general, la cantidad de bacterias después $4m$ horas es $n(4m) = 1000\cdot 2^m$. Considerando $t= 4m$, vemos que el número de bacterias después de $t$ horas es $n(t) = 1000 \cdot 2^{t/ 4}$. Encuentra la cantidad de bacterias después de 6 horas, después de 10 horas, y después de 24 horas.

 |
Cuestión 1.27 |
Dada la función exponencial $f(x) = 100 \cdot 3^{x/ 2}$, evaluar $f(4)$ y $f(10)$.
 Visita el enlace enlace para ver otro ejemplo de crecimiento poblacional exponencial.
Visita el enlace enlace para ver otro ejemplo de crecimiento poblacional exponencial.
Representación de funciones exponenciales
Para cualquier base $b> 0$, $b \neq 1$, la función exponencial $f(x) =b^x$ está definido para todos los números reales $x$ y $b^x> 0$. Por tanto, el dominio de $f(x) =b^x$ es $(-\infty, \infty)$ y el rango es $(0, \infty)$.
Para representar $b^x$, observamos que para $b> 1$, $b^x$ crece en $(-\infty, \infty)$ y $b^x \to \infty$ cuando $x \to \infty$, mientras que $b^x \to 0$ cuando $x \to -\infty$. Por otro lado, si $b$ está comprendido entre 0 y 1, $f(x) =b^x$ decrece en $(-\infty, \infty)$ y $b^x \to 0$ cuando $x \to \infty$ mientras que $b^x \to \infty$ cuando $x \to \infty$ ( Figura 1.44).

Figura 1.44. Si $b> 1$, se tiene que $b^x$ crece en $(-\infty, \infty)$. Si $0 < b < 1$, se cumple $b^x$ decrece en $(-\infty, \infty)$.
 La siguiente escena interactiva, a la que se puede acceder desde este enlace, permite la exploración de las gráficas de funciones exponenciales.
La siguiente escena interactiva, a la que se puede acceder desde este enlace, permite la exploración de las gráficas de funciones exponenciales.
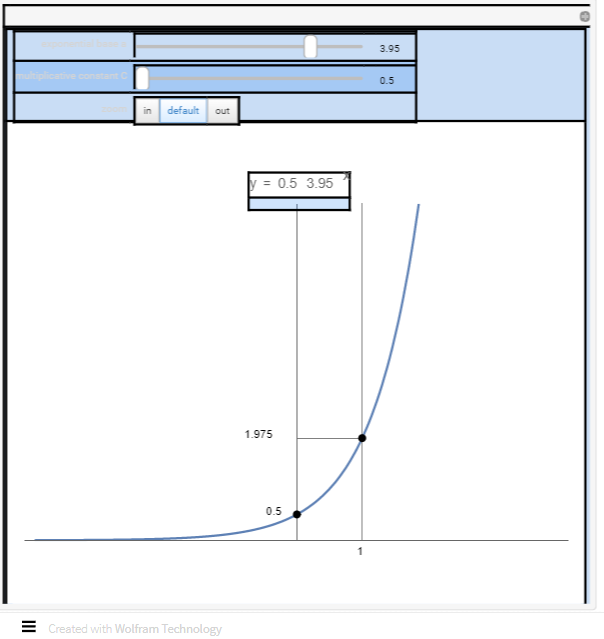
Debemos tener en cuenta que las funciones exponenciales satisfacen las leyes generales de los exponentes. Para recordar estas leyes, las establecemos como reglas.
 |
1.34 Usando las leyes de los exponentes |
Usa las leyes de los exponentes para simplificar cada una de las siguientes expresiones.

 |
Cuestión 1.28 |
Usa las leyes de los exponentes para simplificar $\frac {6x^{-3}y^2} {12x^{-4}y^5}$
En las aplicaciones del mundo real aparece un tipo especial de función exponencial. Para introducirla, consideremos el siguiente ejemplo de crecimiento exponencial que surge del interés compuesto en una cuenta de ahorros. Supongamos que una persona invierte $P$ dólares en una cuenta de ahorros con una tasa de interés anual compuesto, $r$. La cantidad de dinero después de 1 año es $$A(1) =P+rP=P(1+r)$$ La cantidad de dinero después 2 años es $$A(2) =A(1) +rA(1) =P(1+r) +rP(1+r) =P(1+r)^2$$ De manera más general, la cantidad después de $t$ años es $$A(t) =P(1+r)^t$$ Si el dinero se capitaliza 2 veces al año, la cantidad de dinero después de medio año es $$A\left( \frac{1}{2}\right)=P+\left( \frac{r}{2}\right)P=P\left( 1+\frac{r}{2}\right).$$ La cantidad de dinero después de 1 es $$\footnotesize{A(1) =A\left( \frac{1}{2}\right)+\left( \frac{r}{2} \right)A\left(\frac{1}{2}\right)=P\left( 1+\frac{r}{2}\right)+\frac{r}{2}P\left( 1+\frac{r}{2}\right)=P\left( 1+\frac{r}{2}\right)^2}$$ Después de $t$ años, la cantidad de dinero en la cuenta es $$ A(t) =P\left( 1+\frac{r}{2}\right)^{2t}.$$
De manera más general, si el dinero está compuesto $n$ veces al año, la cantidad de dinero en la cuenta después de $t$ años viene dado por la función $$A(t) =P\left( 1+\frac{r}{n}\right)^{nt}.$$ ¿Qué ocurre cuándo $n \to \infty$? Para responder a esta pregunta, denotando $m=n/r$ se tendrá $$\left( 1+\frac{r}{n}\right)^{nt}=\left( 1 + \frac{1}{m} \right) ^{mrt}$$ Examinamos el comportamiento de $(1 + 1 /m)^m$ cuando $m \to \infty$, usando una tabla de valores (Tabla 1.12).
| $m$ | 10 | 100 | 1000 | 10,000 | 100,000 | 1,000,000 |
| $\footnotesize{(1+\frac{1} {m})^m}$ | 2.5937 | 2.7048 | 2.71692 | 2.71815 | 2.718268 | 2.718280 |
Tabla 1.12 Valores de $(1+1/m)^m$ cuando $m \to \infty$.
Mirando esta tabla, parece que $(1 + 1 /m)^m$ se acerca a un número entre 2.7 y 2.8 cuando $m \to \infty$. De hecho, se puede demostrar que $(1 + 1 /m)^m$ converge a un número cuando $m \to \infty$, a este valor le llamaremos número $e$. Con seis cifras decimales de precisión, $e \approx 2.718282$.
La letra $e$ fue utilizado por primera vez para representar este número por el matemático suizo Leonhard Euler durante la década de 1720. Aunque Euler no descubrió el número, mostró muchas conexiones importantes entre $e$ y las funciones logarítmicas.
Todavía usamos la notación $e$ hoy para honrar el trabajo de Euler porque aparece en muchas áreas de las matemáticas y porque podemos usarlo en muchas aplicaciones prácticas.
Volviendo a nuestro ejemplo de cuenta de ahorros, podemos concluir que si una persona pone $P$ dólares en una cuenta a una tasa de interés anual $r$ compuesto continuamente, entonces $A(t)=Pe^{rt}.$ Esta función puede resultarle familiar. Dado que las funciones que contienen términos con el número $e$ surgen a menudo en aplicaciones, llamamos a la función $f(x) =e^x$ la función exponencial natural. Esta función no solo es interesante por la definición del número $e$, sino también, como se analiza a continuación, su gráfica tiene una propiedad importante.
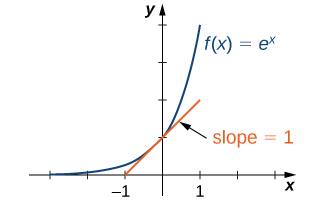
Figura 1.45. La gráfica de $f(x) =e^x$ tiene una recta tangente con pendiente 1 en $x= 0$.
Como $e> 1$, sabemos que $e^x$ es creciente $(-\infty, \infty)$. En la Figura 1.45, mostramos la gráfica de $f(x) =e^x$ junto con una recta tangente a la gráfica en $x= 0$. Aunque daremos una definición precisa de recta tangente en el capítulo dedicado a las derivadas, informalmente, diremos que una recta tangente a una gráfica de $f$ en un punto $x=a$ es una recta que pasa por el punto $(a,f(a))$ y tiene
la misma "pendiente" que $f$ en ese punto. La función $f(x) =e^x$ es la única función exponencial $b^x$ con recta tangente en $x= 0$ que tiene una pendiente con valor 1. Como veremos más adelante en el texto, tener esta propiedad hace que la función exponencial natural sea la función exponencial más simple para usar en muchos casos.
 |
1.35 Interés compuesto |
Supongamos que 500 dólares se invierten en una cuenta a una tasa de interés anual de $r= 5.5\%$, compuesto continuo.

 |
Cuestión 1.29 |
Si 750 dólares se invierten en una cuenta a una tasa de interés anual del $4\%$, compuesto continuo, encuentra una fórmula para la cantidad de dinero en la cuenta después de $t$ años. Encuentra la cantidad de dinero después de 30 años.
Una vez introducidas las funciones exponenciales; podemos analizar sus inversas; que son las funciones logarítmicas. Estos son útiles cuando necesitamos considerar cualquier fenómeno que varíe en una amplia gama de valores; como el pH en química o los decibelios en los niveles de sonido.
La función exponencial $f(x) =b^x$ es uno-uno, con dominio $(-\infty, \infty)$ y rango $(0, \infty)$. Por lo tanto, tiene una función inversa, llamada función logarítmica con base $b$. Para cualquier $b> 0$, $b$ distinto de 1, la función logarítmica con base b, que se denota $log_b$, tiene dominio $(0, \infty)$ y rango $(-\infty, \infty)$, y satisface $$log_b(x) =y \,\,\,\,\text{si y solo si}\,\,\,\ b^y=x.$$ Por ejemplo, $$log_2(8) = 3 \,\,\,\,\text{ya que} \,\,\, 2^3=8$$ $$log_{10}\left(\frac{1}{100}\right) = -2 \,\,\,\,\text{ya que} \,\,\, 10^{-2}=\frac{1}{100}$$ $$log_2(8) = 3 \,\,\,\,\text{ya que} \,\,\,2^3=8$$ $$log_b(1) = 0 \,\,\,\,\text{ya que} \,\,\, b^{0}=1$$ Además, dado que $y= log_b(x)$ y $y=b^x$ son funciones inversas, $$log_b(b^x) =x \text{\,\,\,\,y \,\,\,} b^{log_b(x)}=x.$$ La función logarítmica más utilizada es la función $log_e$ y como utiliza el número $e$ como base, se llama logaritmo natural.
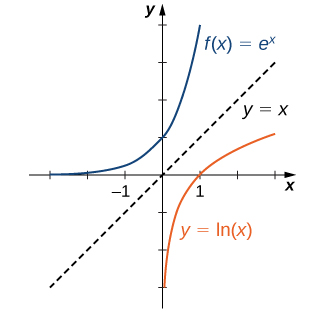
Figura 1.46. Las funciones $y=e^x$ y $y=ln (x)$ son inversas entre sí, por lo que sus gráficas son simétricas con respecto a la recta $y=x$.
 Haciendo clic en el siguiente enlace, puedes ver un ejemplo de una escala logarítmica de base 10.
Haciendo clic en el siguiente enlace, puedes ver un ejemplo de una escala logarítmica de base 10.
En general, para cualquier base $b> 0$, $b$ distinto de 1, la función $g(x) = log_b(x)$ es simétrica con respecto a la recta $y=x$ de la función $f(x) =b^x$. Usando este hecho y las gráficas de las funciones exponenciales, representamos $log_b$ para varios valores de $b> 1$ (Figura 1.47).
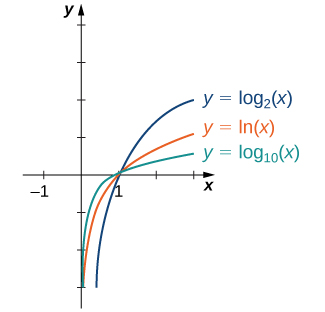
Figura 1.47. Gráficas de $y= log_b(x)$ para los valores $b= 2; \,\,e; \,\,10$.
Antes de resolver algunas ecuaciones en las que aparecen funciones exponenciales y logarítmicas, repasemos las propiedades básicas de los logaritmos.
Si $a,b,c> 0$, siendo $b \neq 1$, y $r$ es un número real, entonces
 |
1.36 Resolver ecuaciones con funciones exponenciales |
Resuelve cada una de las siguientes ecuaciones en $x$:

 |
Cuestión 1.30 |
Resuelve $\frac {e^{2x}} {3+e^{2x}} = 1/2$.
 |
1.37 Resolver ecuaciones con funciones logarítmicas |
Resuelve cada una de las siguientes ecuaciones en $x$.

 |
Cuestión 1.31 |
Resolver $ln(x^3)-4ln(x) = 1.$
Al evaluar una función logarítmica con una calculadora, es posible que haya notado que las únicas opciones son $log_{10}$ o $log$, llamado logaritmo decimal, o $ln$, que es el logaritmo natural. Sin embargo, las funciones exponenciales y las funciones logarítmicas se pueden expresar en términos de cualquier base deseada $b$. Si necesitas usar una calculadora para evaluar una expresión con una base diferente, puedes aplicar primero las fórmulas de cambio de base. Usando este cambio de base, normalmente escribimos una función exponencial o logarítmica dada en términos de las funciones exponencial natural y logarítmica natural.
Prueba
Propiedad 1. Para la primera fórmula de cambio de base, comenzamos haciendo uso de la propiedad de potencia de las funciones logarítmicas. Sabemos que para cualquier base $b> 0$, $b \neq 1$, se tiene $log_b{a^x}=xlog_ba$. Por lo tanto $$b^{log_b{(a^x)}} =b^{xlog_ba}$$
Además, sabemos que $b^x$ y $log_b(x)$ son funciones inversas. Por lo tanto, $$b^{log_b{(a^x)}}=a^x$$ Combinando estas dos últimas igualdades, llegamos a la conclusión de que $$a^x=b^{xlog_ba}$$
Propiedad 2. Mostremos que $$(log_ba)\cdot (log_ax)=log_bx$$Consideramos $u= log_ba$, $v= log_ax$, $w=log_bx$. Mostraremos que $u·v=w$.
Por la definición de funciones logarítmicas, sabemos que $b^u=a$, $a^v=x$ y $b^w=x$. De las ecuaciones anteriores, vemos que $$b^{uv}= (b^u)^v=a^v=x=b^w.$$ Por lo tanto, $b^{uv}=b^w$. Dado que las funciones exponenciales son uno-uno, podemos concluir que $u·v=w$.
 |
1.38 Cambios de base |
Utiliza una herramienta de cálculo y la función logaritmo natural para evaluar $log_37$ mediante la fórmula de cambio de base presentada anteriormente.

 |
Cuestión 1.32 |
Utiliza el cambio de base y una herramienta de cálculo para evaluar $log_46$.
 |
1.39 Apertura del capítulo. La escala de Richter para terremotos |

Figura 1.48. (crédito: modificación del trabajo de Robb Hannawacker, NPS).
En 1935, Charles Richter desarrolló una escala (ahora conocida como escala de Richter) para medir la magnitud de un terremoto. Esta escala es una escala logarítmica de base 10, y se puede describir como se indica a continuación.
Consideremos un terremoto con magnitud $R_1$ en la escala de Richter y un segundo terremoto con magnitud $R_2$ en la escala de Richter. Supongamos $R_1>R_2$, lo que significa el terremoto de magnitud $R_1$ es más fuerte, pero ¿cuánto más fuerte es respecto del otro terremoto?
Una forma de medir la intensidad de un terremoto es usando un sismógrafo para medir la amplitud de las ondas del terremoto. Si $A_1$ es la amplitud medida para el primer terremoto y $A_2$ para el segundo, entonces las amplitudes y magnitudes de los dos terremotos satisfacen la siguiente ecuación: $$R_1-R_2= log_{10}\left(\frac{A_1}{A_2}\right).$$
Consideremos un terremoto que mide 8 en la escala de Richter y un terremoto que mide 7 en la escala de Richter. Luego, $$8-7 = log_{10}\left(\frac{A_1}{A_2}\right).$$ Por lo tanto, $$log_{10}\left(\frac{A_1}{A_2}\right)= 1,$$ lo que implica $\frac{A_1}{A_2}= 10$ o $A_1= 10A_2$. Ya que $A_1$ es 10 veces el tamaño de $A_2$, decimos que el primer terremoto es 10 veces más intenso que el segundo.
Por otro lado, si un terremoto mide 8 en la escala de Richter y otro mide 6, entonces la intensidad relativa de los dos terremotos satisface la ecuación $$log_{10}\left(\frac{A_1}{A_2}\right)=8-6=2$$ Por lo tanto, $A_1= 100 A_2$. Es decir, el primer terremoto es 100 veces más intenso que el segundo.
¿Cómo podemos usar funciones logarítmicas para comparar la severidad relativa del terremoto de magnitud 9 en Japón en 2011 con el terremoto de magnitud 7.3 en Haití en 2010?

 |
Cuestión 1.33 |
Compare la severidad relativa de una magnitud de un terremoto de 8.4 y otro de intensidad 7.4.
Las funciones hiperbólicas se definen en términos de ciertas combinaciones de $e^x$ y $e^{-x}$. Estas funciones surgen de forma natural en diversas aplicaciones de la ingeniería y la física, incluido el estudio de las ondas del agua y las vibraciones de las membranas elásticas. Otro uso común de una función hiperbólica es la representación de una cadena o cable colgante, también conocido como catenaria (Figura 1.49). Si introducimos un sistema de coordenadas de modo que el punto bajo de la cadena se encuentra a lo largo del eje $Y$, podemos describir la altura de la cadena en términos de una función hiperbólica. Empecemos entonces por definir estas funciones.

Figura 1.49. La forma de una hebra de seda en una telaraña se puede describir en términos de una función hiperbólica. La misma forma se aplica a una cadena o cable que cuelga de dos soportes con solo su propio peso. (crédito: "Mtpaley", Wikimedia Commons).
Usando la definición de $cosh(x)$ y principios de la física, se puede demostrar que la altura de una cadena colgante, como la de Figura 1.49, puede ser descrito por la función $h(x) =acosh(x/a) +c$ para ciertas constantes $a$ y $c$.
Pero, ¿por qué estas funciones se denominan funciones hiperbólicas? Para responder a esta pregunta, consideremos la expresión $cosh^2t-senh^2t$. Usando la definición de $cosh$ y $senh$, se tiene $$cosh^2t-senh^2t=\frac{e^{2t}+2+e^{-2t}}{4}- \frac{e^{2t}-2+e^{-2t}}{4}= 1.$$
Esta identidad es análoga a la identidad trigonométrica $$cos^2t+ sen^2t= 1$$Aquí, dado un valor $t$, el punto $(x,y) = (cosht, senht)$ se encuentra en la hipérbola unidad $$x^2-y^2= 1$$ ( Figura 1.50).
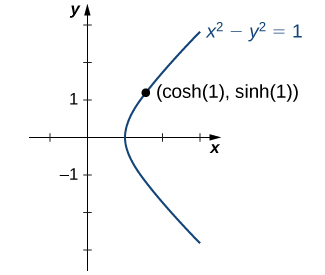
Figura 1.50. La hipérbola unitaria $cosh^2t-senh^2t= 1.$
 En la siguiente escena del Proyecto Descartes se puede comprobar la relación entre las funciones trigonométricas y la circunferencia unidad y las funciones hiperbólicas y la hipérbola unitaria.
En la siguiente escena del Proyecto Descartes se puede comprobar la relación entre las funciones trigonométricas y la circunferencia unidad y las funciones hiperbólicas y la hipérbola unitaria.
Gráficos de funciones hiperbólicas
Para representar la gráfica de $coshx$ y $senhx$, hacemos uso del hecho de que ambas funciones se acercan $(1/2)e^{-x}$ cuando $x \to \infty$, ya que $e^{-x}\to 0$ cuando $x \to \infty$.
Cuando $x \to -\infty$, $coshx$ se aproxima a $1/2e^{-x}$, mientras que $senh(x)$ se aproxima a $-1/2e^{-x}$. Por lo tanto, usando las gráficas de $1/2e^x$, $1/2e^{-x}$, y $-1/2e^{-x}$ como guías, podremos representar $coshx$ y $senh(x)$. Para representar $tanhx$, usamos el hecho de que $tanh (0) = 0$, $-1 < tanh (x) < 1$ para todos los valores $x$, $tanhx \to 1$ cuando $x \to \infty$, y $tanhx \to -1$ cuando $x \to \infty$.
Las gráficas de las otras tres funciones hiperbólicas se pueden bosquejar usando las gráficas de $cosh$, $senhx$, y $tanhx$ ( Figura 1.51).
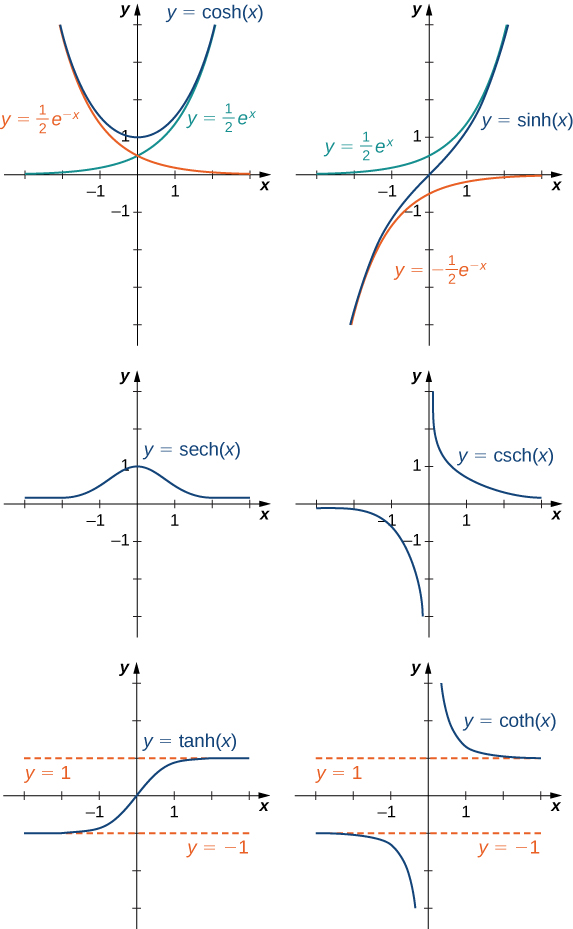
Figura 1.51. Las funciones hiperbólicas implican combinaciones de $e^x$ y $e^{-x}$.
Identidades que incluyen funciones hiperbólicas
La identidad $cosh^2t-senh^2t$, se muestra en la Figura 1.50, es una de varias identidades relativas a las funciones hiperbólicas, algunas de las cuales se enumeran a continuación.
Las primeras cuatro propiedades se derivan fácilmente de las definiciones de seno hiperbólico y coseno hiperbólico. Excepto por algunas diferencias en los signos, la mayoría de estas propiedades son análogas a las identidades de las funciones trigonométricas.
 |
1.40 Evaluación de funciones hiperbólicas |

 |
1.34 Evaluación de funciones hiperbólicas |
Simplifica $cosh (2 \cdot lnx)$.
Funciones hiperbólicas inversas
De las gráficas de las funciones hiperbólicas, vemos que todas ellas son uno-uno excepto $cosh(x)$ y $sech(x)$. Si restringimos los dominios de estas dos funciones al intervalo $[0, \infty)$, entonces todas las funciones hiperbólicas son uno-uno, y podemos definir las funciones hiperbólicas inversas. Dado que las funciones hiperbólicas en sí mismas se definen a partir de las funciones exponenciales, las funciones hiperbólicas inversas se definirán mediante funciones logarítmicas.
Veamos cómo deducir la primera ecuación. Los demás se demostrarían de forma similar. Supongamos $y= senh^{-1}x$. Luego, $x= senh(y)$ y, por la definición de la función del seno hiperbólico, $x=\frac{e^y-e^{-y}}{2}$. Por lo tanto, $$e^y-2x-e^{-y}= 0.$$ Multiplicando esta ecuación por $e^y$, obtenemos $$e^{2y}-2xe^y-1 = 0.$$
Esto se puede resolver como una ecuación cuadrática, con la solución $$e^y=\frac{2x \pm \sqrt{4x^2+4}}{2}=x \pm \sqrt{x^2+1}$$ Ya que $e^y> 0$, la única solución es la que tiene el signo positivo. Aplicando el logaritmo natural a ambos lados de la ecuación, llegamos a la conclusión de que $$y= ln(x+\sqrt{x^2+1}).$$
 |
1.41 Evaluación de funciones hiperbólicas inversas |
Evalúa cada una de las siguientes expresiones: $senh^{-1}(2)$, $tanh^{-1}(1/4)$

 1.6.5 Ejercicios
1.6.5 Ejercicios Para los siguientes ejercicios, evalúa las funciones exponenciales dadas como se indica, con una precisión de dos dígitos significativos después del decimal.
Para los siguientes ejercicios, evalúa las funciones exponenciales dadas como se indica, con una precisión de dos dígitos significativos después del decimal.
229. $f(x)=5^x$, a. $x=3$, b. $x=\frac{1}{2}$, c. $x=\sqrt{2}$ (Solución)
230. $f(x)=(0.3)^x$, a. $x=-1$, b. $x=4$, c. $x=-1.5$
231. $f(x)=10^x$, a. $x=-2$, b. $x=4$, c. $x=\frac{5}{3}$ (Solución)
232. $f(x)=e^x$, a. $x=2$, b. $x=-3.2$, c. $x=\pi$
 Une la función exponencial con el gráfico correcto.
Une la función exponencial con el gráfico correcto.
233.
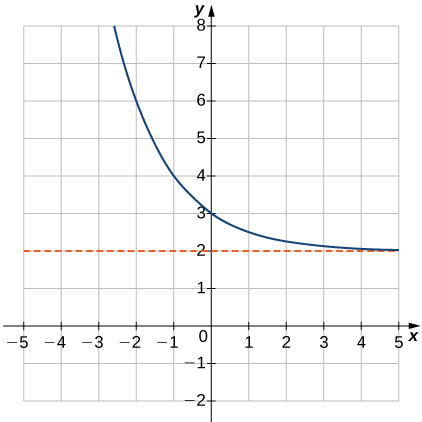 (Solución)
(Solución)
237.
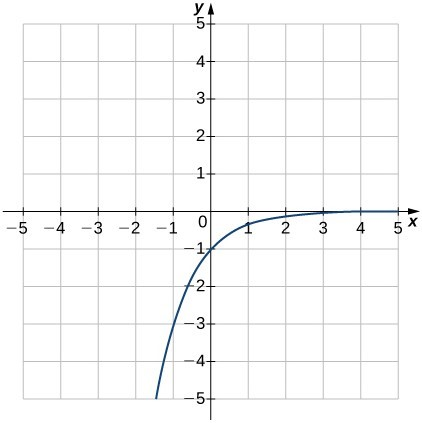 (Solución)
(Solución)
238.
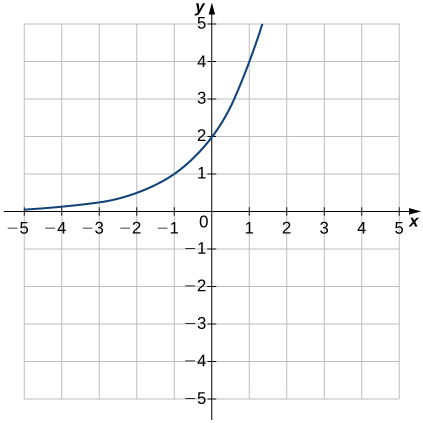
 Para los siguientes ejercicios, dibuja la gráfica de la función exponencial. Determina el dominio, el rango y la asíntota horizontal.
Para los siguientes ejercicios, dibuja la gráfica de la función exponencial. Determina el dominio, el rango y la asíntota horizontal.
239. $f(x)=e^x+2$ (Solución)
240. $f(x)=-2^x$
241. $f(x)=3^{x+1}$ (Solución)
242. $f(x)=4^{x}-1$
243. $f(x)=1-2^{-x}$ (Solución)
244. $f(x)=5^{x+1}+2$
245. $f(x)=e^{-x}-1$ (Solución)
 Para los siguientes ejercicios, escribe la ecuación en forma exponencial equivalente.
Para los siguientes ejercicios, escribe la ecuación en forma exponencial equivalente.
246. $log_{3}{81}=4$
247. $log_{8}{2}=\frac{1}{3}$ (Solución)
248. $log_{5}{1}=0$
249. $log_{5}{25}=2$ (Solución)
250. $log0.1=-1$
251. $ln \left( \frac{1}1{e^3} \right)=-3$ (Solución)
252. $log_9{3}=0.5$
253. $ln1=0.5$ (Solución)
 Para los siguientes ejercicios, escribe la ecuación en forma logarítmica equivalente.
Para los siguientes ejercicios, escribe la ecuación en forma logarítmica equivalente.
254. $2^3=8$
255. $4^{-2}=\frac{1}{16}$ (Solución)
256. $10^{2}=100$
257. $9^{0}=1$ (Solución)
258. $\left( \frac{1}{3} \right)^3=\frac{1}{27}$
259. $\sqrt[3]{64}=4$ (Solución)
260. $e^x=y$
261. $9^y=150$ (Solución)
262. $b^3=45$
263. $4^{-3/2}=0.12$
 Para los siguientes ejercicios, dibuje la gráfica de la función logarítmica. Determine el dominio, el rango y la asíntota vertical.
Para los siguientes ejercicios, dibuje la gráfica de la función logarítmica. Determine el dominio, el rango y la asíntota vertical.
264. $f(x)=3+lnx$
265. $f(x)=ln(x-1)$ (Solución)
266. $f(x)=ln(-x)$
267. $f(x)=1-ln(x)$ (Solución)
268. $f(x)=logx-1$
269. $f(x)=ln(x+1)$ (Solución)
 Para los siguientes ejercicios, usa las propiedades de los logaritmos para escribir las expresiones como suma, diferencia y/o producto de logaritmos.
Para los siguientes ejercicios, usa las propiedades de los logaritmos para escribir las expresiones como suma, diferencia y/o producto de logaritmos.
270. $f(x)=logx^4y$
271. $f(x)=log_3\frac{9a^3}{b}$ (Solución)
272. $f(x)=ln a\sqrt[3]{b}$
273. $f(x)=ln_5 \sqrt{12xy^3}$ (Solución)
274. $f(x)=ln_4 \frac{\sqrt[3]{xy}}{64}$
275. $f(x)=ln \left(\frac{6}{\sqrt{e^3}} \right)$ (Solución)
 Para los siguientes ejercicios, resuelve exactamente la ecuación exponencial.
Para los siguientes ejercicios, resuelve exactamente la ecuación exponencial.
276. $5^x=125$
277. $e^{3x}-1=0$ (Solución)
278. $8^x=4$
279. $4^{x+1}-21=0$ (Solución)
280. $3^{x/14}=\frac{1}{10}$
281. $10^x=7.21$ (Solución)
282. $4 \cdot 2^{3x}-20=0$
283. $7^{3x-2}=11$ (Solución)
 Para los siguientes ejercicios, resuelve, si es posible, la ecuación logarítmica exactamente.
Para los siguientes ejercicios, resuelve, si es posible, la ecuación logarítmica exactamente.
284. $log_3x=0$
285. $log_5x=-2$ (Solución)
286. $log_4(x+5)=0$
287. $log(2x-7)=0$ (Solución)
288. $log\sqrt{x+3}=2$
289. $log_6(x+9)+log_6(x)=2$ (Solución)
290. $log_4(x+2)-log_6(x-1)=0$
291. $lnx+ln(x-2)=ln4$ (Solución)
 Para los siguientes ejercicios, usa la fórmula de cambio de base y base 10 o base e para evaluar las expresiones dadas. Responde en forma exacta y aproximada, redondeando a cuatro cifras decimales.
Para los siguientes ejercicios, usa la fórmula de cambio de base y base 10 o base e para evaluar las expresiones dadas. Responde en forma exacta y aproximada, redondeando a cuatro cifras decimales.
292. $log_5 {47}$
293. $log_7 {82}$ (Solución)
294. $log_6 {103}$
295. $log_{0.5} {211}$ (Solución)
296. $log_2 {\pi}$
297. $log_{0.2} {0.452}$ (Solución)
298. Reescribe las siguientes expresiones en términos de exponenciales y simplifica.
299. [T] El número de bacterias $N$ en un cultivo después de $t$ días puede modelarse mediante la función $N(t) = 1300\cdot(2)^{t/ 4}$. Encuentra la cantidad de bacterias presentes después de 15 días. (Solución)
300. [T] La demanda $D$ (en millones de barriles) de petróleo en un país rico en petróleo está dada por la función $D(p) = 150\cdot (2.7)^{−0.25p}$,donde $p$ es el precio (en dólares) de un barril de petróleo. Encuentra la cantidad de petróleo demandada (al millón de barriles más cercano) cuando el precio está entre 15 y 20 dólares.
301. [T] La cantidad $A$ de una inversión de 100.000 dólares que se paga de forma continua y compuesta durante $t$ años está dada por $A(t) = 100.000 e^{0.055t}$. Encuentra la cantidad $A$ acumulada en 5 años. (Solución)
302. [T] Una inversión se capitaliza mensualmente, trimestralmente o anualmente y viene dada por la función $A=P\left( 1+\frac{j}{n}\right)^{nt}$, dónde $A$
es el valor de la inversión en el momento $t$, $P$ es el principio inicial que se invirtió, $j$ es la tasa de interés anual, y $n$ es la cantidad de veces que se capitaliza el interés por año. Dada una tasa de interés anual del 3.5% y un principio inicial de 100,000 dólares, encuentra la cantidad $A$ acumulados en 5 años por intereses compuestos
303. [T] La concentración de iones de hidrógeno en una sustancia se denota por [H+], medido en moles por litro. El pH de una sustancia está definido por la función logarítmica $pH = −log[H+]$.Esta función se utiliza para medir la acidez de una sustancia. El pH del agua es 7. Una sustancia con un pH inferior a 7 es un ácido, mientras que una que tiene un pH superior a 7 es una base.
304. [T] El yodo-131 es una sustancia radiactiva que se desintegra según la función $Q(t) =Q_0⋅e^{−0.08664t}$, dónde $Q_0$ es la cantidad inicial de una muestra de la sustancia y $t$ está en días. Determina
cuánto tiempo tarda (al día más cercano) para que el 95% de una cantidad decaiga.
305. [T] Según el Banco Mundial, a finales de 2013 (t= 0) la población de Estados Unidos era de 316 millones y estaba aumentando de acuerdo con el siguiente modelo: $P(t) = 316 e^{0.0074t}$, donde $P$ se mide en millones de personas y $t$ se mide en años posteriores a 2013.
306. [T] La cantidad $A$ acumulada después de 1000 dólares se invierte durante $t$ años a una tasa de interés del 4% está modelada por la función $A(t) = 1000 (1.04)^t$.
307. [T]Se sabe que una colonia de bacterias cultivada en un laboratorio se duplica en 12 horas. Supongamos, inicialmente, que hay 1000 bacterias presentes.
308. [T] La población de conejos en una reserva de caza se duplica cada 6 meses. Supongamos que inicialmente había 120 conejos.
309. [T] El terremoto de 1906 en San Francisco tuvo una magnitud de 8.3 en la escala de Richter. Al mismo tiempo, en Japón, un terremoto de magnitud 4.9 causó solo daños menores. Aproximadamente, ¿cuánta más energía fue liberada por el terremoto de San Francisco que por el terremoto de Japón? (Solución)

Figura 2.1La visión de la exploración humana por parte de la Administración Nacional de Aeronáutica y del Espacio (NASA) a partes distantes del universo ilustra la idea de los viajes espaciales a altas velocidades. Pero, ¿hay un límite en la velocidad a la que puede ir una nave espacial? (crédito: NASA)
Los escritores de ciencia ficción a menudo imaginan naves espaciales que pueden viajar a planetas lejanos en galaxias distantes. Sin embargo, en 1905, Albert Einstein demostró que existe un límite de la rapidez con la que puede viajar cualquier objeto. El problema es que cuanto más rápido se mueve un objeto, más masa alcanza (en forma de energía), según la ecuación $$m = {{{m_o}} \over {\sqrt {1 - {{{v^2}} \over {{c^2}}}} }}$$ donde $m_o$ es la masa del objeto en reposo, $v$ es su velocidad y $c$ es la velocidad de la luz. ¿Cuál es este límite de velocidad? (Exploraremos más este problema en el ejemplo 2.12.)
La idea de un límite es fundamental para todo el cálculo. Comenzamos este capítulo examinando por qué los límites son tan importantes. Luego, continuamos describiendo cómo encontrar el límite de una función en un punto dado. No todas las funciones tienen límites en todos los puntos, discutiremos qué significa y cómo podemos saber si una función tiene o no un límite en un valor particular. Este capítulo se introduce de manera informal e intuitiva, aunque no siempre será suficiente este planteamiento si necesitamos probar un enunciado matemático que implica límites. La última sección de este capítulo presenta la definición más precisa de límite y muestra cómo probar si una función tiene límite.
A medida que nos embarquemos en nuestro estudio del cálculo, veremos cómo su desarrollo surgió a partir de soluciones comunes a problemas prácticos en áreas de ingeniería física, como el problema de los viajes espaciales planteado en el primer capítulo. Dos problemas clave llevaron a la formulación inicial del cálculo:
La tasa de cambio es uno de los conceptos más críticos en cálculo. Comenzamos nuestra investigación de las tasas de cambio observando las gráficas de tres rectas: $f (x) = - 2x − 3$, $g (x) = \frac{1}{2}x + 1$, y $h (x) = 2$,
se muestra en la Figura 2.2.
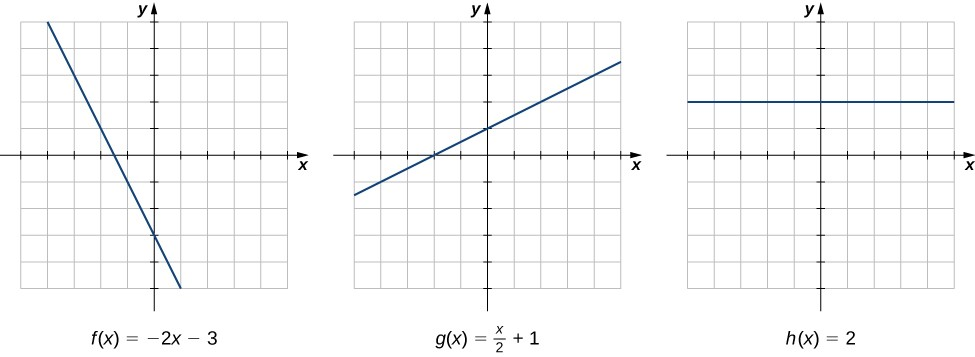
Figura 2.2 La tasa de cambio de una función lineal es constante en cada uno de estos tres gráficos, con la constante determinada por la pendiente.
A medida que nos movemos de izquierda a derecha a lo largo de la gráfica de $f (x) = - 2x − 3$, vemos que la gráfica disminuye a una tasa constante. Por cada 1 unidad que nos movemos hacia la derecha a lo largo del eje $x$, la coordenada y disminuye en 2 unidades. Esta tasa de cambio está determinada por la pendiente de la recta: $−2$. De manera similar, la pendiente de $1/2$ en la función $g (x)$ nos dice que por cada cambio en $x$ de 1 unidad hay un cambio correspondiente en $y$ de $1/2$ unidad. La función $h (x) = 2$ tiene una pendiente de cero, lo que indica que los valores de la función permanecen constantes. Vemos que la pendiente de cada función lineal indica la tasa de cambio de la función.

Figura 2.3 La función $k (x) = x^2$ no tiene una tasa de cambio constante.
Compara las gráficas de estas tres funciones con la gráfica de $k (x) = x^2$ (Figura 2.3).
La gráfica de $k (x) = x^2$ comienza desde la izquierda disminuyendo rápidamente, luego comienza a disminuir más lentamente y se nivela, y finalmente comienza a aumentar, lentamente al principio, seguido de una tasa de aumento creciente a medida que se mueve hacia la derecha. A diferencia de una función lineal, ningún número representa la tasa de cambio de esta función. Naturalmente, preguntamos: ¿Cómo medimos la tasa de cambio de una función no lineal?
Podemos aproximar la tasa de cambio de una función $f (x)$ en un punto $(a, f (a))$ de su gráfica tomando otro punto $(x, f (x))$ en la gráfica de $f (x)$, trazando una recta a través de los dos puntos y calculando la pendiente de esta recta que se llama recta secante.La Figura 2.4 muestra una recta secante a una función $f (x)$ en un punto $(a, f (a))$.

Figura 2.4 La pendiente de una recta secante que pasa por un punto $(a, f (a))$ estima la tasa de cambio de la función en el punto $(a, f (a))$.
Definimos formalmente a continuación una recta secante.
La precisión de aproximar la tasa de cambio de la función con una recta secante depende de qué tan cerca esté $x$ de $a$. Como vemos en la Figura 2.5, si $x$ está más cerca de $a$, la pendiente de la recta secante es una mejor medida de la tasa de cambio de $f (x)$ en $a$.
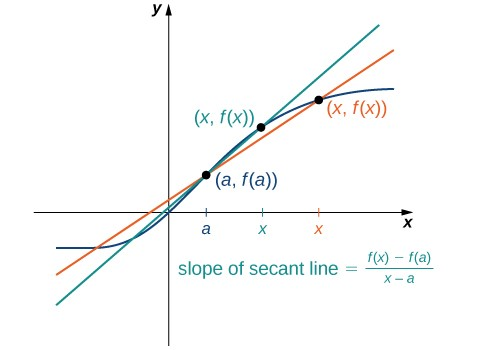
Figura 2.5 A medida que $x$ se acerca a $a$, la pendiente de la recta secante se vuelve una mejor aproximación a la tasa de cambio de la función $f (x)$ en $a$.
Las propias rectas secantes se acercan a una recta que se llama tangente a la función $f (x)$ como se muestra en la Figura 2.6). La pendiente de la recta tangente a la gráfica en $a$ mide la tasa de cambio de la función en dicho punto. Este valor también representa la derivada de la función $f (x)$ en $a$, o la tasa de cambio de la función en este punto. Esta derivada se denota por $f ′ (a)$.
El cálculo diferencial es el campo del cálculo que se ocupa del estudio de las derivadas y sus aplicaciones.

Figura 2.6 Resolución del problema de la tangente: a medida que $x$ se acerca a $a$, las líneas secantes se acercan a la tangente.
 Para obtener una demostración interactiva de la pendiente de una línea secante que puede manipular usted mismo, visite este applet
Para obtener una demostración interactiva de la pendiente de una línea secante que puede manipular usted mismo, visite este applet
Enlace: https://mathinsight.org/applet/secant_line_slope.
 |
2.1 Encontrar pendientes de rectas secantes |
Estima la pendiente de la recta tangente (tasa de cambio) a $f (x) = x^2$ en $x = 1$ encontrando pendientes de las rectas secantes a través de $(1,1)$ y cada uno de los siguientes puntos en la gráfica de $f (x) = x^2$.

 En la siguiente escena interactiva puedes observar cómo cuando $h$ tiende a cero la recta secante se convierte en recta tangente.
En la siguiente escena interactiva puedes observar cómo cuando $h$ tiende a cero la recta secante se convierte en recta tangente.
 |
Cuestión 2.1 |
Estima la pendiente de la recta tangente (tasa de cambio) a $f (x) = x^2$ en $x = 1$ encontrando pendientes de rectas secantes a través de $(1,1)$ y el punto $(54,2516)$ en la gráfica de $f (x) = x^2$.
Continuamos nuestra investigación explorando una pregunta relacionada. Teniendo en cuenta que la velocidad puede considerarse como la tasa de cambio de la posición, suponga que tenemos una función, $s (t)$, que da la posición de un objeto a lo largo de un eje de coordenadas en un momento dado $t$. ¿Podemos usar estas mismas ideas para crear una definición razonable de la velocidad instantánea en un tiempo dado $t = a$?
Comenzamos aproximando la velocidad instantánea con una velocidad promedio. Primero, recuerde que la rapidez de un objeto que viaja a una tasa constante es la razón entre la distancia recorrida y el tiempo que ha viajado. Definimos la velocidad promedio de un objeto durante un período de tiempo como el cambio en su posición dividido por la duración del período de tiempo.
A medida que $t$ se elige más cerca de $a$, la velocidad promedio se acerca a la velocidad instantánea. Tenga en cuenta que encontrar la velocidad promedio de una función de posición durante un intervalo de tiempo es esencialmente lo mismo que encontrar la pendiente de una recta secante a una función.
Además, para encontrar la pendiente de una recta tangente en un punto $a$, dejamos que los valores de $x$ se acerquen a $a$ en la pendiente de la recta secante. De manera similar, para encontrar la velocidad instantánea en el tiempo $a$, dejamos que los valores $t$ se acerquen a $a$ en la velocidad promedio. Este proceso de permitir que $x$ o $t$ se acerquen a $a$ en una expresión se llama calcular un límite. Por tanto, podemos definir la velocidad instantánea como sigue.
El ejemplo 2.2 ilustra este concepto de límites y velocidad media.
 |
2.2 Encontrar la velocidad media |
Se deja caer una roca desde una altura de 64 pies. Se determina que su altura (en pies) sobre el suelo $t$ segundos después (para 0≤t≤2) viene dado por $s (t) = - 16t^2 + 64$. Encuentra la velocidad promedio de la roca en cada uno de los intervalos de tiempo dados. Usa esta información para adivinar la velocidad instantánea de la roca en el tiempo $t = 0.5$.

 |
Cuestión 2.2 |
Un objeto se mueve a lo largo de un eje de coordenadas de modo que su posición en el tiempo $t$ está dada por $s (t) = t^3$. Estima su velocidad instantánea en el tiempo $t = 2$ calculando su velocidad promedio en el intervalo de tiempo $[2,2.001]$.
Ahora dirigimos nuestra atención a una pregunta clásica del cálculo. Muchas cantidades en física, por ejemplo, cantidades de trabajo, pueden interpretarse como el área bajo una curva. Esto nos lleva a plantearnos la pregunta: ¿Cómo podemos encontrar el área entre la gráfica de una función y el eje $x$ en un intervalo (Figura 2.8)?
Figura 2.8 El problema del área: ¿Cómo encontramos el área de la región sombreada?.
Como en la respuesta a nuestras preguntas anteriores sobre la velocidad, primero intentaremos aproximar la solución. Dividimos el intervalo $[a, b]$ en intervalos más pequeños que permitirán definir rectángulos aproximantes. La aproximación del área proviene de sumar las áreas de estos rectángulos (Figura 2.9).
Figura 2.9 El área de la región debajo de la curva se aproxima sumando las áreas de rectángulos delgados.
A medida que los anchos de los rectángulos se vuelven más pequeños (se acercan a cero), las sumas de las áreas de los rectángulos se acercan al área entre la gráfica de $f (x)$ y el eje $x$ sobre el intervalo $[a, b]$.
Una vez más, nos encontramos con un límite. Los límites de este tipo sirven como base para la definición de la integral definida. El cálculo integral es el estudio de integrales y sus aplicaciones.
 |
2.3 Estimación mediante rectángulos |
Estima el área entre el eje $x$ y la gráfica de $f (x) = x^2 + 1$ en el intervalo $[0,3]$ utilizando los tres rectángulos que se muestran en la Figura 2.10.

Figura 2.10 El área de la región bajo la curva de $f (x) = x^2 + 1$ se puede estimar usando rectángulos.
 |
Cuestión 2.3 |
Estima el área entre el eje $x$ y la gráfica de $f (x) = x^2 + 1$ durante el intervalo $[0,3]$ utilizando los tres rectángulos que se muestran en la figura siguiente:
 En la siguiente escena interactiva puedes estimar el área bajo la gráfica de una funcion positiva mediante sumas de áreas de rectángulos. La base de esos rectángulos se calcula en función del número de rectángulos a considerar y la altura se toma el valor de la función en distintos puntos (extremo inferior, extremo superior o punto medio del rectángulo considerado).
En la siguiente escena interactiva puedes estimar el área bajo la gráfica de una funcion positiva mediante sumas de áreas de rectángulos. La base de esos rectángulos se calcula en función del número de rectángulos a considerar y la altura se toma el valor de la función en distintos puntos (extremo inferior, extremo superior o punto medio del rectángulo considerado).
Hasta ahora, hemos estudiado funciones de una sola variable. Estas funciones se pueden representar visualmente mediante gráficos en dos dimensiones; sin embargo, no hay una buena razón para restringir nuestra investigación a dos dimensiones.
Supongamos, por ejemplo, que en lugar de determinar la velocidad de un objeto que se mueve a lo largo de un eje de coordenadas, queremos determinar la velocidad de una roca lanzada desde una catapulta en un momento dado, o de un avión que se mueve en tres dimensiones. Podríamos querer graficar funciones de valor real de dos variables o determinar volúmenes de sólidos del tipo que se muestra en la Figura 2.11.
Estos son solo algunos de los tipos de preguntas que se pueden hacer y responder mediante el cálculo multivariable. De manera informal, el cálculo multivariable se puede caracterizar como el estudio del cálculo de funciones de dos o más variables. Sin embargo, antes de explorar estas y otras ideas, primero debemos sentar las bases para el estudio del cálculo en una variable explorando el concepto de límite.

Figura 2.11 Podemos usar el cálculo multivariable para encontrar el volumen entre una superficie definida por una función de dos variables y un plano.
 Para los siguientes ejercicios, considera los puntos $P (1,2)$
y $Q (x, y)$ que están en la gráfica de la función $f (x) = x^2 + 1$.
Para los siguientes ejercicios, considera los puntos $P (1,2)$
y $Q (x, y)$ que están en la gráfica de la función $f (x) = x^2 + 1$.
1. [T] Completa la siguiente tabla con los valores apropiados: coordenada $y$ de $Q$, el punto $Q (x, y)$, y la pendiente de la recta secante que pasa por los puntos $P$ y $Q$. Redondea tu respuesta a ocho dígitos significativos.
| $x$ | $y$ | $Q(x,y)$ | $m_{sec}$ |
| 1.1 | a | e | i |
| 1.01 | b | f | b |
| 1.001 | c | g | k |
| 1.0001 | d | h | l |
2. Utiliza los valores de la columna derecha de la tabla del ejercicio anterior para adivinar el valor de la pendiente de la recta tangente a $f$ en $x = 1$.
3. Usa el valor del ejercicio anterior para encontrar la ecuación de la recta tangente en el punto $P$. Representa $f (x)$ y la recta tangente. (Solución)
 Para los siguientes ejercicios, considera los los puntos $P (1,1)$ y $Q (x, y)$ que están en la gráfica de la función $f (x) = x^3$.
Para los siguientes ejercicios, considera los los puntos $P (1,1)$ y $Q (x, y)$ que están en la gráfica de la función $f (x) = x^3$.
4. [T] Completa la siguiente tabla con los valores apropiados: coordenada $y$ de $Q$, el punto $Q (x, y)$, y la pendiente de la recta
secante que pasa por los puntos $P$ y $Q$. Redondea tu respuesta a ocho dígitos significativos.
| $x$ | $y$ | $Q(x,y)$ | $m_{sec}$ |
| 1.1 | a | e | i |
| 1.01 | b | f | b |
| 1.001 | c | g | k |
| 1.0001 | d | h | l |
5. Utiliza los valores de la columna derecha de la tabla del ejercicio anterior para adivinar el valor de la pendiente de la recta tangente a $f$ en $x = 1$. (Solución)
6. Usa el valor del ejercicio anterior para encontrar la ecuación de la recta tangente en el punto $P$. Grafica $f (x)$ y la recta tangente.
 Para los siguientes ejercicios, considera los puntos $P (4,2)$ y $Q (x, y)$ que están en la gráfica de la función $f (x) =\sqrt{x}$.
Para los siguientes ejercicios, considera los puntos $P (4,2)$ y $Q (x, y)$ que están en la gráfica de la función $f (x) =\sqrt{x}$.
7. [T] Completa la siguiente tabla con los valores apropiados: coordenada $y$ de $Q$, el punto $Q (x, y)$, y la pendiente de la recta secante que pasa por los puntos $P$ y $Q$. Redondea tu respuesta a ocho dígitos significativos.
| $x$ | $y$ | $Q(x,y)$ | $m_{sec}$ |
| 4.1 | a | e | i |
| 4.01 | b | f | b |
| 4.001 | c | g | k |
| 4.0001 | d | h | l |
8. Utiliza los valores de la columna derecha de la tabla del ejercicio anterior para adivinar el valor de la pendiente de la recta tangente a $f$ en $x = 4$.
9. Utiliza el valor del ejercicio anterior para encontrar la ecuación de la recta tangente en el punto $P$.
(Solución) Para los siguientes ejercicios, considera los puntos $P (1.5,0)$ y $Q (\phi, y)$ que están en la gráfica de la función $f (\phi) = cos (\pi \phi)$.
Para los siguientes ejercicios, considera los puntos $P (1.5,0)$ y $Q (\phi, y)$ que están en la gráfica de la función $f (\phi) = cos (\pi \phi)$.
10. [T] Completa la siguiente tabla con los valores apropiados: coordenada $y$ de $Q$, el punto $Q (\phi, y)$ y la pendiente de la recta secante que pasa por los puntos $P$ y $Q$. Redondea tu respuesta a ocho dígitos significativos.
| $\phi$ | $y$ | $Q(\phi,y)$ | $m_{sec}$ |
| 1.4 | a | e | i |
| 1.49 | b | f | b |
| 1.499 | c | g | k |
| 1.4999 | d | h | l |
11. Utiliza los valores de la columna derecha de la tabla del ejercicio anterior para adivinar el valor de la pendiente de la recta tangente a $f$ en $\phi = 1.5$. (Solución)
12. Utiliza el valor del ejercicio anterior para encontrar la ecuación de la recta tangente en el punto $P$.
 Para los siguientes ejercicios, considera los puntos $P (−1, −1)$ y $Q (x, y)$ que están en la gráfica de la función $f (x) = \frac{1}{x}$.
Para los siguientes ejercicios, considera los puntos $P (−1, −1)$ y $Q (x, y)$ que están en la gráfica de la función $f (x) = \frac{1}{x}$.
13. [T] Completa la siguiente tabla con los valores apropiados: coordenada $y$ de $Q$, el punto $Q (x, y)$ y la pendiente de la recta secante que pasa por los puntos $P$ y $Q$. Redondea tu respuesta a ocho dígitos significativos.
| $x$ | $y$ | $Q(x,y)$ | $m_{sec}$ |
| -1.05 | a | e | i |
| -1,01 | b | f | b |
| -1.005 | c | g | k |
| -1.001 | d | h | l |
14. Usa los valores de la columna derecha de la tabla del ejercicio anterior para adivinar el valor de la pendiente de la recta tangente a $f$ en $x = −1$.
15. Utiliza el valor del ejercicio anterior para encontrar la ecuación de la recta tangente en el punto $P$.
 Para los siguientes ejercicios, la función de posición de una pelota que se deja caer desde lo alto de un edificio de 200 metros de altura viene dada por $s (t) = 200−4.9t^2$, donde la posición $s$ se mide en metros y el tiempo $t$ se mide en segundos. Redondea tu respuesta a ocho dígitos significativos.
(Solución)
Para los siguientes ejercicios, la función de posición de una pelota que se deja caer desde lo alto de un edificio de 200 metros de altura viene dada por $s (t) = 200−4.9t^2$, donde la posición $s$ se mide en metros y el tiempo $t$ se mide en segundos. Redondea tu respuesta a ocho dígitos significativos.
(Solución)
16. [T] Calcula la velocidad promedio de la pelota en los intervalos de tiempo dados.
17. Utiliza el ejercicio anterior para adivinar la velocidad instantánea de la pelota en $t = 5$ segundos.
 Para los siguientes ejercicios, consideremos una piedra lanzada al aire desde el nivel del suelo con una velocidad inicial de 15 m / seg. Su altura en metros en el tiempo $t$ segundos es $h (t) = 15t − 4.9t^2$.
(Solución)
Para los siguientes ejercicios, consideremos una piedra lanzada al aire desde el nivel del suelo con una velocidad inicial de 15 m / seg. Su altura en metros en el tiempo $t$ segundos es $h (t) = 15t − 4.9t^2$.
(Solución)
18. [T] Calcule la velocidad promedio de la piedra en los intervalos de tiempo dados.
19. Utiliza el ejercicio anterior para adivinar la velocidad instantánea de la piedra en $t = 1$ segundo. (Solución)
 Para los siguientes ejercicios, consideremos un cohete lanzado al aire que luego regresa a la Tierra.
Para los siguientes ejercicios, consideremos un cohete lanzado al aire que luego regresa a la Tierra.
La altura del cohete en metros viene dada por $h (t) = 600 + 78.4t − 4.9t^2$, donde $t$ se mide en segundos. (Solución)
20. [T] Calcule la velocidad promedio del cohete en los intervalos de tiempo dados.
21. Utiliza el ejercicio anterior para adivinar la velocidad instantánea del cohete en $t = 9$ segundos. (Solución)
 Para los siguientes ejercicios, consideremos a un atleta que corre una carrera de 40 m. La posición del atleta viene dada por $d (t) = \frac{t^3}{6} + 4t$, donde $d$ es la posición en metros y $t$ es el tiempo transcurrido, medido en segundos.
Para los siguientes ejercicios, consideremos a un atleta que corre una carrera de 40 m. La posición del atleta viene dada por $d (t) = \frac{t^3}{6} + 4t$, donde $d$ es la posición en metros y $t$ es el tiempo transcurrido, medido en segundos.
22. [T] Calcule la velocidad promedio del corredor en los intervalos de tiempo dados.
23. Utiliza el ejercicio anterior para adivinar la velocidad instantánea del corredor en $t = 2$ segundos. (Solución)
 Para los siguientes ejercicios, considera la función $f (x) = | x |$.
Para los siguientes ejercicios, considera la función $f (x) = | x |$.
24. Dibuja la gráfica de $f$ en el intervalo $[−1,2]$ y sombrea la región por encima del eje x.
25. Utiliza el ejercicio anterior para encontrar el valor aproximado del área entre el eje $x$ y la gráfica de $f$ en el intervalo $[−1,2]$ usando rectángulos. Para los rectángulos, usa las unidades cuadradas y haga una aproximación tanto por encima como por debajo de las líneas. Usa geometría para encontrar la respuesta exacta. (Solución)
 Para los siguientes ejercicios, consideremos la función $f (x) = \sqrt{1 − x^2}$.
(Sugerencia: esta es la mitad superior de un círculo de radio 1 y de centro $(0,0)$).
Para los siguientes ejercicios, consideremos la función $f (x) = \sqrt{1 − x^2}$.
(Sugerencia: esta es la mitad superior de un círculo de radio 1 y de centro $(0,0)$).
26. Dibuja la gráfica de $f$ sobre el intervalo $[−1,1]$.
27. Utiliza el ejercicio anterior para encontrar el área aproximada entre el eje $x$ y la gráfica de $f$ en el intervalo $[−1,1]$ usando rectángulos. Para los rectángulos, usa cuadrados de 0,4 por 0,4 unidades y haga una aproximación tanto por encima como por debajo de las líneas. Usa geometría para encontrar la respuesta exacta. (Solución)
 Para los siguientes ejercicios, considere la función $f (x) = - x^2 + 1$.
Para los siguientes ejercicios, considere la función $f (x) = - x^2 + 1$.
28. Dibuje la gráfica de $f$ sobre el intervalo $[−1,1]$.
29. Calcula el área de la región entre el eje $x$ y la gráfica de $f$ en el intervalo $[−1,1]$. (Solución)
El concepto de límite es esencial para la comprensión del cálculo, existe desde hace miles de años. De hecho, los primeros matemáticos utilizaron un proceso de límite para obtener cada vez mejores aproximaciones de áreas de círculos. Sin embargo, la definición formal de límite, tal como la conocemos y entendemos hoy, no apareció hasta finales del siglo XIX. Por lo tanto, comenzamos nuestra búsqueda para comprender los límites, como lo hicieron nuestros antepasados matemáticos, utilizando un enfoque intuitivo. Al final de este capítulo, armados con una comprensión conceptual de los límites, se examinará la definición formal de límite.
Comenzamos nuestra exploración de límites observando las gráficas de las funciones. $f(x) =\frac{x^2−4}{x−2}$, $g(x) = \frac{|x−2|} {x−2}$ y $h(x) = \frac{1}{(x−2)^2}$, que se muestran en la Figura 2.12.
En particular, centremos nuestra atención en el comportamiento de cada gráfico para el valor $y$ alrededor de $x = 2$.

Figura 2.12 Estos gráficos muestran el comportamiento de tres funciones diferentes alrededor de $x = 2$.
Cada una de las tres funciones no está definida en $x = 2$, pero si hacemos esta afirmación, damos una imagen muy incompleta de cómo se comporta cada función en la vecindad de $x = 2$. Para expresar el comportamiento de cada gráfico en las proximidades de 2 de manera más completa, necesitamos introducir el concepto de límite.
Primero echemos un vistazo más de cerca a cómo la función $f (x) = (x^2−4) / (x − 2)$ se comporta alrededor de $x = 2$ en la Figura 2.12. A medida que los valores de $x$ se acercan a $2$ desde cualquier lado de $2$, los valores de $y = f (x)$ se acercan a 4. Matemáticamente, decimos que el límite de $f (x)$ cuando $x$ se acerca a $2$ es $4$.
Simbólicamente, expresamos este límite como $$\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 4.$$
A partir de esta breve mirada informal a un límite, comencemos a desarrollar una definición intuitiva del límite. Podemos pensar en el límite de una función en un número $a$ como el único número real $L$ al que se acercan los valores funcionales cuando los valores de $x$ se acercan al punto $a$, siempre que exista tal número real $L$. Expresado con más cuidado, tenemos la siguiente definición.
Sea $f (x)$ una función definida en todos los valores en un intervalo abierto que contenga $a$, con la posible excepción de $a$, y sea $L$ un número real.
Si todos los valores de la función $f (x)$ se acercan al número real $L$ cuando los valores de $x \neq a$ se acercan al número $a$, entonces decimos que el límite de $f (x)$ cuando $x$ se acerca al punto $a$ es $L$. Más sucintamente, a medida que $x$ se acerca a $a$, $f (x)$ se acerca y permanece cerca de $L$.
Simbólicamente, expresamos esta idea como $$\mathop {\lim }\limits_{x \to a} f\left( x \right) = L \tag{$2.3$}$$
Podemos estimar límites construyendo tablas de valores funcionales y mirando sus gráficos. Este proceso se describe en la siguiente estrategia de resolución de problemas.
| $x$ | $f(x)$ | $x$ | $f(x)$ | |
| $a-0.1$ | $f(a-0.1)$ | $a+0.1$ | $f(a+0.1)$ | |
| $a-0.01$ | $f(a-0.01)$ | $a+0.01$ | $f(a+0.01)$ | |
| $a-0.001$ | $f(a-0.001)$ | $a+0.001$ | $f(a+0.001)$ | |
| $a-0.0001$ | $f(a-0.0001)$ | $a+0.0001$ | $f(a+0.0001)$ |
Tabla 2.1 Tabla de valores para $\mathop {\lim }\limits_{x \to a} f\left( x \right) = L$
En nuestras columnas, miramos la secuencia $f (a − 0.1)$, $f (a − 0.01)$, $f (a − 0.001)$, $f (a − 0.0001)$, y así sucesivamente, y $f (a + 0.1)$, $f (a + 0.01)$, $f (a + 0.001)$, $f (a + 0.0001)$, y así sucesivamente.
Nota: aunque hemos elegido para $x$ los valores $a ± 0,1$, $a ± 0,01$, $a ± 0,001$, $a ± 0,0001$, y así sucesivamente, y estos valores probablemente funcionarán casi siempre, en ocasiones es posible que necesitemos modificar nuestras elecciones.
Usando una calculadora gráfica o un software de ordenador que nos permita representar gráficas de funciones, podemos trazar la función $f(x)$, asegurándose de que los valores funcionales de $f (x)$ para los valores de $x$ cerca de $a$ estén en nuestra ventana gráfica.
Podemos movernos a lo largo del gráfico de la función y observar la lectura del valor $y$ cuando los valores $x$ se acercan a $a$. Si los valores de $y$ se acercan a $L$ cuando nuestros valores de $x$ se acercan a $a$ desde ambas direcciones, entonces $\mathop {\lim }\limits_{x \to a} f\left( x \right) = L$.
Es posible que necesitemos ampliar nuestro gráfico y repetir este proceso varias veces.
 En la siguiente escena interactiva incorporamos un applet que permite aplicar esta estrategia calculando los valores que se consideren y representando la gráfica de la función.
En la siguiente escena interactiva incorporamos un applet que permite aplicar esta estrategia calculando los valores que se consideren y representando la gráfica de la función.
Aplicamos esta estrategia de resolución de problemas para calcular un límite en el Ejemplo 2.4.
 |
2.4 Evaluación de un límite mediante una tabla de valores funcionales |
Evalúa $\mathop {\lim }\limits_{x \to 0} {{senx} \over x}$.

 |
2.5 Evaluación de un límite mediante una tabla de valores funcionales |
Evalúa $\mathop {\lim }\limits_{x \to 4} {{\sqrt x - 2} \over {x - 4}}$ utilizando una tabla de valores funcionales.

 |
Cuestión 2.4 |
Estima $\mathop {\lim }\limits_{x \to 1} {{{1 \over x} - 1} \over {x - 1}}$ utilizando una tabla de valores funcionales. Utiliza un gráfico para confirmar su estimación.
En este punto, vemos desde Ejemplo 2.4 y Ejemplo 2.5 que puede ser tan fácil, si no más fácil, estimar un límite de una función inspeccionando su gráfica como estimar el límite usando una tabla de valores funcionales. En el Ejemplo 2.6, evaluamos un límite exclusivamente mirando un gráfico en lugar de usar una tabla de valores funcionales.
 |
2.6 Evalúa un límite mediante un gráfico |
Para $g (x)$ se muestra en la Figura 2.15, evalúe $\mathop {\lim }\limits_{x \to - 1} g\left( x \right)$.

Figura 2.15 La gráfica de $g (x)$ incluye un valor que no está en una curva suave.

Mirar una tabla de valores funcionales o mirar el gráfico de una función nos proporciona información útil sobre el valor del límite de una función en un punto dado. Sin embargo, estas técnicas se basan demasiado en conjeturas.
Eventualmente, necesitamos desarrollar métodos alternativos para evaluar los límites. Estos nuevos métodos son de naturaleza más algebraica y los exploramos en la siguiente sección; sin embargo, en este punto presentamos dos límites especiales que son fundamentales para las técnicas futuras.
Sea $a$ un número real y $c$ una constante. $$\mathop {\lim }\limits_{x \to a} x = a \tag{$2.4$}$$ $$\mathop {\lim }\limits_{x \to a} c = c \tag{$2.5$}$$
Podemos hacer las siguientes observaciones sobre estos dos límites.
| $x$ | $f(x)=c$ | $x$ | $f(x)=c$ | |
| $a-0.1$ | $c$ | $a+0.1$ | $c$ | |
| $a-0.01$ | $c$ | $a+0.01$ | $c$ | |
| $a-0.001$ | $c$ | $a+0.001$ | $c$ | |
| $a-0.0001$ | $c$ | $a+0.0001$ | $c$ |
Tabla 2.4 Tabla de valores funcionales para $\mathop {\lim }\limits_{x \to a} c = c$
Observamos que para todos los valores de $x$ (independientemente de si se acercan a $a$), los valores $f (x)$ permanecen constante en $c$. No tenemos más remedio que concluir que $\mathop {\lim }\limits_{x \to a} c = c$.
Al considerar el límite en el siguiente ejemplo, debemos tener en cuenta que para que exista el límite de una función en un punto, los valores funcionales deben acercarse a un único valor real en ese punto. Si los valores funcionales no se acercan a un solo valor, entonces el límite no existe.
 |
2.7 Evalúa un límite que no existe |
Evalúa $\mathop {\lim }\limits_{x \to 0} sen\left( {{1 \over x}} \right)$ usando una tabla de valores.

 |
Cuestión 2.6 |
Utiliza una tabla de valores funcionales para evaluar $\mathop {\lim }\limits_{x \to 2} {{\left| {{x^2} - 4} \right|} \over {x - 2}}$, si es posible.
A veces, indicar que el límite de una función no existe en un punto no nos proporciona suficiente información sobre el comportamiento de la función en ese punto en particular. Para ver esto, ahora revisamos la función $g (x) = | x − 2 | / (x − 2)$ introducida al principio de la sección (ver Figura 2.12).
Como elegimos valores de $x$ cercanos a $2$, $g (x)$ no se acerca a un solo valor, por lo que el límite cuando $x$ se acerca a $2$ no existe, es decir, $\mathop {\lim }\limits_{x \to 2} g\left( x \right)\,\,\nexists$. Sin embargo, esta afirmación por sí sola no nos da una imagen completa del comportamiento de la función en torno al valor $2$ de $x$.
Para proporcionar una descripción más precisa, presentamos la idea de un límite lateral. Para todos los valores a la izquierda de $2$, $g (x) = - 1$. Por lo tanto, cuando $x$ se acerca a $2$ por la izquierda, $g (x)$ se aproxima a $-1$. Matemáticamente, decimos que el límite cuando $x$ se acerca a $2$ por la izquierda es $−1$. Simbólicamente, expresamos esta idea como $$\mathop {\lim }\limits_{x \to {2^ - }} g\left( x \right) = - 1$$
De manera similar, cuando $x$ se acerca a $2$ por la derecha, $g (x)$ se aproxima a $1$. Simbólicamente, expresamos esta idea como $$\mathop {\lim }\limits_{x \to {2^ + }} g\left( x \right) = 1$$
Ahora podemos presentar una definición informal de límites laterales.
Si los valores de la función $f (x)$ se acercan al número real $L$ cuando los valores de $x$ (donde $x < a$) se acercan al número $a$, entonces decimos que $L$ es el límite de $f (x)$ cuando $x$ se acerca al punto $a$ por la izquierda. Simbólicamente, expresamos esta idea como $$\mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = L \tag{$2.6$}$$
Si los valores de la función $f (x)$ se acercan al número real $L$ cuando los valores de $x$ (donde $x > a$) se acercan al número $a$, entonces decimos que $L$ es el límite de $f (x)$ cuando $x$ se acerca al punto $a$ por la derecha. Simbólicamente, expresamos esta idea como $$\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = L \tag{$2.7$}$$
 En la siguiente escena interactiva incorporamos un applet que permite practicar con el cálculo de límites laterales.
En la siguiente escena interactiva incorporamos un applet que permite practicar con el cálculo de límites laterales.
 |
2.8 Evaluar límites laterales |
Para la función $\begin{cases} x+1 & \text{si $x < 2$} \\ x^2-4 & \text{si $x \ge 2$} \end{cases} $, $x=1$ evalúa cada uno de los siguientes límites.

 |
Cuestión 2.7 |
Utiliza una tabla de valores funcionales para estimar los siguientes límites, si es posible.
Consideremos ahora la relación entre el límite de una función en un punto y los límites a derecha e izquierda en ese punto. Parece claro que si el límite de la derecha y el límite de la izquierda tienen un valor común, entonces ese valor común es el límite de la función en ese punto.
Del mismo modo, si el límite de la izquierda y el límite de la derecha toman valores diferentes, el límite de la función no existe. Estas conclusiones se resumen en el siguiente teorema.
TEOREMA 2.2. Relacionar limites laterales y el límite
Sea $f (x)$ una función definida en todos los valores en un intervalo abierto que contenga al punto $a$, con la posible excepción del punto $a$, y sea $L$ un número real. Se tiene, $$\mathop {\lim }\limits_{x \to a} f\left( x \right) = L\,\,\,\,si\,\,y\,\,solo\,\,si\,\,\mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = L$$
Evaluar el límite de una función en un punto o evaluar el límite de una función a la derecha o a la izquierda en un punto nos ayuda a caracterizar el comportamiento de una función alrededor de un valor dado. Como veremos, también podemos describir el comportamiento de funciones que no tienen límites finitos.
Ahora dirigimos nuestra atención a $h (x) = 1 / (x − 2)^2$, la tercera y última función presentada al principio de esta sección (ver Figura 2.12 (c)). De su gráfica vemos que a medida que los valores de $x$ se acercan a $2$, los valores de $h (x) = 1 / (x − 2)^2$ se vuelven cada vez más grandes superando a cualquier número real. Matemáticamente, decimos que el límite de $h (x)$ cuando $x$ se acerca a $2$ es infinito positivo. Simbólicamente, expresamos esta idea como $$\mathop {\lim }\limits_{x \to 2} h\left( x \right) = + \infty $$
De manera más general, definimos límites infinitos de la siguiente manera:
Es importante entender que cuando escribimos declaraciones como $\mathop {\lim }\limits_{x \to a} f\left( x \right) = + \infty $ o $\mathop {\lim }\limits_{x \to a} f\left( x \right) = - \infty $ estamos describiendo el comportamiento de la función, tal como la acabamos de definir. No estamos afirmando que exista un límite. Para que exista el límite de una función $f (x)$ en $a$, debe acercarse a un número real $L$ cuando $x$ se acerca al punto $a$.
Dicho esto, si, por ejemplo, $\mathop {\lim }\limits_{x \to a} f\left( x \right) = + \infty $, siempre escribimos $\mathop {\lim }\limits_{x \to a} f\left( x \right) = + \infty$ en lugar de $\mathop {\lim }\limits_{x \to a} f\left( x \right) = + \infty \,\,\nexists$
 En la siguiente escena interactiva incorporamos un applet para practicar los límites infinitos.
En la siguiente escena interactiva incorporamos un applet para practicar los límites infinitos.
 |
2.9 Reconociendo un límite infinito |
Evalúa cada uno de los siguientes límites, si es posible. Usa una tabla de valores funcionales y grafique $f (x) = 1 / x$ para confirmar su conclusión.

 |
Cuestión 2.8 |
Evalúa cada uno de los siguientes límites, si es posible. Usa una tabla de valores funcionales y represente la gráfica de $f (x) = 1 / x^2$ para confirmar su conclusión.
Es útil señalar que funciones de la forma $f (x) = 1 / (x − a)^n$, donde $n$ es un número entero positivo, tiene límites infinitos cuando $x$ se acerca al punto $a$ desde la izquierda o la derecha (Figura 2.20). Estos límites se resumen en el siguiente resultado.
Figura 2.20 La función $f (x) = 1 / (x − a)^n$ tiene límites infinitos en $a$.
TEOREMA 2.3. Límites infinitos de enteros positivos
Si $n$ es un entero par positivo, entonces
$$\mathop {\lim }\limits_{x \to a} {1 \over {{{\left( {x - a} \right)}^n}}} = + \infty $$Si $n$ es un entero impar positivo, entonces
$$\mathop {\lim }\limits_{x \to {a^ + }} {1 \over {{{\left( {x - a} \right)}^n}}} = + \infty $$ $$\mathop {\lim }\limits_{x \to {a^ - }} {1 \over {{{\left( {x - a} \right)}^n}}} = - \infty $$También debemos señalar que en las gráficas de $f (x) = 1 / (x − a)^n$, los puntos en el gráfico que tienen coordenadas $x$ muy cerca de $a$ están muy cerca de la línea vertical $x = a$. Es decir, cuando $x$ se acerca al punto $a$, los puntos en la gráfica de $f (x)$ están más cerca de la recta $x = a$. La recta $x = a$ se llama asíntota vertical del gráfico.
Definimos a continuación formalmente una asíntota vertical.
 |
2.10 Encontrar una asíntota vertical |
Evalúa cada uno de los siguientes límites utilizando Límites infinitos de enteros positivos. Identifica cualquier asíntota vertical de la función $$f (x) = \frac{1} {(x + 3)^4}$$

 |
2.11 Comportamiento de una función en diferentes puntos |
Usa la gráfica de $f (x)$ en la Figura 2.21 para determinar cada uno de los siguientes valores:

Figura 2.21 La gráfica muestra $f (x)$.
 |
Cuestión 2.9 |
Evalúa cada uno de los siguientes límites. Identifica las asíntotas verticales de la función $f (x) = 1/ (x − 2)^3$.

 |
Cuestión 2.10 |
Evalúa $\mathop {\lim }\limits_{x \to 1} f\left( x \right)$ para $f (x)$ mostrado aquí:
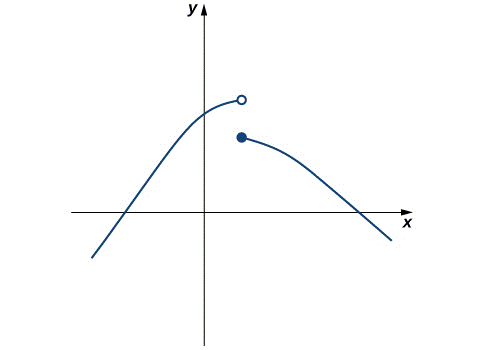
En el siguiente ejemplo ponemos nuestro conocimiento de varios tipos de límites para analizar el comportamiento de una función en varios puntos diferentes.
 |
2.12 Ecuación de Einstein |
En el primer capítulo mencionamos brevemente cómo Albert Einstein demostró que existe un límite a la rapidez con la que puede viajar cualquier objeto. Dada la ecuación de Einstein para la masa de un objeto en movimiento, ¿cuál es el valor de este límite?

Figura 2.22 Crédito: NASA.

 Para los siguientes ejercicios, considera la función $f (x) = \frac{x^2−1} {| x − 1 |}$.
Para los siguientes ejercicios, considera la función $f (x) = \frac{x^2−1} {| x − 1 |}$.
30. [T]Completa la siguiente tabla para la función. Redondea tus soluciones a cuatro decimales.
| $x$ | $f(x)$ | $x$ | $f(x)$ | |
| 0.9 | a | 1.1 | e | |
| 0.99 | b | 1.01 | f | |
| 0.999 | c | 1.001 | g | |
| 0.9999 | d | 1.0001 | h |
31. ¿Qué indican los resultados del ejercicio anterior sobre el límite $\mathop {\lim }\limits_{x \to 1} f\left( x \right)$ Explica la respuesta. (Solución)
 Para los siguientes ejercicios, considera la función $f (x) = (1 + x)^{1 / x}$.
Para los siguientes ejercicios, considera la función $f (x) = (1 + x)^{1 / x}$.
32. [T] Haz una tabla que muestre los valores de $f$ para $x = −0.01, −0.001, −0.0001, −0.00001$ y para $x = 0.01,0.001,0.0001,0.00001$. Redondea tus soluciones a cinco decimales.
| $x$ | $f(x)$ | $x$ | $f(x)$ | |
| -0.01 | a | 1.1 | e | |
| -0.001 | b | 0.001 | f | |
| -0.0001 | c | 0.0001 | g | |
| -0.00001 | d | 0.00001 | h |
33. ¿Qué indica la tabla de valores del ejercicio anterior sobre la función $f (x) = (1 + x)^{1 / x}$? (Solución)
34. ¿A qué constante matemática parece acercarse el límite del ejercicio anterior?
 En los siguientes ejercicios, usa los valores dados para configurar una tabla para evaluar los límites. Redondea tus soluciones a ocho lugares decimales.
En los siguientes ejercicios, usa los valores dados para configurar una tabla para evaluar los límites. Redondea tus soluciones a ocho lugares decimales.
35. [T] $\mathop {\lim }\limits_{x \to 0} {{sen\left( {2x} \right)} \over x};\,\, \pm 0.1,\,\, \pm 0.01,\, \pm 0.001,\,\, \pm 0.00$
| $x$ | $\frac{sen(2x)}{x}$ | $x$ | $\frac{sen(2x)}{x}$ | |
| -0.1 | a | 0.1 | e | |
| -0.01 | b | 0.01 | f | |
| -0.001 | c | 0.001 | g | |
| -0.0001 | d | 0.0001 | h |
36. [T] $\mathop {\lim }\limits_{x \to 0} {{sen\left( {3x} \right)} \over x};\,\, \pm 0.1,\,\, \pm 0.01,\, \pm 0.001,\,\, \pm 0.0001$
| $x$ | $\frac{sen(3x)}{x}$ | $x$ | $\frac{sen(3x)}{x}$ | |
| -0.01 | a | 1.1 | e | |
| -0.001 | b | 0.001 | f | |
| -0.0001 | c | 0.0001 | g | |
| -0.00001 | d | 0.00001 | h |
37. Utiliza los dos ejercicios anteriores para conjeturar (adivinar) el valor del siguiente límite: $\mathop {\lim }\limits_{x \to 0} {{sen\left( {ax} \right)} \over x}$ para $a$ un valor real positivo. (Solución)
 [T]En los siguientes ejercicios, configura una tabla de valores para encontrar el límite indicado. Redondea a ocho dígitos.
[T]En los siguientes ejercicios, configura una tabla de valores para encontrar el límite indicado. Redondea a ocho dígitos.
38. $\mathop {\lim }\limits_{x \to 2} {{{x^2} - 4} \over {{x^2} + x - 6}}$
| $x$ | ${{{x^2} - 4} \over {{x^2} + x - 6}}$ | $x$ | ${{{x^2} - 4} \over {{x^2} + x - 6}}$ | |
| 1.9 | a | 2.1 | e | |
| 1.99 | b | 2.01 | f | |
| 1.999 | c | 2.001 | g | |
| 1.9999 | d | 2.0001 | h |
39. $\mathop {\lim }\limits_{x \to 1} \left( {1 - 2x} \right)$
| $x$ | $1-2x$ | $x$ | $1-2x$ | |
| 0.9 | a | 1.1 | e | |
| 0.99 | b | 1.01 | f | |
| 0.999 | c | 1.001 | g | |
| 0.9999 | d | 1.0001 | h |
40. $\mathop {\lim }\limits_{x \to 0} {5 \over {1 - {e^{1/x}}}}$
| $x$ | $5 \over {1 - {e^{1/x}}}$ | $x$ | $5 \over {1 - {e^{1/x}}}$ | |
| -0.1 | a | 0.1 | e | |
| -0.01 | b | 0.01 | f | |
| -0.001 | c | 0.001 | g | |
| -0.0001 | d | 0.0001 | h |
41. $\mathop {\lim }\limits_{z \to 0} {{z - 1} \over {{z^2}\left( {z + 3} \right)}}$
| $z$ | ${{z - 1} \over {{z^2}\left( {z + 3} \right)}}$ | $z$ | ${{z - 1} \over {{z^2}\left( {z + 3} \right)}}$ | |
| -0.1 | a | 0.1 | e | |
| -0.01 | b | 0.01 | f | |
| -0.001 | c | 0.001 | g | |
| -0.0001 | d | 0.0001 | h |
42. $\mathop {\lim }\limits_{t \to {0^ + }} {{\cos t} \over t}$
| $t$ | ${\cos t} \over t$ |
| 0.1 | a |
| 0.01 | b |
| 0.001 | c |
| 0.0001 | d |
43. $\mathop {\lim }\limits_{x \to 2} {{1 - {2 \over x}} \over {{x^2} - 4}}$
| $x$ | $5 \over {1 - {e^{1/x}}}$ | $x$ | $5 \over {1 - {e^{1/x}}}$ | |
| 1.9 | a | 2.1 | e | |
| 1.99 | b | 2.01 | f | |
| 1.999 | c | 2.001 | g | |
| 1.9999 | d | 2.0001 | h |
 [T] En los siguientes ejercicios, configura una tabla de valores y redondea a ocho dígitos significativos. Con base en la tabla de valores, adivina cuál es el límite. Luego, usa una calculadora para representar la gráfica de la función y determinar el límite. ¿Fue correcta la conjetura? Si no es así, ¿por qué falla el método de utilizar tablas?
[T] En los siguientes ejercicios, configura una tabla de valores y redondea a ocho dígitos significativos. Con base en la tabla de valores, adivina cuál es el límite. Luego, usa una calculadora para representar la gráfica de la función y determinar el límite. ¿Fue correcta la conjetura? Si no es así, ¿por qué falla el método de utilizar tablas?
44. $\mathop {\lim }\limits_{\theta \to 0} sen\left( {{\pi \over \theta }} \right)$
| $\theta$ | $sen\left( {{\pi \over \theta }} \right)$ | $\theta$ | $sen\left( {{\pi \over \theta }} \right)$ | |
| -0.1 | a | 0.1 | e | |
| -0.01 | b | 0.01 | f | |
| -0.001 | c | 0.001 | g | |
| -0.0001 | d | 0.0001 | h |
45. $\mathop {\lim }\limits_{\alpha \to 0} {1 \over \alpha }\cos \left( {{\pi \over \alpha }} \right)$
| $\alpha$ | ${1 \over \alpha }\cos \left( {{\pi \over \alpha }} \right)$ |
| 0.1 | a |
| 0.01 | b |
| 0.001 | c |
| 0.0001 | d |
 En los siguientes ejercicios, considera la gráfica de la función $y = f (x)$
que se muestra.
En los siguientes ejercicios, considera la gráfica de la función $y = f (x)$
que se muestra.
¿Cuál de las afirmaciones sobre $y = f (x)$ son verdaderas y cuales son falsas? Explica por qué es falsa.
46. $\mathop {\lim }\limits_{x \to 10} f\left( x \right) = 0$.
47. $\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 3$. (Solución)
48. $\mathop {\lim }\limits_{x \to 8} f\left( x \right) = f\left( { - 8} \right)$.
49. $\mathop {\lim }\limits_{x \to 6} f\left( x \right) = 5$. (Solución)
 En los siguientes ejercicios, usa la siguiente gráfica de la función $y = f (x)$ para encontrar los valores, si es posible. Estimar cuando sea necesario.
En los siguientes ejercicios, usa la siguiente gráfica de la función $y = f (x)$ para encontrar los valores, si es posible. Estimar cuando sea necesario.
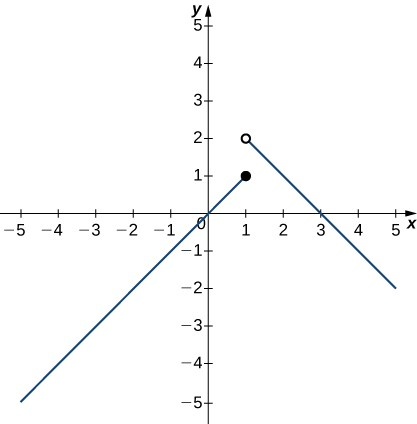
50. $\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)$
51. $\mathop {\lim }\limits_{x \to {1^ +}} f\left( x \right)$ (Solución)
52. $\mathop {\lim }\limits_{x \to {1}} f\left( x \right)$
53. $\mathop {\lim }\limits_{x \to {2}} f\left( x \right)$ (Solución)
54. $f(1)$.
 En los siguientes ejercicios, utiliza la gráfica de la función $y = f (x)$ que
se muestra a continuación para encontrar los valores, si es posible. Estimar cuando sea necesario.
En los siguientes ejercicios, utiliza la gráfica de la función $y = f (x)$ que
se muestra a continuación para encontrar los valores, si es posible. Estimar cuando sea necesario.
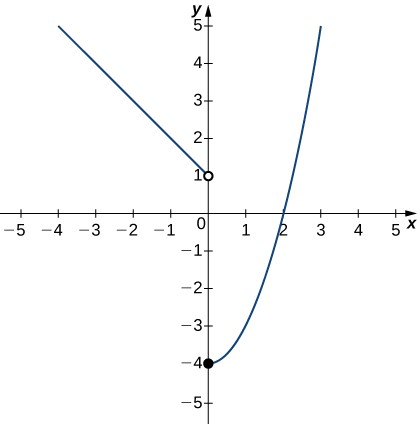
55. $\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right)$ (Solución)
56. $\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right)$
57. $\mathop {\lim }\limits_{x \to {0}} f\left( x \right)$ (Solución)
58. $\mathop {\lim }\limits_{x \to {2 }} f\left( x \right)$
 En los siguientes ejercicios, utiliza la gráfica de la función $y = f (x)$ que se muestra aquí para encontrar los valores, si es posible. Estimar cuando sea necesario.
En los siguientes ejercicios, utiliza la gráfica de la función $y = f (x)$ que se muestra aquí para encontrar los valores, si es posible. Estimar cuando sea necesario.
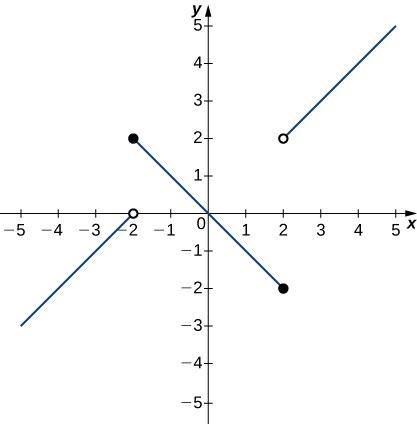
59. $\mathop {\lim }\limits_{x \to -{2^ - }} f\left( x \right)$ (Solución)
60. $\mathop {\lim }\limits_{x \to -{2^ + }} f\left( x \right)$
61. $\mathop {\lim }\limits_{x \to {-2 }} f\left( x \right)$ (Solución)
62. $\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right)$
63. $\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right)$ (Solución)
64. $\mathop {\lim }\limits_{x \to {2}} f\left( x \right)$
 En los siguientes ejercicios, utiliza la gráfica de la función $y = g (x)$
que se muestra a continuación para encontrar los valores, si es posible. Estimar cuando sea necesario.
En los siguientes ejercicios, utiliza la gráfica de la función $y = g (x)$
que se muestra a continuación para encontrar los valores, si es posible. Estimar cuando sea necesario.
65. $\mathop {\lim }\limits_{x \to {0^ - }} g\left( x \right)$ (Solución)
66. $\mathop {\lim }\limits_{x \to {0^ + }} g\left( x \right)$
67. $\mathop {\lim }\limits_{x \to {0 }} g\left( x \right)$ (Solución)
 En los siguientes ejercicios, utiliza la gráfica de la función $y = h (x)$
que se muestra a continuación para encontrar los valores, si es posible. Estimar cuando sea necesario.
En los siguientes ejercicios, utiliza la gráfica de la función $y = h (x)$
que se muestra a continuación para encontrar los valores, si es posible. Estimar cuando sea necesario.
68. $\mathop {\lim }\limits_{x \to {0^ - }} h\left( x \right)$
69. $\mathop {\lim }\limits_{x \to {0^ + }} h\left( x \right)$ (Solución)
70. $\mathop {\lim }\limits_{x \to {0 }} h\left( x \right)$
 En los siguientes ejercicios, utiliza la gráfica de la función $y = f (x)$ que
se muestra a continuación para encontrar los valores, si es posible. Estimar cuando sea necesario.
En los siguientes ejercicios, utiliza la gráfica de la función $y = f (x)$ que
se muestra a continuación para encontrar los valores, si es posible. Estimar cuando sea necesario.

71. $\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right)$ (Solución)
72. $\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right)$
73. $\mathop {\lim }\limits_{x \to {0 }} f\left( x \right)$ (Solución)
74. $\mathop {\lim }\limits_{x \to {1}} f\left( x \right)$
75. $\mathop {\lim }\limits_{x \to {2}} f\left( x \right)$ (Solución)
 En los siguientes ejercicios, esboce la gráfica de una función con las propiedades dadas.
En los siguientes ejercicios, esboce la gráfica de una función con las propiedades dadas.
76. $\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 1\,\,;\,\,\,\mathop {\lim }\limits_{x \to {4^ - }} f\left( x \right) = 3\,\,\,;\,\,\,\mathop {\lim }\limits_{x \to {4^ + }} f\left( x \right) = 6\,\,\,;\,\,f\left( 4 \right)\,\,no\,\,definido\,$
77. $\mathop {\lim }\limits_{x \to -\infty } f\left( x \right) = 0\,\,;\,\,\,\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = - \infty \,\,\,;\,\,\,\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = \infty \,\,\,;\,\,$, $\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right)\,\,;\,\,\,f\left( 0 \right) = 1\,\,\,;\,\,\,\mathop {\lim }\limits_{x \to \infty } f\left( x \right) = - \infty \,\,\,;\,\,$ (Solución)
78. $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2\,\,;\,\,\,\,\mathop {\lim }\limits_{x \to 3} f\left( x \right) = - \infty \,\,\,;\,\,\,\,\,\,\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = \infty $, $\mathop {\lim }\limits_{x \to \infty } f\left( x \right) = 2\,\,;\,\,\,\,f\left( 0 \right) = {{ - 1} \over 3}$
79. $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2\,\,;\,\,\,\mathop {\lim }\limits_{x \to - 2} f\left( x \right) = - \infty \,\,\,;\,\,\,\,\mathop {\lim }\limits_{x \to \infty } f\left( x \right) = 2\,\,\,;\,\,\,f\left( 0 \right) = 0$ (Solución)
80. $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 0\,\,;\,\,\,\mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right) = \infty \,\,\,;\,\,\,\,\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = - \infty $; $f\left( 0 \right) = - 1\,\,;\,\,\,\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = - \infty \,\,\,;\,\,\,\,\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \infty \,;\,\,\,\,\mathop {\lim }\limits_{x \to \infty } f\left( x \right) = 0$
81. Las ondas de choque surgen en muchas aplicaciones físicas, que van desde supernovas hasta ondas de detonación. Aquí se muestra un gráfico de la densidad de una onda de choque con respecto a la distancia, $x$. Estamos interesados principalmente en la ubicación del frente del amortiguador, etiquetado $x_{SF}$ en el diagrama. (Solución)
82. Un entrenador de pista usa una cámara con un obturador rápido para estimar la posición de un corredor con respecto al tiempo. Aquí se da una tabla de los valores de posición del atleta frente al tiempo, donde $x$ es la posición en metros del corredor y $t$ es el tiempo en segundos. ¿Qué es $\mathop {\lim }\limits_{t \to 2} x\left( t \right)$? ¿Qué significa físicamente?
| $t$(segundos) | $x$ (metros) |
| 1.75 | 4.5 |
| 1.95 | 6.1 |
| 1.99 | 6.42 |
| 2.01 | 6.58 |
| 2.05 | 6.9 |
| 2.25 | 8.5 |
Objetivos de aprendizaje
En la sección anterior, evaluamos los límites observando gráficos o construyendo una tabla de valores. En esta sección, establecemos leyes para calcular los límites y aprendemos cómo aplicar estas leyes.
En el Proyecto del estudiante al final de esta sección, tienes la oportunidad de aplicar estas leyes de límites para derivar la fórmula del área de un círculo adaptando un método ideado por el matemático griego Arquímedes.
Comenzamos reafirmando dos resultados de límites útiles de la sección anterior. Estos dos resultados, junto con las leyes de límites, sirven como base para calcular muchos límites.
Las dos primeras leyes de límites se establecieron en dos límites importantes y los repetimos aquí. Estos resultados básicos, junto con las otras leyes de límites, nos permiten evaluar los límites de muchas funciones algebraicas.
 |
2.13 Evaluación de un límite básico |
Evalúa cada uno de los siguientes límites utilizando Resultados del límite básico.

Ahora echamos un vistazo a las leyes de los límites. Las pruebas que sostienen estas reglas se omiten aquí.
Ahora practicamos la aplicación de estas reglas de límites para evaluar un límite.
 |
2.14 Evaluación de un límite mediante leyes de límites |
Utiliza las leyes de límites para evaluar $\mathop {\lim }\limits_{x \to - 2} \left( {4x + 2} \right)$

 |
2.15 Usar leyes de límites repetidamente |
Utiliza las leyes de los límites para evaluar $\mathop {\lim }\limits_{x \to 2} {{2{x^2} - 3x + 1} \over {{x^3} + 4}}$.

 |
Cuestión 2.11 |
Usa las leyes del límite para evaluar $\mathop {\lim }\limits_{x \to 6} \left( {2x - 1} \right)\sqrt {x + 4} $. En cada paso, indica la ley de límites que se aplica.
A estas alturas probablemente hayas notado que, en cada uno de los ejemplos anteriores, se ha dado el caso de que $\mathop {\lim }\limits_{x \to a} f\left( x \right) = f\left( a \right)$. Esto no siempre es cierto, pero es válido para todos los polinomios para cualquier elección de $a$ y para todas las funciones racionales en todos los valores de $a$ para los que esté definida la función racional.
Para ver que este teorema es válido, consideremos el polinomio $p\left( x \right) = {c_n}{x^n} + {c_{n - 1}}{x^{n - 1}} + ... + {c_1}x + {c_0}$ Al aplicar las leyes de la suma, la multiplicació por una constante y la potencia, terminamos con
$$\begin{aligned} \mathop {\lim }\limits_{x \to a} p\left( x \right) & = \mathop {\lim }\limits_{x \to a} \left( {{c_n}{x^n} + {c_{n - 1}}{x^{n - 1}} + ... + {c_1}x + {c_0}} \right)\\ & = {c_n}{\left( {\mathop {\lim }\limits_{x \to a} x} \right)^n} + {c_{n - 1}}{\left( {\mathop {\lim }\limits_{x \to a} x} \right)^{n - 1}} + ... + {c_o}\\ & = {c_n}{a^n} + {c_{n - 1}}{a^{n - 1}} + ... + {c_o}= p\left( a \right) \end{aligned}$$
Ahora se sigue de la ley del cociente, que si $p (x)$ y $q (x)$ son polinomios para los cuales $q (a) \neq 0$, se cumple $$\mathop {\lim }\limits_{x \to a} {{p\left( x \right)} \over {q\left( x \right)}} = {{p\left( a \right)} \over {q\left( a \right)}}$$
 |
2.16 Evaluación de un límite de una función racional |
Evalúa el $\mathop {\lim }\limits_{x \to 3} {{2{x^2} - 3x + 1} \over {x + 4}}$.

 |
Cuestión 2.12 |
Evalúa $\mathop {\lim }\limits_{x \to - 2} \left( {3{x^3} - 2x + 7} \right)$.
Como hemos visto, podemos evaluar fácilmente los límites de los polinomios y los límites de algunas (pero no todas) funciones racionales mediante sustitución directa. Sin embargo, como vimos en la sección introductoria sobre límites, es posible que $\mathop {\lim }\limits_{x \to a} f\left( x \right)$ exista cuando $f (a)$ no esté definido. La siguiente observación nos permite evaluar muchos límites de este tipo:
Para comprender mejor esta idea, consideremos el límite $\mathop {\lim }\limits_{x \to 1} {{{x^2} - 1} \over {x - 1}}$.
La función $$f\left( x \right) = {{{x^2} - 1} \over {x - 1}} = {{\left( {x - 1} \right)\left( {x + 1} \right)} \over {x - 1}}$$ y la función $g (x) = x + 1$ coincide con $f(x)$ para todos los valores de $x \neq 1$.
Los gráficos de estas dos funciones se muestran en la Figura 2.24.
Vemos eso $$\begin{aligned} \mathop {\lim }\limits_{x \to 1} {{{x^2} - 1} \over {x - 1}} & = \mathop {\lim }\limits_{x \to 1} {{\left( {x - 1} \right)\left( {x + 1} \right)} \over {x - 1}} \\ & = \mathop {\lim }\limits_{x \to 1} \left( {x + 1} \right) \\ & = 2 \end{aligned}$$
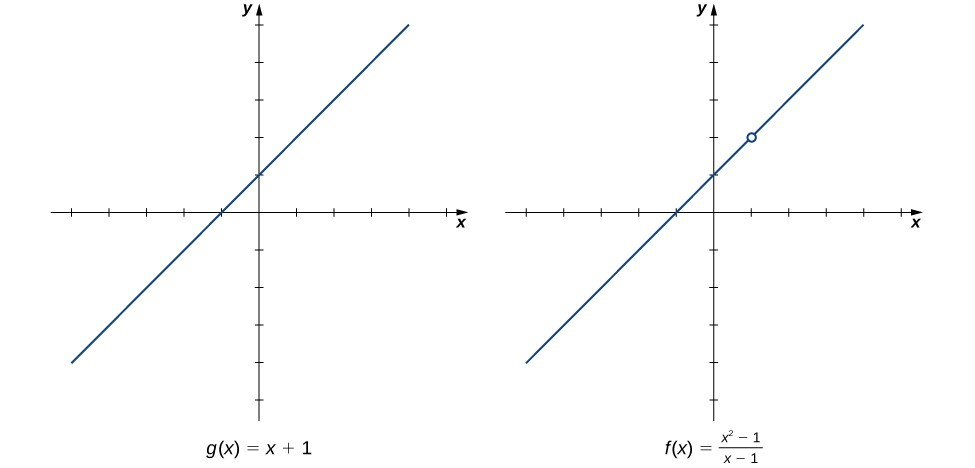
Figura 2.24 Las gráficas de $f (x)$ y $g (x)$ coinciden para todo $x \neq 1$. Sus límites en 1 son iguales.
El límite tiene la forma $\mathop {\lim }\limits_{x \to a} {{f\left( x \right)} \over {g\left( x \right)}}$, donde $\mathop {\lim }\limits_{x \to a} f\left( x \right) = 0$ y $\mathop {\lim }\limits_{x \to a} g\left( x \right) = 0.$ En este caso, decimos que $f (x) / g (x)$ tiene la forma indeterminada $0/0$.
La siguiente estrategia de resolución de problemas proporciona un esquema general para evaluar límites de este tipo.
Los siguientes ejemplos muestran la aplicación de estas estrategias de resolución de problemas: el Ejemplo 2.17 ilustra la técnica de factorización y cancelación; el Ejemplo 2.18 el de la multiplicación por un conjugado y el Ejemplo 2.19, simplificar una fracción compleja.
 |
2.17 Evaluación de un límite factorizando y cancelando |
Evalúa $\mathop {\lim }\limits_{x \to 3} {{{x^2} - 3x} \over {2{x^2} - 5x - 3}}$.

 |
Cuestión 2.13 |
Evalúa $\mathop {\lim }\limits_{x \to - 3} {{{x^2} + 4x + 3} \over {{x^2} - 9}}$.
 |
2.18 Evaluar un límite multiplicando por un conjugado |
Evalúa $\mathop {\lim }\limits_{x \to - 1} {{\sqrt {x + 2} - 1} \over {x + 1}}$.

 |
Cuestión 2.14 |
Evalúa $\mathop {\lim }\limits_{x \to 5} {{\sqrt {x - 1} - 2} \over {x - 5}}$.
 |
2.19 Evaluar un límite simplificando una fracción compleja |
Evalúa $\mathop {\lim }\limits_{x \to 1} {{{1 \over {x + 1}} - {1 \over 2}} \over {x - 1}}$.

 En la siguiente escena interactiva incorporamos un applet que permite aplicar esta estrategia calculando los valores que se consideren y representa la gráfica de la función.
En la siguiente escena interactiva incorporamos un applet que permite aplicar esta estrategia calculando los valores que se consideren y representa la gráfica de la función.
El Ejemplo 2.20 no cae claramente en ninguno de los patrones establecidos en los ejemplos anteriores. Sin embargo, con un poco de creatividad, todavía podemos utilizar estas mismas técnicas.
 |
Cuestión 2.15 |
Evalúa $\mathop {\lim }\limits_{x \to - 3} {{{1 \over {x + 2}} + 1} \over {x + 3}}$.
 |
2.20 Evaluación de un límite cuando las leyes de límites no se aplican |
Evalúa $\mathop {\lim }\limits_{x \to 0} \left( {{1 \over x} + {5 \over {x\left( {x - 5} \right)}}} \right)$.

 |
Cuestión 2.16 |
Evalúa $\mathop {\lim }\limits_{x \to 3} \left( {{1 \over {x - 3}} - {4 \over {{x^2} - 3x - 3}}} \right)$.
Repasemos ahora los límites laterales. Las modificaciones simples en las leyes de límites nos permiten aplicarlas a límites laterales. Por ejemplo, para aplicar las leyes del límite a un límite de la forma $\mathop {\lim }\limits_{x \to {a^ - }} h\left( x \right)$, requerimos que la función $h (x)$ se defina sobre un intervalo abierto de la forma $(b, a)$; para un límite de la forma $\mathop {\lim }\limits_{x \to {a^ + }} h\left( x \right)$, requerimos que la función $h (x)$ se defina sobre un intervalo abierto de la forma $(a, c)$. El Ejemplo 2.21 ilustra este punto.
 |
2.21 Evaluación de un límite lateral utilizando las leyes de límites |
Evalúa cada uno de los siguientes límites, si es posible.

En el Ejemplo 2.22 obtenemos los límites laterales de una función definida por partes y usamos estos límites para sacar una conclusión sobre el límite de la misma función.
 |
2.22 Evaluación de un límite utilizando las leyes de límites |
Para $\begin{cases} 4x-3 & \text{si $x < 2$} \\ (x-3)^2 & \text{si $x \ge 2$} \end{cases} $, evalúa cada uno de los siguientes límites:

 |
Cuestión 2.17 |
Representa $\begin{cases} -x-2 & \text{si $x < -1$} \\ 2 & \text{si $x=-1$} \\ x^3 &\text {si $x\ge 1$} \end{cases} $ y evalúa $\mathop {\lim }\limits_{x \to {{.1}^ - }} f\left( x \right)$.
Ahora enfocamos nuestra atención en evaluar un límite de la forma $\mathop {\lim }\limits_{x \to .a} {{f\left( x \right)} \over {g\left( x \right)}}$, donde $\mathop {\lim }\limits_{x \to .a} f\left( x \right) = \mathop {\lim }\limits_{x \to .a} g\left( x \right) = 0$. Es decir, $f (x) / g (x)$ tiene la forma $K / 0$, con $K \neq 0$ en $a$.
 |
2.23 Evaluación de un límite de la forma $K / 0$, $K \neq 0$ |
Evalúa $\mathop {\lim }\limits_{x \to {{.2}^ - }} {{x - 3} \over {{x^2} - 2x}}$.

 |
Cuestión 2.18 |
Evalúa $\mathop {\lim }\limits_{x \to 1} {{x + 2} \over {{{\left( {x - 1} \right)}^2}}}$.
Las técnicas que hemos desarrollado hasta ahora funcionan muy bien para funciones algebraicas, pero todavía somos incapaces de evaluar los límites de funciones trigonométricas muy básicas. El siguiente teorema, llamado teorema de sandwich, resulta muy útil para establecer límites trigonométricos básicos. Este teorema nos permite calcular límites al “encajar” una función, con un límite en un punto $a$ que es desconocido, entre dos funciones que tienen un límite conocido común en $a$.Figura 2.27 ilustra esta idea.
Figura 2.27 El teorema del sandwich se aplica cuando $f (x) \ge g (x) \ge h (x)$ y $\mathop {\lim }\limits_{x \to a} f\left( x \right) = \mathop {\lim }\limits_{x \to a} h\left( x \right) $.
 |
2.24 Aplicar el teorema de la compresión |
Aplicar el teorema del sandwich para evaluar $\mathop {\lim }\limits_{x \to 0} x\cos \left( x \right)$.

 |
Cuestión 2.19 |
Utiliza el teorema del sandwich para evaluar $\mathop {\lim }\limits_{x \to 0} {x^2}sen\left( {{1 \over x}} \right)$.
Ahora usamos el teorema del sandwich para abordar varios límites muy importantes. Aunque esta discusión es algo extensa, estos límites resultan muy importantes para el desarrollo del material tanto en la siguiente sección como en el próximo capítulo. El primero de estos límites es $\mathop {\lim }\limits_{\theta \to 0} sen\theta $. Consideremos el círculo unitario que se muestra en la Figura 2.29.
En esta figura, vemos que $sen\theta$ es la coordenada $y$ en el círculo unitario y corresponde al segmento de la figura que se muestra en azul. La medida en radianes del ángulo $\theta$ es la longitud del arco que abarca en el círculo unitario. Por tanto, vemos que para $0 < \theta < \frac{\pi}{2}$, se cumple $0 < sen\theta < \theta$.
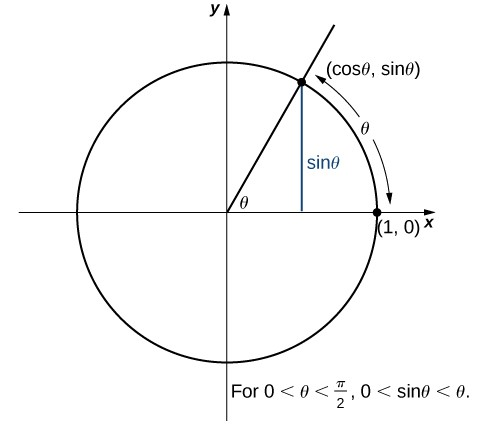
Figura 2.29 El seno se muestra como el segmento azul considerando el círculo unitario.
Dado que $\mathop {\lim }\limits_{\theta \to {0^ + }} 0 = 0$ y $\mathop {\lim }\limits_{\theta \to {0^ + }} \theta = 0$, utilizando el teorema del sandwich concluimos que $$\mathop {\lim }\limits_{\theta \to {0^ + }} sen\theta = 0$$
Para ver que $\mathop {\lim }\limits_{\theta \to {0^ - }} sen\theta = 0$ también, observamos que para $\frac{−\pi}{2} < \theta < 0$, $0 <−\theta < \frac{\pi}{2}$ y por lo tanto, $0 <sin (−\theta) < - \theta$.
En consecuencia, $0 <−sen\theta <−\theta$. De ello se deduce que $0 > sin\theta > \theta$. Una aplicación del teorema del sandwich produce el límite deseado. Por lo tanto, como $\mathop {\lim }\limits_{\theta \to {0^ + }} sen\theta = 0$ y $\mathop {\lim }\limits_{\theta \to {0^ - }} sen\theta = 0$, $$\mathop {\lim }\limits_{\theta \to {0}} sen\theta = 0 \tag{$2.16$}$$ Luego, usando la identidad $\cos \theta = \sqrt {1 - se{n^2}\theta } $ para $\frac{−\pi}{2} < \theta < \frac{\pi}{2}$, vemos que $$\mathop {\lim }\limits_{\theta \to 0} \cos \theta = \mathop {\lim }\limits_{\theta \to 0} \sqrt {1 - se{n^2}\theta } = 1 \tag{$2.17$}$$
Ahora echamos un vistazo a un límite que juega un papel importante en capítulos posteriores, se trata de $\mathop {\lim }\limits_{\theta \to 0} {{sen\theta } \over \theta }$. Para evaluar este límite, usamos el círculo unitario en la Figura 2.30. Observamos que esta figura agrega un triángulo adicional a la Figura 2.30. Vemos que la longitud del lado opuesto al ángulo $\theta$ en este nuevo triángulo es $tan\theta$. Así, vemos que para $0 < \theta < \frac{\pi}{2}$, se cumple $sen\theta <\theta < tan\theta$.
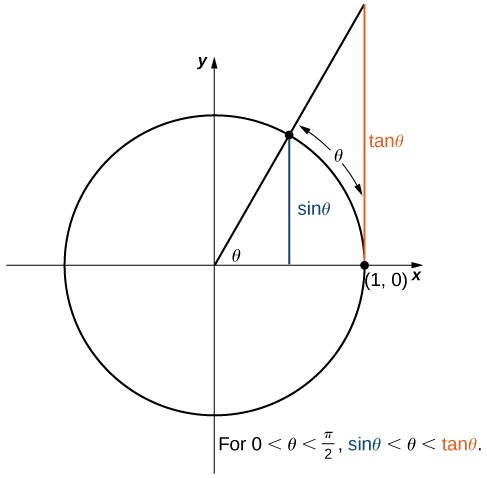
Figura 2.30 Tanto el seno como la tangente se muestran como segmentos en el círculo unitario.
Dividiendo por $sen\theta$ en todas los miembros de la desigualdad, obtenemos $$1 < {\theta \over {sen\theta }} < {1 \over {\cos \theta }}$$ De manera equivalente, tenemos $$1 > {{sen\theta } \over \theta } > \cos \theta $$ Dado que $\mathop {\lim }\limits_{\theta \to {0^ + }} 1 = 1 = \mathop {\lim }\limits_{\theta \to {0^ + }} \cos \theta $, concluimos que $\mathop {\lim }\limits_{\theta \to {0^ + }} {{sen\theta } \over \theta } = 1$. Al aplicar una manipulación similar a la utilizada, podemos demostrar que $$\mathop {\lim }\limits_{\theta \to {0^ - }} {{sen\theta } \over \theta } = 1$$ Así, $$\mathop {\lim }\limits_{\theta \to {0 }} {{sen\theta } \over \theta } = 1 \tag{$2.18$}$$
En el Ejemplo 2.25 usamos este límite para establecer $\mathop {\lim }\limits_{\theta \to 0} {{1 - \cos \theta } \over \theta } = 0.$ Este límite también resulta útil en capítulos posteriores.
 |
2.25 Evaluación de un límite trigonométrico importante |
Evalúa $\mathop {\lim }\limits_{\theta \to 0} {{1 - \cos \theta } \over \theta } = 0$.

 |
Cuestión 2.20 |
Evalúa $\mathop {\lim }\limits_{\theta \to 0} {{1 - \cos \theta } \over {sen\theta }}$.
Derivar la fórmula para el área de un círculo
Algunas de las fórmulas geométricas que damos por sentadas hoy en día se obtuvieron primero mediante métodos que anticipan algunos de los métodos de cálculo. El matemático griego Arquímedes (287-212 a. C.) fue particularmente inventivo, y utilizó polígonos inscritos dentro de círculos para aproximar el área del círculo a medida que aumentaba el número de lados del polígono. Nunca se le ocurrió la idea de un límite, pero podemos usar esta idea para ver qué podrían haber predicho sus construcciones geométricas sobre el límite.
Podemos estimar el área de un círculo calculando el área de un polígono regular inscrito. Piensa en el polígono regular como si estuviera formado por $n$ triángulos. Al tomar el límite cuando el ángulo del vértice de estos triángulos llega a cero, puede obtener el área del círculo.
Para ver esto, sigue los siguientes pasos:
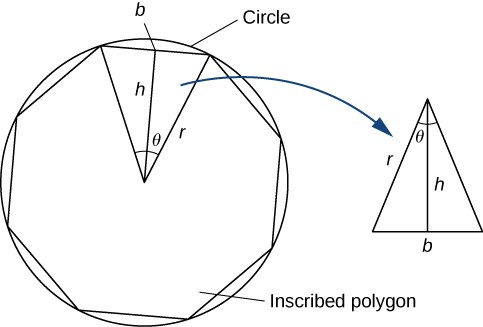
Figura 2.31 .
La técnica de estimar áreas de regiones utilizando polígonos se revisa en el apartado de introducción a la integración.
 En los siguientes ejercicios, utiliza las leyes de límites para evaluar cada límite. Justifica cada paso indicando las leyes de límite apropiadas.
En los siguientes ejercicios, utiliza las leyes de límites para evaluar cada límite. Justifica cada paso indicando las leyes de límite apropiadas.
83. $\mathop {\lim }\limits_{x \to 0} \left( {4{x^2} - 2x + 3} \right)$ (Solución)
84. $\mathop {\lim }\limits_{x \to 1} {{{x^3} + 3{x^2} + 5} \over {4 - 7x}}$
85. $\mathop {\lim }\limits_{x \to - 2} \sqrt {{x^2} - 6x + 3} $ (Solución)
86. $\mathop {\lim }\limits_{x \to - 1} {\left( {9x + 1} \right)^2}$
 En los siguientes ejercicios, utiliza la sustitución directa para evaluar cada límite.
En los siguientes ejercicios, utiliza la sustitución directa para evaluar cada límite.
87. $\mathop {\lim }\limits_{x \to 7} {x^2}$ (Solución)
88. $\mathop {\lim }\limits_{x \to - 2} \left( {4{x^2} - 1} \right)$
89. $\mathop {\lim }\limits_{x \to 0} {1 \over {1 + senx}}$ (Solución)
90. $\mathop {\lim }\limits_{x \to 2} {e^{2x - {x^2}}}$
91. $\mathop {\lim }\limits_{x \to 1} {{2 - 7x} \over {x + 6}}$ (Solución)
92. $\mathop {\lim }\limits_{x \to 3} \ln {e^{3x}}$
 En los siguientes ejercicios, utiliza la sustitución directa para mostrar que cada límite conduce a la forma indeterminada $0/0$. Luego, evalúa el límite.
En los siguientes ejercicios, utiliza la sustitución directa para mostrar que cada límite conduce a la forma indeterminada $0/0$. Luego, evalúa el límite.
93. $\mathop {\lim }\limits_{x \to 4} {{{x^2} - 16} \over {x - 4}}$ (Solución)
94. $\mathop {\lim }\limits_{x \to 2} {{x - 2} \over {{x^2} - 2x}}$
95. $\mathop {\lim }\limits_{x \to 6} {{3x - 18} \over {2x - 12}}$ (Solución)
96. $\mathop {\lim }\limits_{h \to 0} {{{{\left( {1 + h} \right)}^2} - 1} \over h}$
97. $\mathop {\lim }\limits_{t \to 9} {{t - 9} \over {\sqrt t - 3}}$ (Solución)
98. $\mathop {\lim }\limits_{h \to 0} {{{1 \over {a + h}} - {1 \over a}} \over h}$ donde $a$ es una constante de valor real distinta de cero.
99. $\mathop {\lim }\limits_{\theta \to \pi } {{sen\theta } \over {\tan \theta }}$ (Solución)
100. $\mathop {\lim }\limits_{x \to 1} {{{x^3} - 1} \over {{x^2} - 1}}$
101. $\mathop {\lim }\limits_{x \to 1/2} {{2{x^2} + 3x - 2} \over {2x - 1}}$ (Solución)
102. $\mathop {\lim }\limits_{x \to - 3} {{\sqrt {x + 4} - 1} \over {x + 3}}$
 En los siguientes ejercicios, utiliza la sustitución directa para obtener una expresión indeterminada. Luego, usa el método del Ejemplo 2.23 para simplificar la función para ayudar a determinar el límite.
En los siguientes ejercicios, utiliza la sustitución directa para obtener una expresión indeterminada. Luego, usa el método del Ejemplo 2.23 para simplificar la función para ayudar a determinar el límite.
103. $\mathop {\lim }\limits_{x \to - {2^ - }} {{2{x^2} + 7x - 4} \over {{x^2} + x - 2}}$ (Solución)
104. $\mathop {\lim }\limits_{x \to - {2^ + }} {{2{x^2} + 7x - 4} \over {{x^2} + x - 2}}$
105. $\mathop {\lim }\limits_{x \to {1^ - }} {{2{x^2} + 7x - 4} \over {{x^2} + x - 2}}$ (Solución)
106. $\mathop {\lim }\limits_{x \to {1^ + }} {{2{x^2} + 7x - 4} \over {{x^2} + x - 2}}$
 En los siguientes ejercicios, supón que $\mathop {\lim }\limits_{x \to 6} f\left( x \right) = 4$, $\mathop {\lim }\limits_{x \to 6} g\left( x \right) = 9$,
y $\mathop {\lim }\limits_{x \to 6} h\left( x \right) = 6$.
Utiliza estos tres hechos y las leyes de límites para evaluar cada límite.
En los siguientes ejercicios, supón que $\mathop {\lim }\limits_{x \to 6} f\left( x \right) = 4$, $\mathop {\lim }\limits_{x \to 6} g\left( x \right) = 9$,
y $\mathop {\lim }\limits_{x \to 6} h\left( x \right) = 6$.
Utiliza estos tres hechos y las leyes de límites para evaluar cada límite.
107. $\mathop {\lim }\limits_{x \to 6} 2f\left( x \right)g\left( x \right)$ (Solución)
108. $\mathop {\lim }\limits_{x \to 6} {{g\left( x \right) - 1} \over {f\left( x \right)}}$
109. $\mathop {\lim }\limits_{x \to 6} \left( {f\left( x \right) + {1 \over 3}g\left( x \right)} \right)$ (Solución)
110. $\mathop {\lim }\limits_{x \to 6} {{{{\left[ {h\left( x \right)} \right]}^3}} \over 2}$
111. $\mathop {\lim }\limits_{x \to 6} \sqrt {g\left( x \right) - f\left( x \right)} $ (Solución)
112. $\mathop {\lim }\limits_{x \to 6} x \cdot h\left( x \right)$
113. $\mathop {\lim }\limits_{x \to 6} \left( {x + 1} \right) \cdot f\left( x \right)$ (Solución)
114. $\mathop {\lim }\limits_{x \to 6} \left[ {f\left( x \right) \cdot g\left( x \right) - h\left( x \right)} \right]$
 [T] En los siguientes ejercicios, usa una calculadora para dibujar el gráfico de cada función definida por partes y estudie el gráfico para evaluar los límites dados.
[T] En los siguientes ejercicios, usa una calculadora para dibujar el gráfico de cada función definida por partes y estudie el gráfico para evaluar los límites dados.
115. $f(x)=\begin{cases} x^2 & \text{si $x \le 3$} \\ x+4 & \text{si $x > 3$} \end{cases} $
116. $g(x)=\begin{cases} x^3-1 & \text{si $x \le 0$} \\ x+4 & \text{si $x > 0$} \end{cases} $
117. $h(x)=\begin{cases} x^2-2x+1 & \text{si $x < 2$} \\ 3-x & \text{si $x \ge 2$} \end{cases} $
 En los siguientes ejercicios, utiliza los siguientes gráficos y las leyes de límites para evaluar cada límite.
En los siguientes ejercicios, utiliza los siguientes gráficos y las leyes de límites para evaluar cada límite.
118. $$\mathop {\lim }\limits_{x \to - {3^ + }} \left( {f\left( x \right) + g\left( x \right)} \right)$$
119. $\mathop {\lim }\limits_{x \to - {3^ - }} \left( {f\left( x \right) - 3g\left( x \right)} \right)$ (Solución)
120. $\mathop {\lim }\limits_{x \to 0} {{f\left( x \right)g\left( x \right)} \over 3}$
121. $\mathop {\lim }\limits_{x \to -5 } {{2 + g\left( x \right)} \over {f\left( x \right)}}$ (Solución)
122. $\mathop {\lim }\limits_{x \to 1} {\left[ {f\left( x \right)} \right]^2}$
123. $\mathop {\lim }\limits_{x \to 1} \sqrt[3] {f\left( x \right) - g\left( x \right)} $ (Solución)
124. $\mathop {\lim }\limits_{x \to - 7} \left( {x \cdot g\left( x \right)} \right)$
125. $\mathop {\lim }\limits_{x \to - 9} \left( {x \cdot f\left( x \right) + 2 \cdot g\left( x \right)} \right)$ (Solución)
126. [T] ¿Verdadero o falso? Si $2x − 1 \le g (x) \le x^2−2x + 3$, entonces $\mathop {\lim }\limits_{x \to 2} g\left( x \right) = 0$.
 Para los siguientes problemas, evalúa el límite utilizando el teorema del sandwich. Usa una calculadora para representar gráficamente las funciones $f (x)$, $g (x)$,
y $h (x)$ cuando sea posible.
Para los siguientes problemas, evalúa el límite utilizando el teorema del sandwich. Usa una calculadora para representar gráficamente las funciones $f (x)$, $g (x)$,
y $h (x)$ cuando sea posible.
127. [T] $\mathop {\lim }\limits_{\theta \to 0} {\theta ^2}\cos \left( {{1 \over \theta }} \right)$ (Solución)
128. $\mathop {\lim }\limits_{x \to 0} f\left( x \right)$, donde $f(x)=\begin{cases} 0 & \text{si $x$ es racional} \\ x^2 & \text{si $x$ es irracional} \end{cases} $
129. [T] En física, la magnitud de un campo eléctrico generado por una carga puntual a una distancia $r$ en el vacío se rige por la ley de Coulomb:
$$E (r) = \frac{q}{4 \pi \epsilon r^2}$$ donde $E$ representa la magnitud del campo eléctrico, $q$ es la carga de la partícula, $r$ es la distancia entre la partícula y donde se mide la fuerza del campo, y $\frac{1}{4 \pi \epsilon_0}$ es la constante de Coulomb: $8.988 x 10^9N \cdot m^2/C^2$. (Solución)
130. [T] La densidad de un objeto está dada por su masa dividida por su volumen: $\rho = m / V$.
Objetivos de aprendizaje
Muchas funciones tienen la propiedad de que sus gráficas se pueden trazar con un lápiz sin levantar el lápiz de la página. Estas funciones se denominan continuas aunque esta la definición formal de este término no significa exactamente esto.
 En la siguiente escena interactiva se representa la idea intuitiva de continuidad aunque hay funciones continuas para las cuales esto no ocurre.
En la siguiente escena interactiva se representa la idea intuitiva de continuidad aunque hay funciones continuas para las cuales esto no ocurre.
Nota: Hay funciones continuas en las que esta idea intuitiva no es correcta como por ejemplo la función siguiente que es continua en el origen y, sin embargo, no se puede representar su gráfica.$$f(x)=\begin{cases} 0 & \text{si $x$ es racional} \\ x^2 & \text{si $x$ es irracional} \end{cases} $$
Otras funciones tienen puntos en los que se produce una ruptura en el gráfico, pero satisfacen esta propiedad en los intervalos contenidos en sus dominios. Son continuas en estos intervalos y se dice que tienen una discontinuidad en un punto donde ocurre una ruptura.
Comenzamos nuestra investigación de la continuidad explorando lo que significa que una función tenga continuidad en un punto. Intuitivamente, una función es continua en un punto particular si no hay una ruptura en su gráfico en ese punto.
Antes de ver una definición formal de lo que significa que una función sea continua en un punto, consideremos varias funciones que no cumplen con nuestra noción intuitiva de lo que significa ser continua en un punto. Luego creamos una lista de condiciones que previenen tales fallas.
Nuestra primera función de interés se muestra en la Figura 2.32. Vemos que la gráfica de $f (x)$ tiene un "agujero" en $a$. De hecho, $f (a)$ no está definida. Como mínimo, para que $f (x)$ sea continua en $a$, necesitamos la siguiente condición: $$\text{i. $f(a)$ debe estar definida}$$
Figura 2.32 La función $f (x)$ no es continua en $a$ porque $f (a)$ no está definida.
Sin embargo, como vemos en la Figura 2.33, esta condición por sí sola es insuficiente para garantizar la continuidad en el punto $a$. Aunque $f (a)$ está definida, la función tiene un salto en a. En este ejemplo, la brecha existe porque no existe $\mathop {\lim }\limits_{x \to a} f\left( x \right)$. Debemos agregar otra condición para la continuidad en $a$, a saber, $$\text{ii. debe existir $\mathop {\lim }\limits_{x \to a} f\left( x \right)$}$$
Figura 2.33 La función $f (x)$ no es continua en $a$ porque $\mathop {\lim }\limits_{x \to a} f\left( x \right)$ no existe.
Sin embargo, como vemos en la Figura 2.34, estas dos condiciones por sí mismas no garantizan la continuidad en un punto. La función en esta figura satisface nuestras dos primeras condiciones, pero aún no es continua en $a$. Debemos agregar una tercera condición a nuestra lista: $$\text{iii. $\mathop {\lim }\limits_{x \to a} f\left( x \right) = f\left( a \right)$}$$
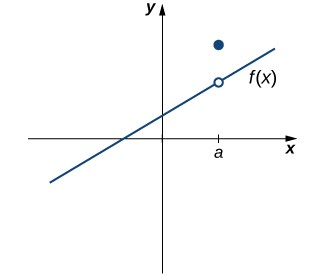
Figura 2.34 La función $f (x)$ no es continua en $a$ porque $\mathop {\lim }\limits_{x \to a} f\left( x \right) \ne f\left( a \right)$.
Ahora juntamos nuestra lista de condiciones y formamos una definición de continuidad en un punto.
El siguiente procedimiento se puede utilizar para analizar la continuidad de una función en un punto utilizando esta definición.
Los siguientes tres ejemplos demuestran cómo aplicar la definición para determinar si una función es continua en un punto dado. Estos ejemplos ilustran situaciones en las que cada una de las condiciones para la continuidad en la definición puede o no cumplirse.
 |
2.26 Determinación de la continuidad en un punto, condición 1 |
Usando la definición, determina si la función $$f\left( x \right) = {{{x^2} - 4} \over {x - 2}}$ es continua en $x = 2$$ Justifica la conclusión.

 |
2.27 Determinación de la continuidad en un punto, condición 2 |
Usando la definición, determina si la función $f(x)=\begin{cases} -x^2+4 & \text{si $x \le 3$} \\ 4x-8 & \text{si $x < 3$} \end{cases} $ es continua en $x = 3$. Justifica la conclusión.

 |
2.28 Determinación de la continuidad en un punto, condición 3 |
Usando la definición, determina si la función $f(x)=\begin{cases} \frac{senx}{x} & \text{si $x \ne 0$} \\ 1 & \text{si $x =0$} \end{cases} $, es continua en $x = 0$.

 |
Cuestión 2.21 |
Usando la definición, determina si la función $$f(x)=\begin{cases} 2x+1 & \text{si $x < 1$} \\ 2 & \text{si $x =1$} \\ -x+4 & \text{si $x > 1$ } \end{cases} $$ es continua en $x = 1$. Si la función no es continua en 1, indica la condición de continuidad en un punto que no se verifica.
Aplicando la definición de continuidad y teoremas previamente establecidos sobre la evaluación de límites, podemos enunciar el siguiente teorema.
Prueba
Anteriormente, mostramos que si $p (x)$ y $q (x)$ son polinomios, $\mathop {\lim }\limits_{x \to a} p\left( x \right) = p\left( a \right)$ para cada polinomio $p (x)$ y $\mathop {\lim }\limits_{x \to a} \frac {p\left( x \right)} {q\left( x \right)}= \frac {p\left( a \right)} {q\left( a \right)}$ siempre que $q (a) \ne 0$.
Por tanto, los polinomios y las funciones racionales son continuas en su dominio.
Ahora aplicamos la continuidad de polinomios y funciones racionales para determinar los puntos en los que una función racional dada es continua.
 |
2.29 Continuidad de una función racional |
¿Para qué valores de $x$ es $f\left( x \right) = {{x + 1} \over {x -5 }}$ continua?

 |
Cuestión 2.22 |
¿Para qué valores de $x$ es $f (x) = 3x^4−4x^2$ continua?
Como hemos visto en el Ejemplo 2.26 y en el Ejemplo 2.27, las discontinuidades pueden ocurrir en distintas situaciones. Clasificamos los tipos de discontinuidades que hemos visto hasta ahora como discontinuidades removibles o evitables, discontinuidades infinitas o discontinuidades de salto.
Intuitivamente, una discontinuidad removible es una discontinuidad para la cual hay un "agujero" en el gráfico, una discontinuidad de salto es una discontinuidad no infinita para la cual las secciones a ambos lados de la función no se encuentran, y una discontinuidad infinita es una discontinuidad ubicada en una asíntota vertical.
La Figura 2.37 ilustra las diferencias en este tipo de discontinuidades. Aunque estos términos brindan una forma práctica de describir tres tipos comunes de discontinuidades, tenga en cuenta que no todas las discontinuidades encajan perfectamente en estas categorías.
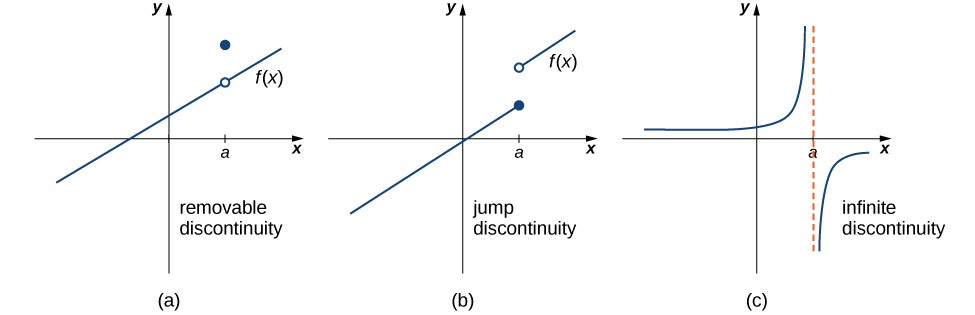
Figura 2.37 Las discontinuidades se clasifican en (a) removibles, (b) saltos o (c) infinitas.
Estas tres discontinuidades se definen formalmente de la siguiente manera:
Nota: cuando establecemos que $\mathop {\lim }\limits_{x \to {a^ - }} $ y $\mathop {\lim }\limits_{x \to {a^ + }} $ ambos existen, queremos decir que ambos son números reales y que ninguno toma los valores $ \pm \infty $.
 |
2.30 Clasificación de una discontinuidad |
En el Ejemplo 2.26, mostramos que $$f (x) =\frac{ x^2−4}{x − 2}$$ es discontinua en $x = 2$. Clasifica esta discontinuidad como removible, salto o infinito.

 |
2.31 Clasificación de una discontinuidad |
En el Ejemplo 2.27, mostramos que $$f(x)=\begin{cases} -x^2+4 & \text{si $x \le 3$} \\ 4x-8 & \text{si $x < 3$} \end{cases} $$ es discontinua en $x = 3$. Clasifica esta discontinuidad como removible, salto o infinito.

 |
2.32 Clasificación de una discontinuidad |
Determina si $f (x) = \frac{x + 2}{x + 1}$ es continua en -1. Si la función es discontinua en −1, clasifica la discontinuidad como removible, salto o infinita.

 |
Cuestión 2.23 |
Se considera la función
determina si $f$ es continua en 1. Si no lo fuera, clasifica la discontinuidad como removible, salto o infinita.
Ahora que hemos explorado el concepto de continuidad en un punto, ampliamos esa idea a la continuidad en un intervalo. A medida que desarrollamos esta idea para diferentes tipos de intervalos, puede ser útil tener en cuenta la idea intuitiva de que una función es continua en un intervalo si podemos usar un lápiz para trazar la función entre dos puntos cualesquiera en el intervalo sin levantar el lápiz del papel. En preparación para definir la continuidad en un intervalo, comenzamos mirando la definición de lo que significa que una función sea continua por la derecha en un punto y continua por la izquierda en un punto.
Una función es continua en un intervalo abierto si es continua en todos los puntos del intervalo. Una función $f (x)$ es continua en un intervalo cerrado de la forma $[a, b]$ si es continua en cada punto en $(a, b)$ y es continua a la derecha en $a$ y es continua a la izquierda en $b$.
De manera análoga, una función $f (x)$ es continua en un intervalo de la forma $(a, b]$ si es continua en $(a, b)$ y es continua por la izquierda en $b$. La continuidad sobre otros tipos de intervalos se define de manera similar.
Requeriendo que $\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right)$ y $\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right)$ se asegura que podemos trazar la gráfica de la función desde el punto $(a, f (a))$ hasta el punto $(b, f (b))$ sin levantar el lápiz . Si, por ejemplo, $\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) \ne f\left( a \right)$, necesitaríamos levantar nuestro lápiz para saltar de $f (a)$ a la gráfica del resto de la función sobre $(a, b]$.
 |
2.33 Continuidad en un intervalo |
Determina si $$f (x) =\frac{x-1}{x^2+2x}$$ es continua.

 |
2.34 Continuidad en un intervalo |
Indica el intervalo o intervalos en los que la función $f (x) =\sqrt{4-x^2}$ es continua.

 |
Cuestión 2.24 |
Indica los intervalos en los que la función $f (x) = \sqrt{x+3}$ es continua.
El teorema de la función compuesta nos permite ampliar nuestra capacidad para calcular límites. En particular, este teorema permitirá demostrar que las funciones trigonométricas son continuas en sus dominios.
Antes de pasar al Ejemplo 2.35, recuerda que en la sección de leyes de límites, mostramos $\mathop {\lim }\limits_{x \to 0} \cos x = 1 = \cos 0$. En consecuencia, sabemos que $f (x) = cosx$ es continua en 0. En el Ejemplo 2.35 vamos ver cómo combinar este resultado con el teorema de la función compuesta.
 |
2.35 Límite de una función coseno compuesta |
Evalúa $\mathop {\lim }\limits_{x \to \pi /2} \cos \left( {x - {\pi \over 2}} \right)$.

 |
Cuestión 2.25 |
Evalúa $\mathop {\lim }\limits_{x \to \pi } sen\left( {x - \pi } \right)$.
La demostración del siguiente resultado usa el teorema de la función compuesta, así como la continuidad de $f (x) = senx$ y $g (x) = cosx$ en el punto 0 para mostrar que las funciones trigonométricas son continuas en todos sus dominios.
Prueba
Comenzamos demostrando que $cosx$ es continua en cada número real. Para hacer esto, debemos mostrar que $\mathop {\lim }\limits_{x \to a} \cos x = \cos a$ para todos los valores de $a$. $$\begin{aligned} \mathop {\lim }\limits_{x \to a} \cos x &= \mathop {\lim }\limits_{x \to a} \cos \left( {\left( {x + a} \right) - a} \right) &\text{(1)}\\ &= \mathop {\lim }\limits_{x \to a} \left( {\cos \left( {x - a} \right)\cos a - sen\left( {x - a} \right)sena} \right) &\text{(2)} \\ &=\cos \left( {\mathop {\lim }\limits_{x \to a} \left( {x - a} \right)} \right)\cos a - sen\left( {\mathop {\lim }\limits_{x \to a} \left( {x - a} \right)} \right)sena &\text{(3)} \\ &=\cos \left( 0 \right)\cos a - sen\left( 0 \right)sena &\text{(4)}\\ &=1 \cdot \cos a - 0 \cdot sena = \cos a \end{aligned}$$ $$\begin{aligned} (1) & \text{escribimos $x=x-a+a$}\\ (2) &\text{aplicamos la expresión del coseno de una suma} \\ (3) &\text{aplicamos que las funciones seno y coseno son continuas en el punto 0} \\ (4) &\text{evaluamos cos(0) y sen(0)}\\ \end{aligned}$$
La prueba de que $senx$ es una función continua en cada número real $a$ es análoga. Debido a que las funciones trigonométricas restantes pueden expresarse en términos de $senx$ y $cosx$, su continuidad se sigue de la ley del límite del cociente.
Como puedes ver, el teorema de la función compuesta permite demostrar la continuidad de las funciones trigonométricas.
Las funciones que son continuas en intervalos de la forma $[a, b]$, donde $a$ y $b$ son números reales, poseen muchas propiedades útiles. A lo largo de nuestro estudio del cálculo, encontraremos muchos teoremas relacionados con tales funciones. El primero de estos teoremas es el Teorema del valor intermedio.
Figura 2.38 Hay un número $c\in (a, b)$ que satisface $f (c) = z$.
 |
2.36 Aplicación del teorema del valor intermedio |
Demuestre que $f (x) = x − cosx$ tiene al menos un cero.

 En la siguiente escena interactiva del Proyecto Descartes puedes ver cómo la aplicación del resultado varias veces permite encontrar los ceros de una función mediante lo que se conoce como el método de la bisección.
En la siguiente escena interactiva del Proyecto Descartes puedes ver cómo la aplicación del resultado varias veces permite encontrar los ceros de una función mediante lo que se conoce como el método de la bisección.
 |
2.37 ¿Cuándo se puede aplicar el teorema del valor intermedio? |
Si $f (x)$ es continua sobre $[0,2]$, $f (0) > 0$ y $f (2)> 0$, ¿podemos usar el teorema del valor intermedio para concluir que $f (x)$ no tiene ceros en el intervalo $[0,2]$? Justifica la respuesta.

 |
2.38 ¿Cuándo se puede aplicar el teorema del valor intermedio? |
Para $f (x) = 1 / x$, $f (−1) = - 1 <0$ y $f (1) = 1> 0$. ¿Podemos concluir que $f (x)$ tiene cero en el intervalo $[−1,1]$?

 |
Cuestión 2.26 |
Demuestra que $f (x) = x^3 − x^2−3x + 1$ tiene un cero en el intervalo $[0,1]$.
 Para los siguientes ejercicios, determina los puntos, si los hay, en los que cada función es discontinua. Clasifica cualquier discontinuidad como salto, removible, infinito u otro.
Para los siguientes ejercicios, determina los puntos, si los hay, en los que cada función es discontinua. Clasifica cualquier discontinuidad como salto, removible, infinito u otro.
131. $f\left( x \right) = {1 \over {\sqrt x }}$ (Solución)
132. $f\left( x \right) = {2 \over {{x^2} + 1}}$
133. $f\left( x \right) = {x \over {{x^2} - x}}$ (Solución)
134. $g(t) =t^{−1}+1$
135. $f\left( x \right) = {5 \over {{e^x} - 2}}$ (Solución)
136. $f\left( x \right) = {{\left| {x - 2} \right|} \over {x - 2}}$
137. $h(x) = tan2x$ (Solución)
138. $f\left( t \right) = {{t + 3} \over {{t^2} + 5t + 6}}$
 Para los siguientes ejercicios, decide si la función es continua en el punto dado. Si es discontinuo, determina qué tipo de discontinuidad tiene.
Para los siguientes ejercicios, decide si la función es continua en el punto dado. Si es discontinuo, determina qué tipo de discontinuidad tiene.
139. $f\left( x \right) = {{2{x^2} - 5x + 3} \over {x - 1}}$ en $x = 1$ (Solución)
140. $h\left( \theta \right) = {{sen\theta - \cos \theta } \over {tg\theta }}$ en $\theta = \pi$
141. $g(u)=\begin{cases} \frac{6u^2+u-2}{2u-1} & \text{si $x \ne \frac{1}{2}$} \\ \frac{7}{2} & \text{si $u = \frac{1}{2}$} \end{cases} $ en $u = \frac{1}{2}$ (Solución)
142. $f\left( y \right) = {{sen\left( {\pi y} \right)} \over {tg\left( {\pi y} \right)}}$ en $y = 1$
143. $f(x)=\begin{cases} x^2-e^x & \text{si $x < 0$} \\ x-1 & \text{si $x \ge 0$} \end{cases} $ en $x = 0$ (Solución)
144. $f(x)=\begin{cases} xsenx & \text{si $x < /pi$} \\ x-1 & \text{si $x \ge 0$} \end{cases} $ en $x = \pi$
 En los siguientes ejercicios, encuentra los valores de $k$ que hacen que cada función sea continua en el intervalo dado.
En los siguientes ejercicios, encuentra los valores de $k$ que hacen que cada función sea continua en el intervalo dado.
145. $f(x)=\begin{cases} 3x+2 & \text{si $x < k$} \\ 2x-3 & \text{si $k \ge x \ge 8$} \end{cases} $ (Solución)
146. $f(\theta)=\begin{cases} sen\theta & \text{si $x \ge\theta; \ge \frac{\pi}{2}$} \\ cos(\theta+k) & \text{si $frac{pi}{2} \ge \theta \ge \phi$} \end{cases} $
147. $f(x)=\begin{cases} \frac{x^2+3x+2}{x+2} & \text{si $x \ne -2$} \\ k & \text{si $x=-2$} \end{cases} $ (Solución)
148. $f(x)=\begin{cases} e^{kx} & \text{si $0 \le x < 4$} \\ x+3 & \text{si $4 \le x \le 8$} \end{cases} $
149. $f(x)=\begin{cases} \sqrt{kx} & \text{si $0 \le x \le 3$} \\ x+1 & \text{si $3 < x \le 10$} \end{cases} $ (Solución)
 En los siguientes ejercicios, usa el Teorema del valor intermedio (TVI).
En los siguientes ejercicios, usa el Teorema del valor intermedio (TVI).
150. Sea $h(x)=\begin{cases} 3x^2-4 & \text{si $x \le 2$} \\ +4x & \text{si $x < 2$} \end{cases} $ en el intervalo $[0,4]$, no hay un valor de $x$ tal que $h (x) = 10$, aunque $h (0) $lt; 10$ y $h (4)> 10$. Explica por qué esto no contradice el TVI.
151. Una partícula que se mueve a lo largo de una recta tiene en cada momento una función de posición $s (t)$ que es continua. Supongamos que $s (2) = 5$ y $s (5) = 2$. Otra partícula se mueve de manera que su posición está dada por $h (t) = s (t) −t$. Explica por qué debe haber un valor $c$ para $2 < c < 5$ tal que $h (c) = 0$. (Solución)
152. [T] Utiliza el enunciado "El coseno de $t$ es igual a $t$ al cubo".
153. Aplica el TVI para determinar si $2x = x^3$ tiene una solución en uno de los intervalos $[1.25,1.375]$ o $[1.375,1.5]$. Explica brevemente la respuesta para cada intervalo. (Solución)
154. Consideremos la gráfica de la función$ y = f (x)$ que se muestra en el siguiente gráfico.
155. Sea $f(x)=\begin{cases} 3x & \text{si $ x > 1$} \\ x^3 & \text{si $x < 1$} \end{cases} $
156. Sea $f (x) = \frac{x^4-1}{x^2-1}$ para $x \ne −1,1$.
157. Dibuja la gráfica de la función $y = f (x)$ que verifique las propiedades i. hasta vii.
158. Dibuja la gráfica de la función $y = f (x)$ cumpliendo las propiedades i. hasta iv.
 En los siguientes ejercicios, supón que $y = f (x)$ está definida para todo $x$. Para cada descripción, dibuja un gráfico con la propiedad indicada.
En los siguientes ejercicios, supón que $y = f (x)$ está definida para todo $x$. Para cada descripción, dibuja un gráfico con la propiedad indicada.
159. Discontinua en $x = 1$ y con $\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = - 1$ y $\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 4$ (Solución)
160. Discontinua en $x = 2$ pero continua en todos los puntos con $\mathop {\lim }\limits_{x \to 0} f\left( x \right) = 1/2$.
 Determina si cada una de las afirmaciones dadas es verdadera. Justifica tu respuesta con una explicación o un contraejemplo.
Determina si cada una de las afirmaciones dadas es verdadera. Justifica tu respuesta con una explicación o un contraejemplo.
161. $f(t) \frac{2}{e^t-e^{-t}}$ es continuo en en todos los puntos. (Solución)
162. Si los límites izquierdo y derecho de $f (x)$ cuando $x$ tiende al punto $a$ existen y son iguales, entonces $f$ no puede ser discontinua en $x = a$.
163. Si una función no es continua en un punto, entonces no está definida en ese punto. (Solución)
164. Según el TVI, $cosx − sinx − x = 2$ tiene una solución en el intervalo $[−1,1]$.
165. Si $f (x)$ es continua cumpliendo que $f (a)$ y $f (b)$ tienen signos opuestos, entonces $f (x) = 0$ tiene exactamente una solución en $[a, b]$. (Solución)
166. La función $f (x) = \frac{x^2−4x + 3}{x^2−1}$ es continua en el intervalo $[0,3]$.
167. Si $f (x)$ es continua en todos los puntos reales y $f (a)$, $f (b)> 0$, entonces no hay raíz de $f (x)$ en el intervalo $[a, b]$. (Solución)
 [T]Los siguientes problemas consideran la forma escalar de la ley de Coulomb, que describe la fuerza electrostática entre dos cargas puntuales, como los electrones. Está dada por la ecuación $F (r) = k_e \frac{| q_1q_2 |}{ r^2}$, donde $k_e$ es la constante de Coulomb, $q_i$
son las magnitudes de las cargas de las dos partículas y $r$ es la distancia entre las dos partículas.
[T]Los siguientes problemas consideran la forma escalar de la ley de Coulomb, que describe la fuerza electrostática entre dos cargas puntuales, como los electrones. Está dada por la ecuación $F (r) = k_e \frac{| q_1q_2 |}{ r^2}$, donde $k_e$ es la constante de Coulomb, $q_i$
son las magnitudes de las cargas de las dos partículas y $r$ es la distancia entre las dos partículas.
168. Para simplificar el cálculo de un modelo con muchas partículas que interactúan, después de algún valor umbral $r = R$, aproximamos $F$ como cero.
169. En lugar de hacer que la fuerza sea 0 en $R$, dejamos que la fuerza sea $10^{−20}$ para $r\ge R$. Considera dos protones, que tienen una magnitud de carga de $1.6022 x 10^{−19}C$, y la constante de Coulomb $k_e = 8.988 x 109Nm^2 / C^2$. ¿Existe un valor $R$ que pueda hacer que este sistema sea continuo? Si es así, calcula este valor.
 Recuerde la discusión sobre las naves espaciales del comienzo del capítulo. Los siguientes problemas consideran el lanzamiento de un cohete desde la superficie de la Tierra. La fuerza de gravedad sobre el cohete viene dada por $F (d) = - mk / d^2$, donde $m$ es la masa del cohete, $d$ es la distancia del cohete desde el centro de la Tierra y $k$ es una constante. (Solución)
Recuerde la discusión sobre las naves espaciales del comienzo del capítulo. Los siguientes problemas consideran el lanzamiento de un cohete desde la superficie de la Tierra. La fuerza de gravedad sobre el cohete viene dada por $F (d) = - mk / d^2$, donde $m$ es la masa del cohete, $d$ es la distancia del cohete desde el centro de la Tierra y $k$ es una constante. (Solución)
170. [T]Determina el valor y las unidades de $k$ dado que la masa del cohete es de 3 millones de kg. Sugerencia: la distancia desde el centro de la Tierra hasta su superficie es de $6378$ km.
171. [T] Después de que ha pasado una cierta distancia $D$, el efecto gravitacional de la Tierra se vuelve bastante insignificante, por lo que podemos aproximar la función de fuerza por $$F(d)= \begin{cases} -\frac{mk}{d^2} & \text{si $d < D$} \\ 10000 & \text{si $d \ge D$} \end{cases} $$ Utilizando el valor de $k$ encontrado en el ejercicio anterior, encuentra la condición necesaria de $D$ para que la función de fuerza permanezca continua. (Solución)
172. A medida que el cohete se aleja de la superficie de la Tierra, hay una distancia $D$ donde el cohete arroja parte de su masa, ya que ya no necesita el exceso de almacenamiento de combustible.
Podemos escribir esta función como $$F(d)= \begin{cases} -\frac{m_1k}{d^2} & \text{si $d < D$} \\ -\frac{m_2k}{d^2} & \text{si $d \ge D$} \end{cases} $$ ¿Existe un valor $D$ tal que esta función sea continua, asumiendo $m_1 \ne m_2$?
 Demuestra que las siguientes funciones son continuas en todos los números reales
Demuestra que las siguientes funciones son continuas en todos los números reales
173. $f(\theta) = sen\theta$ (Solución)
174. $g(x) = |x|$
175. ¿Donde es continua $f(x)=\begin{cases} 0 & \text{si $x$ es irracional} \\ 1 & \text{si $x$ es racional} \end{cases} $? (Solución)
Objetivos de aprendizaje
A este punto, se ha pasado de la definición muy informal de un límite en la introducción de este capítulo a la comprensión intuitiva de un límite y lo que significa el límite de una función y cómo puedes encontrarlo. En esta sección, convertimos esta idea intuitiva de un límite en una definición formal utilizando un lenguaje matemático preciso. La definición formal de límite es posiblemente una de las definiciones más desafiantes que encontrarás al principio del estudio del cálculo; sin embargo, vale la pena cualquier esfuerzo que hagas para reconciliarlo con su noción intuitiva de límite. Comprender esta definición es la clave que abre la puerta a una mejor comprensión del cálculo.
Antes de enunciar la definición formal de límite, debemos introducir algunas ideas preliminares. Recuerda que la distancia entre dos puntos $a$ y $b$ en la recta numérica viene dada por $| a − b |$.
También es importante observar las siguientes equivalencias de valor absoluto:
Con estas aclaraciones, podemos establecer la definición formal épsilon-delta del límite.
Esta definición puede parecer bastante compleja desde un punto de vista matemático, pero se vuelve más fácil de entender si la desglosamos frase por frase. El enunciado en sí implica algo llamado cuantificador universal (para todo $\epsilon > 0$), un cuantificador existencial (existe un $\delta > 0$) y, por último, un enunciado condicional (si $0 < | x − a | < \delta$, entonces $| f (x) −L | < \epsilon$).
Echemos un vistazo a la Tabla 2.9, que desglosa la definición y traduce cada parte.
| Definición | Traducción |
| 1. Para cada $\epsilon > 0$ | 1. Para cada distancia positiva $\epsilon$ desde $L$ |
| 2. existe un $\delta ≥ 0$ | 2. Hay una distancia positiva $\delta$ a partir de $a$ |
| 3. tal que | 3. tal que |
| 4. si $0 < | x − a | < \delta$, entonces $| f (x) −L | < \epsilon$ | 4. si $x$ está a una distancia menor que $\delta$ de $a$ siendo $x\ne a$, entonces $f (x)$ está a una distancia de $L$ menor que $\epsilon$. |
Tabla 2.9 Traducción de la definición del límite epsilon-delta
Podemos manejar mejor esta definición si la observamos geométricamente. La Figura 2.39 muestra posibles valores de $\delta$ para varias opciones de $\epsilon > 0$ para una función dada $f (x)$, un número $a$, y un límite $L$ en $a$.
Observa que cuando elegimos valores más pequeños de $\epsilon$ (la distancia entre la función y el límite), siempre podemos encontrar un $\delta$ lo suficientemente pequeño como para que si hemos elegido un valor de $x$ a una distancia menor que $\delta$ de $a$, entonces el valor de $f (x)$ está a una distancia menor que $\epsilon$ del límite $L$.
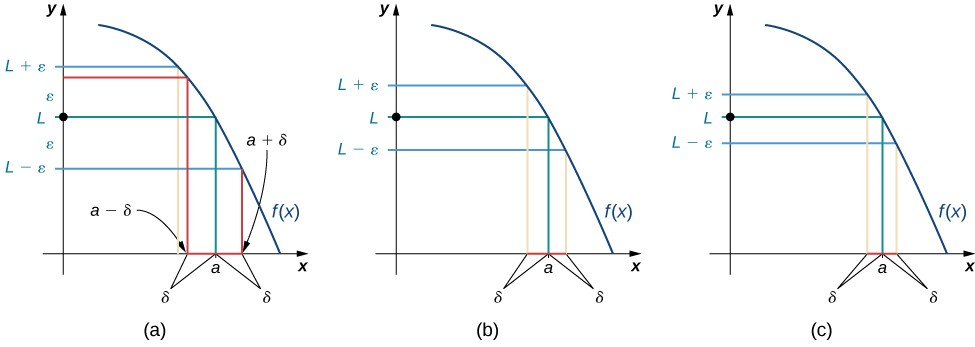
Figura 2.39 Figura 2.39 Estos gráficos muestran posibles valores de $\delta$ para distinas opciones de $\epsilon$ cada vez más pequeños.
 Puedes utilizar el siguiente applet de David Beyler para experimentar con la búsqueda de valores $\delta$ una vez determinados los valores de $\epsilon$ para la función $f(x)=\sqrt{x-1}$.
Puedes utilizar el siguiente applet de David Beyler para experimentar con la búsqueda de valores $\delta$ una vez determinados los valores de $\epsilon$ para la función $f(x)=\sqrt{x-1}$.
En este applet el valor de $a$ se corresponde con $x_0$. Observa que el valor de $\delta$ depende del valor de $\epsilon$ elegido, y que cuanto más pequeño se tome $\epsilon$, se deben considerar puntos $x$ más próximos a $x_0$.
El Ejemplo 2.39 muestra cómo puede usar esta definición para demostrar que un número es el valor de un límite.
 |
2.39 Demostrar el valor de un límite de una función específica |
Demuestre que $\mathop {\lim }\limits_{x \to 1} \left( {2x + 1} \right) = 3$.

 En la siguiente escena interactiva se puede considerar distintos valores de $\epsilon$ y a partir del valor elegido obtener un valor de $\delta$ adecuado con el que comprobar la definición de límite.
En la siguiente escena interactiva se puede considerar distintos valores de $\epsilon$ y a partir del valor elegido obtener un valor de $\delta$ adecuado con el que comprobar la definición de límite.
La siguiente estrategia de resolución de problemas resume el tipo de prueba que hemos elaborado en el Ejemplo 2.39.
Sea $\epsilon > 0$.
Elija $\delta =$ _______.
Supongamos $0 < |x-a| < \delta$.
Por lo tanto, $\mathop {\lim }\limits_{x \to a} f\left( x \right) = L$.
 |
2.40 Demostrar una declaración sobre un límite |
Completa la prueba de que $\mathop {\lim }\limits_{x \to -1}\left( 4x+1 \right) = -3$ rellenando los espacios en blanco.
Sea _____.
Elije $\delta =$ _______.
Supongamos $0 < | $x$ − \text{\_\_\_\_\_\_\_}| < \delta$.
Por lo tanto,
| ________ − _______ | = _____________________________________ $\epsilon$.

 |
Cuestión 2.27 |
Sea _____.
Elije $\delta =$ _______.
Supongamos $0 < | $x$ − \text{\_\_\_\_\_\_\_}| < \delta$.
Por lo tanto,
| ________ − ________ | = _____________________________________ $\epsilon$.
En el Ejemplo 2.39 y el Ejemplo 2.40, las demostraciones eran bastante sencillas, ya que las funciones con las que estábamos trabajando eran lineales. En el Ejemplo 2.41, vemos cómo modificar la demostración para considerar una función no lineal.
 |
2.41 Demostrar el valor de un límite (enfoque geométrico) |
Demuestra que $\mathop {\lim }\limits_{x \to 2} x^2 = 4$

 |
Cuestión 2.28 |
Encuentra $\delta$ correspondiente a $\epsilon > 0$ para una prueba de que $\mathop {\lim }\limits_{x \to 9} \sqrt x = 3$.
El enfoque geométrico para demostrar que el límite de una función adquiere un valor específico, funciona bastante bien para algunas funciones. Además, la comprensión de la definición formal del límite que proporciona este método es invaluable. Sin embargo, también podemos acercarnos a las demostraciones de límite desde un punto de vista puramente algebraico. En muchos casos, un enfoque algebraico puede no solo proporcionarnos información adicional sobre la definición, sino que también puede resultar más simple. Además, un enfoque algebraico es la herramienta principal utilizada en las pruebas de enunciados sobre límites.
En el Ejemplo 2.42, adoptamos un enfoque puramente algebraico.
 |
2.42 Demostrar el valor de un límite (enfoque algebraico) |
Demuestre que $\mathop {\lim }\limits_{x \to - 1} \left( {{x^2} - 2x + 3} \right) = 6$.

 |
Cuestión 2.29 |
Completa la prueba de que $\mathop {\lim }\limits_{x \to 1} x^2 = 1$.
Sea $\epsilon > 0$; elije $\delta = min \left\{1, \epsilon / 3\right\}$; supón $0 < | x − 1 | < \delta$.
Dado que $| x − 1 | < \delta$, podemos concluir que $−\delta < x − 1 < \delta$. Por tanto, $-\delta +2 < x + 1 < 2+\delta$. Por tanto, $| x + 1 | < 2+\delta$.
Descubriras que, en general, cuanto más compleja es una función, más probable es que el enfoque algebraico sea el más fácil de aplicar. El enfoque algebraico también es más útil para probar afirmaciones sobre límites.
Ahora demostramos cómo usar la definición épsilon-delta de un límite para construir una prueba rigurosa de una de las leyes del límite. La desigualdad triangular se usa en un punto clave de la prueba, por lo que primero revisamos esta propiedad del valor absoluto.
Prueba
Demostramos la propiedad anterior de los límites.
Sea $\epsilon > 0$.
Elije $\delta_1 > 0$ de modo que si $0 < | x − a | < \delta_1$, entonces $| f (x) −L | < \epsilon / 2$.
Elije $\delta_2 > 0$ de modo que si $0 <| x − a | < \delta_2$, entonces $| g (x) −M | < \epsilon / 2$.
Elija $\delta = min \left\{\delta_1, \delta_2\right\}$.
Supongamos $0 <| x − a | < \delta$.
Así, $$0 <|x-a| <\delta_1 \,\,\,\,\,\text{y} \,\,\,\,\,0 <|x-a| <\delta_2$$
Por lo tanto, $$| (f(x) +g(x)) - (L+M) | = $$ $$| (f(x) -L) + (g(x) -M) | \le |f(x) -L| + |g(x) -M|$$ $$< \epsilon/2+\epsilon/2=\epsilon.$$
Ahora exploramos qué significa que no exista un límite. El límite ${\mathop {\lim }\limits_{x \to a} f\left( x \right)}$ no existe si no hay un número real $L$ para el cual ${\mathop {\lim }\limits_{x \to a} f\left( x \right)}=L$ o expresado de otra forma, si para todos los números reales $L$, ${\mathop {\lim }\limits_{x \to a} f\left( x \right)}\ne L$.
Para entender lo que esto significa, miramos cada parte de la definición de ${\mathop {\lim }\limits_{x \to a} f\left( x \right)}=L$ junto con su negación tal y como se indica en la Tabla 2.10.
| Definición | Opuesto |
| 1. Para cada $\epsilon > 0$ | 1. Existe $\epsilon > 0$ |
| 2. existe un $\delta ≥ 0$ | 2. para cada $\delta ≥ 0$ |
| 3. si $0 < | x − a | < \delta$, entonces $| f (x) −L | < \epsilon$ | 4. hay un $x$ cumpiendo que $0 < | x − a | < \delta$ de forma que $| f (x) −L | \ge \epsilon$ |
Tabla 2.10 Traducción de la definición del límite y su opuesta
Finalmente, podemos enunciar lo que significa que no exista un límite.
Apliquemos este resultado en el Ejemplo 2.43 para mostrar que no existe un límite.
 |
2.43 Demostrar que no existe un límite |
Demuestre que $\mathop {\lim }\limits_{x \to 0} {{\left| x \right|} \over x}$ no existe. La gráfica de la función
se muestra a continuación:
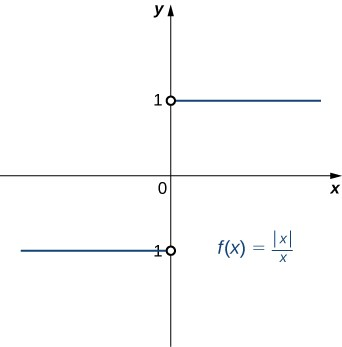

De la misma forma que en el caso de los límites empezamos con una comprensión intuitiva y luego pasamos a una definición más rigurosa, ahora abordaremos la definición formar de los límites laterales. Para hacer esto, modificamos la definición épsilon-delta de un límite para dar definiciones formales épsilon-delta de los límites por la derecha y por la izquierda en un punto. Estas definiciones solo requieren ligeras modificaciones de la definición del límite.
En la definición del límite por la derecha, la desigualdad $0 < x − a < \delta$ reemplaza $0 < | x − a | < \delta$, lo que asegura que solo consideramos valores de $x$ que son mayores que $a$ (a la derecha de $a$). De manera similar, en la definición del límite por la izquierda, la desigualdad $−\delta < x − a < 0$ reemplaza $0 < | x − a | < \delta$, lo que asegura que solo consideremos valores de $x$ que sean menores que $a$ (a la izquierda de $a$).
 En la siguiente escena interactiva puede ayudar a comprender la definición formal de límite lateral de una función en un punto
En la siguiente escena interactiva puede ayudar a comprender la definición formal de límite lateral de una función en un punto
 |
2.44 Demostrar el valor de un límite por la derecha |
Demuestra que $\mathop {\lim }\limits_{x \to a{4^ + }} \sqrt {x - 4} = 0$.

 |
Cuestión 2.30 |
Encuentra $\delta$ correspondiente a $\epsilon$ para demostrar que $\mathop {\lim }\limits_{x \to {1^ - }} \sqrt {1 - x} = 0$
Concluimos el proceso de convertir nuestras ideas intuitivas de varios tipos de límites en definiciones formales rigurosas dando una definición formal de límites infinitos.
Para tener $\mathop {\lim }\limits_{x \to a} f\left( x \right) = + \infty $, queremos que los valores de la función $f (x)$ sean cada vez más grandes a medida que $x$ se acerca al punto $a$.
En lugar del requisito de que $| f (x) −L | < \epsilon$ para $\epsilon$ arbitrariamente pequeño con $0 < | x − a | < \delta$ para $\delta$ suficientemente pequeño, queremos $f (x) > M$ para $M$ positivo y arbitrariamente grande con $0 < | x − a | < \delta$ para valores $\delta$ suficientemente pequeños.
La Figura 2.43 ilustra esta idea mostrando el valor de $\delta$ para valores de $M$ sucesivamente más grandes.
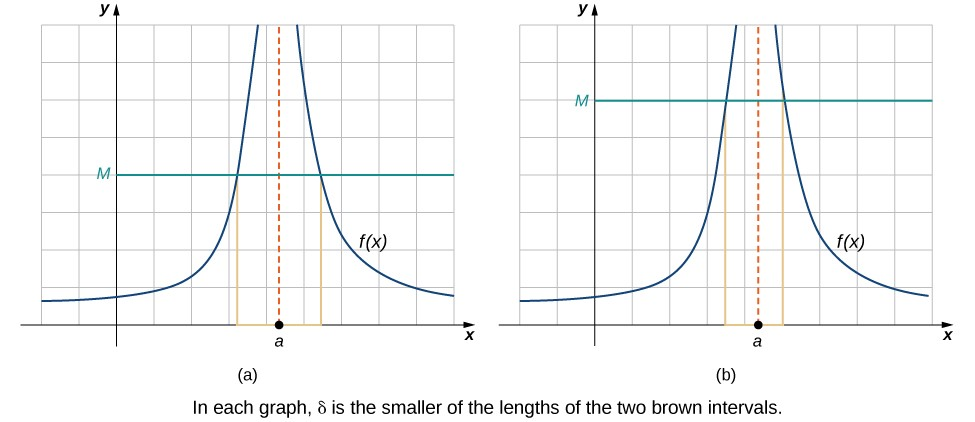
Figura 2.43 Estos gráficos trazan los valores de $\delta$ para distintos valores de $M$ para mostrar que $\mathop {\lim }\limits_{x \to a} f\left( x \right) = + \infty $.
 La siguiente escena interactiva puede ayudar a comprender la definición formal de límite infinito positivo de una función en un punto.
La siguiente escena interactiva puede ayudar a comprender la definición formal de límite infinito positivo de una función en un punto.
 En los siguientes ejercicios, escribe el $\epsilon - \delta$ apropiado
de la definición para cada una de las sentencias dadas.
En los siguientes ejercicios, escribe el $\epsilon - \delta$ apropiado
de la definición para cada una de las sentencias dadas.
176. $\mathop {\lim }\limits_{x \to {a}} f\left( x \right) = N$
177. $\mathop {\lim }\limits_{t \to {b}} g\left( t \right) = M$ (Solución)
178. $\mathop {\lim }\limits_{x \to {c}} h\left( x \right) = L$
179. $\mathop {\lim }\limits_{x \to {a}} \phi\left( x \right) = A$ (Solución)
 La siguiente gráfica de la función $f$ satisface $\mathop {\lim }\limits_{x \to {2 }} f\left( x \right) = 2$. En los siguientes ejercicios, determina un valor de $\delta > 0$
que satisfaga cada afirmación.
La siguiente gráfica de la función $f$ satisface $\mathop {\lim }\limits_{x \to {2 }} f\left( x \right) = 2$. En los siguientes ejercicios, determina un valor de $\delta > 0$
que satisfaga cada afirmación.
180. Si $0 < | x − 2 | < \delta$, entonces $| f (x) −2 | < 1$.
181. Si $0 <| x − 2 | <\delta$, entonces $| f (x) −2 | < 0.5$. (Solución)
 La siguiente gráfica de la función $f$ satisface $\mathop {\lim }\limits_{x \to 3} f\left( x \right) = - 1$. En los siguientes ejercicios, determina un valor de $\delta > 0$
que satisfaga cada afirmación.
La siguiente gráfica de la función $f$ satisface $\mathop {\lim }\limits_{x \to 3} f\left( x \right) = - 1$. En los siguientes ejercicios, determina un valor de $\delta > 0$
que satisfaga cada afirmación.
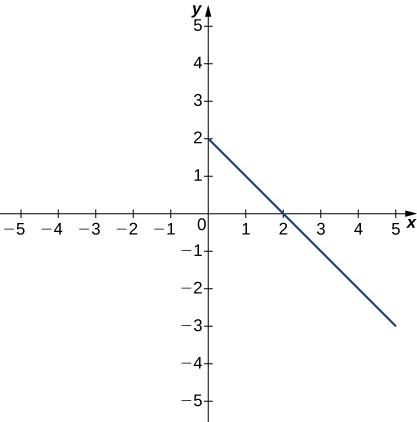
182. Si $0 < | x − 3 | < \delta$, entonces $| f (x) +1 | <1$.
183. Si $0 < | x − 3 | < \delta$ entonces $| f (x) +1 | <2$. (Solución)
 La siguiente gráfica de la función $f$ satisface $\mathop {\lim }\limits_{x \to 3} f\left( x \right) = 2$. En los siguientes ejercicios, para cada valor de $\epsilon$, encuentra un valor de $\delta> 0$ de modo que la definición precisa de límite sea cierta.
La siguiente gráfica de la función $f$ satisface $\mathop {\lim }\limits_{x \to 3} f\left( x \right) = 2$. En los siguientes ejercicios, para cada valor de $\epsilon$, encuentra un valor de $\delta> 0$ de modo que la definición precisa de límite sea cierta.
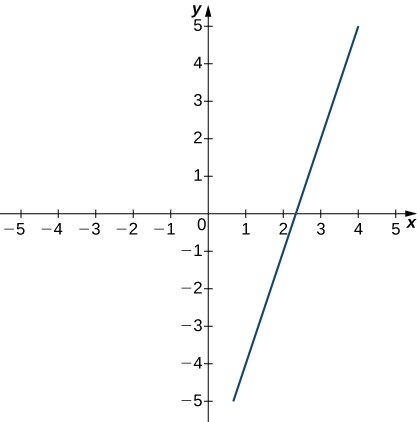
184. $\epsilon= 1.5$
185. $\epsilon= 3$ (Solución)
 [T] En los siguientes ejercicios, usa una calculadora gráfica para encontrar un número $\delta$
tal que las declaraciones sean verdaderas.
[T] En los siguientes ejercicios, usa una calculadora gráfica para encontrar un número $\delta$
tal que las declaraciones sean verdaderas.
186. $|sen(2x)-\frac{1}{2}|<0.1$ siempre que $|x-\frac{\pi}{12}|< \delta$
187. $|\sqrt{x-4}-2|<0.1$ siempre que $|x-8|< \delta$ (Solución)
 En los siguientes ejercicios, utiliza la definición precisa de límite para probar los límites dados.
En los siguientes ejercicios, utiliza la definición precisa de límite para probar los límites dados.
188. $\mathop {\lim }\limits_{x \to 2} \left( {x + 8} \right) = 18$
189. $\mathop {\lim }\limits_{x \to 3} {{{x^2} - 9} \over {x - 3}} = 6$ (Solución)
190. $\mathop {\lim }\limits_{x \to 2} {{2{x^2} - 3x - 2} \over {x - 2}} = $
191. $\mathop {\lim }\limits_{x \to 0} {x^4} = 0$ (Solución)
192. $\mathop {\lim }\limits_{x \to 2} \left( {{x^2} + 2x} \right) = 8$
 En los siguientes ejercicios, utiliza la definición precisa de límite para probar los límites unilaterales dados.
En los siguientes ejercicios, utiliza la definición precisa de límite para probar los límites unilaterales dados.
193. $\mathop {\lim }\limits_{x \to {5^ - }} \sqrt {5 - x} = 0$ (Solución)
194. $\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = - 2$ donde $f(x)=\begin{cases} 8x-3 & \text{si $x < 0$} \\ 4x-2 & \text{si $x \ge 0$} \end{cases} $
195. $\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = 3$ donde $f(x)=\begin{cases} 5x-2 & \text{si $x < 1$} \\ 7x-1 & \text{si $x \ge 1$} \end{cases} $ (Solución)
 En los siguientes ejercicios, usa la definición precisa de límite para probar los límites infinitos dados.
En los siguientes ejercicios, usa la definición precisa de límite para probar los límites infinitos dados.
196. $\mathop {\lim }\limits_{x \to 0} {1 \over {{x^2}}} = \infty $
197. $\mathop {\lim }\limits_{x \to - 1} {3 \over {{{\left( {x + 1} \right)}^2}}} = \infty $ (Solución)
198. $\mathop {\lim }\limits_{x \to 2} - {3 \over {{{\left( {x - 2} \right)}^2}}} = - \infty $
199. Un ingeniero está usando una máquina para cortar un cuadrado plano de aerogel de $144 \,\,cm^2$ de área. Si hay una tolerancia de error máxima en el área de $8 \,\,cm^2$, ¿con qué precisión debe el ingeniero cortar el lado, asumiendo que todos los lados tienen la misma longitud? ¿Cómo se relacionan estos números con $\delta$, $\epsilon$, $a$ y $L$? (Solución)
200. Utiliza la definición precisa de límite para demostrar que el siguiente límite no existe: $\mathop {\lim }\limits_{x \to 1} {{\left| {x - 1} \right|} \over {x - 1}}$.
201. Usando la definición precisa de límite, demuestre que $\mathop {\lim }\limits_{x \to 0} f\left( x \right)$ no existe, dado que $f (x)$ es la función de techo. Sugerencia: prueba cualquier $\delta < 1&.) (Solución)
202. Usando la definición precisa de límite, demuestre que $\mathop {\lim }\limits_{x \to 0} f\left( x \right)$ no existe: $f(x)=\begin{cases} 1 & \text{si $x$ es irracional} \\ 0 & \text{si $x$ es racional} \end{cases} $. Sugerencia: Piense en cómo se puede elegir siempre un número racional $0 < r < d$, pero $| f (r) −0 | = 1$.
203. Usando la definición precisa de límite, determina $\mathop {\lim }\limits_{x \to 0} f\left( x \right)$ para $f(x)=\begin{cases} x & \text{si $x$ es racional} \\ 0 & \text{si $x$ es irracional} \end{cases} $.(Solución) Sugerencia: divide en dos casos, $x$ racional y $x$ irracional.
204. Usando la función del ejercicio anterior, utiliza la definición precisa de límite para mostrar que $\mathop {\lim }\limits_{x \to a} f\left( x \right)$ no existe para $a \ne 0$.
 Para los siguientes ejercicios, suponga que existen los siguientes límites $\mathop {\lim }\limits_{x \to 0} f\left( x \right)=L$
y $\mathop {\lim }\limits_{x \to 0} f\left( x \right)=M$. Utiliza la definición precisa de límite para probar las siguientes leyes de límites:
Para los siguientes ejercicios, suponga que existen los siguientes límites $\mathop {\lim }\limits_{x \to 0} f\left( x \right)=L$
y $\mathop {\lim }\limits_{x \to 0} f\left( x \right)=M$. Utiliza la definición precisa de límite para probar las siguientes leyes de límites:
205. $\mathop {\lim }\limits_{x \to a} \left( {f\left( x \right) + g\left( x \right)} \right) = L + M$ (Solución)
206. $\mathop {\lim }\limits_{x \to a} \left( {cf\left( x \right)} \right) = cL$ para cualquier constante real $c$. Sugerencia: consideremos dos casos: $c = 0$ y $c \ne 0$.
207. $\mathop {\lim }\limits_{x \to a} \left( {f\left( x \right)g\left( x \right)} \right) = LM$.Sugerencia: $$\left| {f\left( x \right)g\left( x \right) - LM} \right| = $$ $$\left| {f\left( x \right)g\left( x \right) - f\left( x \right)M + f\left( x \right)M - LM} \right| \le $$ $$\left| {f\left( x \right)} \right|\left| {g\left( x \right) - M} \right| + \left| M \right|\left| {f\left( x \right) - L} \right|$$ (Solución)

Figura 3.1 El Hennessey Venom GT puede pasar de 0 a 200 mph en 14,51 segundos. (crédito: modificación del trabajo de Codex41, Flickr)
El Hennessey Venom GT es uno de los coches más rápidos del mundo. En 2014, alcanzó una velocidad récord de 270,49 mph (millas por hora). Puede pasar de 0 a 200 mph en 14,51 segundos. Las técnicas de este capítulo se pueden usar para calcular la aceleración que logra Venom en esta hazaña (ver Ejemplo 3.8).
El cálculo de la velocidad y los cambios en la velocidad son aplicaciones importantes del cálculo, pero su utilización se extiende a más situaciones. El cálculo es importante en todas las ramas de las matemáticas, las ciencias y la ingeniería, y también es fundamental para el análisis económico en los negocios y la salud. En este capítulo, exploramos una de las principales herramientas del cálculo, la derivada, y mostramos técnicas convenientes de calcular las derivadas. Aplicamos estas reglas a una variedad de funciones para que luego podamos estudiar sus aplicaciones.
Objetivos de aprendizaje
Ahora que tenemos una comprensión conceptual del límite y la capacidad práctica para calcular límites, hemos establecido las bases para nuestro estudio del cálculo, la rama de las matemáticas en la que calculamos derivadas e integrales. La mayoría de los matemáticos e historiadores están de acuerdo en que el cálculo fue desarrollado independientemente por el inglés Isaac Newton (1643-1727) y el alemán Gottfried Leibniz (1646-1716), cuyos retratos aparecen en la Figura 3.2.
Citamos a Newton y Leibniz como inventores del Cálculo ya que fueron los primeros en comprender la relación entre la derivada y la integral. Ambos matemáticos se beneficiaron del trabajo de predecesores como Barrow, Fermat y Cavalieri.
En un inicio, los dos matemáticos parece que tuvieron una relación amistosa; sin embargo, posteriormente estalló una amarga controversia sobre quién era el autor del trabajo que tenía prioridad. Aunque parece probable que Newton fue el primero que llegó a las ideas sobre las que se sustenta el cálculo, estamos en deuda con Leibniz, entre otras cosas, por la notación que usamos comúnmente en la actualidad para la derivada.

Figura 3.2 A Newton y Leibniz se les atribuye el desarrollo del cálculo de forma independiente.
Comenzamos nuestro estudio del cálculo revisando la noción de líneas secantes y líneas tangentes. Recordemos que usamos la pendiente de una recta secante a una función en un punto $(a, f (a))$ para estimar la tasa de cambio, o la tasa a la que una variable cambia en relación con otra variable.
Podemos obtener la pendiente de la secante eligiendo un valor de $x$ cerca de $a$ y trazando una recta a través de los puntos $(a, f (a))$ y $(x, f (x))$, como se muestra en la Figura 3.3. La pendiente de esta recta viene dada por una ecuación en forma de cociente de diferencias:
$$m_{sec} = \frac{f (x) -f (a)} {x - a}.$$
Figura 3.3 Podemos calcular la pendiente de una recta secante de dos formas.
También podemos calcular la pendiente de una recta secante a una función en un valor $a$ usando esta ecuación y reemplazando $x$ con $a + h$, donde $h$ es un valor cercano a 0. Luego podemos calcular la pendiente de la recta a través de los puntos $(a, f (a))$ y $(a + h, f (a + h))$. En este caso, encontramos que la recta secante tiene una pendiente dada por el siguiente cociente de diferencias con incremento $h$:
$$m_{sec} = \frac{f (a+h) -f (a)} {a+h - a}= \frac{f (a+h) -f (a)} {h}.$$.Sea $f$ una función definida en un intervalo $I$ que contiene $a$. Si $x \neq a$ pertenece a $I$, entonces $$Q =\frac{f (x) -f (a)} {x - a} \tag{$3.1$}$$ es un cociente de diferencias o cociente incremental.
Además, si $h \neq 0$ se elige de modo que $a + h$ esté en I, entonces $$Q =\frac{f (a+h) -f (a)} {h} \tag{$3.2$}$$ es un cociente de diferencia con incremento $h$.
 Puedes utilizar el siguiente applet interactivo para practicar moviendo los puntos $a$ y $a+h$ del eje de abscisas.
Puedes utilizar el siguiente applet interactivo para practicar moviendo los puntos $a$ y $a+h$ del eje de abscisas.
Estas dos expresiones para calcular la pendiente de una recta secante se ilustran en la Figura 3.3. Veremos que estos dos métodos para encontrar la recta tangente tiene interés dependiendo de la situación. La consideración principal para la elección de uno y otro generalmente dependerá de la facilidad de cálculo.
Esta figura consta de dos gráficos etiquetados como a y b. La figura a muestra el plano cartesiano de coordenadas con $0$, $a$ y $x$ marcadas en el eje $X$. Hay una curva etiquetada $y = f (x)$ con puntos marcados $(a, f (a))$ y $(x, f (x))$. También hay una línea recta que cruza estos dos puntos $(a, f (a))$ y $(x, f (x))$. En la parte inferior del gráfico, se da la ecuación $$m_{sec} = \frac {f (x) - f (a)} {x - a}.$$
La figura b muestra un gráfico similar, pero esta vez $a + h$ está marcado en el eje $X$ en lugar de $x$. En consecuencia, la curva etiquetada $y = f (x)$ pasa por $(a, f (a))$ y $(a + h, f (a + h))$ al igual que la línea recta. En la parte inferior del gráfico, se da la ecuación $$m_{sec} = \frac{f (a + h) - f (a)} {h}$$
En la Figura 3.4 (a) vemos que, a medida que los valores de $x$ se acercan a $a$, las pendientes de las rectas secantes proporcionan mejores estimaciones de la tasa de cambio de la función en dicho punto. Además, las rectas secantes se acercan a la recta tangente, que representa su límite.
De manera similar, la Figura 3.4 (b) muestra que, a medida que los valores de $h$ se acercan a 0, las rectas secantes también se acercan a la tangente.
La pendiente de la recta tangente en $a$ es la tasa de cambio de la función en $a$, como se muestra en la Figura 3.4 (c).
Esta figura consta de tres gráficos etiquetados a, b y c. La figura a muestra el plano cartesiano de coordenadas con $0$, $a$, $x_2$ y $x_1$ marcados en orden en el eje $X$. Hay una curva etiquetada con $y = f (x)$ y puntos en ella marcados con $(a, f (a))$, $(x_2, f (x_2))$ y $(x_1, f (x_1))$. Hay tres rectas: la primera une $(a, f (a))$ y $(x_1, f (x_1))$; la segunda une $(a, f (a))$ y $(x_2, f (x_2))$; la tercera solo toca a $(a, f (a))$, siendo la tangente. En la parte inferior del gráfico, se da la ecuación $$m_{tan} = \mathop {\lim } \limits_{x \to a } \frac{f (x) - f (a)} {x - a}$$
Figura 3.4 Las líneas secantes se acercan a la línea tangente (mostrada en verde) cuando el segundo punto se acerca al primero.
La figura b muestra un gráfico similar, pero esta vez se considera $a + h_2$ y $a + h_1$ en el eje $X$ en lugar de $x_2$ y $x_1$. En consecuencia, la curva $y = f (x)$ pasa por $(a, f (a))$, $(a + h_2, f (a + h_2))$, y $(a + h_1, f (a + h_1))$ y las rectas cruzan la gráfica de manera similar a la de la Figura a. En la parte inferior del gráfico, se da la ecuación $$m_{tan} = \mathop {\lim } \limits_{h \to 0 } \frac{f (a+h) - f (a)} {h}$$ La figura c muestra solo la curva $y = f (x)$ y su tangente en el punto $(a, f (a))$.
 En la siguiente escena interactiva puedes observar cómo cuando $h$ tiende a cero la recta secante se convierte en recta tangente.
En la siguiente escena interactiva puedes observar cómo cuando $h$ tiende a cero la recta secante se convierte en recta tangente.
 Puedes utilizar la siguiente escena, accesible desde el siguiente enlace para explorar gráficas y ver si tienen una recta tangente en un punto.
Puedes utilizar la siguiente escena, accesible desde el siguiente enlace para explorar gráficas y ver si tienen una recta tangente en un punto.
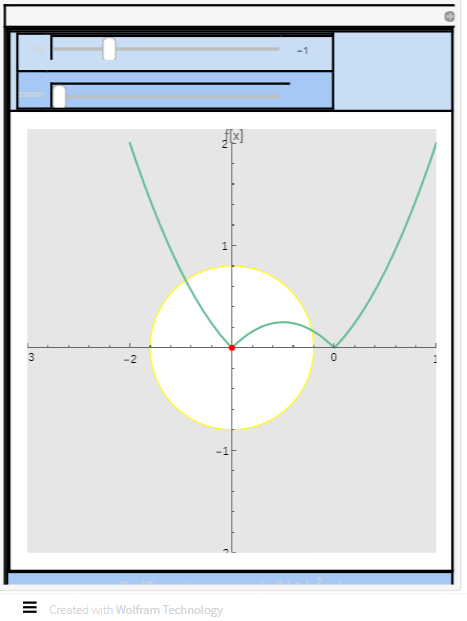
En la Figura 3.5 mostramos la gráfica de $f (x) = \sqrt{x}$ y su recta tangente en $(1,1)$ en una serie de intervalos más ajustados alrededor de $x = 1$. A medida que los intervalos se vuelven más estrechos, la gráfica de la función y su línea tangente parecen coincidir, lo que hace que los valores de la recta tangente sean una buena aproximación a los valores de la función para opciones de $x$ cercanos a 1. De hecho, la propia gráfica de $f (x)$ parece ser localmente lineal en la vecindad inmediata de $x = 1$.
Figura 3.5 Para valores de $x$ cercanos a 1, la gráfica de $f (x) = \sqrt{x}$ y su recta tangente parecen coincidir.
Esta figura consta de cuatro gráficos etiquetados a, b, c y d. La Figura a muestra las gráficas de la raíz cuadrada de $x$ y la ecuación $y = (x + 1) / 2$ con el eje $X$ yendo de 0 a 4 y el eje $Y$ yendo de 0 a 2.5. Los gráficos de estas dos funciones se ven muy próximas una de la otra cerca del de 1; hay un recuadro alrededor de donde se ven estos gráficos.
La Figura b muestra un acercamiento de estas mismas dos funciones en el área del cuadro de la Figura a, específicamente $x$ va de 0 a 2 e $y$ va de 0 a 1.4. La figura c es la misma gráfica que la figura b, pero esta tiene un cuadro de 0 a 1.1 en la coordenada $x$ y 0.8 y 1 en la coordenada $y$. Hay una flecha que indica que esto está aumentado en la Figura d. La figura d muestra una imagen muy cercana del cuadro de la figura c, y las dos funciones parecen estar tocándose durante casi toda la longitud del gráfico.
 Puedes utilizar el siguiente applet interactivo pulsando sobre el botón "animar".
Puedes utilizar el siguiente applet interactivo pulsando sobre el botón "animar".
Formalmente, podemos definir la recta tangente a la gráfica de una función de la siguiente manera.
Sea $f (x)$ una función definida en un intervalo abierto que contiene al punto $a$. La recta tangente a $f (x)$ en $a$ es la recta que pasa por el punto $(a, f (a))$ que tiene pendiente $$m_{tan} = \mathop {\lim } \limits_{x \to a } \frac{f (x) - f (a)} {x-a} \tag{$3.3$}$$ siempre que exista este límite.
De manera equivalente, podemos definir la recta tangente a $f (x)$ en $a$ como la recta que pasa por el punto $(a, f (a))$ que tiene pendiente $$m_{tan} = \mathop {\lim } \limits_{h \to 0 } \frac{f (a+h) - f (a)} {h}\tag{$3.4$}$$ siempre que exista este límite.
Dado que hemos usado dos expresiones diferentes para definir la pendiente de una recta secante, usamos también dos formas diferentes para definir la pendiente de la recta tangente. En este texto usamos ambas formas y, como antes, la elección de la definición dependerá del entorno. Ahora que hemos definido formalmente una recta tangente a una función en un punto, podemos usar esta definición para encontrar sus ecuaciones.
 |
3.1 Encontrar una recta tangente |
Encuentra la ecuación de la recta tangente a la gráfica de $f (x) = x^2$ en $x = 3$.

 |
3.2 La pendiente de una recta tangente |
Utiliza la ecuación 3.4 para encontrar la pendiente de la recta tangente a la gráfica de $f (x) = x^2$ en $x = 3$.

 |
3.3 Encontrar la ecuación de una recta tangente |
Encuentra la ecuación de la recta tangente a la gráfica de $f (x) = 1 / x$ en $x = 2$.

 |
Cuestión 3.1 |
Encuentra la pendiente de la recta tangente a la gráfica de $f (x) = \sqrt{x}$ en $x = 4.$
El tipo de límite que calculamos para encontrar la pendiente de la recta tangente a una función en un punto aparece en muchas aplicaciones de muchas disciplinas. Estas aplicaciones incluyen velocidad y aceleración en física, funciones de ganancia marginal en negocios y tasas de crecimiento en biología. Este límite ocurre con tanta frecuencia que le damos a este valor un nombre especial: la derivada. El proceso de encontrar una derivada se llama derivación.
Sea $f (x)$ una función definida en un intervalo abierto que contiene al punto $a$. La derivada de la función $f (x)$ en $a$, denotada por $f'(a)$, está definida por $$f'\left( a \right) = \mathop {\lim }\limits_{x \to a} \frac{{f\left( x \right) - f\left( a \right)}}{{x - a}} \tag{$3.5$}$$ siempre que exista este límite.
Alternativamente, también podemos definir la derivada de $f (x)$ en a como
$$f'\left( a \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( a+h \right) - f\left( a \right)}}{{h}} \tag{$3.6$}$$
 |
3.4 Estimación de una derivada |
Para $f (x) = x^2$, usa una tabla para estimar $f'(3)$ usando la Ecuación 3.5.

 |
Cuestión 3.2 |
Para $f (x) = x^2$, usa una tabla para estimar $f'(3)$ usando la Ecuación 3.6.
 |
3.5 Encontrar una derivada |
Para $f (x) = 3x^2-4x + 1$, encuentra $f'(2)$ usando la Ecuación 3.5.

 |
3.6 Revisando la derivada |
Para $f (x) = 3x^2-4x + 1$, encuentra $f'(2)$ usando la Ecuación 3.6.

 |
Cuestión 3.3 |
Para $f (x) = x^2 + 3x + 2$, encuentra $f'(1)$.
Ahora que sabemos cómo evaluar una derivada, podemos aplicarla para obtener la velocidad. Recuerda que si $s(t)$ es la posición de un objeto que se mueve a lo largo del eje de coordenadas, la velocidad promedio del objeto en un intervalo de tiempo $[a, t]$ si $t>a$ o $[t, a]$ si $t < a$ se da por el cociente incremental siguiente: $$v_{media} =\frac{ s (t) -s (a)}{ t - a} \tag{$3.7$}$$
A medida que los valores de $t$ se acercan al punto $a$, los valores de $v_{media}$ se acercan al valor que llamamos velocidad instantánea en $a$. Es decir, la velocidad instantánea en $a$, denotada $v(a)$, está dada por
Para comprender mejor la relación entre la velocidad promedio y la velocidad instantánea, se puede consultar la Figura 3.8. En esta figura, la pendiente de la recta tangente (mostrada en rojo) es la velocidad instantánea del objeto en el tiempo $t = a$, cuya posición en el tiempo $t$ está dada por la función $s (t)$. La pendiente de la línea secante (que se muestra en verde) es la velocidad promedio del objeto durante el intervalo de tiempo $[a, t]$.
Esta figura consta del plano cartesiano de coordenadas con 0, a y $t$ marcados en el eje $t$. La función $y = s(t)$ se representa gráficamente en el primer cuadrante junto con dos líneas marcadas como tangente y secante. La recta tangente toca a la curva de $y = s (t)$ en un solo punto, $(a, s (a))$. La recta secante toca a la curva $y = s (t)$ en dos puntos: $(a, s (a))$ y $(t, s (t))$.
Figura 3.8 La pendiente de la recta secante es la velocidad promedio en el intervalo $[a, t]$. La pendiente de la recta tangente es la velocidad instantánea.
Podemos utilizar la Ecuación 3.5 para calcular la velocidad instantánea, o podemos estimar la velocidad de un objeto en movimiento a partir de una tabla de valores y confirmar después la estimación mediante la Ecuación 3.7.
 |
3.7 Estimación de la velocidad |
Un peso de plomo sobre un resorte oscila hacia arriba y hacia abajo. Su posición en el tiempo $t$ con respecto a una recta horizontal fija viene dada por $s (t) = sen t$ (Figura 3.9). Utiliza una tabla de valores para estimar $v (0)$ y verifica la estimación usando la Ecuación 3.5.

Figura 3.9 Un peso de plomo suspendido de un resorte en movimiento oscilatorio vertical.

 |
Cuestión 3.4 |
Se deja caer una roca desde una altura de 64 pies. Su altura sobre el suelo en el tiempo $t$ segundos después, viene dada por $$s (t) = - 16t^2 + 64$, $0 ≤ t ≤ 2$$
Encuentra, usando la Ecuación 3.5, su velocidad instantánea un segundo después de soltarla.
Nota: Un pie equivale a 30.48 centímetros.
Como hemos visto a lo largo de esta sección, la pendiente de una recta tangente a una función y la velocidad instantánea son conceptos relacionados. Cada uno se calcula calculando una derivada y cada uno mide la tasa de cambio instantánea de una función, o la tasa de cambio, en cualquier punto de la función.
La tasa instantánea de cambio de una función $f (x)$ en un valor $a$ es su derivada $f'(a)$.
 |
3.8 Inicio del capítulo: Estimación de la tasa de cambio de velocidad |

Figura 3.10 (crédito: modificación del trabajo de Codex41, Flickr).
Al alcanzar una velocidad máxima de 270,49 mph (millas por hora), el Hennessey Venom GT es uno de los coches más rápidos del mundo. En las pruebas pasó de 0 a 60 mph en 3.05 segundos, de 0 a 100 mph en 5.88 segundos, de 0 a 200 mph en 14.51 segundos y de 0 a 229.9 mph en 19.96 segundos.
Utiliza estos datos para sacar una conclusión sobre la tasa de cambio de velocidad (es decir, su aceleración) cuando se acerca a 229.9 mph. ¿Parece que la velocidad a la que acelera el automóvil aumenta, disminuye o es constante?
Nota: Una milla son 1609 metros.

 |
3.9 Tasa de cambio de temperatura |
Un propietario ajusta el termostato para que la temperatura en la casa comience en $70°$ F a las 9 de la noche y luego empiece a bajar alcanzando un mínimo de $60°$ durante la noche y vuelva a subir a $70°$ a las 7 de la mañana siguiente. Supongamos que la temperatura en la casa está dada por $T (t) = 0.4t^2-4t + 70$ para $0 < t <10$, donde $t$ es el número de horas pasadas desde las 9 de la noche.
Encuentra la tasa instantánea de cambio de temperatura a la medianoche.

 |
3.10 Tasa de cambio de beneficio |
Una empresa de juguetes puede vender $x$ sistemas de juegos electrónicos a un precio de $p = -0,01x + 400$ dólares por sistema de juego. El coste de fabricación de un sistema $x$ viene dado por $C (x) = 100x + 10,000$ dólares.
Encuentra la tasa de cambio de beneficio cuando se producen $10,000$ juegos. ¿Debería la empresa de juguetes aumentar o disminuir la producción?

 |
Cuestión 3.5 |
Una cafetería determina que el beneficioi diario de bollos que se obtiene al cobrar $s$ dólares por bollo es $P (s) = - 20s^2 + 150s - 10$. La cafetería cobra actualmente 3.25 dólares por bollo. Encuentra $P'(3.25)$, esto es, la tasa de cambio del beneficio cuando el precio es 3.25 dólares y decide si la cafetería debería considerar subir o bajar los precios de los bollos.
 3.2.3 Ejercicios
3.2.3 Ejercicios Para los siguientes ejercicios, utiliza la Ecuación 3.1 para encontrar la pendiente de la recta secante entre los valores $x_1$ y $x_2$ de la función $y = f (x)$.
Para los siguientes ejercicios, utiliza la Ecuación 3.1 para encontrar la pendiente de la recta secante entre los valores $x_1$ y $x_2$ de la función $y = f (x)$.
1. $f (x) = 4x + 7$; $x_1 = 2$, $x_2 = 5$ (Solución)
2. $f (x) = 8x-3$; $x_1 = -1$, $x_2 = 3$
3. $f (x) = x^2+2x$; $x_1 = 3$, $x_2 = 3.5$ (Solución)
4. $f (x) = x^2+x+2$; $x_1 = 0.5$, $x_2 = 1.5$
5. $f (x) = \frac{4}{3x-1}$; $x_1 = 1$, $x_2 = 2$ (Solución)
6. $f (x) = \frac{x-7}{2x+1}$; $x_1 = 0$, $x_2 = 2$
7. $f (x) = \sqrt{x}$; $x_1 = 1$, $x_2 = 16$ (Solución)
8. $f (x) = \sqrt{x-9}$; $x_1 = 10$, $x_2 = 13$
9. $f (x) = x^{1/3}+1$; $x_1 = 0$, $x_2 = 8$ (Solución)
10. $f (x) = 6x^{2/3}+2x^{1/3}$; $x_1 = 1$, $x_2 = 27$
 Para las siguientes funciones,
Para las siguientes funciones,
11. $f (x) = 3-4x$; $a = 2$ (Solución)
12. $f (x) =\frac{x}{5}+6$; $a = -1$
13. $f (x) =x^2+x$; $a = 1$ (Solución)
14. $f (x) =1-x-x^2$; $a = 0$
15. $f (x) =\frac{7}{x}$; $a = 3$ (Solución)
16. $f (x) =\sqrt{x+8}$; $a = 1$
17. $f (x) =2-3x^2$; $a = -2$ (Solución)
18. $f (x) =\frac{-3}{x-1}$; $a = 4$
19. $f (x) =\frac{2}{x+3}$; $a = -4$ (Solución)
20. $f (x) =\frac{3}{x^2}$; $a = 3$
 Para las siguientes funciones $y = f (x)$, encuentra $f′(a)$ usando la Ecuación 3.1.
Para las siguientes funciones $y = f (x)$, encuentra $f′(a)$ usando la Ecuación 3.1.
21. $f (x) =5x+4$; $a = -1$ (Solución)
22. $f (x) =-7x+1$; $a = 3$
23. $f (x) =x^2+9x$; $a = 2$ (Solución)
24. $f (x) =3x^2-x+2$; $a = 1$
25. $f (x) =\sqrt{x}$; $a = 2$ (Solución)
26. $f (x) =\sqrt{x-2}$; $a = 6$
27. $f (x) =\frac{1}{x}$; $a = 2$ (Solución)
28. $f (x) =\frac{1}{x-3}$; $a = -1$
29. $f (x) =\frac{1}{x^3}$; $a = 1$ (Solución)
30. $f (x) =\frac{1}{\sqrt{x}}$; $a = 4$
 Para los siguientes ejercicios, dada la función $y = f (x)$,
Para los siguientes ejercicios, dada la función $y = f (x)$,
31. [T] $f (x) =x^2+3x+4$; $P(1,8)$ (redondear a 6 cifras decimales) (Solución)
| x | Pendiente $m_{PQ}$ | $x$ | Pendiente $m_{PQ}$ |
| 1.1 | (i) | 0.9 | (vii) |
| 1.01 | (ii) | 0.99 | (viii) |
| 1.001 | (iii) | 0.999 | (ix) |
| 1.0001 | (iv) | 0.9999 | (x) |
| 1.00001 | (v) | 0.99999 | (xi) |
| 1.000001 | (vi) | 0.999999 | (xii) |
32. [T] $f (x) =\frac{x+1}{x^2-1}$; $P(0,-1)$ (redondear a 6 cifras decimales)
| x | Pendiente $m_{PQ}$ | $x$ | Pendiente $m_{PQ}$ |
| 0.1 | (i) | -0.1 | (vii) |
| 0.01 | (ii) | -0.01 | (viii) |
| 0.001 | (iii) | -0.001 | (ix) |
| 0.0001 | (iv) | -0.0001 | (x) |
| 0.00001 | (v) | -0.00001 | (xi) |
| 0.000001 | (vi) | -0.000001 | (xii) |
33. [T] $f (x) =10e^{0.x}$; $P(0,10)$ (redondear a 4 cifras decimales) (Solución)
| x | Pendiente $m_{PQ}$ |
| -0.1 | (i) |
| -0.01 | (ii) |
| -0.001 | (iii) |
| -0.0001 | (iv) |
| -0.00001 | (v) |
| -0.00001 | (vi) |
34. [T] $f (x) =10e^{0.x}$; $P(0,10)$ (redondear a 4 cifras decimales)
| x | Pendiente $m_{PQ}$ |
| 3.1 | (i) |
| 3.14 | (ii) |
| 3.141 | (iii) |
| 3.1415 | (iv) |
| 3.1159 | (v) |
| 3.14192 | (vi) |
 Para las siguientes funciones de posición $y=s(t)$, un objeto se mueve a lo largo de la recta, donde $t$ es en segundos y $s$ en metros. Encuentra
Para las siguientes funciones de posición $y=s(t)$, un objeto se mueve a lo largo de la recta, donde $t$ es en segundos y $s$ en metros. Encuentra
35. $s(t)=\frac{1}{3}t+5$ (Solución)
36. $s(t)=t^2-2t$
37. $s(t)=2t^3+3$ (Solución)
38. $s(t)=\frac{16}{t^2}-\frac{4}{t}$
39. Utiliza la siguiente gráfica para evaluar a) $f ′ (- 3)$ y b) $f ′ (1,5)$.
 (Solución)
(Solución)
40. Utiliza la siguiente gráfica para evaluar a) $f ′ (- 3)$ y b) $f ′ (1,5)$.
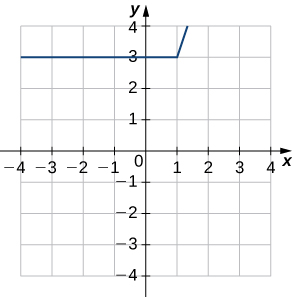
 Para las siguientes funciones utliza la definición de derivada como límite para probar que la derivada no existe en $x=a$
Para las siguientes funciones utliza la definición de derivada como límite para probar que la derivada no existe en $x=a$
41. $f(x)=x^{1/3}$, $x=0$ (Solución)
42. $f(x)=x^{2/3}$, $x=0$
43. $f(x) = \begin{cases} 1 & \text{si $x < 1$} \\ x & \text{si $x \ge 1$} \end{cases} $, $x=1$ (Solución)
44. $f(x)=\frac{|x|}{x}$, $x=0$
45. [T] La posición en pies de un automóvil de carreras a lo largo de una pista recta después de $t$ segundos se modela mediante la función $s (t) = 8t^2−\frac{1}{16}t^3$. (Solución)
46. [T] La distancia en pies que rueda una pelota por una pendiente está modelada por la función $s (t) = 14t^2$, donde $t$ son los segundos después de que la pelota comienza a rodar.
47. Dos vehículos comienzan a viajar uno al lado del otro por una carretera recta. Sus funciones de posición, que se muestran en el siguiente gráfico, están dadas por $s = f (t)$ y $s = g (t)$, donde $s$ se mide en pies y $t$ se mide en segundos. (Solución)
La primera función $s = g (t)$ comienza en $(0, 0)$ y se arquea hacia arriba a través de aproximadamente $(2, 1)$ hasta $(4, 4)$. La segunda función $s = f (t)$ es una recta que pasa por $(0, 0)$ y $(4, 4)$.
48. [T] El coste total $C (x)$, en cientos de dólares, para producir $x$ frascos de mayonesa está dado por $C (x) = 0.000003x^3 + 4x + 300$
49. [T] Para la función $f (x) = x^3−2x^2−11x + 12$, haz lo siguiente.
50. [T] Para la función $f (x) = \frac{x}{1 + x^2}$, haga lo siguiente.
51. Supongamos que $N (x)$ calcula la cantidad de galones de gasolina que usa un vehículo que viaja $x$ millas. Supón que el vehículo gasta 30 mpg (millas por galón).
52. Para la función $f(x)=x^4-5x^2+4$
Objetivos de aprendizaje
Como hemos visto, la derivada de una función en un punto dado nos da la tasa de cambio o pendiente de la recta tangente a la función en ese punto. Si derivamos una función de posición en un momento dado, obtenemos la velocidad en ese momento. Parece razonable concluir que conocer la derivada de la función en cada punto produciría información valiosa sobre el comportamiento de la función.
Sin embargo, el proceso de encontrar la derivada en un conjunto de valores utilizando las técnicas de la sección anterior, parece que sería un trabajo tedioso. En esta sección definimos la función derivada y aprendemos un proceso para encontrarla.
La función derivada asigna la derivada de una función $f$ en cada punto del dominio de $f$. Se define a continuación formalmente la función derivada.
Sea $f$ una función. La función derivada, denotada por $f'$, es la función cuyo dominio consiste en aquellos valores de $x$ tales que existe el siguiente límite: $$f\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right) - f\left( x \right)}}{h} \tag{$3.9$}$$ Se dice que una función $f (x)$ es derivable en $a$ si $f'(a)$ existe. De manera más general, se dice que una función es derivable en un conjunto abierto $S$ si es derivable en cada punto de S, y una función derivable es aquella en la que $f'(x)$ existe en su dominio.
En los siguientes ejemplos usamos la Ecuación 3.9 para encontrar la derivada de una función.
 |
3.11 Hallar la derivada de la función raíz cuadrada |
Encuentra la derivada de $f (x) = \sqrt{x}$.

 |
3.12 Hallar la derivada de una función cuadrática |
Encuentra la derivada de la función $f(x) = x^2-2x$.

 |
Cuestión 3.6 |
Encuentra la derivada de $f (x) = x^2$.
Usamos una variedad de notaciones diferentes para expresar la derivada de una función. En el ejemplo 3.12 mostramos que si $f(x) = x^2-2x$, entonces $f'(x) = 2x - 2$. Si hubiéramos expresado esta función en la forma $y = x^2-2x$, podríamos haber expresado la derivada como $y ' = 2x - 2$ o $\frac{dy}{dx} = 2x - 2$. Podríamos haber transmitido la misma información escribiendo $\frac{d}{dx} (x^2-2x) = 2x - 2$.
Por lo tanto, para la función $y = f (x)$, cualquiera de las siguientes notaciones representa la derivada de $f (x)$: $$f'(x),\,\,\,\, \frac{dy}{dx},\,\,\,\, y ',\,\,\,\, \frac{d}{dx} (f (x))$$
En lugar de $f ' (a)$ también podemos utilizar: ${\left. {\frac{{dy}}{{dx}}} \right|_{x = a}}$
El uso de la notación $\frac{dy}{dx}$ (llamada notación de Leibniz) es bastante común en ingeniería y física. Para entender mejor esta notación, recuerda que la derivada de una función en un punto es el límite de las pendientes de las rectas secantes cuando éstas se acercan a la recta tangente.
Las pendientes de estas rectas secantes a menudo se expresan en la forma $\frac{{\Delta y}}{{\Delta x}}$ donde $\Delta y$ es la diferencia en los valores y correspondientes a la diferencia en los valores x, que se expresan como $\Delta x $ (Figura 3.11. Por tanto, la derivada, que se puede considerar como la tasa instantánea de cambio de y con respecto a $x$, se expresa como
$$\frac{{dy}}{{dx}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}$$La función $y = f (x)$ se representa gráficamente y se muestra como una curva en el primer cuadrante. El eje x está marcado con 0, $a$ y $a + \Delta x$. El eje y está marcado con 0, $f (a)$ y $f (a) + \Delta y$. Hay una recta que corta a $y = f (x)$ en $(a, f (a))$ y $(a + \Delta x, f (a) + \Delta y)$.
Figura 3.11 La derivada se expresa como $\frac{{dy}}{{dx}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}$.
Desde el punto $(a, f (a))$, se traza una recta horizontal; desde el punto $(a + \Delta x, f (a) + \Delta y)$, se traza una recta vertical. La distancia de $(a, f (a)) a (a + \Delta x, f (a))$ se indica como $\Delta x$; la distancia de $(a + \Delta x, f (a) + \Delta y)$ a $(a + \Delta x, f (a))$ se denota como $\Delta y$.
Ya hemos visto cómo representar una función, así que dada la ecuación de una función o la de una función derivada, podríamos representarlas y esperaríamos ver una correspondencia entre sus gráficas, ya que $f ' (x)$ da la tasa de cambio de una función $f (x)$ (o pendiente de la recta tangente a $f (x))$.
En el ejemplo 3.11 encontramos que para $f (x) = \sqrt{x}$, se tenía que $ f ' (x) = \frac{1} {2\sqrt{x}}$. Si graficamos estas funciones en los mismos ejes, como en la Figura 3.12, podemos usar sus gráficas para comprender la relación entre estas dos funciones.
Figura 3.12 La derivada $f'(x)$ es positiva en todas partes porque la función $f(x)$ es creciente.
 En la siguiente escena interactiva se representa la gráfica de la función derivada de la función $a \sqrt{x}$ para distintos valores de $a$.
En la siguiente escena interactiva se representa la gráfica de la función derivada de la función $a \sqrt{x}$ para distintos valores de $a$.
Primero, notamos que $f (x)$ está aumentando en todo su dominio, lo que significa que las pendientes de sus rectas tangentes en todos los puntos son positivas. En consecuencia, esperamos $f ' (x)> 0$ para todos los valores de $x$ en su dominio. Además, a medida que $x$ aumenta, las pendientes de las rectas tangentes a $f (x)$ están disminuyendo y esperamos ver una disminución correspondiente en $f ' (x)$.
También observamos que $f'(0)$ no está definida y que $\mathop {\lim }\limits_{x \to {0^ + }} f'\left( x \right) = \infty $ lo que se corresponde con una tangente vertical a $f (x)$ en el punto $0$.
La función $f (x) = x^2 - 2x$ del ejemplo 3.12 se representa gráficamente junto con su derivada $f '(x) = 2x - 2$ en la siguiente figura.
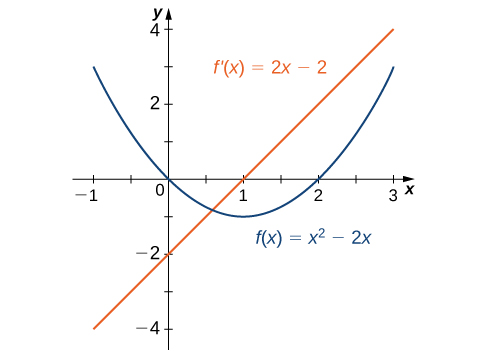
Figura 3.13 La derivada $f'(x) < 0$ donde la función $f (x)$ es decreciente y $f'(x) > 0$ donde $f (x)$ es creciente. La derivada es cero donde la función tiene una tangente horizontal.
 En la siguiente escena interactiva se representa la gráfica de la función derivada de $f (x) = a x^2 + b x$ para distintos valores de $a$ y $b$.
En la siguiente escena interactiva se representa la gráfica de la función derivada de $f (x) = a x^2 + b x$ para distintos valores de $a$ y $b$.
 |
3.13 Dibujar la derivada a partir de una función |
Usa la siguiente gráfica de $f(x)$ para dibujar la gráfica de $f'(x)$. La función $f(x)$ es aproximadamente sinusoidal, comienza en $(-4, 3)$, disminuye hasta un mínimo local en $(-2, 2)$, luego aumenta hasta un máximo local en $(3, 6)$ y se corta en $(7, 2)$.

 En la siguiente escena interactiva se representa la gráfica de la función derivada de $f(x)=a sen(bx+c)$ para distintos valores de $a$, $b$ y $c$.
En la siguiente escena interactiva se representa la gráfica de la función derivada de $f(x)=a sen(bx+c)$ para distintos valores de $a$, $b$ y $c$.
 |
Cuestión 3.7 |
Dibuja la gráfica de $f (x) = x^2-4$. ¿En qué intervalo está la gráfica de $f ' (x)$ por encima del eje $X$?
Ahora que podemos representar la función derivada, examinaremos el comportamiento de las gráficas. Primero, consideremos la relación entre derivabilidad y continuidad. Veremos que si una función es derivable en un punto, debe ser continua en dicho punto; sin embargo, una función que es continua en un punto no es necesariamente derivable en ese punto. De hecho, una función puede ser continua y no derivable enn un punto por diferentes razones.
Sea $f(x)$ una función y $a$ un punto de su dominio. Si $f(x)$ es derivable en $a$, entonces $f$ es continua en $a$.
Prueba
Si $f(x)$ es derivable en $a$, entonces $f'(a)$ existe y $$f'\left( a \right) = \mathop {\lim }\limits_{x \to a} \frac{{f\left( x \right) - f\left( a \right)}}{{x - a}}$$
Queremos demostrar que entonces $f(x)$ es continua en $a$ mostrando que $f\left( a \right) = \mathop {\lim }\limits_{x \to a} f\left( x \right)$. Así,
\[f\left( a \right) = \mathop {\lim }\limits_{x \to a} f\left( x \right) = \mathop {\lim }\limits_{x \to a} \left[ {f\left( x \right) - f\left( a \right) + f\left( a \right)} \right]\]
Multiplicando y dividiendo $f (x) -f (a)$ por $x - a$ \[f(a) = \mathop {\lim }\limits_{x \to a} \left( {\frac{{f\left( x \right) - f\left( a \right)}}{{x - a}}} \right)\mathop {\lim }\limits_{x \to a} \left( {x - a} \right) + \mathop {\lim }\limits_{x \to a} f\left( a \right)\]
\[ f(a) = f'\left( a \right) \cdot 0 + f\left( a \right)\]Por lo tanto, concluimos que $f$ es continua en $a$.
Acabamos de demostrar que la derivabilidad implica continuidad, pero ahora consideramos si la continuidad implica diferenciabilidad. Para determinar una respuesta a esta pregunta, examinamos la función $f (x) = | x |$. Esta función es continua en todo su dominio; sin embargo, $f' (0)$ no está definido y, por lo tanto, la continuidad no implica derivabilidad. Veamos que no esiste la derivada en el cero.
Para $f (x) = | x |$, \[f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to 0} \frac{{|x| - 0}}{{x - 0}} = \mathop {\lim }\limits_{x \to 0} \frac{{|x|}}{x}\] Este límite no existe porque \[\mathop {\lim }\limits_{x \to {0^ - }} \frac{{|x|}}{x} = - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathop {\lim }\limits_{x \to {0^ + }} \frac{{|x|}}{x} = 1\]
Ver la Figura 3.14.
La gráfica de la función $f (x) = | x |$ consta de dos segmentos rectos: el primero tiene por ecuación $y =-x$ y termina en el origen; el segundo tiene por ecuación $y = x$ y comienza en el origen.
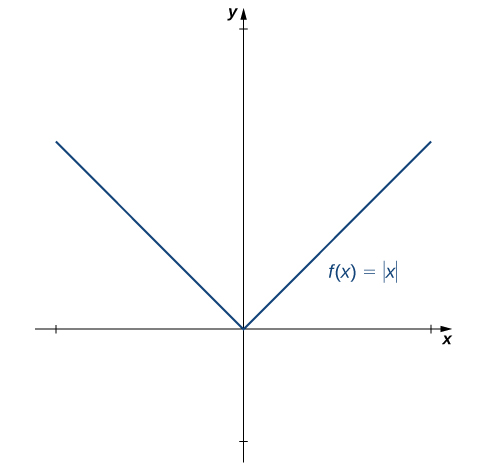
Figura 3.14 La función $f (x) = | x |$ es continua en 0 pero no derivable en dicho punto.
Consideremos algunos ejemplos más en los que una función continua no es derivable. Consideremos la función $f (x) = \sqrt[3]{x}$: \[f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt[3]{x} - 0}}{{x - 0}} = \mathop {\lim }\limits_{x \to 0} \frac{1}{{\sqrt[3]{{{x^2}}}}} = + \infty \] Por tanto, $f'(0)$ no existe. Un vistazo rápido a la gráfica de $f (x) = \sqrt[3]{x}$ muestra que tiene una tangente vertical en 0 (Figura 3.15).
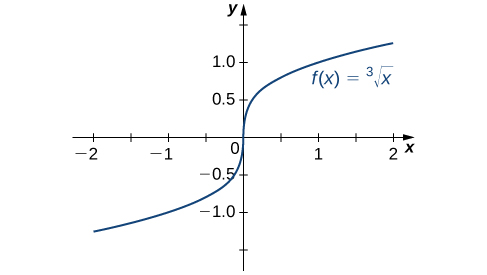
Figura 3.15 La función $f (x) = \sqrt[3]{x}$ tiene una tangente vertical en $x = 0$. Es continua en el punto $0$ pero no derivable en $0$.
La función $$f(x) = \begin{cases} xsen(1/x) & \text{si $x \neq 0$} \\ 0 & \text{si $x = 0$} \end{cases}$$ también tiene una derivada con un comportamiento interesante en el punto 0. Vemos que \[f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{{xsen\left( {\frac{1}{x}} \right) - 0}}{{x - 0}} = \mathop {\lim }\limits_{x \to 0} sen\left( {\frac{1}{x}} \right)\] este límite no existe, esencialmente porque las pendientes de las rectas secantes cambian continuamente de dirección a medida que se acercan a cero (Figura 3.16). Se grafica de la función parece una función sinusoidal que oscila rápidamente con una amplitud que disminuye a 0 en el origen.
Figura 3.16 La función $f(x) = \begin{cases} xsen(1/x) & \text{si $x \neq 0$} \\ 0 & \text{si $x = 0$} \end{cases}$ no es derivable en el punto 0.
En resumen:
 |
3.14 Una función por partes que es continua y diferenciable |
Una empresa de juguetes quiere diseñar una pista para un automóvil que comienza a lo largo de una curva parabólica y luego se convierte en una línea recta (Figura 3.17). La función que describe la pista podría tener la forma siguiente: $$f(x) = \begin{cases} \frac{1}{10} x^2+bx+c & \text{si $x < 0$} \\ -\frac{1}{4} x+\frac{5}{2} & \text{si $x \geq 0$} \end{cases}$$ donde $x$ y $f (x)$ están en pulgadas. Para que el automóvil se mueva suavemente a lo largo de la pista, la función $f (x)$ debe ser continua y derivable en -10. Encuentra los valores de $b$ y $c$ que hagan que $f (x)$ sea continua y derivable.
Se dibuja un carro en una línea que se curva a través de $(-10, 5)$ a ($10, 0)$ con una intersección y aproximadamente $(0, 2)$.
Figura 3.17 Para que el automóvil se mueva suavemente a lo largo de la pista, la función debe ser continua y derivable.

 |
Cuestión 3.8 |
Encuentra los valores de $a$ y $b$ que hagan $$\begin{cases} ax+b & \text{si $x < 3$} \\ x^2 & \text{si $x \geq 3$} \end{cases}$$ tanto continua como derivable en 3.
La derivada de una función es en sí misma una función, por lo que podemos calcular la derivada de una derivada. Por ejemplo, la derivada de una función de posición es la tasa de cambio de la posición o velocidad. La derivada de la velocidad es la tasa de cambio de la velocidad, que es la aceleración. La nueva función que se obtiene al derivar la derivada se denomina segunda derivada. Además, podemos seguir tomando derivadas para obtener sucesivamente la derivada tercera, la derivada cuarta, etc. En conjunto, estas derivadas se denominan derivadas de orden superior. La notación para las derivadas de orden superior de la función $y = f (x)$ se pueden expresar de las siguientes formas: \[f''(x),\,\,\, f'''(x),\,\,\, {f^{(4)}}(x),...,\,\,\,{f^{(n)}}(x)\] \[y''(x),\,\,\, y'''(x),\,\,\, {y^{(4)}}(x),...,\,\,\,{y^{(n)}}(x)\] \[\frac{{{d^2}y}}{{d{x^2}}},\,\,\frac{{{d^3}y}}{{d{x^3}}},\,\,\,\frac{{{d^4}y}}{{d{x^4}}}...\,\frac{{{d^n}y}}{{d{x^n}}}\]
Es interesante notar que la notación para $\frac{{{d^2}y}}{{d{x^2}}}$ puede verse como un intento de expresar de forma más compacta $\frac{d}{{dx}}\left( {\frac{{dy}}{{dx}}} \right)$. De manera análoga, $\frac{d}{{dx}}\left( {\frac{d}{{dx}}\left( {\frac{{dy}}{{dx}}} \right)} \right) = \frac{d}{{dx}}\left( {\frac{{{d^2}y}}{{d{x^2}}}} \right) = \frac{{{d^3}y}}{{d{x^3}}}$.
 |
3.15 Encontrar la segunda derivada |
Dada $f (x) = 2x^2-3x + 1$, encuentra $f '' (x)$.

 |
Cuestión 3.9 |
Encuentra $f '' (x)$ para $f (x) = x^2$.
 |
3.16 Encontrar aceleración |
La posición de una partícula a lo largo de un eje de coordenadas en el tiempo $t$ (en segundos) viene dada por $$s (t) = 3t^2-4t + 1$$ (en metros). Encuentra la función que describe su aceleración en el tiempo $t$.

 |
Cuestión 3.10 |
Para $s (t) = t^3$, encuentra $a(t)$.
 3.3.5 Ejercicios
3.3.5 Ejercicios Para las siguientes funciones, utiliza la definición de derivada y encuentra $f'(x)$
Para las siguientes funciones, utiliza la definición de derivada y encuentra $f'(x)$
54. $f (x) =6$
55. $f (x) =2-3x$ (Solución)
56. $f (x) =\frac{2x}{7}+1$
57. $f (x) =4x^2$ (Solución)
58. $f (x) =5x-x^2$
59. $f (x) =\sqrt{2x}$ (Solución)
60. $f (x) =\sqrt{x-6}$
61. $f (x) =\frac{9}{x}$ (Solución)
62. $f (x) =x+\frac{1}{x}$
63. $f (x) =1/\sqrt{x}$ (Solución)
 Para las siguientes funciones, utiliza la gráfica de $y=f(x)$ para hacer un bosquejo de la gráfica de su derivada $f'(x)$
Para las siguientes funciones, utiliza la gráfica de $y=f(x)$ para hacer un bosquejo de la gráfica de su derivada $f'(x)$
64.
67.
 (Solución)
(Solución)
 Para los siguientes ejercicios, el límite dado representa la derivada de una función $y=f(x)$ en un punto $a$. Encuentra $f(x)$ y $a$
Para los siguientes ejercicios, el límite dado representa la derivada de una función $y=f(x)$ en un punto $a$. Encuentra $f(x)$ y $a$
68. $\mathop {\lim }\limits_{h \to 0} \frac{{{{\left( {1 + h} \right)}^{2/3}} - 1}}{h}$
69. $\mathop {\lim }\limits_{h \to 0} {{\left[ {3{{\left( {2 + h} \right)}^2} + 2} \right] - 14} \over h}$ (Solución)
70. $\mathop {\lim }\limits_{h \to 0} {{\cos \left( {\pi + h} \right) + 1} \over h}$
71. $\mathop {\lim }\limits_{h \to 0} {{{{\left( {2 + h} \right)}^4} - 16} \over h}$ (Solución)
72. $\mathop {\lim }\limits_{h \to 0} {{\left[ {2{{\left( {3 + h} \right)}^2} - \left( {3 + h} \right)} \right] - 15} \over h}$
73. $\mathop {\lim }\limits_{h \to 0} {{{e^h} - 1} \over h}$ (Solución)
 Para las siguientes funciones,
Para las siguientes funciones,
74. $f(x) = \begin{cases} 2\sqrt{x} & \text{si $0 \le x \le 1$} \\ 3x-1 & \text{si $x > 1$} \end{cases} $
75. $f(x) = \begin{cases} 3 & \text{si $x < 1$} \\ 3x & \text{si $x \ge 1$} \end{cases} $ (Solución)
76. $f(x) = \begin{cases} -x^2+2 & \text{si $x \le 1$} \\ x & \text{si $x > 1$} \end{cases} $
77. $f(x) = \begin{cases} 2x & \text{si $x \le 1$} \\ \frac{2}{x} & \text{si $x > 1$} \end{cases} $ (Solución)
 Para las siguientes funciones,
Para las siguientes funciones,
78.
79.
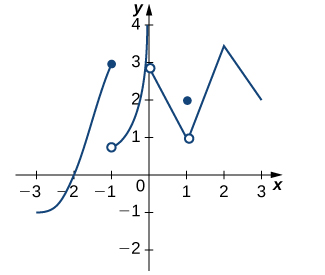 (Solución)
(Solución)
80. Utiliza la gráfica de la función para evaluar a) $f'(-0.5)$, b) $f'(0)$, c) $f'(1)$, d) $f'(2)$ y e) $f'(3)$, si es que existen estos valores
 Para las siguientes funciones, utliza $f''\left( x \right) = \mathop {\lim }\limits_{h \to 0} {{f'\left( {x + h} \right) - f'\left( x \right)} \over h}$ para encontrar $f''(x)$
Para las siguientes funciones, utliza $f''\left( x \right) = \mathop {\lim }\limits_{h \to 0} {{f'\left( {x + h} \right) - f'\left( x \right)} \over h}$ para encontrar $f''(x)$
81. $f(x)=2-3x$ (Solución)
82. $f(x)=4x^2$
83. $f(x)=x+\frac{1}{x}$ (Solución)
 Para las siguientes funciones, utliza una calculadora gráfica para representar $f(x)$. Determina la función $f'(x)$, y usa después una calculadora para representar $f'(x)$
Para las siguientes funciones, utliza una calculadora gráfica para representar $f(x)$. Determina la función $f'(x)$, y usa después una calculadora para representar $f'(x)$
84. [T] $f(x)=-\frac{5}{x}$
85. [T] $f(x)=3x^2+2x+4$ (Solución)
86. [T] $f(x)=\sqrt{x}+3x$
87. [T] $f(x)=\frac{1}{\sqrt{2x}}$ (Solución)
88. [T] $f(x)=1+x+\frac{1}{x}$
89. [T] $f(x)=x^3+1$
(Solución) Para los siguientes ejercicios, describe lo que representan las dos expresiones en términos de cada una de las situaciones dadas. Asegúrate de incluir unidades.
Para los siguientes ejercicios, describe lo que representan las dos expresiones en términos de cada una de las situaciones dadas. Asegúrate de incluir unidades.
90. $P (x)$ denota la población de una ciudad en el tiempo $x$ en años.
91. $C (x)$ denota la cantidad total de dinero (en miles de dólares) gastada en concesiones por $x$ clientes en un parque de diversiones. (Solución)
92. $R (x)$ denota el coste total (en miles de dólares) de fabricación de $x$ radio reloj.
93. $g (x)$ denota la calificación (en puntos porcentuales) recibida en una prueba, dadas $x$ horas de estudio. (Solución)
94. $B (x)$ denota el coste (en dólares) de un libro de texto de sociología en las librerías universitarias de los Estados Unidos en $x$ años desde 1990.
95. $p (x)$ denota la presión atmosférica a una altitud de $x$ pies. (Solución)
96. Dibuja la gráfica de una función $y = f (x)$ con todas las siguientes propiedades:
97. Supón que la temperatura $T$ en grados Fahrenheit a una altura $x$ en pies sobre el suelo está dada por $y = T (x)$. Da una interpretación física, con unidades, de$ T ′ (x)$. Si sabemos que $T ′ (1000) = - 0.1$, explica el significado físico. (Solución)
98. Supón que la ganancia total de una empresa es $y = P (x)$ en miles de dólares cuando se venden $x$ unidades de un artículo.
99. El gráfico de la siguiente figura modela el número de personas $N (t)$ que han contraído la gripe $t$ semanas después de su brote inicial en una ciudad con una población de 50.000 habitantes.
 La función comienza en (0, 3000) y aumenta rápidamente a una asíntota en y = 50000.
La función comienza en (0, 3000) y aumenta rápidamente a una asíntota en y = 50000.
 Para los siguientes ejercicios, usa la siguiente tabla, que muestra la altura $h$ del cohete Saturno V para la misión Apolo 11, $t$ segundos después del lanzamiento.
Para los siguientes ejercicios, usa la siguiente tabla, que muestra la altura $h$ del cohete Saturno V para la misión Apolo 11, $t$ segundos después del lanzamiento.
| Tiempo (segundos) | Altura (metros) |
| 0 | 0 |
| 1 | 2 |
| 3 | 13 |
| 4 | 25 |
| 5 | 32 |
100. ¿Cuál es el significado físico de $h ′ (t)$? ¿Cuáles son las unidades?
101. [T] Construye una tabla de valores para $h'(t)$ y representa tanto $h (t)$ como $h' (t)$ en la misma gráfica. Sugerencia: para los puntos interiores, estima tanto el límite izquierdo como el derecho. Un punto interior de un intervalo I es un elemento de I que no es un punto final del intervalo. (Solución)
102. [T] El mejor ajuste lineal a los datos viene dado por $H (t) = 7.229t − 4.905$, donde $H$ es la altura del cohete (en metros) y $t$ es el tiempo transcurrido desde el despegue. A partir de esta ecuación, determina $H ′ (t)$. Representa la gráfica $H (t)$ con los datos dados y, en un plano de coordenadas separado, representa la gráfica de $H ′ (t)$.
103. [T] El mejor ajuste cuadrático a los datos viene dado por $G(t) = 1.429t^2 + 0.0857t − 0.1429$, donde $G$ es la altura del cohete (en metros) y $t$ es el tiempo transcurrido desde el despegue. A partir de esta ecuación, determina $G ′ (t)$. Representa la gráfica $G (t)$ con los datos dados y, en un plano de coordenadas separado, representa la gráfica de $G ′ (t)$. (Solución)
104. [T] El mejor ajuste cúbico a los datos viene dado por $F (t) = 0.2037t^3 + 2.956t^2−2.705t + 0.4683$, donde $F$ es la altura del cohete (en m) y $t$ es el tiempo transcurrido desde el despegue. A partir de esta ecuación, determina $F ′ (t)$. Representa la gráfica de $F (t)$ con los datos dados y, en un plano de coordenadas separado, representa la gráfica de $F ′ (t)$. ¿La función lineal, cuadrática o cúbica se ajusta mejor a los datos?
105. Utilizando los mejores ajustes lineales, cuadráticos y cúbicos de los datos, determina cuáles son $H '' (t)$, $G '' (t)$ y $F '' (t)$. ¿Cuáles son los significados físicos de $H '' (t)$, $G '' (t)$ y $F '' (t)$, y sus unidades? (Solución)
Encontrar las derivadas de funciones mediante el uso de la definición de derivada puede ser un proceso largo y, para ciertas funciones, bastante desafiante. Por ejemplo, previamente encontramos que $\frac{d}{dx} (\sqrt{x}) = \frac{1}{2\sqrt{x}}$ usando un proceso que involucraba multiplicar una expresión por un conjugado antes de evaluar un límite. El proceso que podríamos usar para evaluar $\frac{d}{dx} (\sqrt[3]{x})$ usando la definición, aunque similar, es más complicado.
Las funciones $f (x) = c$ y $g (x) = x^n$ donde $n$ es un entero positivo son las funciones básicas a partir de los cuales se construyen todos los polinomios y funciones racionales. Para encontrar sus derivadas de manera eficiente, sin recurrir a la definición de límite de la derivada, primero debemos desarrollar fórmulas para derivar estas funciones básicas.
Derivada de una constante
Primero aplicamos la definición de límite de la derivada para encontrar la derivada de la función constante, $f (x) = c$. Para esta función, tanto $f (x) = c$ como $f (x + h) = c$, por lo tanto se obtiene el siguiente resultado: $$\begin{aligned} f'\left( x \right) &= \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right) - f\left( x \right)}}{h} = \\ &= \mathop {\lim }\limits_{h \to 0} \frac{{c - c}}{h} = \mathop {\lim }\limits_{h \to 0} \frac{0}{h} = \mathop {\lim }\limits_{h \to 0} 0 = 0 \end{aligned}$$
La regla para derivar funciones constantes se llama regla de la constante y establece que la derivada de una función constante es cero; es decir, dado que una función constante es una recta horizontal, la pendiente o la tasa de cambio de una función constante es 0. Formulamos esta regla en el siguiente teorema.
TEOREMA 3.2. La regla de la función constante
Sea $c$ una constante. Si $f (x) = c$, entonces $f ' (c) = 0$.
Alternativamente, podemos expresar esta regla como $\frac{d}{dx} (c) = 0$.
 |
3.17 Aplicar la regla de la constante |
Encuentra la derivada de $f (x) = 8$.

 |
Cuestión 3.11 |
Encuentra la derivada de $g (x) = - 3$.
Hemos demostrado que (ejemplos 3.11 y 3.12) $$\frac{d}{dx} (x^2) = 2x \,\,\,\,\,\,\,\text{y}\,\,\,\,\,\,\frac{d}{dx} (x^{1 / 2}) = \frac{1}{2} x^{- 1/2}$$
En este punto, es posible que vea un patrón para derivadas de la forma $\frac{d}{dx} (x^n)$. Vamos a proceder para ello en etapas, comenzando con potencias enteras positivas. Antes de ello, analicemos un caso particular, $\frac{d}{dx} (x^3)$. A medida que avancemos en la derivación de estas funciones, observaremos que la técnica utilizada en este caso es esencialmente la misma que la técnica utilizada para probar el caso general.
 |
3.18 Derivando $x^3$ |
Encuentra $\frac{d}{dx} (x^3)$.

 |
Cuestión 3.12 |
Encuentra $\frac{d}{dx} (x^4)$.
Como veremos, el procedimiento para encontrar la derivada de la forma general $f (x) = x^n$ es muy similar. Aunque a menudo no es prudente sacar conclusiones generales de ejemplos específicos, observamos que cuando derivamos $f (x) = x^3$, la potencia se convierte en el coeficiente de $x^2$ en la derivada y la potencia de $x$ en la derivada disminuye en 1. El siguiente teorema establece que la regla de la potencia es válida para todas las potencias enteras positivas de $x$. Eventualmente ampliaremos este resultado a potencias enteras negativas.
Más adelante, veremos que esta regla también puede extenderse primero a potencias racionales de $x$ y luego a potencias arbitrarias de $x$. Sin embargo, ten en cuenta que esta regla no se aplica a funciones en las que una constante se eleva a una potencia variable, como $f (x) = 3^x$.
TEOREMA 3.3. La regla de la potencia
Sea $n$ un número entero positivo. Si $f (x) = x^n$, entonces $$f ' (x) = nx^{n - 1}$$
Alternativamente, podemos expresar esta regla como
$$\frac{d}{dx}x^n = nx^{n - 1}$$.Prueba
Para $f (x) = x^n$ donde $n$ es un entero positivo, tenemos \[f'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right) - f\left( x \right)}}{h}\] como $$\begin{aligned} {\left( {x + h} \right)^n} &= {x^n} + n{x^{n - 1}}h +{ n \choose 2} {x^{n - 2}}{h^2} + \\ &+{n \choose 3} {x^{n - 3}}{h^3} + ...+ nx{h^{n - 1}} + {h^n} \end{aligned}$$
se tiene $$\begin{aligned} {\left( {x + h} \right)^n} -{x^n} &= n{x^{n - 1}}h +{ n \choose 2} {x^{n - 2}}{h^2} + \\ &+{n \choose 3} {x^{n - 3}}{h^3} + ...+ nx{h^{n - 1}} + {h^n} \end{aligned}$$ Al dividir ambos lados por h: $$\begin{aligned} \frac{{\left( {x + h} \right)^n} -{x^n}}{h} &= n{x^{n - 1}} +{ n \choose 2} {x^{n - 2}}{h} + \\ &+{n \choose 3} {x^{n - 3}}{h^2} + ...+ nx{h^{n - 2}} + {h^{n-1}} \end{aligned}$$ Finalmente, $$\begin{aligned} f' \left( x \right)&= \mathop {\lim }\limits_{h \to 0} [ n{x^{n - 1}} +{ n \choose 2} {x^{n - 2}}{h} + \\ &+{n \choose 3} {x^{n - 3}}{h^2} + ...+ nx{h^{n - 2}} + {h^{n-1}}] &=n{x^{n - 1}} \end{aligned}$$
 |
3.19 Aplicar la regla de la potencia |
Encuentra la derivada de la función $f (x) = x^{10}$ aplicando la regla de la potencia.

 |
Cuestión 3.13 |
Encuentra la derivada de $f (x) = x^7$.
Se resumen en el siguiente teorema las reglas de derivación de la suma, diferencia y producto por constantes de funciones.
TEOREMA 3.4. Reglas de suma, diferencia y múltiplo constante
Sean $f (x)$ y $g (x)$ funciones derivables y $k$ una constante. Entonces se cumple cada una de las siguientes reglas.
Prueba
Aquí solo proporcionamos la prueba de la regla de la suma. Para el resto se procedería de manera similar.
Para funciones diferenciables $f (x)$ y $g (x)$, consideramos $ j (x) = f (x) + g (x)$. Usando la definición límite de la derivada tenemos
\[j'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{j\left( {x + h} \right) - j\left( x \right)}}{h}\] Sustituyendo $$j (x + h) = f (x + h) + g (x + h)$$ $$j (x) = f (x) + g (x)$$ obtenemos \[j'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{\left[ {f\left( {x + h} \right) + g\left( {x + h} \right)} \right] - \left[ {f\left( x \right) + g\left( x \right)} \right]}}{h}\] Reorganizando y reagrupando los términos, tenemos \[j'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right) - f\left( x \right) + g\left( {x + h} \right) - g\left( x \right)}}{h}\] Ahora aplicamos la ley de la suma para los límites y la definición de la derivada para obtener $$\begin{aligned} j'\left( x \right) &= \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right) - f\left( x \right)}}{h} + \mathop {\lim }\limits_{h \to 0} \frac{{g\left( {x + h} \right) - g\left( x \right)}}{h} \\ &= f'\left( x \right) + g'\left( x \right) \end{aligned}$$
 |
3.20 Aplicación de la regla del múltiplo constante |
Encuentra la derivada de $g (x) = 3x^2$ y compárela con la derivada de $f (x) = x^2$.

 |
3.21 Aplicación de reglas de derivadas básicas |
Encuentra la derivada de $f (x) = 2x^5 + 7$.

 |
Cuestión 3.14 |
Encuentra la derivada de $f (x) = 2x^3-6x^2 + 3$.
 |
3.22 Encontrar la ecuación de una recta tangente |
Encuentra la ecuación de la recta tangente a la gráfica de $f (x) = x^2-4x + 6$ en $x = 1$.

 |
Cuestión 3.15 |
Encuentra la ecuación de la recta tangente a la gráfica de $f (x) = 3x^2-11$ en $x = 2$. Usa la ecuación punto-pendiente de la recta.
Ahora que hemos examinado las reglas básicas, podemos comenzar a ver algunas de las reglas más avanzadas. En primer lugar veremos la derivada del producto de dos funciones. Aunque puede resultar tentador suponer que la derivada del producto es el producto de las derivadas, como así ocurría para las reglas de la suma y diferencia de funciones, la regla del producto no sigue este patrón. Para ver por qué no podemos usar este patrón, consideremos la función $f (x) = x^2$, cuya derivada es $f ' (x) = 2x$ y no $\frac{d}{dx} (x) · \frac{d}{dx} (x) = 1·1 = 1$.
TEOREMA 3.5. Regla del producto
Sean $f (x)$ y $g (x)$ funciones diferenciables, se cumple \[\frac{d}{{dx}}(f(x)g(x)) = {\rm{ }}\frac{d}{{dx}}f(x){\rm{ \cdot}}g(x) + \frac{d}{{dx}}g(x){\rm{ \cdot}}f(x)\] Es decir, si $j (x) = f (x) g (x)$, entonces $$j ' (x) = f ' (x) g (x) + g ' (x) f (x)$$ Esto significa que la derivada de un producto de dos funciones es la derivada de la primera función por la segunda función más la derivada de la segunda función por la primera.
Prueba
Comenzamos suponiendo que $f (x)$ y $g (x)$ son funciones derivables. En un punto clave de esta demostración, debemos utilizar el hecho de que, dado que $g (x)$ es derivable, también es continua.
Utilizando el hecho de que $g (x)$ es continua, \[\mathop {\lim }\limits_{h \to 0} g\left( {x + h} \right) = g\left( x \right)\] Al aplicar la definición de la derivada mediante límites a la función $j (x) = f (x) g (x)$, obtenemos \[j'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right)g\left( {x + h} \right) - f\left( x \right)g\left( x \right)}}{h}\] Al sumar y restar $f (x) g (x + h)$ en el numerador, tenemos \[\textstyle j'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right)g\left( {x + h} \right) - f\left( x \right)g\left( {x + h} \right) - f\left( x \right)g\left( x \right) + f\left( x \right)g\left( {x + h} \right)}}{h}\] Después de separar este cociente y aplicar la ley de la suma para los límites, la derivada se convierte en \[\begin{aligned} j'\left( x \right) &= \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right)g\left( {x + h} \right) - f\left( x \right)g\left( x +h\right)}}{h}\\ &+ \mathop {\lim }\limits_{h \to 0} \frac{{f\left( x \right)g\left( {x + h} \right) - f\left( x \right)g\left( {x} \right)}}{h} \end{aligned}\] Reordenando, obtenemos $$\begin{aligned} j'\left( x \right) &= \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right) - f\left( x \right)}}{h} \cdot g\left( x+h \right)\\ &+ \mathop {\lim }\limits_{h \to 0} f\left( x \right) \cdot \frac{{g\left( {x + h} \right) - g\left( x \right)}}{h} \end{aligned}$$ Utilizando la continuidad de $g (x)$, la definición de las derivadas de $f (x)$ y $g (x)$, y aplicando las leyes del límite, llegamos a la regla del producto,
 |
3.23 Aplicación de la regla del producto a funciones en un punto |
Para $j (x) = f (x) g (x)$, usa la regla del producto para encontrar $j ' (2)$ si $f (2) = 3$, $f ' (2) = - 4$, $g (2) = 1$, y $g ' (2) = 6$.

 |
3.24 Aplicar la regla de producto a binomios |
Para $j (x) = (x^2 + 2) (3x^3-5x)$, encuentra $j ' (x)$ aplicando la regla del producto. Verifica el resultado encontrando primero el producto y luego derivando.

 |
Cuestión 3.16 |
Usa la regla del producto para obtener la derivada de $j (x) = 2x^5 (4x^2 + x)$.
Habiendo desarrollado y practicado la regla del producto, ahora consideramos la derivada del cociente de funciones. Como vemos en el siguiente teorema, la derivada del cociente no es el cociente de las derivadas. Es la derivada de la función del numerador por la función del denominador menos la derivada de la función del denominador por la función del numerador, todo dividido por el cuadrado de la función del denominador.
Para comprender mejor por qué no podemos simplemente tomar el cociente de las derivadas, observa que $$\frac{d}{dx} (x^2) = 2x, \text{\,\,\,\,no\,\,\,\,} \frac{\frac{d}{dx} (x^3)}{ \frac{d}{dx} (x)} = \frac{3x^2}{1} = 3x^2$$
TEOREMA 3.6. La regla del cociente
Sean $f (x)$ y $g (x)$ funciones derivables. Se tiene $$\frac{d}{dx} \frac{f (x)}{ g (x)} = \frac {\frac{d}{dx} (f (x)) ·g (x)-\frac{d}{dx} (g (x)) ·f (x)} { g (x)^2.}$$ Es decir, si $j (x) = \frac{f (x)}{ g (x)}$, entonces $$j ' (x) = \frac{f ' (x) g (x) -g ' (x) f (x)}{ g (x)^2}$$La prueba de la regla del cociente es muy similar a la prueba de la regla del producto, por lo que se omite aquí. En cambio, aplicamos esta nueva regla para encontrar derivadas en el siguiente ejemplo.
 |
3.25 Aplicación de la regla del cociente |
Usa la regla del cociente para hallar la derivada de $k (x) = \frac{5x^2}{4x + 3}$.

En este momento, se puede utilizar la regla del cociente para extender la regla de la potencia para encontrar derivadas de funciones de la forma $x^k$ donde $k$ es un número entero negativo.
TEOREMA 3.7. Regla de la potencia extendida
Si k es un entero negativo, entonces $$\frac{d}{dx} (x^k) = kx^{k - 1}$$
Prueba
Si $k$ es un entero negativo, podemos establecer $n = -k$, de modo que $n$ es un entero positivo con $k = -n$. Dado que para cada entero positivo $n$, $x^{- n} = \frac{1}{x^n}$, ahora podemos aplicar la regla del cociente estableciendo $f (x) = 1$ y $g (x) = x^n$. En este caso, $f ' (x) = 0$ y $g ' (x) = nx^{n - 1}$. Así, $$\frac{d}{dx} (x^{- n}) = \frac{0 \cdot (x^n) -1 \cdot (nx^{n - 1})} {(x^n)^2}$$
Simplificando, vemos que $$\frac{d}{dx} (x^{- n}) =\frac{-nx^{n - 1}}{x^{2n}} = -nx^{(n - 1) -2n} = -nx^{ - n - 1}$$ Finalmente, observamos que como $k = -n$, al sustituir tenemos $$\frac{d}{dx} (x^k) = kx^{k - 1}$$
 |
3.26 Usar la regla de potencia extendida |
Encuentra $\frac{d}{dx} (x^{- 4})$.

 |
3.27 Usar la regla de potencia extendida y la regla de multiplicación por una constante |
Usa la regla de la potencia extendida y la regla de la multiplicación por una constante para encontrar la derivada de la función $$f (x) = \frac{6}{x^2}$$

 |
Cuestión 3.18 |
Encuentra la derivada de $g (x) =\frac{ 1}{x^7}$ usando la regla de la potencia extendida.
Como hemos visto a lo largo de los ejemplos de esta sección, rara vez se nos pide que apliquemos una sola regla de derivación para encontrar la derivada de una función dada. En este punto, al combinar las reglas de derivación, podemos encontrar las derivadas de cualquier polinomio o función racional. Más adelante encontraremos combinaciones más complejas de reglas de derivación. Una buena regla general para usar cuando se aplican varias reglas es aplicar las reglas en orden inverso al orden en que evaluaríamos la función.
 |
3.28 Combinando reglas de derivación |
Para $k (x) = 3h (x) + x^2g (x)$, encuentra $k ' (x)$.

 |
3.29 Ampliación de la regla del producto |
Para $k (x) = f (x) g (x) h (x)$, expresa $k ' (x)$ en términos de $f (x)$, $g (x)$, $h (x)$ y sus derivadas.

 |
3.30 Combinando la regla del cociente y la regla del producto |
Para $h (x) =\frac{ 2x^3k (x)}{ 3x + 2}$, encuentra $h' (x)$.

 |
Cuestión 3.19 |
Encuentra $\frac{d}{dx} (3f (x) -2g (x))$.
 |
3.31 Determinar dónde tiene una función una tangente horizontal |
Determina los valores de $x$ para los cuales $f (x) = x^3-7x^2 + 8x + 1$ tiene una recta tangente horizontal.

Figura 3.19 Esta función tiene rectas tangentes horizontales en $x = 2/3$ y $x = 4$.
 |
3.32 Encontrar una velocidad |
La posición de un objeto en un eje de coordenadas en el tiempo $t$ está dada por $s (t) = \frac{t}{t^2 + 1}$. ¿Cuál es la velocidad inicial del objeto?

 |
Cuestión 3.20 |
Encuentra los valores de $x$ para los cuales la gráfica de $f (x) = 4x^2-3x + 2$ tiene una recta tangente paralela a la recta $y = 2x + 3$.
Las carreras de coches de Fórmula Uno pueden ser muy emocionantes de ver y atraer a muchos espectadores. Los diseñadores de pistas de Fórmula Uno deben asegurarse de que haya suficiente espacio en las tribunas alrededor de la pista para acomodar a estos espectadores. Sin embargo, las carreras de coches pueden ser peligrosas y las consideraciones de seguridad son primordiales. Las tribunas deben ubicarse donde los espectadores no estén en peligro si un conductor pierde el control de un automóvil (Figura 3.20).

Figura 3.20 La tribuna junto a una recta del circuito de carreras del Circuito de Barcelona-Cataluña, ubicada donde los espectadores no corren peligro.
La seguridad es especialmente una preocupación en los giros. Si un conductor no reduce la velocidad lo suficiente antes de entrar en la curva, el automóvil puede deslizarse fuera de la pista de carreras. Normalmente, esto solo da como resultado un giro más amplio, lo que ralentiza al conductor. Pero si el conductor pierde el control por completo, el automóvil puede salirse de la pista por completo en un camino tangente a la curva de la pista de carreras.
Supongamos que está diseñando una nueva pista de Fórmula Uno. Una sección de la pista se puede modelar mediante la función $f (x) = x^3 + 3x^2 + x$ (Figura 3.21).
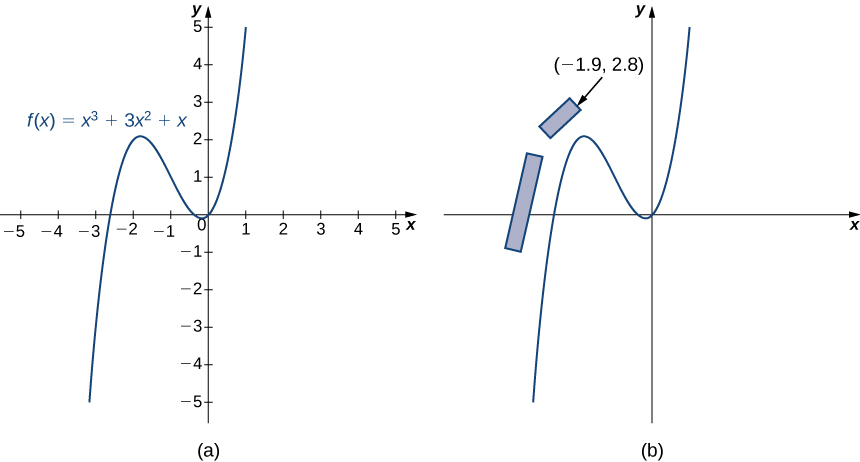
Figura 3.21 (a) Una sección de la pista de carreras se puede modelar mediante la función $f (x) = x^3 + 3x^2 + x$. (b) La esquina delantera de la tribuna se encuentra en $(-1.9,2.8)$.
El plan actual exige la construcción de tribunas a lo largo de la primera recta y alrededor de una parte de la primera curva. Los planos requieren que la esquina frontal de la tribuna se ubique en el punto $(-1.9,2.8)$. Queremos determinar si esta ubicación pone en peligro a los espectadores en el caso de que un conductor pierde el control del automóvil.
Esta figura tiene dos partes etiquetadas como $a$ y $b$. La figura a muestra la gráfica de $f (x) = x^3 + 3x^2 + x$. La figura b muestra el mismo gráfico pero esta vez con dos cuadros. El primer cuadro aparece a lo largo del lado izquierdo del gráfico a ambos lados del eje x aproximadamente paralelo a $f (x)$. El segundo cuadro aparece un poco más alto, también aproximadamente paralelo a $f (x)$, con su esquina frontal ubicada en $(-1,9, 2,8)$. Tenga en cuenta que esta esquina está aproximadamente en línea con el camino directo de la pista antes de que comenzara a girar.
 3.4.7 Ejercicios
3.4.7 Ejercicios Para las siguientes funciones, encuentra $f'(x)$ para cada función
Para las siguientes funciones, encuentra $f'(x)$ para cada función
106. $f(x)=x^7+10$
107. $f(x)=x^3-x+1$ (Solución)
108. $f(x)=4x^2-7x$
109. $f(x)=8x^4+9x^2-1$ (Solución)
110. $f(x)=x^4+\frac{2}{x}$
111. $f(x)=3x\left( 18x^4+\frac{13}{x+1} \right)$ (Solución)
112. $f(x)=(x+2)(2x^2-3)$
113. $f(x)=x^2 \left(\frac{2}{x^2}+\frac{5}{x^3} \right)$ (Solución)
114. $f(x)=\frac{x^3+2x^2-4}{3}$
115. $f(x)=\frac{4x^3-2x^2+1}{x^2}$ (Solución)
116. $f(x)=\frac{x^2+4}{x^2-4}$
117. $f(x)=\frac{x+9}{x^2-7x+1}$
(Solución) Para las siguientes funciones, encuentra la ecuación de la tangente $T(x)$ a la gráfica del la función en el punto indicado. Utiliza una calculadora gráfica para representar dela función y su recta tangente.
Para las siguientes funciones, encuentra la ecuación de la tangente $T(x)$ a la gráfica del la función en el punto indicado. Utiliza una calculadora gráfica para representar dela función y su recta tangente.
118. [T] $y=3x^2+4x+1$ en $(0,1)$
119. [T] $y=2\sqrt{x}+1$ en $(4,5)$ (Solución)
120. [T] $y=\frac{2x}{x-1}$ en $(-1,1)$
121. [T] $y=\frac{2}{x}-\frac{3}{x^2}$ en $(1,-1)$ (Solución)
 Para los siguientes ejercicios, supongamos que $f(x)$ y $g(x)$ son ambas funciones derivables. Encuentra la derivada de cada función $h(x)$
Para los siguientes ejercicios, supongamos que $f(x)$ y $g(x)$ son ambas funciones derivables. Encuentra la derivada de cada función $h(x)$
122. [T] $h(x)=4f(x)+\frac{g(x)}{7}$
123. [T] $h(x)=x^3 f(x)$ (Solución)
124. [T] $h(x)=4\frac{f(x)g(x)}{2}$
125. [T] $h(x)=\frac{3f(x)}{g(x)+2}$ (Solución)
 Para los siguientes ejercicios, supongamos que tanto $f(x)$ como $g(x)$ son derivables.
Para los siguientes ejercicios, supongamos que tanto $f(x)$ como $g(x)$ son derivables.
Utiliza la tabla para calcular las derivadas que se solicitan.
| $x$ | 1 | 2 | 3 | 4 |
| $f(x)$ | 3 | 5 | -2 | 0 |
| $g(x)$ | 2 | 3 | -4 | 6 |
| $f'(x)$ | -1 | 7 | 8 | -3 |
| $g'(x)$ | 4 | 1 | 2 | 9 |
126. Encuentra $h'(1)$ si $h(x)=xf(x)+4g(x)$
127. Encuentra $h'(2)$ si $h(x)=\frac{f(x)}{g(x)}$ (Solución)
128. Encuentra $h'(3)$ si $h(x)=2x+f(x)g(x)$
129. Encuentra $h'(4)$ si $h(x)=\frac{1}{x}+\frac{g(x)}{f(x)}$ (Solución)
 Para los siguientes ejercicios, utiliza las siguientes figuras para encontrar la derivada indicada si es que existe.
Para los siguientes ejercicios, utiliza las siguientes figuras para encontrar la derivada indicada si es que existe.
130. Sea $h(x)=f(x)+g(x)$. Encuentra
131. Sea $h(x)=f(x)g(x)$. Encuentra
132. Sea $h(x)=\frac{f(x)}{g(x)}$. Encuentra
 Para los siguientes ejercicios,
Para los siguientes ejercicios,
133. [T] $f(x)=2x^3+3x-x^2$, $a=2$ (Solución)
134. [T] $f(x)=\frac{1}{x}-x^2$, $a=1$
135. [T] $f(x)=x^2-x^{12}+3x+2$, $a=0$(Solución)
136. [T] $f(x)=\frac{1}{x}-x^{2/3}$, $a=-1$
137. [T] Encuentra la ecuación de la recta tangente a la gráfica de la función $f(x)=2x^3+4x^2-5x-3$, $x=-1$ (Solución)
138. [T] Encuentra la ecuación de la recta tangente a la gráfica de la función $f(x)=x^2+\frac{4}{x}-10$, $x=8$
139. Encuentra la ecuación de la recta tangente a la gráfica de la función $f(x)=(3x-x^2)(3-x-x^2)$, $x=1$(Solución)
140. Encuentra el punto de la gráfica de la función $f(x)=x^3$ tal que la recta tangente en el punto tiene intersección con el eje x en el punto 6
141. Encuentra la ecuación de la recta que pasa por el punto $P(3,2=$ y tangente a la gráfica de la función $f(x)=\frac{6}{x-1}$ (Solución)
142. Determina todos los puntos de la gráfica de $f(x)=x^3+x^2-x-1$ para los cuales
143. Encuentra un polinomio cuadrático tal que $f(1)=5$, $f'(1)=3$ y $f''(1)=-6$. (Solución)
144. Un automóvil que circula por una autopista con tráfico ha recorrido $s (t) = t^3−6t^2 + 9t$ metros en $t$ segundos
145. [T] Un arenque que nada en línea recta ha viajado $s (t) = \frac{t^2}{t^2 + 2}$ pies en $t$ segundos. Determina la velocidad del arenque cuando ha viajado 3 segundos. (Solución)
146. La población en millones de lenguado ártico en el Océano Atlántico se modela mediante la función $P (t) = \frac{8t + 3}{0.2t^2 + 1}$, donde $t$ se mide en años.
147. [T] La concentración de antibiótico en el torrente sanguíneo $t$ horas después de ser inyectado viene dada por la función $C (t) = \frac{2t^2 + t}{t^3 + 50}$, donde $C$ se mide en miligramos por litro de sangre.
148. Un editor de libros tiene una función de coste dada por $C (x) = \frac{x^3 + 2x + 3}{x^2}$, donde $x$ es el número de copias de un libro en miles y C es el coste, por libro, medido en dólares. Evalúa $C ′ (2)$ y explica su significado.
149. [T] Según la ley de Newton de la gravitación universal, la fuerza $F$ entre dos cuerpos de masa constante $m_1$ y $m_2$ viene dada por la fórmula $F = \frac{Gm_1 m_2}{d^2}$, donde $G$ es la constante gravitacional y $d$ es la distancia entre los cuerpos.
Objetivos de aprendizaje
En esta sección, examinamos algunas aplicaciones de la derivada centrándonos en la interpretación de la derivada como la tasa de cambio de una función. Estas aplicaciones incluyen aceleración y velocidad en física, tasas de crecimiento poblacional en biología y funciones marginales en economía.
Una aplicación de las derivadas es estimar un valor desconocido de una función en un punto utilizando un valor conocido de una función en un punto dado junto con su tasa de cambio en ese punto. Si $y=f (x)$ es una función definida en un intervalo $[a, a + h]$, entonces la cantidad de cambio de $f (x)$ en el intervalo es el cambio en los valores $y$ de la función en ese intervalo y está dada por $f (a + h) -f (a)$.
La tasa de cambio promedio de la función $f$ en ese mismo intervalo es la razón entre la cantidad de cambio en ese intervalo y el cambio correspondiente en los valores de $x$. Está dado por $\frac{f (a + h) -f (a)}{ h}$.
Como ya sabemos, la tasa de cambio instantánea de $f (x)$ en $a$ es su derivada \[f'\left( a \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {a + h} \right) - f\left( a \right)}}{h}\]
Para valores suficientemente pequeños de $h$, $f'(a) \approx \frac {f (a + h) -f (a)}{ h}$. Luego, podemos despejar $f (a + h)$ para obtener la fórmula de la cantidad de cambio: \[f\left( {a + h} \right) \approx f\left( a \right) + f'\left( a \right)h\]
Podemos usar esta fórmula si solo conocemos $f (a)$ y $f ' (a)$ y deseamos estimar el valor de $f (a + h)$. Por ejemplo, se puede consdiderar la población actual de una ciudad y la tasa a la que está creciendo para estimar su población en el futuro cercano. Como podemos ver en la Figura 3.22, estamos aproximando $f (a + h)$ por la coordenada $y$ en $a + h$ en la recta tangente a $f (x)$ en $x = a$. Observa que la precisión de esta estimación depende del valor de $h$, así como del valor de $f ' (a)$.
En el plano cartesiano de coordenadas con $a$ y $a + h$ marcadas en el eje $x$, se representa gráficamente la función $f$. Pasa por $(a, f (a))$ y $(a + h, f (a + h))$. Se traza una línea recta a través de $(a, f (a))$ con su pendiente como derivada en ese punto.
Esta recta pasa por $(a + h, f (a) + f '(a) h)$. Hay un segmento de línea que conecta $(a + h, f (a + h))$ y $(a + h, f (a) + f '(a) h)$, y está marcado que este es el error al usar $f ( a) + f '(a) h$ para estimar $f (a + h)$.
Figura 3.22 El nuevo valor de $f(a+h)$ es igual al valor original más la tasa de cambio multiplicada por el intervalo de cambio: $f (a + h) \approx ˜f (a) + f ' (a) h$.
Enlace: en la siguiente página https://demonstrations.wolfram.com/ASnowballsRateOfChange hay una demostración interesante de la tasa de cambio.
 |
3.33 Estimando el valor de una función |
Si $f (3) = 2$ y $f ' (3) = 5$, estime $f (3.2)$.

 |
Cuestión 3.21 |
Dado $f (10) = - 5$ y $f ' (10) = 6$, estime $f (10.1)$.
Otra aplicación de la derivada es analizar el movimiento a lo largo de una recta. Hemos descrito la velocidad como la tasa de cambio de la posición. Si tomamos la derivada de la velocidad, podemos encontrar la aceleración o la tasa de cambio de la velocidad. También es importante introducir la idea de aceleración, que es la magnitud de la velocidad. Por tanto, podemos enunciar las siguientes definiciones matemáticas.
Sea $s (t)$ una función que da la posición de un objeto en el tiempo $t$.
 |
3.34 Comparación entre la velocidad instantánea y la velocidad media |
Se deja caer una pelota desde una altura de 64 pies. Su altura sobre el suelo (en pies) a los $t$ segundos después, está definida por la función $s (t) = - 16t^2 + 64$. En el plano cartesiano de coordenadas, se representa la función $s (t)$, esta función comienza en $(0, 64)$ y disminuye a $(0, 2)$.

 |
3.35 Interpretación de la relación entre $v (t)$ y $a (t)$ |
Una partícula se mueve a lo largo de un eje de coordenadas en la dirección positiva hacia la derecha.
Su posición en el tiempo $t$ está dada por $s (t) = t^3-4t + 2$. Encuentra $v (1)$ y $a (1)$ y usa estos valores para responder las siguientes preguntas.

 |
3.36 Posición y velocidad |
La posición de una partícula que se mueve a lo largo de un eje de coordenadas es $s (t) = t^3-9t^2 + 24t + 4$, $t \leq 0$.


Figura 3.23 El signo de $v (t)$ determina la dirección de la partícula.
 |
Cuestión 3.22 |
Una partícula se mueve a lo largo de un eje de coordenadas. Su posición en el tiempo $t$ está dada por $s (t) = t^2-5t + 1$. ¿Se mueve la partícula de derecha a izquierda o de izquierda a derecha en el tiempo $t = 3$?
Además de analizar la velocidad, la velocidad, la aceleración y la posición, podemos utilizar derivadas para analizar varios tipos de poblaciones, incluidas aquellas tan diversas como colonias de bacterias y ciudades. Podemos considerar una población actual, junto con una tasa de crecimiento, para estimar el tamaño de la población en el futuro. La tasa de crecimiento de la población es su tasa de cambio y, en consecuencia, puede representarse mediante la derivada del tamaño de la población.
DEFINICIÓN
Si $P (t)$ es el número de entidades presentes en una población, entonces la tasa de crecimiento poblacional de $P (t)$ se define como $P ' (t)$.
 |
3.37 Estimación de una población |
La población de una ciudad se triplica cada 5 años. Si su población actual es de 10,000, ¿cuál será su población aproximada dentro de 2 años?

 |
Cuestión 3.23 |
Se sabe que la población actual de una colonia de mosquitos es de 3.000; es decir, $P (0) = 3000$. Si $P ' (0) = 100$, estime el tamaño de la población en 3 días, donde $t$ se mide en días.
Además de analizar el movimiento a lo largo de una recta y el crecimiento de la población, las derivads son útiles para analizar los cambios en los costes, los ingresos y las ganancias. El concepto de función marginal es común en los campos de los negocios y la economía e implica la utilización de derivadas. El coste marginal es la derivada de la función de coste. El ingreso marginal es la derivada de la función de ingreso. La ganancia marginal es la derivada de la función de ganancia, que se basa en la función de coste y la función de ingreso.
DEFINICIÓN
Podemos aproximarnos a \[MC\left( x \right) = C'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{C\left( {x + h} \right) - C\left( x \right)}}{h}\] eligiendo un valor apropiado para $h$. Como $x$ representa objetos, un valor razonable y pequeño para $h$ es 1. Por lo tanto, al sustituir $h = 1$, obtenemos la aproximación $MC (x) = C ' (x) \approx ˜C (x + 1) -C (x)$. En consecuencia, $C ' (x)$ para un valor dado de $x$ se puede considerar como el cambio del coste asociado a la producción de un artículo adicional. De manera similar, $MR (x) = R ' (x)$ aproxima los ingresos obtenidos al vender un artículo adicional, y $MP (x) = P ' (x)$ aproxima la ganancia obtenida al producir y vender un artículo adicional.
 |
3.38 Aplicación de ingresos marginales |
Supongamos que el número de cenas de barbacoa que se pueden vender, $x$, se puede relacionar con el precio cobrado, $p$, mediante la ecuación $p (x) = 9-0.03x$, $0 \le x \le 300$.
En este caso, el ingreso en dólares obtenido por la venta de $x$ cenas de barbacoa viene dado por $$R (x) = xp (x) = x (9-0.03x) = - 0.03x^2 + 9x $$para $0 \le x \le 300$.
Utiliza la función de ingresos marginales para estimar los ingresos obtenidos por la venta de la cena de barbacoa número 101. Compara esto con los ingresos reales obtenidos por la venta de esta cena.

 |
Cuestión 3.24 |
Supongamos que la ganancia obtenida de la venta de $x$ cenas de pescado frito viene dada por $P (x) = - 0.03x^2 + 8x - 50$. Utiliza la función de beneficio marginal para estimar el beneficio de la venta de la 101ª cena de pescado frito.
 3.5.5 Ejercicios
3.5.5 Ejercicios Para los siguientes ejercicios, las funciones representan la posición de una partícula viajando a lo largo de una recta horizontal
Para los siguientes ejercicios, las funciones representan la posición de una partícula viajando a lo largo de una recta horizontal
150. $s(t)=2t^3-3t^2-12t+8$
151. $s(t)=2t^3-15t^2+36t-10$ (Solución)
152. $s(t)=\frac{t}{1+t^2}$
153. Se dispara un cohete verticalmente hacia arriba desde el suelo. La distancia $s$ en pies del cohete desde el suelo después de $t$ segundos viene dada por $s (t) = - 16t^2 + 560t$.
154. Se lanza una pelota hacia abajo con una velocidad de 8 pies/s desde lo alto de un edificio de 64 pies de altura. Después de $t$ segundos, su altura sobre el suelo viene dada por $s (t) = - 16t^2−8t + 64$.
155. La función de posición $s (t) = t^2−3t − 4$ representa la posición de la parte trasera de un automóvil que sale marcha atrás de un camino de entrada y luego conduce en línea recta, donde s está en pies y $t$ en segundos. En este caso, $s (t) = 0$ representa el momento en el que la parte trasera del automóvil está en la puerta del garaje, por lo que $s (0) = - 4$ es la posición inicial del automóvil, 4 pies dentro del garaje.
156. La posición de un colibrí volando a lo largo de una línea recta en t segundos viene dada por s (t) = 3t3−7t metros.
157. Una patata se lanza verticalmente hacia arriba con una velocidad inicial de 100 pies / s desde una pistola de patatas en la parte superior de un edificio de 85 pies de altura. La distancia en pies que recorre la patata desde el suelo después de $t$ segundos viene dada por $s (t) = - 16t^2 + 100t + 85$.
158. La función de posición $s (t) = t^3−8t$ da la posición en millas de un tren de carga donde el este es la dirección positiva y $t$ se mide en horas.
159. El siguiente gráfico muestra la posición $y = s (t)$ de un objeto que se mueve a lo largo de una línea recta. En el plano cartesiano de coordenadas, se representa la gráfica de una función que es parte de una parábola desde el origen hasta $(2, 2)$ con un máximo en $(1.5, 2.25)$. Después la función es constante hasta $(5, 2)$, en cuyo punto se vuelve una parábola nuevamente, disminuyendo despues hasta un mínimo en $(6, 1)$ y luego aumentando a $(7, 2)$.
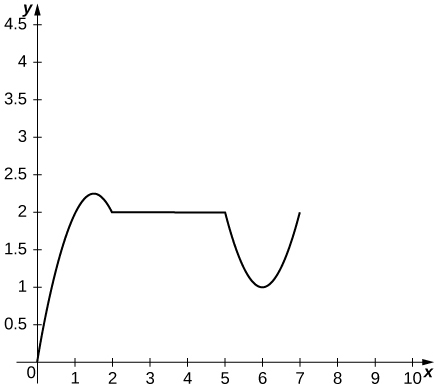
160. La función de coste, en dólares, de una empresa que fabrica procesadores de alimentos está dada por $C (x) = 200 + \frac{7}{x} + \frac{x^2}{7}$, donde $x$ es el número de procesadores de alimentos fabricados.
161. El precio $p$ (en dólares) y la demanda $x$ de un cierto radio reloj digital están relacionados por la función precio-demanda $p = 10−0.001x$.
162. [T] Se obtiene una ganancia cuando los ingresos superan el coste. Supón que la función de ganancias para un fabricante de patinetes viene dada por $P (x) = 30x − 0.3x^2−250$, donde $x$ es el número de patinetes vendidos.
163. [T] En general, la función de ganancias es la diferencia entre las funciones de ingresos y costes: $P (x) = R (x) −C (x)$. Supón que las funciones de precio-demanda y coste para la producción de taladros inalámbricos están dadas respectivamente por $p = 143−0.03x$ y $C (x) = 75,000 + 65x$, donde $x$ es el número de taladros inalámbricos que se venden a un precio de $p$ dólares por taladro y $C (x)$ es el coste de producción de $x$ taladros inalámbricos.
164. Una pequeña ciudad de Ohio encargó a una empresa que realizara un estudio que modelara la tasa de cambio de la población de la ciudad. El estudio encontró que la población de la ciudad (medida en miles de personas) se puede obtener mediante la función $P (t) = - 13t^3 + 64t + 3000$, donde $t$ se mide en años.
165. [T] Un cultivo de bacterias crece en número según la función $N (t) = 3000 \left(1 + \frac{4t}{t^2 + 100}\right)$, donde $t$ se mide en horas.
166. La fuerza centrípeta de un objeto de masa $m$ está dada por $F (r) = \frac{mv^2}{r}$, donde $v$ es la velocidad de rotación y $r$ es la distancia desde el centro de rotación.
 Las siguientes preguntas se refieren a la población (en millones) de Londres por década en el siglo XIX, que se incluyen en la siguiente tabla.
Las siguientes preguntas se refieren a la población (en millones) de Londres por década en el siglo XIX, que se incluyen en la siguiente tabla.
| Años desde 1800 | Población (millones) |
| 1 | 0.8795 |
| 11 | 1.040 |
| 21 | 1.264 |
| 31 | 1.516 |
| 41 | 1.661 |
| 51 | 2.000 |
| 61 | 2.634 |
| 71 | 3.272 |
| 81 | 3.911 |
| 91 | 4.422 |
Tabla 3.4 Población de Londres Fuente: http://en.wikipedia.org/wiki/Demographics_of_London.
167. [T]
168. [T]
 Para los siguientes ejercicios, considera un astronauta en un planeta grande de otra galaxia. Para aprender más sobre la composición de este planeta, el astronauta deja caer un sensor electrónico en una zanja profunda. El sensor transmite su posición vertical cada segundo en relación con la posición del astronauta. El resumen de los datos del sensor de caída se muestra en la siguiente tabla.
Para los siguientes ejercicios, considera un astronauta en un planeta grande de otra galaxia. Para aprender más sobre la composición de este planeta, el astronauta deja caer un sensor electrónico en una zanja profunda. El sensor transmite su posición vertical cada segundo en relación con la posición del astronauta. El resumen de los datos del sensor de caída se muestra en la siguiente tabla.
| Tiempo después de la caída (s) | Posición (m) |
| 0 | 0 |
| 1 | -1 |
| 2 | -2 |
| 3 | -5 |
| 4 | -7 |
| 5 | -14 |
169. [T]
170. [T]
 Los siguientes problemas tratan de las ecuaciones de Holling tipo I, II y III. Estas ecuaciones describen el evento ecológico de crecimiento de una población de depredadores dada la cantidad de presas disponibles para el consumo.
Los siguientes problemas tratan de las ecuaciones de Holling tipo I, II y III. Estas ecuaciones describen el evento ecológico de crecimiento de una población de depredadores dada la cantidad de presas disponibles para el consumo.
171. [T] La ecuación de Holling tipo I se describe mediante $f (x) = ax$, donde $x$ es la cantidad de presas disponibles y $a> 0$ es la velocidad de consumo de presas del depredador.
172. [T] La ecuación de Holling tipo II se describe mediante $f (x) = \frac{ax}{n + x}$, donde $x$ es la cantidad de presas disponibles y $a> 0$ es la tasa máxima de consumo del depredador.
173. [T] La ecuación de Holling tipo III se describe mediante $f (x) = \frac{ax^2}{n^2 + x^2}$, donde $x$ es la cantidad de presas disponibles y $a > 0$ es la tasa máxima de consumo del depredador.
174. [T] Las poblaciones de liebre de patas blancas (en miles) y el lince (en cientos) analizadas durante 7 años desde 1937 hasta 1943 se muestran en la siguiente tabla.
| Población de liebres con patas blancas (miles) | Población de linces (cientos) |
| 20 | 10 |
| 55 | 15 |
| 65 | 55 |
| 95 | 60 |
Tabla 3.5 Poblaciones de liebres de patas blancas y linces
La liebre con patas blancas es la principal presa del lince. Fuente: http://www.biotopics.co.uk/newgcse/predatorprey.html.
Objetivos de aprendizaje
Uno de los tipos de movimiento más importantes en física es el movimiento armónico simple, que está asociado por ejemplo a un objeto con masa que oscila en un resorte. El movimiento armónico simple se puede describir utilizando las funciones seno o coseno. En esta sección ampliamos nuestro conocimiento calculando las derivadas de estas y otras funciones trigonométricas.
Comenzamos con las derivadas de las funciones seno y coseno y luego las usamos para obtener fórmulas para las derivadas de las cuatro funciones trigonométricas restantes. Sabiendo calcular las derivadas de las funciones seno y coseno nos permitirá encontrar la velocidad y la aceleración del movimiento armónico simple.
Comenzamos nuestra exploración de la derivada de la función seno usando la fórmula para hacer una suposición razonable de su derivada. Recuerde que para una función $f (x)$, \[f'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right) - f\left( x \right)}}{h}\]
En consecuencia, para valores de $h$ muy cercanos a $0$, $$f ' (x) \approx ˜f (x + h) -f (x) h$$
Vemos que al usar $h = 0.01$, $$\frac{d}{dx} (senx) \approx \frac{sen (x + 0.01) -sen(x)} {0.01}$$
Considerando $D (x) = \frac{sen (x + 0.01) -senx}{0.01}$ y usando una utilidad gráfica, podemos obtener una gráfica de una aproximación a la derivada de $sen(x) $(Figura 3.25).

Figura 3.25 La gráfica de la función $D (x) = (sen (x + 0.01) - sen x) /0.01$ se parece mucho a una curva de coseno.
Tras la inspección, la gráfica de $D (x)$ parece estar muy cerca de la gráfica de la función coseno. De hecho, demostraremos que $$\frac{d}{dx} (senx) = cosx$$
Si tuviéramos que seguir los mismos pasos para aproximar la derivada de la función coseno, encontraríamos que
$$\frac{d}{dx} (cosx) = - senx$$TEOREMA 3.8. Las derivadas de sen x y cos x
La derivada de la función seno es el coseno y la derivada de la función coseno es el seno negativo.
$$\frac{d}{dx} (senx) = cosx \tag{$3.11$}$$Prueba
Debido a que las demostraciones para $\frac{d}{dx} (sen(x)) = cos(x)$ y $\frac{d}{dx} (cos(x)) = - sen(x)$ usan técnicas similares, proporcionamos solo la prueba para la primera igualdad. Antes de comenzar, recuerde dos límites trigonométricos importantes: \[\mathop {\lim }\limits_{h \to 0} \frac{{senh}}{h} = 1\,\,\,\,\,\,\,\,y\,\,\,\,\,\,\,\,\,\mathop {\lim }\limits_{h \to 0} \frac{{\cos h - 1}}{h} = 0\]
Las gráficas de $y = \frac{senh}{h}$ y $y = \frac{cosh - 1} {h}$ se muestran en la Figura 3.26. Ambas funciones tienen tienen discontinuidades en el punto 0.
Figura 3.26 Estas gráficas muestran dos límites importantes necesarios para establecer las fórmulas derivadas de las funciones seno y coseno.
También recordamos la siguiente identidad trigonométrica para el seno de la suma de dos ángulos: $$sen (x + h) = senx \cdot cosh + cosx \cdot senh$$ Ahora que hemos reunido todas las ecuaciones e identidades necesarias, procedemos con la demostración.
$$\begin{aligned}\frac{d}{dx}senx &=\mathop {\lim }\limits_{h \to 0} \frac{{sen\left( {x + h} \right) - sen\left( x \right)}}{h} \\ &=\mathop {\lim }\limits_{h \to 0} \frac{{senx\cosh + \cos x\,\,senh - sen\left( x \right)}}{h}\\ & = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{senx\cosh - sen\left( x \right)}}{h} + \frac{{\cos x\,\,senh}}{h}} \right)\\ & = \mathop {\lim }\limits_{h \to 0} \left( {senx\frac{{\cosh - 1}}{h} + \cos x\frac{{senh}}{h}} \right)\\ &= senx \cdot 0 + \cos x \cdot 1=cosx\\ \end{aligned}$$La Figura 3.27 muestra la relación entre la gráfica de $f (x) = senx$ y su derivada $f ' (x) = cosx$. Observa que en los puntos donde $f (x) = senx$ tiene una tangente horizontal, su derivada $f ' (x) = cosx$ toma el valor cero.
También vemos que donde $f (x) = senx$ aumenta, $f ' (x) = cosx> 0$ y donde $f (x) = senx$ es decreciente, $f ' (x) = cosx \lt 0$. Se representan las funciones $f (x) = sen x$ y $f '(x) = cos x$. Es evidente que cuando $f (x)$ tiene un máximo o un mínimo, $f '(x) = 0$.
Figura 3.27 Donde $f (x)$ tiene un máximo o un mínimo, $f '(x) = 0$ es decir, $f' (x) = 0$ donde $f (x)$ tiene una tangente horizontal. Estos puntos aparecen representados en la gráfica.
 En la siguiente escena interactiva incorporamos un applet que permite analizar la gráfica de la función coseno como derivada de la función seno.
En la siguiente escena interactiva incorporamos un applet que permite analizar la gráfica de la función coseno como derivada de la función seno.
 |
3.39 Derivar una función que contiene $sen(x)$ |
Encuentra la derivada de $f (x) = 5x^3sen(x)$.

 |
Cuestión 3.25 |
Encuentra la derivada de $f (x) = sen(x)cos(x)$.
 |
3.40 Hallar la derivada de una función que contiene $cos x$ |
Encuentra la derivada de $g (x) = \frac{cosx}{4x^2}$.

 |
Cuestión 3.26 |
Encuentra la derivada de $f (x) = \frac{x}{cosx}$.
 |
3.41 Una aplicación a la velocidad |
Una partícula se mueve a lo largo de un eje de coordenadas de tal manera que su posición en el tiempo $t$ está dada por $s (t) = 2sen(t) - t$ para $0 \le t \le 2\pi $. ¿En qué momentos está en reposo la partícula?

 |
Cuestión 3.27 |
Una partícula se mueve a lo largo de un eje de coordenadas. Su posición en el tiempo $t$ está dada por $s (t) = \sqrt{3}t + 2cost$ para $0 \le t \le 2\pi $. ¿En qué momentos está en reposo la partícula?
Dado que las cuatro funciones trigonométricas restantes pueden expresarse como cocientes que involucran seno, coseno o ambos, podemos usar la regla del cociente para encontrar sus derivadas.
 |
3.42 La derivada de la función tangente |
Encuentra la derivada de $f (x) = tgx$.

 |
Cuestión 3.28 |
Encuentra la derivada de $f (x) = cotx$.
Las derivadas de las funciones trigonométricas restantes pueden obtenerse utilizando técnicas similares. Proporcionamos estas fórmulas en el siguiente teorema.
TEOREMA 3.9. Derivadas de $tgx$, $cotx$, $secx$ y $cscx$
Las derivadas de las funciones trigonométricas restantes son las siguientes: $$\frac{d}{dx} (tgx) = sec^2x \tag{$3.13$}$$ $$\frac{d}{dx} (cotx) = - csc^2x \tag{$3.14$}$$ $$\frac{d}{dx} (secx) = secx \,\,tgx \tag{$3.15$}$$ $$\frac{d}{dx} (cscx) = - cscx\,\,cotx \tag{$3.16$}$$
 |
3.43 Encontrar la ecuación de una recta tangente |
Encuentra la ecuación de una recta tangente a la gráfica de $f (x) = cotx$ en $x = \pi/4$.

 |
3.44 Hallar la derivada de funciones trigonométricas |
Encuentra la derivada de $f (x) = cscx + xtanx$.

 |
Cuestión 3.29 |
Encuentra la derivada de $f (x) = 2tgx - 3cotx$.
 |
Cuestión 3.30 |
Encuentra la pendiente de la recta tangente a la gráfica de $f (x) = tgx$ en $x = \frac{\pi}{6}$.
Las derivadas de orden superior de $sen(x)$ y $cos(x)$ siguen un patrón repetido. Siguiendo el patrón, podemos encontrar cualquier derivada de orden superior de ambas funciones.
 |
3.45 Encontrar derivadas de orden superior de $y = sen(x)$. |
Encuentra las primeras cuatro derivadas de $y = senx$.

Análisis
Una vez que reconocemos el patrón de derivadas, podemos encontrar cualquier derivada de orden superior determinando el paso en el patrón al que corresponde. Por ejemplo, la derivada de orden cualquier múltiplo de 4 de la función $sen x$ es igual a $sen x$, entonces $$\begin{aligned} \frac{{{d^4}}}{{d{x^4}}}\left( {senx} \right) &= \frac{{{d^8}}}{{d{x^8}}}\left( {senx} \right) = \frac{{{d^{12}}}}{{d{x^{12}}}}\left( {senx} \right) \\ &= ... = \frac{{{d^{4n}}}}{{d{x^{4n}}}}\left( {senx} \right) = senx \end{aligned}$$ $$\begin{aligned} \frac{{{d^5}}}{{d{x^5}}}\left( {senx} \right) &= \frac{{{d^9}}}{{d{x^9}}}\left( {senx} \right) = \frac{{{d^{13}}}}{{d{x^{13}}}}\left( {senx} \right) \\ &= ... = \frac{{{d^{4n + 1}}}}{{d{x^{4n + 1}}}}\left( {senx} \right) = \cos x \end{aligned}$$
 |
Cuestión 3.31 |
Para $y = cosx$, encuentra $\frac{d^4y}{dx^4}$.
 |
3.46 Patrón para derivadas de orden superior de $y = sen(x)$ |
Encuentra $\frac{{{d^{74}}}}{{d{x^{74}}}}\left( {senx} \right)$.

 |
Cuestión 3.32 |
Para $y = senx$, encuentra $\frac{{{d^{59}}}}{{d{x^{59}}}}\left( {senx} \right)$.
 |
3.47 Una aplicación a la aceleración |
Una partícula se mueve a lo largo de un eje de coordenadas de tal manera que su posición en el tiempo $t$ viene dada por $s (t) = 2 - sen(t)$. Encuentra $v (\pi / 4)$ y $a (\pi / 4)$. Compara estos valores y decide si la partícula se está acelerando o desacelerando.

 |
Cuestión 3.33 |
Un bloque unido a un resorte se mueve verticalmente. Su posición en el tiempo $t$ viene dada por $s (t) = 2sent$. Encuentra $v (5\pi/6)$ y $a (5\pi/6)$. Compare estos valores y decide si el bloque se acelera o se ralentiza.
 3.6.4 Ejercicios
3.6.4 Ejercicios Para los siguientes ejercicios, encuentra $\frac{dy}{dx}$ para las funciones consideradas.
Para los siguientes ejercicios, encuentra $\frac{dy}{dx}$ para las funciones consideradas.
175. $y=x^2-secx+1$ (Solución)
176. $y=3cscx+\frac{5}{x}$
177. $y=x^2cotgx$ (Solución)
178. $y=x-x^3sen(x)$
179. $y=\frac{secx}{x}$ (Solución)
180. $y=sen(x)tg(x)$
181. $y=(x+cos(x))(1-sen(x))$ (Solución)
182. $y=\frac{tg(x)}{1-sec(x)}$
183. $y=\frac{1-cot(x)}{1+cot(x)}$(Solución)
184. $y=cos(x)(1+csc(x))$
 Para los siguientes ejercicios, encuentra la ecuación de la recta tangente a cada una de las funciones dadas en los valores indicados de $x$. Luego usa una calculadora para graficar tanto la función como la recta tangente para asegurarse que la ecuación de la recta tangente sea correcta.
Para los siguientes ejercicios, encuentra la ecuación de la recta tangente a cada una de las funciones dadas en los valores indicados de $x$. Luego usa una calculadora para graficar tanto la función como la recta tangente para asegurarse que la ecuación de la recta tangente sea correcta.
185. [T] $f (x) = - sen(x)$, $x = 0$.(Solución)
186. [T] $f (x) = - csc(x)$, $x = \frac{\pi}{2}$.
187. [T] $f (x) = 1+cos(x)$, $x = \frac{3\pi}{2}$. (Solución)
188. [T] $f (x) = sec(x)$, $x = \frac{\pi}{4}$.
189. [T] $f (x) = x^2-tg(x)$, $x = 0$. (Solución)
190. [T] $f (x) =cot(x)$, $x = \frac{\pi}{4}$.
 Para los siguientes ejercicios, encuentra $\frac{d^2y}{dx^2}$ considerando las funciones dadas.
Para los siguientes ejercicios, encuentra $\frac{d^2y}{dx^2}$ considerando las funciones dadas.
191. [T] $y =xsen(x)-cos(x)$. (Solución)
192. [T] $y =sen(x)cos(x)$.
193. [T] $y =x-\frac{1}{2}sen(x)$.(Solución)
194. [T] $y =\frac{1}{x}+tg(x)$.
195. [T] $y =2csc(x)$. (Solución)
196. [T] $y =sec^2(x)$.
197. Encuentra todos los valores de $x$ en la gráfica de $f (x) = - 3sin(x)cos(x)$ donde la recta tangente es horizontal. (Solución)
198. Encuentra todos los valores de $x$ en la gráfica de $f (x) = x − 2cosx$ para $0 < x < 2\pi$ donde la recta tangente tiene pendiente 2.
199. Sea $f (x) = cot(x)$. Determina los puntos en la gráfica de $f$ para $0 < x < 2\pi$ donde la(s) recta(s) tangente es(son) paralelas a la recta $y = −2x$. (Solución)
200. [T] Una masa en un resorte rebota hacia arriba y hacia abajo en un movimiento armónico simple, modelado por la función $s (t) = - 6cost$ donde $s$ se mide en pulgadas y $t$ se mide en segundos. Encuentra la tasa a la que el resorte oscila en $t = 5$ s.
201. Supongamos que la posición de un péndulo oscilante en movimiento armónico simple viene dada por $s (t) = acos(t) + bsin(t)$ donde $a$ y $b$ son constantes, $t$ mide el tiempo en segundos y $s$ mide la posición en centímetros. Si la posición es 0 cm y la velocidad es 3 cm/s cuando $t = 0$, encuentra los valores de $a$ y $b$. (Solución)
202. Después de que un buzo salte de un trampolín, el borde del trampolín oscila con la posición dada por $s (t) = - 5cos(t)$ cm en $t$ segundos después del salto.
203. El número de hamburguesas vendidas en un restaurante de comida rápida en Pasadena, California, viene dado por $y = 10 + 5sinx$ donde $y$ es el número de hamburguesas vendidas y $x$ representa el número de horas después de que el restaurante abriera a las 11 am hasta las 11 pm que es la hora de cierre. Encuentra $y'$ y determina los intervalos en los que aumenta la cantidad de hamburguesas que se venden. (Solución)
204. [T] La cantidad de lluvia por mes en Phoenix, Arizona, se puede aproximar por $y (t) = 0.5 + 0.3cost$, donde $t$ son los meses trascurridos desde enero. Encuentra $y ′$ y usa una calculadora para determinar los intervalos en los que la cantidad de lluvia que cae está disminuyendo.
 Para los siguientes ejercicios, usa la regla del cociente para derivar las ecuaciones dadas.
Para los siguientes ejercicios, usa la regla del cociente para derivar las ecuaciones dadas.
205. $\frac{d}{dx} (cotx) = - csc^2(x)$(Solución)
206. $\frac{d}{dx} (secx) = sec(x)tan(x)$
207. $\frac{d}{dx} (cscx) = - csc(x)cot(x)$ (Solución)
208. Usa la definición de derivada y la identidad $cos (x + h) = cosx \cdot cosh − senx \cdot senh$ para demostrar que $\frac{d (cosx)}{ dx} = −senx$.
 Para los siguientes ejercicios, encuentra la derivada de orden superior solicitada para las funciones dadas.
Para los siguientes ejercicios, encuentra la derivada de orden superior solicitada para las funciones dadas.
209. $\frac{d^3y}{dx^3}$ de $y = 3cosx$(Solución)
210. $\frac{d^2y}{dx^2}$ de $y = 3sinx + x^2cosx$
211. $\frac{d^4y}{dx^4}$ de $y = 5cosx$(Solución)
212. $\frac{d^2y}{dx^2}$ de $y = secx + cotx$
213. $\frac{d^3y}{dx^3}$ de $y = x^10 − secx$ (Solución)
Objetivos de aprendizaje
Hemos visto las técnicas para derivar funciones básicas ($x^n$, $sen(x)$, $cos(x)$, etc.) así como las reglas para derivar las sumas, diferencias, productos, cocientes y producto por constantes de estas funciones. Sin embargo, estas técnicas no nos permiten derivar funciones compuestas, como $h (x) = sen (x^3)$ o $k (x) = \sqrt{3x^2 + 1}$. En esta sección, estudiamos la regla para encontrar la derivada de la composición de dos o más funciones.
Cuando tenemos una función que es una composición de dos o más funciones, podríamos usar todas las técnicas que ya hemos aprendido para derivarla. Sin embargo, considerar estas técnicas para dividir una función en partes más simples que podamos derivar puede resultar engorroso. En cambio, resulta más fácil utilizar la regla de la cadena, que establece que la derivada de una función compuesta es la derivada de la función externa evaluada en la función interna multiplicada por la derivada de la función interna.
Para poner esta regla en contexto, echemos un vistazo a un ejemplo: $h (x) = sen (x^3)$. Podemos pensar en la derivada de esta función con respecto a $x$ como la tasa de cambio de $sen (x^3)$ en relación con la variación de $x$. En consecuencia, queremos saber cómo cambia $sen (x^3)$ a medida que cambia $x$. Podemos pensar en este situación como una reacción en cadena: a medida que $x$ cambia, $x^3$ cambia, lo que conduce a un cambio en $sen (x^3)$. Esta reacción en cadena nos da pistas sobre lo que implica el cálculo de la derivada de $sen (x^3)$. En primer lugar, un cambio en $x$ que obliga a un cambio en $x^3$ sugiere que de alguna manera está involucrada la derivada de $x^3$. Además, el cambio en $x^3$ que obliga a un cambio en $sen(x^3)$ sugiere que la derivada de $sen(u)$ con respecto a $u$, donde $u = x^3$, también es parte de la derivada final.
Podemos echar un vistazo más formal a la derivada de $h (x) = sen (x^3)$ estableciendo el límite que nos daría la derivada en un valor específico $a$ en el dominio de $h (x) = sen(x^3)$. \[h'\left( a \right) = \mathop {\lim }\limits_{x \to a} \frac{{sen\left( {{x^3}} \right) - sen\left( {{a^3}} \right)}}{{x - a}}\]
Esta expresión no parece particularmente útil; sin embargo, podemos modificarla multiplicando y dividiendo por la expresión $x^3 - a^3$ para obtener \[h'\left( a \right) = \mathop {\lim }\limits_{x \to a} \frac{{sen\left( {{x^3}} \right) - sen\left( {{a^3}} \right)}}{{x^3 - a^3}} \cdot \frac{{{x^3} - {a^3}}}{{x - a}}\]
De la definición de la derivada, podemos ver que el segundo factor es la derivada de $x^3$ en $x = a$. Es decir, \[\mathop {\lim }\limits_{x \to a} \frac{{{x^3} - {a^3}}}{{x - a}} = \frac{d}{{dx}}{\left( {{x^3}} \right)_{x = a}} = 3{a^2}\]
Sin embargo, podría ser un poco más difícil reconocer que el primer término también es una derivada. Podemos ver esto haciendo $u = x 3$ y observando que cuando $x \to a$, $u \to {a^3}$: \[\mathop {\lim }\limits_{x \to a} \frac{{sen\left( {{x^3}} \right) - sen\left( {{a^3}} \right)}}{{{x^3} - {a^3}}} = \mathop {\lim }\limits_{u \to {a^3}} \frac{{sen\left( u \right) - sen\left( {{a^3}} \right)}}{{u - {a^3}}}\] \[ = \frac{d}{{du}}{\left( {senu} \right)_{u = {a^3}}} = \cos \left( {{a^3}} \right)\]
Por tanto, $h ' (a) = cos (a^3) ·3a^2$.
En otras palabras, si $h (x) = sen (x^3)$, entonces $h ' (x) = cos (x^3) ·3x^2$. Por lo tanto, si pensamos en $h (x) = sen (x^3)$ como la composición $(f \circ g) (x) = f (g (x))$ donde $f (x) = sen x$ y $g (x) = x^3$, entonces la derivada de $h (x) = sen (x^3)$ es el producto de la derivada de $g (x) = x^3$ y la derivada de la función $f (x) = sen(x)$ evaluada en la función $g (x) = x^3$. En este punto, anticipamos que para $h (x) = sen (g (x))$, es muy probable que $h ' (x) = cos (g (x)) g ' (x)$. Como determinamos anteriormente, este es el caso de $h (x) = sen (x^3)$
Ahora que hemos visto un ejemplo de derivada, planteamos el caso general y luego lo aplicaremos a otras funciones compuestas. Se proporciona una prueba informal al final de la sección.
Regla: la regla de la cadena
Sean $f$ y $g$ funciones. Para todo $x$ en el dominio de $g$ de forma que $g$ es derivable en $x$ y $f$ es derivable en $g (x)$, la derivada de la función compuesta $h (x) = (f \circ g) (x) = f (g (x))$ viene dada por $$h ' (x) = f ' (g (x)) g ' (x) \tag{$3.17$}$$
Puedes ver una interpretación de la regla de la cadena en este http://webspace.ship.edu/msrenault/ que incluye la escena que se muestra en la página siguiente.
 En la siguiente escena interactiva se muestra un ejemplo de la regla de la cadena.
En la siguiente escena interactiva se muestra un ejemplo de la regla de la cadena.
En el applet vemos una rueda $x$, una rueda $u$ y una rueda $y$. Podemos cambiar la velocidad de la rueda $x$, y se pueden conectar las ruedas con correas y cambiar sus radios. Usaremos este modelo para explorar la regla de la cadena y tratar de obtener una comprensión intuitiva de la fórmula que nos da la derivada de la función compuesta.
Nota: Al aplicar la regla de la cadena a la composición de dos o más funciones, tenga en cuenta que trabajamos desde la función exterior hacia adentro. También es útil recordar que la derivada de la composición de dos funciones se puede considerar como tener dos partes; la derivada de la composición de tres funciones tiene tres partes; y así. Además, recuerda que nunca evaluamos una derivada en una derivada.
Las reglas de la cadena y de la potencia combinadas
Ahora podemos aplicar la regla de la cadena a funciones compuestas, pero debemos tener en cuenta que a menudo necesitamos usarla combinada con con otras reglas. Por ejemplo, para encontrar las derivadas de funciones de la forma $h (x) = (g (x))^n$, necesitamos usar la regla de la cadena combinada con la regla de la potencia.
Para hacerlo, podemos pensar en $h (x) = (g (x))^n $ como $f (g (x))$ donde $f (x) = x^n.$ Entonces $f ' (x) = nx^{n - 1}$. Por lo tanto, $f ' (g (x)) = n (g (x))^{n - 1}$. Esto nos lleva a la derivada de una función potencial usando la regla de la cadena, $$h ' (x) = n (g (x))^{n - 1}g ' (x)$$
Regla de la potencia para la composición de funciones
Para todos los valores de $x$ para los que está definida la derivada, si $h (x) = \left(g (x)\right)^ n$ entonces $$h ' (x) = n (g (x))^{n - 1}g ' (x) \tag{$3.18$}$$
 |
3.48 Reglas de la cadena y de la potencia |
Encuentra la derivada de $h (x) = \frac{1} {(3x2 + 1)^2}$.

 |
Cuestión 3.34 |
Encuentra la derivada de $h (x) = (2x^3 + 2x - 1)^4$.
 |
3.49 Reglas de la cadena y la potencia con una función trigonométrica |
Encuentra la derivada de $h (x) = sen^3x$.

 |
3.50 Encontrar la ecuación de una recta tangente |
Encontrar la ecuación de la recta tangente a la gráfica de $h (x) = \frac{1} {(3x - 5)^2}$ en $x = 2$
.
 |
Cuestión 3.35 |
Encuentra la ecuación de la recta tangente a la gráfica de $f (x) = (x^2-2)^3$ en $x = -2.$
Ahora que podemos combinar la regla de la cadena y la regla de la potencia, examinamos cómo combinar la regla de la cadena con las otras reglas que hemos aprendido. En particular, podemos usarlo con las fórmulas para las derivadas de funciones trigonométricas o con la regla del producto.
 |
3.51 Regla de la cadena en una función coseno general |
Encuentra la derivada de $h (x) = cos (g (x))$.

En el siguiente ejemplo aplicamos la regla que acabamos de obtener en el ejemplo anterior.
 |
3.52 Usar la regla de la cadena en una función coseno |
Encuentra la derivada de $h (x) = cos (5x^2)$.

 |
3.53 Usar la regla de la cadena en otra función trigonométrica |
Encuentra la derivada de $h (x) = sec (4x^5 + 2x)$.

 |
Cuestión 3.36 |
Encuentra la derivada de $h (x) = sen (7x + 2)$.
En este punto, proporcionamos una lista de fórmulas derivadas que se pueden obtener aplicando la regla de la cadena junto con las fórmulas para derivadas de funciones trigonométricas. Sus derivadas son similares a las utilizadas en el ejemplo 3.51 y el ejemplo 3.53. Por conveniencia, las fórmulas también se dan en la notación de Leibniz, que algunos estudiantes encuentran más fácil de recordar. (Discutimos la regla de la cadena usando la notación de Leibniz al final de esta sección.)
No es absolutamente necesario memorizarlas como fórmulas separadas ya que todas son aplicaciones de la regla de la cadena a fórmulas aprendidas previamente.
TEOREMA 3.10. Usar la regla de la cadena con funciones trigonométricas
Para todos los valores de $x$ para los que se define la derivada,
 |
3.54 Combinando la regla de la cadena con la regla del producto |
Encuentra la derivada de $h (x) = (2x + 1)^5 (3x - 2)^7$.

 |
Cuestión 3.37 |
Encuentra la derivada de $h (x) = \frac{x} {(2x + 3)^3}$.
Ahora podemos combinar la regla de la cadena con otras reglas para derivar funciones, cuado estemos derivando la composición de tres o más funciones, necesitaremos aplicar la regla de la cadena más de una vez. Si miramos esta situación en términos generales, podemos generar una fórmula, pero no necesitamos recordarla, ya que simplemente podemos aplicar la regla de la cadena varias veces.
En primer lugar debemos detectar las funciones $f$, $g$ y $h$ de forma que $$k (x) = h (f (g (x)))$$
Posteriormente, se apica la regla de la cadena una vez, obteniendo $$k ' (x) = \frac{d}{dx} (h (f (g (x))) = h '(f (g (x))) ·\frac{d}{dx}f ((g (x)))$$
Aplicando la regla de la cadena nuevamente, obtenemos $$k ' (x) = h ' (f (g (x)) f ' (g (x)) g ' (x))$$
Para todos los valores de $x$ para los cuales la función es derivable, si $k (x) = h (f (g (x))),$
se cumpmle $$k ' (x) = h ' (f (g (x))) f ' (g (x)) g ' (x).$$
Observa que la derivada de la composición de tres funciones tiene tres factores. De manera similar, la derivada de la composición de cuatro funciones tiene cuatro factores, y así sucesivamente. Además, recuerda, siempre podemos trabajar de afuera hacia adentro, tomando una derivada a la vez.
 |
3.55 Derivar una función compuesta de tres funciones |
Encuentra la derivada de $k (x) = cos^4(7x^2 + 1)$.

 |
Cuestión 3.38 |
Encuentra la derivada de $h (x) = sen^6 (x^3)$.
 |
3.56 Usando la regla de la cadena en un problema de velocidad |
Una partícula se mueve a lo largo de un eje de coordenadas. Su posición en el tiempo $t$ está dada por $s (t) = sen (2t) + cos (3t)$. ¿Cuál es la velocidad de la partícula en el tiempo $t = \pi/6$?

 |
Cuestión 3.39 |
Una partícula se mueve a lo largo de un eje de coordenadas. Su posición en el tiempo $t$ viene dada por $s (t) = sen (4t)$. Encuentra su aceleración en el tiempo $t$.
Prueba
En este punto, presentamos una prueba muy informal de la regla de la cadena. En aras de la simplicidad, ignoramos ciertos problemas: por ejemplo, asumimos que $g (x) \neq g (a)$ para $x \neq a$ en algún intervalo abierto que contenga al punto $a$. Comenzamos aplicando la definición límite de la derivada a la función $h (x)$ para obtener $h ' (a)$: \[h'\left( a \right) = \mathop {\lim }\limits_{x \to a} \frac{{f\left( {g\left( x \right)} \right) - f\left( {g\left( a \right)} \right)}}{{x - a}}\] Reescribiendo, obtenemos
Aunque está claro que \[\mathop {\lim }\limits_{x \to a} \frac{{g\left( x \right) - g\left( a \right)}}{{x - a}} = g'\left( a \right)\] no es obvio que \[\mathop {\lim }\limits_{x \to a} \frac{{f\left( {g\left( x \right)} \right) - f\left( {g\left( a \right)} \right)}}{{g(x) - g(a)}} = f'\left( {g\left( a \right)} \right)\] Para ver que esto es cierto, primero recuerda que dado que $g$ es derivable en $a$, $g$ también es continua en $a$. Así, \[\mathop {\lim }\limits_{x \to a} g\left( x \right) = g\left( a \right)\]
Luego, considerando la sustitución $y = g (x)$ y $b = g (a)$ y usando el cambio de variables en el límite se obtiene \[\mathop {\lim }\limits_{x \to a} \frac{{f\left( {g\left( x \right)} \right) - f\left( {g\left( a \right)} \right)}}{{x - a}} = \mathop {\lim }\limits_{y \to b} \frac{{f\left( y \right) - f\left( f \right)}}{{y - b}} = f'\left( b \right) = f'\left( {g\left( a \right)} \right)\]
Finalmente, \[h'\left( a \right) = \mathop {\lim }\limits_{x \to a} \frac{{f\left( {g\left( x \right)} \right) - f\left( {g\left( a \right)} \right)}}{{g\left( x \right) - g\left( a \right)}} \cdot \frac{{g\left( x \right) - g\left( a \right)}}{{x - q}} = f'\left( {g\left( a \right)} \right)g'\left( a \right)\]
 |
3.57 Usando la regla de la cadena con valores funcionales |
Sea $h (x) = f (g (x))$. Si $g (1) = 4$, $g ' (1) = 3$ y f$ ' (4) = 7$, calcula $h ' (1)$.

 |
Cuestión 3.40 |
Dado $h (x) = f (g (x))$. Si $g (2) = - 3$, $g ' (2) = 4$ y $f ' (- 3) = 7$, encuentra $h ' (2)$.
Al igual que con otras derivadas que hemos visto, podemos expresar la regla de la cadena utilizando la notación de Leibniz. Esta notación para la regla de la cadena se usa mucho en aplicaciones físicas.
Para $h (x) = f (g (x))$, sea $u = g (x)$ e $y = h (x) = f (u)$. Así, $$h ' (x) = \frac{dy}{dx}, f ' (g (x)) = f ' (u) =\frac{dy}{du} \,\,\,\,y\,\,\,\,g ' (x) = \frac{du}{dx}.$$
Por consiguiente, $$\frac{dy}{dx}= h ' (x) = f ' (g (x)) g ' (x) = \frac{dy}{du}· \frac{du}{dx}.$$
Regla de cadena usando la notación de Leibniz
Si $y$ es una función de $u$, y $u$ es una función de $x$, entonces $$\frac{dy}{dx} = \frac{dy}{du}· \frac{du}{dx}.$$
 |
3.58 Calcular la derivada usando la notación de Leibniz, Ejemplo 1 |
Encuentra la derivada de $y = (\frac{x}{3x + 2})^5$.

 |
3.59 Calcular la derivada usando la notación de Leibniz, Ejemplo 2 |
Encuentra la derivada de $y = tg(4x^2-3x + 1)$

 |
Cuestión 3.41 |
Usa la notación de Leibniz para encontrar la derivada de $y = cos (x^3)$. Asegúrate de que la respuesta final se exprese enteramente en términos de la variable $x$.
 3.7.5 Ejercicios
3.7.5 Ejercicios Para los siguientes ejercicios, dado $y=f(u)$ y $u=g(x)$, encuentra $\frac{dy}{dx}$ utilizando la notación de Leibniz para la regla de la cadena $\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$
Para los siguientes ejercicios, dado $y=f(u)$ y $u=g(x)$, encuentra $\frac{dy}{dx}$ utilizando la notación de Leibniz para la regla de la cadena $\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$
214. $y=3u-6$, $u=2x^2$
215. $y=6u^3$, $u=7x-4$ (Solución)
216. $y=sen(u)$, $u=x-1$
217. $y=cos(u)$, $u=\frac{-x}{8}$ (Solución)
218. $y=tg(u)$, $u=9x+2$
219. $y=\sqrt(4u+3)$, $u=x^2-6x$ (Solución)
 Para cada un de los siguientes ejercicios
Para cada un de los siguientes ejercicios
220. $y=(3x-2)^6$
221. $y=(3x^2+1)^3$ (Solución)
222. $y=sen^5(x)$
223. $y=\left(\frac{x}{7}+\frac{7}{x}\right)^7$ (Solución)
224. $y=tan(sec(x))$
225. $y=csc(\pi x+1)$ (Solución)
227. $y=-6sen^{-3}x$ (Solución)
 Para los siguientes ejericios, encuentra $\frac{dy}{dx}$.
Para los siguientes ejericios, encuentra $\frac{dy}{dx}$.
228. $y=\left( 3x^2+3x-1 \right)^4$
229. $y=\left( 5-2x \right)^{-2}$ (Solución)
230. $y=cos^3(\pi x)$
231. $y=\left( 2x^3-x^2+6x+1 \right)^3$ (Solución)
232. $y=\frac{1}{sen^2(x)}$
233. $y=(tgx+senx)^{-3}$ (Solución)
234. $y=x^2 cos^4(x)$
235. $y=sen(cos(7x))$ (Solución)
236. $y=\sqrt{6+sec(\pi x^2)}$
237. $y=cot^3(4x+1)$ (Solución)
238. Sea $y=[f(x)]^3$ y supongamos que $f\prime(1)=4$ y $\frac{dy}{dx}=10$ donde $x=1$. Encuentra $f(1)$.
239. Sea $y=(f(x)+x^2)^4$ y supongamos que $f(-1)=-4$ y $\frac{dy}{dx}=3$ donde $x=-1$. Encontrar $f\prime(-1)$. (Solución)
240. Sea $y=(f(u)+3x)^2$ y $u=x^3-2x$. Si $f(1)=6$ y $\frac{dy}{dx}=18$ donde $x=2$. Encontrar $f\prime(4)$.
241. [T] Encuentra la ecuación de la recta tangente a $y=-sen\left(\frac{x}{2}\right)$ en el origen. Utiliza una calculadora gráfica para representar juntas la función y la recta tangente. (Solución)
242. [T] Encuentra la ecuación de la recta tangente a $y=\left(3x+\frac{1}{x}\right)$ en el punto $(1,16)$. Utiliza una calculadora gráfica para representar juntas la función y la recta tangente.
243. Encuentra la coordenada $x$ en la que la tangente a $y = {\left( {x - {6 \over x}} \right)^8}$ es horizontal. (Solución)
244. [T] Encuentra la ecuación de la recta tangente que es normal a $g(\theta)=sen^{2}(\pi \theta)$ en el punto $\left( \frac{1}{4},\frac{1}{2} \right)$. Utiliza una calculadora para representar en una misma gráfica la función y la recta normal.
 Para las siguientes ejercicios, utiliza la información de la tabla y encuentra $h\prime(a)$ en el valor dado para $a$.
Para las siguientes ejercicios, utiliza la información de la tabla y encuentra $h\prime(a)$ en el valor dado para $a$.
| $x$ | $f(x)$ | $f\prime(x)$ | $g(x)$ | $g\prime(x)$ |
| 0 | 2 | 5 | 0 | 2 |
| 1 | 1 | -2 | 3 | 0 |
| 2 | 4 | 4 | 1 | -1 |
| 3 | 3 | -5 | 2 | 3 |
245. $h(x)=f(g(x))$, $a=0$
246. $h(x)=g(f(x))$, $a=0$
247. $h(x)=\left(x^4+g(x)\right)^{-2}$, $a=1$ (Solución)
248. $h(x)=\left( \frac{f(x)}{g(x)} \right)^{-2}$, $a=3$
249. $h(x)=f\left( x+f(x)\right)^{-2}$, $a=1$ (Solución)
250. $h(x)=f\left( 1+g(x)\right)^{3}$, $a=2$
251. $h(x)=g\left( 2+f(x^2)\right)$, $a=1$ (Solución)
252. $h(x)=f\left( f(sen(x))\right)$, $a=0$
253. [T] La función de posición de un tren de carga viene dado por $s(t)=100(t+1)^{-2}$, con $s$ en metros y $t$ en segundos. En el instante $t=6 seg.$, encuentra
254. [T] Una masa que cuelga de un resorte vertical está en movimiento armónico simple dado por la siguiente función de posición: $s(t)=-3cos\left(\pi t + \frac{pi}{4} \right)$, donde $t$ se mide en segundos y $s$ está en pulgadas.
255. El coste total para producir $x$ cajas de las galletas Thin Mint Girl Scout son $C$ dólares, donde $C = 0.0001x^3 - 0.02x^2 + 3x + 300$. En $t$ semanas la producción se estima en $x = 1600 + 100t$ cajas.
256. [T] La fórmula para el área de un círculo es $A = \pi r^2$, donde $r$ es el radio del círculo. Supongamos que un círculo está expandiéndose, lo que significa que tanto el área $A$ como el radio $r$ (en pulgadas) se están expandiendo.
257. [T] La fórmula para el volumen de una esfera es $S = \frac{4}{3} \pi r^3$, donde $r$ (en pies) es el radio de la esfera. Suponga que una bola de nieve esférica se derrite al sol.
258. [T] La temperatura diaria en grados Fahrenheit de Phoenix en el verano se puede modelar por la función $T(x) = 94 - 10cos\left[ {{\pi \over {12}}(x - 2)} \right]$,donde $x$ es el número de horas a partir de la medianoche. Encuentra la velocidad a la que la temperatura está cambiando a las 4 p.m.
259. [T]La profundidad (en pies) del agua en un dique cambia con la subida y bajada de las mareas. La profundidad está modelada por la función $D(t) = 5sen\left( {{\pi \over 6} - {{7\pi } \over 6}} \right)$ donde $t$ es el número de horas después de la medianoche. Encuentra la tasa a la que la profundidad está cambiando a las 6 a.m. (Solución)
Objetivos de aprendizaje
En esta sección exploramos la relación entre la derivada de una función y la derivada de su inversa. Para funciones cuyas derivadas ya conocemos, podemos usar esta relación para encontrar derivadas de sus funciones inversas sin tener que usar la definición de límite de la derivada. En particular, lo aplicaremos a las funciones trigonométricas. Esta fórmula también se puede usar para extender la regla de la potencia a exponentes racionales.
Comenzamos considerando una función y su inversa. Si $f (x)$ es invertible y derivable, parece razonable que la inversa de $f (x)$ también sea derivable. La Figura 3.28 muestra la relación entre una función $f (x)$ y su inversa $f ^{- 1}(x)$. Observa el punto $(a, f^{- 1} (a))$ en la gráfica de $f^{- 1} (x)$ que tiene una recta tangente con una pendiente de $(f^{- 1}) ' (a) = \frac{p}{q}$. Este punto corresponde a un punto $(f^{- 1}(a), a)$ en la gráfica de $f (x)$ que tiene una recta tangente con una pendiente de $f ' (f^{- 1} (a)) = \frac{q}{p}$.
Por lo tanto, si $f^{- 1}(x)$ es derivable en $a$, entonces se tiene que $$(f^{ - 1}) ' (a) = \frac{1}{f ' (f^{- 1} (a))}.$$
Figura 3.28 Las rectas tangentes de una función y su inversa están relacionadas; también lo son las derivadas de estas funciones.
 En la siguiente escena interactiva incorporamos un applet que permite relacionar la derivada de una función y su inversa.
En la siguiente escena interactiva incorporamos un applet que permite relacionar la derivada de una función y su inversa.
Estas funciones son simétricas con respecto a la recta $y = x$. La recta tangente de la función $f (x)$ en el punto $(f^{- 1} (a), a)$ y la recta tangente de la función $f^{- 1} (x)$ en $(a, f ^{- 1}(a))$ también son simétricas sobre la recta $y = x$. Específicamente, si la pendiente de uno fuera $p / q$, entonces la pendiente del otro sería $q / p$. Por último, sus derivadas también son simétricas con respecto a la recta $y = x$.
También podemos obtener la fórmula para la derivada de la inversa recordando primero que $x = f (f^{- 1}(x))$. Luego, al derivar ambos lados de esta ecuación (usando la regla de la cadena a la derecha), obtenemos $$1 = f ' (f^{- 1}(x)) (f^{- 1}) ' (x)).$$ Despejando $(f^{- 1}) ' (x)$, obtenemos $$(f^{- 1}) ' (x) = \frac{1}{f ' (f^{- 1} (x))} \tag{$3.19$}$$
Resumimos este resultado en el siguiente teorema.
TEOREMA 3.11. Teorema de la función inversa
Sea $f (x)$ una función que es invertible y derivable. Sea $y = f^{- 1} (x)$ la función inversa de $f (x)$. Para todo $x$ que satisfaga $f ' (f - 1 (x)) \neq 0$, $$\frac{dy}{dx} = \frac{d}{dx} (f^{- 1} (x)) = (f^{- 1}) ' (x) = \frac{1}{f ' (f^{- 1} (x))}.$$
 |
3.60 Aplicación del teorema de la función inversa |
Usa el teorema de la función inversa para encontrar la derivada de $g (x) =\frac{ x + 2}{x}$. Compara la derivada resultante con la obtenida al derivar la función directamente.

 |
Cuestión 3.42 |
Usa el teorema de la función inversa para encontrar la derivada de $g (x) = \frac{1}{x + 2}$. Compara el resultado obtenido al derivar $g (x)$ directamente.
 |
Cuestión 3.43 |
Encuentra la derivada de $g (x) =\sqrt[5]{x}$ aplicando el teorema de la función inversa.
 |
3.61 Aplicación del teorema de la función inversa |
Usa el teorema de la función inversa para encontrar la derivada de $g (x) =\sqrt[3]{x}$.

En el ejemplo anterior, vemos que podemos usar el teorema de la función inversa para extender la regla de la potencia a exponentes de la forma $\frac{1}{n}$, donde $n$ es un número entero positivo. Esta extensión finalmente nos permitirá derivar $x^q$, donde $q$ es cualquier número racional.
TEOREMA 3.12. Extendiendo la regla de la potencia a exponentes racionales
La regla de la potencia se puede extender a exponentes racionales. Es decir, si $n$ es un número entero positivo, entonces $$\frac{d}{dx} (x^{1 / n}) = \frac{1}{n}x^{(1 / n) -1}. \tag{$3.20$}$$
Además, si $n$ es un número entero positivo y $m$ es un número entero arbitrario, entonces $$\frac{d}{dx} (x^{m / n}) = \frac{m}{n}x^{(m / n) -1}. \tag{$3.21$}$$
Prueba
La función $g (x) = x^{1 / n}$ es la inversa de la función $f (x) = x^n$. Dado que $ g ' (x) = \frac{1}{f ' (g (x))}$, comenzamos por encontrar $f ' (x)$. Así, $$f ' (x) = nx^{n - 1}\,\,\,\,\,\, y\,\,\,\,\,\,f ' (g (x)) = n (x^{1 / n})^{n - 1} = nx^{(n - 1) / n}.$$ Finalmente, $$g ' (x) = \frac{1}{n}x^{(n - 1) / n} = \frac{1}{n}x^{(1 - n) / n} = \frac{1}{n}x^{(1 / n) -1}.$$ Para derivar $x^{m / n}$ debemos reescribirlo como $(x^{1 / n})^m$ y aplicar la regla de la cadena. Así, $$\frac{d}{dx} (x^{m / n}) = \frac{d}{dx} ((x^{1 / n})^m) =$$ $$=m (x^{1 / n}) {m - 1}·\frac{1}{n}x ^{1 / n) -1} = \frac{m}{n}x^{(m / n) -1}.$$
 |
3.62 Aplicación de la regla del poder a un poder racional |
Encuentra la ecuación de la recta tangente a la gráfica de $y = x^{2 / 3}$ en $x = 8$.

 |
Cuestión 3.44 |
Encuentra la derivada de $s (t) = \sqrt{2t+1}$.
Ahora dirigimos nuestra atención a encontrar derivadas de funciones trigonométricas inversas. Estas derivadas resultarán de aplicación en el estudio de la integración en la parte II de este libro. Las derivadas de funciones trigonométricas inversas son bastante sorprendentes porque sus derivadas son en realidad funciones algebraicas. Anteriormente, las derivadas de funciones algebraicas han demostrado ser funciones algebraicas y las derivadas de funciones trigonométricas han demostrado ser funciones trigonométricas. Aquí, por primera vez, vemos que la derivada de una función no necesita ser del mismo tipo que la función original.
 |
3.63 Derivada de la función inversa del seno |
Usa el teorema de la función inversa para encontrar la derivada de $g (x) = sen^{- 1}x$.

 |
3.64 Aplicación de la regla de la cadena a la función inversa del seno |
Aplica la regla de la cadena a la fórmula obtenida en el Ejemplo 3.61 para encontrar la derivada de $h (x) = sen^{- 1} (g (x))$ y usa este resultado para encontrar la derivada de $h (x) = sen^{- 1} (2x^3)$.

 |
Cuestión 3.45 |
Usa el teorema de la función inversa para encontrar la derivada de $g (x) = tg^{- 1}x$.
Las derivadas de las funciones trigonométricas inversas restantes también se pueden encontrar utilizando el teorema de la función inversa. Estas fórmulas se proporcionan en el siguiente teorema.
TEOTEMA 3.13. Derivadas de funciones trigonométricas inversas
$$\frac{d}{dx}sen^{- 1}x = \frac{1}{\sqrt{1-x^2}} \tag{$3.22$}$$$$\frac{d}{dx}cos^{- 1}x = \frac{-1}{\sqrt{1-x^2}} \tag{$3.23$}$$ $$\frac{d}{dx}tan^{- 1}x = \frac{1}{1+x^2} \tag{$3.24$}$$ $$\frac{d}{dx}cot^{- 1}x = \frac{-1}{1+x^2} \tag{$3.25$}$$ $$\frac{d}{dx}sec^{- 1}x = \frac{1}{|x| \sqrt{x^2-1}} \tag{$3.26$}$$ $$\frac{d}{dx}csc ^{- 1}x = \frac{-1}{|x| \sqrt{x^2-1}} \tag{$3.27$}$$
 |
3.65 Aplicar fórmulas de derivación a una función de tangente inversa |
Encuentra la derivada de $f (x) = tg^{- 1} (x^2)$.

 |
3.66 Aplicando fórmulas de derivación a una función inversa del seno |
Encuentra la derivada de $h (x) = x^2sen^{ - 1}x$.

 |
Cuestión 3.46 |
Encuentra la derivada de $h (x) = cos^{- 1} (3x - 1)$.
 |
3.67 Aplicar la función inversa de la tangente |
La posición de una partícula en el tiempo $t$ viene dada por $s (t) = tan^{- 1} \left(\frac{1}{t}\right)$ para $t=12$. Encuentra la velocidad de la partícula en el tiempo $t = 1$.

 |
Cuestión 3.47 |
Encuentra la ecuación de la recta tangente a la gráfica de $f (x) = sen^{- 1}{x}$ en $x = 0$.
 3.8.3 Ejercicios
3.8.3 Ejercicios Para los siguientes ejercicios, utilizando la gráfica de $y = f (x)$
Para los siguientes ejercicios, utilizando la gráfica de $y = f (x)$
260.
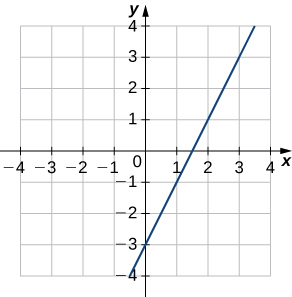
261.
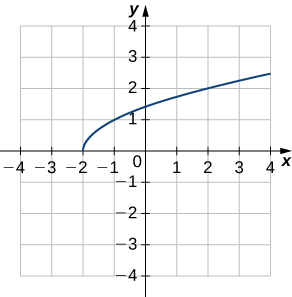 (Solución)
(Solución)
262. 
263. 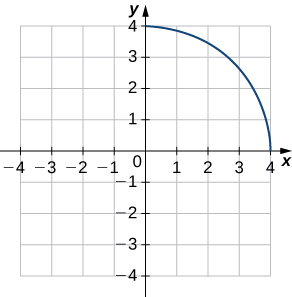 (Solución)
(Solución)
 Para los siguientes ejercicios, usa las funciones $y = f (x)$ para encontrar
Para los siguientes ejercicios, usa las funciones $y = f (x)$ para encontrar
264. $f (x) = 6x − 1$, $x = −2$
265. $f (x) = 2x^3−3$, $x = 1$ (Solución)
266 $f (x) = 9 − x^2$, $0\le x \le 3$, $x = 2$
267. $f (x) = senx$, $x = 0$ (Solución)
 Para cada una de las siguientes funciones, encuentra $(f^{− 1})'(a)$.
Para cada una de las siguientes funciones, encuentra $(f^{− 1})'(a)$.
268. $f (x) = x^2 + 3x + 2$, $x\ge \frac{− 3}{2}$, $a = 2$
269. $f (x) = x^3 + 2x + 3$, $a = 0$ (Solución)
270. $f (x) = x + \sqrt{x}$, $a = 2$
271. $f (x) = x − \frac{2}{x}$, $x < 0$, $a = 1$ (Solución)
272. $f (x) = x + senx$, $a = 0$
273. $f (x) = tanx + 3x^2$, $a = 0$ (Solución)
 Para cada una de las funciones dadas $y = f (x)$,
Para cada una de las funciones dadas $y = f (x)$,
274. $f (x) = \frac{4}{1+x^2}$, $P (2,1)$
275. $f (x) =\sqrt{x-4}$, $P (2,8)$ (Solución)
276. $f (x) = (x^3 + 1)^4$, $P (16,1)$
277. $f (x) = - x^3 − x + 2$, $P (−8,2)$ (Solución)
278. $f (x) = x^5 + 3x^3−4x − 8$, $P (−8,1)$
 Para los siguientes ejercicios, encuentra $\frac{dy}{dx}$ para la función dada.
Para los siguientes ejercicios, encuentra $\frac{dy}{dx}$ para la función dada.
279. $y = sin^{− 1} (x^2)$ (Solución)
280. $y = cos^{− 1} (\sqrt{x})$
281. $y = sec^{− 1} \left( \frac{1}{x} \right)$ (Solución)
282. $y = \sqrt{csc^{− 1}x}$
283. $y = \left(1 + tan^{− 1}x \right)^3$ (Solución)
284. $y = cos^{− 1}(2x) \cdot sin^{− 1} (2x)$
285. $y = \frac{1}{tan^{− 1} (x)}$ (Solución)
286. $y = sec^{− 1} (−x)$
287. $y = cot^{− 1}\sqrt{4 − x^2}$ (Solución)
288. $y = x \cdot csc^{− 1}x$
 Para los siguientes ejercicios, usa los valores dados para encontrar $(f^{− 1})'(a)$.
Para los siguientes ejercicios, usa los valores dados para encontrar $(f^{− 1})'(a)$.
289. $f (\pi) = 0$, $f'(\pi) = - 1$, $a = 0$ (Solución)
290. $f(6) = 2$, $f'(6) = 13$, $a = 2$
291. $f \left(\frac{1}{3}\right) = - 8$, $f '\left(\frac{1}{3}\right) = 2$, $a = −8$ (Solución)
292. $f (\sqrt{3}) = 12$, $f'(\sqrt{3}) = \frac{2}{3}$, $a = \frac{1}{2}$
293. $f(1) = - 3$, $f'(1) = 10$, $a = −3$ (Solución)
294. $f (1) = 0$, $f'(1) = - 2$, $a = 0$
295. [T] La posición de un disco de hockey en movimiento después de $t$ segundos es $s (t) = tan`{− 1}t$ donde $s$ está en metros.
296. [T] Un edificio de 225 pies de altura proyecta una sombra de varias longitudes $x$ a medida que pasa el día. Un ángulo de elevación $\theta$ está formado por líneas desde la parte superior e inferior del edificio hasta la punta de la sombra, como se ve en la siguiente figura.
Encuentra la tasa de cambio del ángulo de elevación $\frac{d\theta}{dx}$ cuando x = 272 pies.
297. [T] Un poste mide 75 pies de alto. Se forma un ángulo $\theta$ cuando se conectan cables de varias longitudes de $x$ pies desde el suelo hasta la parte superior del poste, como se muestra en la siguiente figura.
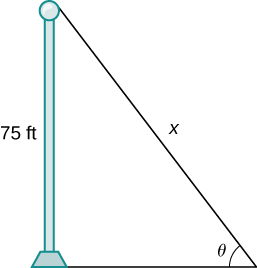
Encuentra la tasa de cambio del ángulo $\frac{d\theta}{dx}$ cuando se conecta un cable de 90 pies de longitud. (Solución)
298. [T] Una cámara de televisión a nivel del suelo está a 2000 pies de distancia de la plataforma de lanzamiento de un cohete espacial que está configurado para despegar verticalmente, como se ve en la siguiente figura.
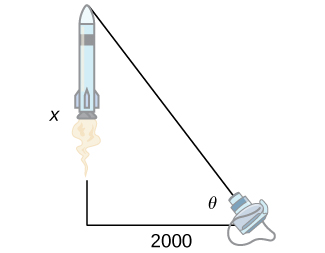
El ángulo de elevación de la cámara se puede encontrar mediante $\theta = tan^{− 1} \left(\frac{x}{2000}\right)$, donde $x$ es la altura del cohete. Encuentra la tasa de cambio del ángulo de elevación después del lanzamiento cuando la cámara y el cohete están separados por 5000 pies.
299. [T] Un cine local con una pantalla de 30 pies de altura que está a 10 pies por encima del nivel de los ojos de una persona cuando está sentada tiene un ángulo de visión $\theta$ (en radianes) dado por $\theta = cot^{− 1}\frac{x}{40} − cot^{− 1}\frac{x}{10}$, donde $x$ es la distancia en pies de la pantalla de cine a la que está sentada la persona, como se muestra en la siguiente figura.
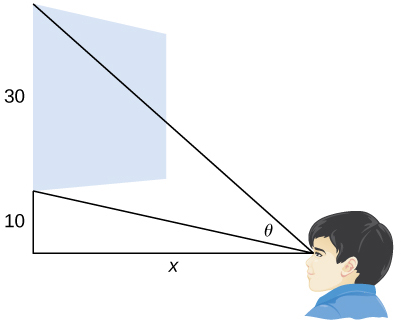
Objetivos de aprendizaje
Ya hemos estudiado cómo encontrar ecuaciones de rectas tangentes a funciones y la tasa de cambio de una función en un punto específico. En todos estos casos teníamos la ecuación explícita para la función y derivábamos estas funciones explícitamente. Supongamos, en cambio, que queremos determinar la ecuación de una recta tangente a una curva arbitraria o la tasa de cambio de una curva arbitraria en un punto. En esta sección, resolvemos estos problemas encontrando las derivadas de funciones que definen $y$ implícitamente en términos de $x$.
En la mayoría de las discusiones sobre matemáticas, si la variable dependiente $y$ es una función de la variable independiente $x$, expresamos $y$ en términos de $x$. Si este es el caso, decimos que $y$ es una función explícita de $x$. Por ejemplo, cuando escribimos la ecuación $y = x^2 + 1$, estamos definiendo $y$ explícitamente en términos de $x$. Por otro lado, si la relación entre la función $y$ y la variable $x$ se expresa mediante una ecuación en la que y no se expresa completamente en términos de $x$, decimos que la ecuación define $y$ implícitamente en términos de $x$. Por ejemplo, la ecuación $y - x^2 = 1$ define la función $y = x^2 + 1$ implícitamente.
La derivación implícita nos permite encontrar pendientes de tangentes a curvas que claramente no son funciones (fallan la prueba de la línea vertical). Estamos usando la idea de que porciones de $y$ son funciones que satisfacen la ecuación dada, pero que $y$ no es realmente una función de $x$.
En general, una ecuación define una función implícitamente si la función satisface esa ecuación. Una ecuación puede definir implícitamente muchas funciones diferentes. Por ejemplo, las funciones
$$y = \sqrt{25 - x^2}$$ $$y = \begin{cases} \sqrt{25-x^2} & \text{si $-5<x\lt $} \\ -\sqrt{25-x^2} & \text{si $0 <x<5$} \end{cases} $$ que se ilustran en la Figura 3.30, son solo tres de las muchas funciones definidas implícitamente por la ecuación $x^2 + y^2 = 25$.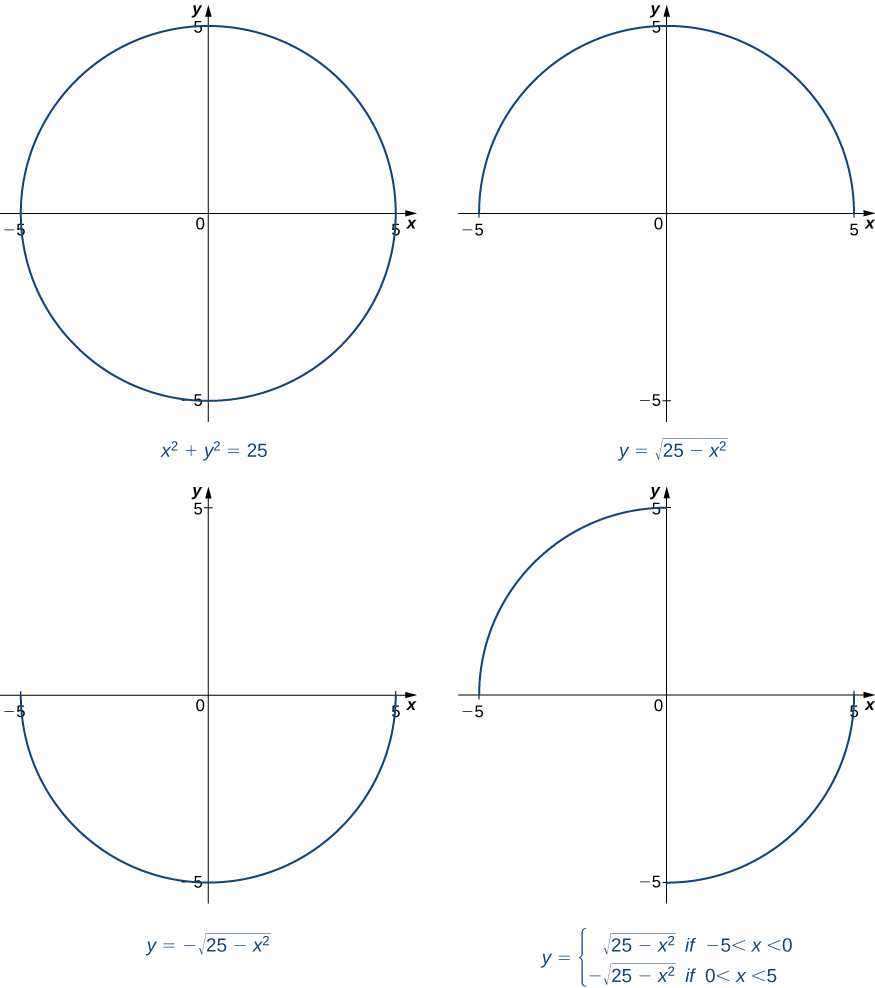
Figura 3.30 La ecuación $x^2 + y^2 = 25$ define muchas funciones implícitamente.
La circunferencia con radio 5 y centro en el origen está representado completamente en una imagen. A su derecha, solo se representa su gráfica en los cuadrantes I y II. En la parte inferior izquierda, se representa su gráfica en los cuadrantes III y IV y, a su derecha aparece su gráfica en los cuadrantes II y IV.
Si queremos encontrar la pendiente de la recta tangente a la gráfica de $x^2 + y^2 = 25$ en el punto $(3,4)$, podríamos evaluar la derivada de la función $y = \sqrt{25 - x^2}$ en $x = 3$. Por otro lado, si queremos la pendiente de la recta tangente en el punto $(3, -4)$, podríamos usar la derivada de $y = -\sqrt{25 - x^2}$. Sin embargo, no siempre es fácil despejar $y$ en una función definida implícitamente por una ecuación. Afortunadamente, la técnica de derivación implícita nos permite encontrar la derivada de una función definida implícitamente sin tener que despejar la función explícitamente. El proceso de encontrar $\frac{dy}{dx}$ usando la derivación implícita se describe en la siguiente estrategia de resolución de problemas.
Para realizar una derivación implícita en una ecuación que define una función y implícitamente en términos de una variable $x$, utiliza los siguientes pasos:
 |
3.68 Usar la derivación implícita |
Suponiendo que $y$ se define implícitamente por la ecuación $x^2 + y^2 = 25$, encuentra $\frac{dy}{dx}$.

 En la siguiente escena interactiva incorporamos un applet que permite obtener la derivada de varias funciones definidas de forma implícita utlizando la estrategia dada anteriormente.
En la siguiente escena interactiva incorporamos un applet que permite obtener la derivada de varias funciones definidas de forma implícita utlizando la estrategia dada anteriormente.
 |
3.69 Usa la derivación implícita y la regla del producto |
Suponiendo que $y$ se define implícitamente por la ecuación $x^3seny + y = 4x + 3$, encuentra $\frac{dy}{dx}$.

 |
3.70 Usando la derivación implícita para encontrar una segunda derivada |
Encuentra $\frac{d^2y}{dx^2}$ si $x^2 + y^2 = 25$.

 |
Cuestión 3.48 |
Encuentra $\frac{dy}{dx}$ para $y$ definida implícitamente por la ecuación $4x^5 + tg(y) = y^2 + 5x$.
Ahora que hemos visto la técnica de la derivación implícita, podemos aplicarla al problema de encontrar las ecuaciones de las rectas tangentes a curvas descritas implícitamente.
 |
3.71 Encontrando la recta tangente a una circunferencia |
Encuentra la ecuación de la recta tangente a la curva $x^2 + y^2 = 25$ en el punto $(3, -4)$.

 |
3.72 Hallar la ecuación de la recta tangente a una curva |
Encuentra la ecuación de la recta tangente a la gráfica de la curva $y^3 + x^3-3xy = 0$ en el punto $(32,32)$ (Figura 3.32). Esta curva se conoce como folio (u hoja) de Descartes. Se muestra un folio, que es una línea que crea un bucle que se cruza sobre sí mismo, en este caso,$(0, 0)$. Se muestra su recta tangente en $(3/2, 3/2)$.

 |
3.73 Aplicar la derivación implícita |
En un videojuego simple, un cohete viaja en una órbita elíptica cuya trayectoria se describe mediante la ecuación $4x^2 + 25y^2 = 100$.
El cohete puede disparar misiles a lo largo de líneas tangentes a su trayectoria. El objetivo del juego es destruir un asteroide entrante que viaja a lo largo del eje $X$ positivo hacia $(0,0)$. Si el cohete dispara un misil cuando está ubicado en $(3,85)$, ¿dónde se cruzará con el eje $X$?

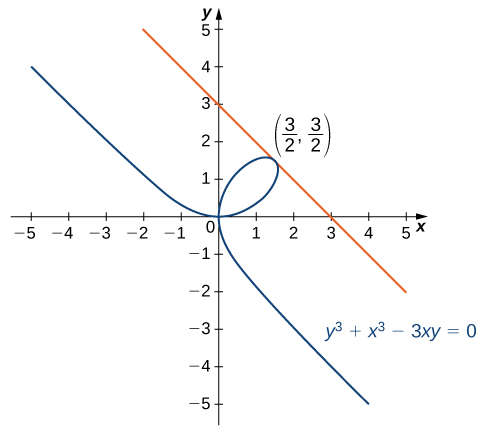
Figura 3.32 Encontrar la recta tangente al folio de Descartes en $(3/2,3/2)$.
 En la siguiente escena interactiva incorporamos un applet que permite obtener la derivada del folio de Descartes en distintos puntos.
En la siguiente escena interactiva incorporamos un applet que permite obtener la derivada del folio de Descartes en distintos puntos.
 |
Cuestión 3.49 |
Encuentra la ecuación de la recta tangente a la hipérbola $x^2 - y^2 = 16$ en el punto $(5,3)$.
 3.9.3 Ejercicios
3.9.3 Ejercicios Para los siguientes ejercicios, usa la derivación implícita y encuentra $\frac{dy}{dx}$.
Para los siguientes ejercicios, usa la derivación implícita y encuentra $\frac{dy}{dx}$.
300. $x^2 − y^2 = 4$
301. $6x^2 + 3y^2 = 12$ (Solución)
302. $x^2y = y − 7$
303. $3x^3 + 9xy^2 = 5x^3$ (Solución)
304. $xy − cos (xy) = 1$
305. $y\sqrt{x+4}= xy + 8$ (Solución)
306. $−xy − 2 = \frac{x}{7}$
307. $ysen (xy) = y^2 + 2$ (Solución)
308. $(xy)^2 + 3x = y^2$
309. $x^3y + xy^3 = −8$
 Para los siguientes ejercicios, encuentra la ecuación de la recta tangente a la gráfica de la función implícita dada en el punto indicado. Usa una calculadora o software de computadora para representar gráficamente la función y la recta tangente.
(Solución)
Para los siguientes ejercicios, encuentra la ecuación de la recta tangente a la gráfica de la función implícita dada en el punto indicado. Usa una calculadora o software de computadora para representar gráficamente la función y la recta tangente.
(Solución)
310. [T] $x^4y − xy^3 = −2$, $(- 1, −1)$
311. [T] $x^2y^2 + 5xy = 14$, $(2,1)$ (Solución)
312. [T] $tan (xy) = y$, $\left(\frac{\pi}{4},1\right)$
313. [T] $xy^2 + sen \left(\frac{pi}{y}\right) −2x^2 = 10$, $(2, −3)$ (Solución)
314. [T] $\frac{x}{y }+ 5x − 7 = −\frac{3}{4}y$, $(1,2)$
315. [T] $xy + sin (x) = 1$, $\left(\frac{\pi}{2},0\right)$ (Solución)
316.
[T] La gráfica de un folio de Descartes de ecuación $2x^3 + 2y^3−9xy = 0$ se da en la siguiente gráfica.
317. Para la ecuación $x^2 + 2xy − 3y^2 = 0$,
318. Encuentra todos los puntos en la gráfica de $y^3−27y = x^2−90$ en los que la recta tangente es vertical.
319. Para la ecuación $x^2 + xy + y^2 = 7$,
320. Encuentra la ecuación de la recta tangente a la gráfica de la ecuación $sen^{− 1}x + sen ^{− 1}y = \frac{\pi}{6}$ en el punto $(0,12)$.
321. Encuentra la ecuación de la recta tangente a la gráfica de la ecuación $tan^{− 1} (x + y) = x^2 + \frac{\pi}{4}$ en el punto $(0,1)$. (Solución)
322. Encuentra $y′$ y $y''$ para $x^2 + 6xy − 2y^2 = 3$.
323. [T] El número de teléfonos móviles producidos al gastar x dólares en mano de obra y se invierte un capital $y$ dólares por un fabricante puede modelarse mediante la ecuación $60x^{3 / 4}y^{1 / 4 }= 3240$.
324. [T] El número de automóviles producidosal gastar x dólares en mano de obra y se invierte un capital $y$ dólares por un fabricante puede modelarse mediante la ecuación $30x^{1 / 3}y^{2 / 3 }= 360$.(Tanto $x$ como $y$ se miden en miles de dólares).
325. El volumen de un cono circular recto de radio $x$ y altura $y$ viene dado por $V = \frac{1}{3}\pix^2y$. Suponga que el volumen del cono es $85\pi cm^3$. Encuentra $\frac{dy}{dx}$ cuando $x = 4$ e $y = 16$. (Solución)
 Para los siguientes ejercicios, consideremos una caja rectangular cerrada con una base cuadrada de lado $x$ y altura $y$.
Para los siguientes ejercicios, consideremos una caja rectangular cerrada con una base cuadrada de lado $x$ y altura $y$.
326. Encuentra una ecuación para el área de la superficie de la caja rectangular, $S (x, y)$.
327. Si el área de la superficie de la caja rectangular es 78 pies cuadrados, encuentra $\frac{dy}{dx}$ cuando $x = 3$ pies e $y = 5$ pies. (Solución)
 Para los siguientes ejercicios, usa la derivación implícita para determinar $y′$. ¿La respuesta coincide con las fórmulas que hemos determinado previamente?
Para los siguientes ejercicios, usa la derivación implícita para determinar $y′$. ¿La respuesta coincide con las fórmulas que hemos determinado previamente?
328. $x = seny$
329. $x = cosy$ (Solución)
330. $x = tany$
Objetivos de aprendizaje
Hasta ahora, hemos aprendido a derivar una variedad de funciones, incluidas funciones trigonométricas, inversas e implícitas. En esta sección, exploramos las derivadas de funciones exponenciales y logarítmicas. Como discutimos en enel primer capítulo, las funciones exponenciales juegan un papel importante en muchas aplicaciones como, por ejemplo, en el modelado del crecimiento de la población y la desintegración de materiales radiactivos.
Las funciones logarítmicas pueden ayudar a cambiar la escala de grandes cantidades y son particularmente útiles para reescribir expresiones complicadas.
Al igual que para las derivadas de otras funciones, podemos encontrar las derivadas de funciones exponenciales y logarítmicas usando fórmulas. A medida que desarrollamos estas fórmulas, necesitamos hacer ciertas suposiciones básicas. Las pruebas que sostienen estos supuestos están más allá del alcance de este libro.
En primer lugar, partimos del supuesto de que la función $B (x) = b^x$, con $b> 0$, está definida para cada número real y es continua. Los valores de las funciones exponenciales para todos los números racionales se define comenzando con la definición de $b^n$, donde $n$ es un número entero positivo, como el producto de $b$ multiplicado por sí mismo $n$ veces. Más tarde, definimos $b^0 = 1$, $b^{- n} = \frac{1}{b^n}$, para un número entero positivo $n$, y $b^{s / t} = \sqrt[t]{b^s}$ para números enteros positivos $s$ y $t$.
Estas definiciones no incluyen cómo obtener el valor de $b^r$ donde $r$ es un número real arbitrario. Suponiendo la continuidad de $B (x) = b^x$, con $b> 0$, podemos interpretar $b^r$ como $\mathop {\lim }\limits_{x \to r} {b^x}$ donde los valores de $x$ los tomamos como racionales. Por ejemplo, podemos ver $4^\pi$ como el número que satisface \[{4^3} < {4^\pi } < {4^4},\,\,\,\,{4^{3.1}} < {4^\pi } < {4^{3.2}},\,\,\,\,\,{4^{3.14}} < {4^\pi } < {4^{3.15}}\] \[{4^{3.1414}} < {4^\pi } < {4^{3.142}},\,\,\,\,{4^{3.1415}} < {4^\pi } < {4^{3.1416}}...\]
Como vemos en la siguiente tabla, $4^{\pi} \approx 77.88$.
| $x$ | $4^x$ | $x$ | $4^x$ |
| $4^3$ | $64$ | $4^{3.141593}$ | $77.88027104862$ |
| $4^{3.1}$ | $73.5166947198$ | $4^{3.1416}$ | $77.8810268071$ |
| $4^{3.14}$ | $77.7084726013$ | $4^{3.142}$ | $78.7932424541$ |
| $4^{3.141}$ | $77.8162741237$ | $4^{3.15}$ | $78.7932424541$ |
| $4^{3.1415}$ | 77.8702309526$ | $4^{3.3}$ | $84.4485062895$ |
| $4^{3.14159}$ | $77.8799471543$ | $4^{4}$ | $256$ |
Tabla 3.6. Aproximación del valor de $4^x$
También asumimos que para $B (x) = b^x$, $b> 0$, el valor de la derivada $B ' (0)$ existe. En esta sección, mostramos que al hacer esta suposición adicional, es posible probar que la función $B (x)$ es derivable en todos los puntos.
Finalmente supongamos también que hay un valor único de $b> 0$para el cual $B ' (0) = 1$. Definimos este valor único ccmo $e$, como hicimos en el apartado Introducción a funciones y gráficos.
La Figura 3.33 proporciona las gráficas de las funciones $y = 2^x$, $y = 3^x$, $y = 2.7^x$ y $y = 2.8^x$. Una estimación visual de las pendientes de las rectas tangentes a estas funciones en 0 proporciona evidencia que el valor de $e$ se encuentra entre $2.7$ y $2.8$. La función $E (x) = e^x$ se llama función exponencial natural. Su inversa, $L (x) = {\log _e}x = lnx$ se llama función logarítmica natural.
Se muestran las gráficas de $3^x$, $2.8^x$, $2.7^x$ y $2^x$. En el cuadrante I, su orden de menor a mayor es $2^x$, $2.7^x$, $2.8^x$ y $3^x$. En el cuadrante II, este orden se invierte. Todos cruzan el eje $y$ en (0, 1).
Figura 3.33 La gráfica de $E (x) = e^x$ está entre $y = 2^x$ y $y = 3^x$.
Para una mejor estimación de $e$, podemos construir una tabla de estimaciones de $B ' (0)$ para funciones de la forma $B (x) = b^x$. Antes de hacer esto, recuerde que \[B'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{{{b^x} - {b^0}}}{{x - 0}} = \mathop {\lim }\limits_{x \to 0} \frac{{{b^x} - 1}}{x} \approx \frac{{{b^x} - 1}}{x}\] para valores de $x$ muy cercanos a cero. Para nuestras estimaciones, elegimos $x = 0.00001$ y $x = -0.00001$ para obtener la estimación \[\frac{{{b^{ - 0.000001}} - 1}}{{ - 0.000001}} < B'\left( 0 \right) < \frac{{{b^{0.000001}} - 1}}{{0.000001}}\]
Consulta la siguiente tabla.
| $b$ | $\frac{{{b^{ - 0.000001}} - 1}}{{ - 0.000001}} < B'\left( 0 \right) < \frac{{{b^{0.000001}} - 1}}{{0.000001}}$ | $b$ | $\frac{{{b^{ - 0.000001}} - 1}}{{ - 0.000001}} < B'\left( 0 \right) < \frac{{{b^{0.000001}} - 1}}{{0.000001}}$ |
| $2$ | $0,693145 <B ' (0) <0,69315$ | $2.7183$ | $1,000002 <B ' (0) <1,0000012$ |
| $2.7$ | $0,993247 <B ' (0) <0,993257$ | $2.719$ | $1.000259 <B ' (0) <1.000269$ |
| $2.71$ | $0,996944 <B ' (0) <0,996954$ | $2,72$ | $1.000627 <B ' (0) <1.000637$ |
| $2.718$ | $0,999891 <B ' (0) <0,999901$ | $2,8$ | $1.029614 <B ' (0) <1.029625$ |
| $2.7182$ | $ 0,999965 <B ' (0) <0,999975$ | $3$ | $1.098606 <B ' (0) <1.098618$ |
Tabla 3.7. Estimación del valor de $e$
La evidencia de la tabla sugiere que $2.7182 <e <2.7183$.
La gráfica de $E (x) = e^x$ junto con la recta $y = x + 1$ se muestran en la Figura 3.34. Esta recta es tangente a la gráfica de $ E (x) = e^x$ en $x = 0$.
Ahora que hemos establecido nuestras suposiciones básicas, comenzamos nuestra investigación explorando la derivada de $B (x) = b^x$, $b> 0$. Recuerda que asumimos que existe $B ' (0)$. Al aplicar la definición de límite a la derivada, concluimos que \[B'\left( 0 \right) = \mathop {\lim }\limits_{h \to 0} \frac{{{b^{0 + h}} - {b^0}}}{h} = \mathop {\lim }\limits_{h \to 0} \frac{{{b^h} - 1}}{h}\]
Figura 3.34 La recta tangente a $E (x) = e^x$ en $x = 0$ tiene pendiente 1.
Considerando $B ' (x)$, obtenemos lo siguiente. $$\begin{aligned} B'\left( x \right) &= \mathop {\lim }\limits_{h \to 0} \frac{{{b^{x + h}} - {b^x}}}{h} &\text{Aplicamos la definición de derivada}\\ & = \mathop {\lim }\limits_{h \to 0} \frac{{{b^x}{b^h} - {b^x}}}{h}\\ &= \mathop {\lim }\limits_{h \to 0} \frac{{{b^x}\left( {{b^h} - 1} \right)}}{h} \\ & = {b^x}\mathop {\lim }\limits_{h \to 0} \frac{{{b^h} - 1}}{h} \\ &= {b^x} \, B'\left( 0 \right) \\ \end{aligned}$$
Vemos que sobre la base del supuesto de que $B (x) = b^x$ es derivable en $0$, $B (x)$ no solo es derivable en todas sus puntos, sino que su derivada es $$B ' (x) = b^xB ' (0). \tag{$3.29$}$$
Para $E (x) = e^x$, $E ' (0) = 1$. Entonces, tenemos $E ' (x) = e^x$. El valor de $B ' (0)$ para una función arbitraria de la forma $B (x) = b^x$, $b> 0$, se obtendrá más adelante.
TEOREMA 3.14. Derivada de la función exponencial natural
Sea $E (x) = e^x$ la función exponencial natural. Luego $E ' (x) = e^x$.
En general, $$\frac{d}{dx} (e^{g(x)})) = e^{g(x)} g ' (x).$$
 |
3.74 Derivada de una función exponencial |
Encuentra la derivada de $f (x) = e^{tg(2x)}$.

 |
3.75 Combinando reglas de derivación |
Encuentra la derivada de $y = \frac{e^{x^2}}{x}$.

 |
Cuestión 3.50 |
Encuentra la derivada de $h (x) = xe^{2x}$.
 |
3.76 Aplicar la función exponencial natural |
Una colonia de mosquitos tiene una población inicial de 1000. Después de $t$ días, la población viene dada por $A (t) = 1000e^{0.3t}$. Demuestra que la razón entre la tasa de cambio de la población, $A ' (t)$, y la población, $A (t)$ es constante.

 |
Cuestión 3.51 |
Si $A (t) = 1000e^{0.3t}$ describe la población de mosquitos después de $t$ días, como en el ejemplo anterior, ¿cuál es la tasa de cambio de $A (t)$ después de 4 días?
Ahora que tenemos la derivada de la función exponencial natural, podemos usar la derivación implícita para encontrar la derivada de su inversa, la función logarítmica natural.
TEOREMA 3.15. La derivada de la función logarítmica natural
Si $x> 0$ y $y = lnx$, entonces $$\frac{dy}{dx} = \frac{1}{x}. \tag{$3.30$}$$ De manera más general, sea $g (x)$ una función derivable. Para todos los valores de $x$ para los cuales $g ' (x)> 0$, la derivada de $h (x) = ln (g (x))$ viene dada por $$h ' (x) = \frac{1}{g (x)} g ' (x). \tag{$3.31$}$$
Prueba
Si $x> 0$ e $y = lnx$, entonces $e^y = x$. Derivando ambos lados de esta ecuación da como resultado la ecuación $$e^y\frac{dy}{dx} = 1.$$ Despejando $\frac{dy}{dx}$ $$\frac{dy}{dx} = \frac{1}{e^y}.$$ Finalmente, sustituimos $x = e^y$ para obtener $$\frac{dy}{dx} = \frac{1}{x}.$$ También podemos obtener este resultado aplicando el teorema de la función inversa, como vamos a ver a continuación. Como $y = g (x) = lnx$ es la inversa de $f (x) = e^x$, aplicando el teorema de la función inversa tenemos $$\frac{dy}{dx} = \frac{1}{f ' (g (x))} = \frac{1}{e^{lnx}} = \frac{1}{x}.$$ Usando este resultado y aplicando la regla de la cadena a $h (x) = ln (g (x))$ se obtiene $$h ' (x) = \frac{1}{g (x)} g ' (x).$$
La gráfica de $y = lnx$ y su derivada $\frac{dy}{dx} = \frac{1}{x}$ se muestran en la Figura 3.35.
La función $ln x$ aumenta en $(0, +\infty )$. Su derivada es decreciente pero mayor que 0 en $(0, +\infty)$.

Figura 3.35 La función $y = lnx$ aumenta en $(0, +\infty)$. Su derivada $y '= 1/x$ es mayor que cero en $(0, +\infty)$.
 |
3.77 Tomando una derivada de un logaritmo natural |
Encuentra la derivada de $f (x) = ln (x^3 + 3x - 4)$.

 |
Usar propiedades de logaritmos en una derivada |
Encuentra la derivada de $f (x) = ln \left(\frac{x^2senx}{2x + 1}\right)$.

 |
Cuestión 3.52 |
Derivar: $f (x) = ln (3x + 2)^5$.
Ahora que podemos derivar la función logarítmica natural, podemos usar este resultado para encontrar las derivadas de ${\log _b}x$ y $y = b^x$ para $b> 0$, $b \neq 1$.
TEOREMA 3.16. Derivadas de funciones logarítmicas y exponenciales generales
Sea $b> 0$, $b \neq 1$, y sea $g (x)$ una función derivable.
Más general, si $h (x) = b^{g (x)}$, entonces $$h ' (x) = b^g (x) g '(x) lnb \tag{$3.35$}$$
Prueba
Si $y = {log_b}x$, entonces $b^y = x$. De ello se deduce que $ln (b^y) = lnx$. Entonces $ylnb = lnx$. Despejando $y$, tenemos $y = \frac{lnx}{lnb}$. Derivando y teniendo en cuenta que $lnb$ es una constante, vemos que $$\frac{dy}{dx} = \frac{1}{xlnb}.$$
La derivada de la ecuación 3.33 se obtiene de la regla de la cadena.
Si $ y= b^x$, entonces $lny = xlnb$. Usando la derivación implícita, y teniendo en cuenta que $lnb$ es constante, se deduce que $\frac{1}{y}\frac{dy}{dx} = lnb$. Despejando $\frac{dy}{dx}$ y sustituyendo $y = b^x$, vemos que $$\frac{dy}{dx} = ylnb = b^xlnb.$$ La derivada más general (Ecuación 3.35) se sigue de la regla de la cadena.
 |
3.79 Aplicanado fórmulas derivadas |
Encuentra la derivada de $h (x) = \frac{3^x}{3x + 2}$.

 |
3.80 Pendiente de una recta tangente |
Encuentra la pendiente de la recta tangente a la gráfica de $y = {log_2}(3x + 1)$ en $x = 1$.

 |
Cuestión 3.53 |
Encuentra la pendiente de la recta tangente a $y = 3^x$ en $x = 2$.
En este punto, podemos tomar derivadas de funciones de la forma $y = (g (x))^n$ para ciertos valores de $n$, así como funciones de la forma $y = b^{g (x)}$, donde $b> 0$ y $b \neq 1$. Desafortunadamente, todavía no conocemos las derivadas de funciones como $y = x^x$ o $y = x^{\pi}$.
Estas funciones requieren una técnica llamada derivación logarítmica, que nos permite derivar cualquier función de la forma $h (x) = {g (x)}^{f (x)}$.. También se puede usar para convertir un problema de derivaciíon muy complejo en uno más simple, como encontrar la derivada de $y = \frac{x\sqrt{2x+1}}{e^x*sen^3x}$. Describimos esta técnica en la siguiente estrategia de resolución de problemas.
 |
3.81 Usar derivación logarítmica |
Encuentra la derivada de $y = (2x^4 + 1)^{tgx}$.

 |
3.82 Usar derivación logarítmica |
Encuentra la derivada de $y = \frac{x \sqrt{2x+1}}{e^x swn^3x}$.

 |
3.83 Ampliando la regla del poder |
Encuentra la derivada de $y = x^r$ donde $r$ es un número real arbitrario.

 |
Cuestión 3.54 |
Usa la derivación logarítmica para encontrar la derivada de $y = x^x$.
 |
Cuestión 3.55 |
Encuentra la derivada de $y = {(tgx)}^x$.
 3.10.4 Ejercicios
3.10.4 Ejercicios Para los siguientes ejercicios encuentra $f'(x)$
Para los siguientes ejercicios encuentra $f'(x)$
331. $f(x)=x^2e^x$ (Solución)
332. $f(x)=\frac{e^{−x}}{x}$
333. $f(x)=e^{x^3lnx}$ (Solución)
334. $f(x)=\sqrt{e^{2x}+2x}$
335. $f(x)=\frac{e`x-e^{-x}}{e^x+e^{-x}}$ (Solución)
336. $f(x)=\frac{10^x}{ln10}$
337. $f(x)=2^{4x}+4x^2$ (Solución)
338. $f(x)=3^{sen3x}$
339. $f(x)=x^{\pi}{\pi}^x$ (Solución)
340. $f(x)=ln(4x^3+x)$
341. $f(x)=ln \sqrt{5x-7}$ (Solución)
342. $f(x)=x^2ln9x$
343. $f(x)=log(secx)$ (Solución)
344. $f(x)=log_7(6x^4+3)^5$
345. $f(x)=2^x⋅log_37^{x^2−4}$ (Solución)
 En los siguientes ejercicios utiliza la derivación logarítmica para encontrar $\frac{dy}{dx}$.
En los siguientes ejercicios utiliza la derivación logarítmica para encontrar $\frac{dy}{dx}$.
346. $y=x^{\sqrt{x}}$
347. $y=(sin2x)^{4x}$ (Solución)
348. $y=(lnx)^{lnx}
349. $y=x^{log_2x}$ (Solución)
350. $y=(x^2−1)^{lnx}$
351. $y=x^{cotx}$ (Solución)
352. $y=\frac{x+11}{\sqrt[3]{x^2−4}}$
353. $y=x^{−1/2}(x^2+3)^{2/3}(3x−4)^4$ (Solución)
354. [T] Encuentra la ecuación de la recta tangente a la gráfica de la función $f(x)=4xe^{(x^2−1)}$ en el punto donde $x=−1$. Representa en una misma gráfica la función y la recta tangente.
355. [T] Encuentra la ecuación de la recta que es normal a la gráfica de $f(x)=x\cdot 5^x$ en el pnnto en el que $x=1$. Representa en una misma gráfica la función y la recta normal. (Solución)
356. [T] Encuentra la ecuación de la recta tangente a la gráfica de $x^3 − xlny + y^3 = 2x + 5$ en el punto donde $x = 2$. (Sugerencia: uutiliza la derivación implícita para encontrar $\frac{dy}{dx}$). Grafique tanto la curva como la tangente.
357. Consideremos la función $y = x^{1 / x}$ para $x > 0$.
358. La fórmula $I(t) = \frac{sent}{e^t}$ es la fórmula para una corriente alterna. Completa la siguiente tabla con los valores adecuados.
| $t$ | $\frac{sint}{e^t}$ |
| 0 | (i) |
| $\frac{\pi}{2}$ | (ii) |
| $\pi$ | (iii) |
| $\frac{3\pi}{2}$ | (iv) |
| $2\pi$ | (v) |
| $\frac{5\pi}{2}$ | (vi) |
| $3 \pi$ | (ii) |
Utilizando solo los valores de la tabla, determina dónde es horizontal la recta tangente a la gráfica de $I (t)$.
359. [T] La población de Toledo, Ohio, en 2000 era de aproximadamente 500.000. Supongamos que la población está aumentando a una tasa del 5% anual.
360. [T] Un isótopo del elemento erbio tiene una vida media de aproximadamente 12 horas. Inicialmente hay presentes 9 gramos del isótopo.
361. [T] El número de casos de gripe en la ciudad de Nueva York desde principios de 1960 hasta principios de 1961 está modelado por la función $N (t) = 5.3e^{0.093t2−0.87t}$, $(0 \le t \le 4)$, donde $N (t)$ da el número de casos (en miles) y $t$ se mide en años, con $t = 0$ correspondiente al comienzo de 1960.
362. [T] La tasa relativa de cambio de una función derivable $y = f (x)$ está dada por $\frac{100 \cdot f'(x)}{f (x)} \%$. Un modelo para el crecimiento de la población es una función de crecimiento de Gompertz, dada por $P(x) = ae^{− b\cdot e^{− cx}}$ donde $a$, $b$ y $c$ son constantes.
 Para los siguientes ejercicios, usa la población de la ciudad de New York desde 1790 a 1860, que se muestra en la siguiente tabla.
Para los siguientes ejercicios, usa la población de la ciudad de New York desde 1790 a 1860, que se muestra en la siguiente tabla.
| Añaos desde 1790 | Poblacion |
| 0 | 22,131 |
| 10 | 60,515 |
| 20 | 96,373 |
| 30 | 123,706 |
| 40 | 202,300 |
| 50 | 312,710 |
| 60 | 515,547 |
| 70 | 813,669 |
Tabla 3.8 Población de la ciudad de Nueva York sobre Fuente: http://en.wikipedia.org/wiki/.
363. [T] Utilizando un programa de computadora o una calculadora, calcule un curva de crecimiento a los datos de la forma $p = ab^t$. (Solución)
364. [T] Usando el mejor ajuste exponencial para los datos, escribe una tabla que contenga las derivadas evaluadas en cada año.
365. [T] Utilizando el mejor ajuste exponencial para los datos, escribe una tabla que contenga las segundas derivadas evaluadas en cada año. (Solución)
366. [T] A partir de las tablas de la primera y segunda derivada y el mejor ajuste, responde a las siguientes preguntas: