Solución

La tabla 2.5 enumera los valores para la función $sen (1 / x)$ para los valores dados de $x$.

Tabla 2.5 Tabla de valores funcionales para $\mathop {\lim }\limits_{x \to 0} sen\left( {{1 \over x}} \right)$

Después de examinar la tabla de valores funcionales, podemos ver que los valores de y no parecen acercarse a ningún valor único. Parece que el límite no existe, pero antes de llegar a esta conclusión, adoptemos un enfoque más sistemático. Consideremos la siguiente secuencia de valores $x$ cercanos a 0:

$\frac{2}{\pi}$, $\frac{2}{3\pi}$, $\frac{2}{5\pi}$, $\frac{2}{7\pi}$, $\frac{2}{9\pi}$, $\frac{2}{11\pi}$...

Los valores de y correspondientes son: 1, −1, 1, −1, 1, −1,….

En este momento podemos concluir que $\mathop {\lim }\limits_{x \to 0} sen\left( {{1 \over x}} \right)$ no existe. Los matemáticos abrevian frecuentemente "no existe" como $\nexists$. Por lo tanto, escribiríamos $\mathop {\lim }\limits_{x \to 0} sen\left( {{1 \over x}} \right)$ $\nexists$.

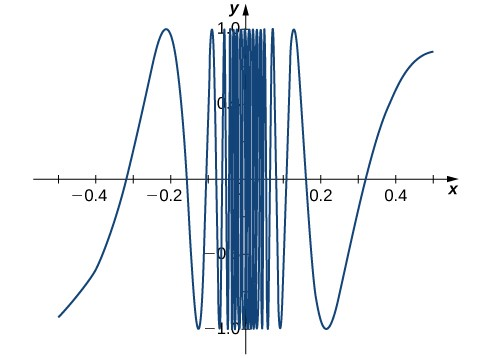
La gráfica de $f (x) = sin (1 / x)$ se muestra en la Figura 2.17 y da una imagen más clara del comportamiento de $sin (1 / x)$ cuando $x$ se acerca a 0. Puedes ver que $sin (1 / x)$ oscila cada vez más rápidamente entre -1 y 1 a medida que $x$ se acerca a 0.

Figura 2.17 La gráfica de $f (x) = sen(1/x)$ oscila entre -1 y 1 cuando $x$ se acerca a 0.