Solución

Aunque podríamos encontrar esta ecuación sin usar la derivación implícita, usar ese método lo hace mucho más fácil. En el ejemplo 3.68, encontramos $\frac{dy}{dx} = −\frac{x}{y}$.

La pendiente de la recta tangente se calcula sustituyendo $(3, −4)$ en esta expresión. En consecuencia, la pendiente de la recta tangente es ${\left. {\frac{{dy}}{{dx}}} \right|_{\left( {3, - 4} \right)}} = - \frac{3}{{ - 4}} = \frac{3}{4}$.

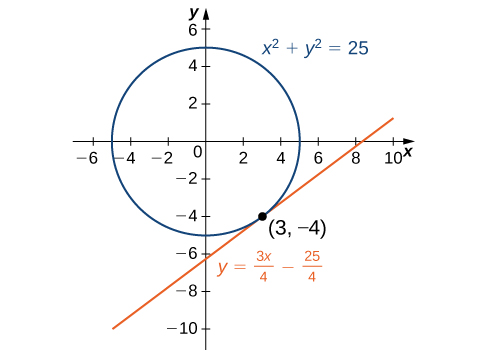
Usando el punto $(3, −4)$ y la pendiente $\frac{3}{4}$ en la ecuación punto-pendiente de la recta, obtenemos la ecuación $y = \frac{3}{4}x − \frac{25}{4}$ (Figura 3.31). Se representa gráficamente la circunferencia con radio $5$ y centro en el origen. Se traza una recta tangente a través del punto $(3, −4)$.

Figura 3.30 La recta $y = \frac{3}{4}x − \frac{25}{4}$ es tangente a $x^2 + y^2 = 25$ en el punto $(3, −4)$.