Solución

Apartado a

Evaluando la función de ingresos de $p= 5$ y $p= 17$, podemos concluir que $$R(5) = - 1.04 (5)^2+26 (5) = 104$$ por lo que los ingresos son 104,000 dólares. $$R(17) = - 1.04 (17)^2+26 (17) = 141,44$$ por lo que los ingresos son 141,440 dólares.

Apartado b

Los ceros de esta función se pueden encontrar resolviendo la ecuación $$−1,04p^2+26p= 0$$ Cuando factorizamos la expresión cuadrática, obtenemos $$p(−1,04p+26) = 0$$ Las soluciones de esta ecuación están dadas por $p= 0,25$. Para estos valores de $p$,los ingresos son cero. Cuando $p=0$ dólares,los ingresos son cero porque la empresa regala su mercancía. Cuando $p= 25$ dólares, los ingresos son cero porque el precio es demasiado alto y nadie comprará ningún artículo.

Apartado c

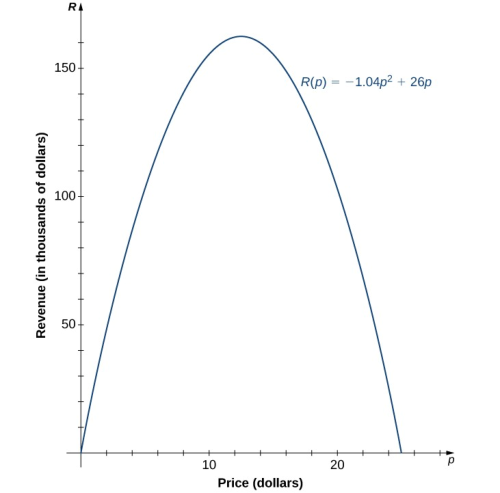
Sabiendo que la función es cuadrática, la gráfica es una parábola. Dado que el coeficiente principal es negativo, la parábola se abre hacia abajo. Una propiedad de las parábolas es que son simétricas con respecto a su eje, por lo que, dado que los ceros están $p= 0$ y $p= 25$, la parábola debe ser simétrica con respecto a la línea vertical que es su punto medio, $p= 12,5$.

Apartado d

La función es una parábola con ceros en $p= 0$ y $p= 25$, y es simétrico sobre la línea $p= 12,5$, por lo que el ingreso máximo se produce a un precio de $p=12.5$ dólares por artículo. A ese precio, los ingresos en dólares serían $$R(p) = - 1,04 (12,5)^2+26 (12,5) = 162,500$$