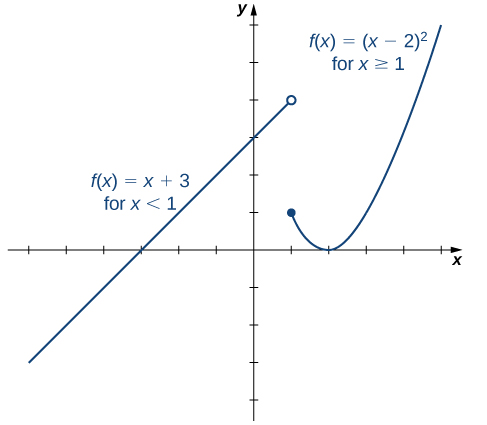
Representamos la función lineal $y=x+3$ en el intervalo $(−∞, 1)$ y grafica la función cuadrática $y= (x−2)^2$ en el intervalo $[1, ∞)$. Dado que el valor de la función en $x= 1$ está dado por la fórmula $f(x) = (x−2)^2$, vemos que $f(1) = 1$. Para indicar esto en el gráfico, dibujamos un círculo cerrado en el punto $(1,1)$. El valor de la función viene dado por $f(x) =x+2$ para todos $x$ menores que 1, pero no en $x= 1$. Para indicar esto en el gráfico, dibujamos un círculo abierto en $(1,4)$.

Figura 1.22 Esta función definida por partes es lineal para $x<1$ y cuadrática para $x≥1$.