Solución

La Figura 2.26ilustra la función $f (x)$ y ayuda a comprender estos límites.

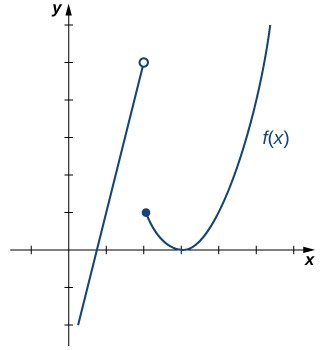
Figura 2.26 La gráfica muestra la función $f\left( x \right)$.

Apartado a

Como $f(x)=4x-3$ para todo $x$ en $(-\infty,2)$, sustituimos $f(x)$ por $4x-3$ en el límite y aplicamos las propiedades de los límites

Apartado b

Como $f(x)={(x-3)}^2$ para todo $x$ en $(2,\infty)$, sustituimos $f(x)$ en el límite por ${(x-3)}^2$ y aplicamos las propiedades de los límites

Apartado c

Como $\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = 5$ y $\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 1$, concluimos que $\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = 5$ no existe