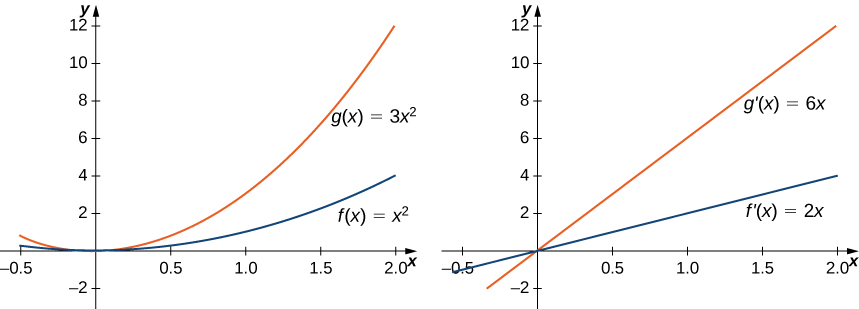
Usamos la regla de la derivada de una potencia: $$g'(x) = \frac{d}{dx} (3x^2) = 3\frac{d}{dx} (x^2) = 3 (2x) = 6x.$$ Como $f (x) = x^2$ tiene como derivada f ′ (x) = 2x, vemos que la derivada de $g (x)$ es 3 veces la derivada de $f (x)$. Esta relación se ilustra en la Figura 3.18.
Se muestran dos gráficos. El primer gráfico muestra $g (x) = 3x^2$ y $f (x) = x^2$. El segundo gráfico muestra $g '(x) = 6x$ y $f' (x) = 2x$. En el primer gráfico, $g (x)$ aumenta tres veces más rápido que $f (x)$. En el segundo gráfico, $g '(x)$ aumenta tres veces más rápido que $f' (x)$.
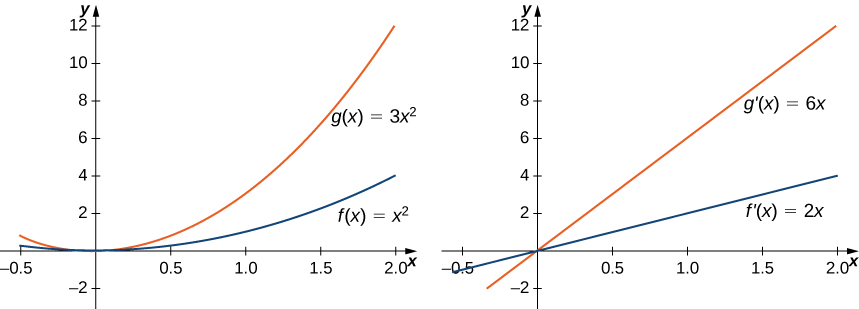
Figura 3.18 La derivada de $g (x)$ es 3 veces la derivada de $f (x)$.