Solución

Sea $\epsilon > 0$.

La primera parte de la definición comienza con "Para todo $\varepsilon > 0$".

Esto significa que debemos demostrar que todo lo que sigue es cierto sin importar qué valor positivo de $\epsilon$ que se elija. Al indicar "Sea $\epsilon > 0$", indicamos nuestra intención de hacerlo.

Elija $\delta = \frac{\epsilon} {2}$.

La definición continúa con “existe un $\delta > 0$".

La frase "existe" en un enunciado matemático siempre es una señal para una búsqueda del tesoro. En otras palabras, debemos encontrar $\delta$. Pero, ¿cómo saber que $\delta = \epsilon / 2$? Hay dos enfoques básicos para rastrear $\delta$.Un método es puramente algebraico y el otro es geométrico.

Comenzamos abordando el problema desde un punto de vista algebraico.

Dado que en última instancia queremos $| (2x + 1) −3 | < \epsilon$, comenzamos manipulando esta expresión: $| (2x + 1) −3 | < ε$ es equivalente a $| 2x − 2 | < \epsilon$, que a su vez es equivalente a $|2 || x − 1 | <\epsilon$.

Por último, esto es equivalente a $| x − 1 | < \epsilon / 2$. Así, parecería que $\delta = \epsilon / 2$ es apropiado.

También podemos encontrar $\delta$ a través de métodos geométricos. La Figura 2.40 demuestra cómo se elige $\delta$.

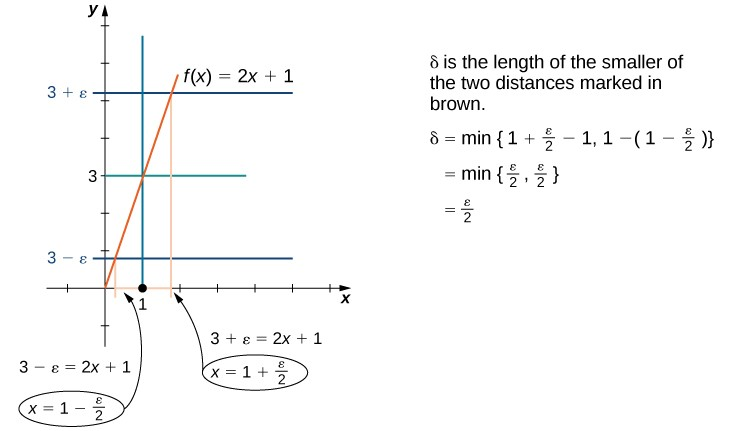
Figura 2.40 Este gráfico muestra cómo encontramos δ geométricamente.

Supongamos $0 < | x − 1 | < \delta$.

Cuando se ha elegido $\delta$, nuestro objetivo es mostrar que si $0 <| x − 1 | < \delta$, entonces $| (2x + 1) −3 | < \epsilon$.

Así, $$\begin{aligned} \left| {\left( {2x + 1} \right) - 3} \right| \\ &= \left| {2x - 2} \right| &\text{propiedad del valor absoluto} \\ & = \left| {2\left( {x - 1} \right)} \right| \\ & = \left| 2 \right|\left| {x - 1} \right| \\ & = 2\left| {x - 1} \right|\\ & < 2\delta &\text{aquí usamos que hemos supuesto } 0\left|x-1\right| < \delta\\ & = 2 \cdot {\varepsilon \over 2} = \varepsilon &\text{aquí usamos que } \delta=\epsilon/2 \end{aligned}$$

Análisis

En esta parte de la demostración, comenzamos con $| (2x + 1) −3 |$ y usamos nuestro supuesto $0 < | x − 1 | < \delta$ en una parte clave de la cadena de desigualdades para obtener que $| (2x + 1) −3 |$ sea menor que $\epsilon$.

Con la misma facilidad podríamos haber manipulado la desigualdad asumida $0 <| x − 1 | < \delta$ para llegar a $| (2x + 1) −3 | < \epsilon$ como sigue: $$\begin{aligned} 0 < \left| {x - 1} \right| < \delta &\Rightarrow \left| {x - 1} \right| < \delta & \Rightarrow - \delta < x - 1 < \delta \\ & \Rightarrow - {\varepsilon \over 2} < x - 1 < {\varepsilon \over 2} \\ & \Rightarrow - \varepsilon < 2x - 2 < \varepsilon \\ & \Rightarrow \left| {2x - 2} \right| < \varepsilon \\ & \Rightarrow \left| {\left( {2x + 1} \right) - 3} \right| < \varepsilon \end{aligned}$$ Por lo tanto, $\mathop {\lim }\limits_{x \to 1} \left( {2x + 1} \right) = 3$. (Habiendo completado la prueba, declaramos lo que hemos logrado).

Versión final

Después de eliminar todos los comentarios, aquí hay una versión final de la prueba:

Sea $\epsilon < 0$.

Elija δ = ε / 2.

Supongamos $0 < | x − 1 | < \delta$.

Así, $$\begin{aligned} \left| {\left( {2x + 1} \right) - 3} \right| &= \left| {2x - 2} \right| \\ & = \left| {2\left( {x - 1} \right)} \right| \\ & = \left| 2 \right|\left| {x - 1} \right| \\ & = 2\left| {x - 1} \right|\\ & < 2\delta \\ & = 2 \cdot {\varepsilon \over 2} = \varepsilon \end{aligned}$$ Por lo tanto, $\mathop {\lim }\limits_{x \to 1} \left( {2x + 1} \right) = 3$.