Solución

Podemos usar la tabla de valores funcionales que se muestra en la Tabla 2.6. Observa que para valores de xx menores que 2, usamos f(x)=x+1f (x) = x + 1 y para valores de xx mayores que 2, usamos f(x)=x2−4f (x) = x^2−4.

xx f(x)=x+1f(x)=x+1 xx f(x)=x2−4f(x)=x^2-4
1.9  2.9    2.1   0.41  
1.99  2.99    2.01   0.0401  
1.999  2.999    2.001   0.004001  
1.9999  2.9999    2.0001   0.00040001  
1.99999  2.99999    2.00001   0,0000400001  

Tabla 2.6 Tabla de valores funcionales para f(x)={x+1si x<2x2−4si x≥2f(x) = \begin{cases} x+1 & \text{si $x < 2$} \\ x^2-4 & \text{si $x \ge 2$} \end{cases}

Con base en esta tabla, podemos concluir que lim⁡x→2−f(x)=3            lim⁡x→2+f(x)=0\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = 3 \,\,\,\,\,\,\,\,\,\,\,\, \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 0

Por lo tanto, el límite (bilateral) de f (x) no existe en x=2x = 2. La Figura 2.18 muestra una gráfica de f(x)f (x) y refuerza nuestra conclusión sobre estos límites.

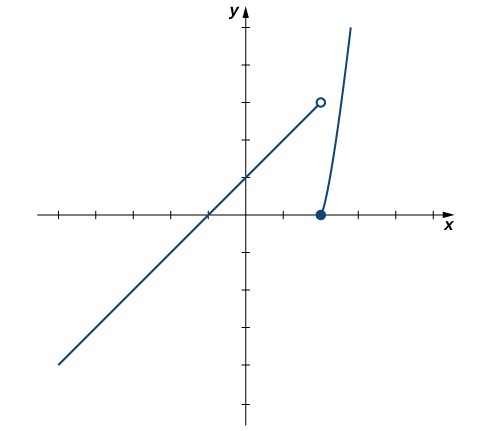
Figura 2.18 La gráfica de f(x)={x+1si x<2x2−4si x≥2f(x) = \begin{cases} x+1 & \text{si $x < 2$} \\ x^2-4 & \text{si $x \ge 2$} \end{cases} tiene un salto en x=2x=2.