Solución

Empezamos por construir una tabla de valores funcionales.

Apartado a

Los valores de $1 / x$ disminuyen sin límite cuando $x$ se aproxima a 0 por la izquierda. Concluimos que $$\mathop {\lim }\limits_{x \to {0^ - }} {1 \over x} = - \infty$$

Apartado b

Los valores de $1 /x$ aumenta sin límite cuando $x$ se aproxima a 0 por la derecha. Concluimos que $$\mathop {\lim }\limits_{x \to {0^ - }} {1 \over x} = + \infty$$ Como $$\mathop {\lim }\limits_{x \to {0^ - }} {1 \over x} \ne \mathop {\lim }\limits_{x \to {0^ + }} {1 \over x}$$ concluimos que no existe $\mathop {\lim }\limits_{x \to 0} {1 \over x}$.

Apartado c

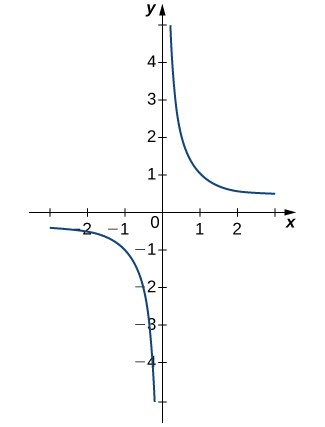
La gráfica de $f (x) = 1 / x$ que se muestra en la Figura 2.19 confirma estas conclusiones.

Figura 2.19 La gráfica de $f (x) = 1/x$ confirma que el límite cuando $x$ se acerca a 0 no existe.