Solución

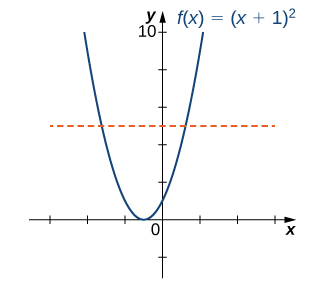
Apartado a

La gráfica de ff es la gráfica de y=x2y = x^2 desplazado a la izquierda una unidad. Dado que existe una recta horizontal que corta a la gráfica más de una vez, ff no es uno-uno.

Apartado b

En el intervalo [−1,∞)[−1, ∞), ff es uno-uno.

El dominio y rango de f1f^{1} se corresponden con el rango y el dominio de ff , respectivamente. Por tanto, el dominio de f−1f^−1 es [0,∞)[0, ∞) y el rango de f−1f^−1 es [−1,∞)[−1, ∞).

Para encontrar la expresión de f−1f^−1, resolvemos la ecuación y=(x+1)2y = (x + 1)^2 en xx.

Si y=(x+1)2y = (x + 1)^2, se tiene que x=−1±yx= −1 ± \sqrt{y} Dado que estamos restringiendo el dominio al intervalo donde x≥−1x ≥ −1, necesitamos ±y≥0±\sqrt{ y} ≥ 0. Por lo tanto, x=−1+yx = −1 + \sqrt{y} Intercambiando xx e yy,escribiendo y=−1+xy = −1 + \sqrt{x} y concluimos entonces que f−1(x)=−1+xf^{−1}(x) = −1 + \sqrt{x}