Solución

1. La velocidad es la derivada de la función de posición: $$v (t) = s'(t) = 3t^2-18t + 24.$$
2. La partícula está en reposo cuando $v (t) = 0$, así que $3t^2-18t + 24 = 0$. Factorizando el lado izquierdo de la igualdad se tiene $$3 (t - 2) (t - 4) = 0.$$ Resolviendo, encontramos que la partícula está en reposo en $t = 2$ y $t = 4$.
   La partícula se mueve de izquierda a derecha cuando $v (t)> 0$ y de derecha a izquierda cuando $v (t) <0$. La Figura 3.23 muestra el análisis del signo de $v (t)$ para $t \ge \ 0$, pero no representa el eje a lo largo del cual se mueve la partícula.
   

   

   Figura 3.23 El singo de $v(t)$ determina la dirección de la partícula

   
   
   • Dado que $3t^2-18t + 24> 0$ en $[0,2) \cup (2, + 8)$, la partícula se mueve de izquierda a derecha en estos intervalos.
   • Dado que $3t^2-18t + 24 <0$ en $(2,4)$, la partícula se mueve de derecha a izquierda en este intervalo.
3. Antes de que podamos dibujar la gráfica de la partícula, necesitamos saber su posición en el momento en que comienza a moverse ($t = 0$) y en los momentos en que cambia de dirección ($t = 2.4$). Tenemos $s (0) = 4$, $s (2) = 24$ y $s (4) = 20$. Esto significa que la partícula comienza en el eje de coordenadas en $4$ y cambia de dirección en $0$ y $20$ en el eje de coordenadas.
   La trayectoria de la partícula se muestra en un eje de coordenadas en la Figura 3.23. Se da una recta numérica y encima de ella serpentea una recta, comenzando en $t = 0$ arriba de 4 en la recta numérica. Entonces la recta en $t = 2$ está por encima de $24$ en la recta numérica. Luego, la recta disminuye en $t = 4$ para estar por encima de 20 en la recta numérica, momento en el que la recta cambia de dirección nuevamente y aumenta indefinidamente.

   

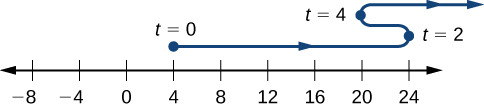
   Figura 3.24 La trayectoria de la partícula se puede determinar analizando $v (t)$.