Solución

La solución se muestra en el siguiente gráfico. Observa que $f (x)$ es creciente y $f ′ (x)> 0$ en $(–2,3)$. Además, $f (x)$ es decreciente y $f ′ (x) <0$ en $(−∞, −2)$ y en $(3, + ∞)$. Se debe tener en cuenta también que $f (x)$ tiene tangentes horizontales en $–2$ y $3$, y $f ′ (- 2) = 0$ y $f ′ (3) = 0$.

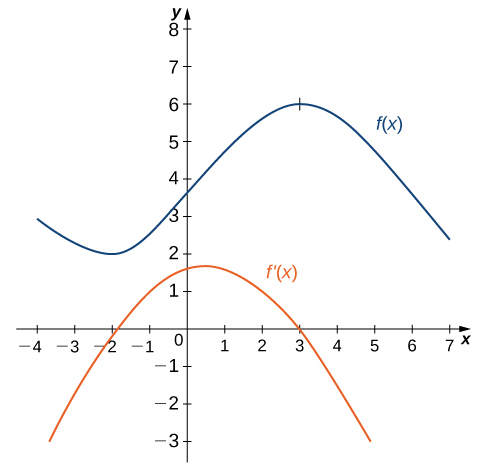
Aquí se representan dos funciones: $f (x)$ y $f '(x)$. La función $f (x)$ es la misma que la gráfica anterior, es decir, aproximadamente sinusoidal, comenzando en $(−4, 3)$, disminuyendo a un mínimo local en $(−2, 2)$, luego aumentando a un máximo local en $( 3, 6)$ y pasa por el punto $(7, 2)$. La función $f '(x)$ es una parábola orientada hacia abajo con vértice cerca de $(0.5, 1.75)$, se corta con el eje $y$ en $(0, 1.5)$ y corta al eje $x$ en los puntos $(−1.9, 0)$ y $(3, 0)$.