Solución

Para encontrar los valores de $x$ para los cuales $f (x)$ tiene una recta tangente horizontal, debemos resolver $f ′ (x) = 0$. Como $$f'(x) = 3x^2−14x + 8 = (3x − 2) (x − 4),$$ debemos resolver $(3x − 2) (x − 4) = 0$.

Vemos que la función tiene rectas tangentes horizontales en $x = \frac{2}{3}$ y $x = 4$ como se muestra en el siguiente gráfico. En la gráfica se representa $f (x) = x^3 - 7x^2 + 8x + 1$, y las rectas tangentes $x = 2/3$ y $x = 4$.

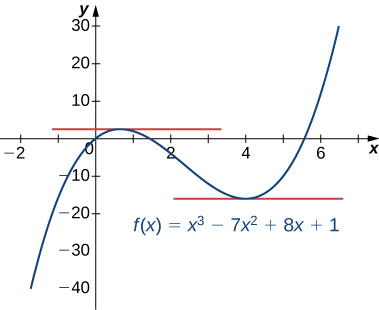
Figura 3.19 Tiene rectas tangentes en $x=2/3$ y $x=4$.