Apartado a
Para encontrar los ceros, resolvemos $ \sqrt{x + 3} + 1 = 0$. Esta ecuación implica $ \sqrt{x + 3} = −1$. Como $\sqrt{x + 3} ≥ 0$ para todo $x$, esta ecuación no tien soluciones, y por ello $f$ no tiene ceros.
Apartado b
La intersección con el eje $y$ es $(0, f (0))= (0,\sqrt{3}+ 1)$.
Apartado c
Para representar esa función, debemos dibujar una tabla de valores. Como necesitamos $x + 3 ≥ 0$, necesitamos elegir $x ≥ −3$. Elegimos valores que hagan sencillo evaluar la raíz cuadrada.
| $x$ | −3 | −2 | −1 |
| $f(x)$ | 1 | 2 | 3 |
Tabla 1.2
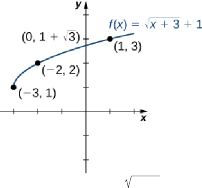
Haciendo uso de la tabla y sabiendo que, como la función es una raíz cuadrada, el gráfico será similar al de $y=\sqrt{x}$, la gráfica se muestra a continuación (Figura 1.10) Figure 1.10 El gráfico de $f (x) = \sqrt{x + 3} + 1$ tiene intersección con el eje $y$ pero no con el eje $x$
Figura. 1.10 Intersección $x$, $(1/2, 0$) e intersección $y$ $(0, 2)$