Cálculo VectorialParte I INTERACTIVO
Juan Guillermo Rivera Berrío
Institución Universitaria Pascual Bravo
Elena E. Álvarez Sáiz
Universidad de Cantabria


Fondo Editorial Pascual Bravo
Medellín2020
Título de la obra:
Cálculo Vectorial - Parte I
Interactivo
Autores:
Juan Guillermo Rivera Berrío
Elena Esperanza Álvarez Sáiz
Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Obra derivada del libro Calculus Volume 3 de: Gilbert Strang (Massachusetts Institute of Technology) Edwin “Jed” Herman (University of Wisconsin-Stevens Point)
LICENCIA
Este libro digital interactivo se ha diseñado con fundamento en la filosofía del Proyecto Descartes: "Trabajando altruistamente por la comunidad educativa de la aldea global", que sólo busca desarrollar contenidos educativos para el provecho de la comunidad académica, esperando únicamente como retribución el uso y difusión de estos contenidos. El contenido del libro, al igual que los objetos interactivos se han diseñado de tal forma que se puedan leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin. El libro se puede descargar para su uso en local sin dependencia con la red. Algunos de los objetos interactivos se han diseñado con el Editor DescartesJS.
El contenido del libro se basa en un recurso de OpenStax, organización sin fines de lucro de la Universidad de Rice, cuya misión, similar a la nuestra, es mejorar el acceso de los estudiantes a la educación. El libro corresponde al Volumen 3 de Cálculo, que cubre ecuaciones paramétricas y coordenadas polares, vectores, funciones de varias variables, integración múltiple y ecuaciones diferenciales de segundo orden.
Este libro de texto "Cálculo Vectorial" se ha trabajado para hacer que el cálculo sea interesante y accesible para los estudiantes, manteniendo el rigor matemático inherente a la asignatura. Con este objetivo en mente, el contenido se ha desarrollado y organizado para proporcionar una progresión lógica de conceptos fundamentales a conceptos más avanzados, basándose en lo que los estudiantes ya han aprendido y enfatizando en las conexiones entre temas y entre teoría y aplicaciones. El objetivo es permitir que los estudiantes no solo reconozcan los conceptos, sino que trabajen con ellos de manera que sean útiles en cursos posteriores y carreras futuras. La organización y las características pedagógicas fueron desarrolladas y examinadas con comentarios de educadores matemáticos dedicados al proyecto.
Las derivaciones y explicaciones se basan en años de experiencia en el aula por parte de profesores de cálculo desde hace mucho tiempo, luchando por un equilibrio de claridad y rigor que haya demostrado ser exitoso con sus estudiantes. El libro incluye evaluaciones al final de cada apartado para que los estudiantes puedan aplicar lo que han aprendido a través de problemas de práctica. Muchos ejercicios están marcados con una [T] para indicar que son adecuados para la solución por tecnología, incluidas las calculadoras o los sistemas de álgebra computacional (CAS), como GeoGebra. Las respuestas para los ejercicios seleccionados están disponibles para los numerales impares.
El texto original, desarrollado por Gilbert Strang y Edwin “Jed” Herman, ha sido publicado en versiones html y pdf. Esta obra derivada, en español y como libro interactivo, creada por Rivera J.G. y Álvarez E.E., presenta las siguientes aportaciones: traducción al español, diseño en formato ebook, incorporación de 81 objetos interactivos de aprendizaje, 66 de ellos diseñados con el editor DescartesJS y 15 con GeoGebra.
Para evitar, al máximo, la dependencia con la conectividad en la red, las expresiones matemáticas se han construido recurriendo al API de $\KaTeX$.
En otra obra, que hemos titulado "Curvas y superficies paramétricas", puedes encontrar un gran cantidad de curvas y superficies, de las cuales hemos seleccionado la miscelánea diseñada por Ildefonso Fernández Trujillo, José Román Galo Sánchez y Ángel Cabezudo Bueno como motivación de este libro:

Figura 1. El nautilus de cámara es un animal marino que vive en el Océano Pacífico tropical. Los científicos creen que han existido prácticamente sin cambios durante unos 500 millones de años (crédito: modificación del trabajo de Jitze Couperus, Flickr)
El nautilus de cámara es una criatura fascinante. Este animal se alimenta de cangrejos ermitaños, peces y otros crustáceos. Tiene una cubierta exterior dura con muchas cámaras conectadas en forma de espiral, y puede retraerse en su cubierta para evitar a los depredadores. Cuando se corta parte de la cáscara se revela una espiral perfecta, con cámaras en su interior que son algo similares a los anillos de crecimiento en un árbol.
La función matemática que describe una espiral se puede expresar utilizando coordenadas rectangulares (o cartesianas). Sin embargo, si cambiamos nuestro sistema de coordenadas a algo que funcione un poco mejor con los patrones circulares, la función se vuelve mucho más sencilla de describir. El sistema de coordenadas polares es adecuado para describir curvas de este tipo.
En este capítulo también estudiamos las ecuaciones paramétricas, que nos brindan una manera conveniente de describir curvas o de estudiar la posición de una partícula u objeto en dos dimensiones en función del tiempo. Usaremos ecuaciones paramétricas y coordenadas polares para describir muchos temas más adelante en este texto.
En esta sección examinamos las ecuaciones paramétricas y sus gráficas. En el sistema de coordenadas bidimensional, las ecuaciones paramétricas son útiles para describir curvas que no son necesariamente funciones. El parámetro es una variable independiente de la que tanto x como y dependen, y a medida que aumenta el parámetro, los valores de $x$ e $y$ trazan un camino a lo largo de una curva plana. Por ejemplo, si el parámetro es $t$ (una opción común), entonces $t$ podría representar el tiempo. Luego, $x$ e $y$ se definen como funciones de tiempo, y $(x(t), y(t))$ puede describir la posición en el plano de un objeto dado a medida que se mueve a lo largo de una trayectoria curva.
Considera la órbita de la Tierra alrededor del Sol. Nuestro año dura aproximadamente 365.25 días, pero para esta discusión usaremos 365 días.
El 1 de enero de cada año, la ubicación física de la Tierra con respecto al Sol es casi la misma, excepto en los años bisiestos, cuando el retraso introducido por los 14 días adicionales de tiempo de órbita se incluye en el calendario. Llamamos al 1 de enero "día 1" del año. Luego, por ejemplo, el día 31 es el 31 de enero, el día 59 es el 28 de febrero y así sucesivamente.
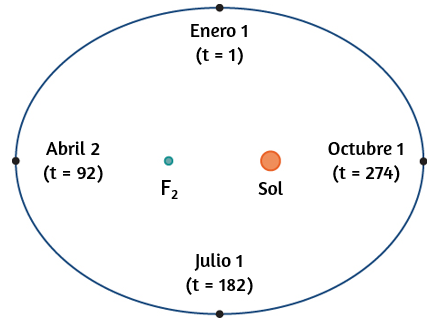
Figura 1.1. La órbita de la Tierra alrededor del Sol en un año.
El número del día en un año puede considerarse una variable que determina la posición de la Tierra en su órbita. A medida que la Tierra gira alrededor del Sol, su ubicación física cambia en relación con el Sol. Después de un año completo, estamos de vuelta donde empezamos y comienza un nuevo año. Según las leyes de Kepler sobre el movimiento planetario, la forma de la órbita es elíptica, con el Sol en un foco de la elipse. Estudiamos esta idea con más detalle en las secciones cónicas.
La figura muestra la órbita de la Tierra alrededor del Sol durante un año. El punto etiquetado $F_2$ es uno de los focos de la elipse; el otro foco está ocupado por el sol.
Si superponemos los ejes de coordenadas sobre este gráfico, entonces podemos asignar pares ordenados a cada punto de la elipse (Figura 1.2). Luego, cada valor de $x$ en el gráfico es un valor de posición en función del tiempo, y cada valor de $y$ también es un valor de posición en función del tiempo. Por lo tanto, cada punto en el gráfico corresponde a un valor de la posición de la Tierra en función del tiempo.
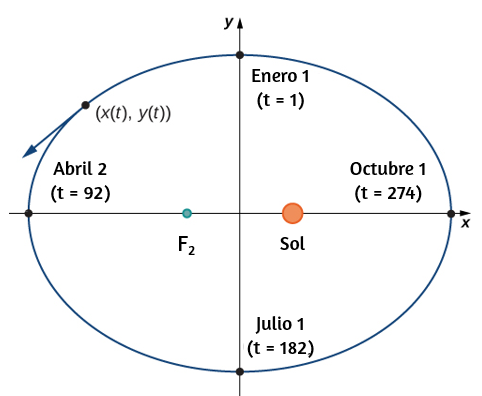
Figura 1.2. Ejes de coordenadas superpuestos a la órbita de la Tierra.
Podemos determinar las funciones para $x(t)$ y $y(t)$, parametrizando así la órbita de la Tierra alrededor del Sol. La variable $t$ se llama parámetro independiente y, en este contexto, representa el tiempo relativo al comienzo de cada año.
Una curva en el plano $(x, y)$ puede representarse paramétricamente. Las ecuaciones que se utilizan para definir la curva se denominan ecuaciones paramétricas.
Observa en esta definición que $x$ e $y$ se usan de dos maneras. La primera es como funciones de la variable independiente t. Como t varía en el intervalo $I$, las funciones $x(t)$ e $y(t)$ generan un conjunto de pares ordenados $(x, y)$. Este conjunto de pares ordenados genera la gráfica de las ecuaciones paramétricas. En este segundo uso, para designar los pares ordenados, $x$ e $y$ son variables. Es importante distinguir las variables $x$ e $y$ de las funciones $x(t)$ y $y(t)$.
 |
Graficando una curva definida paramétricamente |
a. $x(t) = t − 1,\; y(t) = 2t + 4,\; −3 ≤ t ≤ 2$
b. $x(t) = t^2 − 3,\; y(t) = 2t + 1,\; −2 ≤ t ≤ 3$
c. $x(t) = 4cost, \;y(t) = 4sent,\; 0 ≤ t ≤\; 2π$
Haz clic en el siguiente botón, para ver la solución al ejercicio.

 |
Dibuja la curva descrita por las ecuaciones paramétricas:
$$x(t) = 3t + 2,\; y (t) = t^2 − 1,\; −3 ≤ t ≤ 2$$Sugerencia: Haz una tabla de valores para $x(t)$ y $y(t)$ usando valores de $t$ de $−3$ a $2$.

Para comprender mejor la gráfica de una curva representada de manera paramétrica, es útil reescribir las dos ecuaciones como una sola ecuación que relaciona las variables $x$ e $y$. Luego podemos aplicar cualquier conocimiento previo de ecuaciones de curvas en el plano para identificar la curva. Por ejemplo, las ecuaciones que describen la curva plana en la parte b del primer ejercicio, son:
$$x(t) = t^2 − 3,\; y(t) = 2t + 1,\; −2 ≤ t ≤ 3$$Resolviendo la segunda ecuación para t, obtenemos:
$$t = \frac{y - 1}{2}$$Este resultado puede ser sustituido en la primera ecuación:
$$x=\left(\frac{y-1}{2}\right)^2 - 3 = \frac{y^2-2y+1}{4} -3 = \frac{y^2-2y-11}{4}$$Esta ecuación describe $x$ como una función de $y$. Estos pasos dan un ejemplo de eliminación del parámetro. La gráfica de esta función es una parábola que se abre hacia la derecha. Recuerda que la curva plana comenzó en $(1, −3)$ y terminó en $(6, 7)$. Estas terminaciones se debieron a la restricción del parámetro $t$.
 |
Eliminando el parámetro |
Elimina el parámetro para cada una de las curvas planas descritas por las siguientes ecuaciones paramétricas y describe el gráfico resultante.
$a.\; x(t) = \sqrt{2t + 4},\; y(t) = 2t + 1,\; −2 ≤ t ≤ 6\\ b.\; x(t) = 4cost,\; y(t) = 3sent,\; 0 ≤ t ≤ 2π$

 |
Elimina el parámetro para la curva plana definida por las siguientes ecuaciones paramétricas y describe el gráfico resultante.
$$x(t) = 2 + \frac{3}{t},\; y(t) = t − 1,\; 2 ≤ t ≤ 6$$Sugerencia: Resuelve una de las ecuaciones para t y sustitúyela en la otra ecuación.

Hasta ahora hemos visto el método de eliminar el parámetro, asumiendo que conocemos un conjunto de ecuaciones paramétricas que describen una curva plana. ¿Qué pasa si nos gustaría comenzar con la ecuación de una curva y determinar un par de ecuaciones paramétricas para esa curva? Esto es ciertamente posible, y de hecho es posible hacerlo de muchas maneras diferentes para una curva dada. El proceso se conoce como parametrización de una curva.
 |
Parametrizando una curva |
Encuentra dos pares de ecuaciones paramétricas diferentes para representar la gráfica de $y = 2x^2 − 3$.
Haz clic en el botón para observar la solución:

 |
Encuentra dos conjuntos diferentes de ecuaciones paramétricas para representar la gráfica de $y = x^2 + 2x$.
Sugerencia: Sigue los pasos del ejercicio anterior. Recuerda que tenemos libertad para elegir la parametrización de $x(t)$.

Imagínate paseando en bicicleta por el país. Los neumáticos permanecen en contacto con la carretera y giran en un patrón predecible. Ahora supongamos que una hormiga muy decidida está cansada después de un largo día y quiere llegar a casa. Así que se cuelga del lado del neumático y consigue un viaje gratis. El camino que esta hormiga recorre por un camino recto se llama cicloide (Figura 1.3). Una cicloide generada por un círculo (o rueda de bicicleta) de radio a, está dada por las ecuaciones paramétricas:
$$x(t) = a(t − sen t),\; y(t) = a(1 − cos t).$$Para ver por qué esto es cierto, considera el camino que toma el centro de la rueda. El centro se mueve a lo largo del eje $x$ a una altura constante igual al radio de la rueda. Si el radio es $a$, entonces las coordenadas del centro pueden ser dadas por las ecuaciones
$$x(t) = at,\; y(t) = a$$para cualquier valor de $t$. A continuación, considera la hormiga, que gira alrededor del centro a lo largo de un camino circular. Si la bicicleta se mueve de izquierda a derecha, las ruedas giran en el sentido de las agujas del reloj.
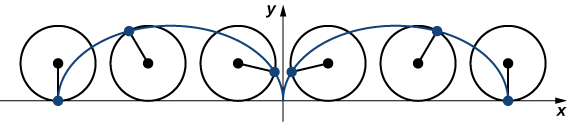
Figura 1.3. Una rueda que recorre una carretera sin resbalarse; el punto en el borde de la rueda traza un cicloide.
Una posible parametrización del movimiento circular de la hormiga (en relación con el centro de la rueda) está dada por
$$x(t) = -asen t, y(t) = -acos t.$$(El signo negativo es necesario para invertir la orientación de la curva. Si el signo negativo no estuviera allí, tendríamos que imaginar la rueda girando en sentido contrario a las agujas del reloj). Sumar estas ecuaciones juntas da las ecuaciones para la cicloide.
$$x(t) = a(t − sen t), \;y(t) = a(1 − cos t).$$Este tipo de curva recibió el nombre de "Helena de los geométras"Véase en Carrillo & Llamas, el trazado de algunas curvas (Revista Suma, 1999).. Pese a que fue Mersenne, en 1615, quien la define como cicloide, su estudio fue de mucho interés para Galileo, Torricelli, Fermat, Descartes, Huygens y Pascal (Ibid).
Dado su gran interés para estos ilustres matemáticos, vamos a describir su construcción geométrica y, posteriormente, las ecuaciones paramétricas que la definen.
De la miscelánea (Ruleta cicloidal), diseñada por Rita Jiménez Igea, Ildefonso Fernández Trujillo y Ángel Cabezudo Bueno, encontramos que,
Una ruleta cicloidal es una curva plana que describe la trayectoria de un punto vinculado a una circunferencia, llamada generatriz, que rueda tangencialmente sin deslizarse sobre otra curva plana llamada directriz. Según sea la curva directriz sobre la que rueda la circunferencia, la ruleta cicloidal recibe nombres diferentes. Se llama cicloide a la ruleta cicloidal que rueda sobre una recta. El punto vinculado a la circunferencia puede ser interior, exterior o estar en la circunferencia; en este último caso se dice que la cicloide es normal.
En la escena interactiva de la página siguiente, al pulsar el botón animar/parar, vemos cómo se genera la cicloide normal. El punto vinculado a la circunferencia es el punto $P$ que inicialmente hace contacto con la recta.
Supongamos ahora que la rueda de la bicicleta no viaja por una carretera recta, sino que se mueve por el interior de una rueda más grande, como se muestra en la figura 1.4. En este gráfico, el círculo verde se desplaza alrededor del círculo azul en sentido contrario a las agujas del reloj. Un punto en el borde del círculo verde traza el gráfico rojo, que se llama hipocicloide.
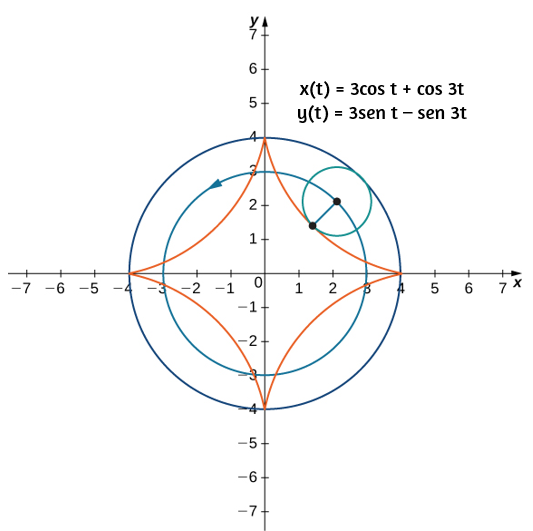
Figura 1.4. Gráfico del hipocicloide descrito por las ecuaciones paramétricas mostradas.
Otra curva de gran interés es la hipocicloide. Las ecuaciones paramétricas generales para una hipocicloide son:
$$x(t) = (a − b)cost + bcos\left(\frac{a - b}{b}\right)t\\ y(t) = (a − b)sent − bsen\left(\frac{a - b}{b}\right)t$$Estas ecuaciones son un poco más complicadas, pero la deducción es algo similar a las ecuaciones para la cicloide. En este caso, asumimos que el radio del círculo más grande es $a$ y el radio del círculo más pequeño es $b$. Luego, el centro de la rueda se desplaza a lo largo de un círculo de radio $a − b$. Este hecho explica el primer término en cada ecuación anterior. El período de la segunda función trigonométrica tanto en $x(t)$ como en $y(t)$ es igual a $\frac{2πb}{a - b}$
En la siguiente escena interactiva, observa cómo se generan las hipocicloides, a partir de punto P de una circunferencia de radio $b$ que rota interiormente y sin deslizamiento sobre otra circunferencia de radio $a$.
La relación $\frac{a}{b}$ está relacionada con el número de cúspides en el gráfico (las cúspides son las esquinas o los extremos puntiagudos del gráfico), como se ilustra en la figura 1.4. Esta relación puede llevar a algunos gráficos muy interesantes, dependiendo de si la relación es racional o no. La figura corresponde a $a = 4$ y $b = 1$. El resultado es un hipocicloide con cuatro cúspides, llamada astroide.
Inicialmente, la escena presenta la relación $\frac{a}{b} = 3$, que corresponde a una hipocicloide llamada deltoide, cambia el valor de $a$ por 4 y observarás la astroide.En la escena interactiva puedes obtener otras posibilidades.
Ahora, haz clic en el botón Inicio para cambiar el valor de $t$ a cero y usas el botón animar/parar, para que observes la construcción geométrica de la hipocicloide, puedes hacerlo más lento con el pulsador $t$.
En la figura 1.5, presentamos algunas de esas posibilidades para que las reproduzcas en el interactivo. Las dos últimas hipocicloides tienen valores irracionales para $a/b$. En estos casos, los hipocicloides tienen un número infinito de cúspides, por lo que nunca vuelven a su punto de partida, por ello, debes recurrir a los pulsadores $t$ y zoom. Estos son ejemplos de lo que se conoce como curvas de relleno de espacio.
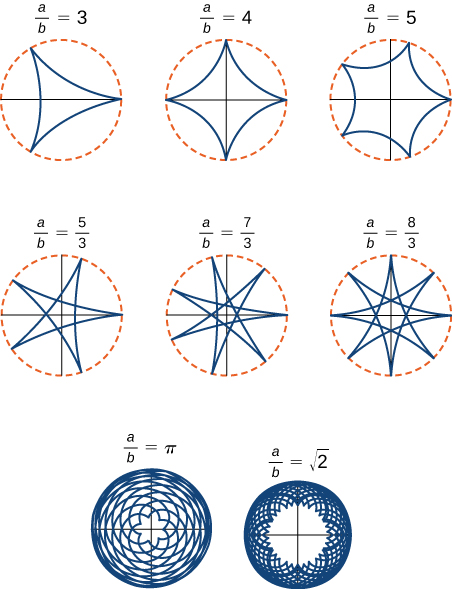
Figura 1.5. Gráfico de varios hipocicloides correspondientes a diferentes valores de a/b.
Muchas curvas planas en matemáticas llevan el nombre de las personas que las investigaron por primera vez, como el folio de Descartes o la espiral de Arquímedes. Sin embargo, quizás el nombre más extraño para una curva es la bruja de Agnesi. ¿Por qué una bruja?
Maria Gaetana Agnesi (1718–1799) fue una de las pocas mujeres matemáticas reconocidas en la Italia del siglo XVIII. Escribió un libro popular sobre geometría analítica, publicado en 1748, que incluía una curva interesante que había estudiado Fermat en 1630. El matemático Guido Grandi mostró en 1703 cómo construir esta curva, que más tarde llamó la "versoria", una Término latino para una cuerda usada en la navegación. Agnesi usó el término italiano para esta cuerda, "versiera", pero en latín, esta misma palabra significa "duende femenino". Cuando el libro de Agnesi se tradujo al inglés en 1801, el traductor usó el término "bruja" para la curva, en lugar de la cuerda. El nombre "bruja de Agnesi" se ha pegado desde entonces.
La bruja de Agnesi es una curva definida de la siguiente manera: Comienza con un círculo de radio $a$ para que los puntos $(0,0)$ y $(0,2a)$ sean puntos en el círculo (Figura 1.6). Dejemos que $O$ denote el origen. Elige cualquier otro punto $A$ en el círculo y traza la recta secante $OA$. Sea $B$ el punto en el cual la recta OA inyterseca la recta horizontal a través de $(0,2a)$. La recta vertical a través de $B$ interseca la recta horizontal a través de $A$ en el punto $P$. A medida que el punto $A$ varía, la trayectoria que recorre el punto $P$ es la curva de la bruja de Agnesi para el círculo dado.
Las curvas de la bruja de Agnesi tienen aplicaciones en física, que incluyen el modelado de ondas de agua y la distribución de líneas espectrales.
En la teoría de la probabilidad, la curva describe la función de densidad de probabilidad de la distribución de Cauchy. En este apartado parametrizarás estas curvas.
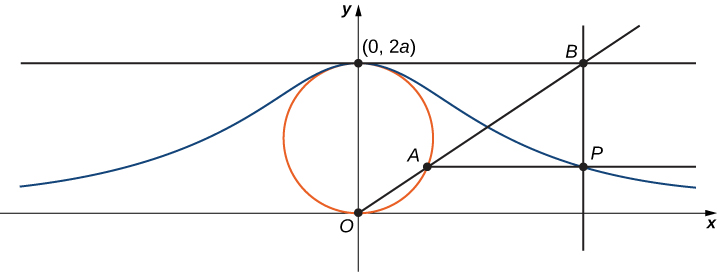
Figura 1.6. A medida que el punto $A$ se mueve alrededor del círculo, el punto $P$ traza la curva de la bruja de Agnesi para el círculo dado.
El objetivo de este apartado es parametrizar a la bruja utilizando $θ$ como parámetro. Para hacer esto, escribe ecuaciones para x e y en términos de solo $θ$.
En la siguiente escena interactiva hemos emulado la figura 1.6. En esta escena puedes generar la curva de la bruja de Agnesi aumentando el valor del parámetro $t$, también puedes cambiar el valor del radio.
Anteriormente en esta sección, observamos las ecuaciones paramétricas de una cicloide, que es el camino que un punto en el borde de una rueda traza a medida que la rueda gira a lo largo de un camino recto. En este proyecto, observamos dos variaciones diferentes de la cicloide, denominadas cicloides acortadas (curtata) y alargadas (prolata).
Primero, revisemos la derivación de las ecuaciones paramétricas para una cicloide. Recordemos que consideramos una hormiga tenaz que intenta llegar a casa colgada del borde de un neumático de bicicleta. Hemos asumido que la hormiga se subió al neumático en el borde, donde el neumático toca el suelo.
A medida que la rueda gira, la hormiga se mueve con el borde del neumático (Figura 1.7).
Como hemos discutido, tenemos mucha flexibilidad al parametrizar una curva. En este caso, dejamos que nuestro parámetro $t$ represente el ángulo por el que ha girado el neumático. Al observar la Figura, vemos que después de que el neumático haya girado en un ángulo $t$, la posición del centro de la rueda, $C = (x_C, y_C)$, viene dada por
$$x_C = at\; e\; y_C = a$$
Figura 1.7. (a) La hormiga se adhiere al borde del neumático de la bicicleta a medida que el neumático se desplaza por el suelo. (b) Usar la geometría para determinar la posición de la hormiga después de que el neumático haya girado en un ángulo $t$.
Además, al dejar que $A = (x_A, y_A)$ denote la posición de la hormiga, notamos que
$$x_C − x_A = asent \;e\; y_C − y_A = acost$$Entonces
$$x_A = x_C − asent = at − asent = a(t − sent)$$Observa que estas son las mismas representaciones paramétricas que teníamos antes, pero ahora hemos asignado un significado físico a la variable paramétrica $t$.
Después de un tiempo, la hormiga se está mareando al dar vueltas y vueltas en el borde del neumático. Entonces sube uno de los radios hacia el centro de la rueda. Al subir hacia el centro de la rueda, la hormiga ha cambiado su trayectoria de movimiento. La nueva ruta tiene menos movimiento hacia arriba y hacia abajo y se denomina cicloide curtata (Figura 1.8). Como se muestra en la figura, permitimos que $b$ denote la distancia a lo largo del radio desde el centro de la rueda hasta la hormiga. Como antes, dejamos que $t$ represente el ángulo por el que ha girado el neumático. Además, permitimos que $C = (x_C, y_C)$ represente la posición del centro de la rueda y $A = (x_A, y_A)$ represente la posición de la hormiga.
Una vez que la cabeza de la hormiga se aclara, se da cuenta de que el ciclista ha dado un giro y ahora se está alejando de su casa. Así que se deja caer del neumático de la bicicleta y mira a su alrededor. Afortunadamente, hay un conjunto de vías de tren cercanas, dirigidas de regreso en la dirección correcta. Así que la hormiga se dirige a las vías del tren para esperar.
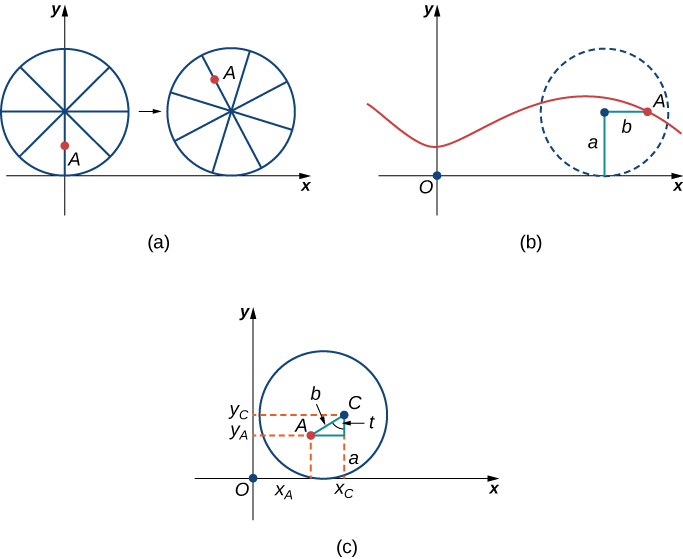
Figura 1.8. (a) La hormiga sube por uno de los radios hacia el centro de la rueda. (b) La trayectoria de movimiento de la hormiga después de que se acerca más al centro de la rueda. Esto se llama una cicloide curtata o acortada. (c) La nueva configuración, ahora que la hormiga se ha acercado al centro de la rueda.
Al cabo de un rato, pasa un tren en dirección correcta, y logra saltar y simplemente atrapar el borde de la rueda del tren (¡sin ser aplastada!).
La hormiga todavía está preocupada por marearse, pero la rueda del tren está resbaladiza y no tiene radios para trepar, por lo que decide simplemente aferrarse al borde de la rueda y esperar lo mejor. Ahora, las ruedas del tren tienen una pestaña para mantener la rueda funcionando en las vías.
Entonces, en este caso, dado que la hormiga cuelga del borde de la pestaña, la distancia desde el centro de la rueda a la hormiga es en realidad mayor que el radio de la rueda (Figura 1.9).
La configuración aquí es esencialmente la misma que cuando la hormiga subió el radio en la rueda de la bicicleta. Dejamos que $b$ denote la distancia desde el centro de la rueda a la hormiga, y dejamos que $t$ represente el ángulo por el que ha girado el neumático. Además, dejamos que $C = (x_C, y_C)$ represente la posición del centro de la rueda y $A = (x_A, y_A)$ represente la posición de la hormiga (Figura 1.9).
Cuando la distancia desde el centro de la rueda a la hormiga es mayor que el radio de la rueda, su trayectoria de movimiento se llama una cicloide prolata.
Tanto las cicloides curtatas como prolatas, son denominadas trocoides. En la escena interactiva de la Página 35 hemos representado una trocoide, en la cual moviendo los parámetros $a$ y $r$ en los controles de la escena, puedes observar que en el caso de que el punto se encuentre en el exterior de la circunferencia ($a > r$), la trocoide tiene "lazos" (prolata) y en el caso contrario no los tiene.
Esta curva fué estudiada por Durero en 1525 y Rømer en 1674. Su nombre se deriva del griego trokhos: rueda.
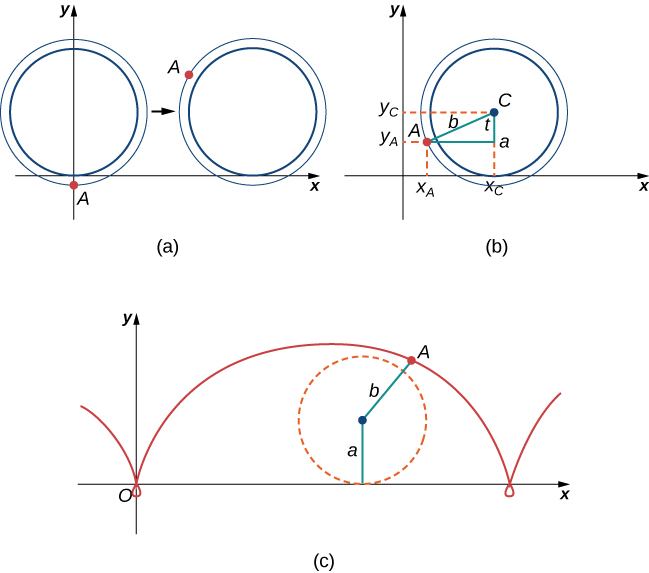
Figura 1.9. (a) La hormiga cuelga de la brida de la rueda del tren. (b) La nueva configuración, ahora que la hormiga ha saltado a la rueda del tren. (c) La hormiga viaja a lo largo de una cicloide prolata.
En la siguiente escena interactiva puedes observar una cicloide alargada, reduce el valor de $a$ para obtener una cicloide acortada.

A continuación, encontrará varios ejercicios para que confrontes lo aprendido. Lo ejercicios correspondientes a numerales impares, presentan la solución.
 Para los siguientes ejercicios, dibuja las curvas eliminando el parámetro $t$. Indica la orientación de la curva.
Para los siguientes ejercicios, dibuja las curvas eliminando el parámetro $t$. Indica la orientación de la curva.
1. $x = t^2 + 2t, \;y = t + 1$ (Solución)
2. $x = cos(t), \;y = sen(t),\; (0,2π]$
3. $x = 2t + 4,\; y = t − 1$ (Solución)
4. $x = 3 − t,\; y = 2t − 3,\; 1.5 ≤ t ≤ 3$
 En el siguiente ejercicio, elimina el parámetro y dibuja los gráficos.
En el siguiente ejercicio, elimina el parámetro y dibuja los gráficos.
5. $x = 2t^2, \;y = t^4 + 1$ (Solución)
 Para los siguientes ejercicios, usa la tecnología (CAS o calculadora) para dibujar las ecuaciones paramétricas.
Para los siguientes ejercicios, usa la tecnología (CAS o calculadora) para dibujar las ecuaciones paramétricas.
6. [T] $x = t^2 + t,\; y = t^2 − 1$
7. [T] $x = e^{-t},\; y = e^{2t} − 1$ (Solución)
8. [T] $x = 3cost,\; y = 4sent$
9. [T] $x = sect,\; y = cost$ (Solución)
 Para los siguientes ejercicios, dibuja las ecuaciones paramétricas eliminando el parámetro. Indica cualquier asíntota del gráfico.
Para los siguientes ejercicios, dibuja las ecuaciones paramétricas eliminando el parámetro. Indica cualquier asíntota del gráfico.
10. $x = e^t,\; y = e^{2t} + 1$
11. $x = 6sen(2θ),\; y = 4cos(2θ)$ (Solución)
12. $x = cosθ,\; y = 2sen(2θ)$
13. $x = 3 − 2cosθ,\; y = −5 + 3senθ$ (Solución)
14. $x = 4 + 2cosθ,\; y = −1 + senθ$
15. $x = sect,\; y = tant$ (Solución)
16. $x = ln(2t),\; y = t^2$
17. $x = e^t,\; y = e^{2t}$ (Solución)
18. $x = e^{−2t},\; y = e^{3t}$
19. x = $t^3,\; y = 3lnt$ (Solución)
20. $x = 4secθ,\; y = 3tanθ$
 Para los siguientes ejercicios, convierte las ecuaciones paramétricas de una curva en forma rectangular. No es necesario ningún boceto. Condición del dominio de la forma rectangular.
Para los siguientes ejercicios, convierte las ecuaciones paramétricas de una curva en forma rectangular. No es necesario ningún boceto. Condición del dominio de la forma rectangular.
21. $x = t^2 − 1,\; y = \frac{t}{2}$ (Solución)
22. $x = \frac{1}{\sqrt{t + 1}},\; y = \frac{1}{t + 1},\; t > -1$
23. $x = 4cosθ,\; y = 3senθ,\; t ∈ (0,2π]$ (Solución)
24. $x = cosht, \;y = senht$
25. $x = 2t − 3,\; y = 6t − 7$ (Solución)
26. $x = t^2,\; y = t^3$
27. $x = 1 + cost,\; y = 3 − sent$ (Solución)
28. $x = \sqrt{t},\; y = 2t + 4$
29. $x = sect,\; y = tant,\; π ≤ t ≤ 3π/2$ (Solución)
30. $x = 2cosht,\; y = 4senht$
31. $x = cos(2t),\; y = sent$ (Solución)
32. $x = 4t + 3, y = 16t^2 − 9$
33. $x = t^2,\; y = 2lnt,\; t ≥ 1$ (Solución)
34. $x = t^3, \;y = 3lnt,\; t ≥ 1$
35. $x = t^n,\; y = nlnt,\; t ≥ 1$, donde $n$ es un número natural (Solución)
36. $x = ln(5t),\; y = ln(t^2);$ donde $1 ≤ t ≤ e$
37. $x = 2sen(8t),\; y = 2cos(8t)$ (Solución)
38. $x = tan t,\; y = sec^2 t - 1$
 Para los siguientes ejercicios, los pares de ecuaciones paramétricas representan rectas, parábolas, círculos, elipses o hipérbolas. Nombra el tipo de curva básica que representa cada par de ecuaciones.
Para los siguientes ejercicios, los pares de ecuaciones paramétricas representan rectas, parábolas, círculos, elipses o hipérbolas. Nombra el tipo de curva básica que representa cada par de ecuaciones.
39. $x = 3t + 4,\; y = 5t − 2$ (Solución)
40. $x − 4 = 5t,\; y + 2 = t$
41. $x = 2t + 1,\; y = t^2 − 3$ (Solución)
42. $x = 3cost,\; y = 3sent$
43. $x = 2cos(3t),\; y = 2sen(3t)$ (Solución)
44. $x = cosht,\; y = senht$
45. $x = 3cost,\; y = 4sent$ (Solución)
46. $x = 2cos(3t),\; y = 5sen(3t)$
47. $x = 3cosh(4t),\; y = 4senh(4t)$ (Solución)
48. $x = 2cosht,\; y = 2senht$
 Para los siguientes ejercicios, usa una utilidad gráfica para graficar la curva representada por las ecuaciones paramétricas e identificar la curva a partir de su ecuación.
Para los siguientes ejercicios, usa una utilidad gráfica para graficar la curva representada por las ecuaciones paramétricas e identificar la curva a partir de su ecuación.
49. $x = θ + senθ,\; y = 1 − cosθ$ (Solución)
50. $x = 2t − 2sent,\; y = 2 − 2cost$
51. $x = t − 0.5sent,\; y = 1 − 1.5cost$ (Solución)
52. Un avión que viaja horizontalmente a 100 m/s sobre terreno plano a una altura de 4000 metros debe dejar caer un paquete de emergencia en un objetivo en el suelo.
La trayectoria del paquete viene dada por $x = 100t,\; y = −4.9t^2 + 4000,\; t ≥ 0$ donde el origen es el punto en el suelo directamente debajo del plano en el momento del lanzamiento. ¿Cuántos metros horizontales antes del objetivo se debe lanzar el paquete para golpear el objetivo?
53. La trayectoria de una bala viene dada por
$x = v_0(cosα)t,\; y = v_0(senα)t − \frac{1}{2}gt^2$ donde $v_0 = 500 m/s, \;g = 9.8 m/s^2$, y $α = 30^\circ$. ¿Cuándo llegará la bala al suelo? ¿A qué distancia del cañón caerá la bala al suelo? (Solución)
54. Usa la tecnología para dibujar la curva representada por $x = sen(4t),\; y = sen(3t),\; 0 ≤\; t ≤\; 2π$.
55. Usa la tecnología para dibujar $x = 2tan(t),\; y = 3sec(t),\; -π ≤ t ≤ π$. (Solución)
56. Dibuja la curva conocida como epitrocoide, que da la trayectoria de un punto en un círculo de radio $b$ a medida que rueda en el exterior de un círculo de radio $a$. Las ecuaciones son
$$x = (a + b)cost − c•cos\left(\frac{(a + b)t}{b}\right)\\
y = (a + b)sent − c•sen\left(\frac{(a + b)t}{b}\right)$$
haz $a = 1, \;b = 2, \;c = 1$.
57. Usa la tecnología para dibujar la curva espiral dada por $x = tcos(t),\; y = tsen(t),\; −2π ≤ t ≤ 2π$. (Solución)
58. Usa la tecnología para graficar la curva dada por las ecuaciones paramétricas
$$x = 2cot(t),\; y = 1 − cos(2t),\; -π/2 ≤ t ≤ π/2.$$
Esta curva es conocida como la bruja de Agnesi.
59. Dibuja la curva dada por las ecuaciones paramétricas $x = cosh(t),\; y = senh(t)$, donde −2 ≤ $t$ ≤ 2. (Solución)
Ahora que hemos introducido el concepto de una curva parametrizada, nuestro siguiente paso es aprender cómo trabajar con este concepto en el contexto del cálculo. Por ejemplo, si conocemos una parametrización de una curva dada, ¿es posible calcular la pendiente de una recta tangente a la curva? ¿Qué tal la longitud de arco de la curva? ¿O el área bajo la curva?
Otro escenario: supongamos que nos gustaría representar la ubicación de una pelota de béisbol después de que la pelota deja la mano de un lanzador. Si la posición de la pelota de béisbol está representada por la curva plana $(x(t),\; y(t))$, entonces deberíamos poder usar el cálculo para encontrar la velocidad de la pelota en cualquier momento dado. Además, deberíamos poder calcular la distancia que ha recorrido esa bola en función del tiempo.
Comenzamos preguntando cómo calcular la pendiente de una recta tangente a una curva paramétrica en un punto. Considera la curva plana definida por las ecuaciones paramétricas.
$$x(t) = 2t + 3,\; y(t) = 3t − 4,\; −2 ≤ t ≤ 3.$$La gráfica de esta curva aparece en la figura 1.10. Es un segmento de recta que comienza en $(−1, −10)$ y termina en $(9, 5)$.
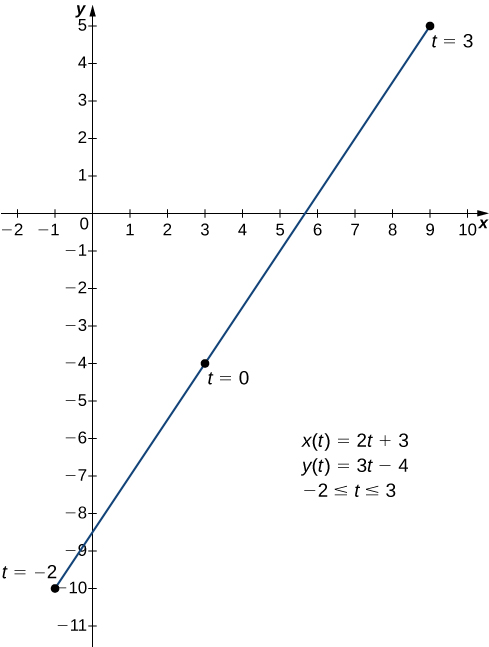
Figura 1.10. Gráfico del segmento de recta descrito por las ecuaciones paramétricas dadas.
Podemos eliminar el parámetro resolviendo primero la ecuación $x(t) = 2t + 3$ para t:
$$\begin{aligned} x(t) &= 2t + 3\\ x - 3 &= 2t\\ t &= \frac{x-3}{2} \end{aligned}$$Sustituyendo en $y(t)$, obtenemos
$$\begin{aligned} y(t) &= 3t - 4\\ y &= 3\left(\frac{x - 3}{2}\right) - 4\\ y &= \frac{3x}{2} - \frac{9}{2} - 4\\ y &= \frac{3x}{2} - \frac{17}{2} \end{aligned}$$La pendiente de esta recta está dada por $\frac{dy}{dx} = \frac{3}{2}$. Luego calculamos $x'(t)\; e\; y'(t)$. Esto da $x'(t) = 2\; e\; y'(t) = 3$. Ten en cuenta que $\frac{dy}{dx} = \frac{dy/dt}{dx/dt} = \frac{3}{2}$. Esto no es una coincidencia, como se describe en el siguiente teorema.
Demostración
Este teorema puede ser probado usando la Regla de la Cadena.
En particular, supón que el parámetro $t$ puede eliminarse, dando como resultado una función diferenciable $y = F(x)$. Entonces $y(t) = F(x(t))$. Diferenciando ambos lados de esta ecuación usando los resultados de la regla de la cadena
$$y'(t) = F'(x(t))x'(t)$$entonces
$$F'(x(t)) = \frac{y'(t)}{x'(t)}$$Pero $F'(x(t)) = \frac{dy}{dx}$, lo que prueba el teorema.
La ecuación se puede utilizar para calcular derivadas de curvas planas, así como puntos críticos. Recuerda que un punto crítico de una función diferenciable $y = f(x)$ es cualquier punto $x = x_0$ tal que $f'(x_0) = 0$ o $f'(x_0)$ no existe. La ecuación da una fórmula para la pendiente de una recta tangente a una curva definida paramétricamente, independiente de si la curva se puede describir mediante una función $y = f(x)$ o no.
 |
Encontrando la derivada de una curva paramétrica |
Calcula la derivada $\frac{dy}{dx}$ para cada una de las siguientes curvas planas definidas paramétricamente y ubica los puntos críticos en sus gráficos respectivos.
a. $x(t) = t^2 − 3,\; y(t) = 2t − 1,\; −3 ≤ t ≤ 4$
$b. \;x(t) = 2t + 1,\; y(t) = t^3 − 3t + 4,\; −2 ≤ t ≤ 2$
c. $x(t) = 5cost,\; y(t) = 5sent,\; 0 ≤ t ≤ 2π$

 |
Calcula la derivada $dy/dx$ para la curva plana definida por las ecuaciones
$$x(t) = t^2 − 4t, \;y(t) = 2t^3 − 6t,\; −2 ≤ t ≤ 3$$y ubicar los puntos críticos en su gráfica.
Sugerencia
Calcula $x'(t)$ e $y'(t)$ y usa la ecuación.

 |
Encuentra una recta tangente |
Encuentra la ecuación de la recta tangente a la curva definida por las ecuaciones
$$x(t) = t^2 − 3,\; y(t) = 2t − 1,\; −3 ≤ t ≤ 4,\; \text{cuando } t = 2$$
Luego de haber solucionado el ejercicio, interactúa con la siguiente escena diseñada en GeoGebra:
 |
Encuentra la ecuación de la recta tangente a la curva definida por las ecuaciones
$$x(t) = t^2 − 4t,\; y(t) = 2t^3 − 6t,\; −2 ≤ t ≤ 3, \text{cuando }t = 5$$
Nuestro siguiente objetivo es ver cómo tomar la segunda derivada de una función definida paramétricamente. La segunda derivada de una función $y = f(x)$ se define como la derivada de la primera derivada; es decir,
$$\frac{d^2y}{dx^2}=\frac{d}{x}\left(\frac{dy}{dx}\right)$$Dado que $\frac{dy}{dx} = \frac{dy/dt}{dx/dt^2}$, podemos reemplazar la $y$ en ambos lados de esta ecuación con $\frac{dy}{dx}$. Esto nos da
$$\frac{d^2y}{dx^2}=\frac{d}{dx}\left(\frac{dy}{dx}\right)=\frac{(d/dt)(dy/dx)}{dx/dt} \tag{$1.2$}$$Si conocemos $dy/dx$ como una función de $t$, entonces esta fórmula es sencilla de aplicar.
 |
Encuentra la segunda derivada |
Calcula la segunda derivada $d^2y/dx^2$ para la curva plana definida por las ecuaciones paramétricas
$$x(t) = t^2 − 3,\; y(t) = 2t − 1,\; −3 ≤ t ≤ 4.$$
 |
Calcula la segunda derivada $d^2y/dx^2$ para la curva plana definida por las ecuaciones
$$x(t) = t^2 − 4t,\; y(t) = 2t^3 − 6t,\; −2 ≤ t ≤ 3$$y ubicar los puntos críticos en su gráfica.

Ahora que hemos visto cómo calcular la derivada de una curva plana, la siguiente pregunta es: ¿Cómo podemos encontrar el área bajo una curva definida paramétricamente? Recuerda el cicloide definido por las ecuaciones $x(t) = t − sent,\; y(t) = 1 − cos t$.
Supongamos que queremos encontrar el área de la región sombreada en el siguiente gráfico.
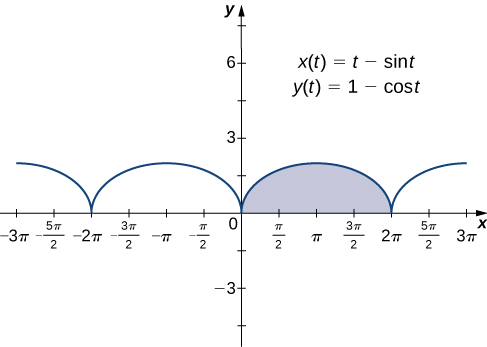
Figura 1.11. Gráfico de una cicloide con el arco sobre [0, 2π] resaltado.
Al derivar una fórmula para el área bajo la curva definida por las funciones
$$x = x(t),\; y = y(t),\; a ≤ t ≤ b,$$asumimos que $x(t)$ es diferenciable y comenzamos con una partición igual del intervalo a $≤ t ≤ b$. Supón que $t_0 = a < t_1 < t_2 < ...< t_n = b$ y considera la siguiente gráfica.
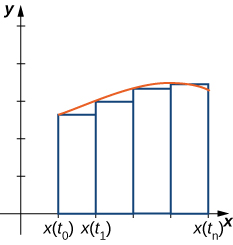
Figura 1.12. Aproximando el área bajo una curva definida paramétricamente.
Usamos rectángulos para aproximar el área debajo de la curva. La altura de un rectángulo típico en esta parametrización es $y(x(\bar{t}_i))$ para algún valor $\bar{t}_i$ en el subintervalo $i$, y el ancho se puede calcular como $x(t_i) − x(t_{i - 1})$. Así, el área del rectángulo $i$ está dada por
$$A_i = y(x(\bar{t}_i))(x(t_i) − x(t_{i - 1})).$$Entonces una suma de Riemann para el área es
$$A_n = \sum_{i=1}^n y(x(\bar{t}_i))(x(t_i) − x(t_{i - 1}))$$Multiplicando y dividiendo cada área por $t_i − t_{i - 1}$, obtenemos:
Tomando el límite cuando n se acerca al infinito
$$A = \lim_{n \to{+}\infty}{A_n} = \int_{a}^{b} y(t)x'(t)dt$$Esto nos lleva al siguiente teorema.
 |
Encontrando el área bajo una curva paramétrica |
Encuentra el área bajo la curva de la cicloide definida por las ecuaciones
$$x(t) = t − sen t,\; y(t) = 1 − cos t,\; 0 ≤ t ≤ 2π.$$
La siguiente escena interactiva, permite calcular el área bajo la cicloide. Cambia los límites de integración para obtener otras áreas.
 |
Encuentra el área bajo la curva del hipocicloide definida por las ecuaciones
$$x(t) = 3cos t + cos 3t,\; y(t) = 3sen t − sen 3t,\; 0 ≤ t ≤ π$$ |
Sugerencia |
Usa la ecuación, junto con las identidades $senαsenβ = \frac{1}{2}[cos(α − β) − cos(α + β)]$ y $sen^2t = \frac{1 − cos 2t}{2}$

La hipocicloide del ejercicio es conocida como Astroide (hipocicloide de cuatro ramas). En la siguiente escena interactiva, verifica el cálculo del área en el intervalo [0, 2π] y observa que su construcción es de derecha a izquierda, en la mitad de dicho intervalo.
Además de encontrar el área bajo una curva paramétrica, a veces necesitamos encontrar la longitud del arco de una curva paramétrica. En el caso de un segmento de recta, la longitud del arco es la misma que la distancia entre los puntos finales.
Si una partícula viaja desde el punto $A$ hasta el punto $B$ a lo largo de una curva, entonces la distancia que recorre esa partícula es la longitud del arco. Para desarrollar una fórmula para la longitud del arco, comenzamos con una aproximación por segmentos de recta como se muestra en el siguiente gráfico.
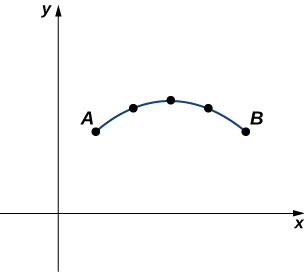
Figura 1.13. Aproximación de una curva por segmentos de recta.
Dada una curva plana definida por las funciones $x = x(t),\; y = y(t),\; a ≤ t ≤ b$, comenzamos dividiendo el intervalo $[a, b]$ en $n$ subintervalos iguales: $t_0 = a < t_1 < t_2 < ... < t_n = b$. El ancho de cada subintervalo viene dado por $Δt = (b − a)/n$. Podemos calcular la longitud de cada segmento de recta:
$$d_1 = \sqrt{(x(t_1)- x(t_0))^2 + (y(t_1)- y(t_0))^2}$$ $$d_2 = \sqrt{(x(t_2)- x(t_1))^2 + (y(t_2)- y(t_1))^2},\; etc.$$Luego los sumamos. Dejamos que $s$ denote la longitud de arco exacta y $s_n$ denote la aproximación por n segmentos de recta:
$$s \approx \sum_{k=1}^n s_k = \sum_{k=1}^n\sqrt{(x(t_k)- x(t_{k - 1}))^2 + (y(t_k)- y(t_{k - 1}))^2} \tag{$1.4$}$$
Si asumimos que $x(t)$ e $y(t)$ son funciones diferenciables de $t$, entonces se aplica el teorema del valor medio, por lo que en cada subintervalo $[t_{k − 1}, t_k]$ existen $\widehat{t}_k$ y $\bar{t}_k$ tal que
$$x(t_k) - x(t_{k - 1}) = x'(\widehat{t}_k)(t_k - t_{k - 1}) = x'(\widehat{t}_k)Δt\\ y(t_k) - y(t_{k - 1}) = y'(\bar{t}_k)(t_k - t_{k - 1}) = y'(\bar{t}_k)Δt$$Por lo tanto, la ecuación se convierte en
$$\begin{aligned} s &\approx \sum_{k=1}^N s_k\\ &= \sum_{k=1}^n \sqrt{(x'(\widehat{t}_k)Δt)^2 + (y'(\bar{t}_k)Δt)^2}\\ &= \sum_{k=1}^n \sqrt{(x'(\widehat{t}_k)^2(Δt)^2 + (y'(\bar{t}_k)^2(Δt)^2}\\ &= \left(\sum_{k=1}^n \sqrt{(x'(\widehat{t}_k))^2 + (y'(\bar{t}_k))^2}\right)Δt \end{aligned}$$Esta es una suma de Riemann que se aproxima a la longitud del arco sobre una partición del intervalo $[a, b]$. Si asumimos además que las derivadas son continuas y permitimos que el número de puntos en la partición aumente sin límite, la aproximación se aproxima a la longitud exacta del arco. Esto da
Al tomar el límite, los valores de $\widehat{t}_k$ y $\bar{t}_k$ están contenidos dentro del mismo intervalo cada vez menor de ancho $Δt$, por lo que deben converger al mismo valor. Podemos resumir este método en el siguiente teorema.
En este punto, una derivación lateral conduce a una fórmula anterior para la longitud del arco. En particular, supón que el parámetro se puede eliminar, lo que lleva a una función $y = F(x)$. Luego $y(t) = F(x(t))$ y por Regla de la cadena $y′(t) = F′(x(t))x′(t)$. Sustituyendo esto en la ecuación 1.5, obtenemos:
$$\begin{aligned} s &= \int_{t_1}^{t_2}\sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2}dt\\ &= \int_{t_1}^{t_2}\sqrt{\left(\frac{dx}{dt}\right)^2 + \left(F'(x)\frac{dx}{dt}\right)^2}dt\\ &= \int_{t_1}^{t_2}\sqrt{\left(\frac{dx}{dt}\right)^2 \left(1+(F'(x)\right)^2}dt\\ &= \int_{t_1}^{t_2} x'(t)\sqrt{1+\left(\frac{dy}{dx}\right)^2}dt \end{aligned}$$Aquí hemos asumido que $x'(t)> 0$, que es una suposición razonable. La regla de la cadena nos dice que $dx = x'(t)dt$, y dejando $a = x(t_1)$ y $b = x(t_2)$, obtenemos la fórmula
$$s=\int_{a}^{b} \sqrt{1+\left(\frac{dy}{dx}\right)^2}dx,$$la cuál es la fórmula para la longitud del arco obtenida en la Introducción en los libros de integración.
 |
Encontrar la longitud del arco de una curva paramétrica |
Encuentra la longitud del arco del semicírculo definido por las ecuaciones
$$x(t) = 3cost,\; y(t) = 3sent,\; 0≤t≤π.$$
Ahora volvemos al problema planteado al comienzo de la sección sobre una pelota de béisbol que deja la mano de un lanzador. Ignorando el efecto de la resistencia del aire (¡a menos que sea una bola curva!), La bola recorre un camino parabólico. Suponiendo que la mano del lanzador está en el origen y la bola viaja de izquierda a derecha en la dirección del eje x positivo, las ecuaciones paramétricas para esta curva se pueden escribir como
$$x(t)=140t,\;y(t)=−16t^2+2t$$donde t representa el tiempo. Primero calculamos la distancia que recorre la pelota en función del tiempo. Esta distancia está representada por la longitud del arco. Podemos modificar la fórmula de la longitud del arco ligeramente. Primero reescribe las funciones $x(t)$ e $y(t)$ usando $v$ como variable independiente, para eliminar cualquier confusión con el parámetro $t$:
$$x(v) = 140v,\; y(v) = - 16v^2 + 2v$$.Luego escribimos la fórmula de la longitud del arco de la siguiente manera:
$$\begin{aligned} s(t) &= \int_{0}^{t}\sqrt{\left(\frac{dx}{dv}\right)^2+\left(\frac{dy}{dv}\right)^2}dv\\ &= \int_{0}^{t}\sqrt{140^2+(−32v+2)^2}dv \end{aligned}$$La variable $v$ actúa como una variable ficticia que desaparece después de la integración, dejando la longitud del arco en función del tiempo $t$. Para integrar esta expresión podemos usar una tabla de integrales, en la cual encontrarás esta expresión:
$$\int \sqrt{a^2+u^2}du = \frac{u}{2}\sqrt{a^2+u^2}+\frac{a^2}{2}ln|u+\sqrt{a^2+u^2}|+C$$Establecemos $a = 140$ y $u = −32v + 2$. Esto da $du = −32dv$, entonces $dv = −\frac{1}{32}du$. Por lo tanto
$\int\sqrt{140^2+(−32v+2)^2}dv = -\frac{1}{32}\int\sqrt{a^2+u^2}du$$=-\frac{1}{32}\left(\frac{(-32v+2)}{2}\sqrt{140^2 +(−32v+2)^2}+\frac{140^2}{2}ln|(−32v+2)+\sqrt{140^2+(−32v+2)^2}|\right)\\+C$
y
$s(t)= -\frac{1}{32}\left(\frac{(-32v+2)}{2}\sqrt{140^2 +(−32v+2)^2}+\frac{140^2}{2}ln|(−32v+2)+\sqrt{140^2+(−32v+2)^2}|\right)\\ +\frac{1}{32}\left(\sqrt{140^2+2^2}+\frac{140^2}{2}ln|2+\sqrt{140^2+2^2}\right)$
$s(t)=\left(\frac{t}{2}-\frac{1}{32}\right) \sqrt{1024t^2−128t+19604} -\frac{1225}{4}ln|(−32t+2)+\\ \sqrt{1024t^2−128t+19604}|+\frac{\sqrt{19604}}{32}+\frac{1225}{4}ln(2+\sqrt{19604}).$
Esta función representa la distancia recorrida por la pelota en función del tiempo. Para calcular la velocidad, toma la derivada de esta función con respecto a $t$. Si bien esto puede parecer una tarea desalentadora, es posible obtener la respuesta directamente del Teorema fundamental del cálculo:
$$\frac{d}{dx}\int_{0}^{x}f(u)du = f(x).$$Por lo tanto
$$\begin{aligned} s'(t) &= \frac{d}{dt}s(t)\\ &= \frac{d}{dt}\int_{0}^{t}\sqrt{140^2+(-32v+2)^2}dv\\ &= \sqrt{140^2+(-32v+2)^2}\\ &= \sqrt{1024t^2−128t+19604}\\ &= 2\sqrt{256t^2−32t+4901} \end{aligned}$$Un tercio de segundo después de que la pelota deja la mano del lanzador, la distancia que recorre es igual a
$s(\frac13) = (\frac{1/3}{2}-\frac{1}{32})\sqrt{1024(1/3)^2−128(1/3)+19604}\\ -\sqrt{125}{4}|(-32(1/3)+2)+\sqrt{1024(1/3)^2−128(1/3)+19604}|\\ +\frac{\sqrt{19604}}{32}+\frac{1225}{4}ln(2+\sqrt{19604})\\ \approx 46.69 pies.$Este valor es un poco más de tres cuartos del camino al plato de home. La velocidad de la pelota es
$$s'(\frac13) = 2\sqrt{256(\frac13)^2 - 16(\frac13) + 4901} \approx 140.34\; pies/s$$Esta velocidad se traduce en aproximadamente 95 mph, una bola rápida de grandes ligas.
Recordemos el problema de encontrar el área de la superficie de un volumen de revolución. Una fórmula para encontrar el área de la superficie de un volumen generado por una función $y = f(x)$ desde $x = a$ a $x = b$, girada alrededor del eje $x$ es:
$$ S = 2π\int_{a}^{b} f(x)\sqrt{1+(f'x))^2}dx\tag{$1.6$}$$Ahora consideramos un volumen de revolución generado al girar una curva definida paramétricamente como $x = x(t), \;y = y(t),\;\\ a \le t \le b$ alrededor del eje x como se muestra en la siguiente figura.
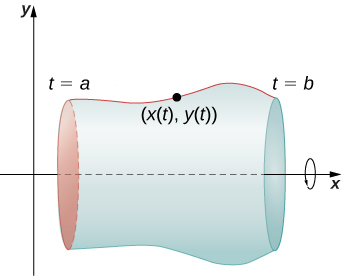
Figura 1.15 Una superficie de revolución generada por una curva definida paramétricamente.
La fórmula análoga para una curva definida paramétricamente es
$$ S = 2π\int_{a}^{b} y(t)\sqrt{(x'(t))^2+(y'(t))^2}dt$$siempre que $y(t)$ no sea negativo en $[a, b]$.
 |
Encontrar la superficie de área |
Encuentra el área de la superficie de una esfera de radio $r$ centrada en el origen.

Una demostración interesante, nos la presenta Anthony OR 柯志明 en la siguiente escena de GeoGebra.
Arrastra el punto rojo para ver cómo se puede diseccionar una esfera en $n$ pirámides (aproximadas) de alturas iguales al radio $r$. Deja que $A_1$, $A_2$, ..., $A_n$ sean las áreas de las bases de las pirámides.
(a) Demuestra que
$$\frac13(A_1 + A_2 + ... + A_n) r \approx \text{Volumen de la esfera}$$
(b) Cuando $n$ tiende al infinito, demuestra que $\frac13 Sr = V$, donde $V$ y $S$ son el volumen y el área de superficie de la esfera, respectivamente.
Por lo tanto, demuestra que $S = 4πr^2$.
¡Haz clic en la esquina superior derecha de la escena, para verla en un tamaño mayor!

A continuación, encontrarás varios ejercicios para que confrontes lo aprendido. Lo ejercicios correspondientes a numerales impares, presentan la solución.
 Para los siguientes ejercicios, cada conjunto de ecuaciones paramétricas representa una recta. Sin eliminar el parámetro, encuentre la pendiente de cada recta.
Para los siguientes ejercicios, cada conjunto de ecuaciones paramétricas representa una recta. Sin eliminar el parámetro, encuentre la pendiente de cada recta.
62. $x=3+t,\; y=1−t$
63. $x=8+2t,\; y=1$ (Solución)
64. $x=4−3t,\; y=−2+6t$
65. $x=−5t+7,\; y=3t−1$ (Solución)
 Para los siguientes ejercicios, determina la pendiente de la recta tangente, luego encuentra la ecuación de la recta tangente en el valor dado del parámetro.
Para los siguientes ejercicios, determina la pendiente de la recta tangente, luego encuentra la ecuación de la recta tangente en el valor dado del parámetro.
66. $x=3sent,\;y=3cost,\;t=\fracπ4$
67. $x=cost,\;y=8sent,\;t=\fracπ2$ (Solución)
68. $x=2t,\;y=t^3,\;t=−1$
69. $x=t+1t,\;y=t−\frac1t,\;t=1$ (Solución)
70. $x=\sqrt{t},\;y=2t,\;t=4$
 Para los siguientes ejercicios, encuentra todos los puntos en la curva que tengan la pendiente dada.
Para los siguientes ejercicios, encuentra todos los puntos en la curva que tengan la pendiente dada.
71. $x = 4cost,\; y = 4sent$, pendiente = 0.5 (Solución)
72. $x = 2cost,\; y = 8sent$, pendiente = −1
73. $x = t + \frac1t,\; y = t − 1t$, pendiente = 1 (Solución)
74. $x = 2 + \sqrt{t},\; y = 2−4t$, pendiente = 0
 Para los siguientes ejercicios, escribe la ecuación de la recta tangente en coordenadas cartesianas para el parámetro dado $t$.
Para los siguientes ejercicios, escribe la ecuación de la recta tangente en coordenadas cartesianas para el parámetro dado $t$.
75. $x = e^{\sqrt{t}},\; y = 1 − lnt^2,\; t = 1$ (Solución)
76. $x = tlnt,\; y = sen^2t,\; t = \fracπ4$
77. $x = e^t,\; y = (t − 1)^2,\; en\; (1,1)$ (Solución)
78. Para $x = sen(2t),\; y = 2sent$, donde $0 \le t \lt 2π$. Encuentra todos los valores de $t$ en los que existe una recta tangente horizontal.
79. Para $x = sen(2t),\; y = 2sent$, donde $0 \le t \lt 2π$. Encuentra todos los valores de t en los que existe una recta tangente vertical. (Solución)
80. Encuentra todos los puntos en la curva $x = 4cos(t),\; y = 4sen(t)$ que tienen la pendiente de $\frac12$.
81. Encuentra $\frac{dy}{dx}$ para $x = sen(t),\; y = cos(t)$. (Solución)
82. Encuentra la ecuación de la recta tangente a $x = sen(t),\; y = cos(t)\; en\; t = \fracπ4$.
83. Para la curva $x = 4t,\; y = 3t − 2$, encuentra la pendiente y la concavidad de la curva en $t = 3$. (Solución)
84. Para la curva paramétrica cuya ecuación es $x = 4cosθ,\; y = 4senθ$, encuentra la pendiente y la concavidad de la curva en $θ = \fracπ4$.
85. Encuentra la pendiente y la concavidad de la curva cuya ecuación es $x = 2 + secθ,\; y = 1 + 2tanθ\; en\; θ = \fracπ6$. (Solución)
86. Encuentra todos los puntos en la curva $x = t + 4,\; y = t^3−3t$ en los que hay tangentes verticales y horizontales.
87. Encuentra todos los puntos en la curva $x = secθ,\; y = tanθ$ en los que existen tangentes horizontales y verticales. (Solución)
 Para los siguientes ejercicios, encuentra $\frac{d^2y}{dx^2}$.
Para los siguientes ejercicios, encuentra $\frac{d^2y}{dx^2}$.
88. $x=t^4−1,\;y=t−t^2$
89. $x=sen(πt),\;y=cos(πt)$ (Solución)
90. $x=e^{−t},y=te^{2t}$
 Para los siguientes ejercicios, encuentra puntos en la curva en los que la recta tangente sea horizontal o vertical.
Para los siguientes ejercicios, encuentra puntos en la curva en los que la recta tangente sea horizontal o vertical.
91. $x=t(t^2−3),\;y=3(t^2−3)$ (Solución)
92. $x=\frac{3t}{1+t^3},\;y=\frac{3t^2}{1+t^3}$
 Para los siguientes ejercicios, encuentra dy/dx en el valor del parámetro.
Para los siguientes ejercicios, encuentra dy/dx en el valor del parámetro.
93. $x=cost,\;y=sent,\;t=\frac{3π}{4}$ (Solución)
94. $x=\sqrt{t},\;y=2t+4,\;t=9$
95. $x=4cos(2πs),\;y=3sen(2πs),\;s=−\frac14$ (Solución)
 Para los siguientes ejercicios, encuentra $d^2y/dx^2$ en el punto dado sin eliminar el parámetro.
Para los siguientes ejercicios, encuentra $d^2y/dx^2$ en el punto dado sin eliminar el parámetro.
96. $x = \frac12t^2,\; y = \frac13t^3,\; t = 2$
97. $x = \sqrt{t},\; y = 2t + 4,\; t = 1$ (Solución)
98. Encuentra los intervalos $t$ en los que la curva $x = 3t^2,\; y = t^3 − t$ es cóncava hacia arriba y cóncava hacia abajo.
99. Determina la concavidad de la curva $x = 2t + lnt,\; y = 2t − lnt$. (Solución)
100. Dibuja y encuentra el área debajo de un arco del cicloide $x = r(θ − senθ),\; y = r(1 − cosθ)$.
101. Encuentra el área delimitada por la curva $x = cost,\; y = e^t, 0 \le t \le \fracπ2$ y las rectas $y = 1$ y $x = 0$. (Solución)
102. Encuentra el área encerrada por la elipse $x = acosθ,\; y = bsenθ,\; 0 \le θ \lt 2π$.
103. Encuentra el área de la región delimitada por $x = 2sen2θ,\; y = 2sen2θtanθ,\; para\; 0 \le θ \le \fracπ2$. (Solución)
 Para los siguientes ejercicios, encuentra el área de las regiones delimitadas por las curvas paramétricas y los valores indicados del parámetro.
Para los siguientes ejercicios, encuentra el área de las regiones delimitadas por las curvas paramétricas y los valores indicados del parámetro.
104. $x = 2cotθ,\; y = 2sin^2θ,\; 0 \le θ \le π$
105. [T] $x = 2acost − acos(2t),\; y = 2asent − asen(2t),\\ 0 \le t \lt 2π$ (Solución)
106. [T] $x = asen(2t),\; y = bsen(t),\; 0 \le t \lt 2π$ (el "reloj de arena")
107. [T] $x = 2acost − asen(2t),\; y = bsent,\; 0 \le t \lt 2π$ (la "lágrima") (Solución)
 Para los siguientes ejercicios, encuentra la longitud del arco de la curva en el intervalo indicado del parámetro.
Para los siguientes ejercicios, encuentra la longitud del arco de la curva en el intervalo indicado del parámetro.
108. $x = 4t + 3,\; y = 3t − 2,\;0 \le t \le 2$
109. $x = \frac13t^3,\; y = \frac12t^2,\;0 \le t \le 1$ (Solución)
110. $x = cos(2t),\; y = sen(2t),\; 0 \le t \le \fracπ2$
111. $x = 1 + t^2,\; y = (1 + t)^3,\;0 \le t \le 1$ (Solución)
112. $x = e^tcost,\; y = e^tsent,\; 0 \le t \le \fracπ2$ (expresa la respuesta como un decimal redondeado a tres lugares)
113. $x = acos^3θ,\; y = asen^3θ$ en el intervalo $[0,2π)$ (el hipocicloide) (Solución)
114. Halla la longitud de un arco del cicloide $x = 4(t − sent), \;y = 4(1 − cost)$.
115. Encuentra la distancia recorrida por una partícula con posición $(x, y)$ ya que $t$ varía en el intervalo de tiempo dado: $x = sen^2t,\; y = cos^2t,\; 0 \le t \le 3π$.
116. Halla la longitud de un arco del cicloide $x = θ − senθ,\; y = 1 − cosθ$. (Solución)
117. Demuestra que la longitud total de la elipse $x = 4senθ,\; y = 3cosθ$ es $L = 16 \int_{0}^{π/2} \sqrt{1 − e^2sen^2θ}dθ\;$, donde $e = \frac{c}{a}$ y $c = \sqrt{a^2 − b^2}$.
118. Encuentra la longitud de la curva $x = e^t − t,\; y = 4e^{t/2}, −8 \le t \le 3$.
 Para los siguientes ejercicios, encuentra el área de la superficie obtenida girando la curva dada sobre el eje x.
Para los siguientes ejercicios, encuentra el área de la superficie obtenida girando la curva dada sobre el eje x.
119. $x = t^3,\; y = t^2,\;0 \le t \le 1$ (Solución)
120. $x = acos^3θ,\; y = asen^3θ,\; 0 \le θ\le π/2$
121. [T] Usa un CAS para encontrar el área de la superficie generada al girar $x = t + t^3,\; y = t − \frac{1}{t^2},\;1 \le t \le 2$ alrededor del eje x. (Responde con tres decimales). (Solución)
122. Encuentra el área de superficie obtenida girando $x = 3t^2,\; y = 2t^3,\;0 \le t \le 5\;$ alrededor del eje y.
123. Encuentra el área de la superficie generada al girar $x = t^2,\; y = 2t,\; 0 \le t \le 4$ alrededor del eje x. (Solución)
124. Encuentra el área de superficie generada al girar $x = t^2,\; y = 2t^2,\;0 \le t \le 1$ alrededor del eje $y$.
El sistema de coordenadas rectangulares (o plano cartesiano) proporciona un medio de mapear puntos a pares ordenados y pares ordenados a puntos. Esto se denomina mapeo uno a uno desde puntos en el plano hasta pares ordenados. El sistema de coordenadas polares proporciona un método alternativo de mapeo de puntos a pares ordenados. En esta sección veremos que, en algunas circunstancias, las coordenadas polares pueden ser más útiles que las coordenadas rectangulares.
Para encontrar las coordenadas de un punto en el sistema de coordenadas polares, considera la figura 1.17. El punto $P$ tiene coordenadas cartesianas $(x, y)$. El segmento de recta que conecta el origen al punto $P$ mide la distancia desde el origen a $P$ y tiene una longitud $r$. El ángulo entre el eje x positivo y el segmento de recta tiene la medida $θ$. Esta observación sugiere una correspondencia natural entre el par de coordenadas $(x, y)$ y los valores $r$ y $θ$. Esta correspondencia es la base del sistema de coordenadas polares. Ten en cuenta que cada punto en el plano cartesiano tiene dos valores (de ahí el término par ordenado) asociado a él. En el sistema de coordenadas polares, cada punto también tiene dos valores asociados: $r$ y $θ$.
Usando la trigonometría del triángulo rectángulo, las siguientes ecuaciones son verdaderas para el punto $P$:
$$cosθ = \frac{x}{r}\;\text{entonces}\;\;x=rcosθ$$ $$senθ=\frac{y}{r}\;\text{entonces }\;\;y=rsenθ$$Por lo tanto
$$r^2=x^2+y^2\;\;y\;\;tanθ=\frac{y}{x}$$.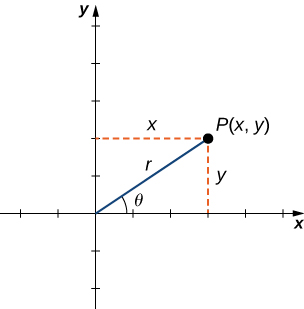
Figura 1.17 Un punto arbitrario en el plano cartesiano.
Por lo tanto, cada punto $(x, y)$ en el sistema de coordenadas cartesianas se puede representar como un par ordenado $(r, θ)$ en el sistema de coordenadas polares. La primera coordenada se llama coordenada radial y la segunda coordenada se llama coordenada angular. Cada punto en el plano se puede representar de esta forma.
Observa que la ecuación $tanθ = y/x$ tiene un número infinito de soluciones para cualquier par ordenado $(x, y)$.
Sin embargo, si restringimos las soluciones a valores entre $0$ y $2π$, entonces podemos asignar una solución única al cuadrante en el que se encuentra el punto original $(x, y)$. Entonces el valor correspondiente de $r$ es positivo, entonces $r^2 = x^2 + y^2$.
 |
Conversión entre coordenadas rectangulares y polares |
Convierte cada uno de los siguientes puntos en coordenadas rectangulares.
$e.(3, π/3)\\ f.(2,3π/2)\\ g.(6, −5π/6)$
La representación polar de un punto no es única. Por ejemplo, las coordenadas polares $(2, \fracπ3)$ y $(2,\frac{7π}{3})$ representan el punto $(1,\sqrt{3})$ en el sistema rectangular. Además, el valor de $r$ puede ser negativo. Por lo tanto, el punto con coordenadas polares $(−2,\frac{4π}{3})$ también representa el punto $(1,\sqrt{3})$ en el sistema rectangular, como podemos ver usando la Ecuación 1.8:
| $$\begin{aligned} x &= rcosθ\\ &=-2cos(\frac{π}{3})\\ &=-2(-\frac12)=1 \end{aligned}$$ | y | $$\begin{aligned} y &= rsenθ\\ &= -2sen(\frac{4π}{3})\\ &= -2(-\frac{\sqrt{3}}{2})=\sqrt{3} \end{aligned}$$ |
Cada punto en el plano tiene un número infinito de representaciones en coordenadas polares. Sin embargo, cada punto en el plano tiene solo una representación en el sistema de coordenadas rectangular.
Ten en cuenta que la representación polar de un punto en el plano también tiene una interpretación visual.
En particular, $r$ es la distancia dirigida que el punto se encuentra desde el origen, y $θ$ mide el ángulo que el segmento de recta desde el origen hasta el punto forma con el eje x positivo. Los ángulos positivos se miden en sentido antihorario y los ángulos negativos se miden en sentido horario. El sistema de coordenadas polares aparece en la siguiente figura.
Figura 1.18 El sistema de coordenadas polares
El segmento de recta que comienza desde el centro del gráfico hacia la derecha (llamado eje $x$ positivo en el sistema cartesiano) es el eje polar.
El punto central es el polo, u origen, del sistema de coordenadas, y corresponde a $r = 0$. El círculo más interno que se muestra en la figura 1.18 contiene todos los puntos a una distancia de una unidad del polo, y está representado por la ecuación $r = 1$. Entonces $r = 2$ es el conjunto de puntos a 2 unidades del polo, y así sucesivamente. Los segmentos de recta que emanan del polo corresponden a ángulos fijos. Para trazar un punto en el sistema de coordenadas polares, comienza con el ángulo. Si el ángulo es positivo, mida el ángulo desde el eje polar en sentido antihorario. Si es negativo, mídelo en sentido horario. Si el valor de $r$ es positivo, mueva esa distancia a lo largo del rayo terminal del ángulo. Si es negativo, muévase a lo largo del rayo opuesto al rayo terminal del ángulo dado.
En la siguiente escena, diseñada por Elena E. Álvarez SaizElena usa la notación $φ$ para el ángulo, en lugar de $θ$., haz clic en el botón "ver ejemplos", para diferentes posiciones del punto $P$.
En esta otra escena interactiva de Elena E. Álvarez Saiz, puedes observar la conversión de un sistema a otro, haciendo clic en los botones "ver ejemplos". Recuerda que haciendo clic en la esquina superior derecha, puedes ver la escena en una ventana ampliada.
 |
Trazar puntos en el plano polar |
Traza cada uno de los siguientes puntos en el plano polar.
$a. (2,\fracπ4)$ $b. (−3,\frac{2π}{3})$ $c. (4,\frac{5π}{4})$
Ahora que sabemos cómo trazar puntos en el sistema de coordenadas polares, podemos discutir cómo trazar curvas. En el sistema de coordenadas rectangulares, podemos graficar una función $y = f(x)$ y crear una curva en el plano cartesiano. De manera similar, podemos graficar una curva generada por una función $r = f(θ)$.
La idea general detrás de graficar una función en coordenadas polares es la misma que graficar una función en coordenadas rectangulares. Comienza con una lista de valores para la variable independiente ($θ$ en este caso) y calcula los valores correspondientes de la variable dependiente $r$. Este proceso genera una lista de pares ordenados, que se pueden trazar en el sistema de coordenadas polares. Finalmente, conecta los puntos y aprovecha cualquier patrón que pueda aparecer. La función puede ser periódica, por ejemplo, lo que indica que solo se necesita un número limitado de valores para la variable independiente.
 |
Graficar una función en coordenadas polares |
Grafica la curva definida por la función $r = 4senθ$. Identifica la curva y reescribe la ecuación en coordenadas rectangulares.

En este ejercicio obtendrás una circunferencia que contiene al polo. En la siguiente escena interactiva, también de Elena E. Álvarez Saiz, puedes observar otra ecuación en el sistema de coordenadas polares, que define dos tipos de circunferencia (con centro en el polo o conteniendo el polo). Cambia el valor de $φ_0$ a $pi/2$ y obtendrás la circunferencia del ejercicio anterior.
La gráfica en el ejercicio anterior era la de una circunferencia. La ecuación de la circunferencia se puede transformar en coordenadas rectangulares utilizando las fórmulas de transformación de la Ecuación 1.8, tal como lo puedes observar en el siguiente ejercicio.
 |
Transformación de ecuaciones polares en coordenadas rectangulares |
Reescribe cada una de las siguientes ecuaciones en coordenadas rectangulares e identifica el gráfico.
$a.\;θ=\frac{π}{3}\\ b.\;r=3 \\ c.\;r=6cos\theta−8sen\theta$
Hemos visto varios ejemplos de dibujar gráficos de curvas definidas por ecuaciones polares. Un resumen de algunas curvas comunes se da en las siguientes tablas (Figuras 1.21 y 1.22). En cada ecuación, $a$ y $b$ son constantes arbitrarias.
Haz clic sobre las imágenes para interactuar con las curvas. Las cuatro primeras fueron diseñadas por Elena E. Álvarez Saiz con DescartesJS, las dos últimas las diseñamos con GeoGebra.
| Nombre | Ecuación | Ejemplo |
| Recta pasando por el origen | $θ = k$ |  |
| Circunferencia | $r = acos(θ)+bsen(θ)$ | 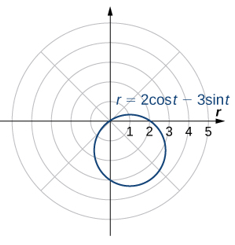 |
| Espiral | $r = a+b(θ)$ | 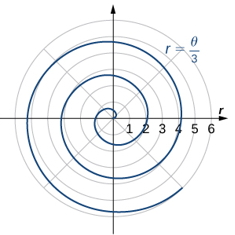 |
Figura 1.21
| Nombre | Ecuación | Ejemplo |
| Cardioide | $r=a(1+cosθ)\\r=a(1-cosθ)\\r=a(1+senθ)\\r=a(1-senθ)$ | 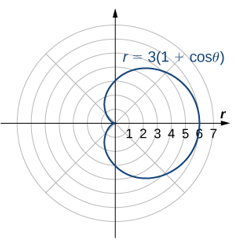 |
| Limaçon | $r = acosθ+b\\asenθ+b$ | 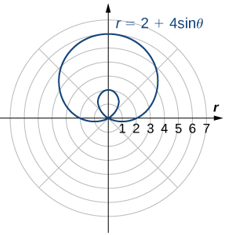 |
| Rosa | $r = acos(bθ)\\r = asen(bθ)$ | 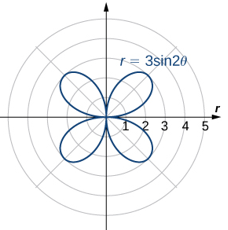 |
Figura 1.22
Sin interactuaste con las curvas, habrás observado que un cardioide es un caso especial de un limaçon (pronunciado "lee-mah-son"). La rosa es una curva muy interesante. Observa que la gráfica de $r = 3sen2θ$ tiene cuatro pétalos. Sin embargo, la gráfica de $r = 3sen3θ$ tiene tres pétalos como se muestra en la siguiente figura.
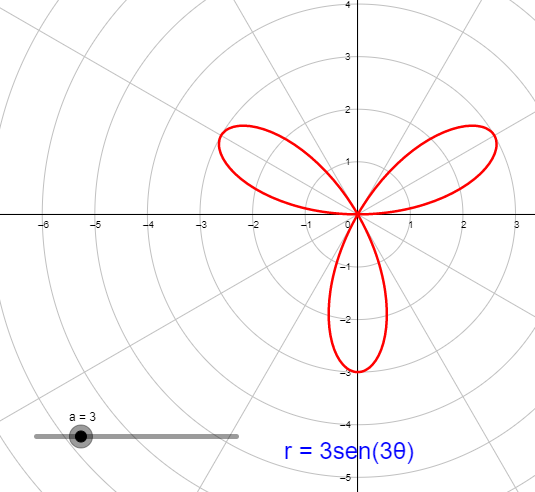
Figura 1.23 Gráfico de $r = 3sen3θ$.
Si el coeficiente de $θ$ es par, la gráfica tiene el doble de pétalos que el coeficiente. Si el coeficiente de $θ$ es impar, entonces el número de pétalos es igual al coeficiente. Te recomendamos explorar por qué sucede esto. Incluso surgen gráficos más interesantes cuando el coeficiente de $θ$ no es un número entero. Por ejemplo, si es racional, entonces la curva está cerrada; es decir, finalmente termina donde comenzó (ver escena interactiva a continuación). Sin embargo, si el coeficiente es irracional, entonces la curva nunca se cierra.
Aunque puede parecer que la curva está cerrada, un examen más detallado revela que los pétalos justo por encima del eje x positivo son ligeramente más gruesos. Esto se debe a que el pétalo no coincide con el punto de partida.
En la escena, cambia el valor de $a$ por números pares, impares o racionales.
Como la curva definida por la gráfica de $r = 3sen(πθ)$ nunca se cierra, la curva representada es solo una representación parcial. De hecho, este es un ejemplo de una curva que llena espacios. Una curva de relleno de espacio es aquella que, de hecho, ocupa un subconjunto bidimensional del plano real. En este caso, la curva ocupa el círculo de radio 3 centrado en el origen.
 |
Apertura del capítulo: Describiendo una espiral |
Recordemos el nautilo de cámara introducido en el primer apartado. Esta criatura muestra una espiral cuando se corta la mitad de la capa exterior. Es posible describir una espiral usando coordenadas rectangulares. La figura 1.25 muestra una espiral en coordenadas rectangulares. ¿Cómo podemos describir esta curva matemáticamente?
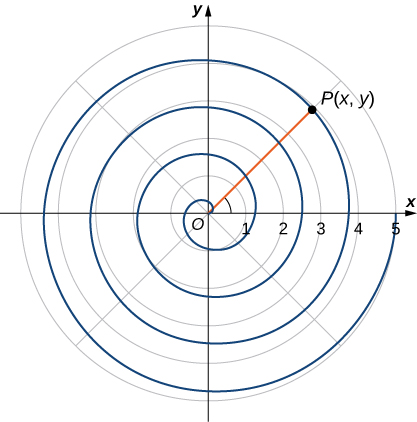
Figura 1.25 ¿Cómo podemos describir una gráfica espiral matemáticamente?

Supón que se describe una curva en el sistema de coordenadas polares a través de la función $r = f(θ)$. Dado que tenemos fórmulas de conversión de coordenadas polares a rectangulares dadas por
$$x = rcosθ$$ $$y = rsenθ$$es posible reescribir estas fórmulas usando la función
$$x = f(θ)cosθ$$ $$y = f(θ)senθ$$Este paso proporciona una parametrización de la curva en coordenadas rectangulares utilizando θ como parámetro. Por ejemplo, la fórmula espiral $r = a + bθ$ de la figura 1.21 se convierte en
$$x = (a+bθ)cosθ$$ $$y = (a+bθ)senθ$$Dejando que θ varíe de $−\infty$ a $\infty$ genera toda la espiral.
Al estudiar la simetría de funciones en coordenadas rectangulares (es decir, en la forma $y = f(x)$), hablamos de simetría con respecto al eje $y$ y simetría con respecto al origen.
En particular, si $f(−x) = f(x)$ para todas las $x$ en el dominio de $f$, entonces $f$ es una función par y su gráfica es simétrica con respecto al eje $y$. Si $f(−x) = -f (x)$ para todas las $x$ en el dominio de $f$, entonces $f$ es una función impar y su gráfica es simétrica con respecto al origen. Al determinar qué tipos de simetría exhibe un gráfico, podemos aprender más sobre la forma y el aspecto del gráfico. La simetría también puede revelar otras propiedades de la función que genera el gráfico. La simetría en las curvas polares funciona de manera similar.
La siguiente tabla muestra ejemplos de cada tipo de simetría.
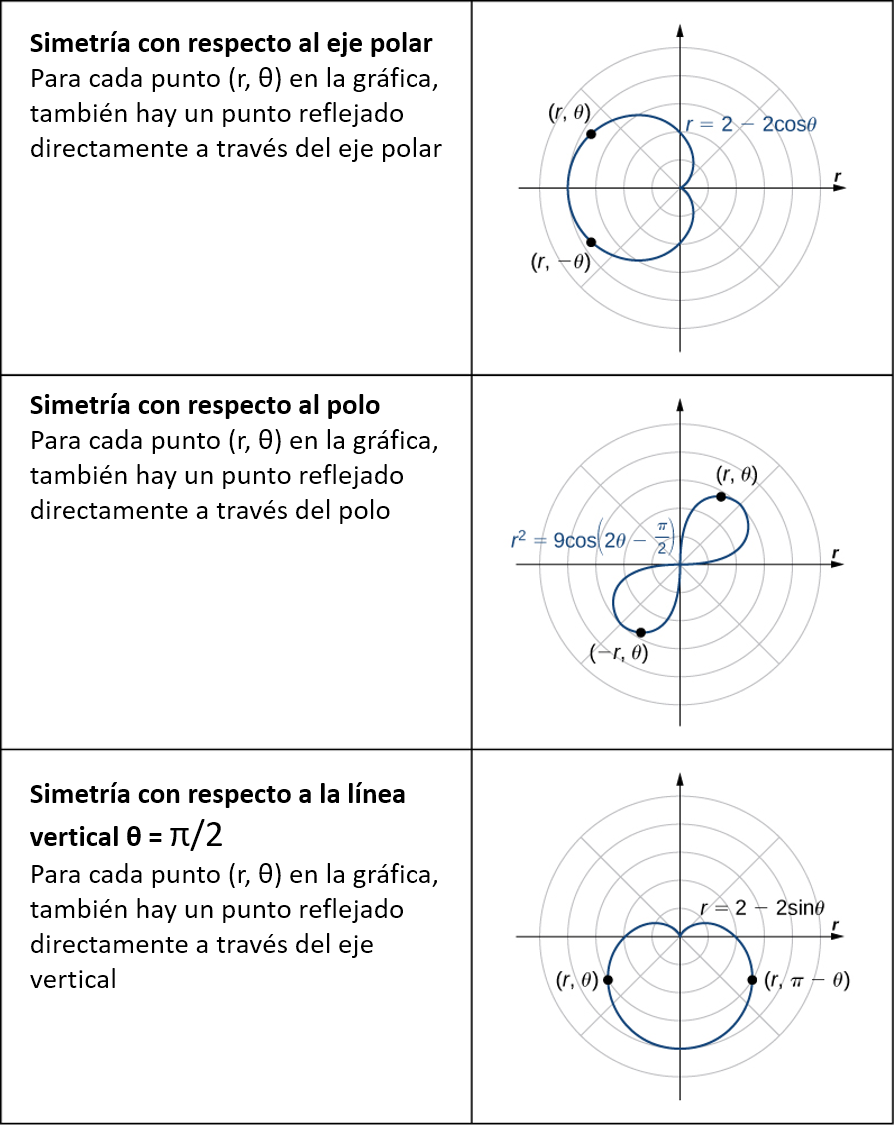
 |
Usando la simetría para graficar una ecuación polar |
Encuentra la simetría de la rosa definida por la ecuación $r = 3sen(2θ)$ y crea una gráfica.


A continuación, encontrarás varios ejercicios para que confrontes lo aprendido. Lo ejercicios correspondientes a numerales impares, presentan la solución.
 En los siguientes ejercicios, traza el punto cuyas coordenadas polares se dan construyendo primero el ángulo $θ$ y luego marcando la distancia $r$ a lo largo del rayo.
En los siguientes ejercicios, traza el punto cuyas coordenadas polares se dan construyendo primero el ángulo $θ$ y luego marcando la distancia $r$ a lo largo del rayo.
 Para los siguientes ejercicios, considera el gráfico polar a continuación. Da dos conjuntos de coordenadas polares para cada punto.
Para los siguientes ejercicios, considera el gráfico polar a continuación. Da dos conjuntos de coordenadas polares para cada punto.
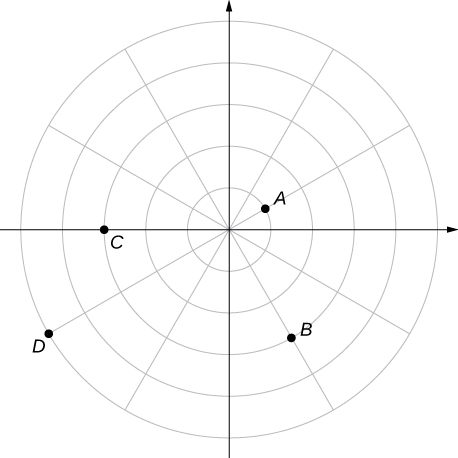 132. $\;\text{Coordenadas del punto A}$
132. $\;\text{Coordenadas del punto A}$ Para los siguientes ejercicios, se dan las coordenadas rectangulares de un punto. Encuentra dos conjuntos de coordenadas polares para el punto en $(0,2π)$. Redondea a tres decimales.
Para los siguientes ejercicios, se dan las coordenadas rectangulares de un punto. Encuentra dos conjuntos de coordenadas polares para el punto en $(0,2π)$. Redondea a tres decimales.
137. $\; (3,−4)$ (Solución)
138. $\; (8,15)$
139. $\; (−6,8)$ (Solución)
140. $\; (4,3)$
141. $\; (3,−\sqrt{3})$ (Solución)
 Para los siguientes ejercicios, encuentra coordenadas rectangulares para el punto dado en coordenadas polares.
Para los siguientes ejercicios, encuentra coordenadas rectangulares para el punto dado en coordenadas polares.
 Para los siguientes ejercicios, determina si las gráficas de la ecuación polar son simétricas con respecto al eje x, el eje y o el origen.
Para los siguientes ejercicios, determina si las gráficas de la ecuación polar son simétricas con respecto al eje x, el eje y o el origen.
 Para los siguientes ejercicios, describe la gráfica de cada ecuación polar. Confirma cada descripción convirtiéndola en una ecuación rectangular.
Para los siguientes ejercicios, describe la gráfica de cada ecuación polar. Confirma cada descripción convirtiéndola en una ecuación rectangular.
 Para los siguientes ejercicios, convierte la ecuación rectangular a forma polar y dibuja su gráfica.
Para los siguientes ejercicios, convierte la ecuación rectangular a forma polar y dibuja su gráfica.
 Para los siguientes ejercicios, convierte la ecuación rectangular a forma polar y dibuja su gráfica.
Para los siguientes ejercicios, convierte la ecuación rectangular a forma polar y dibuja su gráfica.
 Para los siguientes ejercicios, convierte la ecuación polar a forma rectangular y dibuja su gráfica.
Para los siguientes ejercicios, convierte la ecuación polar a forma rectangular y dibuja su gráfica.
 Para los siguientes ejercicios, dibuja un gráfico de la ecuación polar e identifica cualquier simetría.
Para los siguientes ejercicios, dibuja un gráfico de la ecuación polar e identifica cualquier simetría.
178. [T] La gráfica de $r = 2cos(2θ)sec(θ)$ se llama estrofoide. Usa una utilidad gráfica para dibujar el gráfico y, a partir del gráfico, determina la asíntota.
179. [T] Usa una utilidad gráfica y dibuja la gráfica de $r = \frac{6}{2senθ} − 3cosθ$. (Solución)
180. [T] Usa una utilidad gráfica para representar gráficamente
$r = \frac{1}{1 − cosθ}$.
181. [T] Usa la tecnología para graficar $r = e^{sen(θ)} −2cos(4θ)$. (Solución)
182. [T] Usa la tecnología para trazar $r = sen(\frac{3θ}{7})$ (usa el intervalo $ 0 \le θ \le 14π$).
En el sistema de coordenadas rectangulares, la integral definida proporciona una forma de calcular el área bajo una curva. En particular, si tenemos una función $y = f(x)$ definida de $x = a$ a $x = b$ donde $f(x) \gt 0$ en este intervalo, el área entre la curva y el eje $x$ viene dada por $A = \int_{a}^{b} f(x)dx$. Este hecho, junto con la fórmula para evaluar esta integral, se resume en el Teorema fundamental del cálculo. Del mismo modo, la longitud del arco de esta curva viene dada por $L = \int_{a}^{b} \sqrt{1+(f'(x))^2}dx$. En esta sección, estudiamos fórmulas análogas para el área y la longitud del arco en el sistema de coordenadas polares.
Hemos estudiado las fórmulas para el área bajo una curva definida en coordenadas rectangulares y curvas definidas paramétricamente. Ahora dirigimos nuestra atención a derivar una fórmula para el área de una región limitada por una curva polar.
Recuerda que la prueba del Teorema fundamental del cálculo utilizó el concepto de una suma de Riemann para aproximar el área bajo una curva mediante el uso de rectángulos. Para las curvas polares usamos nuevamente la suma de Riemann, pero los rectángulos se reemplazan por sectores de un círculo.
Considera una curva definida por la función $r = f(\theta)$, donde
$\alpha \le \theta \le \beta$. Nuestro primer paso es dividir el intervalo $[\alpha, \beta]$ en $n$ subintervalos de igual ancho. El ancho de cada subintervalo viene dado por la fórmula $\Delta\theta = (\beta − \alpha)/n$, y el i-ésimo punto de partición $\theta_i$ viene dado por la fórmula $\theta_i = \alpha + i\Delta\theta$.
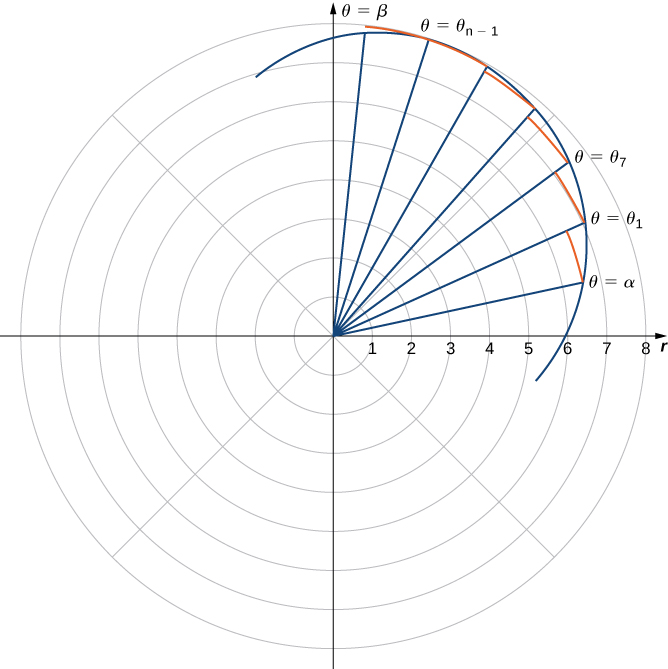
Figura 1.29 Una partición de una curva típica en coordenadas polares.
Cada punto de partición $\theta = \theta_i$ define una recta con pendiente $tan\theta_i$ que pasa a través del polo como se muestra en el gráfico anterior. Los segmentos de recta están conectados por arcos de radio constante. Esto define sectores cuyas áreas se pueden calcular utilizando una fórmula geométrica. El área de cada sector se usa para aproximar el área entre segmentos de recta sucesivos. Luego sumamos las áreas de los sectores para aproximar el área total. Este enfoque proporciona una aproximación de suma de Riemann para el área total.
En la siguiente escena interactiva, diseñada por Tom Ahlschwede, puedes visualizar el límite de la suma de las áreas del sector. El límite inferior y el límite superior se pueden cambiar, también cambia la forma de la ecuación polar $r = a_2sen(\theta)$
La fórmula para el área de un sector de un círculo se ilustra en la siguiente figura.
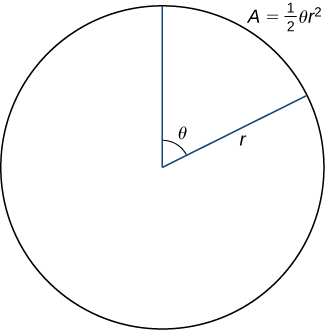
Figura 1.30 El área de un sector de un círculo viene dada por $A = \frac12\theta r^2$
Recuerda que el área de un círculo es $A = \pi r^2$. Al medir ángulos en radianes, 360 grados es igual a $2\pi$ radianes. Por lo tanto, una fracción de un círculo se puede medir por el ángulo central $\theta$. La fracción del círculo está dada por $\frac{\theta}{2\pi}$, por lo que el área del sector es esta fracción multiplicada por el área total:
$$A=\left(\frac{\theta}{2\pi}\right)\pi r^2= \frac12\theta r^2$$Dado que el radio de un sector típico en la Figura 1.29 viene dado por $r_i = f(\theta_i)$, el área del sector iésimo está dada por
$$A_i = \frac12(\Delta\theta)(f(\theta_i))^2$$Por lo tanto, una suma de Riemann que se aproxima al área viene dada por
Tomamos el límite como $n \to\infty$ para obtener el área exacta:
$$\lim_{n \to\infty} \sum_{i=1}^n A_i = \frac12\int_{\alpha}^{\beta}(f(\theta))^2d\theta$$Esto nos da el siguiente teorema.
 |
Encontrar el área de una región polar |
Encuentra el área de un pétalo de la rosa definida por la ecuación $r = 3sen (2\theta)$.

En la siguiente escena interactiva, diseñada por Tom Ahlschwede, puedes interactuar con la rosa y los segmentos usados para hallar el área. El límite inferior y el límite superior se pueden cambiar, también cambia la forma de la ecuación polar.
El ejemplo anterior involucraba encontrar el área dentro de una curva. También podemos usar el área de una región limitada por una curva polar para encontrar el área entre dos curvas polares. Sin embargo, a menudo necesitamos encontrar los puntos de intersección de las curvas y determinar qué función define la curva externa o la curva interna entre estos dos puntos.
 |
Encontrar el área entre dos curvas polares |
Encuentra el área fuera del cardioide $r = 2 + 2sen\theta$ y dentro del círculo $r = 6sen\theta$.

Una escena interactiva, diseñada por Tim Brzezinski, permite obtener la respuesta al ejercicio anterior. Esta escena permite, además, modificar las funciones polares, el intervalo $[t_{min}, t_{max}]$ y el número de sectores ($n$) en los que deseas dividir el intervalo $[t_{min}, t_{max}]$ (Nota: para ingresar un valor como $2\pi/3$, simplemente escribes "2pi/3" en el cuadro de entrada).
Interactúa con la escena haciendo clic en la siguiente imagen:
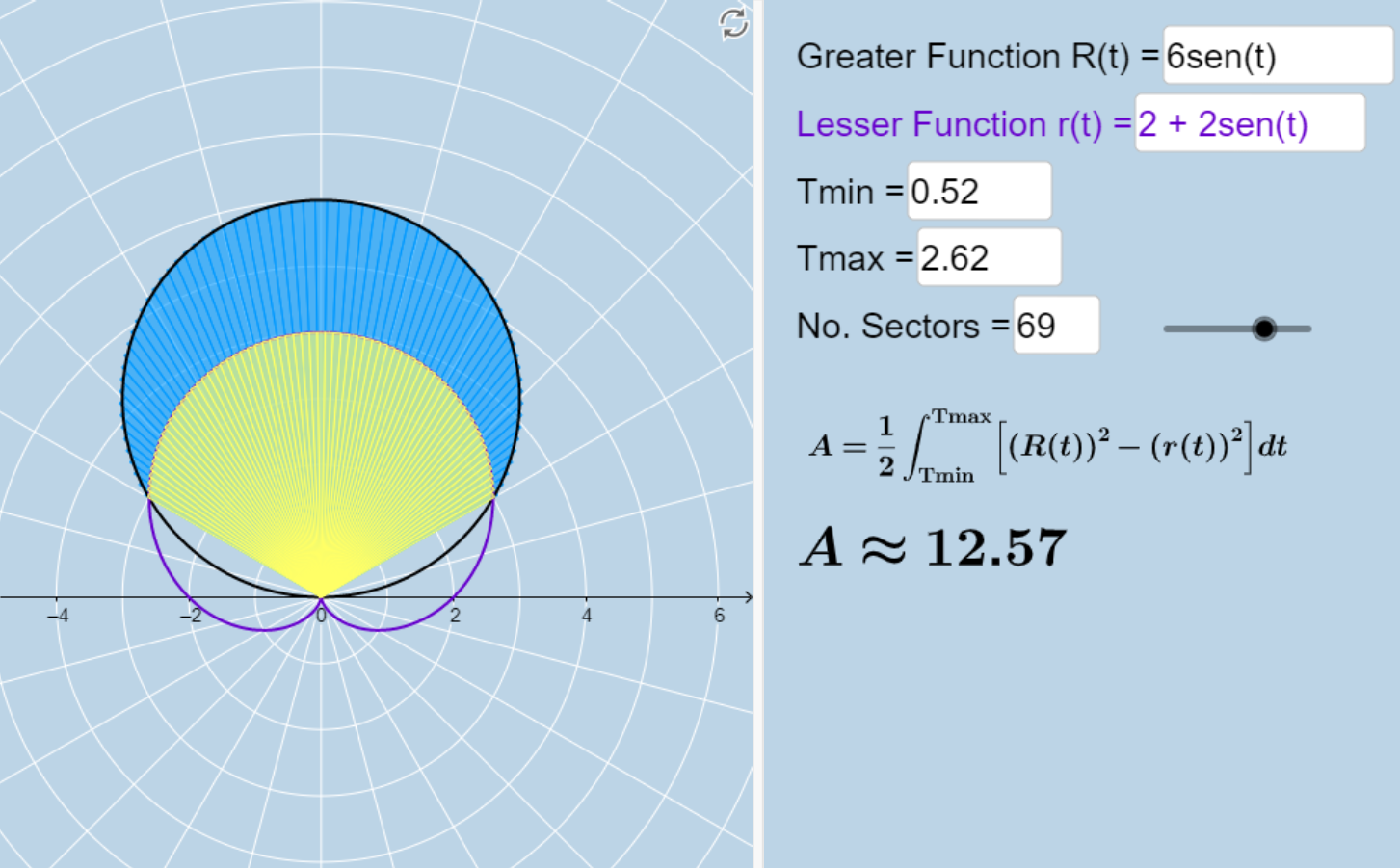
En la solución del ejercicio encontramos el área dentro del círculo y fuera del cardioide al encontrar primero sus puntos de intersección.
Observa que resolver la ecuación directamente para $\theta$ produjo dos soluciones: $\theta = \frac{\pi}{6}$ y $\theta = \frac{5\pi}{6}$. Sin embargo, en el gráfico hay tres puntos de intersección. El tercer punto de intersección es el origen. La razón por la cual este punto no apareció como solución es porque el origen está en ambos gráficos, pero para diferentes valores de $\theta$. Por ejemplo, para el cardioide obtenemos
$$\begin{aligned} 2+2sen\theta &= 0\\ sen\theta &= 1 \end{aligned}$$entonces los valores para $\theta$ que resuelven esta ecuación son
$\theta = \frac{3\pi}{2} + 2n\pi$, donde $n$ es cualquier número entero. Para el círculo obtenemos
Las soluciones a esta ecuación son de la forma $\theta = n\pi$ para cualquier valor entero de $n$. Estos dos conjuntos de soluciones no tienen puntos en común. Independientemente de este hecho, las curvas se intersecan en el origen. Este caso siempre debe tenerse en cuenta.
Aquí deduciremos una fórmula para la longitud del arco de una curva definida en coordenadas polares.
En coordenadas rectangulares, la longitud del arco de una curva parametrizada $(x(t), y(t))$ para $a \le t \le b$ viene dada por
$$L=\int_a^b \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt$$En coordenadas polares definimos la curva mediante la ecuación $r = f(\theta)$, donde $\alpha \le \theta \le \beta$. Para adaptar la fórmula de longitud de arco para una curva polar, usamos las ecuaciones
$$x = rcos\theta = f(\theta)cos\theta\;\;,\;\;\;y =rsen\theta = f(\theta)sen\theta$$y consideramos el parámetro $\theta$ en lugar de $t$. Se cumple
$$\begin{aligned} \frac{dx}{d\theta} &= f'(\theta)cos(\theta)-f(\theta)sen(\theta)\\ \frac{dy}{d\theta} &= f'(\theta)sen(\theta)-f(\theta)cos(\theta) \end{aligned}$$Reemplazamos $dt$ por $d\theta$, y los límites inferior y superior de integración son $\alpha$ y $\beta$, respectivamente. Entonces la fórmula de la longitud del arco se convierte en
$$\begin{aligned} L &= \int_a^b \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt\\ &= \int_{\alpha}^{\beta} \sqrt{\left(\frac{dx}{d\theta}\right)^2+\left(\frac{dy}{d\theta}\right)^2}d\theta\\ &= \int_{\alpha}^{\beta} \sqrt{(f'(\theta)cos(\theta)-f(\theta)sen(\theta))^2 + (f'(\theta)sen(\theta)-f(\theta)cos(\theta))^2}d\theta\\ &= \int_{\alpha}^{\beta} \sqrt{(f'(\theta))^2(cos^2\theta+sen^2\theta) + (f(\theta))^2(cos^2\theta+sen^2\theta)}d\theta\\ &= \int_{\alpha}^{\beta} \sqrt{(f'(\theta))^2 + (f(\theta))^2}d\theta\\ &= \int_{\alpha}^{\beta} \sqrt{r^2 + \left(\frac{dr}{d\theta}\right)^2}d\theta \end{aligned}$$
Esto conduce al siguiente teorema
$$L = \int_{\alpha}^{\beta} \sqrt{|f(\theta)|^2 + |f'(\theta)|^2}d\theta = \int_{\alpha}^{\beta} \sqrt{r^2 + \left(\frac{dr}{d\theta}\right)^2}d\theta \tag{$1.10$}$$
 |
Encontrar la longitud del arco de una curva polar |
Encuentra la longitud del arco del cardioide $r = 2 + 2cos\theta$.

En las guiente escena interactiva, diseñada por Ron Smith, puedes observar la solución aproximada de la longitud de arco del cardioide. Igualmente, la escena permite hallar el área aproximada de la región interior del cardioide, seleccionando la casilla Sectores.
La escena, además, permite que cambies la curva en la casilla de entrada, lo cual puedes hacerlo tal como lo indica el vídeo que está a continuación de la escena.

A continuación, encontrarás varios ejercicios para que confrontes lo aprendido. Los ejercicios de numerales impares, presentan la solución; sin embargo, puedes recurrir a la escena de Ron Smith para encontrar algunos resultados de los numerales pares (Obviamente, debes tener en cuenta que el intervalo en la escena es $[0, 2\pi]$; por ejemplo, para la rosa de cuatro pétalos la longitud de arco obtenida es cuatro veces la de un pétalo cuyo intervalo es $[0, \pi/2]$.
 Para los siguientes ejercicios, determina una integral definida que represente el área.
Para los siguientes ejercicios, determina una integral definida que represente el área.
188. Región encerrada por $r = 4$
189. Región encerrada por $r = 3sen\theta$ (Solución)
190. Región en el primer cuadrante dentro del cardioide $r = 1 + sen\theta$
191. Región encerrada por un pétalo de $r = 8sen(2\theta)$ (Solución)
192. Región encerrada por un pétalo de $r = cos(3\theta)$
193. Región debajo del eje polar y encerrada por $r = 1 − sen\theta$ (Solución)
194. Región en el primer cuadrante encerrada por $r = 2 − cos\theta$
195. Región encerrada por el bucle interno de $r = 2−3sen\theta$ (Solución)
196. Región encerrada por el bucle interno de $r = 3−4cos\theta$
197. Región encerrada por $r = 1−2cos\theta$ y fuera del bucle interno (Solución)
198. Región común a $r = 3sen\theta$ y $r = 2 − sen\theta$
199. Región común a $r = 2$ y $r = 4cos\theta$ (Solución)
200. Región común a $r = 3cos\theta$ y $r = 3sen\theta$
 Para los siguientes ejercicios, encuentre el área de la región descrita.
Para los siguientes ejercicios, encuentre el área de la región descrita.
 Para los siguientes ejercicios, encuentra una integral definida que represente la longitud del arco.
Para los siguientes ejercicios, encuentra una integral definida que represente la longitud del arco.
214. $r=4cos\theta$ en el intervalo $0 \le \theta \le \pi/2$
215. $r=1+sen\theta$ en el intervalo $0 \le \theta \le 2\pi$ (Solución)
216. $r=2sec\theta$ en el intervalo $0 \le \theta \le \pi/3$
217. $r=e^{\theta}$ en el intervalo $0 \le \theta \le 1$ (Solución)
 Para los siguientes ejercicios, encuentre la longitud de la curva en el intervalo dado.
Para los siguientes ejercicios, encuentre la longitud de la curva en el intervalo dado.
218. $r=6$ en el intervalo $0 \le \theta \le \pi/2$
219. $r=^{e3\theta}$ en el intervalo $0 \le \theta \le 2$ (Solución)
220. $r=6cos\theta$ en el intervalo $0 \le \theta \le \pi/2$
221. $r=8+8cos\theta$ en el intervalo $0 \le \theta \le \pi$ (Solución)
222. $r=1−sen\theta$ en el intervalo $0 \le \theta \le 2\pi$
 Para los siguientes ejercicios, usa las capacidades de integración de una calculadora para aproximar la longitud de la curva (o, también, la escena interactiva anterior).
Para los siguientes ejercicios, usa las capacidades de integración de una calculadora para aproximar la longitud de la curva (o, también, la escena interactiva anterior).
223. [T] $r=3\theta$ en el intervalo $\pi \le \theta \le \pi/2$ (Solución)
224. [T] $r=\frac{2}{\theta}$ en el intervalo $\pi \le \theta \le 2\pi$
225. [T] $r=sen^2(\frac{\theta}{2})$ en el intervalo $0 \le \theta \le \pi$ (Solución)
226. [T] $r=2\theta^2$ en el intervalo $0 \le \theta \le \pi$
227. [T] $r=sen(3cos\theta)$ en el intervalo $0 \le \theta \le \pi$ (Solución)
 Para los siguientes ejercicios, usa la fórmula familiar de la geometría para encontrar el área de la región descrita y luego confirma usando la integral definida.
Para los siguientes ejercicios, usa la fórmula familiar de la geometría para encontrar el área de la región descrita y luego confirma usando la integral definida.
228. $r=3sen\theta$ en el intervalo $0 \le \theta \le \pi$
229. $r=sen\theta+cos\theta$ en el intervalo $0 \le \theta \le \pi$ (Solución)
230. $r=6sen\theta+8cos\theta$ en el intervalo $0 \le \theta \le \pi$
 Para los siguientes ejercicios, usa la fórmula familiar de la geometría para encontrar la longitud de la curva y luego confirme con la integral definida.
Para los siguientes ejercicios, usa la fórmula familiar de la geometría para encontrar la longitud de la curva y luego confirme con la integral definida.
231. $r=3sen\theta$ en el intervalo $0 \le \theta \le \pi$ (Solución)
232. $r=sen\theta + cos\theta$ en el intervalo $0 \le \theta \le \pi$
233. $r=6sen\theta + 8cos\theta$ en el intervalo $0 \le \theta \le \pi$ (Solución)
234. Verifica que si $y = rsen\theta = f(\theta) sen\theta$ entonces
$\frac{dy}{d\theta} = f'(\theta)sen\theta + f(\theta)cos\theta$.
 Para los siguientes ejercicios, encuentra la pendiente de una recta tangente a una curva polar $r = f(θ)$. Toma $x = rcos\theta = f(\theta)cos\theta$ e $y = rsen\theta = f(\theta)sen\theta$, por lo que la ecuación polar $r = f(\theta)$ ahora se escribe en forma paramétrica.
Para los siguientes ejercicios, encuentra la pendiente de una recta tangente a una curva polar $r = f(θ)$. Toma $x = rcos\theta = f(\theta)cos\theta$ e $y = rsen\theta = f(\theta)sen\theta$, por lo que la ecuación polar $r = f(\theta)$ ahora se escribe en forma paramétrica.
235. Usa la definición de la derivada $\frac{dy}{dx} = \frac{dy/dθ}{dx/dθ}$ y la regla del producto para deducir la derivada de una ecuación polar. (Solución)
236. $r = 1 − senθ; (\frac12, \frac{\pi}{6})$
237. $r = 4cos\theta; (2, \frac{\pi}{3})$ (Solución)
238. $r = 8sen\theta; (4,\frac{5\pi}{6})$
239. $r = 4 + sen\theta; (3,\frac{3\pi}{2})$ (Solución)
240. $r = 6 + 3cos\theta; (3, \pi)$
241. $r = 4cos (2\theta)$; puntas de las hojas. (Solución)
242. $r = 2sen (3\theta)$; puntas de las hojas
243. $r = 2\theta; (\frac{\pi}{2}, \frac{\pi}{4})$ (Solución)
244. Encuentra los puntos en el intervalo $−\pi \le \theta \le \pi$ en el que el cardioide $r = 1 − cos\theta$ tiene una recta tangente vertical u horizontal.
245. Para el cardioide $r = 1 + sen\theta$, encuentra la pendiente de la recta tangente cuando $\theta = \frac{\pi}{3}$. (Solución)
 Para los siguientes ejercicios, encuentra la pendiente de la recta tangente a la curva polar dada en el punto dado por el valor de $\theta$.
Para los siguientes ejercicios, encuentra la pendiente de la recta tangente a la curva polar dada en el punto dado por el valor de $\theta$.
246. $r=3cos\theta,\theta=\frac{\pi}{3}$
247. $r=\theta, \theta=\frac{\pi}{2}$ (Solución)
248. $r=ln\theta, \theta = e$
249. [T] Usa tecnología: $r=2+4cos\theta en \theta=\frac{\pi}{6}$ (Solución)
 Para los siguientes ejercicios, encuentra los puntos en los que las siguientes curvas polares tienen una recta tangente horizontal o vertical.
Para los siguientes ejercicios, encuentra los puntos en los que las siguientes curvas polares tienen una recta tangente horizontal o vertical.
250. $r = 4cos\theta$
251. $r^2 = 4cos(2\theta)$ (Solución)
252. $r = 2sen(2\theta)$
253. El cardioide $r = 1 + sen\theta$ (Solución)
254. 254. Demuestra que la curva $r = sen\theta tan\theta$ (llamada cissoide de Diocles) tiene la recta $x = 1$ como asíntota vertical.

Figura 2.1. La gran matriz de Karl G. Jansky, ubicada en Socorro, Nuevo México, consiste en una gran cantidad de radiotelescopios que pueden recolectar ondas de radio y cotejarlas como si estuvieran reuniendo ondas en un área enorme sin espacios en la cobertura (crédito: modificación del trabajo de CGP Gray, Wikimedia Commons)
Los observatorios astronómicos modernos a menudo consisten en una gran cantidad de reflectores parabólicos, conectados por computadoras, utilizados para analizar ondas de radio. Cada plato enfoca los haces paralelos entrantes de ondas de radio en un punto focal preciso, donde pueden sincronizarse por computadora. Si la superficie de uno de los reflectores parabólicos se describe mediante la ecuación $\frac{x^2}{100} + \frac{y^2}{100} = z^4$, ¿dónde está el punto focal del reflector?
Ahora estamos a punto de comenzar una nueva parte del curso de cálculo, cuando estudiamos las funciones de dos o tres variables independientes en el espacio multidimensional.
Muchos de los cálculos son similares a los del estudio de funciones de variable única, pero también hay muchas diferencias. En este capítulo, examinamos los sistemas de coordenadas para trabajar en un espacio tridimensional, junto con los vectores, que son una herramienta matemática clave para tratar cantidades en más de una dimensión. Comencemos aquí con las ideas básicas y avancemos hasta las herramientas más generales y poderosas de las matemáticas en capítulos posteriores.
Cuando se describe el movimiento de un avión en vuelo, es importante comunicar dos datos: la dirección en la que viaja el avión y la velocidad del avión. Al medir una fuerza, como el empuje de los motores del avión, es importante describir no solo la intensidad de esa fuerza, sino también la dirección en la que se aplica. Algunas cantidades se definen en términos del tamaño (también llamado magnitud) y dirección. Una cantidad que tiene magnitud y dirección se llama vector. En este texto, denotamos vectores con letras en negrita, como v.
Un vector en un plano está representado por un segmento de recta dirigida (una flecha). Los puntos finales del segmento se denominan punto inicial y punto terminal o final del vector. Una flecha desde el punto inicial al punto terminal indica la dirección del vector. La longitud del segmento de recta representa su magnitud.
Usamos la notación $\|$v$\|$ para denotar la magnitud del vector v. Un vector con un punto inicial y un punto terminal que son iguales se llama vector cero, denotado como 0. El vector cero es el único vector sin dirección, y por convención se puede considerar que tiene cualquier dirección conveniente para el problema en cuestión.
Los vectores con la misma magnitud y dirección se denominan vectores equivalentes. Tratamos los vectores equivalentes como iguales, incluso si tienen puntos iniciales diferentes. Por lo tanto, si v y w son equivalentes, escribimos
v = w
Las flechas en la (Figura 2.2 (b)) son equivalentes. Cada flecha tiene la misma longitud y dirección. Un concepto estrechamente relacionado es la idea de vectores paralelos. Se dice que dos vectores son paralelos si tienen las mismas direcciones o direcciones opuestas. Exploramos esta idea con más detalle más adelante en el capítulo. Un vector se define por su magnitud y dirección, independientemente de dónde se encuentre su punto inicial.
El uso de negrita y letras minúsculas para nombrar vectores es una representación común en la impresión, pero hay anotaciones alternativas. Al escribir el nombre de un vector a mano, por ejemplo, es más fácil dibujar una flecha sobre la variable que simular el tipo de negrita: $\vec{v}$. Cuando un vector tiene un punto inicial $P$ y un punto terminal $Q$, la notación $\vec{PQ}$ es útil porque indica la dirección y ubicación del vector.
Figura 2.2. (a) Un vector está representado por un segmento de recta dirigida desde su punto inicial hasta su punto final. (b) Los vectores $v_1$ a $v_5$ son equivalentes.
 |
Dibujando vectores |
Dibuja un vector en el plano desde el punto inicial $P (1,1)$ hasta el punto terminal $Q (8,5)$.

Los vectores tienen muchas aplicaciones en la vida real, incluidas situaciones que implican fuerza o velocidad. Por ejemplo, considera las fuerzas que actúan en un bote que cruza un río. El motor del bote genera una fuerza en una dirección, y la corriente del río genera una fuerza en otra dirección. Ambas fuerzas son vectores.
Debemos tener en cuenta tanto la magnitud como la dirección de cada fuerza si queremos saber a dónde irá el bote.
Un segundo ejemplo que involucra vectores es un mariscal de campo lanzando una pelota de fútbol. El mariscal de campo no lanza la pelota paralela al suelo, sino que apunta hacia el aire. La velocidad de su lanzamiento puede ser representada por un vector. Si sabemos con qué fuerza arroja la pelota (magnitud, en este caso, velocidad) y el ángulo (dirección), podemos decir qué tan lejos viajará la pelota por el campo.
Un número real a menudo se llama escalar en matemáticas y física. A diferencia de los vectores, generalmente se considera que los escalares solo tienen una magnitud, pero no una dirección. Multiplicar un vector por un escalar cambia la magnitud del vector. Esto se llama multiplicación por un escalar. Ten en cuenta que cambiar la magnitud de un vector no indica un cambio en su dirección. Por ejemplo, el viento que sopla de norte a sur puede aumentar o disminuir su velocidad mientras mantiene su dirección de norte a sur.
Como es de esperar, si k = −1, denotamos el producto kv como
$$k \bold{v} = (−1) \bold{v} = −\bold{v}$$Observa que −v tiene la misma magnitud que v, pero tiene la dirección opuesta (Figura 2.4 (d)).

Figura 2.4. (a) El vector original v tiene una longitud $n$ unidades. (b) La longitud de 2v es igual a 2$n$ unidades. (c) La longitud de v/2 es $n$/2 unidades. (d) Los vectores v y −v tienen la misma longitud pero direcciones opuestas.
Otra operación que podemos realizar es la suma de vectores, pero como cada vector puede tener su propia dirección, el proceso es diferente de sumar dos números. El método gráfico más común para sumar dos vectores, que consiste en colocar el punto inicial del segundo vector en el punto terminal del primero, como en la Figura 2.5 (a). Para ver por qué esto tiene sentido, supongamos, por ejemplo, que ambos vectores representan un desplazamiento. Si un objeto se mueve primero desde el punto inicial hasta el punto terminal del vector v, luego desde el punto inicial hasta el punto terminal del vector w, el desplazamiento general es el mismo que si el objeto hubiera hecho un solo movimiento desde el punto inicial hasta el punto final del vector v + w. Por razones obvias, este enfoque se llama el método del triángulo. Tenga en cuenta que si hubiéramos cambiado el orden, de modo que w fuera nuestro primer vector y v fuera nuestro segundo vector, habríamos terminado en el mismo lugar (nuevamente, observa la Figura 2.5 (a)). Por lo tanto, v + w = w + v.
Un segundo método para agregar vectores se llama método o regla del paralelogramo. Con este método, colocamos los dos vectores para que tengan el mismo punto inicial, y luego dibujamos un paralelogramo con los vectores como dos lados adyacentes, como en la Figura 2.5 (b). La longitud de la diagonal del paralelogramo es la suma. Comparando la Figura 2.5 (b) y la Figura 2.5 (a), podemos ver que obtenemos la misma respuesta usando cualquiera de los métodos. El vector v + w se llama suma vectorial.
Figura 2.5. (a) Al sumar vectores por el método del triángulo, el punto inicial de w es el punto final de v. (b) Al sumar vectores por el método del paralelogramo, los vectores v y w tienen el mismo punto inicial.
También es apropiado aquí discutir la sustracción de vectores. Definimos v − w como v + (- w) = v + (- 1)w. El vector v − w se llama la diferencia vectorial. Gráficamente, el vector v − w se representa dibujando un vector desde el punto final de w hasta el punto final de v (Figura 2.6).
En la Figura 2.5 (a), el punto inicial de v + w es el punto inicial de v. El punto final de v + w es el punto final de w. Estos tres vectores forman los lados de un triángulo. Se deduce que la longitud de cualquier lado es menor que la suma de las longitudes de los lados restantes. Entonces tenemos
Esto se conoce más generalmente como la desigualdad del triángulo o desigualdad triangular. Sin embargo, hay un caso en el que el vector resultante v + w tiene la misma magnitud que la suma de las magnitudes de v y w. Esto sucede solo cuando v y w tienen la misma dirección.
Figura 2.6. (a) La diferencia vectorial v − w se representa dibujando un vector desde el punto final de w al punto final de v. (b) El vector v − w es equivalente al vector v + (-w).
Si necesitamos sumar tres o más vectores, repetimos la regla del paralelogramo para los pares de vectores hasta que encontremos la resultante de todos los resultados. Para tres vectores, por ejemplo, primero encontramos la resultante del vector 1 y el vector 2, y luego encontramos la resultante de este vector con el vector 3.
En la siguiente escena interactiva, podrás observar tres vídeos que muestran los métodos para la suma vectorial (en lo vídeos se usan las expresiones "cabeza" y "cola", en lugar de "inicio" y "final".
En la siguiente escena interactiva se explica, paso a paso, el método del paralelogramo. Puedes cambiar la dirección de los vectores, usando el botón pulsador.
 |
Combinando vectores |
Dados los vectores v y w que se muestran en la Figura 2.7, dibuja los vectores
Figura 2.7. Los vectores v y w se encuentran en el mismo plano.

Trabajar con vectores en un plano es más fácil cuando estamos trabajando en un sistema de coordenadas. Cuando los puntos iniciales y los puntos terminales de los vectores se dan en coordenadas cartesianas, los cálculos se vuelven sencillos.
 |
Comparación de vectores |
¿Son v y w vectores equivalentes?

Hemos visto cómo trazar un vector cuando se nos da un punto inicial y un punto final. Sin embargo, debido a que un vector se puede colocar en cualquier lugar de un plano, puede ser más fácil realizar cálculos con un vector cuando su punto inicial coincide con el origen. Llamamos a un vector con su punto inicial en el origen un vector de posición estándar. Dado que se sabe que el punto inicial de cualquier vector en posición estándar es (0,0), podemos describir el vector mirando las coordenadas de su punto final. Por lo tanto, si el vector v tiene su punto inicial en el origen y su punto final en (x, y), escribimos el vector en sus componentes como
$$\bold{v} = \lang x,y \rang$$Cuando un vector se escribe en forma de componentes como este, los escalares x e y se denominan componentes de v.
Recuerda que los vectores se nombran con letras minúsculas en negrita o dibujando una flecha sobre su nombre. También hemos aprendido que podemos nombrar un vector por su forma componente, con las coordenadas de su punto final entre paréntesis angulares. Sin embargo, al escribir la forma componente de un vector, es importante distinguir entre $\lang x,y \rang$ y (x, y). El primer par ordenado usa corchetes angulares para describir un vector, mientras que el segundo usa paréntesis para describir un punto en un plano. El punto inicial de $\lang x,y \rang$ es (0,0); El punto final de $\lang x,y \rang$ es $(x, y)$.
Cuando tenemos un vector que aún no está en posición estándar, podemos determinar su forma componente de una de dos maneras. Podemos usar un enfoque geométrico, en el que dibujamos el vector en el plano de coordenadas, y luego dibujamos un vector de posición estándar equivalente. Alternativamente, podemos encontrarlo algebraicamente, usando las coordenadas del punto inicial y el punto terminal. Para encontrarlo algebraicamente, restamos la coordenada $x$ del punto inicial de la coordenada $x$ del punto final para obtener el componente $x$, y restamos la coordenada $y$ del punto inicial de la coordenada $y$ del punto final para obtener el componente $y$.
 |
Expresando vectores en forma de componente |

Para encontrar la magnitud de un vector, calculamos la distancia entre su punto inicial y su punto final. La magnitud del vector $\bold{v} = \lang x, y\rang$ se denota $\|v\|$, o $|\bold{v}|$, y se puede calcular utilizando la fórmula
$$\|v\| = \sqrt{x^2 + y^2}$$Observa que debido a que este vector está escrito en forma de componente, es equivalente a un vector en posición estándar, con su punto inicial en el punto de origen y final $(x, y)$. Por lo tanto, es suficiente calcular la magnitud del vector en posición estándar. Usando la fórmula de la distancia para calcular la distancia entre el punto inicial $(0,0)$ y el punto final $(x, y)$, tenemos
Con base en esta fórmula, está claro que para cualquier vector v, $\|v\| \ge 0$ y $\|v\| = 0$ si y solo si v = 0.
La magnitud de un vector también se puede derivar usando el teorema de Pitágoras, como en la siguiente figura.
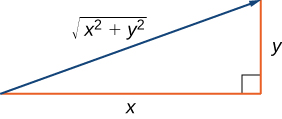
Figura 2.13. Si usas los componentes de un vector para definir un triángulo rectángulo, la magnitud del vector es la longitud de la hipotenusa del triángulo.
Hemos definido la multiplicación por un escalar y la suma de vectores geométricamente. La expresión de vectores en forma de componentes nos permite realizar estas mismas operaciones algebraicamente.
 |
Realizar operaciones en forma componente |

Ahora que hemos establecido las reglas básicas de la aritmética vectorial, podemos establecer las propiedades de las operaciones vectoriales. Probaremos dos de estas propiedades. Las otras pueden ser probadas de manera similar.
Prueba de la propiedad conmutativa
Sea $\bold{u} = \lang x_1, y_1\rang$ y $\bold{v} = \lang x_2, y_2\rang$. Aplica la propiedad conmutativa para números reales:
$$\bold{u} + \bold{v} = \lang x_1 + x_2, y_1 + y_2\rang = \lang x_2 + x_1, y_2 + y_1\rang = \bold{v} + \bold{u}$$Prueba de la propiedad distributiva
Aplica la propiedad distributiva para números reales:
$$\begin{aligned} r(\bold{u} + \bold{v}) &= r\cdot\lang x_1 + x_2, y_1 + y_2\rang\\ &= \lang r(x_1 + x_2), r(y_1 + y_2)\rang\\ &= \lang rx_1 + rx_2, ry_1 + ry_2\rang\\ &= \lang rx_1, ry_1\rang + \lang rx_2, ry_2\rang\\ &= r\bold{u} + r\bold{v} \end{aligned}$$Hemos encontrado los componentes de un vector dados sus puntos iniciales y finales. En algunos casos, solo podemos tener la magnitud y la dirección de un vector, no los puntos. Para estos vectores, podemos identificar los componentes horizontal y vertical usando trigonometría (Figura 2.15).
Figura 2.15. Los componentes de un vector forman los catetos de un triángulo rectángulo, con el vector como hipotenusa.
Considera el ángulo θ formado por el vector v y el eje x positivo. Podemos ver desde el triángulo que los componentes del vector v son $\lang \| \bold{v}\| cosθ, \| \bold{v}\| senθ\rang$. Por lo tanto, dado un ángulo y la magnitud de un vector, podemos usar el coseno y el seno del ángulo para encontrar las componentes del vector.
 |
Forma componente |
Encuentra la forma componente de un vector con magnitud 4 que forma un ángulo de -45° con el eje x

Un vector unitario es un vector con magnitud 1. Para cualquier vector distinto de cero v, podemos usar la multiplicación por un escalar para encontrar un vector unitario u que tenga la misma dirección que v. Para hacer esto, multiplicamos el vector por el recíproco de su magnitud:
$$\bold{u} = \frac{1}{\|\bold{v}\|}\bold{v}$$Recuerda que cuando definimos la multiplicación escalar, notamos que $\| k\bold{v}\| = |k|\cdot\|\bold{v}\|$. Para $\bold{u} = \frac{1}{\|\bold{v}\|}\bold{v}$, se deduce que $\|\bold{u}\| = \frac{1}{\|\bold{v}\|}(\|\bold{v}\|) = 1$. Decimos que u es el vector unitario en la dirección de v (figura 2.17). El proceso de usar la multiplicación escalar para encontrar un vector unitario con una dirección dada se llama normalización.

Figura 2.17. El vector v y el vector unitario asociado $\bold{u} = \frac{1}{\|\bold{v}\|}\bold{v}$. En este caso, $\|\bold{v}\| \gt 1$.
 |
Encontrar un vector unitario |
Dado $\bold{v} = \lang 1, 2\rang$.

Hemos visto lo conveniente que puede ser escribir un vector en forma de componente. Sin embargo, a veces es más conveniente escribir un vector como la suma de un vector horizontal y un vector vertical. Para facilitar esto, veamos los vectores unitarios estándar. Los vectores unitarios estándar son los vectores $\bold{i} = \lang 1, 0\rang$ y $\bold{j} = \lang 0, 1\rang$ (Figura 2.18).
Figura 2.18. Los vectores unitarios estándar i y j.
Al aplicar las propiedades de los vectores, es posible expresar cualquier vector en términos de i y j en lo que llamamos una combinación lineal:
$$\bold{v} = \lang x, y\rang = \lang x, 0\rang + \lang 0, y\rang = x\lang 1,0\rang + y\lang 0,1\rang = x\bold{i} + y\bold{j}$$Por lo tanto, v es la suma de un vector horizontal con magnitud x, y un vector vertical con magnitud y, como en la siguiente figura.
Figura 2.19. El vector v es la suma de xi e yj.
 |
Usar vectores unitarios estándar |

Debido a que los vectores tienen dirección y magnitud, son herramientas valiosas para resolver problemas que involucran aplicaciones tales como movimiento y fuerza. Recordemos el ejemplo del barco que describimos anteriormente. Aquí nos fijamos en otros dos ejemplos en detalle.
 |
El auto de Jane está atrapado en el barro. Lisa y Jed vienen en un camión para ayudarla a sacarla. Atan un extremo de una correa de remolque a la parte delantera del automóvil y el otro extremo al enganche de remolque del camión, y el camión comienza a tirar. Mientras tanto, Jane y Jed se ponen detrás del auto y empujan. El camión genera una fuerza horizontal de 300 lb sobre el automóvil. Jane y Jed empujan ligeramente hacia arriba y generan una fuerza de 150 lb sobre el automóvil. Estas fuerzas pueden representarse mediante vectores, como se muestra en la figura 2.21. El ángulo entre estos vectores es de 15°. Encuentra la fuerza resultante (la suma de los vectores) y su magnitud a la décima de libra más cercana y, además, su ángulo de dirección desde el eje x positivo.

Figura 2.21. Dos fuerzas que actúan sobre un automóvil en diferentes direcciones.

 |
Encontrar la velocidad resultante |
Un avión vuela hacia el oeste a una velocidad de 425 mph. El viento sopla del noreste a 40 mph. ¿Cuál es la velocidad de avance del avión? ¿Cuál es el rumbo del avión?

Otra aplicación la encontramos en el cálculo de la resultante de varias fuerzas coplanares, con un método gráfico o analítico. La siguiente escena interactiva, muestra varios ejemplos de aplicación en la Física Estática.

A continuación, encontrarás varios ejercicios para que confrontes lo aprendido. Los ejercicios de numerales impares, presentan la solución.
 Para los siguientes ejercicios, considera los puntos P (−1,3), Q (1,5) y R (−3,7). Determina los vectores solicitados y expresa cada uno de ellos a. en forma de componente y b. utilizando los vectores unitarios estándar.
Para los siguientes ejercicios, considera los puntos P (−1,3), Q (1,5) y R (−3,7). Determina los vectores solicitados y expresa cada uno de ellos a. en forma de componente y b. utilizando los vectores unitarios estándar.
1. $\overrightarrow{PQ}$ (Solución)
2. $\overrightarrow{PR}$
3. $\overrightarrow{QP}$ (Solución)
4. $\overrightarrow{RP}$
5. $\overrightarrow{PQ} + \overrightarrow{PR}$ (Solución)
6. $\overrightarrow{PQ} - \overrightarrow{PR}$
7. $2\overrightarrow{PQ} - 2\overrightarrow{PR}$ (Solución)
8. $2\overrightarrow{PQ} + \frac{1}{2}\overrightarrow{PR}$ 9. El vector unitario en la dirección de $\overrightarrow{PQ}$ (Solución) 10. El vector unitario en la dirección de $\overrightarrow{PR}$ 11. Un vector v tiene un punto inicial (−1, −3) y un punto final (2,1). Encuentra el vector unitario en la dirección de v. Expresa la respuesta en forma de componente. (Solución) 12. Un vector v tiene un punto inicial (−2,5) y un punto final (3, −1). Encuentra el vector unitario en la dirección de v. Expresa la respuesta en forma de componente.
13. El vector v tiene el punto inicial P (1,0) y el punto final Q que está en el eje y y por encima del punto inicial. Encuentra las coordenadas del punto final Q de modo que la magnitud del vector v sea $\sqrt{5}$. (Solución) 14. El vector v tiene el punto inicial P (1,1) y el punto final Q que está en el eje xy a la izquierda del punto inicial. Encuentra las coordenadas del punto final Q de tal manera que la magnitud del vector v sea $\sqrt{10}$.
 Para los siguientes ejercicios, usa los vectores dados a y b.
Para los siguientes ejercicios, usa los vectores dados a y b.
15. a = 2i + j, b = i + 3j (Solución) 16. a = 2i, b = −2i + 2j 17. Sea a un vector de posición estándar con un punto final (−2, −4). Sea b un vector con punto inicial (1,2) y punto final (−1,4). Encuentre la magnitud del vector −3a + b − 4i + j. (Solución) 18. Sea a un vector de posición estándar con un punto final en (2,5). Sea b un vector con un punto inicial (−1,3) y un punto final (1,0). Encuentra la magnitud del vector a − 3b + 14i − 14j.
19. Sea u y v dos vectores distintos de cero que no son equivalentes. Considera los vectores a = 4u + 5v y b = u + 2v definidos en términos de u y v. Encuentra el escalar λ tal que los vectores a + λb y u − v sean equivalentes. (Solución) 20. Sea u y v dos vectores distintos de cero que no son equivalentes. Considera los vectores a = 2u − 4v y b = 3u − 7v definidos en términos de u y v. Encuentre los escalares α y β de manera que los vectores αa + βb y u − v sean equivalentes. 21. Considera el vector a(t) = $\lang cost, sent\rang$ con componentes que dependen de un número real t. A medida que el número t varía, los componentes de a(t) también cambian, dependiendo de las funciones que los definen. (Solución)
23. Demuestra que los vectores $\bold{a}(t) = \lang cost, sent\rang$ y $\bold{a}(x) = \big\lang x, \sqrt{1 − x^2}\big\rang$ son equivalentes para x = 1 y t = 2kπ, donde k es un número entero. (Solución) 24. Demuestra que los vectores $\lang a(t) = \lang cost, sent\rang$ y $\bold{a}(x) = \big\lang x, \sqrt{1 − x^2}\big\rang$ son opuestos a x = r y t = π + 2kπ, donde k es entero.
 Para los siguientes ejercicios, encuentra el vector v con la magnitud dada y en la misma dirección que el vector u.
Para los siguientes ejercicios, encuentra el vector v con la magnitud dada y en la misma dirección que el vector u.
25. $\| \bold{v}\| = 7, \bold{u} = \lang 3, 4\rang$ (Solución) 26. $\| \bold{v}\| = 3, \bold{u} = \lang −2,5\rang$ 27. $\| \bold{v}\| = 7, \bold{u} = \lang 3,−5\rang$ (Solución) 28. $\| \bold{v}\| = 10, \bold{u} = \lang 2,−1\rang$
 Para los siguientes ejercicios, encuentra la forma componente del vector u, dada su magnitud y el ángulo que forma el vector con el eje x positivo. Da respuestas exactas cuando sea posible.
Para los siguientes ejercicios, encuentra la forma componente del vector u, dada su magnitud y el ángulo que forma el vector con el eje x positivo. Da respuestas exactas cuando sea posible.
29. $\| \bold{u}\| = 2, \theta =30°$ (Solución) 30. $\| \bold{u}\| = 6, \theta = 60^o$ 31. $\| \bold{u}\| = 5, \theta = \frac{\pi}{2}$ (Solución) 32. $\| \bold{u}\| = 8, \theta = \pi $ 33. $\| \bold{u}\| = 10, \theta = \frac{5\pi}{6} $ (Solución) 34. $\| \bold{u}\| = 50, \theta = \frac{3\pi}{4}$
 Para los siguientes ejercicios, se proporciona el vector u. Encuentra el ángulo $\theta\isin [0,2\pi )$ que el vector u forma con la dirección positiva del eje x, en sentido antihorario.
Para los siguientes ejercicios, se proporciona el vector u. Encuentra el ángulo $\theta\isin [0,2\pi )$ que el vector u forma con la dirección positiva del eje x, en sentido antihorario.
35. $\bold{u} = 5\sqrt{2}\bold{i} − 5\sqrt{2}\bold{j}$ (Solución) 36. $\bold{u} = −\sqrt{3}\bold{i} − \bold{j}$ 37. Sea $\bold{a} = \lang a_1, a_2\rang, \bold{b} = \lang b_1, b_2\rang$ y $\bold{c} = \lang c_1, c_2\rang$ tres vectores distintos de cero. Si $a_1b_2 − a_2b_1 \ne 0$, demuestra que hay dos escalares, α y β, de modo que c = αa + βb. (Solución) 38. Considera los vectores $\bold{a} = \lang 2, −4\rang, \bold{b} = \lang − 1,2\rang$ y $\bold{c} = 0$. Determina los escalares α y β de manera que c = αa + βb. 39. Sea $P(x_0, f(x_0))$ un punto fijo en la gráfica de la función diferencial f con un dominio que es el conjunto de números reales. (Solución)
42. Encuentre $x \isin \R$ tal que los vectores $\bold{a} = \lang x, senx\rang$ y $\bold{b} = \lang x, cosx\rang$ sean equivalentes. 43. Calcula las coordenadas del punto D de manera que ABCD sea un paralelogramo, con A(1,1), B(2,4) y C(7,4). (Solución) 44. Considera los puntos A(2,1), B(10,6), C(13,4) y D 16, −2). Determina la forma componente del vector $\overrightarrow{AD}$. 45. La velocidad de un objeto es la magnitud de su vector de velocidad relacionado. Un balón de fútbol lanzado por un quarterback tiene una velocidad inicial de 70 mph y un ángulo de elevación de 30°. Determina el vector de velocidad en mph y exprésalo en forma de componente (Redondear a dos decimales). (Solución)
46. Un jugador de béisbol lanza una pelota de béisbol en un ángulo de 30° con la horizontal. Si la velocidad inicial de la pelota es 100 mph, encuentra los componentes horizontal y vertical del vector de velocidad inicial de la pelta (Redondear a dos decimales).
| 47. Se dispara una bala con una velocidad inicial de 1500 ft/seg en un ángulo de 60° con la horizontal. Encuentra los componentes horizontal y vertical del vector de velocidad de la bala (Redondear a dos decimales). (Solución) | 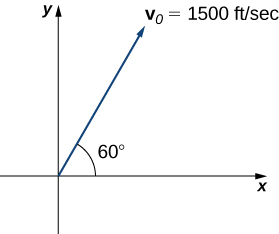 |
48. [T] Un velocista de 65 kg ejerce una fuerza de 798 N en un ángulo de 19° con respecto al suelo en el bloque de inicio en el instante en que comienza una carrera. Encuentra el componente horizontal de la fuerza (Redondear a dos decimales). 49. [T] Dos fuerzas, una fuerza horizontal de 45 lb y otra de 52 lb, actúan sobre el mismo objeto. El ángulo entre estas fuerzas es de 25°. Encuentra la magnitud y el ángulo de dirección del eje x positivo de la fuerza resultante que actúa sobre el objeto (Redondear a dos decimales). (Solución)
50. [T] Dos fuerzas, una fuerza vertical de 26 lb y otra de 45 lb, actúan sobre el mismo objeto. El ángulo entre estas fuerzas es de 55°. Encuentra la magnitud y el ángulo de dirección con el eje x positivo de la fuerza resultante que actúa sobre el objeto (Redondear a dos decimales). 51. [T] Tres fuerzas actúan sobre el objeto. Dos de las fuerzas tienen las magnitudes 58 N y 27 N, y forman ángulos de 53° y 152°, respectivamente, con el eje x positivo. Encuentre la magnitud y el ángulo de dirección desde el eje x positivo de la tercera fuerza de tal manera que la fuerza resultante que actúa sobre el objeto sea cero (Redondear a dos decimales). (Solución)
52. Tres fuerzas con magnitudes de 80 lb, 120 lb y 60 lb actúan sobre un objeto en ángulos de 45°, 60° y 30°, respectivamente, con el eje x positivo. Encuentra la magnitud y el ángulo de dirección con el eje x positivo de la fuerza resultante (Redondear a dos decimales).
53. [T] Un avión vuela en dirección a 43° al noreste (también abreviado como N43E) a una velocidad de 550 mph. Un viento con una velocidad de 25 mph viene del suroeste con una dirección de N15E. ¿Cuáles son la velocidad de avance y la nueva dirección del avión? (Solución)
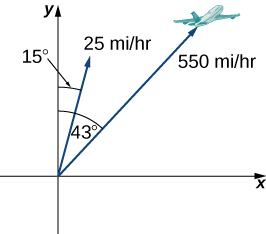
54. [T] Un barco viaja en el agua a 30 mph en una dirección de N20E (es decir, 20° al noreste). Una corriente fuerte se mueve a 15 mph en una dirección de N45E. ¿Cuáles son la nueva velocidad y dirección del barco?
55. [T] Un cable cuelga un peso de 50 lb para que las dos porciones del cable formen ángulos de 40° y 53°, respectivamente, con la horizontal. Encuentra las magnitudes de las fuerzas de tensión $T_1$ y $T_2$ en los cables si la fuerza resultante que actúa sobre el objeto es cero (Redondear a dos decimales). (Solución)
56. [T] Un peso de 62 lb cuelga de una cuerda que forma los ángulos de 29° y 61°, respectivamente, con la horizontal. Encuentra las magnitudes de las fuerzas de tensión $T_1$ y $T_2$ en los cables si la fuerza resultante que actúa sobre el objeto es cero (Redondear a dos decimales). 57. [T] Una embarcación de 1500 lb está estacionada en una rampa que forma un ángulo de 30° con la horizontal. El vector de peso del barco apunta hacia abajo y es una suma de dos vectores: un vector horizontal $\bold{v}_1$ que es paralelo a la rampa y un vector vertical $\bold{v}_2$ que es perpendicular a la superficie inclinada. Las magnitudes de los vectores $\bold{v}_1$ y $\bold{v}_2$ son el componente horizontal y vertical, respectivamente, del vector de peso del barco. Encuentra las magnitudes de $\bold{v}_1$ y $\bold{v}_2$ (Redondear al entero más cercano). (Solución)
58. [T] Una caja de 85 lb está en reposo en una inclinación de 26°. Determina la magnitud de la fuerza paralela a la inclinación necesaria para evitar que la caja se deslice (Redondear al entero más cercano).
59. Un cable de sujeción soporta un poste de 75 pies de altura. Un extremo del cable está unido a la parte superior del poste y el otro extremo está anclado al suelo a 50 pies de la base del poste. Determina los componentes horizontal y vertical de la fuerza de tensión en el cable si su magnitud es de 50 lb (Redondea al entero más cercano). (Solución)
60. Un cable de poste de teléfono tiene un ángulo de elevación de 35° con respecto al suelo. La fuerza de tensión en el cable de conexión es de 120 lb. Encuentra los componentes horizontal y vertical de la fuerza de tensión (Redondear al entero más cercano).
Los vectores son herramientas útiles para resolver problemas bidimensionales. La vida, sin embargo, ocurre en tres dimensiones. Para expandir el uso de vectores a aplicaciones más realistas, es necesario crear un marco para describir el espacio tridimensional. Por ejemplo, aunque un mapa bidimensional es una herramienta útil para navegar de un lugar a otro, en algunos casos la topografía del terreno es importante. ¿Tu ruta planeada va a través de las montañas? ¿Tienes que cruzar un río? Para apreciar completamente el impacto de estas características geográficas, debes usar tres dimensiones. Esta sección presenta una extensión natural del plano de coordenadas cartesianas bidimensional en tres dimensiones.
Como hemos aprendido, el sistema de coordenadas rectangulares bidimensionales contiene dos ejes perpendiculares: el eje horizontal x y el eje vertical y. Podemos agregar una tercera dimensión, el eje z, que es perpendicular tanto al eje x como al eje y. Llamamos a este sistema el sistema de coordenadas rectangulares tridimensionales. Representa las tres dimensiones que encontramos en la vida real.
En la figura 2.23 (a), el eje z positivo se muestra sobre el plano que contiene los ejes x e y. El eje x positivo aparece a la izquierda y el eje y positivo está a la derecha. Una pregunta natural es: ¿Cómo se determinó el acuerdo? El sistema que se muestra sigue la regla de la mano derecha. Si tomamos nuestra mano derecha y alineamos los dedos con el eje x positivo, luego doblamos los dedos para que apunten en la dirección del eje y positivo, nuestro pulgar apunta en la dirección del eje z positivo. En este texto, siempre trabajamos con sistemas de coordenadas configurados de acuerdo con la regla de la mano derecha. Algunos sistemas siguen una regla de la mano izquierda, pero la regla de la mano derecha se considera la representación estándar.
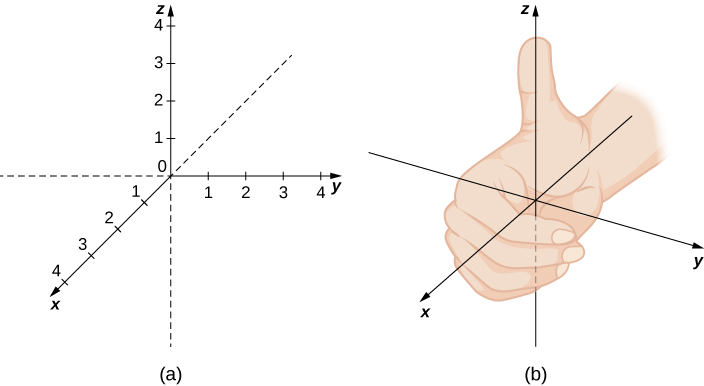
Figura 2.23. (a) Podemos extender el sistema de coordenadas rectangulares bidimensionales agregando un tercer eje, el eje z, que es perpendicular tanto al eje x como al eje y. (b) La regla de la mano derecha se usa para determinar la ubicación de los ejes de coordenadas en el plano cartesiano estándar.
En dos dimensiones, describimos un punto en el plano con las coordenadas $(x, y)$. Cada coordenada describe cómo se alinea el punto con el eje correspondiente. En tres dimensiones, se agrega una nueva coordenada, z, para indicar la alineación con el eje z: $(x, y, z)$. Un punto en el espacio se identifica por las tres coordenadas (Figura 2.24). Para trazar el punto $(x, y, z)$, vaya $x$ unidades a lo largo del eje x, luego $y$ unidades en la dirección del eje y, luego, $z$ unidades en la dirección del eje z.
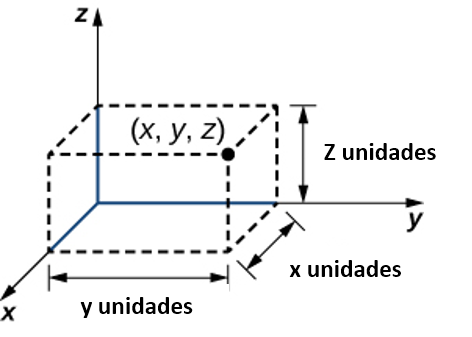
Figura 2.24. Para trazar el punto (x, y, z) vaya x unidades a lo largo del eje x, luego y unidades en la dirección del eje y, luego z unidadesen la dirección del eje z.
 |
Localizando puntos en el espacio |
Dibuja el punto $(1, −2, 3)$ en el espacio tridimensional.

En la siguiente escena interactiva, diseñada por María José García Cebrian y Elena E. Álvarez Sáiz, puedes observar el punto del ejercicio anterior y, si lo deseas, modificar los valores del punto utilizando los pulsadores. Puedes, también, rotar el espacio con clic sostenido.
En el espacio bidimensional, el plano de coordenadas está definido por un par de ejes perpendiculares. Estos ejes nos permiten nombrar cualquier ubicación dentro del plano. En tres dimensiones, definimos planos de coordenadas por los ejes de coordenadas, tal como en dos dimensiones. Ahora hay tres ejes, por lo que hay tres pares de ejes que se intersecan. Cada par de ejes forma un plano de coordenadas: el plano xy, el plano xz y el plano yz (Figura 2.26).
Definimos formalmente el plano xy como el siguiente conjunto: ${(x, y, 0): x, y \isin \Reals}$. Del mismo modo, el plano xz y el plano yz se definen como ${(x, 0, z): x, z \isin \Reals}$ y ${(0, y, z): y, z\isin \Reals}$, respectivamente.
Para visualizar esto, imagina que estás construyendo una casa y estás parado en una habitación con solo dos de las cuatro paredes terminadas (supón que las dos paredes terminadas son adyacentes entre sí). Si te paras de espaldas a la esquina donde se encuentran las dos paredes terminadas, de frente a la habitación, el piso es el plano xy, la pared a tu derecha es el plano $xz$, y la pared a su izquierda es el plano $yz$.

Figura 2.26. El plano que contiene los ejes $x$ y $y$ se llama plano $xy$. El plano que contiene los ejes $x$ y $z$ se llama plano $xz$, y los ejes $y$ y $z$ definen el plano $yz$.
En la siguiente escena interactiva, puedes observar con más detalle los planos al rotar el espacio con clic sostenido.
En dos dimensiones, los ejes de coordenadas dividen el plano en cuatro cuadrantes. Del mismo modo, los planos de coordenadas dividen el espacio entre ellos en ocho regiones alrededor del origen, llamadas octantes. Los octantes llenan $\Reals ^3$ de la misma manera que los cuadrantes llenan $\Reals ^2$, como se muestra en la figura 2.27.
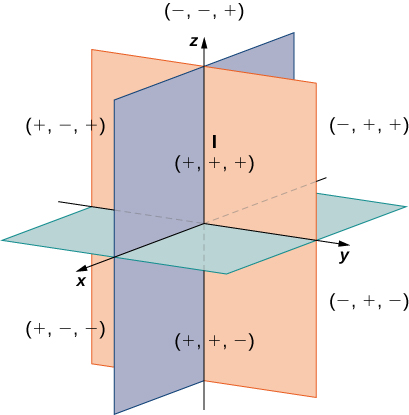
Figura 2.26. Los puntos que se encuentran en octantes tienen tres coordenadas distintas de cero.
La mayoría del trabajo en el espacio tridimensional es una extensión cómoda de los conceptos correspondientes en dos dimensiones. En esta sección, usamos nuestro conocimiento de los círculos para describir las esferas, luego ampliamos nuestra comprensión de los vectores a tres dimensiones. Para lograr estos objetivos, comenzamos adaptando la fórmula de la distancia al espacio tridimensional.
Si dos puntos se encuentran en el mismo plano de coordenadas, entonces es sencillo calcular la distancia entre ellos. Consideramos que la distancia $d$ entre dos puntos $(x_1, y_1)$ y $(x_2, y_2)$ en el plano de coordenadas $xy$ viene dada por la fórmula
La fórmula para la distancia entre dos puntos en el espacio es una extensión natural de esta fórmula.
La prueba de este teorema se deja como un ejercicio (sugerencia: Primero encuentra la distancia $d_1$ entre los puntos $(x_1, y_1, z_1)$ y $(x_2, y_2, z_2)$ como se muestra en la Figura 2.28).
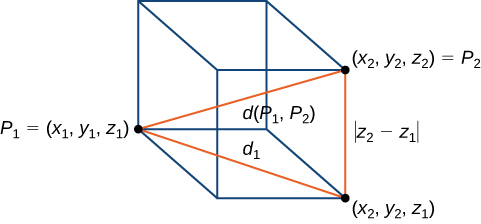
Figura 2.28. La distancia entre $P_1$ y $P_2$ es la longitud de la diagonal del prisma rectangular que tiene $P_1$ y $P_2$ como esquinas opuestas.
 |
Distancia en el espacio |
Encuentra la distancia entre los puntos $P_1 = (3, −1, 5)$ y $P_2 = (2, 1, −1)$.

Figura 2.29. Encuentra la distancia entre los dos puntos.

Antes de pasar a la siguiente sección, veamos cómo $\Reals ^3$ difiere de $\Reals ^2$. Por ejemplo, en $\Reals ^2$, las rectas que no son paralelas siempre deben intersecarse. Este no es el caso en $\Reals ^3$. Por ejemplo, considera la recta que se muestra en la Figura 2.30. Estas dos rectas no son paralelas, ni se intersecan.
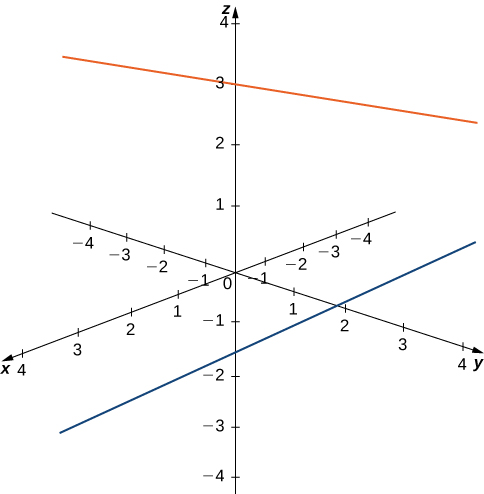
Figura 2.30. Estas dos rectas no son paralelas, pero no se intersecan.
También puedes tener circunferencias que estén interconectadas pero que no tengan puntos en común, como en la figura 2.31.
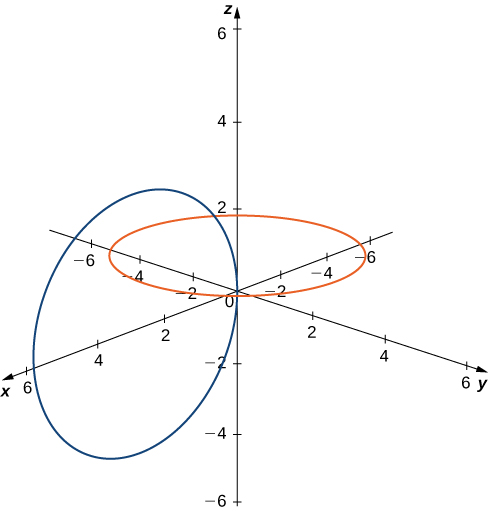
Figura 2.31. Estas circunferencias están interconectadas, pero no tienen puntos en común.
Tenemos mucha más flexibilidad trabajando en tres dimensiones que si trabajamos con solo dos dimensiones.
Ahora que podemos representar puntos en el espacio y encontrar la distancia entre ellos, podemos aprender a escribir ecuaciones de objetos geométricos como rectas, curvas, planos y superficies n $\Reals ^3$. Primero, comenzamos con una ecuación simple. Compara las gráficas de la ecuación $x = 0$ en $\Reals$, $\Reals ^2$ y $\Reals ^3$ (Figura 2.32).
A partir de estos gráficos, podemos ver que la misma ecuación puede describir un punto, una recta o un plano.

Figura 2.32. (a) En $\Reals$, la ecuación $x = 0$ describe un solo punto. (b) En $\Reals ^2$, la ecuación $x = 0$ describe una recta, el eje y. (c) En $\Reals ^3$, la ecuación $x = 0$ describe un plano, el plano yz.
En el espacio, la ecuación $x = 0$ describe todos los puntos $(0, y, z)$. Esta ecuación define el plano $yz$. Del mismo modo, el plano $xy$ contiene todos los puntos de la forma $(x, y, 0)$. La ecuación $z = 0$ define el plano $xy$ y la ecuación $y = 0$ describe el plano $xz$ (Figura 2.33).
Comprender las ecuaciones de los planos de coordenadas nos permite escribir una ecuación para cualquier plano que sea paralelo a uno de los planos de coordenadas. Cuando un plano es paralelo al plano $xy$, por ejemplo, la coordenada $z$ de cada punto en el plano tiene el mismo valor constante. Solo las coordenadas $x$ e $y$ de los puntos en ese plano varían de un punto a otro.
Figura 2.33. (a) En el espacio, la ecuación $z = 0$ describe el plano $xy$. (b) Todos los puntos en el plano $xz$ satisfacen la ecuación $y = 0$.
 |
Escribir ecuaciones de planos paralelos a planos coordinados |

Como hemos visto, en $\Reals ^2$ la ecuación $x = 5$ describe la recta vertical que pasa por el punto $(5, 0)$. Esta recta es paralela al eje y. En una extensión natural, la ecuación $x = 5$ en $\Reals ^3$ describe el plano que pasa por el punto $(5, 0, 0)$, que es paralelo al plano $yz$. Otra extensión natural de una ecuación familiar se encuentra en la ecuación de una esfera.
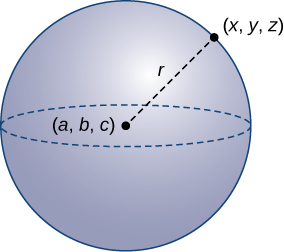
Figura 2.33. Cada punto $(x, y, z)$ en la superficie de una esfera está $r$ unidades lejos del centro $(a, b, c)$.
La ecuación de una circunferencia se deriva usando la fórmula de la distancia en dos dimensiones. Del mismo modo, la ecuación de una esfera se basa en la fórmula tridimensional de la distancia.
 |
Encontrar una ecuación de una esfera |
Encuentra la ecuación estándar de la esfera con centro $(10, 7, 4)$ y punto $(−1, 3, −2)$, como se muestra en la figura 2.35.

Figura 2.35. La esfera centrada en $(10, 7, 4)$ que contiene el punto $(−1, 3, −2)$.
 |
Encontrar una ecuación de una esfera |
Supongamos que $P = (- 5, 2, 3)$ y $Q = (3, 4, −1)$, y supongamos que el segmento de recta $PQ$ forma el diámetro de una esfera (Figura 2.36). Encuentra la ecuación de la esfera. .

Figura 2.36. Segmento de recta $PQ$.
En la siguiente escena interactiva, puedes apreciar los resultados del ejercicio anterior (recuerda que puedes rotar el espacio).
 |
Graficar otras ecuaciones en tres dimensiones |
Describe el conjunto de puntos que satisface $(x − 4)(z − 2) = 0$, y grafica el conjunto.

 |
Graficar otras ecuaciones en tres dimensiones |
Describe el conjunto de puntos que satisface $(x − 2)^2 + (y − 1)^2 = 4$, y grafica el conjunto.

Al igual que los vectores bidimensionales, los vectores tridimensionales son cantidades con magnitud y dirección, y están representados por segmentos de recta dirigidos (flechas). Con un vector tridimensional, usamos una flecha tridimensional.
Los vectores tridimensionales también se pueden representar en forma de componente. La notación $\bold{v} = \lang x, y, z\rang$ es una extensión natural del caso bidimensional, que representa un vector con el punto inicial en el origen, $(0, 0, 0)$ y el punto final $(x, y, z )$.
El vector cero es $\bold{0} = \lang 0, 0, 0\rang$. Entonces, por ejemplo, el vector tridimensional $\bold{v} = \lang 2, 4, 1\rang$ está representado por un segmento de línea dirigidos desde el punto $(0, 0, 0)$ al punto $(2, 4, 1)$ (Figura 2.39).
Figura 2.39. El vector $\bold{v} = \lang 2, 4, 1\rang$ está representado por un segmento de recta dirigida desde el punto $(0, 0, 0)$ al punto $(2, 4, 1)$.
La suma vectorial y la multiplicación por un escalar se definen de manera análoga al caso bidimensional. Si $\bold{v} = \lang x_1, y_1, z_1\rang$ y $\bold{w} = \lang x_2, y_2, z_2\rang$ son vectores y $k$ es un escalar, entonces
$$\bold{v} + \bold{w} = \lang x_1 + x_2, y_1 + y_2, z_1 + z_2\rang\; y\; k\bold{v} = \lang kx_1, ky_1, kz_1\rang$$Si $k = −1$, entonces $k\bold{v} = (- 1)\bold{v}$ se escribe como $−\bold{w}$, y la resta vectorial se define por $\bold{v} − \bold{w} = \bold{v} + (-\bold{w}) = \bold{v} + (-1)\bold{w}$.
Los vectores unitarios estándar también se extienden fácilmente en tres dimensiones:
$\bold{i} = \lang 1, 0, 0\rang , \bold{j} = \lang 0, 1, 0\rang\; y\; \bold{k} = \lang 0, 0 ,1\rang$, y los usamos de la misma forma en que usamos los vectores unitarios estándar en dos dimensiones. Por lo tanto, podemos representar un vector en $\Reals^3$ de la siguiente manera:
$$\bold{v} = \lang x, y, z\rang = x\bold{i} + y\bold{j} + z\bold{k}$$ |
Representaciones vectoriales |
Sea $\overrightarrow{PQ}$ el vector con el punto inicial $P = (3, 12, 6)$ y el punto terminal $Q = (- 4, −3, 2)$ como se muestra en la Figura 2.40. Expresa $\overrightarrow{PQ}$ en ambos componentes y utilizando vectores unitarios estándar.
Figura 2.40. El vector con el punto inicial $P = (3, 12, 6)$ y el punto final $Q = (- 4, −3, 2)$.

Como se describió anteriormente, los vectores en tres dimensiones se comportan de la misma manera que los vectores en un plano. La interpretación geométrica de la suma de vectores, por ejemplo, es la misma en el espacio bidimensional y tridimensional, tal como se aprecia en la figura 2.41.
Figura 2.41. Para sumar vectores en tres dimensiones, seguimos los mismos procedimientos que aprendimos para dos dimensiones.
Ya hemos visto cómo algunas de las propiedades algebraicas de los vectores, como la suma de vectores y la multiplicación por un escalar, pueden extenderse a tres dimensiones.
Otras propiedades pueden ampliarse de manera similar. Se resumen aquí para nuestra referencia.
Hemos visto que la adición de vectores en dos dimensiones satisface las propiedades inversas conmutativas, asociativas y aditivas. Estas propiedades de las operaciones vectoriales también son válidas para vectores tridimensionales. La multiplicación por un escalar de vectores satisface la propiedad distributiva, y el vector cero actúa como una identidad aditiva. Las pruebas para verificar estas propiedades en tres dimensiones son extensiones directas de las pruebas en dos dimensiones.
Del libro Geometría analítica del espacio, cuyas autoras son María José García Cebrian y Elena E. Álvarez Sáiz, hemos tomado la siguiente escena interactiva, para que practiques y comprendas mejor algunas propiedades de los vectores en el espacio.
 |
Operaciones vectoriales en tres dimensiones |
Sean $\bold{v} = \lang − 2, 9, 5\rang$ y $\bold{w} = \lang 1, −1, 0\rang$ (Figura 2.42). Encuentra los siguientes vectores.
Figura 2.42. Los vectores $\bold{v} = \lang − 2, 9, 5\rang$ y $\bold{w} = \lang 1, −1, 0\rang$

 |
Lanzar un pase hacia adelante |
Un mariscal de campo está de pie en el campo de fútbol preparándose para lanzar un pase. Su receptor está parado 20 yardas por el campo y 15 yardas a la izquierda del mariscal de campo. El mariscal de campo lanza la pelota a una velocidad de 60 mph hacia el receptor en un ángulo ascendente de 30° (ver la siguiente figura). Escribe el vector de velocidad inicial de la pelota, $\bold{v}$, en forma de componente.

A continuación, presentamos los ejercicios propuestos para esta sesión. Recuerda que los ejercicios correspondientes a numerales impares, presentan la solución.

61. Considera una caja rectangular con uno de los vértices en el origen, como se muestra en la siguiente figura. Si el punto $A (2, 3, 5)$ es el vértice opuesto al origen, entonces encuentra
 Para los siguientes ejercicios, describe y grafica el conjunto de puntos que satisface la ecuación dada.
Para los siguientes ejercicios, describe y grafica el conjunto de puntos que satisface la ecuación dada.
63. $(y − 5)(z − 6) = 0$ (Solución) 64. $(z − 2)(z −5 ) = 0$ 65. $(y − 1)^2 + (z − 1)^2 = 1$ (Solución) 66. $(x − 2)^2 + (z − 5)^2 = 4$ 67. Escribe la ecuación del plano que pasa por el punto $(1,1,1)$ que es paralelo al plano $xy$. (Solución) 68. Escribe la ecuación del plano que pasa por el punto $(1, −3,2)$ que es paralelo al plano $xz$. 69. Encuentra una ecuación del plano que pasa por los puntos $(1, −3, −2)$, $(0,3, −2)$ y $(1,0, −2)$. (Solución) 70. Encuentra una ecuación del plano que pasa por los puntos $(1,9,2)$, $(1,3,6)$ y $(1, −7,8)$.
 Para los siguientes ejercicios, encuentra la ecuación de la esfera en forma estándar que satisfaga las condiciones dadas.
Para los siguientes ejercicios, encuentra la ecuación de la esfera en forma estándar que satisfaga las condiciones dadas.
71. Centro $C (−1,7,4)$ y radio $4$ (Solución) 72. Centro $C (−4,7,2)$ y radio $6$ 73. Diámetro $PQ$, donde $P (−1,5,7)$ y $Q (−5,2,9)$ (Solución) 74. Diámetro $PQ$, donde $P (−16, −3,9)$ y $Q (−2,3,5)$
 Para los siguientes ejercicios, encuentra el centro y el radio de la esfera con una ecuación en forma general que se proporciona.
Para los siguientes ejercicios, encuentra el centro y el radio de la esfera con una ecuación en forma general que se proporciona.
75. $x^2+y^2+z^2−4z+3=0$ (Solución) 76. $x^2+y^2+z^2−6x+8y−10z+25=0$
 Para los siguientes ejercicios, expresa el vector $\overrightarrow{PQ}$ con el punto inicial en $P$ y el punto final en $Q$
Para los siguientes ejercicios, expresa el vector $\overrightarrow{PQ}$ con el punto inicial en $P$ y el punto final en $Q$
77. $P(3,0,2)$ y $Q(−1,−1,4)$ (Solución) 78. $P(0,10,5)$ y $Q(1,1,−3)$ 79. $P (−2,5, −8)$ y $M (1, −7,4)$, donde M es el punto medio del segmento de recta PQ (Solución) 80. $Q (0,7, −6)$ y $M (−1,3,2)$, donde M es el punto medio del segmento de recta PQ 81. Encuentra el punto final Q del vector $\overrightarrow{PQ} = \lang 7, −1,3\rang$ con el punto inicial en $P (−2,3,5)$ (Solución) 82. Encuentra el punto inicial P del vector $\overrightarrow{PQ} = \lang − 9,1,2\rang$ con el punto final en $Q (10,0, −1)$.
 Para los siguientes ejercicios, usa los vectores a y b dados para encontrar y expresar los vectores a + b, 4a y −5a + 3b en forma de componente.
Para los siguientes ejercicios, usa los vectores a y b dados para encontrar y expresar los vectores a + b, 4a y −5a + 3b en forma de componente.
83. . $\bold{a}=\lang −1,−2,4\rang$, $\bold{b}=\lang −5,6,−7\rang$ (Solución) 84. $\bold{a}=\lang 3,−2,4\rang$, $\bold{b}=\lang −5,6,−9\rang$ 85. $\bold{a}=−k$, $ \bold{B}=−\bold{i}$ (Solución) 86. $\bold{a}=\bold{i}+\bold{j}+\bold{k}$, $\bold{b}=2\bold{i}−3\bold{j}+2\bold{k}$
 Para los siguientes ejercicios, se dan los vectores u y v. Encuentra las magnitudes de los vectores u − v y −2u.
Para los siguientes ejercicios, se dan los vectores u y v. Encuentra las magnitudes de los vectores u − v y −2u.
87. 87. $\bold{u} = 2\bold{i} + 3\bold{j} + 4\bold{k}, \bold{v} = −\bold{i} + 5\bold{j} − \bold{k}$ (Solución) 88. $\bold{u} = \bold{i} + \bold{j}, \bold{v} = \bold{j} − \bold{k}$ 89. $\bold{u} = \lang 2cost, −2sent, 3\rang, \bold{v} = \lang 0,0,3\rang$, donde t es un número real. (Solución) 90. $\bold{u} = \lang 0,1, sinht\rang, \bold{v} = \lang 1,1,0\rang$, donde t es un número real.
 Para los siguientes ejercicios, encuentra el vector unitario en la dirección del vector dado a y exprésalo usando vectores unitarios estándar.
Para los siguientes ejercicios, encuentra el vector unitario en la dirección del vector dado a y exprésalo usando vectores unitarios estándar.
91. $\bold{a} = 3\bold{i} − 4\bold{j}$ (Solución) 92. $\bold{a} = \lang 4, −3,6\rang$ 93. $\bold{a} = \overrightarrow{PQ}$, donde $P (−2,3,1)$ y $Q (0, −4,4)$ (Solución) 94. $\bold{a} = \overrightarrow{OP}$, donde $P (−1, −1,1)$ 95. $\bold{a} = \bold{u} − \bold{v} + \bold{w}$, donde $\bold{u} = \bold{i} − \bold{j} − \bold{k}, \bold{v} = 2\bold{i} − \bold{j} + \bold{k}$, y $\bold{w} = −\bold{i} + \bold{j} + 3\bold{k}$ (Solución) 96. $\bold{a} = 2\bold{u} + \bold{v} − \bold{w}$, donde $\bold{u} = \bold{i} − \bold{k}, \bold{v} = 2\bold{j}$ y $\bold{q} = \bold{i} − \bold{j}$ 97. Determina si $\overrightarrow{AB}$ y $\overrightarrow{OP}$ son vectores equivalentes, donde $A (1,1,1), B (3,3,3), P (1,4,5)$ y $Q (3,6,7)$ (Solución). 98. Determina si los vectores $\overrightarrow{AB}$ y $\overrightarrow{OP}$ son equivalentes, donde $A (1,4,1), B (−2,2,0), P (2,5,7) y Q (−3,2 1)$
 Para los siguientes ejercicios, encuentra el vector u con una magnitud dada y que satisfaga las condiciones dadas.
Para los siguientes ejercicios, encuentra el vector u con una magnitud dada y que satisfaga las condiciones dadas.
99. $\bold{v} = \lang 7, −1,3\rang, \|\bold{u}\| = 10$, $\bold{u}$ y $\bold{v}$ tienen la misma dirección (Solución) 100. $\bold{v} = \lang 2,4,1\rang, \|\bold{u}\| = 15$, $\bold{u}$ y $\bold{v}$ tienen la misma dirección 101. $\bold{v} = \lang 2sent, 2cost, 1\rang, \|\bold{u}\| = 2$, $\bold{u}$ y $\bold{v}$ tienen direcciones opuestas para cualquier t, donde t es un número real (Solución) 102. $\bold{v} = \lang 3senht, 0,3\rang, \|\bold{u}\| = 5$, $\bold{u}$ y $\bold{v}$ tienen direcciones opuestas para cualquier t, donde t es un número real
103. Determina un vector de magnitud 5 en la dirección del vector $\overrightarrow{AB}$, donde $A (2,1,5)$ y $B (3,4, −7)$ (Solución). 104. Encuentra un vector de magnitud 2 que apunte en la dirección opuesta al vector $\overrightarrow{AB}$, donde $A (−1, −1,1)$ y B $(0,1,1)$. ExpresA la respuesta en forma de componente. 105. Considera los puntos $A (2, \alpha, 0), B (0,1, \beta)$ y $C (1,1, \beta )$, donde $\alpha$ y $\beta$ son números reales negativos. Encuentre $\alpha$ y $\beta$ de manera que $\|\overrightarrow{AB} − \overrightarrow{OB} + \overrightarrow{OC}\| = \|\overrightarrow{OB}\| = 4$ (Solución). 106. Considera los puntos $A (\alpha , 0,0), B (0, \beta , 0)$ y $C (\alpha , \beta , \beta )$, donde $\alpha$ y $\beta$ son números reales positivos. Encuentre $\alpha$ y $\beta$ de manera que $\|\overline{OA} + \overline{OB}\| = \sqrt{2}$ y $\|\overline{OC}\| = \sqrt{3}$. 107. Sea $P (x, y, z)$ un punto situado a la misma distancia de los puntos $A (1, −1,0)$ y $B (−1,2,1)$. Muestra que el punto $P$ se encuentra en el plano de la ecuación $−2x + 3y + z = 2$. 108. Sea $P (x, y, z)$ un punto situado a una distancia igual del origen y el punto $A (4,1,2)$. Demuestra que las coordenadas del punto $P$ satisfacen la ecuación $8x + 2y + 4z = 21$. 109. Los puntos $A, B y C$ son colineales (en este orden) si se satisface la relación $\|\overrightarrow{AB}\| + \|\overrightarrow{BC}\| = \|\overrightarrow{AC}\|$. Muestra que $A (5,3, −1), B (−5, −3,1)$ y $C (−15, −9,3)$ son puntos colineales.
110. Muestra que los puntos $A (1,0,1), B (0,1,1)$ y $C (1,1,1)$ no son colineales. 111. [T] Una fuerza F de 50N actúa sobre una partícula en la dirección del vector $\overrightarrow{OP}$, donde $P (3,4,0)$ (Solución).
Sean $\bold{F_1} = \lang 10,6,3\rang, \bold{F2} = \lang 0,4,9\rang$, y $\bold{F_3} = \lang 10, −3, −9\rang$ tres fuerzas que actúan sobre una caja. Encuentra la fuerza $\bold{F_4}$ que actúa sobre la caja de modo que la caja esté en equilibrio estático. Expresa la respuesta en forma de componente (Solución). 116. [T] Sean $F_k = \lang 1, k, k_2\rang, k = 1, ..., n$ n fuerzas que actúan sobre una partícula, con $n \ge 2$.

119. [T] Un bloque de cemento de 30 kg está suspendido por tres cables de igual longitud que están anclados en los puntos $P (−2,0,0), Q (1,-\sqrt{3}, 0)$ y $R (1 , -\sqrt{3}, 0)$. La carga se encuentra en $S (0,0, −2\sqrt{3})$, como se muestra en la siguiente figura. Supongamos que $F_1, F_2$ y $F_3$ son las fuerzas de tensión resultantes de la carga en los cables $RS, QS$ y $PS$, respectivamente (Solución).
120. Dos jugadores de fútbol están practicando para un próximo juego. Uno de ellos corre 10 m desde el punto $A$ hasta el punto $B$. Luego gira a la izquierda a 90° y corre 10 m hasta llegar al punto $C$. Luego patea la pelota con una velocidad de 10 m/seg en un ángulo ascendente de 45° a su compañera de equipo, que se encuentra en el punto $A$. Escribe la velocidad de la pelota en forma de componente.
121. Sea $r(t) = \lang x (t), y (t), z (t)\rang$ el vector de posición de una partícula en el momento $t \isin [0, T]$, donde $x$, $y$ y $z$ son funciones llanas en $[0, T]$. La velocidad instantánea de la partícula en el tiempo $t$ está definida por el vector $v(t) = \lang x'(t), y'(t), z'(t)\rang$, con componentes que son las derivadas con respecto a $t$, de las funciones $x, y$ y $z$, respectivamente. La magnitud $\|v(t)\|$ del vector de velocidad instantánea se denomina velocidad de la partícula en el tiempo $t$. El vector $a(t) = \lang x^{\prime\prime}(t), y^{\prime\prime}(t), z^{\prime\prime}(t)\rang$, con componentes que son las segundas derivadas con respecto a $t$, de las funciones $x$, $y$ y $z$, respectivamente, da la aceleración de la partícula en el tiempo $t$. Considera $r(t) = \lang cost, sent, 2t\rang$ el vector de posición de una partícula en el tiempo $t\isin [0,30]$, donde las componentes de $r$ se expresan en centímetros y el tiempo se expresa en segundos (Solución).
b. Usa un CAS para visualizar la ruta de la partícula definida por los puntos $(t, 2t^2,4t^2)$, donde $t\isin [0,60]$.
Si aplicamos una fuerza a un objeto para que el objeto se mueva, decimos que el trabajo lo realiza la fuerza. En las aplicaciones de la integración observamos una fuerza constante y asumimos que la fuerza se aplica en la dirección del movimiento del objeto. En esas condiciones, el trabajo puede expresarse como el producto de la fuerza que actúa sobre un objeto y la distancia que se mueve el objeto. En este capítulo, sin embargo, hemos visto que tanto la fuerza como el movimiento de un objeto pueden representarse mediante vectores.
En esta sección, desarrollaremos una operación llamada producto punto, que nos permite calcular el trabajo en el caso en que el vector de fuerza y el vector de movimiento tienen direcciones diferentes. El producto punto esencialmente nos dice cuánto del vector de fuerza se aplica en la dirección del vector de movimiento. El producto punto también puede ayudarnos a medir el ángulo formado por un par de vectores y la posición de un vector en relación con los ejes de coordenadas. Incluso proporciona una prueba simple para determinar si dos vectores se encuentran en ángulo recto.
Ya hemos aprendido cómo sumar y restar vectores. En este capítulo, investigamos dos tipos de multiplicación de vectores. El primer tipo de multiplicación entre vectores se llama producto punto, en función de la notación que usamos para él, y se define de la siguiente manera:
Observa que si $\bold{u}$ y $\bold{v}$ son vectores bidimensionales, calculamos el producto escalar de manera similar. Por lo tanto, si $\bold{u} = \lang u_1, u_2\rang$ y $\bold{v} = \lang v_1, v_2\rang$, entonces
$$\bold{u}\cdot\bold{v} = u_1v_1 + u_2v_2$$Cuando dos vectores se combinan bajo suma o resta, el resultado es un vector. Cuando dos vectores se combinan usando el producto punto, el resultado es un escalar. Por esta razón, el producto punto a menudo se llama producto escalar. También se le puede llamar el producto interno.
 |
Calculando productos punto |

Al igual que la suma y resta de vectores, el producto punto tiene varias propiedades algebraicas. Probamos tres de estas propiedades y dejamos el resto como ejercicios.
Prueba
Sea $\bold{u} = \lang u_1, u_2, u_3\rang$ y $\bold{v} = \lang v_1, v_2, v_3\rang$. Luego
$$\begin{aligned} \bold{u}\cdot\bold{v} &= \lang u_1,u_2,u_3\rang \cdot \lang v_1,v_2,v_3\rang\\ &= u_1 v_1 + u_2 v_2 + u_3 v_3\\ &= v_1 u_1 + v_2 u_2 + v_3 u_3\\ &= \lang v_1,v_2,v_3\rang\cdot \lang u_1,u_2,u_3\rang\\ &= \bold{v}\cdot\bold{u} \end{aligned}$$La propiedad asociativa se parece a la propiedad asociativa para la multiplicación de números reales, pero presta mucha atención a la diferencia entre los objetos escalares y vectoriales:
La prueba de que $c(\bold{u}\cdot\bold{v}) = \bold{u}\cdot(c\bold{v})$ es similar.
La cuarta propiedad muestra la relación entre la magnitud de un vector y su producto punto consigo mismo:
$$\begin{aligned} \bold{v}\cdot\bold{v} &= \lang v_1,v_2,v_3\rang\cdot\lang v_1,v_2,v_3\rang\\ &= (v_1)^2+(v_2)^2+(v_3)^2\\ &= \bigg[\sqrt{(v_1)^2+(v_2)^2+(v_3)^2}\bigg]^2\\ &= \|\bold{v}\|^2 \end{aligned}$$Observa que la definición del producto punto produce $0\cdot\bold{v} = \bold{0}$. Por propiedad iv., si $\bold{v}\cdot\bold{v} = 0$, entonces $\bold{v} = \bold{0}$.
 |
Usando las propiedades del producto punto |
Sean $\bold{a} = \lang 1,2, −3\rang$, $\bold{b} = \lang 0,2,4\rang$, y $\bold{c} = \lang 5, −1,3\rang$. Encuentra cada uno de los siguientes productos.

Cuando dos vectores distintos de cero se colocan en posición estándar, ya sea en dos dimensiones o en tres dimensiones, forman un ángulo entre ellos (Figura 2.44). El producto punto proporciona una forma de encontrar la medida de este ángulo. Esta propiedad es el resultado del hecho de que podemos expresar el producto escalar en términos del coseno del ángulo formado por dos vectores.
Figura 2.44. Sea el ángulo entre dos vectores distintos de cero $\bold{u}$ y $\bold{v}$, de modo que $0 \le \theta \le \pi$.
Prueba
Coloca los vectores $\bold{u}$ y $\bold{v}$ en la posición estándar y considera el vector $\bold{v} − \bold{u}$ (Figura 2.45). Estos tres vectores forman un triángulo con longitudes laterales $\|\bold{u}\|, \|\bold{v}\|$ y $\|\bold{v} − \bold{u}\|$.
Figura 2.45. Las longitudes de los lados del triángulo están dadas por las magnitudes de los vectores que forman el triángulo.
En la página siguiente puedes observar e interactuar con el tríangulo en una escena tridimensional.
Recordemos de la trigonometría que la ley de los cosenos describe la relación entre las longitudes laterales del triángulo y el ángulo $\theta$. La aplicación de la ley de cosenos aquí da
$$\|\bold{v} − \bold{u}\| = \|\bold{u}\|^2 + \|\bold{v}\|^2 − 2\|\bold{u}\|\|\bold{v}\|cos\theta$$El producto punto proporciona una forma de reescribir el lado izquierdo de esta ecuación:
$$\begin{aligned} \|\bold{v} − \bold{u}\|^2 &= (\bold{v}−\bold{u})\cdot(\bold{v}−\bold{u})\\ &= (\bold{v}−\bold{u})\cdot\bold{v}−(\bold{v}−\bold{u})\cdot\bold{u}\\ &= \bold{v}\cdot\bold{v}−\bold{u}\cdot\bold{v}−\bold{v}\cdot\bold{u}+\bold{u}\cdot\bold{u}\\ &= \bold{v}\cdot\bold{v}−\bold{u}\cdot\bold{v}−\bold{u}\cdot\bold{v}+\bold{u}\cdot\bold{u}\\ &= \|\bold{v}\|^2−2\bold{u}\cdot\bold{v}+\|\bold{u}\|^2 \end{aligned}$$Aplicando la ley de cosenos
$$\begin{aligned} \|\bold{v} − \bold{u}\|^2 &= \|\bold{u}\|^2+\|\bold{v}\|^2−2\|\bold{u}\|\|\bold{v}\|cos\theta\\ \|\bold{v}\|^2−2\bold{u}\cdot\bold{v}+\|\bold{u}\|^2 &= \|\bold{u}\|^2+\|\bold{v}\|^2−2\|\bold{u}\|\|\bold{v}\|cos\theta\\ −2\bold{u}\cdot\bold{v} &= −2\|\bold{u}\|\|\bold{v}\|cos\theta\\ \bold{u}\cdot\bold{v} &= \|\bold{u}\|\|\bold{v}\|cos\theta \end{aligned}$$Podemos usar esta expresión para encontrar la medida del ángulo entre dos vectores distintos de cero. La siguiente ecuación reorganiza la ecuación 2.3 para resolver el coseno del ángulo:
$$cos\theta = \frac{\bold{u}\cdot\bold{v}}{\|\bold{u}\|\|\bold{v}\|}\tag{$2.5$}$$Usando esta ecuación, podemos encontrar el coseno del ángulo entre dos vectores distintos de cero. Como estamos considerando el ángulo más pequeño entre los vectores, suponemos $0^o\le\theta\le 180^o$ (o $0\le\theta\le\pi$ si estamos trabajando en radianes). El coseno inverso es único en este rango, por lo que podemos determinar el ángulo $\theta$.
 |
Encontrar el ángulo entre dos vectores |
Encuentra la medida del ángulo entre cada par de vectores.

El ángulo entre dos vectores puede ser agudo ($0 \lt cos\theta\lt 1$), obtuso ($−1 \lt cos\theta \lt 0$) o llano ($cos\theta = −1$). Si $cos\theta = 1$, ambos vectores tienen la misma dirección. Si $cos\theta = 0$, entonces los vectores, cuando se colocan en posición estándar, forman un ángulo recto (Figura 2.46). Podemos formalizar este resultado en un teorema con respecto a los vectores ortogonales (perpendiculares).
Figura 2.46. (a) Un ángulo agudo tiene $0 \lt cos\theta\lt 1$. (b) Un ángulo obtuso tiene $−1 \lt cos\theta \lt 0$. (c) Una línea recta tiene $cos\theta = -1$. (d) Si los vectores tienen la misma dirección, $cos\theta = 1$. (e) Si los vectores son ortogonales (perpendiculares), $cos\theta = 0$.
Prueba
Supongamos que $\bold{u}$ y $\bold{v}$ son vectores distintos de cero y que $\theta$ denota el ángulo entre ellos. Primero, supón que $\bold{u}\cdot\bold{v} = 0$. Luego
$$\|\bold{u}\|\|\bold{v}\|cos\theta = 0$$Sin embargo, $\|\bold{u}\| \cancel{=} 0$ y $\|\bold{v}\| \cancel{=} 0$, por lo que debemos tener $cos\theta = 0$. Por lo tanto, $\theta = 90^o$, y los vectores son ortogonales.
Ahora supón que $\bold{u}$ y $\bold{v}$ son ortogonales. Entonces $\theta = 90^o$ y tenemos
$$\bold{u}\cdot\bold{v} = \|\bold{u}\|\|\bold{v}\|cos\theta = \|\bold{u}\|\|\bold{v}\|cos90^o = \|\bold{u}\|\|\bold{v}\|\cdot 0 = 0$$Los términos ortogonal, perpendicular y normal indican que los objetos matemáticos se cortan en ángulo recto. El uso de cada término está determinado principalmente por su contexto. Decimos que los vectores son ortogonales y las rectas son perpendiculares. El término normal se usa con mayor frecuencia cuando se mide el ángulo hecho con un plano u otra superficie.
En la siguiente escena interactiva (adaptación de una escena del libro Geometría analítica del espacio), modifica los vectores y observa qué ocurre.
 |
Identificando vectores ortogonales |
Determina si $p = \lang 1,0,5\rang $ y $q = \lang 10,3, −2\rang $ son vectores ortogonales.

 |
Medición del ángulo formado por dos vectores |
Dado = $\lang 2,3,3\rang$. Encuentra las medidas de los ángulos formados por los siguientes vectores.

El ángulo que forma un vector con cada uno de los ejes de coordenadas, llamado ángulo director, es muy importante en los cálculos prácticos, especialmente en un campo como la ingeniería. Por ejemplo, en ingeniería astronáutica, el ángulo en el que se lanza un cohete debe determinarse con mucha precisión. Un error muy pequeño en el ángulo puede hacer que el cohete se desplace cientos de millas. Los ángulos directores a menudo se calculan utilizando el producto escalar y los cosenos de los ángulos, llamados cosenos directores. Por lo tanto, definimos ambos ángulos y sus cosenos.
Figura 2.48. El ángulo $\alpha$ está formado por el vector $\bold{v}$ y el vector unitario $\bold{i}$. El ángulo $\beta$ está formado por el vector $\bold{v}$ y el vector unitario $\bold{j}$. El ángulo $\gamma$ está formado por el vector $\bold{v}$ y el vector unitario $\bold{k}$.
En el ejercicio anterior, los cosenos directores de $\bold{v} = \lang 2,3,3\rang$ son $cos\alpha = \frac{2}{\sqrt{22}}, cos\beta = \frac{3}{\sqrt{22}}\; y \; cos\gamma = \frac{3}{\sqrt{22}}$. Los ángulos directores de $\bold{v}$ son $\alpha = 1.130rad, \beta = 0.877rad\; y\; \gamma = 0.877rad$.
Hasta ahora, nos hemos centrado principalmente en vectores relacionados con la fuerza, el movimiento y la posición en el espacio físico tridimensional. Sin embargo, los vectores a menudo se usan de formas más abstractas. Por ejemplo, supongamos que un vendedor de frutas vende manzanas, plátanos y naranjas. En un día determinado, vende 30 manzanas, 12 plátanos y 18 naranjas. Podrías usar un vector de cantidad, $\bold{q} = \lang 30,12,18\rang$, para representar la cantidad de fruta que vendió ese día.
De manera similar, podrías usar un vector de precios, $\bold{p} = \lang 0.50,0.25,1\rang$, para indicar que vende sus manzanas por 50 ¢ cada una, plátanos por 25 ¢ cada una y naranjas por $ 1 cada una. En este ejemplo, aunque todavía podríamos graficar estos vectores, no los interpretamos como representaciones literales de posición en el mundo físico. Simplemente estamos usando vectores para realizar un seguimiento de piezas particulares de información sobre manzanas, plátanos y naranjas.
Esta idea puede parecer un poco extraña, pero si simplemente consideramos los vectores como una forma de ordenar y almacenar datos, descubrimos que pueden ser una herramienta bastante poderosa. Volviendo al vendedor de frutas, pensemos en el producto punto, $\bold{q}\cdot\bold{p}$. Lo calculamos multiplicando el número de manzanas vendidas (30) por el precio por manzana (50 ¢), el número de plátanos vendidos por el precio por plátano y el número de naranjas vendidas por el precio por naranja. Luego agregamos todos estos valores juntos. Entonces, en este ejemplo, el producto punto nos dice cuánto dinero tenía el vendedor de frutas en ventas ese día en particular.
Cuando usamos vectores de esta manera más general, no hay razón para limitar el número de componentes a tres. ¿Qué pasa si el vendedor de fruta decide comenzar a vender toronja? En ese caso, le gustaría usar vectores de cantidad y precio de cuatro dimensiones para representar la cantidad de manzanas, plátanos, naranjas y toronjas vendidas, y sus precios unitarios. Como es de esperar, para calcular el producto escalar de los vectores de cuatro dimensiones, simplemente agregamos los productos de los componentes como antes, pero la suma tiene cuatro términos en lugar de tres.
 |
AAA Party Supply Store vende invitaciones, favores de fiesta, decoraciones y artículos para el servicio de alimentos como platos de papel y servilletas. Cuando AAA compra su inventario, paga 25 ¢ por paquete por invitaciones y favores de fiesta. Las decoraciones cuestan 50 ¢ cada una, y los artículos de servicio de comida cuestan 20 ¢ por paquete. AAA vende invitaciones por $\text{\$}$ 2.50 por paquete y favores de fiesta por $\text{\$}$ 1.50 por paquete. Las decoraciones se venden por $\text{\$}$4.50 cada una y los artículos de servicio de comida por $\text{\$}$ 1.25 por paquete.
Durante el mes de mayo, AAA Party Supply Store vende 1258 invitaciones, 342 favores de fiesta, 2426 decoraciones y 1354 artículos de servicio de alimentos. Usa vectores y productos punto para calcular cuánto dinero ganó AAA en ventas durante el mes de mayo. ¿Cuánto ganó la tienda en ganancias?

Como hemos visto, la suma combina dos vectores para crear un vector resultante. Pero, ¿qué pasa si se nos da un vector y necesitamos encontrar sus partes componentes? Utilizamos proyecciones vectoriales para realizar el proceso opuesto; puedes descomponer un vector en sus componentes. La magnitud de una proyección vectorial es una proyección escalar. Por ejemplo, si un niño tira del asa de un vagón en un ángulo de 55°, podemos usar proyecciones para determinar qué parte de la fuerza sobre el asa está realmente moviendo el vagón hacia adelante (Figura 2.49).
Volveremos a este ejemplo y aprenderemos cómo resolverlo después de ver cómo calcular las proyecciones.

Figura 2.49. Cuando un niño tira de una carreta, solo el componente horizontal de la fuerza impulsa la carreta hacia adelante.
Analiza la definición de la siguiente página y luego interactúa (en pantalla ampliada) con la siguiente escena interactiva (adaptación de una escena del libro Geometría analítica del espacio)
Si comparaste la definición con la escena interactiva, habrás notado que en la primera se define $\|proy_u\bold{v}\| = \frac{\bold{u}\cdot\bold{v}}{\|\bold{u}\|}$, mientras que en la escena interactiva se tiene $\|proy_v\bold{u}\| = \frac{\bold{u}\cdot\bold{v}}{\|\bold{v}\|}$; es decir, en una se obtiene la proyección de $\bold{v}$ sobre $\bold{u}$ y, en la escena, la proyección de $\bold{u}$ sobre $\bold{v}$. Veamos un ejemplo:

Figura 2.50. La proyección de $\bold{v}$ sobre $\bold{u}$ muestra el componente del vector $\bold{v}$ en la dirección de $\bold{u}$.
 |
Encontrar proyecciones |
Encuentra la proyección de $\bold{v}$ sobre $\bold{u}$.

A veces es útil descomponer vectores, es decir, separar un vector en una suma. Este proceso se llama resolución de un vector en componentes. Las proyecciones nos permiten identificar dos vectores ortogonales que tienen una suma deseada. Por ejemplo, sea $\bold{v} = \lang 6, −4\rang$ y sea $\bold{u} = \lang 3,1\rang$. Queremos descomponer el vector $\bold{v}$ en componentes ortogonales de modo que uno de los vectores componentes tenga la misma dirección que $\bold{u}$.
Primero encontramos el componente que tiene la misma dirección que $\bold{u}$ proyectando $\bold{v}$ sobre $\bold{u}$. Sea $\bold{p} = proy_\bold{u}\bold{v}$. Entonces tenemos
$$\begin{aligned} \bold{p} &= \frac{\bold{u}\cdot\bold{v}}{\|\bold{u}\|}\bigg(\frac{1}{\|\bold{u}\|}u\bigg) = \frac{\bold{u}\cdot\bold{v}}{\|\bold{u}\|^2}u = \frac{18-4}{9+1}\bold{u}\\ &= \frac{7}{5}\bold{u}\ = \frac{7}{5}\lang 3,1\rang = \bigg\lang \frac{21}{5}, \frac{7}{5} \bigg\rang \end{aligned}$$Ahora considera el vector $\bold{q} = \bold{v} − \bold{p}$. Tenemos
$$\begin{aligned} \bold{q} &= \bold{v} − \bold{p}\\ &= \lang 6,−4\rang − \bigg\lang \frac{21}{5}, \frac{7}{5} \bigg\rang = \bigg\lang \frac{9}{5}, -\frac{27}{5} \bigg\rang \end{aligned}$$Claramente, por la forma en que definimos $\bold{q}$, tenemos $\bold{v} = \bold{q} + \bold{p}$, y
$$\begin{aligned} \bold{q}\cdot\bold{p} &= \bigg\lang \frac{9}{5}, -\frac{27}{5} \bigg\rang\cdot\bigg\lang \frac{21}{5}, \frac{7}{5} \bigg\rang\\ &= \frac{9(21)}{25} + \frac{-27(7)}{25} = \frac{189}{25} - \frac{189}{25} = 0 \end{aligned}$$Por lo tanto, $\bold{q}$ y $\bold{p}$ son ortogonales.
 |
Resolviendo vectores en componentes |
Expresa $\bold{v} = \lang 8, −3, −3\rang$ como una suma de vectores ortogonales de modo que uno de los vectores tenga la misma dirección que $\bold{u} = \lang 2,3,2\rang$

 |
Proyeccion Escalar de Velocidad |
Un barco de contenedores sale del puerto y viaja 15° al noreste. Su motor genera una velocidad de 20 nudos a lo largo de ese camino (ver la siguiente figura). Además, la corriente oceánica mueve el barco hacia el noreste a una velocidad de 2 nudos. Considerando tanto el motor como la corriente, ¿qué tan rápido se mueve el barco en la dirección 15° al noreste? Redondea la respuesta a dos decimales.

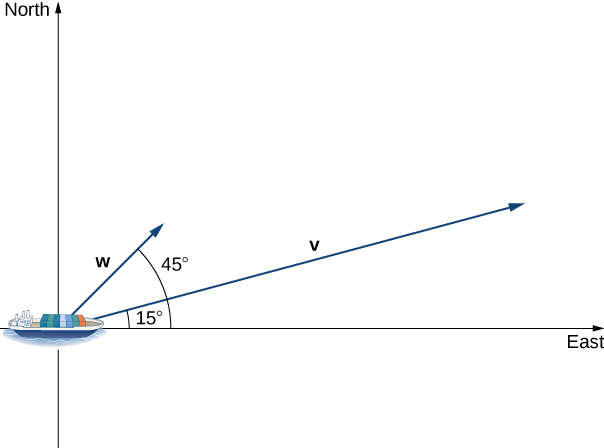
Ahora que entendemos el producto punto, podemos ver cómo aplicarlos a situaciones de la vida real. La aplicación más común del producto escalar de dos vectores está en el cálculo del trabajo.
Por física, sabemos que el trabajo se realiza cuando un objeto es movido por una fuerza. Cuando la fuerza es constante y se aplica en la misma dirección en que se mueve el objeto, definimos el trabajo realizado como el producto de la fuerza y la distancia que recorre el objeto: $\bold{W} = \bold{F}d$. Vimos varios ejemplos de este tipo en capítulos anteriores.
Ahora imagina que la dirección de la fuerza es diferente de la dirección del movimiento, como en el ejemplo de un niño que tira de un carro. Para encontrar el trabajo realizado, necesitamos multiplicar el componente de la fuerza que actúa en la dirección del movimiento por la magnitud del desplazamiento. El producto punto nos permite hacer precisamente eso. Si representamos una fuerza aplicada por un vector $\bold{F}$ y el desplazamiento de un objeto por un vector $\bold{s}$, entonces el trabajo realizado por la fuerza es el producto escalar de $\bold{F}$ y $\bold{s}$.
Volvamos al problema del carro del niño presentado anteriormente. Supongamos que un niño tira de un carro con una fuerza que tiene una magnitud de 8 lb sobre el mango en un ángulo de 55°. Si el niño tira de la carreta 50 pies, encuentra el trabajo realizado por la fuerza (Figura 2.51).
Tenemos
$$\bold{W} = \|\bold{F}\|\|\overrightarrow{PQ}\|cos\theta = 8\cdot 50 \cdot cos(55^o) \approx 229 ft\cdot lb$$En unidades estándar de EE. UU., medimos la magnitud de la fuerza $\|\bold{F}\|$ en libras.
La magnitud del vector de desplazamiento $\|\overrightarrow{PQ}\|$ nos dice qué tan lejos se movió el objeto, y se mide en pies. La unidad de medida habitual para el trabajo, entonces, es la libra-pie. Una libra-pie es la cantidad de trabajo requerida para mover un objeto que pesa 1 libra a una distancia de 1 pie. En el sistema métrico, la unidad de medida de la fuerza es el newton (N), y la unidad de medida de magnitud para el trabajo es un newton-metro $(N\cdot m)$, o un julio (J).
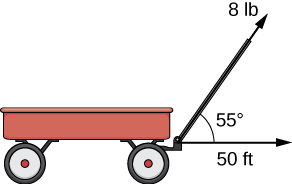
Figura 2.51. La componente horizontal de la fuerza es la proyección de $\bold{F}$ sobre el eje x positivo.
 |
Calculando el trabajo |
Una cinta transportadora genera una fuerza $\bold{F} = 5\bold{i} − 3\bold{j} + \bold{k}$ que mueve una maleta desde el punto $(1,1,1)$ al punto $(9,4,7)$ a lo largo de una línea recta. Encuentra el trabajo realizado por la cinta transportadora. La distancia se mide en metros y la fuerza se mide en newtons.


 Para los siguientes ejercicios, se dan los vectores $\bold{u}$ y $\bold{v}$. Calcula el producto punto $\bold{u}\cdot\bold{v}$.
Para los siguientes ejercicios, se dan los vectores $\bold{u}$ y $\bold{v}$. Calcula el producto punto $\bold{u}\cdot\bold{v}$.
123. $\bold{u} = \lang 3,0\rang, \bold{v}=\lang 2,2\rang$ (Solución) 124. $\bold{u} =\lang 3,−4\rang , \bold{v} = \lang 4,3\rang$ 125. $\bold{u} = \lang 2,2,−1\rang , \bold{v} = \lang −1,2,2\rang$ (Solución) 126. $\bold{u} = \lang 4,5,−6\rang , \bold{v} = \lang 0,−2,−3\rang$
 Para los siguientes ejercicios, se dan los vectores $\bold{a}, \bold{b}$ y $\bold{c}$. Determina los vectores $(\bold{a}\cdpt\bold{b})\bold{c}$ y $(\bold{a}\cdpt\bold{c})\bold{b}$. Expresar los vectores en forma de componente.
Para los siguientes ejercicios, se dan los vectores $\bold{a}, \bold{b}$ y $\bold{c}$. Determina los vectores $(\bold{a}\cdpt\bold{b})\bold{c}$ y $(\bold{a}\cdpt\bold{c})\bold{b}$. Expresar los vectores en forma de componente.
127. $\bold{a}=\lang 2,0,−3\rang, \bold{b}=\lang −4,−7,1\rang, \bold{c}=\lang 1,1,−1\rang$ (Solución) 128. $\bold{a}=\lang 0,1,2\rang, \bold{b}=\lang −1,0,1\rang, \bold{c}=\lang 1,0,−1\rang$ 129. $\bold{a}=\bold{i}+\bold{j}, \bold{b}=\bold{i}−\bold{k}, \bold{c}=\bold{i}−2\bold{k}$ (Solución) 130. $\bold{a}=\bold{i}−\bold{j}+\bold{k}, \bold{b}=\bold{j}+3\bold{k}, \bold{c}=−\bold{i}+2\bold{j}−4\bold{k}$
 Para los siguientes ejercicios, se dan los vectores bidimensionales $\bold{a}$ y $\bold{b}$.
Para los siguientes ejercicios, se dan los vectores bidimensionales $\bold{a}$ y $\bold{b}$.
131. [T] $\bold{a}=\lang 3,−1\rang , \bold{b}=\lang −4,0\rang$ (Solución) 132. [T] $\bold{a}=\lang 2,1\rang, \bold{b}=\lang −1,3\rang$ 133. $\bold{u}=3\bold{i}, \bold{v}=4\bold{i}+4\bold{j}$ (Solución) 134. $\bold{u}=5\bold{i}, \bold{v}=−6\bold{i}+6\bold{j}$
 Para los siguientes ejercicios, encuentra la medida del ángulo entre los vectores tridimensionales $\bold{a}$ y $\bold{b}$. Expresa la respuesta en radianes redondeados a dos decimales, si no es posible expresarla exactamente.
Para los siguientes ejercicios, encuentra la medida del ángulo entre los vectores tridimensionales $\bold{a}$ y $\bold{b}$. Expresa la respuesta en radianes redondeados a dos decimales, si no es posible expresarla exactamente.
 Para los siguientes ejercicios, determine si los vectores dados son ortogonales.
Para los siguientes ejercicios, determine si los vectores dados son ortogonales.
141. $\bold{a} = \lang x, y\rang, \bold{b} = \lang − y, x\rang$, donde x e y son números reales distintos de cero (Solución) 142. $\bold{a} = \lang x, x\rang, \bold{b} = \lang − y, y\rang$, donde x e y son números reales distintos de cero 143. $\bold{a} = 3\bold{i} − \bold{j} − 2\bold{k}, \bold{b} = −2\bold{i} − 3\bold{j} + \bold{k}$ (Solución) 144. $\bold{a} = \bold{i} − \bold{j}, \bold{b} = 7\bold{i} + 2\bold{j} − \bold{k}$
145. Encuentra todos los vectores bidimensionales a ortogonales al vector $\bold{b} = \lang 3,4\rang$. Expresa la respuesta en forma de componente. (Solución) 146. Encuentra todos los vectores bidimensionales a ortogonales al vector $\bold{b} = \lang 5, −6\rang$. Expresa la respuesta utilizando vectores unitarios estándar. 147. Determina todos los vectores tridimensionales u ortogonales al vector $\bold{v} = \lang 1,1,0\rang$. Expresa la respuesta utilizando vectores unitarios estándar. (Solución) 148. Determina todos los vectores tridimensionales u ortogonales al vector $\bold{v} = \bold{i} − \bold{j} − \bold{k}$. Expresa la respuesta en forma de componente. 149. Determina el número real $\alpha$ de manera que los vectores $\bold{a} = 2\bold{i} + 3\bold{j}$ y $\bold{b} = 9\bold{i} + \alpha\bold{j}$ sean ortogonales. (Solución) 150. Determina el número real $\alpha$ de manera que los vectores $\bold{a} = −3\bold{i} + 2\bold{j}$ y $\bold{b} = 2\bold{i} + \alpha\bold{j}$ sean ortogonales. 151. [T] Considera los puntos $P (4,5)$ y $Q (5, −7)$. (Solución)
153. Determina la medida del ángulo A en el triángulo ABC, donde $A (1,1,8), B (4, −3, −4)$ y $C (−3,1,5)$. Expresa tu respuesta en grados redondeados a dos decimales. (Solución) 154. Considera los puntos $P (3,7, −2)$ y $Q (1,1, −3)$. Determina el ángulo entre los vectores $\overrightarrow{OP}$ y $\overrightarrow{OQ}$. Expresa la respuesta en grados redondeados a dos decimales.
 Para los siguientes ejercicios, determina qué pares (si los hay) de los siguientes vectores son ortogonales.
Para los siguientes ejercicios, determina qué pares (si los hay) de los siguientes vectores son ortogonales.
155. $\bold{u} = \lang 3,7, −2\rang, \bold{v} = \lang 5, −3, −3\rang, \bold{w} = \lang 0,1, −1\rang$ (Solución) 156. $\bold{u} = \bold{i} − \bold{k}, \bold{v} = 5\bold{j} − 5\bold{k}, \bold{w} = 10\bold{j}$ 157. Usa vectores para mostrar que un paralelogramo con diagonales iguales es un cuadrado. 158. Usa vectores para mostrar que las diagonales de un rombo son perpendiculares. 159. Demuestre que $\bold{u}\cdot(\bold{v} + \bold{w}) = \bold{u}\cdot\bold{v} + \bold{u}\cdot\bold{w}$ es verdadero para cualquier vector $\bold{u}, \bold{v}$ y $\bold{w}$. 160. Verifica la identidad $\bold{u}\cdot(\bold{v} + \bold{w}) = \bold{u}\cdot\bold{v}+ \bold{u}\cdot\bold{w}$ para los vectores $\bold{u} = \lang 1,0,4\rang, \bold{v} = \lang − 2,3,5\rang$, y $\bold{w} = \lang 4, −2, 6\rang$.
 Para los siguientes problemas, se proporciona el vector $\bold{u}$.
Para los siguientes problemas, se proporciona el vector $\bold{u}$.
161. $\bold{u} = \lang 2,2,1\rang$ (Solución) 162. $\bold{u} = \bold{i} − 2\bold{j} + 2\bold{k}$
163. $\bold{u} = \lang − 1,5,2\rang$ (Solución) 164. $\bold{u} = \lang 2,3,4\rang$ 165. Considere $\bold{u} = \lang a, b, c\rang$ un vector tridimensional distinto de cero. Supón que $cos\alpha, cos\beta$ y $cos\gamma$ sean los cosenos directores de $\bold{u}$. Demuestra que $cos2\alpha + cos2\beta + cos2\gamma = 1$. 166. Determina los cosenos directores del vector $\bold{u} = \bold{i} + 2\bold{j} + 2\bold{k}$ y demuestra que satisfacen $cos2\alpha + cos2\beta + cos2\gamma = 1$.
 Para los siguientes ejercicios, se dan los vectores $\bold{u}$ y $\bold{v}$.
Para los siguientes ejercicios, se dan los vectores $\bold{u}$ y $\bold{v}$.
167. $\bold{u}=5\bold{i}+2\bold{j}, \bold{v}=2\bold{i}+3\bold{j}$ (Solución) 168. $\bold{u}=\lang −4,7\rang, \bold{v}=\lang3,5\rang$ 169. $\bold{u}=3\bold{i}+2\bold{k}, \bold{v}=2\bold{j}+4\bold{k}$ (Solución) 170. $\bold{u}=\lang4,4,0\rang, \bold{v}=\lang0,4,1\rang$
171. Considera los vectores $\bold{u} = 4\bold{i} − 3\bold{j}$ y $\bold{v} = 3\bold{i} + 2\bold{j}$ (Solución).
172. Considera los vectores $\bold{u} = 2\bold{i} + 4\bold{j}$ y $\bold{v} = 4\bold{j} + 2\bold{k}$
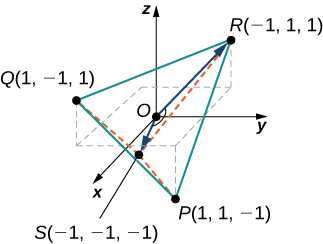 174. [T] Encuentra los vectores que unen el centro de un reloj a las horas 1:00, 2:00 y 3:00. Supón que el reloj es circular con un radio de 1 unidad.
174. [T] Encuentra los vectores que unen el centro de un reloj a las horas 1:00, 2:00 y 3:00. Supón que el reloj es circular con un radio de 1 unidad.
175. Encuentra el trabajo realizado por la fuerza $\bold{F} = \lang 5,6, −2\rang$ (medido en Newtons) que mueve una partícula desde el punto $P (3, −1,0)$ al punto $Q (2,3,1)$ a lo largo de una línea recta (la distancia se mide en metros) (Solución). 176. [T] Se tira de un trineo ejerciendo una fuerza de 100 N sobre una cuerda que forma un ángulo de 25° con la horizontal. Encuentra el trabajo realizado al tirar del trineo 40 m. (Redondea la respuesta a un decimal).
177. [T] Un padre tira de su hijo en un trineo en un ángulo de 20° con la horizontal con una fuerza de 25 lb (ver la siguiente imagen). Tira del trineo en un camino recto de 50 pies. ¿Cuánto trabajo hizo el hombre que tira del trineo? (Redondea la respuesta al entero más cercano) (Solución).
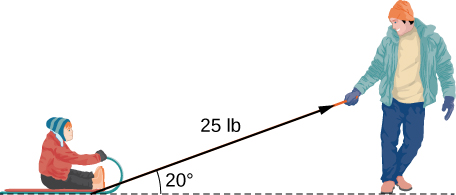
178. [T] Se remolca un automóvil con una fuerza de 1600 N. La cuerda utilizada para tirar del automóvil forma un ángulo de 25° con la horizontal. Encuentra el trabajo realizado en remolcar el coche 2 km. Expresa la respuesta en julios ($1J = 1N\cdot m$) redondeada al entero más cercano. 179. [T] Un barco navega hacia el norte con la ayuda de un viento que sopla en una dirección de N30°E con una magnitud de 500 lb. ¿Cuánto trabajo realiza el viento cuando el barco se mueve 100 pies? (Redondea la respuesta a dos decimales) (Solución).
180. El vector $\bold{p} = \lang 150,225,375\rang$ representa el precio de ciertos modelos de bicicletas que se venden en una tienda de bicicletas. El vector $\bold{n} = \lang 10,7,9\rang$ representa el número de bicicletas vendidas de cada modelo, respectivamente. Calcula el producto punto $\bold{p}\cdot\bold{n}$ y establece su significado. 181. [T] Dos fuerzas $\bold{F_1}$ y $\bold{F_2}$ están representadas por vectores con puntos iniciales que están en el origen. La primera fuerza tiene una magnitud de 20 lb y el punto final del vector es el punto $P (1,1,0)$ (Solución).
La segunda fuerza tiene una magnitud de 40 lb y el punto final de su vector es el punto $Q (0,1,1)$. Sea $\bold{F}$ la fuerza resultante de las fuerzas $\bold{F_1}$ y $\bold{F_2}$.
b. Usa un CAS para ver el vector de velocidad instantánea y el plano normal en el punto P y la trayectoria de la partícula.
Imagina a un mecánico girando una llave para apretar un perno. El mecánico aplica una fuerza al final de la llave. Esto crea rotación, o torque, que aprieta el perno. Podemos usar vectores para representar la fuerza aplicada por el mecánico y la distancia (radio) desde el perno hasta el final de la llave. Entonces, podemos representar el par mediante un vector orientado a lo largo del eje de rotación. Ten en cuenta que el vector de torque es ortogonal tanto para el vector de fuerza como para el vector de radio.
En esta sección, desarrollaremos una operación llamada producto cruz, que nos permite encontrar un vector ortogonal a dos vectores dados. Calcular el par es una aplicación importante de los productos cruz, y examinamos el par con más detalle más adelante en la sección.
El producto punto es una multiplicación de dos vectores que da como resultado un escalar. En esta sección, presentamos un producto de dos vectores que genera un tercer vector ortogonal a los dos primeros. Considera cómo podríamos encontrar ese vector. Sean $\bold{u} = \lang u_1, u_2, u_3\rang$ y $\bold{v} = \lang v_1, v_2, v_3\rang$ vectores distintos de cero. Queremos encontrar un vector $\bold{w} = \lang w_1, w_2, w_3\rang$ ortogonal a $\bold{u}$ y $\bold{v}$, es decir, queremos encontrar $\bold{w}$ tal que $\bold{u}\cdot\bold{w} = 0$ y $\bold{v}\cdot\bold{w} = 0$. Por lo tanto, $w_1, w_2$ y $w_3$ deben satisfacer
$$u_1w_1+u_2w_2+u_3w_3=0\\ v_1w_1+v_2w_2+v_3w_3=0$$Si multiplicamos la ecuación superior por $v_3$ y la ecuación inferior por $u_3$ y restamos, podemos eliminar la variable $w_3$, que da
$$(u_1v_3 − v_1u_3) w_1 + (u_2v_3 − v_2u_3) w_2 = 0$$Si seleccionamos
$$w_1 = u_2v_3 − u_3v_2\\ w_2 = -(u_1v_3 − u_3v_1)$$obtenemos un posible vector de solución. Sustituir estos valores nuevamente en las ecuaciones originales da
$$w_3 = u_1v_2 − u_2v_1$$Es decir, el vector
$$\bold{w} = \lang {u}_2 {v}_3 − {u}_3 {v}_2, - ({u}_1{v}_3 − {u}_3{v}_1), {u}_1{v}_2 − {u}_2{v}_1\rang$$es ortogonal a $\bold{u}$ y $\bold{v}$, lo que nos lleva a definir la siguiente operación, llamada producto cruz.
Por la forma en que hemos desarrollado $\bold{u} \times \bold{v}$, debe quedar claro que el producto cruz es ortogonal tanto para $\bold{u}$ como para $\bold{v}$. Sin embargo, nunca está de más comprobarlo. Para mostrar que $\bold{u} \times \bold{v}$ es ortogonal a $\bold{u}$, calculamos el producto escalar de $\bold{u}$ y $\bold{u} \times \bold{v}$.
$$\begin{aligned} \bold{u}\cdot(\bold{u} \times \bold{v}) &= \lang {u}_1, {u}_2, {u}_3\rang\cdot \lang {u}_2{v}_3−{u}_3{v}_2, −{u}_1{v}_3 + {u}_3{v}_1,{u}_1{v}_2−{u}_2{v}_1\rang\\ &= {u}_1({u}_2{v}_3 − {u}_3{v}_2) + {u}_2(−{u}_1{v}_3 + {u}_3{v}_1) + {u}_3({u}_1{v}_2−{u}_2{v}_1)\\ &= {u}_1{u}_2{v}_3 − {u}_1{u}_3{v}_2 − {u}_1{u}_2{v}_3 + {u}_2{u}_3{v}_1 + {u}_1{u}_3{v}_2 − {u}_2{u}_3{v}_1\\ &= ({u}_1{u}_2{v}_3 − {u}_1{u}_2{v}_3) + (−{u}_1{u}_3{v}_2 + {u}_1{u}_3{v}_2) + ({u}_2{u}_3{v}_1 − {u}_2{u}_3{v}_1)\\ &= 0 \end{aligned}$$
De manera similar, podemos mostrar que el producto cruz también es ortogonal a $\bold{v}$.
 |
Encontrar un producto cruz |
Sean $\bold{p} = \lang − 1,2,5\rang$ y $\bold{q} = \lang 4,0, −3\rang$ (Figura 2.53). Encuentra $\bold{u} \times \bold{v}$.

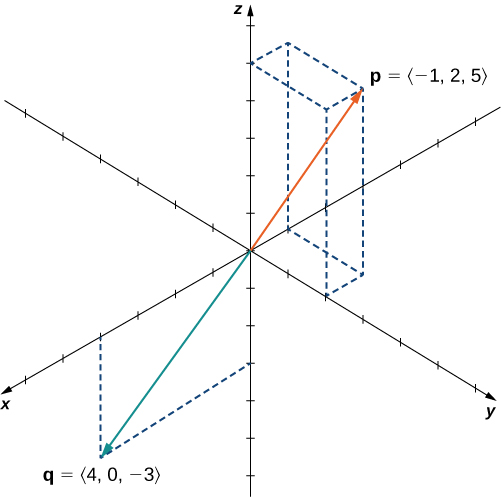
Figura 2.53. Encontrar un producto cruz para dos vectores dados.
En la siguiente escena interactiva (adaptación de una escena del libro Geometría analítica del espacio), puedes verificar la ortogonalidad de los vectores $\color{Red}\bold{p}$ y $\color{Green}\bold{q}$ con el producto cruz $\color{Blue}\bold{p}\times\bold{q}$. Usa la barra de escala para apreciar el vector azul. Puedes modificar los valores de $\bold{p}$ y $\bold{q}$ para hallar otros productos vectoriales.
Prueba que si $\color{Red}\bold{p}$ y $\color{Green}\bold{q}$ sen encuentran en el plano XY, entonces $\color{Blue}\bold{p}\times\bold{q}$ irá en dirección Z; por ejemplo, $\color{Red}\bold{p} = \lang 3,0,0\rang$ y $\color{Green}\bold{q} = \lang 1,3,0 \rang$, tendrá como producto cruz $\color{Blue}\bold{p}\times\bold{q} = \lang 0,0,9 \rang$; es decir $\color{Blue}9\bold{k}$
Aunque puede no ser obvio en la Ecuación 2.9, la dirección de $\bold{u}\times\bold{v}$ viene dada por la regla de la mano derecha. Si levantamos la mano derecha con los dedos apuntando en la dirección de $\bold{u}$, luego doblamos los dedos hacia el vector $\bold{v}$, el pulgar apunta en la dirección del producto cruz, como se muestra en la figura 2.54.
Después de la figura, observa la escena interactiva (en pantalla ampliada es mejor) en la que se explica la regla de la mano derecha en "Física Estática", para el caso de torques o momentos.
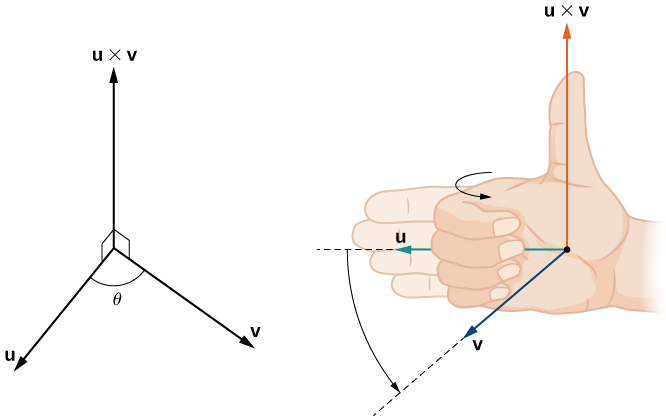
Figura 2.54. La dirección de $\bold{u}\times\bold{v}$ está determinada por la regla de la mano derecha.
Observa lo que esto significa para la dirección de $\bold{v}\times\bold{u}$. Si aplicamos la regla de la mano derecha a $\bold{v}\times\bold{u}$, comenzamos con nuestros dedos apuntando en la dirección de $\bold{v}$, luego doblamos nuestros dedos hacia el vector $\bold{u}$. En este caso, el pulgar apunta en la dirección opuesta de $\bold{u}\times\bold{v}$. (¡Intentalo!)
 |
Anticommutatividad del producto cruz |
Sean $\bold{u} = \lang 0,2,1\rang$ y $\bold{v} = \lang 3, −1,0\rang$. Calcula $\bold{u}\times\bold{v}$ y $\bold{v}\times\bold{u}$ y grafícalos.

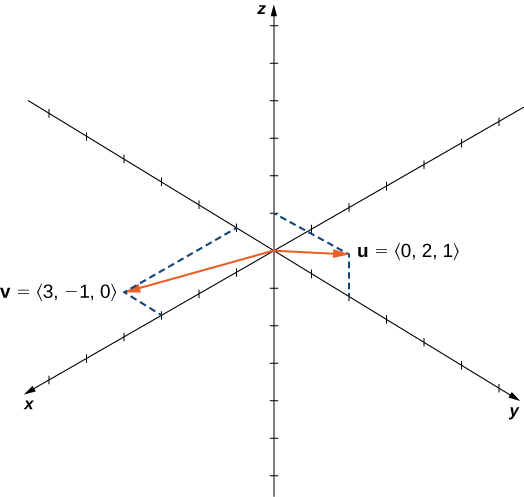
Figura 2.55. ¿Los productos cruz $\bold{u}\times\bold{v}$ y $\bold{v}\times\bold{u}$ están en la misma dirección?
Los productos cruz de los vectores unitarios $\bold{i}, \bold{j}$ y $\bold{k}$ pueden ser útiles para simplificar algunos cálculos. Una aplicación directa de la definición muestra que
$$\bold{i}\times\bold{i} = \bold{j}\times\bold{j} = \bold{k}\times\bold{k} = \bold{0}$$El producto cruz de dos vectores es un vector, por lo que cada uno de estos productos da como resultado el vector cero, no el escalar 0. Verifica los cálculos por tu cuenta.
Además, debido a que el producto cruz de dos vectores es ortogonal a cada uno de estos vectores, sabemos que el producto cruz de $\bold{i}$ y $\bold{j}$ es paralelo a $\bold{k}$. Del mismo modo, el producto vectorial de $\bold{i}$ y $\bold{k}$ es paralelo a $\bold{j}$, y el producto vectorial de $\bold{j}$ y $\bold{k}$ es paralelo a $\bold{i}$. Podemos usar la regla de la mano derecha para determinar la dirección de cada producto. Entonces tenemos
| $$\begin{aligned} \bold{i}\times\bold{j} &= \bold{k}\\ \bold{j}\times\bold{k} &= \bold{i}\\ \bold{k}\times\bold{i} &= \bold{j} \end{aligned}$$ | $$\begin{aligned} \bold{j}\times\bold{i} &= -\bold{k}\\ \bold{k}\times\bold{j} &= -\bold{i}\\ \bold{i}\times\bold{k} &= -\bold{j} \end{aligned}$$ |
 |
Producto cruz de vectores unitarios estándar |
Encuentra $\bold{i}\times(\bold{j}\times\bold{k})$

Como hemos visto, el producto punto a menudo se llama producto escalar porque da como resultado un escalar. El producto cruz da como resultado un vector, por lo que a veces se denomina producto vectorial. Estas operaciones son versiones de multiplicación de vectores, pero tienen propiedades y aplicaciones muy diferentes. Exploremos algunas propiedades del producto cruz. Probamos solo algunos de ellos. Las pruebas de las otras propiedades se dejan como ejercicios.
| $\text{i.}\\\text{ii.}\\\text{iii.}\\\text{iv.}\\\text{v.}\\\text{vi.}$ | $\begin{aligned} \bold{u}\times\bold{v} &= -\bold{v}\times\bold{u}\; \text{(Anticommutativa)}\\ \bold{u}\times(\bold{v}+\bold{w}) &= \bold{u}\times\bold{v} + \bold{u}\times\bold{w}\;\text{(Distributiva)}\\ c(\bold{u}\times\bold{v}) &= (c\bold{u})\times\bold{v} = \bold{u}\times(c\bold{v})\\ \bold{u}\times\bold{0} &= \bold{0}\times\bold{u}\;\text{(Producto cruz del vector cero)}\\ \bold{v}\times\bold{v} &= \bold{0}\;\text{Producto de un vector consigo mismo}\\ \bold{u}\cdot (\bold{v}\times\bold{w}) &= (\bold{u}\times\bold{v})\cdot\bold{w}\;\text{(Triple producto escalar)} \end{aligned}$ |
Prueba
Para la propiedad i., queremos demostrar $\bold{u}\times\bold{v} = -(\bold{v}\times\bold{u})$. Tenemos
A diferencia de la mayoría de las operaciones que hemos visto, el producto cruz no es conmutativo. Esto tiene sentido si pensamos en la regla de la mano derecha.
La propiedad iv. se deduce directamente de la definición del producto cruz. Tenemos
$$\begin{aligned} \bold{u}\times\bold{0} &= \lang u_2\cdot 0−u_3\cdot 0,−(u_2\cdot 0−u_3\cdot 0),u_1\cdot 0−u_2\cdot 0\rang\\ &= \lang 0,0,0\rang =\bold{0} \end{aligned}$$Entonces, por propiedad i., $\bold{0}\times\bold{u} = \bold{0}$. Recuerda que el producto escalar de un vector y el vector cero es el escalar 0, mientras que el producto cruz de un vector con el vector cero es el vector $\bold{0}$.
Propiedad vi. se parece a la propiedad asociativa, pero ten en cuenta el cambio en las operaciones:
$$\begin{aligned} \bold{u}\cdot (\bold{v}\times\bold{w}) &= \bold{u}\cdot \lang v_2w_3−v_3w_2,−v_1w_3+v_3w_1,v_1w_2−v_2w_1\rang\\ &= u_1(v_2w_3−v_3w_2)+u_2(−v_1w_3+v_3w_1)+u_3(v_1w_2−v_2w_1)\\ &= u_1v_2w_3−u_1v_3w_2−u_2v_1w_3+u_2v_3w_1+u_3v_1w_2−u_3v_2w_1\\ &= (u_2v_3−u_3v_2)w_1+(u_3v_1−u_1v_3)w_2+(u_1v_2−u_2v_1)w_3\\ &= \lang u_2v_3−u_3v_2,u_3v_1−u_1v_3,u_1v_2−u_2v_1\rang\cdot\lang w_1,w_2,w_3\rang\\ &= (\bold{u}\times\bold{v})\cdot\bold{w} \end{aligned}$$
 |
Uso de las propiedades del producto cruz |
Usa las propiedades del producto cruz para calcular $(2\bold{i}\times 3\bold{j})\times \bold{j}$

Hasta ahora en esta sección, nos hemos preocupado por la dirección del vector $\bold{u}\times\bold{v}$, pero no hemos discutido su magnitud. Resulta que hay una expresión simple para la magnitud de $\bold{u}\times\bold{v}$ que involucra las magnitudes de $\bold{u}$ y $\bold{v}$, y el seno del ángulo entre ambos vectores.
Prueba
Sean $\bold{u} = \lang u_1, u_2, u_3\rang$ y $\bold{v} = \lang v_1, v_2, v_3\rang$ los vectores, y $\theta$ el ángulo entre ellos.
Luego
Tomando raíces cuadradas y observando que $\sqrt{sen^2\theta} = sen\theta$ para $0\le \theta \le 180^o$, tenemos el resultado deseado:
$$\|\bold{u}\times\bold{v}\| = \|\bold{u}\|\cdot\|\bold{v}\|sen\theta$$Esta definición del producto cruz nos permite visualizar o interpretar el producto geométricamente. Está claro, por ejemplo, que el producto cruz se define solo para vectores en tres dimensiones, no para vectores en dos dimensiones. En dos dimensiones, es imposible generar un vector simultáneamente ortogonal a dos vectores no paralelos.
 |
Cálculo del producto cruz |
Usa las propiedades del producto cruz para encontrar la magnitud del producto cruz de $\bold{u} = \lang 0,4,0\rang$ y $\bold{v} = \lang 0,0, −3\rang$.

Usar la ecuación 2.9 para encontrar el producto cruz de dos vectores es sencillo y presenta el producto cruz en la forma de componente. La fórmula, sin embargo, es complicada y difícil de recordar. Afortunadamente, tenemos una alternativa. Podemos calcular el producto cruz de dos vectores usando la notación determinante.
Un determinante 2 $\times$ 2 se define por
$$ \begin{vmatrix} a_1 & a_2 \\ b_1 & b_2 \end{vmatrix} = a_1b_2−b_1a_2$$Por ejemplo
$$ \begin{vmatrix} 3 & -2 \\ 5 & 1 \end{vmatrix} = 3(1)−5(−2)=3+10=13$$Un determinante 3 $\times$ 3 se define en términos de determinantes 2 $\times$ 2 de la siguiente manera:
$$ \begin{vmatrix} a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\\c_1 & c_2 & c_3\end{vmatrix} = a_1\begin{vmatrix} b_2 & b_3 \\ c_2 & c_3 \end{vmatrix} - a_2\begin{vmatrix} b_1 & b_3 \\ c_1 & c_3 \end{vmatrix} + a_3\begin{vmatrix} b_1 & b_2 \\ c_1 & c_2 \end{vmatrix}\tag{$2.10$}$$
La ecuación 2.10 se conoce como la expansión del determinante a lo largo de la primera fila. Observa que los multiplicadores de cada uno de los determinantes 2 $\times$ 2 en el lado derecho de esta expresión son las entradas en la primera fila del determinante 3 $\times$ 3. Además, cada uno de los determinantes 2 $\times$ 2 contiene las entradas del determinante 3 $\times$ 3 que quedarían si se tacharan la fila y la columna que contiene el multiplicador. Por lo tanto, para el primer término a la derecha, $a_1$ es el multiplicador, y el determinante 2 $\times$ 2 contiene las entradas que quedan si se tachan la primera fila y la primera columna del determinante 3 $\times$ 3. Del mismo modo, para el segundo término, el multiplicador es $a_2$, y el determinante 2 $\times$ 2 contiene las entradas que quedan si se tachan la primera fila y la segunda columna del determinante 3 $\times$ 3. Observa, sin embargo, que el coeficiente del segundo término es negativo. El tercer término se puede calcular de manera similar.
 |
Uso de la expansión a lo largo de la primerra fila para calcular un determinante 3 $\times$ 3 |

Técnicamente, los determinantes se definen solo en términos de matrices de números reales. Sin embargo, la notación determinante proporciona un dispositivo mnemónico útil para la fórmula del producto cruz.
 |
Usando la notación determinante para encontrar el producto cruz |
Sean $\bold{p} = \lang − 1,2,5\rang$ y $\bold{q} = \lang 4,0, −3\rang$. Encuentra $\bold{p}\times\bold{q}$.

El producto cruz es muy útil para varios tipos de cálculos, que incluyen encontrar un vector ortogonal a dos vectores dados, calcular áreas de triángulos y paralelogramos, e incluso determinar el volumen de la forma geométrica tridimensional hecha de paralelogramos conocidos como paralelepípedos.
Los siguientes ejemplos ilustran estos cálculos.
 |
Encontrar un vector unitario ortogonal a dos vectores dados |
Dados $\bold{a} = \lang 5,2, −1\rang$ y $\bold{b} = \lang 0, −1,4\rang$. Encuentra un vector unitario ortogonal a los vectores $\bold{a}$ y $\bold{b}$.

Para usar el producto cruz para calcular áreas, establecemos y probamos el siguiente teorema.
Demostramos que la magnitud del producto cruz es igual a la base por la altura del paralelogramo.
$$\begin{aligned} \text{Área de un paralelogramo} &= \text{base }\times\text{ altura}\\ &= \|\bold{u}\|(\|\bold{v}\|sen\theta)\\ &= \|\bold{u}\|\times\|\bold{v}\| \end{aligned}$$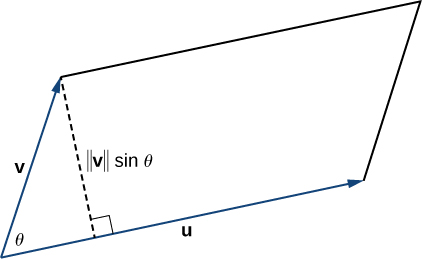
Figura 2.57. El paralelogramo con lados adyacentes $\bold{u}$ y $\bold{v}$ tiene base $\|\bold{u}\|$ y altura $\|\bold{v}\| sen\theta$.
 |
Encontrar el área de un triángulo |
Sean $P = (1,0,0), Q = (0,1,0)$ y $R = (0,0,1)$ los vértices de un triángulo (Figura 2.58). Encuentra su área
Figura 2.58. Encontrar el área de un triángulo usando el producto cruz.

Nuevamente recurrimos al libro Geometría analítica del espacio de María José García Cebrian y Elena E. Álvarez Sáiz, que nos ofrecen la siguiente escena interactiva:
Debido a que el producto cruz de dos vectores es un vector, es posible combinar el producto escalar y el producto cruz. El producto escalar de un vector con el producto cruz de otros dos vectores se llama producto triple escalar o producto mixto porque el resultado es escalar.
 |
Cálculo del producto triple escalar |
Sean $\bold{u} = \lang 1,3,5\rang, \bold{v} = \lang 2, −1,0\rang$ y $\bold{w}= \lang − 3,0, −1\rang$. Calcula el producto triple escalar $\bold{u}\cdot(\bold{v}\times\bold{w})$

Cuando creamos una matriz a partir de tres vectores, debemos tener cuidado con el orden en que los enumeramos. Si los enumeramos en una matriz en un orden y luego reorganizamos las filas, el valor absoluto del determinante permanece sin cambios. Sin embargo, cada vez que dos filas cambian de lugar, el determinante cambia de signo:
$$\begin{vmatrix} a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\\c_1 & c_2 & c_3\end{vmatrix} = d\;\;\begin{vmatrix} b_1 & b_2 & b_3\\ a_1 & a_2 & a_3\\c_1 & c_2 & c_3\end{vmatrix} = -d$$ $$\begin{vmatrix} b_1 & b_2 & b_3\\ c_1 & c_2 & c_3\\a_1 & a_2 & a_3\end{vmatrix} = d\;\;\begin{vmatrix} c_1 & c_2 & c_3\\ b_1 & b_2 & b_3\\a_1 & a_2 & a_3\end{vmatrix} = -d$$Verificar este hecho es sencillo, pero bastante desordenado. Echemos un vistazo a esto con un ejemplo:
$$\begin{aligned} \begin{vmatrix} 1 & 2 & 1\\ -2 & 0 & 3\\4 & 1 & -1\end{vmatrix} &= \begin{vmatrix} 0 & 3\\ 1 & -1\end{vmatrix} -2\begin{vmatrix} -2 & 3\\ 4 & -1\end{vmatrix} + \begin{vmatrix} -2 & 0\\ 4 & 1\end{vmatrix}\\ &= (0−3)−2(2−12)+(−2−0)=−3+20−2=15 \end{aligned}$$Cambiando las dos filas superiores tenemos
$$\begin{aligned} \begin{vmatrix} -2 & 0 & 3\\ 1 & 2 & 1\\4 & 1 & -1\end{vmatrix} &= -2\begin{vmatrix} 2 & 1\\ 1 & -1\end{vmatrix} +3\begin{vmatrix} 1 & 2\\ 4 & -1\end{vmatrix} + 3\begin{vmatrix} 1 & 2\\ 4 & 1\end{vmatrix}\\ &= −2(−2−1)+3(1−8)=6−21=−15 \end{aligned}$$Reorganizar los vectores en los productos triples es equivalente a reordenar las filas en la matriz del determinante. Sean $\bold{u} = u_1\bold{i} + u_2\bold{j} + u_3\bold{k}, \bold{v} = v_1\bold{i} + v_2\bold{j} + v_3\bold{k}$, y $\bold{w} = w_1\bold{i} + w_2\bold{j} + w_3\bold{k}$. Aplicando el cálculo de un producto triple escalar, tenemos
$$\bold{u}\cdot(\bold{v}\times\bold{w}) = \begin{vmatrix} u_1 & u_2 & u_3\\ v_1 & v_2 & v_3\\w_1 & w_2 & w_3\end{vmatrix}\;\;\text{ y }\;\\ \bold{u}\cdot(\bold{w}\times\bold{v}) = \begin{vmatrix} u_1 & u_2 & u_3\\ w_1 & w_2 & w_3\\v_1 & v_2 & v_3\end{vmatrix}$$Podemos obtener el determinante para calcular $\bold{u}\cdot(\bold{w}\times\bold{v})$ cambiando las dos filas inferiores de $\bold{u}\cdot(\bold{v}\times\bold{w})$. Por lo tanto, $\bold{u}\cdot(\bold{v}\times\bold{w}) = - \bold{u}\cdot(\bold{w}\times\bold{v})$
Siguiendo este razonamiento y explorando las diferentes formas en que podemos intercambiar variables en el producto triple escalar, se obtienen las siguientes identidades:
$$\bold{u}\cdot(\bold{v}\times\bold{w}) = - \bold{u}\cdot(\bold{w}\times\bold{v})$$ $$\bold{u}\cdot(\bold{v}\times\bold{w}) = \bold{v}\cdot(\bold{w}\times\bold{u}) = \bold{w}\cdot(\bold{u}\times\bold{v})$$Sean $\bold{u}$ y $\bold{v}$ dos vectores en posición estándar. Si $\bold{u}$ y $\bold{v}$ no son múltiplos escalares entre sí, entonces estos vectores forman lados adyacentes de un paralelogramo. Vimos que el área de este paralelogramo es $\|\bold{u}\times\bold{v}\|$. Ahora supongamos que agregamos un tercer vector $\bold{w}$ que no se encuentra en el mismo plano que $\bold{u}$ y $\bold{v}$ pero que aún comparte el mismo punto inicial. Luego, estos vectores forman tres bordes de un paralelepípedo, un prisma tridimensional con seis caras que son cada uno paralelogramos, como se muestra en la figura 2.59. El volumen de este prisma es el producto de la altura de la figura y el área de su base. El producto triple escalar de $\bold{u}$, $\bold{v}$ y $\bold{w}$ proporciona un método simple para calcular el volumen del paralelepípedo definido por estos vectores.
Observa que, como su nombre lo indica, el producto triple escalar produce un escalar. La fórmula de volumen que se acaba de presentar utiliza el valor absoluto de una cantidad escalar.
Figura 2.59. La altura del paralelepípedo viene dada por $\|proy_{\bold{v}\times\bold{w}}\bold{u}\|$.
El área de la base del paralelepípedo viene dada por $\|\bold{v}\times\bold{w}\|$. La altura de la figura viene dada por $\|proy_{\bold{v}\times\bold{w}}\bold{u}\|$. El volumen del paralelepípedo es el producto de la altura y el área de la base, por lo que tenemos
$$\begin{aligned} V &= \|proy_{\bold{v}\times\bold{w}}\bold{u}\|\|\bold{v}\times\bold{w}\bold{u}\|\\ &= \bigg|\frac{\bold{u}\cdot(\bold{v}\times\bold{w})}{\|\bold{v}\times\bold{w}\|}\bigg|\|\bold{v}\times\bold{w}\|\\ &= |\bold{u}\cdot(\bold{v}\times\bold{w})| \end{aligned}$$ |
Cálculo del volumen de un paralelepípedo |
Sean $\bold{u} = \lang − 1, −2,1\rang , \bold{v} = \lang 4,3,2\rang$ y $\bold{w}= \lang 0, −5, −2\rang$. Encuentra el volumen del paralelepípedo con bordes adyacentes $\bold{u}, \bold{v}$ y $\bold{w}$ (Figura 2.60).


Figura 2.60. Paralelepípedo con bordes adyacentes $\bold{u}, \bold{v}$ y $\bold{w}$
En la página siguiente, puedes interactuar con una escena de GeoGebra, diseñada por Juan Carlos Ponce Campuzano, en la que puedes cambiar los valores del los vectores $\bold{u}, \bold{v}$ y $\bold{w}$ moviendo sus puntos finales en la ventana tridimensional.
Interactúa con la escena en una pantalla ampliada (clic en la esquina superior derecha).
El producto cruz aparece en muchas aplicaciones prácticas en matemáticas, física e ingeniería. Examinemos algunas de estas aplicaciones aquí, incluida la idea del par, con el que comenzamos esta sección.
 |
Uso del producto triple escalar |
Usa el producto triple escalar para mostrar que los vectores $\bold{u} = \lang 2,0,5\rang, \bold{v} = \lang 2,2,4\rang$ y $\bold{w} = \lang 1, −1,3\rang$ son coplanares, es decir, muestra que estos vectores se encuentran en el mismo plano

 |
Hallando un vector ortogonal |
Solo uno y solo un plano puede pasar a través de cualquier conjunto de tres puntos no colineales. Encuentra un vector ortogonal al plano que contenga los puntos $P = (9, −3, −2), Q = (1,3,0)$ y $R = (- 2,5,0)$.

Hemos visto cómo usar el producto escalar triple y cómo encontrar un vector ortogonal a un plano. Ahora aplicamos el producto cruz a situaciones del mundo real.
Algunas veces una fuerza hace que un objeto gire. Por ejemplo, girar un destornillador o una llave crea este tipo de efecto de rotación, llamado torque.
Figura 2.61. El par o torque mide cómo una fuerza hace que un objeto gire.
Piensa en usar una llave para apretar un tornillo. El torque $\bold{\tau}$ aplicado al perno depende de cuán fuerte empujemos la llave (fuerza) y cuán lejos del mango apliquemos la fuerza (distancia). El par aumenta con una mayor fuerza sobre la llave a una mayor distancia del perno. Las unidades comunes de torque son el newton-metro o pie-libra. Aunque el torque es dimensionalmente equivalente al trabajo (tiene las mismas unidades), los dos conceptos son distintos. El par se usa específicamente en el contexto de rotación, mientras que el trabajo generalmente implica movimiento a lo largo de una recta.
 |
Calculando un torque |
Se aprieta un perno aplicando una fuerza de 6 N a una llave de 0,15 m (Figura 2.62). El ángulo entre la llave y el vector de fuerza es de 40°. Encuentra la magnitud del par sobre el centro del perno. Redondea la respuesta a dos decimales.

Figura 2.62. El torque describe la acción de torsión de la llave.
En Física Estática, el torque se suele llamar "momento de una fuerza", tal como se explica a continuación:
Observa otros ejemplos de aplicación de torques o momentos:

 Para los siguientes ejercicios, se dan los vectores $\bold{u}$ y $\bold{v}$.
Para los siguientes ejercicios, se dan los vectores $\bold{u}$ y $\bold{v}$.
183. $\bold{u}= \lang 2,0,0\rang, \bold{v}=\lang 2,2,0\rang$ (Solución) 184. $\bold{u}=\lang 3,2,−1\rang, \bold{v}=\lang 1,1,0\rang$ 185. $\bold{u}=2\bold{i}+3\bold{j}, \bold{v}=\bold{j}+2\bold{k}$ (Solución) 186. $\bold{u}=2\bold{j}+3\bold{k}, \bold{v}=3\bold{i}+\bold{k}$
187. Simplifica $(\bold{i}\times\bold{i}−2\bold{i}\times\bold{j}−4\bold{i}\times\bold{k}+3\bold{j}\times\bold{k})\times\bold{i}$ (Solución) 188. Simplifica $\bold{j}\times(\bold{k}\times\bold{j}+2\bold{j}\times\bold{i}−3\bold{j}\times\bold{j}+5\bold{i}\times\bold{k})$
 En los siguientes ejercicios, se dan los vectores $\bold{u}$ y $\bold{v}$. Encuentra el vector unitario $\bold{w}$ en la dirección del vector de producto cruz $\bold{u}\times\bold{v}$. Expresa su respuesta usando vectores unitarios estándar.
En los siguientes ejercicios, se dan los vectores $\bold{u}$ y $\bold{v}$. Encuentra el vector unitario $\bold{w}$ en la dirección del vector de producto cruz $\bold{u}\times\bold{v}$. Expresa su respuesta usando vectores unitarios estándar.
189. $\bold{u} = \lang 3, −1,2\rang, \bold{v} = \lang − 2,0,1\rang$ (Solución) 190. $\bold{u} = \lang 2,6,1\rang, \bold{v} = \lang 3,0,1\rang$ 191. $\bold{u} = \overrightarrow{AB}, \bold{v} = \overrightarrow{AC}$, donde $A (1,0,1), B (1, −1,3)$ y $C (0,0,5)$ (Solución) 192. $\bold{u} = \overrightarrow{OP}, \bold{v} = \overrightarrow{PQ}$, donde $P (−1,1,0)$ y $Q (0,2,1)$ 193. Determina el número real $\alpha$ tal que $\bold{u} \times \bold{v}$ e $\bold{i}$ son ortogonales, donde $\bold{u} = 3\bold{i} + \bold{j} − 5\bold{k}$ y $\bold{v} = 4\bold{i} − 2\bold{j} + \alpha\bold{k}$ (Solución) 194. Demuestra que $\bold{u} \times \bold{v}$ y $2\bold{i} − 14\bold{j} + 2\bold{k}$ no pueden ser ortogonales para ningún número real $\alpha$, donde $\bold{u} = \bold{i} + 7\bold{j} − \bold{k} y \bold{v} = \alpha\bold{i} + 5\bold{j} + \bold{k}$ 195. Demuestra que $\bold{u} \times \bold{v}$ es ortogonal a $\bold{u} + \bold{v}$ y $\bold{u} − \bold{v}$, donde $\bold{u}$ y $\bold{v}$ son vectores distintos de cero. 196. Demuestra que $\bold{v} \times \bold{u}$ es ortogonal a $(\bold{u}\cdot\bold{v}) (\bold{u} + \bold{v}) + \bold{u}$, donde $\bold{u}$ y $\bold{v}$ son vectores distintos de cero.
197. Calcula el determinante: $\begin{vmatrix} \bold{i} & \bold{j} & \bold{k}\\1 & -1 & 7\\2 & 0 & 3\end{vmatrix}$ (Solución)
198. Calcula el determinante: $\begin{vmatrix} \bold{i} & \bold{j} & \bold{k}\\0 & 3 & -4\\1 & 6 & -1\end{vmatrix}$
 Para los siguientes ejercicios, se dan los vectores $\bold{u}$ y $\bold{v}$. Utiliza la notación determinante para encontrar el vector ortogonal a los vectores $\bold{u}$ y $\bold{v}$.
Para los siguientes ejercicios, se dan los vectores $\bold{u}$ y $\bold{v}$. Utiliza la notación determinante para encontrar el vector ortogonal a los vectores $\bold{u}$ y $\bold{v}$.
199. $\bold{u} = \lang − 1,0, e^t\rang, \bold{v} = ⟨1, e^{−t}, 0\rang$, donde $t$ es un número real (Solución). 200. $\bold{u} = \lang 1,0, x\rang, \bold{v} = \lang \frac{2}{x}, 1,0\rang$, donde x es un número real distinto de cero. 201. Encuentra el vector $(\bold{a} − 2\bold{b}) \times\bold{c}$, donde $\bold{a} = \begin{vmatrix} \bold{i} & \bold{j} & \bold{k}\\2 & -1 & 5\\0 & 1 & 8\end{vmatrix}$, $\bold{b} = \begin{vmatrix} \bold{i} & \bold{j} & \bold{k}\\0 & 1 & 1\\2 & -1 & -2\end{vmatrix}$, y $\bold{c}=\bold{i}+\bold{j}+\bold{k}$ (Solución)
202. Encuentra el vector $\bold{c}\times(\bold{a} +3\bold{b})$, donde $\bold{a} = \begin{vmatrix} \bold{i} & \bold{j} & \bold{k}\\5 & 0 & 9\\0 & 1 & 0\end{vmatrix}$, $\bold{b} = \begin{vmatrix} \bold{i} & \bold{j} & \bold{k}\\0 & -1 & 1\\7 & 1 & -1\end{vmatrix}$, y $\bold{c}=\bold{i}-\bold{k}$
203. [T] Usa el producto cruz $\bold{u}\times\bold{v}$ para encontrar el ángulo agudo entre los vectores $\bold{u}$ y $\bold{v}$, donde $\bold{u} = \bold{i} + 2j$ y $\bold{v} = \bold{i} + \bold{k}$. Expresa la respuesta en grados redondeados al entero más cercano (Solución).
204. [T] Usa el producto cruz $\bold{u} \times \bold{v}$ para encontrar el ángulo obtuso entre los vectores $\bold{u}$ y $\bold{v}$, donde $\bold{u} = −\bold{i} + 3\bold{j} + \bold{k}$ y $\bold{v} = \bold{i} − 2\bold{j}$. Expresa la respuesta en grados redondeados al entero más cercano.
205. Usa el seno y el coseno del ángulo entre dos vectores distintos de cero $\bold{u}$ y $\bold{v}$ para demostrar la identidad de Lagrange: $\|\bold{u} \times \bold{v}\|^2 = \|\bold{u}\|^2\|\bold{v}\|^2 − (\bold{u}\cdot\bold{v})^2$ 206. Verifica la identidad de Lagrange $\|\bold{u} \times \bold{v}\|^2 = \|\bold{u}\|^2\|\bold{v}\|^2 − (\bold{u}\cdot\bold{v})^2$ para los vectores $\bold{u} = −\bold{i} + \bold{j} − 2\bold{k}$ y $\bold{v} = 2\bold{i} − \bold{j}$. 207. Los vectores distintos de cero $\bold{u}$ y $\bold{v}$ se denominan colineales si existe un escalar $\alpha$ distinto de cero tal que $\bold{v} = \alpha\bold{u}$. Demuestra que $\bold{u}$ y $\bold{v}$ son colineales si y solo si $\bold{u} \times \bold{v} = 0$. 208. Los vectores distintos de cero $\bold{u}$ y $\bold{v}$ se denominan colineales si existe un $\alpha$ escalar distinto de cero tal que $\bold{v} = \alpha\bold{u}$. Demuestra que los vectores $\overrightarrow{AB}$ y $A\overrightarrow{AC}$ son colineales, donde $A (4,1,0), B (6,5, −2)$ y $C (5,3, −1)$. 209. Encuentra el área del paralelogramo con lados adyacentes $\bold{u} = \lang 3,2,0\rang$ y $\bold{v} = \lang 0,2,1\rang$ (Solución). 210. Encuentra el área del paralelogramo con lados adyacentes $\bold{u} = \bold{i} + \bold{j}$ y $\bold{v} = \bold{i} + \bold{k}$.
211. Considera los puntos $A (3, −1,2), B (2,1,5)$, y $C (1, −2, −2)$ (Solución).
212. Considera los puntos $A (2, −3,4), B (0,1,2)$, y $C (−1,2,0)$.
 En los siguientes ejercicios, los vectores $\bold{u}, \bold{v}$ y $\bold{w}$ son dados.
En los siguientes ejercicios, los vectores $\bold{u}, \bold{v}$ y $\bold{w}$ son dados.
213. $\bold{u} = \bold{i} + \bold{j}, \bold{v} = \bold{j} + \bold{k}$, y $\bold{w} = \bold{i} +\bold{k}$ (Solución) 214. $\bold{u} = \lang − 3,5, −1\rang, \bold{v} = \lang 0,2, −2\rang$ y $\bold{w} = \lang 3,1,1\rang$ 215. Calcula los productos escalares triples $\bold{v}\cdot(\bold{u} \times \bold{w})$ y $\bold{w}\cdot(\bold{u} \times \bold{v})$, donde $\bold{u} = \lang 1,1,1\rang, \bold{v} = \lang 7,6,9\rang$ y $\bold{w} = \lang 4,2,7\rang$ (Solución). 216. Calcula los productos escalares triples $\bold{w}cdot(\bold{v} \times \bold{u})$ y $\bold{u}\cdot(\bold{w} \times \bold{v})$, donde $\bold{u} = \lang 4,2, −1\rang, \bold{v} = \lang 2,5, −3\rang$ y $\bold{w} = \lang 9,5, −10\rang$.
217. Encuentra los vectores $\bold{a}, \bold{b}$ y $\bold{c}$ con un producto escalar triple dado por el determinante $\begin{vmatrix} 1 & 2 & 3\\0 & 2 & 5\\8 & 9 & 2\end{vmatrix}$. Determina su producto triple escalar (Solución). 218. El producto triple escalar de los vectores $\bold{a}, \bold{b}$ y $\bold{c}$ está dado por el determinante $\begin{vmatrix} 0 & -2 & 1\\0 & 1 & 4\\1 & -3 & 7\end{vmatrix}$. Encuentra el vector $\bold{a}-\bold{b}+\bold{c}$
219. Considera el paralelepípedo con bordes $OA, OB$, y $OC$, donde $A (2,1,0), B (1,2,0)$ y $C (0,1, \alpha)$ (Solución).
220. Considera los puntos $A (\alpha, 0,0), B (0, \beta, 0)$, y $C (0,0, \gamma)$, con $\alpha$, $\beta$ y $\gamma$ números reales positivos.
221. Sean $\bold{u}, \bold{v}$, y $\bold{w}$ vectores tridimensionales y $c$ un número real. Demuestra las siguientes propiedades del producto cruz.
222. Demuestra que los vectores $\bold{u} = \lang 1,0, −8\rang, \bold{u} = \lang 0,1,6\rang$, y $\bold{w} = \lang − 1,9,3\rang$ satisfacen las siguientes propiedades del producto cruz.
223. Vectores distintos de cero $\bold{u}, \bold{v}$, y $\bold{w}$ se dice que son linealmente dependientes si uno de los vectores es una combinación lineal de los otros dos. Por ejemplo, existen dos números reales distintos de cero $\alpha$ y $\beta$, de modo que $\bold{w} = \alpha\bold{u} + \beta\bold{v}$. De lo contrario, los vectores se denominan linealmente independientes. Demuestra que $\bold{u}, \bold{v}$, y $\bold{w}$ son coplanarios si y solo si son linealmente dependientes. 224. Considera los vectores $\bold{u} = \lang 1,4, −7\rang, \bold{u} = \lang 2, −1,4\rang, \bold{w} = \lang 0, −9,18\rang$, y $\bold{p} = \lang 0, −9,17\rang$.
225. Considera los puntos $A (0,0,2), B (1,0,2), C (1,1,2)$ y $D (0,1,2)$. ¿Son los vectores $\overrightarrow{AB}, \overrightarrow{AC}$ y $\overrightarrow{AD}$ linealmente dependientes (es decir, uno de los vectores es una combinación lineal de los otros dos)? (Solución) 226. Demuestra que los vectores $\bold{i} + \bold{j}, \bold{i} − \bold{j}$ e $\bold{i} + \bold{j} + \bold{k}$ son linealmente independientes, es decir, existen dos números reales distintos de cero $\alpha$ y $\beta$, de modo que $\bold{i} + \bold{j} + \bold{k} = \alpha (\bold{i} + \bold{j}) + \beta (\bold{i} − \bold{j})$. 227. Sea $\bold{u} = \lang u_1, u_2\rang$ y $\bold{v} = \lang v_1, v_2\rang$ vectores bidimensionales. El producto cruz de los vectores $\bold{u}$ y $\bold{v}$ no está definido. Sin embargo, si los vectores se consideran tridimensionales $\tilde{\bold{u}} = \lang u_1, u_2,0\rang$ y $\tilde{\bold{v}} = \lang v1, v2,0\rang$, respectivamente, entonces, en este caso, podemos definir el producto cruz de $\tilde{\bold{u}}$ y $\tilde{\bold{v}}$. En particular, en notación determinante, el producto cruz de $\tilde{\bold{u}}$ y $\tilde{\bold{v}}$ viene dado por $$\tilde{\bold{u}}\times\tilde{\bold{v}} = \begin{vmatrix} \bold{i} & \bold{j} & \bold{k}\\u_1 & u_2 & 0\\v_1 & v_2 & 0\end{vmatrix}$$ Usa este resultado para calcular $(\bold{i}cos\theta + \bold{j}sen\theta) \times (\bold{i}sen\theta − \bold{j}cos\theta)$, donde $\theta$ es un número real (Solución).
228. Considera los puntos $P (2,1), Q (4,2)$ y $R (1,2)$.
229. Determina un vector de magnitud 10, perpendicular al plano que pasa por el eje $x$ y el punto $P (1,2,4)$ (Solución).
230. Determina un vector unitario perpendicular al plano que pasa por el eje $z$ y el punto $A (3,1, −2)$. 231. Considera $\bold{u}$ y $\bold{v}$ dos vectores tridimensionales. Si la magnitud del vector de producto cruz $\bold{u} \times\bold{v}$ es $k$ veces mayor que la magnitud del vector $\bold{u}$, demuestra que la magnitud de $\bold{v}$ es mayor o igual a $k$, donde $k$ es un número natural. 232. [T] Supón que se conocen las magnitudes de dos vectores distintos de cero $\bold{u}$ y $\bold{v}$. La función $f(θ) = \|\bold{u}\|\|\bold{v}\|sen\theta$ define la magnitud del vector producto cruz $\bold{u}\times\bold{v}$, donde $\theta\isin [0, \pi]$ es el ángulo entre $\bold{u}$ y $\bold{v}$
233. Encuentra todos los vectores $\bold{w} = \lang w_1, w_2, w_3\rang$ que satisfacen la ecuación $\lang 1,1,1\rang \times \bold{w} = \lang − 1, −1,2\rang$ (Solución).
234. Resuelve la ecuación $\bold{w} \times \lang 1,0, −1\rang = \lang 3,0,3\rang$, donde $\bold{w} = \lang w_1, w_2, w_3\rang$ es un vector distinto de cero con una magnitud de 3.
235. [T] Un mecánico utiliza una llave de 12 pulgadas para girar un perno. La llave hace un ángulo de 30° con la horizontal. Si el mecánico aplica una fuerza vertical de 10 lb en el mango de la llave, ¿cuál es la magnitud del torque en el punto $P$ (consulta la siguiente figura)? Expresa la respuesta en libras-pie redondeadas a dos decimales (Solución).
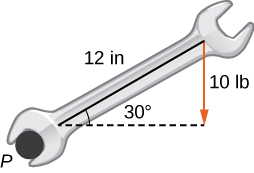
236. [T] Un niño aplica los frenos en una bicicleta aplicando una fuerza hacia abajo de 20 lb en el pedal cuando la manivela forma un ángulo de 40° con la horizontal (observa la siguiente figura). Encuentra el torque en el punto $P$. Expresa tu respuesta en libras-pie redondeadas a dos decimales.
237. [T] Encuentra la magnitud de la fuerza que debe aplicarse al extremo de una llave de 20 cm ubicada en la dirección positiva del eje $y$ si la fuerza se aplica en la dirección $\lang 0,1, −2\rang$ y produce $100\;N\cdot m$ de par al perno ubicado en el origen (Solución).
238. [T] ¿Cuál es la magnitud de la fuerza requerida para ser aplicada al extremo de una llave de 1 pie en un ángulo de $35^o$? para producir un par de $20\;N\cdot m$
239. [T] El vector fuerza $\bold{F}$ actuando sobre un protón con una carga eléctrica de $1.6 \times 10^{−19}C$ (en coulombs) que se mueve en un campo magnético $B$ donde el vector de velocidad $\bold{v}$ viene dado por $\bold{F} = 1.6 \times 10^{−19} (\bold{v}\times\bold{B})$ (aquí, $\bold{v}$ se expresa en metros por segundo, $\bold{B}$ está en tesla [T] y $\bold{F}$ está en newtons [N]). Encuentra la fuerza que actúa sobre un protón que se mueve en el plano $xy$ a una velocidad $\bold{v} = 10^5\bold{i} + 10^5\bold{j}$ (en metros por segundo) en un campo magnético dado por $\bold{B} = 0.3\bold{j}$ (Solución). 240. [T] El vector de fuerza $\bold{F}$ actuando sobre un protón con una carga eléctrica de $1.6 \times 10^{−19}C$ que se mueve en un campo magnético $\bold{B}$ donde el vector de velocidad $\bold{v}$ viene dado por $ \bold{F} = 1.6 \times 10^{−19} ( \bold{v} \times \bold{B})$ (aquí, $\bold{v}$ se expresa en metros por segundo , $\bold{B}$ en T y $\bold{F}$ en N). Si la magnitud de la fuerza $\bold{F}$ que actúa sobre un protón es $5.9 \times 10^{−17} N$ y el protón se mueve a una velocidad de 300 m/seg en el campo magnético $\bold{B}$ de magnitud 2.4 T, encuentra el ángulo entre el vector de velocidad $\bold{v}$ del protón y el campo magnético $\bold{B}$. Expresa la respuesta en grados redondeados al entero más cercano. 241. [T] Considera $r (t) = \lang cost, sent, 2t\rang$ el vector de posición de una partícula en el tiempo $t\isin [0,30]$, donde las componentes de $\bold{r}$ se expresan en centímetros y el tiempo en segundos. Sea $\overrightarrow{OP}$ el vector de posición de la partícula después de 1 segundo (Solución).
242. Un panel solar está montado en el techo de una casa. El panel puede considerarse posicionado en los puntos de coordenadas (en metros) $A (8,0,0), B (8,18,0), C (0,18,8)$ y $D (0,0,8)$ (ver la siguiente figura).

Por ahora, estamos familiarizados con la escritura de ecuaciones que describen una recta en dos dimensiones. Para escribir una ecuación para una recta, debemos conocer dos puntos en la recta, o debemos conocer la dirección de la recta y al menos un punto a través del cual pasa la recta. En dos dimensiones, usamos el concepto de pendiente para describir la orientación o dirección de una recta. En tres dimensiones, describimos la dirección de una recta usando un vector paralelo a la recta. En esta sección, examinamos cómo usar ecuaciones para describir rectas y planos en el espacio.
Primero exploremos lo que significa que dos vectores sean paralelos. Recuerda que los vectores paralelos deben tener la misma dirección o direcciones opuestas. Si dos vectores distintos de cero, $\bold{u}$ y $\bold{v}$, son paralelos, afirmamos que debe haber un escalar, $k$, tal que $\bold{u} = k\bold{v}$. Si $\bold{u}$ y $\bold{v}$ tienen la misma dirección, simplemente elige $k = \frac{\|\bold{u}\|}{\|\bold{v}\|}$. Si $\bold{u}$ y $\bold{v}$ tienen direcciones opuestas, elige $k = -\frac{\|\bold{u}\|}{\|\bold{v}\|}$. Tenga en cuenta que lo contrario se mantiene también. Si $u = kv$ para algún escalar $k$, entonces $\bold{u}$ y $\bold{v}$ tienen la misma dirección $(k \gt 0)$ o direcciones opuestas $(k \lt 0)$, entonces $\bold{u}$ y $\bold{v}$ son paralelas. Por lo tanto, dos vectores distintos de cero $\bold{u}$ y $\bold{v}$ son paralelos si y solo si $\bold{u} = k\bold{v}$ para algún $k$ escalar. Por convención, el vector cero $\bold{0}$ se considera paralelo a todos los vectores.
Como en dos dimensiones, podemos describir una recta en el espacio usando un punto en la recta y la dirección de la recta, o un vector paralelo, que llamamos el vector de dirección (Figura 2.63). Sea $L$ una recta en el espacio que pasa por el punto $P (x_0, y_0, z_0)$.
Sea $\bold{v} = \lang a, b, c\rang$ un vector paralelo a $L$. Luego, para cualquier punto en la recta $Q (x, y, z)$, $\overrightarrow{PQ}$ es paralela a $\bold{v}$. Por lo tanto, como acabamos de discutir, hay un escalar, $t$, tal que $\overrightarrow{PQ} = t\bold{v}$, que da
$$\begin{aligned} \overrightarrow{PQ} &= t\bold{v}\\ \lang x−x_0,y−y_0,z−z_0\rang &= t\lang a,b,c\rang\tag{$2.11$}\\ \lang x−x_0,y−y_0,z−z0_\rang &= \lang ta,tb,tc\rang \end{aligned}$$
Figura 2.63. El vector $\bold{v}$ es el vector de dirección para $\overrightarrow{PQ}$.
Usando operaciones vectoriales, podemos reescribir la ecuación 2.11 como
$$\begin{aligned} \lang x−x_0,y−y_0,z−z_0\rang &= \lang ta,tb,tc\rang\\ \lang x,y,z\rang - \lang x_0,y_0,z_0\rang &= t\lang a,b,c\rang\\ \lang x,y,z\rang &= \lang x_0,y_0,z_0\rang +t\lang a,b,c\rang \end{aligned}$$Configurando $\bold{r} = \lang x, y, z\rang$ y $\bold{r}_0 = \lang x_0, y, z_0\rang$, ahora tenemos la ecuación vectorial de una recta:
$$\bold{r}=\bold{r}_0+tv\tag{$2.12$}$$La ecuación 2.11 muestra que las siguientes ecuaciones son simultáneamente verdaderas: $x − x_0 = ta, y − y_0 = tb$ y $z − z_0 = tc$. Si resolvemos cada una de estas ecuaciones para las variables $x, y$, y $z$, obtenemos un conjunto de ecuaciones en las que cada variable se define en términos del parámetro $t$ y que, juntas, describen la recta. Este conjunto de tres ecuaciones forma un conjunto de ecuaciones paramétricas de una recta:
$$x=x_0+ta\;\;\;\;\;\;y=y_0+tb\;\;\;\;\;\;z=z_0+tc$$Si resolvemos cada una de las ecuaciones para $t$ asumiendo que $a, b$ y $c$ no son cero, obtenemos una descripción diferente de la misma recta:
$$\frac{x-x_0}{a}=t\;\;\;\;\;\;\frac{y-y_0}{b}=t\;\;\;\;\;\;\frac{z-z_0}{c}=t$$Como cada expresión es igual a $t$, todas tienen el mismo valor. Podemos establecerlos iguales entre sí para crear ecuaciones simétricas de una recta:
$$\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}$$Resumimos los resultados en el siguiente teorema.
Las siguientes ecuaciones paramétricas pueden describir una recta $L$ paralela al vector $\bold{v} = \lang a, b, c\rang$ y que pasa por el punto $P (x_0, y_0, z_0)$: $$x=x_0+ta,\;\;\;y=y_0+tb,\;\;\text{y}\;z=z_0+tc\tag{$2.13$}$$
Si las constantes $a, b$ y $c$ no son todas cero, entonces $L$ puede describirse mediante la ecuación simétrica de la recta:
$$\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}\tag{$2.14$}$$Las ecuaciones paramétricas de una recta no son únicas. El uso de un vector paralelo diferente o un punto diferente en la recta conduce a una representación equivalente diferente. Cada conjunto de ecuaciones paramétricas conduce a un conjunto relacionado de ecuaciones simétricas, por lo que se deduce que una ecuación simétrica de una recta tampoco es única.
 |
Ecuaciones de una recta en el espacio |
Encuentra las ecuaciones paramétricas y simétricas de la recta que pasa por los puntos $(1,4, −2)$ y $(−3,5,0)$

En la siguiente escena interactiva, puedes observar la recta que pasa por los puntos del ejercicio anterior. Puedes, además, modificar las coordenadas de los puntos y observar cómo el interactivo calcula las ecuaciones de la recta. Te puede servir, también, para verificar los resultados de algunos ejercicios propuestos al final de este apartado.
A veces no queremos la ecuación de una recta completa, solo un segmento de recta. En este caso, limitamos los valores de nuestro parámetro $t$.
Por ejemplo, sea $P (x_0, y_0, z_0)$ y $Q (x_1, y_1, z_1)$ puntos en una recta, y sean $\bold{p} = \lang x_0, y_0, z_0\rang$ y $\bold{q} = \lang x_1, y_1, z_1\rang$ los vectores de posición asociados. Además, sea $\bold{r} = \lang x, y, z\rang$. Queremos encontrar una ecuación vectorial para el segmento de recta entre $P$ y $Q$. Usando $P$ como nuestro punto conocido en la recta, y $\overrightarrow{PQ} = \lang x_1 − x_0, y_1 − y_0, z_1 − z_0\rang$ como la ecuación del vector direccional, con la ecuación 2.12 obtenenmos
$$\bold{r} = \bold{p} + t\big(\overrightarrow{PQ}\big)$$Usando las propiedades de los vectores:
$$\begin{aligned} \bold{r} = \bold{p} + t\big(\overrightarrow{PQ}\big)\\ &= \lang x_0,y_0,z_0\rang + t\lang x_1−x_0,y_1−y_0,z_1−z_0\rang\\ &= \lang x_0,y_0,z_0\rang + t(\lang x_1,y_1,z_1\rang − \lang x_0,y_0,z_0\rang)\\ &= \lang x_0,y_0,z_0\rang +t\lang x_1,y_1,z_1\rang −t\lang x_0,y_0,z_0\rang\\ &= (1−t)\lang x_0,y_0,z_0\rang+t\lang x_1,y_1,z_1\rang\\ &= (1−t)\bold{p}+t\bold{q} \end{aligned}$$Por lo tanto, la ecuación vectorial de la recta que pasa por $P$ y $Q$ es
$$\bold{r} = (1−t)\bold{p}+t\bold{q}$$Recuerda que no queríamos la ecuación de la recta completa, solo el segmento de recta entre $P$ y $Q$. Observa que cuando $t = 0$, tenemos $\bold{r} = \bold{p}$, y cuando $t = 1$, tenemos $\bold{r} = \bold{q}$. Por lo tanto, la ecuación vectorial del segmento de recta entre $P$ y $Q$ es
$$\bold{r}=(1−t)\bold{p}+t\bold{q} \;\;\;,\;\;\; 0\le t \le 1\tag{$2.15$}$$Volviendo a la ecuación 2.12, también podemos encontrar ecuaciones paramétricas para este segmento de recta. Tenemos
$$\begin{aligned} \bold{r} = \bold{p} + t\big(\overrightarrow{PQ}\big)\\ \lang x,y,z\rang &= \lang x_0,y_0,z_0\rang + t\lang x_1−x_0,y_1−y_0,z_1−z_0\rang\\ &= \lang x_0+t(x_1−x_0),y_0+t(y_1−y_0),z_0+t(z_1−z_0)\rang \end{aligned}$$Entonces, las ecuaciones paramétricas son:
$$x=x_0+t(x_1−x_0),\;\;y=y_0+t(y_1−y_0),\\z=z_0+t(z_1−z_0),\;\;\;0 \le t \le 1\tag{$2.16$}$$ |
Ecuaciones paramétricas de un segmento de recta |
Encuentra las ecuaciones paramétricas del segmento de recta entre los puntos $P (2,1,4)$ y $Q (3, −1,3)$

En la siguiente escena interactiva, puedes observar el segmento y, si lo deseas, cambiar los valores de los puntos.
Ya sabemos cómo calcular la distancia entre dos puntos en el espacio. Ahora ampliamos esta definición para describir la distancia entre un punto y una recta en el espacio. Existen varios contextos del mundo real cuando es importante poder calcular estas distancias.
Al construir una casa, por ejemplo, los constructores deben considerar los requisitos de "retroceso", cuando las estructuras o los accesorios deben estar a una cierta distancia de la recta de la propiedad. Los viajes aéreos ofrecen otro ejemplo. Las aerolíneas están preocupadas por las distancias entre las áreas pobladas y las rutas de vuelo propuestas.
Sea $L$ una recta en el plano y $M$ sea cualquier punto que no esté en la recta. Luego, definimos la distancia $d$ de $M$ a $L$ como la longitud del segmento de recta $\overline{MP}$, donde $P$ es un punto en $L$ tal que $\overline{MP}$ es perpendicular a $L$ (Figura 2.64).
Figura 2.64. La distancia desde el punto $M$ hasta la recta $L$ es la longitud de $\overline{MP}$.
Cuando buscamos la distancia entre una recta y un punto en el espacio, todavía se aplica la figura 2.64. Definimos la distancia como la longitud del segmento de recta perpendicular que conecta el punto con la recta. En el espacio, sin embargo, no hay una manera clara de saber qué punto de la recta crea un segmento de recta tan perpendicular, por lo que seleccionamos un punto arbitrario en la recta y utilizamos las propiedades de los vectores para calcular la distancia.
Por lo tanto, sea $P$ un punto arbitrario en la recta $L$ y sea $\bold{v}$ un vector de dirección para $L$ (Figura 2.65).
Figura 2.65. Los vectores $\overrightarrow{PM}$ y $\bold{v}$ forman dos lados de un paralelogramo con base $\|\bold{v}\|$ y altura $d$, que es la distancia entre una recta y un punto en el espacio.
Los vectores $\overrightarrow{PM}$ y $\bold{v}$ forman dos lados de un paralelogramo con área $\bigg\|\overrightarrow{PM} \times \bold{v}\bigg\|$. Usando una fórmula de geometría, el área de este paralelogramo también se puede calcular como el producto de su base y altura:
$$\bigg\|\overrightarrow{PM} \times \bold{v}\bigg\| = \|\bold{v}\|\cdot d$$Podemos usar esta fórmula para encontrar una fórmula general para la distancia entre una recta en el espacio y cualquier punto que no esté en la recta.
 |
Cálculo de la distancia de un punto a una recta |
Encuentra la distancia entre el punto $M = (1,1,3)$ y la recta $\frac{x − 3}{4} = \frac{y + 1}{2} = z − 3$.

Dadas dos rectas en el plano bidimensional, las rectas son iguales, son paralelas pero no iguales, o se cortan en un solo punto. En tres dimensiones, es posible un cuarto caso. Si dos rectas en el espacio no son paralelas, pero no se intersectan, entonces se dice que las rectas son rectas oblicuas (Figura 2.67).

Figura 2.67. En tres dimensiones, es posible que dos rectas no se crucen, incluso cuando tienen direcciones diferentes.
Para clasificar las rectas como paralelas pero no iguales, iguales, intersectantes u oblicuas, necesitamos saber dos cosas: si los vectores direccionales son paralelos y si las rectas comparten un punto (Figura 2.68).
Figura 2.68. Determina la relación entre dos rectas en función de si sus vectores direccionales son paralelos o si comparten un punto.
 |
Clasificación de rectas en el espacio |
Para cada par de rectas, determina si las rectas son iguales, paralelas pero no iguales, oblicuas o intersectadas.

Sabemos que una recta está determinada por dos puntos. En otras palabras, para dos puntos distintos, hay exactamente una recta que pasa a través de esos puntos, ya sea en dos dimensiones o en tres. Del mismo modo, dados tres puntos que no todos se encuentran en la misma recta, hay un plano único que pasa por estos puntos. Así como una recta está determinada por dos puntos, un plano está determinado por tres.
Esta puede ser la forma más sencilla de caracterizar un plano, pero también podemos usar otras descripciones. Por ejemplo, dadas dos rectas distintas que se intersectan, hay exactamente un plano que contiene ambas rectas.
Un plano también está determinado por una recta y cualquier punto que no se encuentre en la recta. Estas caracterizaciones surgen naturalmente de la idea de que un plano está determinado por tres puntos. Quizás la caracterización más sorprendente de un plano es en realidad la más útil.
Imagina un par de vectores ortogonales que comparten un punto inicial. Visualiza agarrando uno de los vectores y girándolo. A medida que gira, el otro vector gira y barre un plano. Aquí, describimos ese concepto matemáticamente. Sea $\bold{n} = \lang a, b, c\rang$ un vector y $P = (x_0, y_0, z_0)$ un punto. Entonces, el conjunto de todos los puntos $Q = (x, y, z)$ tal que $\overrightarrow{PQ}$ es ortogonal a $\bold{n}$ forma un plano (Figura 2.69). Decimos que $\bold{n}$ es un vector normal, o perpendicular al plano. Recuerda, el producto escalar de los vectores ortogonales es cero. Este hecho genera la ecuación vectorial de un plano: $\bold{n}\cdot\overrightarrow{PQ} = 0$. Reescribir esta ecuación proporciona formas adicionales de describir el plano:
$$\begin{aligned} \bold{n}\cdot\overrightarrow{PQ} &= 0\\ \lang a,b,c\rang\cdot\lang x−x_0,y−y_0,z−z_0\rang &= 0\\ a(x−x_0)+b(y−y_0)+c(z−z_0) &= 0 \end{aligned}$$
Figura 2.69. Dado un punto $P$ y un vector $\bold{n}$, el conjunto de todos los puntos $Q$ con $\overrightarrow{PQ}$ ortogonal a $\bold{n}$ forma un plano.
Como se describió anteriormente en esta sección, los tres puntos que no están todos en la misma recta determinan un plano. Dados tres de estos puntos, podemos encontrar una ecuación para el plano que contiene estos puntos.
 |
Escribir una ecuación de un plano dados tres puntos |
Escribe una ecuación para el plano que contiene los puntos $P = (1,1, −2), Q = (0,2,1)$ y $R = (- 1, −1,0)$ en forma estándar y general.

Las ecuaciones escalares de un plano varían según el vector normal y el punto elegido.
 |
Escribir una ecuación para un plano dado un punto y una recta |
Encuentra una ecuación del plano que pasa por el punto $(1,4,3)$ y contiene la recta dada por $x = \frac{y − 1}{2} = z + 1$.

Usa los resultados de los dos ejercicios para observar el plano resultante en la siguiente escena interactiva:
Ahora que podemos escribir una ecuación para un plano, podemos usar la ecuación para encontrar la distancia $d$ entre un punto $P$ y el plano. Se define como la distancia más corta posible desde $P$ hasta un punto en el plano.
Figura 2.70. Queremos encontrar la distancia más corta desde el punto $P$ al plano. Sea el punto $R $en el plano de modo que, para cualquier otro punto en el plano $Q$, $\big\|\overrightarrow{RP}\big\| \lt \big\|\overrightarrow{QP}\big\|$.
Así como encontramos la distancia bidimensional entre un punto y una recta calculando la longitud de un segmento de recta perpendicular a la recta, encontramos la distancia tridimensional entre un punto y un plano calculando la longitud de un segmento de recta perpendicular al plano. Sea $R$ el punto en el plano de modo que $\overrightarrow{RP}$ sea ortogonal al plano, y sea $Q$ un punto arbitrario en el plano. Luego, la proyección del vector $\overrightarrow{QP}$ sobre el vector normal describe el vector $\overrightarrow{RP}$, como se muestra en la Figura 2.70.
 |
Distancia entre un punto y un plano |
Encuentre la distancia entre el punto $P = (3,1,2)$ y el plano dado por $x − 2y + z = 5$ (observa la primera figura de la página siguiente).

Hemos discutido las diversas relaciones posibles entre dos rectas en dos dimensiones y tres dimensiones. Cuando describimos la relación entre dos planos en el espacio, solo tenemos dos posibilidades: los dos planos distintos son paralelos o se intersecan. Cuando dos planos son paralelos, sus vectores normales son paralelos. Cuando dos planos se intersectan, la intersección es una recta (Figura 2.71).
Figura 2.71. La intersección de dos planos no paralelos es siempre una recta.
Podemos usar las ecuaciones de los dos planos para encontrar ecuaciones paramétricas para la recta de intersección.
 |
Encontrar la recta de intersección para dos planos |
Encuentra ecuaciones paramétricas y simétricas para la recta formada por la intersección de los planos dados por $x + y + z = 0$ y $2x − y + z = 0$ (observa la siguiente figura).

Del libro Geometría analítica del espacio, hemos adaptado la siguiente escena interactiva. Observa que las ecuaciones corresponden al ejercicio anterior. Interactúa con la escena, de tal forma que construyas planos paralelos.
Además de encontrar la ecuación de la recta de intersección entre dos planos, es posible que necesitemos encontrar el ángulo formado por la intersección de dos planos.
Por ejemplo, los constructores que construyen una casa necesitan saber el ángulo donde se encuentran las diferentes secciones del techo para saber si el techo se verá bien y se drenará correctamente. Podemos usar vectores normales para calcular el ángulo entre los dos planos. Podemos hacer esto porque el ángulo entre los vectores normales es el mismo que el ángulo entre los planos. La figura 2.72 se muestra por qué esto es cierto.
Figura 2.72. El ángulo entre dos planos tiene la misma medida que el ángulo entre los vectores normales para los planos.
Podemos encontrar la medida del ángulo $\theta$θ entre dos planos de intersección al encontrar primero el coseno del ángulo, usando la siguiente ecuación:
$$cos\theta =\frac{|\bold{n}_1\cdot\bold{n}_2|}{\|\bold{n}_1\|\|\bold{n}_2\|}$$Entonces podemos usar el ángulo para determinar si dos planos son paralelos u ortogonales o si se intersectan en algún otro ángulo.
 |
Encontrar el ángulo entre dos planos |
Determina si cada par de planos es paralelo, ortogonal o ninguno. Si los planos se intersecan, pero no son ortogonales, encuentra la medida del ángulo entre ellos. Da la respuesta en radianes y redondea a dos decimales.

Cuando descubrimos que dos planos son paralelos, es posible que necesitemos encontrar la distancia entre ellos. Para encontrar esta distancia, simplemente seleccionamos un punto en uno de los planos. La distancia desde este punto al otro plano es la distancia entre los planos.
Anteriormente, presentamos la fórmula para calcular esta distancia en la ecuación 2.19:
$$d = \frac{\overrightarrow{QP}\cdot\bold{n}}{\|\bold{n}\|}$$donde $Q$ es un punto en el plano, $P$ es un punto que no está en el plano y $\bold{n}$ es el vector normal que pasa por el punto $Q$. Considera la distancia desde el punto $(x_0, y_0, z_0)$ al plano $ax + by + cz + k = 0$.
Sea $(x_1, y_1, z_1)$ cualquier punto del plano. Sustituyendo en la fórmula se obtiene
$$\begin{aligned} d &= \frac{|a(x_0−x_1)+b(y_0−y_1)+c(z_0−z_1)|}{\sqrt{a^2+b^2+c^2}}\\ &= \frac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}} \end{aligned}$$Establecemos este resultado formalmente en el siguiente teorema.
 |
Encontrar la distancia entre planos paralelos |
Encuentra la distancia entre los dos planos paralelos dada por $2x+y−z=2$ y $2x+y−z=8$.

Distancia entre dos rectas oblicuas
Figura 2.72. Las instalaciones de tuberías industriales a menudo cuentan con tuberías que funcionan en diferentes direcciones. ¿Cómo podemos encontrar la distancia entre dos tubos oblicuos?
Encontrar la distancia desde un punto a una recta o desde una recta a un plano parece un procedimiento bastante abstracto. Pero, si las rectas representan tuberías en una planta química o tubos en una refinería de petróleo o carreteras en una intersección de autopistas, confirmar que la distancia entre ellas cumple con las especificaciones puede ser importante y difícil de medir.
Una forma es modelar las dos tuberías como rectas, utilizando las técnicas de este capítulo, y luego calcular la distancia entre ellas. El cálculo implica formar vectores a lo largo de las direcciones de las rectas y usar tanto el producto cruz como el producto punto.
Las formas simétricas de dos rectas, $L_1$ y $L_2$, son
$$L_1: \frac{x-x_1}{a_1}= \frac{y-y_1}{b_1} = \frac{z-z_1}{c_1}$$ $$L_2: \frac{x-x_2}{a_2}= \frac{y-y_2}{b_2} = \frac{z-z_2}{c_2}$$Debes desarrollar una fórmula para la distancia $d$ entre estas dos rectas, en términos de los valores $a_1, b_1, c_1; a_2, b_2, c_2; x_1, y_1, z_1$; y $x_2, y_2, z-2$. La distancia entre dos rectas generalmente se toma como la distancia mínima, por lo que esta es la longitud de un segmento de recta o la longitud de un vector que es perpendicular a ambas rectas e intersecta ambas rectas.
Para minimizar el costo, planean instalar estos puntales en los puntos más cercanos entre tuberías inclinadas adyacentes. Debido a que tienen esquemas detallados de la estructura, pueden determinar las longitudes correctas de los puntales necesarios y, por lo tanto, fabricarlos y distribuirlos a los equipos de instalación sin perder un tiempo valioso haciendo mediciones. La estructura del marco rectangular tiene las dimensiones $4.0 \times 15.0 \times 10.0$ (altura, ancho y profundidad, medidas en metros). Un sector tiene una tubería que ingresa en la esquina inferior de la unidad de marco estándar y sale en la esquina diametralmente opuesta (la más alejada en la parte superior); llama a esto $L_1$. Un segundo tubo entra y sale en las dos esquinas inferiores opuestas diferentes; llama a esto $L_2$ (Figura 2.74).
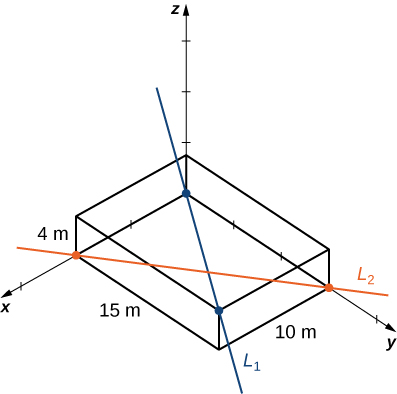
Figura 2.72. Dos tubos cruzan a través de una unidad de marco estándar.

 En los siguientes ejercicios, se dan los puntos $P$ y $Q$. Sea $L$ la recta que pasa por los puntos $P$ y $Q$.
En los siguientes ejercicios, se dan los puntos $P$ y $Q$. Sea $L$ la recta que pasa por los puntos $P$ y $Q$.
243. $P(−3,5,9), Q(4,−7,2)$ (Solución) 244. $P(4,0,5),Q(2,3,1)$ 245. $P(−1,0,5), Q(4,0,3)$ (Solución) 246. $P(7,−2,6), Q(−3,0,6)$
 Para los siguientes ejercicios, se dan el punto $P$ y el vector $\bold{v}$. Sea $L$ la recta que pasa por el punto $P$ con dirección $\bold{v}$.
Para los siguientes ejercicios, se dan el punto $P$ y el vector $\bold{v}$. Sea $L$ la recta que pasa por el punto $P$ con dirección $\bold{v}$.
247. $P(1,−2,3), \bold{v} = \lang 1,2,3\rang$ (Solución) 248. $P(3,1,5), \bold{v} = \lang 1,1,1\rang$
249. $P(3,1,5), \bold{v}=\overrightarrow{QR}$, donde $Q(2,2,3)$ y $R(3,2,3)$ (Solución) 250. $P(2,3,0), \bold{v}=\overrightarrow{QR}$, donde $Q(0,4,5)$ y $R(0,4,6)$
 Para los siguientes ejercicios, se proporciona la recta $L$.
Para los siguientes ejercicios, se proporciona la recta $L$.
251. $x = 1 + t, y = 3 + t, z = 5 + 4t, t\isin\Reals$ (Solución) 252. $−x = y + 1, z = 2$ 253. Encuentra la distancia entre el punto $A (−3,1,1)$ y la recta de ecuaciones simétricas $x = −y = −z$(Solución) 254. Encuentra la distancia entre el punto $A (4,2,5)$ y la recta de ecuaciones paramétricas $x = −1 − t, y = −t, z = 2, t\isin\Reals$
 Para los siguientes ejercicios, se dan las rectas $L_1$ y $L_2$.
Para los siguientes ejercicios, se dan las rectas $L_1$ y $L_2$.
255. $L_1: x = 1 + t, y = t, z = 2 + t, t\isin\Reals, L_2: x − 3 = y − 1 = z − 3$ (Solución) 256. $L_1: x = 2, y = 1, z = t, L_2: x = 1, y = 1, z = 2−3t, t\isin\Reals$
257. Demuestra que la recta que pasa por los puntos $P (3,1,0)$ y $Q (1,4, −3)$ es perpendicular a la recta con la ecuación $x = 3t, y = 3 + 8t, z = −7 + 6t, t \isin\Reals$ 258. ¿Son las rectas de ecuaciones $x = −2 + 2t, y = −6, z = 2 + 6t y x = −1 + t, y = 1 + t, z = t, t\isin\Reals$, perpendiculares entre sí? 259. Encuentra el punto de intersección de las rectas de ecuaciones $x = −2y = 3z y x = −5 − t, y = −1 + t, z = t − 11, t\isin\Reals$ (Solución) 260. Encuentra el punto de intersección del eje $x$ con la recta de ecuaciones paramétricas $x = 10 + t, y = 2−2t, z = −3 + 3t, t\isin\Reals
 Para los siguientes ejercicios, se dan las rectas $L_1$ y $L_2$. Determina si las rectas son iguales, paralelas pero no iguales, oblicuas o intersectadas.
Para los siguientes ejercicios, se dan las rectas $L_1$ y $L_2$. Determina si las rectas son iguales, paralelas pero no iguales, oblicuas o intersectadas.
261. $L_1: x = y − 1 = −z$ y $L_2: x − 2 = −y = \frac{z}{2}$ (Solución) 262. $L_1: x = 2t, y = 0, z = 3, t\isin\Reals$ y $L_2: x = 0, y = 8 + s, z = 7 + s, s\isin\Reals$ 263. $L_1: x = −1 + 2t, y = 1 + 3t, z = 7t, t\isin\Reals$ y $L_2: x − 1 = \frac{2}{3} (y − 4) = \frac{2}{7}z − 2$ (Solución) 264. $L_1: 3x = y + 1 = 2z$ y $L_2: x = 6 + 2t, y = 17 + 6t, z = 9 + 3t, t\isin\Reals$ 265. Considera la recta $L$ de ecuaciones simétricas $x − 2 = −y = \frac{z}{2}$ y punto $A (1,1,1)$ (Solución).
266. Considera la recta $L$ de ecuaciones paramétricas $x = t, y = 2t, z = 3, t\isin\Reals$.
 Para los siguientes ejercicios, se dan el punto $P$ y el vector $\bold{n}$.
Para los siguientes ejercicios, se dan el punto $P$ y el vector $\bold{n}$.
 Para los siguientes ejercicios, se da la ecuación de un plano.
Para los siguientes ejercicios, se da la ecuación de un plano.
271. [T] $4x + 5y + 10z − 20 = 0$ (Solución) 272. $3x + 4y − 12 = 0$ 273. $3x − 2y + 4z = 0$ (Solución) 274. $x + z = 0$ 275. Dado el punto $P (1,2,3)$ y el vector $\bold{n} = \bold{i} + \bold{j}$, encuentra el punto $Q$ en el eje $x$ tal que $\overrightarrow{PQ}$ y $\bold{n}$ sean ortogonales. (Solución) 276. Demuestra que no hay un plano perpendicular a $\bold{n} = \bold{i} + \bold{j}$ que pase por los puntos $P (1,2,3)$ y $Q (2,3,4)$. 277. Encuentra las ecuaciones paramétricas de la recta que pasa por el punto $P (−2,1,3)$ que es perpendicular al plano de la ecuación $2x − 3y + z = 7$. (Solución) 278. Encuentra las ecuaciones simétricas de la recta que pasa por el punto $P (2,5,4)$ que es perpendicular al plano de la ecuación $2x + 3y − 5z = 0$. 279. Demuestra que la recta $x − 12 = y + 13 = z − 24$ es paralela al plano $x − 2y + z = 6$. 280. Encuentra el número real $\alpha$ tal que la recta de ecuaciones paramétricas $x = t, y = 2 − t, z = 3 + t, t\isin\Reals$ es paralela al plano de la ecuación $\alpha x + 5y + z − 10 = 0$.
 Para los siguientes ejercicios, se dan los puntos $P, Q$ y $R$.
Para los siguientes ejercicios, se dan los puntos $P, Q$ y $R$.
281. $P (1,1,1), Q (2,4,3)$ y $R (−1, −2, −1)$ (Solución) 282. $P (−2,1,4), Q (3,1,3)$ y $R (−2,1,0)$ 283. Considera los planos de ecuaciones $x + y + z = 1$ y $x + z = 0$. (Solución)
284. Considera los planos de las ecuaciones $−y + z − 2 = 0$ y $x − y = 0$.
285. Encuentra la ecuación escalar del plano que pasa por el punto $P (−1,2,1)$ y es perpendicular a la recta de intersección de los planos $x + y − z − 2 = 0$ y $2x − y + 3z − 1 = 0$ (Solución).
286. Encuentra la ecuación general del plano que pasa por el origen y es perpendicular a la recta de intersección de los planos $−x + y + 2 = 0$ y $z − 3 = 0$. 287. Determina si la recta de ecuaciones paramétricas $x = 1 + 2t, y = −2t, z = 2 + t, t\isin\Reals$ intersecta el plano con la ecuación $3x + 4y + 6z − 7 = 0$. Si se intersecan, encuentra el punto de intersección (Solución). 288. Determina si la recta de ecuaciones paramétricas $x = 5, y = 4 − t, z = 2t, \isin\Reals$ interseca el plano con la ecuación $2x − y + z = 5$. Si se intersecan, encuentra el punto de intersección. 289. Encuentra la distancia desde el punto $P (1,5, −4)$ al plano de la ecuación $3x − y + 2z − 6 = 0$ (Solución). 290. Encuentra la distancia desde el punto $P (1, −2,3)$ al plano de la ecuación $(x − 3) +2 (y + 1) −4z = 0$.
 Para los siguientes ejercicios, se dan las ecuaciones de dos planos.
Para los siguientes ejercicios, se dan las ecuaciones de dos planos.
291. [T] $x + y + z = 0, 2x − y + z − 7 = 0$ (Solución) 292. $5x − 3y + z = 4, x + 4y + 7z = 1$ 293. $x − 5y − z = 1, 5x − 25y − 5z = −3$ (Solución) 294. [T] $x − 3y + 6z = 4, 5x + y − z = 4$
295. Demuestra que las rectas de ecuaciones $x = t, y = 1 + t, z = 2 + t, t\isin\Reals$ y $\frac{x}{2} = \frac{y − 1}{3} = z − 3$ son asimétricas, y encuentra la distancia entre ellas (Solución). 296. Demuestra que las rectas de ecuaciones $x = −1 + t, y = −2 + t, z = 3t, t\isin\Reals$ y $x = 5 + s, y = −8 + 2s, z = 7s, s\isin\Reals$ son oblicuas, y encontrar la distancia entre ellos. 297. Considera el punto $C (−3,2,4)$ y el plano de la ecuación $2x + 4y − 3z = 8$ (Solución).
299. Dos niños están jugando con una pelota. La niña tira la pelota al niño. La pelota viaja en el aire, se curva 3 pies hacia la derecha y cae 5 pies lejos de la niña (observa la siguiente figura). Si el plano que contiene la trayectoria de la pelota es perpendicular al suelo, encuentra su ecuación (Solución).
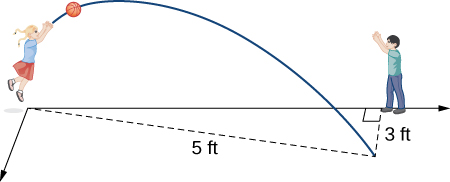
300. [T] John asigna $d$ dólares para consumir mensualmente tres bienes de precios a, $b$ y $c$. En este contexto, la ecuación presupuestaria se define como $ax + by + cz = d$, donde $x \ge 0, y \ge 0$ y $z \ge 0$ representan el número de artículos comprados de cada uno de los bienes. El conjunto de presupuesto viene dado por ${(x, y, z) | ax + por + cz \le d, x \ge 0, y \ge 0, z \ge 0}$, y el plano de presupuesto es la parte del plano de la ecuación $ax + por + cz = d$ para el cual $x \ge 0, y \ge 0, z \ge 0$. Considere $a = \text{\$}8, b = \text{\$}5, c = \text{\$}10$ y $d = \text{\$}500$. Usa un CAS para representar gráficamente el conjunto de presupuesto y el plano de presupuesto. Para z = 25, encuentra la nueva ecuación de presupuesto y grafica el conjunto de presupuesto en el mismo sistema de coordenadas.
301. [T] Considera $\bold{r}(t) = \lang sent, cost, 2t\rang$ el vector de posición de una partícula en el tiempo $t\isin [0,3]$, donde los componentes de $\bold{r}$ se expresan en centímetros y el tiempo se mide en segundos. Sea $overroghtarrow{OP}$ el vector de posición de la partícula después de 1 seg (Solución).
302. [T] Un panel solar está montado en el techo de una casa. El panel puede considerarse posicionado en los puntos de coordenadas (metros) $A (8,0,0), B (8,18,0), C (0,18,8)$ y $D (0,0, 8)$.
Hemos estado explorando vectores y operaciones de vectores en un espacio tridimensional, y hemos desarrollado ecuaciones para describir rectas, planos y esferas. En esta sección, usaremos nuestro conocimiento de planos y esferas, que son ejemplos de figuras tridimensionales llamadas superficies, para explorar una variedad de otras superficies que se pueden graficar en un sistema de coordenadas tridimensional.
La primera superficie que examinaremos es el cilindro. Aunque la mayoría de la gente piensa inmediatamente en una tubería hueca o una pajita de refresco cuando escuchan la palabra cilindro, aquí usamos el amplio significado matemático del término. Como hemos visto, las superficies cilíndricas no tienen que ser circulares. Un conducto de calentamiento rectangular es un cilindro, al igual que una estera de yoga enrollada, cuya sección transversal tiene forma de espiral.
En el plano de coordenadas bidimensional, la ecuación $x^2 + y^2 = 9$ describe una circunferencia centrada en el origen con radio $3$. En el espacio tridimensional, esta misma ecuación representa una superficie. Imagina copias de una cicunferencias apilada una encima de la otra centradas en el eje $z$ (Figura 2.75), formando un tubo hueco. Luego podemos construir un cilindro a partir del conjunto de rectas paralelas al eje $z$ que pasan a través de la circunferencia $x^2 + y^2 = 9$ en el plano $xy$, como se muestra en la figura. De esta manera, cualquier curva en uno de los planos de coordenadas puede extenderse para convertirse en una superficie.
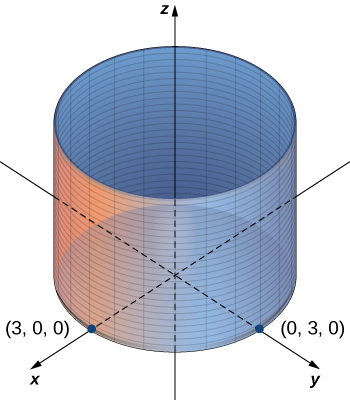
Figura 2.75. En el espacio tridimensional, la gráfica de la ecuación $x^2 + y^2 = 9$ es un cilindro con radio $3$ centrado en el eje z. Continúa indefinidamente en las direcciones positivas y negativas.
En la siguiente escena interactiva puedes verificar el acercamiento a un cilindro,cuando el número de circunferencias aumenta en el mismo intervalo en el eje $z$
A partir de la anterior definición, podemos ver que todavía tenemos un cilindro en el espacio tridimensional, incluso si la curva no es una circunferencia. Cualquier curva puede formar un cilindro, y las reglas que componen el cilindro pueden ser paralelas a cualquier recta dada (Figura 2.76).
Figura 2.76. En el espacio tridimensional, la gráfica de la ecuación $z = x^3$ es un cilindro o una superficie cilíndrica con resoluciones paralelos al eje $y$.
 |
Graficando Superficies Cilíndricas |
Dibuja los gráficos de las siguientes superficies cilíndricas.

La superficie correspondiente a $y=senx$, en el ejercicio anterior, la hemos diseñado en DescartesJS:
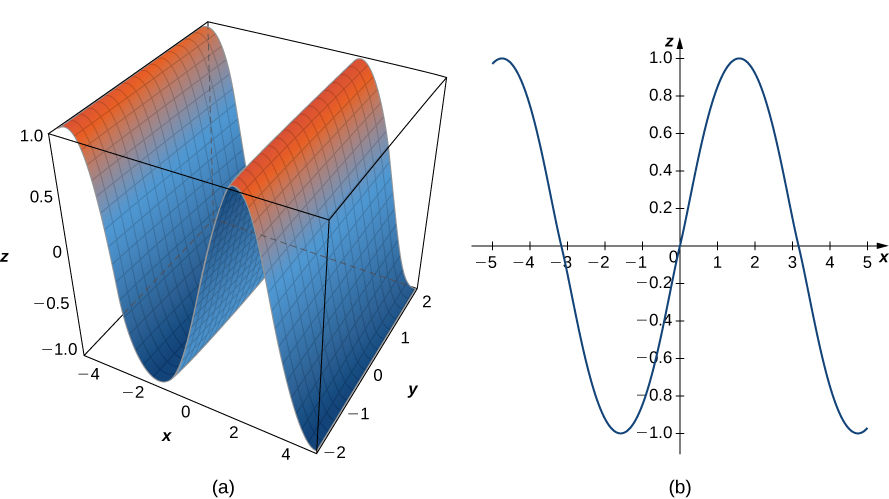
Figura 2.80. (a) Esta es una vista de la gráfica de la ecuación $z = senx$. (b) Para encontrar la traza de la gráfica en el plano $xz$, establece $y = 0$. La traza es simplemente una onda sinusoidal bidimensional.
Las trazas son útiles para dibujar superficies cilíndricas. Sin embargo, para un cilindro en tres dimensiones, solo es útil un conjunto de trazas. Observa, en la figura 2.80, que la traza de la gráfica de $z = senx$ en el plano $xz$ es útil para construir la gráfica. Sin embargo, la traza en el plano $xy$ es solo una serie de rectas paralelas, y la traza en el plano $yz$ es simplemente una recta.
Las superficies cilíndricas están formadas por un conjunto de rectas paralelas. Sin embargo, no todas las superficies en tres dimensiones se construyen de manera tan simple. Ahora exploraremos superficies más complejas, y las trazas son una herramienta importante en esta investigación.
Hemos aprendido sobre superficies en tres dimensiones descritas por ecuaciones de primer orden; estas son planos. Algunos otros tipos comunes de superficies se pueden describir mediante ecuaciones de segundo orden. Podemos ver estas superficies como extensiones tridimensionales de las secciones cónicas que discutimos anteriormente: la elipse, la parábola y la hipérbola. Llamamos a estos gráficos superficies cuadráticas.
Cuando una superficie cuádrica se corta con un plano de coordenadas, la traza es una sección cónica.
Un elipsoide es una superficie descrita por una ecuación de la forma $\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1$. Establece $x = 0$ para ver la traza del elipsoide en el plano $yz$. Para ver las trazas en los planos $xy$ y $xz$, establece $z = 0$ e $y = 0$, respectivamente. Observa que, si $a = b$, la traza en el plano $xy$ es un círculo. De manera similar, si $a = c$, la traza en el plano $xz$ es un círculo y, si $b = c$, entonces la traza en el plano $yz$ es un círculo. Una esfera, entonces, es un elipsoide con $a = b = c$.
 |
Dibujando un elipsoide |
Dibuja el elipsoide
$$\frac{x^2}{2^2} + \frac{y^2}{3^2} + \frac{z^2}{5^2} = 1$$
La superficie del anterior ejercicio, la hemos diseñado en DescartesJS:
La traza de un elipsoide es una elipse en cada uno de los planos de coordenadas. Sin embargo, este no tiene que ser el caso para todas las superficies cuádricas. Muchas superficies cuadráticas tienen trazas que son diferentes tipos de secciones cónicas, y esto generalmente se indica con el nombre de la superficie. Por ejemplo, si una superficie puede describirse mediante una ecuación de la forma $\frac{x^2}{a^2} + \frac{y^2}{b^2} = \frac{z}{c}$, entonces llamamos a esa superficie un paraboloide elíptico. La traza en el plano $xy$ es una elipse, pero las trazas en el plano $xz$ y el plano $yz$ son parábolas (Figura 2.83). Otros paraboloides elípticos pueden tener otras orientaciones simplemente intercambiando las variables para darnos una variable diferente en el término lineal de la ecuación $\frac{x^2}{a^2} + \frac{z^2}{c^2} = \frac{y}{b}$ o $\frac{y^2}{b^2} + \frac{z^2}{c^2} = \frac{x}{a}$.
Figura 2.83. Esta superficie cuádrica se llama paraboloide elíptico.
 |
Identificación de trazas de superficies cuadráticas |
Describir las trazas del paraboloide elíptico
$$x^2 + \frac{y^2}{2^2} = \frac{z}{5}$$
Observa las trazas en el siguiente paraboloide elíptico:
Los hiperboloides de una hoja tienen algunas propiedades fascinantes. Por ejemplo, se pueden construir utilizando líneas rectas, como en la escultura de la Figura 2.85 (a). De hecho, las torres de enfriamiento para centrales nucleares a menudo se construyen en forma de hiperboloide. Los constructores pueden usar vigas de acero rectas en la construcción, lo que hace que las torres sean muy fuertes mientras usan relativamente poco material (Figura 2.85 (b)).

Figura 2.85. (a) Una escultura en forma de hiperboloide puede construirse con líneas rectas. (b) Las torres de enfriamiento para centrales nucleares a menudo se construyen en forma de hiperboloide.
 |
Encontrar el foco de un reflector parabólico |
La energía que golpea la superficie de un reflector parabólico se concentra en el punto focal del reflector (Figura 2.86). Si la superficie de un reflector parabólico se describe mediante la ecuación $\frac{x^2}{100} + \frac{y^2}{100} = \frac{z}{4}$, ¿dónde está el punto focal del reflector?

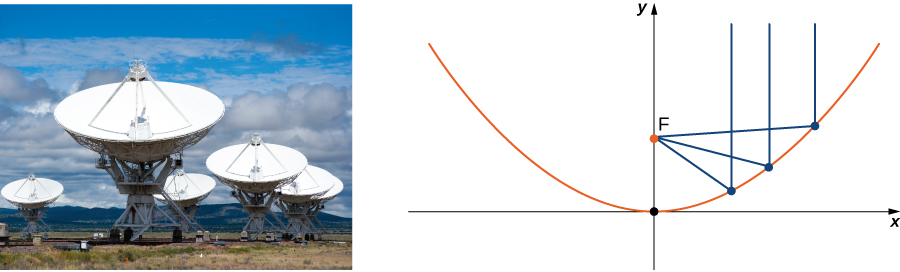
Figura 2.86. La energía se refleja en el reflector parabólico y se recoge en el punto focal (crédito: modificación de CGP Gray, Wikimedia Commons).
Diecisiete superficies cuadráticas estándar pueden derivarse de la ecuación general
$$Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0$$Las siguientes figuras resumen las más importantes.
Haz clic sobre cada imagen para que abras la escena con la superficie correpondiente. Las últimas cinco escenas interactivas, fueron tomadas del libro Curvas y superficies paramétricas, de Navarro y Rivera (2018), las cuales, además de la rotación con clic sostenido, permiten modificar los parámetros de las superficies, para un mejor análisis de sus propiedades.
| Elipsoide $$\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1$$ Trazas En el plano $z=p$: una elipse En el plano $y=q$: una elipse En el plano $x=r$: una elipse Si $a=b=c$, entonces la superficie es una esfera. |  |
| Hiperboloide de una hoja $$\frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1$$ Trazas En el plano $z=p$: una elipse En el plano $y=q$: una hipérbola En el plano $x=r$: una hipérbola En la ecuación, dos de las variables tienen coeficientes positivos y una tiene coeficiente negativo. El eje de la superficie corresponde a la variable con coeficiente negativo. |  |
| Hiperboloide de dos hojas $$\frac{x^2}{a^2} - \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1$$ Trazas En el plano $z=p$: una elipse o conjunto vacío En el plano $y=q$: una hipérbola En el plano $x=r$: una hipérbola En la ecuación, dos de las variables tienen coeficientes negativos y una tiene coeficiente positivo. El eje de la superficie corresponde a la variable con coeficiente positivo. La superficie on intersecta el plano de coordenadas perpendicular al eje. |  |
| Cono elíptico $$\frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1$$ Trazas En el plano $z=p$: una elipse En el plano $y=q$: una hipérbola En el plano $x=r$: una hipérbola El eje de la superficie corresponde a la variable con coeficiente negativo. |  |
| Paraboloide elíptico $$z = \frac{x^2}{a^2} + \frac{y^2}{b^2}$$ Trazas En el plano $z=p$: una elipse En el plano $y=q$: una parábola En el plano $x=r$: una parábola El eje de la superficie corresponde a la variable lineal. |  |
| Paraboloide hiperbólico $$z = \frac{x^2}{a^2} - \frac{y^2}{b^2}$$ Trazas En el plano $z=p$: una hipérbola En el plano $y=q$: una hipérbola En el plano $x=r$: una hipérbola El eje de la superficie corresponde a la variable con coeficiente negativo. |  |
 |
Identificación de ecuaciones de superficies cuadráticas |
Identifica las superficies representadas por las ecuaciones dadas.


 Para los siguientes ejercicios, dibuja y describe la superficie cilíndrica de la ecuación dada.
Para los siguientes ejercicios, dibuja y describe la superficie cilíndrica de la ecuación dada.
303. [T] $x^2+z^2=1$ (Solución) 304. [T] $x^2+y^2=9$ 305. [T] $z=cos(\frac{\pi}{2}+x)$ (Solución) 306. [T] $z=e^x$ 307. [T] $z=9−y^2$ (Solución) 308. [T] $z=ln(x)$
 Para los siguientes ejercicios, se proporciona la gráfica de una superficie cuadrática.
Para los siguientes ejercicios, se proporciona la gráfica de una superficie cuadrática.
309. (Solución)
 310.
310.
311. (Solución) 312.
312.
 Para los siguientes ejercicios, combina la superficie cuadrática dada con su ecuación correspondiente en forma estándar.
Para los siguientes ejercicios, combina la superficie cuadrática dada con su ecuación correspondiente en forma estándar.
313. Hiperboloide de dos hojas (Solución) 314. Elipsoide 315. Paraboloide elíptico (Solución) 316. Paraboloide hiperbólico 317. Hiperboloide de una hoja (Solución) 318. Cono elíptico
 Para los siguientes ejercicios, reescribe la ecuación dada de la superficie cuadrática en forma estándar. Identifica la superficie.
Para los siguientes ejercicios, reescribe la ecuación dada de la superficie cuadrática en forma estándar. Identifica la superficie.
319. $−x^2+36y^2+36z_2=9$ (Solución) 320. $−4x^2+25y^2+z_2=100$ 321. $−3x^2+5y^2−z^2=10$ (Solución) 322. $3x^2−y^2−6z^2=18$ 323. $5y=x^2−z^2$ (Solución) 324. $8x^2−5y^2−10z=0$
325. $x^2+5y^2+3z^2−15=0$ (Solución) 326. $63x^2+7y^2+9z^2−63=0$ 327. $x_2+5y_2−8z_2=0$ (Solución) 328. $5x_2−4y_2+20z_2=0$ 329. $6x=3y_2+2z_2$ (Solución) 330. $49y=x_2+7z_2$
 Para los siguientes ejercicios, encuentra la traza de la superficie cuadrática dada en el plano de coordenadas especificado y haz un esbozo.
Para los siguientes ejercicios, encuentra la traza de la superficie cuadrática dada en el plano de coordenadas especificado y haz un esbozo.
331. [T] $x^2+z^2+4y=0,z=0$ (Solución) 332. [T] $x^2+z^2+4y=0,x=0$ 333. [T] $−4x^2+25y^2+z^2=100,x=0$ (Solución) 334. [T] $−4x^2+25y^2+z^2=100,y=0$ 335. [T] $x^2+\frac{y^2}{4}+\frac{z^2}{100}=1,x=0$ (Solución) 336. [T] $x^2−y−z^2=1,y=0$
337. Usa la gráfica de la superficie cuadrática dada para responder las preguntas (Solución).
338. Usa la gráfica de la superficie cuadrática dada para responder las preguntas.
 Para los siguientes ejercicios, se da la ecuación de una superficie cuadrática.
Para los siguientes ejercicios, se da la ecuación de una superficie cuadrática.
339. $x^2+2z^2+6x−8z+1=0$ (Solución) 340. $4x^2−y^2+z^2−8x+2y+2z+3=0$ 341. $x^2+4y^2−4z^2−6x−16y−16z+5=0$ (Solución) 342. $x^2+z^2−4y+4=0$ 343. $x^2+\frac{y^2}{4}−\frac{z^2}{3}+6x+9=0$ (Solución) 344. $x^2−y^2+z^2−12z+2x+37=0$
345. Escriba la forma estándar de la ecuación del elipsoide centrado en el origen que pasa por los puntos $A (2,0,0), B (0,0,1)$ y $C (\frac{1}{2},\sqrt{11}, \frac{1}{2})$ (Solución). 346. Escribe la forma estándar de la ecuación del elipsoide centrado en el punto $P (1,1,0)$ que pasa por los puntos $A (6,1,0), B (4,2,0)$ y $C (1,2,1 )$ 347. Determina los puntos de intersección del cono elíptico $x^2 − y^2 − z^2 = 0$ con la recta de ecuaciones simétricas $\frac{x − 1}{2} = \frac{y + 1}{3} = z$ (Solución). 348. Determina los puntos de intersección del hiperboloide parabólico $z = 3x^2−2y^2$ con la recta de ecuaciones paramétricas $x = 3t, y = 2t, z = 19t$, donde $t\isin\Reals$. 349. Encuentra la ecuación de la superficie cuadrática con los puntos $P (x, y, z)$ que son equidistantes del punto $Q (0, −1,0)$ y el plano de la ecuación $y = 1$. Identifica la superficie (Solución).
350. Encuentra la ecuación de la superficie cuadrática con los puntos $P (x, y, z)$ que son equidistantes del punto $Q (0,2,0)$ y el plano de la ecuación $y = −2$. Identifica la superficie. 351. Si la superficie de un reflector parabólico se describe mediante la ecuación $400z = x^2 + y^2$, encuentra el punto focal del reflector (Solución). 352. Considera el reflector parabólico descrito por la ecuación $z = 20x^2 + 20y^2$. Encuentra su punto focal. 353. Muestra que la superficie cuadrática $x^2 + y^2 + z^2 + 2xy + 2xz + 2yz + x + y + z = 0 $ se reduce a dos planos paralelos. 354. Demuestra que la superficie cuadrática $x^2 + y^2 + z^2−2xy − 2xz + 2yz − 1 = 0$ se reduce a dos planos paralelos. 355. [T] La intersección entre el cilindro $(x − 1)^2 + y^2 = 1$ y la esfera $x^2 + y^2 + z^2 = 4$ se llama curva de Viviani (Solución).
356. El hiperboloide de una hoja $25x^2 + 25y^2 − z^2 = 25$ y el cono elíptico $−25x^2 + 75y^2 + z^2 = 0$ se representan en la siguiente figura junto con sus curvas de intersección. Identifica las curvas de intersección y encuentra sus ecuaciones (Sugerencia: encuentra $y$ del sistema que consiste en las ecuaciones de las superficies).
357. [T] Usa un CAS para crear la intersección entre el cilindro $9x^2 + 4y^2 = 18$ y el elipsoide $36x^2 + 16y^2 + 9z^2 = 144$, y encuentra las ecuaciones de las curvas de intersección (Solución).
358. [T] Un esferoide es un elipsoide con dos semiejes iguales. Por ejemplo, la ecuación de un esferoide con el eje $z$ como eje de simetría viene dada por $\frac{x^2}{a^2} + \frac{y^2}{a^2} + \frac{z^2}{c^2} = 1$, donde $a$ y $c$ son números reales positivos. El esferoide se llama oblato si $c \lt a$, y prolado para $c\gt a$.
359. [T] En cartografía, la Tierra es aproximada por un esferoide achatado en lugar de una esfera. Los radios en el ecuador y los polos son de aproximadamente $3963 mi$ y $3950 mi$, respectivamente (Solución).
360. [T] Un conjunto de imanes de acrobacias (o “huevos de serpiente de cascabel”) incluye dos imanes brillantes, pulidos y súper fuertes con forma de esferoides, conocidos por el entretenimiento de los niños. Cada imán mide $1.625$ pulgadas de largo y $0.5 $ pulgadas de ancho en el medio. Mientras los lanzan al aire, crean un zumbido mientras se atraen.
En la siguiente pagína presentamos dos escenas interactivas que corresponden a las soluciones de los ejercicios 355 y 361. En la primera se presenta la "curva de Viviani", variante de la "curva Clelia". La segunda escena es una superficie curiosa que muestra una forma similar a un "corazón". Estas escenas son tomadas del libro Curvas y superficies paramétricas de Navarro y Rivera (2018).
El sistema de coordenadas cartesianas proporciona una forma sencilla de describir la ubicación de los puntos en el espacio. Sin embargo, algunas superficies pueden ser difíciles de modelar con ecuaciones basadas en el sistema cartesiano. Este es un problema familiar; recuerda que en dos dimensiones, las coordenadas polares a menudo proporcionan un sistema alternativo útil para describir la ubicación de un punto en el plano, particularmente en casos que involucran circunferencias. En esta sección, veremos dos formas diferentes de describir la ubicación de los puntos en el espacio, ambas basadas en extensiones de coordenadas polares. Como su nombre lo indica, las coordenadas cilíndricas son útiles para tratar problemas que involucran cilindros, como calcular el volumen de un tanque de agua redondo o la cantidad de aceite que fluye a través de una tubería. Del mismo modo, las coordenadas esféricas son útiles para tratar problemas relacionados con esferas, como encontrar el volumen de estructuras abovedadas.
Cuando expandimos el sistema tradicional de coordenadas cartesianas de dos dimensiones a tres, simplemente agregamos un nuevo eje para modelar la tercera dimensión. Comenzando con coordenadas polares, podemos seguir este mismo proceso para crear un nuevo sistema de coordenadas tridimensional, llamado sistema de coordenadas cilíndricas. De esta manera, las coordenadas cilíndricas proporcionan una extensión natural de las coordenadas polares a tres dimensiones.
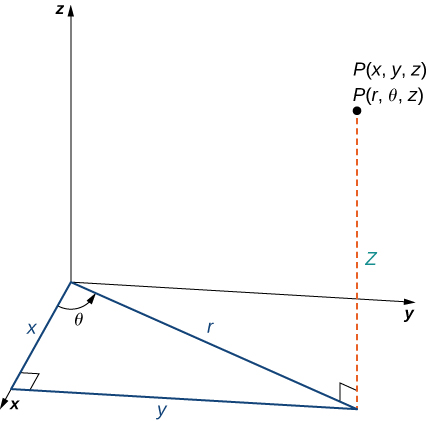
Figura 2.89. El triángulo rectángulo se encuentra en el plano $xy$. La longitud de la hipotenusa es $r$ y $\theta$ es la medida del ángulo formado por el eje $x$ positivo y la hipotenusa. La coordenada $z$ describe la ubicación del punto encima o debajo del plano $xy$.
En el plano $xy$, el triángulo rectángulo que se muestra en la figura 2.89 proporciona la clave para la transformación entre coordenadas cilíndricas y cartesianas, o rectangulares.
| $$\begin{aligned} x &= rcos\theta\\ y &= rsen\theta\\ z &= z \end{aligned}$$ | Estas ecuaciones se utilizan para convertir de coordenadas cilíndricas a coordenadas rectangulares. |
| $$\begin{aligned} r^2 &= x^2 + y^2\\ tan\theta &= \frac{y}{x}\\ z &= z \end{aligned}$$ | Estas ecuaciones se utilizan para convertir coordenadas rectangulares a coordenadas cilíndricas. |
Como cuando discutimos la conversión de coordenadas rectangulares a coordenadas polares en dos dimensiones, debe notarse que la ecuación $tan\theta = \frac{y}{x}$ tiene un número infinito de soluciones. Sin embargo, si restringimos $\theta$ a valores entre $0$ y $2\pi$, entonces podemos encontrar una solución única basada en el cuadrante del plano $xy$ en el que se encuentra el punto original $(x, y, z)$.
Ten en cuenta que si $x = 0$, entonces el valor de $\theta$ es $\frac{\pi}{2}, \frac{3\pi}{2}$ o $0$, dependiendo del valor de $y$. Observa que estas ecuaciones se derivan de las propiedades de los triángulos rectángulos.
Para que sea fácil de ver, considera el punto $P$ en el plano $xy$ con coordenadas rectangulares $(x, y, 0)$ y con coordenadas cilíndricas $(r, \theta, 0)$, como se muestra en la siguiente figura.
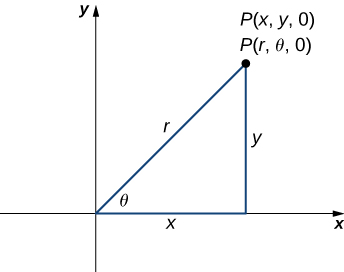
Figura 2.90. El teorema de Pitágoras proporciona la ecuación $r^2 = x^2 + y^2$. Las relaciones del triángulo rectángulo nos dicen que $x = rcos\theta, y = rsen\theta$ y $tan\theta = y/x$.
Consideremos las diferencias entre las coordenadas rectangulares y cilíndricas al observar las superficies generadas cuando cada una de las coordenadas se mantiene constante. Si $c$ es una constante, entonces en coordenadas rectangulares, las superficies de la forma $x = c, y = c$, o $z = c$ son todos planos. Los planos de estas formas son paralelos al plano $yz$, al plano $xz$ y al plano $xy$, respectivamente. Cuando convertimos a coordenadas cilíndricas, la coordenada $z$ no cambia. Por lo tanto, en coordenadas cilíndricas, las superficies de la forma $z = c$ son planos paralelos al plano $xy$.
Ahora, pensemos en las superficies de la forma $r = c$. Los puntos en estas superficies están a una distancia fija del eje $z$. En otras palabras, estas superficies son cilindros circulares verticales. Por último, ¿qué pasa con $\theta = c$? Los puntos en una superficie de la forma $\theta = c$ están en un ángulo fijo desde el eje $x$, lo que nos da un semiplano que comienza en el eje $z$ (Figura 2.91 y Figura 2.92).
Figura 2.91. En coordenadas rectangulares, (a) las superficies de la forma $x = c$ son planos paralelos al plano $yz$, (b) las superficies de la forma $y = c$ son planos paralelos al plano $xz$, y (c) las superficies de la forma $z = c$ son planos paralelos al plano $xy$.
Figura 2.92. En coordenadas cilíndricas, (a) las superficies de la forma $r = c$ son cilindros verticales de radio $r$, (b) las superficies de la forma $\theta = c$ son semiplanos en ángulo $\theta$ desde el eje $x$, y (c) las superficies de la forma $z = c$ son planos paralelos al plano $xy$.
 |
Conversión de coordenadas cilíndricas a rectangulares |
Traza el punto con coordenadas cilíndricas $(4,\frac{2\pi}{3}, −2)$ y expresa su ubicación en coordenadas rectangulares.

Si este proceso parece familiar, es con buena razón. Este es exactamente el mismo proceso que seguimos en el primer capítulo sobre ecuaciones paramétricas y coordenadas polares, para convertir de coordenadas polares a coordenadas rectangulares bidimensionales.
 |
Conversión de coordenadas rectangulares a cilíndricas |
Convierte las coordenadas rectangulares $(1, −3,5)$ en coordenadas cilíndricas.

El uso de coordenadas cilíndricas es común en campos como la física. Los físicos que estudian las cargas eléctricas y los condensadores utilizados para almacenar estas cargas han descubierto que estos sistemas a veces tienen una simetría cilíndrica.
Estos sistemas tienen ecuaciones de modelado complicadas en el sistema de coordenadas cartesianas, lo que dificulta su descripción y análisis. Las ecuaciones a menudo se pueden expresar en términos más simples usando coordenadas cilíndricas. Por ejemplo, el cilindro descrito por la ecuación $x^2 + y^2 = 25$ en el sistema cartesiano puede representarse mediante la ecuación cilíndrica $r = 5$.
 |
Identificación de superficies en el sistema de coordenadas cilíndricas |
Describe las superficies con las ecuaciones cilíndricas dadas.

Practica con la siguiente escena interactiva, adaptación realizada a partir de la miscelánea "Coordenadas cilíndricas", diseñada por Elena E. Álvarez Sáiz, y publicada en el portal del Proyecto Descartes.
En el menún "elige", selecciona una de las variables; por ejemplo, para $r$ constante obtendrás el cilindro $r=c$.
En el sistema de coordenadas cartesianas, la ubicación de un punto en el espacio se describe utilizando un triple ordenado en el que cada coordenada representa una distancia. En el sistema de coordenadas cilíndricas, la ubicación de un punto en el espacio se describe usando dos distancias ($r$ y $z$) y una medida de ángulo ($\theta$). En el sistema de coordenadas esféricas, nuevamente usamos un triple ordenado para describir la ubicación de un punto en el espacio. En este caso, el triple describe una distancia y dos ángulos. Las coordenadas esféricas facilitan la descripción de una esfera, al igual que las coordenadas cilíndricas facilitan la descripción de un cilindro. Las líneas de cuadrícula para coordenadas esféricas se basan en medidas de ángulo, como las de coordenadas polares.
La anterior escena interactiva, es una adaptación realizada a partir de la miscelánea "Coordenadas esféricas", diseñada por Elena E. Álvarez Sáiz, y publicada en el portal del Proyecto Descartes.

Figura 2.97. La relación entre coordenadas esféricas, rectangulares y cilíndricas.
Por convención, el origen se representa como (0,0,0) en coordenadas esféricas.
A continuación, presentamos un Teorema que indica cómo realizar la conversión entre coordenadas esféricas, cilíndricas y rectangulares, la fórmulas presentadas pueden parecer complejas, pero son aplicaciones sencillas de trigonometría.
| $$\begin{aligned} x &= \rho sen\phi cos\theta\\ y &= \rho sen\phi sen\theta\\ z &= \rho cos\phi \end{aligned}$$ | Estas ecuaciones se utilizan para convertir coordenadas esféricas en coordenadas rectangulares. |
| $$\begin{aligned} \rho ^2 &= x^2 + y^2 +z^2\\ tan\theta &= \frac{y}{x}\\ \phi &= arccos \bigg(\frac{z}{\sqrt{x^2+y^2+z^2}}\bigg) \end{aligned}$$ | Estas ecuaciones se utilizan para convertir coordenadas rectangulares en coordenadas esféricas. |
| $$\begin{aligned} r &= \rho sen\theta\\ \theta &= \theta\\ z &= \rho cos\theta \end{aligned}$$ | Estas ecuaciones se utilizan para convertir de coordenadas esféricas a coordenadas cilíndricas. |
| $$\begin{aligned} \rho &= \sqrt{r^2 +z^2}\\ \theta &= \theta\\ \phi &= arccos \bigg(\frac{z}{\sqrt{r^2+z^2}}\bigg) \end{aligned}$$ | Estas ecuaciones se utilizan para convertir coordenadas cilíndricas en coordenadas esféricas. |
Mirando la Figura 2.98, es fácil ver que $r = \rho sen\phi$. Luego, mirando el triángulo en el plano $xy$ con $r$ como su hipotenusa, tenemos $x = rcos\theta = \rho sen\phi cos\theta$. La derivación de la fórmula para $y$ es similar. La figura 2.96 también muestra que $\rho^2 = r^2 + z^2 = x^2 + y^2 + z^2$ y $z = \rho cos\phi$. Resolver esta última ecuación para $\phi$ y luego el sustituir $\rho = \sqrt{r^2 +z^2}$ (de la primera ecuación) se produce $\phi = arccos \bigg(\frac{z}{\sqrt{r^2+z^2}}\bigg)$. Además, ten en cuenta que, como antes, debemos tener cuidado al usar la fórmula $tan\theta = \frac{y}{x}$ para elegir el valor correcto de $\theta$.
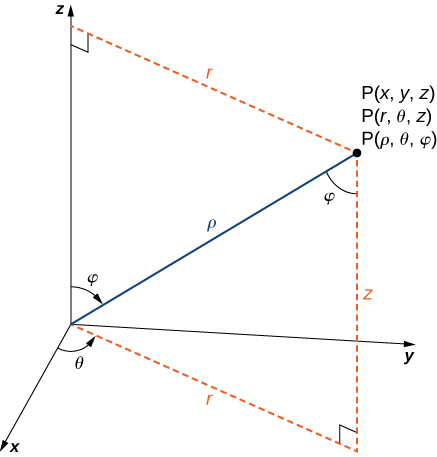
Figura 2.98. Las ecuaciones que se convierten de un sistema a otro se derivan de las relaciones del triángulo rectángulo.
Como hicimos con las coordenadas cilíndricas, consideremos las superficies que se generan cuando cada una de las coordenadas se mantiene constante. Deja que c sea una constante y considera las superficies de la forma $\rho = c$. Los puntos en estas superficies están a una distancia fija del origen y forman una esfera. La coordenada $\theta$ en el sistema de coordenadas esféricas es la misma que en el sistema de coordenadas cilíndricas, por lo que las superficies de la forma $\theta = c$ son semiplanos, como antes. Por último, considera las superficies de la forma $\phi = c$. Los puntos en estas superficies están en un ángulo fijo desde el eje $z$ y forman un medio cono (Escena interactiva y Figura 2.99).
Figura 2.99. En coordenadas esféricas, las superficies de la forma $\rho = c$ son esferas de radio $\rho$ (a), las superficies de la forma $\theta = c$ son semiplanos en un ángulo $\theta$ desde el eje $x$ (b), y las superficies de la forma $\phi = c$ son medios conos en un ángulo $\phi$ desde el eje $z$ (c).
 |
Conversión de coordendas esféricas |
Traza el punto con coordenadas esféricas $(8, \frac{\pi}{3}, \frac{\pi}{6})$ y expresa su ubicación en coordenadas rectangulares y cilíndricas.

 |
Conversión de coordenadas rectangulares |
Convierte las coordenadas rectangulares $(−1,1,\sqrt{6})$ en coordenadas esféricas y cilíndricas.

 |
Identificación de superficies en el sistema de coordenadas esféricas |
Describe las superficies con las ecuaciones esféricas dadas. a. $\theta =\frac{\pi}{3}$ b. $\phi = \frac{5\pi}{6}$ c. $\rho = 6$ d. $\rho= sen\theta sen\phi$

Las coordenadas esféricas son útiles para analizar sistemas que tienen cierto grado de simetría sobre un punto, como el volumen del espacio dentro de un estadio abovedado o la velocidad del viento en la atmósfera de un planeta. Una esfera que tiene la ecuación cartesiana $x^2 + y^2 + z^2 = c^2$ tiene la ecuación simple $\rho = c$ en coordenadas esféricas.
En geografía, la latitud y la longitud se utilizan para describir ubicaciones en la superficie de la Tierra, como se muestra en la Figura 2.104. Aunque la forma de la Tierra no es una esfera perfecta, utilizamos coordenadas esféricas para comunicar la ubicación de los puntos en la Tierra. Supongamos que la Tierra tiene la forma de una esfera con un radio de $4000\; mi$. Expresamos las medidas de los ángulos en grados en lugar de radianes porque la latitud y la longitud se miden en grados.
Figura 2.104. En el sistema de latitud y longitud, los ángulos describen la ubicación de un punto en la Tierra en relación con el ecuador y el meridiano principal.
Supón que el centro de la Tierra sea el centro de la esfera, con el rayo desde el centro a través del Polo Norte que representa el eje $z$ positivo. El meridiano principal representa la traza de la superficie a medida que se interseca con el plano $xz$. El ecuador es la traza de la esfera que se interseca con el plano $xy$.
Analiza los triángulos en la esfera terrestre en la siguiente escena interactiva, diseñada por Jose Galo, en la cual seguro te preguntarás ¿Cómo es que la suma de los ángulos de un triángulo es superior a 180º? (consulta la unidad Geometría esférica).
 |
Conversión de latitud y longitud a coordenadas esféricas |
La latitud de Columbus, Ohio, es de 40° N y la longitud es de 83° W, lo que significa que Columbus está a 40° al norte del ecuador.
Imagina un rayo desde el centro de la Tierra a través de Columbus y un rayo desde el centro de la Tierra a través del ecuador directamente al sur de Columbus. La medida del ángulo formado por los rayos es de 40°. Del mismo modo, midiendo desde el primer meridiano, Columbus se encuentra a 83° hacia el oeste. Expresa la ubicación de Columbus en coordenadas esféricas.

Las coordenadas cilíndricas y esféricas nos dan la flexibilidad de seleccionar un sistema de coordenadas apropiado para el problema en cuestión. Una elección cuidadosa del sistema de coordenadas puede hacer que un problema sea mucho más fácil de resolver, mientras que una mala elección puede conducir a cálculos innecesariamente complejos. En el siguiente ejercicio, examinamos varios problemas diferentes y discutimos cómo seleccionar el mejor sistema de coordenadas para cada uno.
 |
Elegir el mejor sistema de coordenadas |
En cada una de las siguientes situaciones, determinamos qué sistema de coordenadas es el más apropiado y describimos cómo orientaríamos los ejes de coordenadas. Podría haber más de una respuesta correcta sobre cómo deberían orientarse los ejes, pero seleccionamos una orientación que tenga sentido en el contexto del problema. Nota: No hay suficiente información para configurar o resolver estos problemas; simplemente seleccionamos el sistema de coordenadas (Figura 2.105).

Figura 2.105. (crédito: (a) modificación del trabajo de scl hua, Wikimedia, (b) modificación del trabajo de DVIDSHUB, Flickr, (c) modificación del trabajo de Michael Malak, Wikimedia, (d) modificación del trabajo de Sean Mack, Wikimedia, (e) modificación del trabajo de Elvert Barnes, Flickr)


Usa la siguiente figura como ayuda para identificar la relación entre los sistemas de coordenadas rectangulares, cilíndricos y esféricos.
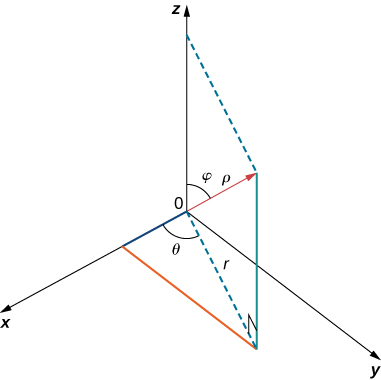
 Para los siguientes ejercicios, se dan las coordenadas cilíndricas $(r, \theta, z)$ de un punto. Encuentra las coordenadas rectangulares $(x, y, z)$ del punto.
Para los siguientes ejercicios, se dan las coordenadas cilíndricas $(r, \theta, z)$ de un punto. Encuentra las coordenadas rectangulares $(x, y, z)$ del punto.
363. $(4,\frac{\pi}{6},3)$ (Solución) 364. $(3,\frac{\pi}{3},5)$ 365. $(4,\frac{7\pi}{6},3)$ (Solución) 366. $(2,π,−4)$
 Para los siguientes ejercicios, se dan las coordenadas rectangulares $(x, y, z)$ de un punto. Encuentra las coordenadas cilíndricas $(r, \theta, z)$ del punto.
Para los siguientes ejercicios, se dan las coordenadas rectangulares $(x, y, z)$ de un punto. Encuentra las coordenadas cilíndricas $(r, \theta, z)$ del punto.
367. $(1,\sqrt{3},2)$ (Solución) 368. $(1,1,5)$ 369. $(3,−3,7)$ (Solución) 370. $(−2\sqrt{2},2\sqrt{2},4)$
 Para los siguientes ejercicios, se da la ecuación de una superficie en coordenadas cilíndricas. Encuentra la ecuación de la superficie en coordenadas rectangulares. Identificar y graficar la superficie.
Para los siguientes ejercicios, se da la ecuación de una superficie en coordenadas cilíndricas. Encuentra la ecuación de la superficie en coordenadas rectangulares. Identificar y graficar la superficie.
371. [T] $r=4$ (Solución) 372. [T] $z=r^2cos^2\theta$ 373. [T] $r^2cos(2\theta)+z^2+1=0$ (Solución) 374. [T] $r=3sen\theta$ 375. [T] $r=2cos\theta$ (Solución) 376. [T] $r^2+z^2=5$ 377. [T] $r=2sec\theta$ (Solución) 378. [T] $r=3csc\theta$
 Para los siguientes ejercicios, se da la ecuación de una superficie en coordenadas rectangulares. Encuentra la ecuación de la superficie en coordenadas cilíndricas.
Para los siguientes ejercicios, se da la ecuación de una superficie en coordenadas rectangulares. Encuentra la ecuación de la superficie en coordenadas cilíndricas.
379. $z=3$ (Solución)
380. $x=6$ 381. $x^2+y^2+z^2=9$ (Solución) 382. $y=2x^2$ 383. $x^2+y^2−16x=0$ (Solución) 384. $x^2+y^2−3\sqrt{x^2+y^2}+2=0$
 Se dan las coordenadas esféricas $(\rho, \theta, \phi)$ de un punto. Encuentra las coordenadas rectangulares $(x, y, z)$ del punto.
Se dan las coordenadas esféricas $(\rho, \theta, \phi)$ de un punto. Encuentra las coordenadas rectangulares $(x, y, z)$ del punto.
385. $(3,0,\pi)$ (Solución) 386. $(1,\frac{\pi}{6},\frac{\pi}{6})$ 387. $(12,−\frac{\pi}{4},\frac{\pi}{4})$ (Solución) 388. $(3,\frac{\pi}{4},\frac{\pi}{6})$
 Se dan las coordenadas rectangulares $(x, y, z)$ de un punto. Encuentra las coordenadas esféricas $(\rho, \theta, \phi)$ del punto. Expresa la medida de los ángulos en grados redondeados al entero más cercano.
Se dan las coordenadas rectangulares $(x, y, z)$ de un punto. Encuentra las coordenadas esféricas $(\rho, \theta, \phi)$ del punto. Expresa la medida de los ángulos en grados redondeados al entero más cercano.
389. $(4,0,0)$ (Solución) 390. $(−1,2,1)$ 391. $(0,3,0)$ (Solución) 392. $(−2,2\sqrt{3},4)$
 Para los siguientes ejercicios, se da la ecuación de una superficie en coordenadas esféricas. Encuentra la ecuación de la superficie en coordenadas rectangulares. Identificar y graficar la superficie.
Para los siguientes ejercicios, se da la ecuación de una superficie en coordenadas esféricas. Encuentra la ecuación de la superficie en coordenadas rectangulares. Identificar y graficar la superficie.
393. [T] $\rho=3$ (Solución) 394. [T] $\phi=\frac{\pi}{3}$ 395. [T] $\rho=2cos\phi$ (Solución) 396. [T] $\rho=4csc\phi$ 397. [T] $\phi=\frac{\pi}{2}$ (Solución) 398. [T] $\rho=6csc\phi sec\theta$
 Para los siguientes ejercicios, se da la ecuación de una superficie en coordenadas rectangulares. Encuentra la ecuación de la superficie en coordenadas esféricas. Identifica la superficie.
Para los siguientes ejercicios, se da la ecuación de una superficie en coordenadas rectangulares. Encuentra la ecuación de la superficie en coordenadas esféricas. Identifica la superficie.
399. $x^2+y^2−3z^2=0$, $z\cancel{=}0$ (Solución) 400. $x^2+y^2+z^2−4z=0$ 401. $z=6$ (Solución) 402. $x^2+y^2=9$
 Para los siguientes ejercicios, se dan las coordenadas cilíndricas de un punto. Encuentra sus coordenadas esféricas asociadas, con la medida del ángulo $\phi$ en radianes redondeado a cuatro decimales.
Para los siguientes ejercicios, se dan las coordenadas cilíndricas de un punto. Encuentra sus coordenadas esféricas asociadas, con la medida del ángulo $\phi$ en radianes redondeado a cuatro decimales.
403. [T] $(1,\frac{π}{4},3)$ (Solución) 404. [T] $(5,π,12)$ 405. $(3,\frac{π}{2},3)$ (Solución) 406. $(3,−\frac{π}{6},3)$
 Para los siguientes ejercicios, se dan las coordenadas esféricas de un punto. Encuentra sus coordenadas cilíndricas asociadas.
Para los siguientes ejercicios, se dan las coordenadas esféricas de un punto. Encuentra sus coordenadas cilíndricas asociadas.
407. $(2,−\frac{\pi}{4},\frac{\pi}{2})$ (Solución) 408. $(4,\frac{\pi}{4},\frac{\pi}{6})$ 409. $(8,\frac{\pi}{3},\frac{\pi}{2})$ (Solución) 410. $(9,−\frac{\pi}{6},\frac{\pi}{3})$
 Para los siguientes ejercicios, encuentra el sistema de coordenadas más adecuado para describir los sólidos.
Para los siguientes ejercicios, encuentra el sistema de coordenadas más adecuado para describir los sólidos.
411. El sólido situado en el primer octante con un vértice en el origen y encerrado por un cubo de longitud de borde $a$, donde $a \gt 0$ (Solución)
412. Una capa esférica determinada por la región entre dos esferas concéntricas centradas en el origen, de radios $a$ y $b$, respectivamente, donde $b \gt a \gt 0$
413. Una esfera interior sólida $x^2 + y^2 + z^2 = 9$ y fuera del cilindro $(x − \frac{3}{2})^2 + y^2 = \frac{9}{4}$ (Solución)
414. Una carcasa cilíndrica de altura $10$ determinado por la región entre dos cilindros con el mismo centro, resoluciones paralelas y radios de $2$ y $5$, respectivamente.
415. [T] Usa un CAS para graficar en coordenadas cilíndricas la región entre el paraboloide elíptico $z = x^2 + y^2$ y el cono $x^2 + y^2 − z^2 = 0$ (Solución).
416. [T] Usa un CAS para graficar en coordenadas esféricas la “región del cono de helado” situada sobre el plano $xy$ entre la esfera $x^2 + y^2 + z^2 = 4$ y el cono elíptico $x^2 + y^2 − z^2 = 0$.
417. Washington, DC, se encuentra a $39^o$ N y $77^o$ W (ver la siguiente figura). Supón que el radio de la Tierra es de $4000\; mi$. Expresa la ubicación de Washington, DC, en coordenadas esféricas (Solución).
418. San Francisco se encuentra a $37.78^o$ N y $122,42^o$ O. Supón que el radio de la Tierra es $4000\; mi$. Expresa la ubicación de San Francisco en coordenadas esféricas.
419. Encuentra la latitud y longitud de Río de Janeiro si sus coordenadas esféricas son $(4000, −43.17^o, 102.91^o)$ (Solución).
420. Encuentra la latitud y longitud de Berlín si sus coordenadas esféricas son $(4000,13.38^o$, 37.48^o$)$.
421. [T] Considera el toro de la ecuación $(x^2 + y^2 + z^2 + R^2 − r^2)^2 = 4R^2(x^2 + y^2)$, donde $R\ge r\gt 0$ (Solución).
422. [T] La “esfera irregular” con una ecuación en coordenadas esféricas es $\rho = a + bcos (m\theta)sen(n\phi)$, con $\theta\isin [0,2\pi]$ y $\phi\isin [0, \pi]$, donde $a$ y $b$ son números positivos y $m$ y $n$ son enteros positivos, pueden usarse en matemática aplicada para modelar el crecimiento tumoral.

Figura 2.1. El cometa Halley apareció a la vista de la Tierra en 1986 y volverá a aparecer en 2061.
En 1705, utilizando las nuevas leyes de movimiento de Sir Isaac Newton, el astrónomo Edmond Halley hizo una predicción. Dijo que los cometas que habían aparecido en 1531, 1607 y 1682 eran en realidad el mismo cometa y que reaparecería en 1758. Halley demostró estar en lo cierto, aunque no vivió para verlo. Sin embargo, el cometa fue nombrado más tarde en su honor.
El cometa Halley sigue un camino elíptico a través del sistema solar, con el Sol apareciendo en un foco de la elipse. Este movimiento es predicho por la primera ley de movimiento planetario de Johannes Kepler, que mencionamos brevemente en la Introducción a las ecuaciones paramétricas y las coordenadas polares.
Las funciones con valor vectorial proporcionan un método útil para estudiar varias curvas tanto en el plano como en el espacio tridimensional.
Podemos aplicar este concepto para calcular la velocidad, la aceleración, la longitud del arco y la curvatura de la trayectoria de un objeto. En este capítulo, examinamos estos métodos y mostramos cómo se usan.
Nuestro estudio de las funciones de valor vectorial combina ideas de nuestro examen anterior del cálculo de una sola variable con nuestra descripción de vectores en tres dimensiones del capítulo anterior. En esta sección ampliamos conceptos de capítulos anteriores y también examinamos nuevas ideas sobre curvas en el espacio tridimensional. Estas definiciones y teoremas apoyan la presentación de material en el resto de este capítulo y también en los capítulos restantes del texto.
Nuestro primer paso para estudiar el cálculo de las funciones con valor vectorial es definir qué es exactamente una función con valor vectorial. Luego, podemos ver gráficos de funciones con valor vectorial y ver cómo definen curvas en dos y tres dimensiones.
El parámetro $t$ puede estar entre dos números reales: $a\le t\le b$. Otra posibilidad es que el valor de $t$ pueda tomar todos los reales. Por último, las funciones de los componentes pueden tener restricciones de dominio que imponen restricciones sobre el valor de $t$.
 |
Evaluación de funciones con valor vectorial y determinación de dominios |
Para cada una de las siguientes funciones con valor vectorial, evalúa $\bold{r}(0), \bold{r}(\frac{\pi}{2})$ y $\bold{r}(\frac{2\pi}{3})$. ¿Alguna de estas funciones tiene restricciones de dominio?

El ejercicio ilustra un concepto importante. El dominio de una función con valor vectorial se compone de números reales. El dominio puede ser todos los números reales o un subconjunto de los números reales. El rango se compone de vectores. Cada número real en el dominio de una función con valor vectorial se asigna a un vector bidimensional o tridimensional.
Recuerda que un vector plano consta de dos cantidades: dirección y magnitud. Dado cualquier punto en el plano (el punto inicial), si nos movemos en una dirección específica para una distancia específica, llegamos a un segundo punto. Esto representa el punto terminal del vector. Calculamos los componentes del vector restando las coordenadas del punto inicial de las coordenadas del punto terminal.
Se considera que un vector está en posición estándar si el punto inicial se encuentra en el origen. Al graficar una función con valor vectorial, generalmente graficamos los vectores en el dominio de la función en posición estándar, porque hacerlo garantiza la unicidad del gráfico. Esta convención se aplica también a los gráficos de funciones tridimensionales con valor vectorial. La gráfica de una función con valor vectorial de la forma $\bold{r}(t) = f (t)\bold{i} + g(t)\bold{j}$ consiste en el conjunto de todos $(t, \bold{r}(t))$, y la ruta que traza se llama curva plana.
La gráfica de una función de valor vectorial de la forma $\bold{r}(t) = f (t)\bold{i} + g(t)\bold{j} + h(t) \bold{k}$ consiste en el conjunto de todos $(t, \bold{r}(t))$, y el camino que traza se llama curva espacial. Cualquier representación de una curva plana o una curva espacial usando una función de valor vectorial se llama parametrización vectorial de la curva.
 |
Graficar una función con valor vectorial |
Crea un gráfico de cada una de las siguientes funciones con valor vectorial:

Puedes notar que las gráficas en las partes a. y b. son idénticas. Esto sucede porque la función que describe la curva b es una llamada reparametrización de la función que describe la curva a. De hecho, cualquier curva tiene un número infinito de reparametrizaciones; por ejemplo, podemos reemplazar $t$ con $2t$ en cualquiera de las tres curvas anteriores sin cambiar la forma de la curva.
El intervalo sobre el cual se define $t$ puede cambiar, pero eso es todo. Volvemos a esta idea más adelante en este capítulo cuando estudiamos la parametrización de longitud de arco.
Como se mencionó, el nombre de la forma de la curva de la gráfica en el ejemplo 3.2c. es una hélice (figura 3.4). La curva se asemeja a un resorte, con una sección transversal circular que mira hacia abajo a lo largo del eje $z$. Es posible que una hélice sea también elíptica en sección transversal. Por ejemplo, la función de valor vectorial $\bold{r}(t) = 4cost\;\bold{i} + 3sent\;\bold{j} + t\;\bold{k}$ describe una hélice elíptica. La proyección de esta hélice en el plano $xy$ es una elipse. Por último, las flechas en el gráfico de esta hélice indican la orientación de la curva a medida que $t$ progresa de $0$ a $4\pi$.
En este punto, puedes notar una similitud entre las funciones de valor vectorial y las curvas parametrizadas. De hecho, dada una función de valor vectorial $\bold{r}(t) = f(t)\;\bold{i} + g(t)\;\bold{j}$, podemos definir $x = f(t)$ e $y = g(t)$. Si existe una restricción en los valores de $t$ (por ejemplo, $t$ está restringido al intervalo $[a, b]$ para algunas constantes $a \lt b$), entonces esta restricción se aplica al parámetro. El gráfico de la función parametrizada estaría de acuerdo con el gráfico de la función con valor vectorial, excepto que el gráfico con valor vectorial representaría vectores en lugar de puntos. Como podemos parametrizar una curva definida por una función $y = f (x)$, también es posible representar una curva plana arbitraria mediante una función de valor vectorial.
En la siguiente escena interactiva, diseñada por Brenda Casandra Vargas Rocha (Instituto de Ciencia e Ingeniería de Materiales, UNAM), puedes observar y cambiar las ecuaciones paramétricas de una hélice. Te recomendamos explorar la escena en forma ampliada.
Cambia el valor de $b$ a 2 y observa cómo se transforma en una hélice elíptica. Puedes, también, cambiar el intervalo, por ejemplo, escribe 2pi en la casilla para $t_2$. Notarás que la curva puede quedar segmentada, pues el editor DescartesJS construye las curvas con $N$ segmentos, por ello, se ha dejado un control $N$ para que aumentes este número de intervalos y mejorar el aspecto de la curva.
Ahora echamos un vistazo al límite de una función con valor vectorial. Es importante entender esto para estudiar el cálculo de las funciones con valores vectoriales.
Esta es una definición rigurosa del límite de una función con valor vectorial. En la práctica, utilizamos el siguiente teorema:
En el siguiente ejercicio, mostramos cómo calcular el límite de una función con valor vectorial.
 |
Evaluación del límite de una función con valor vectorial |
Para cada una de las siguientes funciones vectoriales, calcula $\lim\limits_{t \to 3}\bold{r}(t)$ para

Ahora que sabemos cómo calcular el límite de una función con valor vectorial, podemos definir la continuidad en un punto para dicha función.
De manera similar, la función de valor vectorial $\bold{r}(t) = f(t)\bold{i} + g(t)\bold{j} + h(t)\bold{k}$ es continua en el punto $t = a$ si se cumplen las siguientes tres condiciones:

1. Obtén las funciones componentes $x = f(t)$ e $y = g(t)$ para la función con valor vectorial $\bold{r}(t) = 3sect\bold{i} + 2tant\bold{j}$ (Solución).
2. Dado $\bold{r}(t) = 3sect\bold{i} + 2tant\bold{j}$, encuentra los siguientes valores (si es posible).
3. Dibuja la curva de la función con valor vectorial $\bold{r}(t) = 3sect\bold{i} + 2tant\bold{j}$ y dA la orientación de la curva. Dibuja asíntotas como una guía para el gráfico (Solución).
4. Evaluar $\lim\limits_{t\to 0} \bigg\lang et^\bold{i} + \frac{sent}{t}\bold{j} + e^{−t}\bold{k} \bigg\rang$.
5. Dada la función con valor vectorial $\bold{r}(t) = \lang cost, sent\rang$, encuentra los siguientes valores (Solución):
6. Dada la función con valor vectorial $\bold{r}(t) = \lang t, t^2 + 1\rang$, encuentra los siguientes valores:
7. Sea $\bold{r}(t) = e^t\bold{i} + sent\bold{j} + lnt\bold{k}$. Encuentra los siguientes valores (Solución):
 Encuentra el límite de las siguientes funciones con valores vectoriales en el valor indicado de $t$.
Encuentra el límite de las siguientes funciones con valores vectoriales en el valor indicado de $t$.
8. $\lim\limits_{t\to 4} \bigg\lang \sqrt{t-3},\frac{\sqrt{t}-2}{t-4},tan(\frac{\pi}{t})\bigg\rang$ 9. $\lim\limits_{t\to \frac{\pi}{2}} \bold{r}(t)$, para $\bold{r}(t) = e^t\bold{i}+sent\bold{j}+lnt\bold{k}$ (Solución) 10. $\lim\limits_{t\to \infin}\bigg\lang e^{-2t},\frac{2t+3}{3t-1}, arctan(2t)\bigg\rang$ 11. $\lim\limits_{t\to e^2} \bigg\lang tlnt(t),\frac{ln t}{t^2}, \sqrt{ln(t^2)}\bigg\rang$ (Solución) 12. $\lim\limits_{t\to \frac{\pi}{6}} \lang cos^2t, sen^2t,1\rang $
13. $\lim\limits_{t\to \infin} \bold{r}(t)$, para $\bold{r}(t) = 2e^{-t}\bold{i}+e^{-t}\bold{j}+ln(t-1)\bold{k}$ (Solución) 14. Describe la curva definida por la función con valor vectorial $\bold{r}(t) = (1 + t)\bold{i} + (2 + 5t)\bold{j} + (- 1 + 6t)\bold{k}$.
 Encuentra el dominio de las funciones con valores vectoriales.
Encuentra el dominio de las funciones con valores vectoriales.
15. $\bold{r}(t) = \lang t^2, tant, ln t\rang$ (Solución) 16. $\bold{r}(t) = \bigg\lang t^2, \sqrt{t-3}, \frac{3}{2t+1}\bigg\rang$ 17. $\bold{r}(t) = \big\lang csc(t), \frac{1}{\sqrt{t-3}}, ln(t-2)\big\rang$ (Solución)
 Toma $\bold{r}(t) = \lang cost, t, sent\rang$ y úsalo para responder las siguientes preguntas.
Toma $\bold{r}(t) = \lang cost, t, sent\rang$ y úsalo para responder las siguientes preguntas.
18. ¿Para qué valores de $t$ es $\bold{r}(t)$ continua? 19. Dibuja la gráfica de $\bold{r}(t)$ (Solución). 20. Encuentra el dominio de $\bold{r}(t) = 2e^{-t}\bold{i} + e^{-t}\bold{j} + ln (t − 1)\bold{k}$. 21. Para qué valores de $t$ es $\bold{r}(t) = 2e^{-t}\bold{i} e^{-t}\bold{j} + ln (t − 1)\bold{k}$ continua? (Solución)
 Elimina el parámetro $t$, escribe la ecuación en coordenadas cartesianas, luego dibuja las gráficas de las funciones con valores vectoriales.
Elimina el parámetro $t$, escribe la ecuación en coordenadas cartesianas, luego dibuja las gráficas de las funciones con valores vectoriales.
22. $\bold{r}(t) = 2t\bold{i} + t^2\bold{j}$ (Sugerencia: Haz $x = 2t$ e $y = t^2$. Resuelve la primera ecuación para $x$ en términos de $t$ y sustituye este resultado en la segunda ecuación).
23. $\bold{r}(t) =t^3\bold{i}+2t\bold{j}$ (Solución) 24. $\bold{r}(t) = 2(senht)\bold{i}+2(cosht)\bold{j}$, $t\gt 0$ 25. $\bold{r}(t) = 3(cost)\bold{i}+3(sent)\bold{j}$ (Solución) 26. $\bold{r}(t) = \lang 3sent,3cost\rang$
 Usa una utilidad gráfica para dibujar cada una de las siguientes funciones con valores vectoriales:
Usa una utilidad gráfica para dibujar cada una de las siguientes funciones con valores vectoriales:
27. [T] $\bold{r}(t) =2cost2\bold{i} + (2 − \sqrt{t})\bold{j}$ (Solución) 28. [T] $\bold{r}(t) = \lang e^{cos (3t)}, e^{− sen (t)}\rang$ 29. [T] $\bold{r}(t) = \lang 2 − sen (2t), 3 + 2cost\rang$ (Solución) 30. $4x^2 + 9y^2 = 36$; en sentido horario y antihorario. 31. $\bold{r}(t) = \lang t, t^2\rang $, de izquierda a derecha (Solución). 32. La recta a través de $P$ y $Q$ donde $P$ es $(1,4, −2)$ y $Q$ es $(3,9,6)$
 Considera la curva descrita por la función de valor vectorial $\bold{r}(t) = (50e^{-t}cost)\bold{i} + (50e^{-t}sent)\bold{j} + (5−5e^{-t})\bold{k}$.
Considera la curva descrita por la función de valor vectorial $\bold{r}(t) = (50e^{-t}cost)\bold{i} + (50e^{-t}sent)\bold{j} + (5−5e^{-t})\bold{k}$.
33. ¿Cuál es el punto inicial de la ruta correspondiente a $\bold{r}(0)$? (Solución)
34. ¿Cuál es el $\lim\limits_{t\to \infin} \bold{r}(t)$?
35. [T] Usa la tecnología para dibujar la curva (Solución).
36. Elimina el parámetro $t$ para mostrar que $z = 5 − \frac{r}{10}$ donde $r^2 = x^2 + y^2$.
37. [T] Sea $\bold{r}(t) = cost\bold{i} + sent\bold{j} + 0.3sen (2t)\bold{k}$. Usa la tecnología para graficar la curva (llamada curva de la montaña rusa) durante el intervalo $[0,2\pi)$. Elige al menos dos vistas para determinar los picos y valles (Solución).
38. [T] Usa el resultado del problema anterior para construir una ecuación de una montaña rusa con una fuerte caída desde el pico y una fuerte inclinación desde el "valle". Luego, usa la tecnología para graficar la ecuación.
39. Usa los resultados de los dos problemas anteriores para construir una ecuación de una ruta de una montaña rusa con más de dos puntos de giro (picos y valles) (Solución).
40.
En la página siguiente, puedes observar las gráficas tridimensionales correspondientes a las funciones con valores vectoriales de los ejercicios 29 y 37. Recuerda que puedes ampliarlas hacienco clic en la esquina superior derecha.
En esta escena, hemos dejado los controles $N$ y $c$, sólo para que verifiques que se trata de una variante de la curva tipo "hélice", obteniendo una curva similar a la curva "Ocho", también llamada lemniscata de Gerono o lemniscata de Huygens, o curva en forma de ocho.
Para estudiar el cálculo de funciones con valores vectoriales, seguimos un camino similar al que tomamos al estudiar funciones con valores reales. Primero, definimos la derivada, luego examinamos las aplicaciones de la derivada, luego pasamos a definir integrales. Sin embargo, encontraremos algunas ideas nuevas e interesantes a lo largo del camino como resultado de la naturaleza vectorial de estas funciones y las propiedades de las curvas espaciales.
Ahora que hemos visto qué es una función con valor vectorial y cómo tomar su límite, el siguiente paso es aprender a diferenciarla. La definición de la derivada de una función con valor vectorial es casi idéntica a la definición de una función de valor real de una variable. Sin embargo, debido a que el rango de una función con valor vectorial consiste en vectores, lo mismo es cierto para el rango de la derivada de una función con valor vectorial.
Muchas de las reglas para calcular derivadas de funciones con valor real se pueden aplicar también al cálculo de derivadas de funciones con valor vectorial. Recuerda que la derivada de una función de valor real puede interpretarse como la pendiente de una recta tangente o la tasa de cambio instantánea de la función.
La derivada de una función con valor vectorial también puede entenderse como una tasa de cambio instantánea; por ejemplo, cuando la función representa la posición de un objeto en un punto dado en el tiempo, la derivada representa su velocidad en ese mismo punto en el tiempo.
Ahora lo demostraremos tomando la derivada de una función con valor vectorial.
 |
Encontrar la derivada de una función con valor vectorial |
Usa la definición para calcular la derivada de la función
$$\bold{r}(t)=(3t+4)\bold{i}+(t^2−4t+3)\bold{j}.$$
Observa que en los cálculos del ejercicio anterior, también podríamos obtener la respuesta calculando primero la derivada de cada componente de la función, luego volviendo a colocar estas derivadas en la función con valor vectorial. Esto siempre es cierto para calcular la derivada de una función con valor vectorial, ya sea en dos o tres dimensiones. Establecemos esto en el siguiente teorema. La prueba de este teorema se deriva directamente de las definiciones del límite de una función con valor vectorial y la derivada de una función con valor vectorial.
 |
Cálculo de la derivada de funciones con valor vectorial |
Utiliza la diferenciación de funciones con valores vectoriales para calcular la derivada de cada una de las siguientes funciones.

Antes de continuar, te invitamos a interactuar con la siguiente escena interactiva, diseñada por Yin Bon Ku en GeoGebra.
Aproxima $\Delta t$ a $0$ y observa como $\frac{\bold{r}(t+\Delta t)-\bold{r}(t)}{\Delta t}$ se aproxima a la tangente a la curva en el punto dado.
Interactúa en la escena con los dos deslizadores $t$ y $\Delta t$, rota la gráfica para que verifiques la fórmula 3.5, a medida que $\Delta t$ se aproxima a $0$. Recuerda que puedes ampliar la escena.
Podemos extender a las funciones de valor vectorial las propiedades de la derivada de variable real. En particular, las reglas de suma y diferencia, la regla del producto y la regla de la cadena se extienden a las funciones de valor vectorial. Sin embargo, en el caso de la regla del producto, en realidad hay tres extensiones: (1) para una función de valor real multiplicada por una función de valor vectorial, (2) para el producto punto de dos funciones de valor vectorial, y (3) para el producto cruz de dos funciones vectoriales.
| i. | $$\frac{d}{dt}[c\bold{r}(t)] = c\bold{r'}(t)$$ | Multiplicación por escalar |
| ii. | $$\frac{d}{dt}[\bold{r}(t) \pm \bold{u}(t)] = \bold{r'}(t) \pm \bold{r'}(u)$$ | Suma y diferencia |
| iii. | $$\frac{d}{dt}[f(t)\bold{u}(t)] = f'(t)\bold{u}(t) + f(t)\bold{u'}(t)$$ | Producto escalar |
| iv. | $$\frac{d}{dt}[\bold{r}(t)\cdot\bold{u}(t)] = \bold{u}(t)\cdot\bold{r'}(t) + \bold{r}(t)\cdot\bold{u'}(t)$$ | Producto punto |
| v. | $$\frac{d}{dt}[\bold{r}(t)\times\bold{u}(t)] = \bold{u}(t)\times\bold{r'}(t) + \bold{r}(t)\times\bold{u'}(t)$$ | Producto cruz |
| vi. | $$\frac{d}{dt}[\bold{r}(t)(f(t))] = \bold{r'}(f(t))\cdot f'(t)$$ | Regla de la cadena |
| vii. | Si $\bold{r}(t)\cdot\bold{r}(t)=c$, entonces $\bold{r}(t)\cdot\bold{r'}(t)=0$ |
Las pruebas de las dos primeras propiedades se derivan directamente de la definición de la derivada de una función con valor vectorial. La tercera propiedad se puede derivar de las dos primeras propiedades, junto con la regla del producto. Sea $\bold{u(t)} = g(t)\bold{i} + h(t)\bold{j}$. Luego
$$\begin{aligned} \frac{d}{dt}[f(t)\bold{u}(t)] &= \frac{d}{dt}[f(t)(g(t)\bold{i}+h(t)\bold{j})]\\ &= \frac{d}{dt}[f(t)g(t)\bold{i}+f(t)h(t)\bold{j}]\\ &= (f′(t)g(t)+f(t)g′(t))\bold{i}+(f′(t)h(t)+f(t)h′(t))\bold{j}\\ &= f′(t)\bold{u}(t)+f(t)\bold{u′}(t) \end{aligned}$$Para probar la propiedad iv. sea $\bold{r}(t) = f_1(t)\bold{i} + g_1(t)\bold{j}$ y $\bold{u}(t) = f_2(t)\bold{i} + g_2(t)\bold{j}$. Luego
$$\begin{aligned} \frac{d}{dt}[\bold{r}(t)\cdot\bold{u}(t)] &= \frac{d}{dt}[f_1(t)f_2(t)+g_1(t)g_2(t)]\\ &= f_1′(t)f_2(t)+f_1(t)f_2′(t)+g_1′(t)g_2(t)+g_1(t)g_2′(t)\\ &= f_1′(t)f_2(t)+g_1′(t)g_2(t)+f_1(t)f_2′(t)+g_1(t)g_2′(t)\\ &= f_1′\bold{i}+g_1′\bold{j})\cdot(f_2\bold{i}+g_2\bold{j})+(f_1\bold{i}+g_1\bold{j})\cdot(f_2′\bold{i}+g_2′\bold{j})\\ &= \bold{u}(t)\cdot\bold{r'}(t) + \bold{r}(t)\cdot\bold{u'}(t) \end{aligned}$$La prueba de propiedad v es similar a la de propiedad iv. La propiedad vi puede probarse usando la regla de la cadena. Por último, la propiedad vii se desprende de la propiedad iv:
Ahora, veamos un ejercicio usando estas propiedades.
 |
Uso de las propiedades de derivadas de funciones con valores vectoriales |
Dadas las funciones con valores vectoriales
$$\bold{r}(t)=(6t+8)\bold{i}+(4t^2+2t−3)\bold{j}+5t\bold{k}$$y
$$\bold{u}(t)=(t^2−3)\bold{i}+(2t+4)\bold{j}+(t^3−3t)\bold{k},$$calcula cada una de las siguientes derivadas utilizando las propiedades de la derivada de funciones con valores vectoriales.

Recuerda que la derivada en un punto puede interpretarse como la pendiente de la recta tangente a la gráfica en ese punto. En el caso de una función de valor vectorial, la derivada proporciona un vector tangente a la curva representada por la función. Considera la función de valor vectorial $\bold{r}(t) = cost\bold{i} + sent\bold{j}$. La derivada de esta función es $\bold{r'}(t) = - sent\bold{i} + cost\bold{j}$. Si sustituimos el valor $t = \frac{\pi}{6}$ en ambas funciones obtenemos
$$\bold{r}(\frac{\pi}{6}) = \frac{\sqrt{3}}{2}\bold{i} + \frac{1}{2}\bold{j}\;\text{ y }\; \bold{r'}(\frac{\pi}{6}) = -\frac{1}{2}\bold{i} +\frac{\sqrt{3}}{2}\bold{j}$$El gráfico de esta función aparece en la figura 3.5, junto con los vectores $\bold{r} (\frac{\pi}{6})$ y $\bold{r′}(\frac{\pi}{6})$.
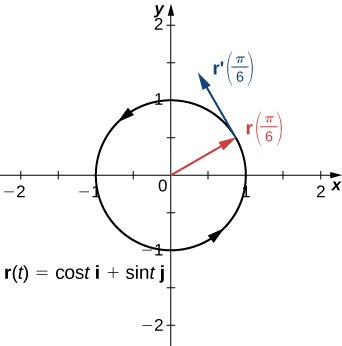
Figura 3.5. La recta tangente en un punto se calcula a partir de la derivada de la función de valor vectorial $\bold{r}(t)$.
Observa que el vector $\bold{r'}(\frac{\pi}{6})$ es tangente a la circunferencia en el punto correspondiente a $t = \frac{\pi}{6}$. Este es un ejemplo de un vector tangente a la curva plana definida por $\bold{r}(t) = cost\bold{i} + sent\bold{j}$.
Para otros valores de $t$ interactúa con la siguiente escena:
 |
Encontrar un vector tangente unitario |
Encuentra el vector tangente unitario para cada una de las siguientes funciones con valores vectoriales:

Ya habrás estudiado las antiderivadas o primitivas de funciones de valor real en cursos previos. Cada uno de estos conceptos se puede extender a funciones con valores vectoriales. Además, así como podemos calcular la derivada de una función con valor vectorial diferenciando las funciones componentes por separado, podemos calcular la antiderivada de la misma manera. Además, el teorema fundamental del cálculo se aplica también a las funciones de valor vectorial.
La antiderivada de una función de valor vectorial aparece en las aplicaciones. Por ejemplo, si una función de valor vectorial representa la velocidad de un objeto en el tiempo $t$, entonces su antiderivada representa la posición. O, si la función representa la aceleración del objeto en un momento dado, entonces la antiderivada representa su velocidad.
Dado que la integral indefinida de una función de valor vectorial implica integrales indefinidas de las funciones componentes,
cada una de estas integrales componentes contiene una constante de integración. Todos pueden ser diferentes. Por ejemplo, en el caso bidimensional, podemos tener
$$\int f(t)dt = F(t) + C_1\;\text{ y }\; \int g(t)dt = G(t)+C_2,$$donde $F$ y $G$ son antiderivadas de $f$ y $g$, respectivamente. Luego
$$\begin{aligned} \int [f(t)\bold{i}+g(t)\bold{j}]dt &= \bigg[\int f(t)dt\bigg]\bold{i}+ \bigg[\int g(t)dt\bigg]\bold{j}\\ &= (F(t)+C_1)\bold{i}+(G(t)+C_2)\bold{j}\\ &= F(t)\bold{i}+G(t)\bold{j}+C_1\bold{i}+C_2\bold{j}\\ &= F(t)\bold{i}+G(t)\bold{j}+C \end{aligned}$$donde $C = C_1\bold{i} + C_2\bold{j}$. Por lo tanto, la constante de integración se convierte en un vector constante.
 |
Integrando funciones con valores vectoriales |
Calcula cada una de las siguientes integrales:


 Calcula las derivadas de las funciones con valores vectoriales.
Calcula las derivadas de las funciones con valores vectoriales.
41. $\bold{r}(t)=t^3\bold{i}+3t^2\bold{j}+\frac{t^3}{6}\bold{k}$ (Solución)
42. $\bold{r}(t)=sen(t)\bold{i}+cos(t)\bold{j}+e^t\bold{k}$
43. $\bold{r}(t) = e^{−t}\bold{i} + sen(3t)\bold{j} + \sqrt{10}t\bold{k}$. Aquí se muestra un boceto del gráfico. Observa la naturaleza periódica variable del gráfico (Solución).
 44. $\bold{r}(t)=e^t \bold{i}+2e^t\bold{j}+\bold{k}$
45. $\bold{r}(t)=\bold{i}+\bold{j}+\bold{k}$ (Solución)
44. $\bold{r}(t)=e^t \bold{i}+2e^t\bold{j}+\bold{k}$
45. $\bold{r}(t)=\bold{i}+\bold{j}+\bold{k}$ (Solución)
46. $\bold{r}(t)=te^t\bold{i}+tln(t)\bold{j}+sen(3t)\bold{k}$ 47. $\bold{r}(t)=\frac{1}{t+1}\bold{i}+arctan(t)\bold{j}+lnt3\bold{k}$ (Solución) 48. $\bold{r}(t)=tan(2t)\bold{i}+sec(2t)\bold{j}+sen^2(t)\bold{k}$ 49. $\bold{r}(t)=3\bold{i}+4sen(3t)\bold{j}+tcos(t)\bold{k}$ (Solución) 50. $\bold{r}(t)=t^2\bold{i}+te^{−2t}\bold{j}−5e^{−4t}\bold{k}$
 Para los siguientes problemas, encuentra un vector tangente en el valor indicado de $t$.
Para los siguientes problemas, encuentra un vector tangente en el valor indicado de $t$.
51. $\bold{r}(t)=t\bold{i}+sen(2t)\bold{j}+cos(3t)\bold{k};t=\frac{\pi}{3}$ (Solución) 52. $\bold{r}(t)=3t^3\bold{i}+2t^2\bold{j}+\frac{1}{t}\bold{k};t=1$ 53. $\bold{r}(t)=3e^t\bold{i}+2e^{−3t}\bold{j}+4e^{2t}\bold{k}; t=ln(2)$ (Solución) 54. $\bold{r}(t)=cos(2t)\bold{i}+2sent\bold{j}+t^2\bold{k};t=\frac{\pi}{2}$
 Encuentra el vector tangente unitario para las siguientes curvas parametrizadas.
Encuentra el vector tangente unitario para las siguientes curvas parametrizadas.
55. $\bold{r}(t) = 6\bold{i} + cos (3t)\bold{j} + 3sen (4t)\bold{k}, 0\le t \lt 2\pi$. Aquí se presenta una vista de esta curva (Solución):
Y aquí una escena interactiva:
563. $\bold{r}(t)=cost\bold{i}+sent\bold{j}+sent\bold{k}, 0\le t\lt 2\pi$ 57. $\bold{r}(t)=3cos(4t)\bold{i}+3sen(4t)\bold{j}+5t\bold{k},1\le t\le 2$ (Solución) 58. $\bold{r}(t)=t\bold{i}+3t\bold{j}+t2\bold{k}$
 Sea $\bold{r}(t) = t\bold{i} + t^2\bold{j} − t^4\bold{k}$ y $\bold{s}(t) = sen(t)\bold{i} + e^t\bold{j} + cos (t)\bold{k}$. Aquí está el gráfico de la función:
Sea $\bold{r}(t) = t\bold{i} + t^2\bold{j} − t^4\bold{k}$ y $\bold{s}(t) = sen(t)\bold{i} + e^t\bold{j} + cos (t)\bold{k}$. Aquí está el gráfico de la función:
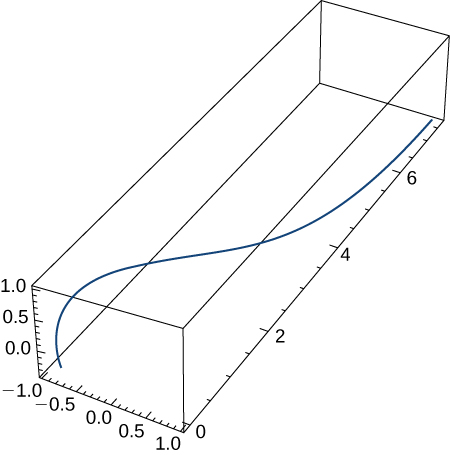
Encuentra lo siguiente: 59. $\frac{d}{dt} [\bold{r} (t^2)]$ (Solución) 60. $\frac{d}{dt} [t^2\cdot\bold{s}(t)]$ 61. $\frac{d}{dt} [\bold{r}(t)\cdot\bold{s}(t)]$ (Solución) 62. Calcula las derivadas primera, segunda y tercera de $\bold{r}(t) = 3t\bold{i} + 6ln(t)\bold{j} + 5e^{−3t}\bold{k}$ 63. Encuentra $\bold{r'}(t)\cdot\bold{r''}(t)$, para $\bold{r}(t) = - 3t^5\bold{i} + 5t\bold{j} + 2t^2\bold{k}$ (Solución) 64. La función de aceleración, la velocidad inicial y la posición inicial de una partícula son: $\bold{a}(t) = - 5cost\bold{i} − 5sent\bold{j}, \bold{v}(0) = 9\bold{i} + 2\bold{j}$, y $\bold{r}(0) = 5\bold{i}$. Encuentra $\bold{v}(t)$ y $\bold{r}(t)$. 65. El vector de posición de una partícula es $\bold{r}(t) = 5sec(2t)\bold{i} − 4tan(t)\bold{j} + 7t^2\bold{k}$ (Solución).
66. Encuentra la velocidad y la rapidez de una partícula con la función de posición $\bold{r}(t) = \bigg(\frac{2t − 1}{2t + 1}\bigg)\bold{i} + ln (1−4t^2)\bold{j}$. La rapidez de una partícula es la magnitud de la velocidad y está representada por $\|\bold{r′}(t)\|$.
 Una partícula se mueve en una trayectoria circular de radio $b$ de acuerdo con la función $\bold{r}(t) = bcos(\omega t)\bold{i} + bsen(\omega t)\bold{j}$, donde $\omega$ es la velocidad angular, $d\theta /dt$.
Una partícula se mueve en una trayectoria circular de radio $b$ de acuerdo con la función $\bold{r}(t) = bcos(\omega t)\bold{i} + bsen(\omega t)\bold{j}$, donde $\omega$ es la velocidad angular, $d\theta /dt$.
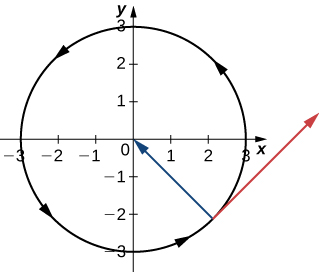
67. Encuentra la función de velocidad y demuestre que $\bold{v}(t)$ siempre es ortogonal a $\bold{r}(t)$ (Solución). 68. Demuestra que la velocidad de la partícula es proporcional a la velocidad angular. 69. Evalúa $\frac{d}{dt}[\bold{u}(t)\times\bold{u′}(t)]$ dado $\bold{u}(t) = t^2\bold{i} − 2t\bold{j} + \bold{k}$ (Solución). 70. Encuentra la antiderivada de $\bold{r'}(t) = cos (2t)\bold{i} − 2sent\bold{j} + \frac{1}{1 + t^2}\bold{k}$ que satisface la condición inicial $\bold{r}(0) = 3\bold{i} − 2\bold{j} +\bold{k}$.
71. Evalúa (Solución).
$$\int_0^3 \|t\bold{i} + t^2\bold{j}\|dt$$72. Un objeto comienza desde el reposo en el punto $P (1,2,0)$ y se mueve con una aceleración de $\bold{a}(t) = \bold{j} + 2\bold{k}$, donde $\|\bold{a}(t)\|$ se mide en pies por segundo cuadrado. Encuentra la ubicación del objeto después de $t = 2 seg$. 73. Demuestra que si la velocidad de una partícula que viaja a lo largo de una curva representada por una función con valor vectorial es constante, entonces la función de velocidad siempre es perpendicular a la función de aceleración (Solución). 74. Dado $\bold{r}(t) = t\bold{i} + 3t\bold{j} + t^2\bold{k}$ y $\bold{u}(t) = 4t\bold{i} + t^2\bold{j} + t^3\bold{k}$, encuentra $\frac{d}{dt}(\bold{r}(t)\times\bold{u}(t))$. 75. Dado $\bold{r}(t) = \lang t + cost, t − sent\rang$, encuentra la velocidad y la rapidez en cualquier momento (Solución). 76. Encuentra el vector de velocidad para la función $\bold{r}(t) = \lang e^t, e^{−t}, 0\rang$. 77. Encuentra la ecuación de la recta tangente a la curva $\bold{r}(t) = \lang e^t, e^{−t}, 0\rang$ en $t = 0$ (Solución). 78. Describe y dibuja la curva representada por la función de valor vectorial $\bold{r}(t) = \lang 6t, 6t − t^2\rang$. 79. Localiza el punto más alto en la curva $\bold{r}(t) = \lang 6t, 6t − t^2\rang$ y obtén el valor de la función en este punto (Solución).
 El vector de posición para una partícula es $\bold{r}(t) = t\bold{i} + t^2\bold{j} + t^3\bold{k}$ El gráfico se muestra a continuación:
El vector de posición para una partícula es $\bold{r}(t) = t\bold{i} + t^2\bold{j} + t^3\bold{k}$ El gráfico se muestra a continuación:
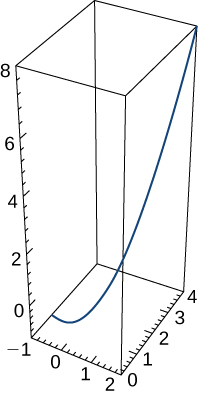
80. Encuentra el vector de velocidad en cualquier momento. 81. Encuentra la velocidad de la partícula en el tiempo $t = 2 seg$ (Solución). 82. Encuentra la aceleración en el tiempo $t = 2 seg$.
 Una partícula viaja a lo largo de la trayectoria de una hélice con la ecuación $\bold{r}(t) = cos(t)\bold{i} + sen(t)\bold{j} + t\bold{k}$.
Una partícula viaja a lo largo de la trayectoria de una hélice con la ecuación $\bold{r}(t) = cos(t)\bold{i} + sen(t)\bold{j} + t\bold{k}$.
83. Encuentra la velocidad de la partícula en cualquier momento (Solución). 84. Encuentra la rapidez de la partícula en cualquier momento. 85. Encuentra la aceleración de la partícula en cualquier momento (Solución). 86. Encuentra el vector tangente unitario para la hélice.
El gráfico se muestra a continuación:
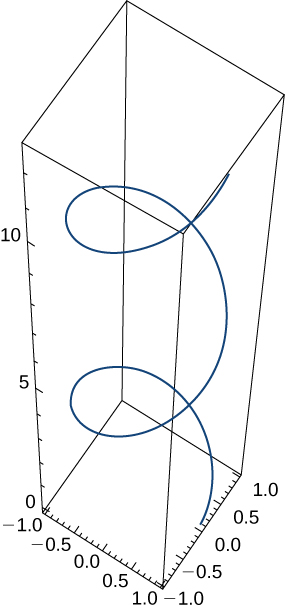
 Una partícula viaja a lo largo del camino de una elipse con la ecuación $\bold{r}(t) = cost\bold{i} + 2sent\bold{j} + 0\bold{k}$. Encuentra lo siguiente:
Una partícula viaja a lo largo del camino de una elipse con la ecuación $\bold{r}(t) = cost\bold{i} + 2sent\bold{j} + 0\bold{k}$. Encuentra lo siguiente:
87. Velocidad de la partícula (Solución) 88. Rapidez de la partícula en $t = \pi/4$ 89. Aceleración de la partícula en $t = \pi/4$ (Solución)
 Dada la función de valor vectorial $\bold{r}(t) = \lang tant, sect, 0\rang$ (el gráfico se muestra en la página siguiente), encuentra lo siguiente:
Dada la función de valor vectorial $\bold{r}(t) = \lang tant, sect, 0\rang$ (el gráfico se muestra en la página siguiente), encuentra lo siguiente:
90. Velocidad 91. Rapidez (Solución) 92. Aceleración 93. Encuentra la velocidad mínima de una partícula que viaja a lo largo de la curva $\bold{r}(t) = \lang t + cost, t − sent\rang\;\; t\isin [0,2\pi)$ (Solución).
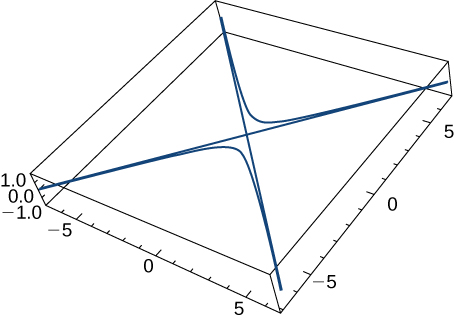
 Dado $\bold{r}(t) = t\bold{i} + 2sent\bold{j} + 2cost\bold{k}$ y $\bold{u}(t) = \frac{1}{t}\bold{i} + 2sent\bold{j} + 2cost\bold{k}$, encuentra lo siguiente:
Dado $\bold{r}(t) = t\bold{i} + 2sent\bold{j} + 2cost\bold{k}$ y $\bold{u}(t) = \frac{1}{t}\bold{i} + 2sent\bold{j} + 2cost\bold{k}$, encuentra lo siguiente:
94. $\bold{r}(t)\times\bold{u}(t)$ 95. $\frac{d}{dt}(\bold{r}(t)\times\bold{u}(t))$ (Solución) 96. Ahora, usa la regla del producto para la derivada del producto cruz de los dos vectores y demuestra que este resultado es el mismo que la respuesta para el problema anterior.
 Encuentra el vector tangente unitario $\bold{T}(t)$ para las siguientes funciones con valores vectoriales.
Encuentra el vector tangente unitario $\bold{T}(t)$ para las siguientes funciones con valores vectoriales.
97. $\bold{r}(t) = \lang t, \frac{1}{t}\rang$ (Solución). El gráfico se muestra a continuación:
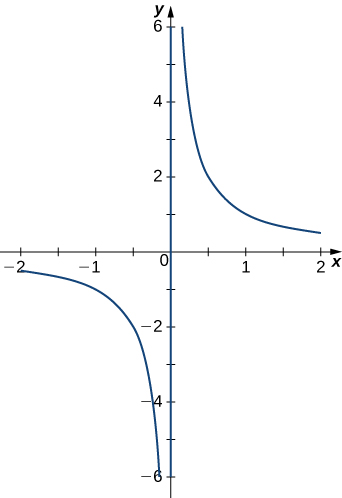
98. $\bold{r}(t)= \lang tcost,tsent\rang$ 99. $\bold{r}(t)= \lang t+1,2t+1,2t+2\rang$ (Solución)
 Evalúa las siguientes integrales:
Evalúa las siguientes integrales:
100. $$\int (e^t\bold{i}+sent\bold{j}+\frac{1}{2t−1}\bold{k})dt$$
101. (Solución). $$\int_0^1 \bold{r}(t)dt,\;\text{ donde }\;\; \bold{r}(t)=\bigg \lang \sqrt[3]{t},\frac{1}{t+1},e^{−t}\bigg \rang$$
En esta sección, estudiaremos fórmulas relacionadas con curvas en dos y tres dimensiones, y veremos cómo están relacionadas con varias propiedades de la misma curva. Por ejemplo, supongamos que una función con valor vectorial describe el movimiento de una partícula en el espacio. Nos gustaría determinar qué tan lejos ha viajado la partícula en un intervalo de tiempo determinado, que puede describirse por la longitud del arco de la ruta que sigue. O supón que la función de valor vectorial describe una carretera que estamos construyendo y queremos determinar qué tan bruscamente se curva la carretera en un punto dado. Esto se describe por la curvatura de la función en ese punto.
Hemos visto cómo una función de valor vectorial describe una curva en dos o tres dimensiones. Recuerda las fórmulas alternativas para la curvatura, que establece que la fórmula para la longitud del arco de una curva definida por las funciones paramétricas $x = x(t), y = y(t), t_1\le t\le t_2$ viene dada por
$$s = \int_{t_1}^{t_2}\sqrt{(x′(t))^2+(y′(t))^2}dt$$De manera similar, si definimos una curva usando una función de valor vectorial $\bold{r}(t) = f(t)\bold{i} + g(t)\bold{j}$, donde $a\le t\le b$, la longitud del arco viene dada por la fórmula
$$s = \int_a^b\sqrt{(f^{\prime}(t))^2+(g^{\prime}(t))^2}dt$$En tres dimensiones, si la función de valor vectorial se describe por $\bold{r}(t) = f(t)\bold{i} + g(t)\bold{j} + h(t)\bold{k}$ durante el mismo intervalo $a\le t\le b$, se da la longitud del arco por
$$s = \int_a^b\sqrt{(f′(t))^2+(g′(t))^2+(h′(t))^2}dt$$Las dos fórmulas son muy similares; solo difieren en el hecho de que una curva espacial tiene tres funciones componentes en lugar de dos. Ten en cuenta que las fórmulas se definen para curvas suaves; es decir, curvas donde la función de valor vectorial $\bold{r}(t)$ es diferenciable con una derivada distinta de cero.
La condición de suavidad garantiza que la curva no tenga cúspides (o esquinas) que puedan hacer que la fórmula sea problemática.
 |
Encontrar la longitud de arco |
Calcula la longitud de arco para cada una de las siguientes funciones con valores vectoriales:

Ahora volvemos a la hélice presentada anteriormente en este capítulo. Una función de valor vectorial que describe una hélice se puede escribir en la forma
$$\bold{r}(t)=Rcos\bigg(\frac{2\pi Nt}{h}\bigg)\bold{i} + Rsen\bigg(\frac{2\pi Nt}{h}\bigg)\bold{j} + t\bold{k}, 0\le t\le h$$donde R representa el radio de la hélice, h representa la altura (distancia entre dos giros consecutivos) y la hélice completa N giros. Deduzcamos una fórmula para la longitud del arco de esta hélice usando la Ecuación 3.12:
$$\bold{r'}(t)=-\frac{2\pi NR}{h}sen\bigg(\frac{2\pi Nt}{h}\bigg)\bold{i} + \frac{2\pi NR}{h}cos\bigg(\frac{2\pi Nt}{h}\bigg)\bold{j} +\bold{k}$$Por lo tanto,
$$\begin{aligned} s &= \|\bold{r'}(t)\|dt\\ &= \int_0^h \sqrt{\bigg(-\frac{2\pi NR}{h}sen\bigg(\frac{2\pi Nt}{h}\bigg)\bigg)^2 + \bigg(\frac{2\pi NR}{h}cos\bigg(\frac{2\pi Nt}{h}\bigg)\bigg)^2 + 1^2}dt\\ &= \int_0^h \sqrt{\frac{4\pi^2 N^2R^2}{h^2}\bigg(sen^2\bigg(\frac{2\pi Nt}{h}\bigg) + cos^2\bigg(\frac{2\pi Nt}{h}\bigg)\bigg)+1}dt\\ &= \int_0^h \sqrt{\frac{4\pi^2 N^2R^2}{h^2} +1}dt\\ &= \bigg[t\sqrt{\frac{4\pi^2 N^2R^2}{h^2} +1}\bigg]_0^1\\ &= h\sqrt{\frac{4\pi^2N^2R^2+h^2}{h^2}}\\ &= \sqrt{4\pi^2N^2R^2+h^2} \end{aligned}$$Esto proporciona una fórmula para la longitud de un cable necesario para formar una hélice con $N$ vueltas que tiene radio $R$ y altura $h$.
Ahora tenemos una fórmula para la longitud del arco de una curva definida por una función con valor vectorial. Avancemos un paso más y examinemos qué es una función de longitud de arco.
Si una función de valor vectorial representa la posición de una partícula en el espacio como una función del tiempo, entonces la función de longitud de arco mide qué tan lejos viaja esa partícula en función del tiempo. La fórmula para la función de longitud de arco se sigue directamente de la fórmula para la longitud de arco:
Si suponemos que $\bold{r} (t)$ define una curva suave, entonces la longitud del arco siempre aumenta, por lo que $s'(t)\gt 0$ para $t\gt a$. Por último, si $\bold{r} (t)$ es una curva en la que $\| \bold{r'} (t)\| = 1$ para todo $t$, entonces
$$s(t) = \int_a^t \|\bold{r'}(u)\|du = \int_a^t 1du = t-a$$lo que significa que $t$ representa la longitud de arco siempre que $a = 0$.
Una aplicación útil de este teorema es encontrar una parametrización alternativa de una curva dada, llamada parametrización de longitud de arco. Recuerda que cualquier función de valor vectorial se puede volver a parametrizar mediante un cambio de variables. Por ejemplo, si tenemos una función $r(t) = \lang 3cost, 3sent\rang, 0\le t\le 2\pi$ que parametriza un círculo de radio $3$, podemos cambiar el parámetro de $t$ a $4t$, obteniendo una nueva parametrización $\bold{r}(t) = \lang 3cos4t, 3sen4t\rang$. La nueva parametrización todavía define un círculo de radio 3, pero ahora solo necesitamos usar los valores $0\le t\le \pi/2$ para atravesar el círculo una vez.
Supongamos que encontramos la función de longitud de arco $s (t)$ y somos capaces de resolver esta función para $t$ como una función de $s$. Luego podemos volver a parametrizar la función original $r (t)$ sustituyendo la expresión por $t$ nuevamente en $r (t)$. La función de valor vectorial ahora se escribe en términos del parámetro $s$.
Como la variable $s$ representa la longitud del arco, llamamos a esto una parametrización de la función original $\bold{r} (t)$. Una ventaja de encontrar la parametrización de longitud de arco es que la distancia recorrida a lo largo de la curva a partir de $s = 0$ ahora es igual al parámetro $s$. La parametrización de longitud de arco también aparece en el contexto de la curvatura (que examinaremos más adelante en esta sección) y las integrales de línea, que estudiaremos en el capítulo de cálculo vectorial.
Antes de presentar un ejemplo, observa otra dedución para la longitud de arco en la siguiente escena interactiva, diseñada por Yin Bon Ku en GeoGebra (amplía la escena para una mejor interacción).
 |
Encontrar una parametrización de la longitud de arco |
Encuentra la parametrización de longitud de arco para cada una de las siguientes curvas:

Un tema importante relacionado con la longitud de arco es la curvatura. El concepto de curvatura proporciona una manera de medir cuán bruscamente gira una curva suave. Una circunferencia tiene una curvatura constante. Cuanto más pequeño es el radio de la circunferencia, mayor es la curvatura.
Piensa en conducir por una carretera. Supongamos que el camino se encuentra en un arco de una gran circunferencia. En este caso, apenas tendrías que girar la rueda para mantenerte en el camino. Ahora supón que el radio es más pequeño. En este caso, deberás girar más bruscamente para mantenerte en el camino. En el caso de una curva que no sea una circunferencia, a menudo es útil primero inscribir una circunferencia en la curva en un punto dado para que sea tangente a la curva en ese punto y "abrace" la curva lo más cerca posible en un vecindad del punto (Figura 3.6). La curvatura del gráfico en ese punto se define entonces como la curvatura de la circunferencia inscrita.

Figura 3.6. El gráfico representa la curvatura de una función $y = f (x)$. Cuanto más afinado es el giro en el gráfico, mayor es la curvatura y menor es el radio del círculo inscrito.
La fórmula en la definición de curvatura no es muy útil en términos de cálculo. Para usar la fórmula de curvatura, primero es necesario expresar $\bold{r}(t)$ en términos del parámetro de longitud de arco $s$, luego encontrar el vector tangente unitario $\bold{T}(s)$ para la función $r(s)$, luego tomar la derivada de $\bold{T}(s)$ con respecto a $s$.
Este es un proceso tedioso. Afortunadamente, hay fórmulas equivalentes para la curvatura.
Si $C$ es una curva tridimensional, la fórmula puede dar la curvatura
$$\kappa = \frac{\|\bold{r^{\prime}}(t)\times\bold{r^{\prime\prime}}\|}{\|\bold{r^{\prime}}(t)\|^3}\tag{$3.16$}$$Si $C$ es la gráfica de una función $y = f (x)$ y existen $y^{\prime}$ e $y^{\prime\prime}$, entonces la curvatura $\kappa$ en el punto $(x, y)$ viene dada por
$$\kappa = \frac{|y^{\prime\prime}|}{[1+(y^{\prime})^2]^(3/2)}\tag{$3.17$}$$La primera fórmula se sigue directamente de la regla de la cadena:
$$\frac{d\bold{T}}{dt} = \frac{d\bold{T}}{ds}\frac{ds}{dt}$$donde $s$ es la longitud del arco a lo largo de la curva $C$. Dividiendo ambos lados por $ds / dt$, y tomando la magnitud, obtenemos:
$$\bigg\|\frac{d\bold{T}}{ds}\bigg\| = \bigg\|\frac{\bold{T^{\prime}}(t)}{\frac{ds}{dt}} \bigg\|$$Como $ds/dt = \|\bold{r^{\prime}}(t)\|$, esto proporciona la fórmula para la curvatura $\kappa$ de una curva $C$ en términos de cualquier parametrización de $C$:
$$\kappa = \frac{\|\bold{T^{\prime}}(t)\|}{\|\bold{r^{\prime}}(t)\|}$$En el caso de una curva tridimensional, comenzamos con las fórmulas $\bold{T}(t) = (\bold{r^{\prime}}(t))/ \|\bold{r^{\prime}}(t)\|$ y $ds/dt = \|\bold{r^{\prime}}(t)\|$. Por lo tanto, $\bold{r^{\prime}}(t) = (ds/dt)\bold{T}(t)$. Podemos tomar la derivada de esta función usando la fórmula del producto escalar:
$$\bold{r^{\prime\prime}}(t)=\frac{d^2s}{dt^2}\bold{T}(t) + \frac{ds}{dt}\bold{T^{\prime}}(t)$$Usando estas dos últimas ecuaciones obtenemos
$$\begin{aligned} \bold{r^{\prime}}(t)\times\bold{r^{\prime\prime}}(t) &= \frac{ds}{dt}\bold{T}(t)\times\bigg(\frac{d^2s}{dt^2}\bold{T}(t) + \frac{ds}{dt}\bold{T^{\prime}}(t)\bigg)\\ &= \frac{ds}{dt}\bold{T}(t)\times\bold{T}(t) + \big(\frac{ds}{dt}\big)^2\bold{T}(t)\times\bold{T'}(t) \end{aligned}$$Como $\bold{T}(t)\times\bold{T}(t) = 0$, esto se reduce a
$$\bold{r^{\prime}}(t)\times\bold{r^{\prime\prime}}(t) = \bigg(\frac{ds}{dt}\bigg)^2\bold{T}(t)\times\bold{T^{\prime}}(t)$$Como $\bold{T^{\prime}}$ es paralelo a $N$ y $\bold{T}$ es ortogonal a $N$, se deduce que $\bold{T}$ y $\bold{T^{\prime}}$ son ortogonales. Esto significa que $\|\bold{T}\times\bold{T^{\prime}}\| = \|\bold{T}\|\|\bold{T^{\prime}}\|sen (\pi/2) = \|\bold{T^{\prime}}\|$, entonces
$$\bold{r^{\prime}}(t)\times\bold{r^{\prime\prime}}(t) = \bigg(\frac{ds}{dt}\bigg)^2\|\bold{T'}(t)\|$$Ahora resolvemos esta ecuación para $\|\bold{T^{\prime}}(t)\|$ y usamos el hecho de que $ds/dt = \|\bold{r^{\prime}}(t)\|$:
$$|\bold{T^{\prime}}(t)\| = \frac{\|\bold{r^{\prime}}(t)\times\bold{r^{\prime\prime}}(t)\|}{\|\bold{r^{\prime}}(t)\|^2}$$Luego, dividimos ambos lados entre $\|\bold{r'}(t)\|$. Esto da
$$\kappa = \frac{|\bold{T^{\prime}}(t)\|}{|\bold{r^{\prime}}(t)\|} = \frac{\|\bold{r^{\prime}}(t)\times\bold{r^{\prime\prime}}(t)\|}{\|\bold{r^{\prime}}(t)\|^3}$$Esto prueba la ecuación 3.16. Para probar la Ecuación 3.17, comenzamos con el supuesto de que la curva $C$ está definida por la función $y = f (x)$. Entonces, podemos definir $\bold{r}(t) = x\bold{i} + f(x)\bold{j} + 0\bold{k}$. Usando la fórmula anterior para la curvatura:
$$\begin{aligned} \bold{r^{\prime}}(t) &= \bold{i} +f^{\prime}(x)\bold{j}\\ \bold{r^{\prime\prime}}(t) &= f^{\prime\prime}(x)\bold{j}\\ \bold{r^{\prime}}(t)\times\bold{r^{\prime\prime}}(t) &= \begin{vmatrix} \bold{i} & \bold{j} & \bold{k}\\ 1 & f^{\prime}(x) & 0\\ 0 & f^{\prime\prime}(x) & 0 \end{vmatrix} = f^{\prime\prime}(x)\bold{k} \end{aligned}$$Por lo tanto,
 |
Encontrar la curvatura |
Encuentra la curvatura para cada una de las siguientes curvas en el punto dado:

En la página siguiente, puedes interactuar con una escena interactiva, diseñada por Bed Prasad Dhakal en GeoGebra. Observa que hemos parametrizado la primera curva del ejercicio anterior, para la cual, la curvatura es $\kappa = \frac{4}{25} = 0.16$ y es constante para cualquier valor de $t$. Puedes cambiar los componentes de la curva y el valor del parámetro $t$ (amplía la escena para una mejor interacción).
Hemos visto que la derivada $\bold{r^{\prime}}(t)$ de una función con valor vectorial es un vector tangente a la curva definida por $\bold{r}(t)$, y el vector tangente unitario $\bold{T}(t)$ se puede calcular dividiendo $\bold{r^{\prime}}(t)$ por su magnitud.
Al estudiar el movimiento en tres dimensiones, otros dos vectores son útiles para describir el movimiento de una partícula a lo largo de un camino en el espacio: el vector normal principal unitario y el vector binormal.
Observa que, por definición, el vector binormal es ortogonal tanto al vector tangente unitario como al vector normal. Además, $\bold{B}(t)$ es siempre un vector unitario. Esto se puede demostrar usando la fórmula para la magnitud de un producto cruz
$$\|\bold{B}(t)\| = \|\bold{T}(t)\times\bold{N}\| = \|\bold{T}(t)\|\|\bold{N}(t)\|sen\theta$$donde $\theta$ es el ángulo entre $\bold{T}(t)$ y $\bold{N}(t)$. Dado que $\bold{N}(t)$ es la derivada de un vector unitario, la propiedad (vii) de la derivada de una función con valor vectorial nos dice que $\bold{T}(t)$ y $\bold{N}(t)$ son ortogonales entre sí, por lo que $\theta =\pi/2$. Además, ambos son vectores unitarios, por lo que su magnitud es $1$. Por lo tanto, $\|\bold{T}(t)\|\|\bold{N}(t)\|sen\theta = (1)(1)sen(\pi /2) = 1$ y $\bold{B}(t)$ es un vector unitario.
El vector normal unitario principal puede ser difícil de calcular porque el vector tangente unitario implica un cociente, y este cociente a menudo tiene una raíz cuadrada en el denominador. En el caso tridimensional, encontrar el producto cruz del vector tangente unitario y el vector normal unitario puede ser aún más engorroso. Afortunadamente, tenemos fórmulas alternativas para encontrar estos dos vectores, que se presentan en el próximo apartado.
 |
Encontrar el vector normal principal unitario y el vector binormal |
Para cada una de las siguientes funciones con valores vectoriales, encuentra el vector normal principal unitario. Luego, si es posible, encuentra el vector binormal.

Para cualquier curva suave en tres dimensiones que esté definida por una función de valor vectorial, ahora tenemos fórmulas para el vector tangente unitario $\bold{T}$, el vector normal unitario $\bold{N}$ y el vector binormal $\bold{B}$. El vector normal unitario y el vector binormal forman un plano que es perpendicular a la curva en cualquier punto de la curva, llamado plano normal. Además, estos tres vectores forman un marco de referencia en un espacio tridimensional llamado marco de referencia de Frenet (también llamado marco TNB) (Figura 3.7). El plano determinado por los vectores $\bold{T}$ y $\bold{N}$ forman el plano osculador de $C$ en cualquier punto $P$ de la curva.
Figura 3.7. Esta figura representa un marco de referencia de Frenet. En cada punto $P$ en una curva tridimensional, los vectores tangente unitario, normal unitario y binormal forman un marco de referencia tridimensional.
Supongamos que formamos un círculo en el plano osculador de $C$ en el punto $P$ de la curva. Supón que el círculo tiene la misma curvatura que la curva en el punto $P$ y deja que el círculo tenga un radio $r$. Luego, la curvatura del círculo viene dada por $1/r$. Llamamos $r$ el radio de curvatura de la curva, y es igual al recíproco de la curvatura. Si este círculo se encuentra en el lado cóncavo de la curva y es tangente a la curva en el punto $P$, entonces este círculo se llama círculo osculador de $C$ en $P$, como se muestra en la siguiente figura y en la escena interactiva anterior.
Figura 3.8. En este círculo osculador, el círculo es tangente a la curva $C$ en el punto $P$ y comparte la misma curvatura.
 |
Encontrar la ecuación de un círculo osculador |
Encuentra la ecuación del círculo osculador de la hélice definida por la función $y = x^3−3x + 1$ en $x = 1$.


 Encuentra la longitud del arco de la curva en el intervalo dado.
Encuentra la longitud del arco de la curva en el intervalo dado.
102. $\bold{r}(t) = t^2\bold{i} + 14t\bold{j}, 0\le t \le 7$. Esta parte del gráfico se muestra aquí:
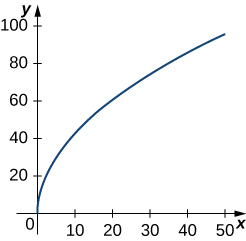
103. $\bold{r}(t) = t^2\bold{i}+(2t^2+1)\bold{j}, 1\le t \le 3$ (Solución)
104. $\bold{r}(t)= \lang 2sent,5t,2cost\rang ,0\le t\le \pi$. Esta parte del gráfico se muestra aquí:
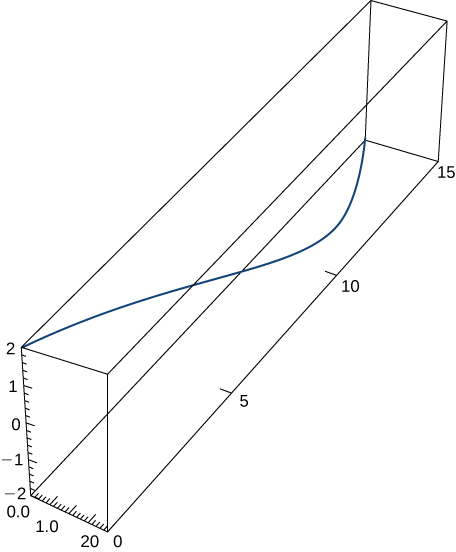
105. $\bold{r}(t) = \lang t^2 + 1,4t^3 + 3\rang , −1\le t\le 0$ (Solución) 106. $\bold{r}(t) = \lang e^{−t}cost, e^{−t}sent\rang$ durante el intervalo $[0, \frac{\pi}{2}]$. Aquí está la parte del gráfico en el intervalo indicado:
107. Encuentra la longitud de una vuelta de la hélice dada por $\bold{r}(t) = 12cost\bold{i} + 12sent\bold{j} + \sqrt{\frac{3}{4}}t\bold{k}$ (Solución) 108. Encuentra la longitud del arco de la función de valor vectorial $\bold{r}(t) = - t\bold{i} + 4t\bold{j} + 3t\bold{k}$ sobre $[0,1]$. 109. Una partícula viaja en un círculo con la ecuación de movimiento $\bold{r}(t) = 3cost\bold{i} + 3sent\bold{j} + 0\bold{k}$. Encuentra la distancia recorrida alrededor del círculo por la partícula (Solución). 110. Establece una integral para encontrar la circunferencia de la elipse con la ecuación $\bold{r}(t) = cost\bold{i} + 2sent\bold{j} + 0\bold{k}$. 111. Encuentra la longitud de la curva $\bold{r}(t) = \lang \sqrt{2t}, e^t, e^{−t}\rang$ en el intervalo $0\le t\le 1$. El gráfico se muestra aquí (Solución):
112. Encuentra la longitud de la curva $\bold{r}(t) = \lang 2sent, 5t, 2cost\rang$ para $t\isin [−10,10]$. 113. La función de posición para una partícula es $\bold{r}(t) = acos (\omega t)\bold{i} + bsen(\omega t)\bold{j}$. Encuentra el vector tangente unitario y el vector normal unitario en $t = 0$ (Solución). 114. Dado $\bold{r}(t) = acos(\omega t)\bold{i} + bsen(\omega t)\bold{j}$, encuentra el vector binormal $\bold{B}(0)$.
115. Dado $\bold{r}(t) = \lang 2e^t, e^tcost, e^tsent\rang$, determina el vector tangente $\bold{T}(t)$ (Solución). 116. Dado $\bold{r}(t) = \lang 2e^t, e^tcost, e^tsent\rang$, determina la unidad de vector tangente $\bold{T}(t)$ evaluada en $t = 0$. 117. Dado $\bold{r}(t) = \lang 2e^t, e^tcost, e^tsent\rang$, encuentra el vector normal unitario $\bold{N}(t)$ evaluado en $t = 0, \bold{N}(0)$ (Solución). 118. Dado $\bold{r}(t) = \lang 2e^t, e^tcost, e^tsent\rang$, encuentra el vector normal unitario evaluado en $t = 0$. 119. Dado $\bold{r}(t) = t\bold{i} + t^2\bold{j} + t\bold{k}$, encuentra el vector tangente unitario $\bold{T}(t)$. El gráfico se muestra aquí (Solución):
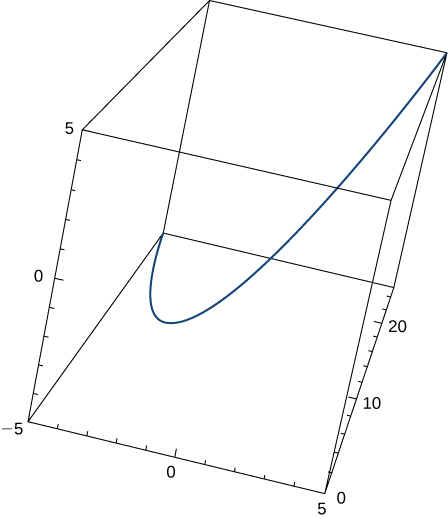
120. Encuentra el vector tangente unitario $\bold{T}(t)$ y el vector normal unitario $\bold{N}(t)$ en $t = 0$ para la curva plana $\bold{r}(t) = \lang t^3−4t, 5t^2−2\rang$. El gráfico se muestra aquí:
121. Encuentra la unidad de vector tangente $\bold{T}(t)$ para $\bold{r}(t) = 3t\bold{i} + 5t^2\bold{j} + 2t\bold{k}$ (Solución) 122. Encuentra el vector normal principal para la curva $\bold{r}(t) = \lang 6cost, 6sent\rang$ en el punto determinado por $t = π / 3$. 123. Encuentra $\bold{T}(t)$ para la curva $\bold{r}(t) = (t^3−4t)\bold{i} + (5t^2−2)\bold{j}$ (Solución). 124. Encuentra $\bold{N}(t)$ para la curva $\bold{r}(t) = (t^3−4t)\bold{i} + (5t^2−2)\bold{j}$. 125. Encuentra la unidad del vector normal $\bold{N}(t)$ para $\bold{r}(t) = \lang 2sent, 5t, 2cost\rang$ (Solución). 126. Encuentra el vector tangente unitario $\bold{T}(t)$ para $\bold{r}(t) = \lang 2sent, 5t, 2cost\rang$. 127. Encuentra la función de longitud de arco $s(t)$ para el segmento de recta dado por $\bold{r}(t) = \lang 3−3t, 4t\rang$. Escribe $r$ como parámetro de $s$ (Solución). 128. Parametriza la hélice $\bold{r}(t) = cost\bold{i} + sent\bold{j} + t\bold{k}$ utilizando el parámetro de longitud de arco $s$, desde $t = 0$.
129. Parametriza la curva usando el parámetro de longitud de arco $s$, en el punto en el que $t = 0$ para $\bold{r}(t) = e^tsent\bold{i} + e^tcost\bold{j}$ (Solución). 130. Encuentra la curvatura de la curva $\bold{r}(t) = 5cost\bold{i} + 4sent\bold{j}$ en $t = π / 3$. (Nota: el gráfico es una elipse).
131. Encuentra la coordenada $x$ en la que la curvatura de la curva $y = 1 / x$ es un valor máximo (Solución). 132. Encuentra la curvatura de la curva $\bold{r}(t) = 5cost\bold{i} + 5sent\bold{j}$. ¿La curvatura depende del parámetro $t$? 133. Encuentra la curvatura $\kappa$ para la curva $y = x − \frac{1}{4}x^2$ en el punto $x = 2$ (Solución). 134. Encuentra la curvatura $\kappa$ para la curva $y = \frac{1}{3}x^3$ en el punto $x = 1$. 135. Encuentra la curvatura $\kappa$ de la curva $\bold{r}(t) = t\bold{i} + 6t^2\bold{j} + 4t\bold{k}$. El gráfico se muestra a continuación (Solución):
136. Encuentra la curvatura de $\bold{r}(t) = \lang 2sent, 5t, 2cost\rang$. 137. Encuentra la curvatura de $\bold{r}(t) = \sqrt{2}t\bold{i} + e^t\bold{j} + e^{−t}\bold{k}$ en el punto $P (0,1,1)$ (Solución). 138. ¿En qué punto la curva $y = e^x$ tiene curvatura máxima? 139. ¿Qué le sucede a la curvatura cuando $x \to \infin$ para la curva $y = e^x$? (Solución) 140. Encuentra el punto de curvatura máxima en la curva $y = lnx$. 141. Encuentra las ecuaciones del plano normal y el plano osculador de la curva $\bold{r}(t) = \lang 2sen(3t), t, 2cos(3t)\rang$ en el punto $(0, \pi, −2)$ (Solución). 142. Encuentra las ecuaciones de los círculos osculantes de la elipse $4y^2 + 9x^2 = 36$ en los puntos $(2,0)$ y $(0,3)$. 143. Encuentra la ecuación para el plano osculador en el punto $t = \pi/4$ en la curva $\bold{r}(t) = cos(2t)\bold{i} + sen(2t)\bold{j} + t$ (Solución). 144. Encuentra el radio de curvatura de $6y = x^3$ en el punto $(2,\frac{4}{3})$.
145. Encuentra la curvatura en cada punto $(x, y)$ en la hipérbola $\bold{r}(t) = \lang acosh(t), bsenh(t)\rang$ (Solución). 146. Calcula la curvatura de la hélice circular $\bold{r}(t) = rsen(t)\bold{i} + rcos(t)\bold{j} + t\bold{k}$. 147. Encuentra el radio de curvatura de $y = ln (x + 1)$ en el punto $(2, ln3)$ (Solución). 148. Encuentra el radio de curvatura de la hipérbola $xy = 1$ en el punto $(1,1)$.
 Una partícula se mueve a lo largo de la curva plana $C$ descrita por $\bold{r}(t) = t\bold{i} + t^2\bold{j}$. Resuelve los siguientes problemas.
Una partícula se mueve a lo largo de la curva plana $C$ descrita por $\bold{r}(t) = t\bold{i} + t^2\bold{j}$. Resuelve los siguientes problemas.
149. Encuentra la longitud de la curva sobre el intervalo $[0,2]$ (Solución). 150. Encuentra la curvatura de la curva plana en $t = 0,1,2$. 151. Describe la curvatura a medida que $t$ aumenta de $t = 0$ a $t = 2$ (Solución).
 La superficie de una copa grande se forma al girar la gráfica de la función $y = 0.25x^{1.6}$ de $x = 0$ a $x = 5$ alrededor del eje y (medido en centímetros).
La superficie de una copa grande se forma al girar la gráfica de la función $y = 0.25x^{1.6}$ de $x = 0$ a $x = 5$ alrededor del eje y (medido en centímetros).
152. [T] Usa la tecnología para graficar la superficie. 153. Encuentra la curvatura $kappa$ de la curva generadora en función de $x$ (Solución). 154. [T] Usa tecnología para graficar la función de curvatura.
Ahora hemos visto cómo describir curvas en el plano y en el espacio, y cómo determinar sus propiedades, como la longitud de arco y la curvatura. Todo esto lleva al objetivo principal de este capítulo, que es la descripción del movimiento a lo largo de curvas planas y curvas espaciales. Ahora tenemos todas las herramientas que necesitamos. En esta sección, reunimos estas ideas y veremos cómo usarlas.
Nuestro punto de partida es utilizar funciones con valores vectoriales para representar la posición de un objeto en función del tiempo. Todo el material siguiente se puede aplicar a curvas en el plano o a curvas espaciales. Por ejemplo, cuando observamos la órbita de los planetas, todas las curvas que definen estas órbitas se encuentran en un plano porque son elípticas. Sin embargo, una partícula que viaja a lo largo de una hélice se mueve en una curva en tres dimensiones.
Como $\bold{r}(t)$ puede estar en dos o tres dimensiones, estas funciones con valores vectoriales pueden tener dos o tres componentes. En dos dimensiones, definimos $\bold{r}(t) = x(t)\bold{i} + y(t)\bold{r}$ y en tres dimensiones $\bold{r}(t) = x(t)\bold{i} + y(t)\bold{j} + z(t)\bold{k}$. Entonces, la velocidad, la aceleración y la rapidez se pueden escribir como se muestra en la siguiente tabla.
| Cantidad | Dos dimensiones | Tres dimensiones |
| Posición | $\bold{r}(t) = x(t)\bold{i}+y(t)\bold{j}$ | $\bold{r}(t) = x(t)\bold{i}+y(t)\bold{j}+z(t)\bold{k}$ |
| Velocidad | $\bold{v}(t) = x^{\prime}(t)\bold{i}+y^{\prime}(t)\bold{j}$ | $\bold{v}(t) = x^{\prime}(t)\bold{i}+y^{\prime}(t)\bold{j}+z^{\prime}(t)\bold{k}$ |
| Aceleración | $\bold{a}(t) = x^{\prime\prime}(t)\bold{i}+y^{\prime\prime}(t)\bold{j}$ | $\bold{a}(t) = x^{\prime\prime}(t)\bold{i}+y^{\prime\prime}(t)\bold{j}+z^{\prime\prime}(t)\bold{k}$ |
| Rapidez | $v(t) = (x^{\prime}(t))^2+(y^{\prime}(t))^2$ | $v(t) = (x^{\prime}(t))^2+(y^{\prime}(t))^2+(z^{\prime}(t))^2$ |
Tabla 3.4 Fórmulas para posición, velocidad, aceleración y rapidez
 |
Estudiar el movimiento a lo largo de una parábola |
Una partícula se mueve en una trayectoria parabólica definida por la función de valor vectorial $\bold{r}(t) = t^2\bold{i} + \sqrt{5 − t^2}\bold{j}$, donde $t$ mide el tiempo en segundos.

Para obtener una mejor comprensión de los vectores de velocidad y aceleración, imagina que conduces por una carretera con curvas. Si no giras el volante, continuarías en línea recta y saldrías corriendo de la carretera. La velocidad a la que viajas cuando sales de la carretera, junto con la dirección, proporciona un vector que representa tu velocidad, como se ilustra en la siguiente figura.
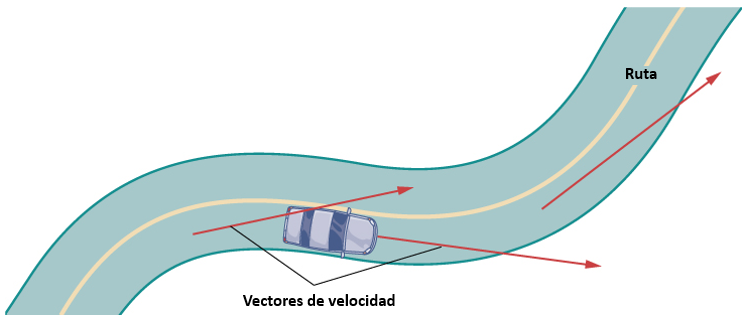
Figura 3.12. En cada punto a lo largo de una carretera recorrida por un automóvil, el vector de velocidad del automóvil es tangente a la ruta recorrida por el automóvil.
Sin embargo, el hecho de que debes girar el volante para permanecer en el camino indica que tu velocidad siempre está cambiando (incluso si tu rapidez no lo está) porque tu dirección cambia constantemente para mantenerte en el camino.
A medida que giras a la derecha, tu vector de aceleración también apunta a la derecha. A medida que giras hacia la izquierda, tu vector de aceleración apunta hacia la izquierda. Esto indica que tus vectores de velocidad y aceleración cambian constantemente, independientemente de si tu rapidez real varía (Figura 3.13).
Figura 3.13. La línea punteada representa la trayectoria de un objeto (un automóvil, por ejemplo). El vector de aceleración apunta hacia el interior del giro en todo momento.
Podemos combinar algunos de los conceptos discutidos en el apartado anterior sobre Longitud de arco y Curvatura con el vector de aceleración para obtener una comprensión más profunda de cómo este vector se relaciona con el movimiento en el plano y en el espacio.
Recuerda que el vector tangente unitario $\bold{T}$ y el vector normal unitario $\bold{N}$ forman un plano osculador en cualquier punto $P$ en la curva definida por una función de valor vectorial $\bold{r}(t)$. El siguiente teorema muestra que el vector de aceleración $\bold{a}(t)$ se encuentra en el plano de osculación y puede escribirse como una combinación lineal del vector tangente unitario y los vectores unitarios normales.
Debido a que $\bold{v}(t) = \bold{r^{\prime}}(t)$ y $\bold{T}(t) = \frac{\bold{r^{\prime}}(t)}{\|\bold{r^{\prime}}(t)\|}$, tenemos $\bold{v}(t) = \|\bold{r^{\prime}}(t)\|\bold{T}(t) = v(t)\bold{T}(t)$. Ahora diferenciamos esta ecuación:
$$\bold{a}(t) = \bold{v^{\prime}}(t) = \frac{d}{dt}(v(t)\bold{T}(t)) = v^{\prime}(t)\bold{T}(t) + v(t)\bold{T^{\prime}}(t)$$Como $\bold{N}(t) = \frac{\bold{T^{\prime}}(t)}{\|\bold{T^{\prime}}(t)\|}$, sabemos que $\bold{T^{\prime}}(t) = \|\bold{T^{\prime}}(t)\|\bold{N}(t)$, entonces
Una fórmula para la curvatura es $\kappa = \frac{\|\bold{T^{\prime}}(t)\|}{\|\bold{r^{\prime}}(t)\|}$, entonces $\|\bold{T^{\prime}}(t)\| = \kappa \|\bold{r^{\prime}}(t)\| = \kappa v(t)$. Esto da $\bold{a}(t) = v^{\prime}(t)\bold{T}(t) + \kappa (v(t))^2\bold{T}(t)$.
Los coeficientes de $\bold{T}(t)$ y $\bold{N}(t)$ se denominan componente tangencial de la aceleración y componente normal de la aceleración, respectivamente. Escribimos $a_{\bold{T}}$ para denotar el componente tangencial y $a_{\bold{N}}$ para denotar el componente normal.
El componente normal de la aceleración también se denomina componente centrípeto de la aceleración o, a veces, componente radial de la aceleración. Para comprender la aceleración centrípeta, supón que viajas en un automóvil en una pista circular a una velocidad constante. Luego, como vimos anteriormente, el vector de aceleración apunta hacia el centro de la pista en todo momento. Como conductor del automóvil, sientes un tirón hacia el exterior de la pista porque estás girando constantemente. Esta sensación actúa en la dirección opuesta de la aceleración centrípeta. Lo mismo es válido para los caminos no circulares. La razón es que tu cuerpo tiende a viajar en línea recta y resiste la fuerza resultante de la aceleración que te empuja hacia un lado. Ten en cuenta que en el punto $B$ de la figura 3.14, el vector de aceleración apunta hacia atrás. Esto se debe a que el automóvil está desacelerando a medida que avanzas en la curva.
Figura 3.14. Los componentes tangencial y normal de la aceleración pueden usarse para describir el vector de aceleración.
Los vectores unitarios tangencial y normal, en cualquier punto dado de la curva, proporcionan un marco de referencia en ese punto. Los componentes tangencial y normal de la aceleración son las proyecciones del vector de aceleración en $\bold{T}$ y $\bold{N}$, respectivamente.
 |
Encontrar los componentes de aceleración |
Una partícula se mueve en una ruta definida por la función de valor vectorial $\bold{r}(t) = t^2\bold{i} + (2t − 3)\bold{j} + (3t^2−3t)\bold{k}$, donde $t$ mide el tiempo en segundos y la distancia se mide en pies.

Ahora veamos una aplicación de funciones con valores vectoriales. En particular, consideremos el efecto de la gravedad en el movimiento de un objeto a medida que viaja por el aire y cómo determina la trayectoria resultante de ese objeto. A continuación, ignoramos el efecto de la resistencia del aire. Esta situación, con un objeto que se mueve con una velocidad inicial pero sin fuerzas que actúen sobre él aparte de la gravedad, se conoce como movimiento de proyectiles. Describe el movimiento de objetos desde pelotas de golf hasta pelotas de béisbol y desde flechas hasta balas de cañón.
Primero tenemos que elegir un sistema de coordenadas. Si estamos parados en el origen de este sistema de coordenadas, entonces elegimos que el eje $y$ positivo esté hacia arriba, el eje $y$ negativo hacia abajo, y el eje $x$ positivo hacia adelante (es decir, lejos del lanzador de el objeto).
El efecto de la gravedad es hacia abajo, por lo que la segunda ley de Newton nos dice que la fuerza sobre el objeto resultante de la gravedad es igual a la masa del objeto multiplicada por la aceleración resultante de la gravedad, o $\bold{F}_g = mg$, donde $\bold{F}_g$ representa la fuerza de la gravedad y $g$ representa la aceleración resultante de la gravedad en la superficie de la Tierra. El valor de $g$ en el sistema de medición inglés es de aproximadamente $32 pies / seg^2$ y de aproximadamente $9.8 m / seg^2$ en el sistema métrico. Esta es la única fuerza que actúa sobre el objeto. Como la gravedad actúa en dirección descendente, podemos escribir la fuerza resultante de la gravedad en la forma $\bold{F}_g = −mg\bold{j}$, como se muestra en la siguiente figura.
Figura 3.15. Un objeto está cayendo bajo la influencia de la gravedad.
La segunda ley de Newton también nos dice que $\bold{F} = m\bold{a}$, donde $\bold{a}$ representa el vector de aceleración del objeto. Esta fuerza debe ser igual a la fuerza de la gravedad en todo momento, por lo que sabemos que
$$\begin{aligned} \bold{F} &= \bold{F}_g\bold{j}\\ m\bold{a} &= -mg\\ \bold{a} &= -g\bold{j} \end{aligned}$$Ahora recurrimos al hecho de que el vector de aceleración es la primera derivada del vector de velocidad. Por lo tanto, podemos reescribir la última ecuación en la forma
$$\bold{v^{\prime}}(t) = - g\bold{j}$$Al tomar la antiderivada de cada lado de esta ecuación obtenemos
$$\begin{aligned} \bold{v}(t) &= \int - g\bold{j}dt\\ &= -gt\bold{j} + \bold{C_1} \end{aligned}$$para algún vector constante $\bold{C_1}$. Para determinar el valor de este vector, podemos usar la velocidad del objeto en un tiempo fijo, digamos en el tiempo $t = 0$. Llamamos a esta velocidad la velocidad inicial: $\bold{v}(0) = \bold{v_0}$. Por lo tanto, $\bold{v}(0) = - g(0)\bold{j} + \bold{C_1} = \bold{v_0}$ y $\bold{C_1} = \bold{v_0}$. Esto da el vector de velocidad como $\bold{v}(t) = - gt\bold{j} + \bold{v_0}$.
A continuación, usamos el hecho de que la velocidad $\bold{v}(t)$ es la derivada de la posición $\bold{s}(t)$. Esto da la ecuación
$$\bold{s^{\prime}}(t) = - gt\bold{j} + \bold{v_0}$$Tomar la antiderivada de ambos lados de esta ecuación conduce a
$$\begin{aligned} \bold{s}(t) &= \int (-gt\bold{j}+\bold{v_0})dt\\ &= -\frac{1}{2}gt^2\bold{j}+\bold{v_0}t + \bold{C_2} \end{aligned}$$con otro vector constante desconocido $\bold{C_2}$. Para determinar el valor de $\bold{C_2}$, podemos usar la posición del objeto en un momento dado, digamos en el tiempo $t = 0$.
Llamamos a esta posición la posición inicial: $\bold{s}(0) = \bold{s_0}$. Por lo tanto, $\bold{s}(0) = -(1/2)g(0)^2\bold{j} + \bold{v_0}(0) + \bold{C_2} = \bold{s_0}$ y $\bold{C_2} = \bold{s_0}$. Esto proporciona la posición del objeto en cualquier momento como
$$\bold{s}(t) = -\frac{1}{2}gt^2\bold{j}+\bold{v_0}t+\bold{s_0}$$Echemos un vistazo más de cerca a la velocidad inicial y la posición inicial. En particular, supón que el objeto se lanza hacia arriba desde el origen en un ángulo $\theta$ con la horizontal, con una velocidad inicial $\bold{v_0}$
¿Cómo podemos modificar el resultado anterior para reflejar este escenario? Primero, podemos suponer que se arroja desde el origen. Si no, entonces podemos mover el origen al punto desde donde se arroja. Por lo tanto, $\bold{s_0} = 0$, como se muestra en la siguiente figura.
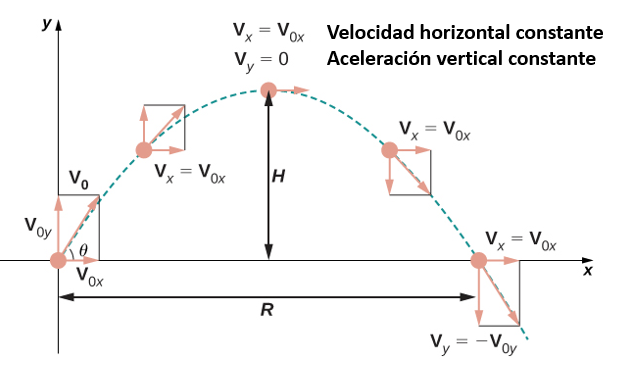
Figura 3.16. Movimiento del proyectil cuando el objeto se lanza hacia arriba en un ángulo $\theta$. El movimiento horizontal está a velocidad constante y el movimiento vertical está a aceleración constante.
Podemos reescribir el vector de velocidad inicial en la forma $\bold{v_0} = v_0 cos\theta \bold{i} + v_0 sen\theta\bold{j}$. Entonces la ecuación para la función de posición $\bold{s}(t)$ se convierte en
$$\begin{aligned} \bold{s}(t) &= −\frac{1}{2}gt^2\bold{j}+v_0tcos\theta\bold{i}+ v_0 tsen\theta\bold{j}\\ &= v_0 tcos\theta\bold{i}+v_0 tsen\theta\bold{j}−\frac{1}{2}gt^2\bold{j}\\ &= v_0 tcos\theta\bold{i}+(v_0 tsen\theta−\frac{1}{2}gt^2)\bold{j} \end{aligned}$$El coeficiente de $\bold{i}$ representa la componente horizontal de $\bold{s}(t)$ y es la distancia horizontal del objeto desde el origen en el tiempo $t$. El valor máximo de la distancia horizontal (medido a la misma altitud inicial y final) se denomina rango $R$. El coeficiente de $\bold{j}$ representa la componente vertical de $\bold{s}(t)$ y es la altitud del objeto en el tiempo $t$.
El valor máximo de la distancia vertical es la altura $H$.
 |
Movimiento de una bala de cañón |
Durante una celebración, se dispara una bala de cañón desde un cañón en un acantilado hacia el agua. El cañón apunta a un ángulo de $30^o$ sobre la horizontal y la velocidad inicial de la bala de cañón es de $600\; pies / seg$. El acantilado está a 100 pies sobre el agua (Figura 3.17).
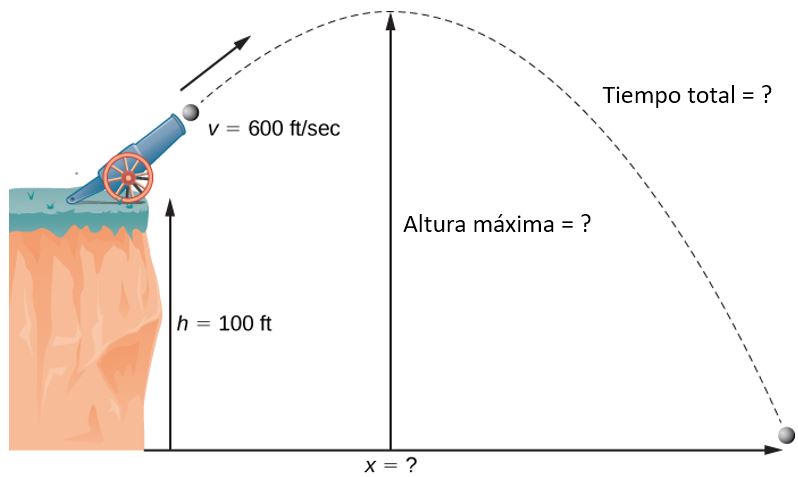
Figura 3.17. El vuelo de una bala de cañón (ignorando la resistencia del aire) es un movimiento de un proyectil.

En la siguiente escena interactiva, tomada de PhET Interactive Simulations de la University of Colorado Boulder, puedes lanzar diferentes tipos de objetos desde un cañón, con el objetivo de dar en el blanco. Sin embargo, si seleccionas la opción "vectores", puedes observar los componentes vectoriales de la velocidad y la aceleración y verificar que la velocidad horizontal y la aceleración vertical permanecen constantes; para ello, activa los componentes de velocidad y aceleración y, luego, pulsas el botón "pausa" y vas adelantando lentamente la animación.
Queda una última pregunta: en general, ¿cuál es la distancia máxima que puede recorrer un proyectil, dada su velocidad inicial? Para determinar esta distancia, asumimos que el proyectil se dispara desde el nivel del suelo y deseamos que regrese al nivel del suelo.
En otras palabras, queremos determinar una ecuación para el rango. En este caso, la ecuación de movimiento de proyectil es
$$\bold{s}(t) = v_0 tcos\theta\bold{i}+\big(v_0 tsen\theta −\frac{1}{2}gt^2\big)\bold{j}$$Hacer el segundo componente igual a cero y resolver $t$ produce
$$\begin{aligned} v_0 tsen\theta −\frac{1}{2}gt^2)\bold{j} &= 0\\ t\big(v_0 sen\theta−\frac{1}{2}gt\big) \end{aligned}$$Por lo tanto, $t = 0$ o $t = \frac{2v_0 sen\theta}{g}$. Estamos interesados en el segundo valor de $t$, por lo que lo sustituimos en $\bold{s}(t)$, que da
$$\begin{aligned} \bold{s}\bigg(\frac{2v_0 sen\theta}{g}\bigg) &= v_0\bigg(\frac{2v_0 sen\theta}{g}\bigg)cos\theta\bold{i} +\Bigg(v_0\bigg(\frac{2v_0 sen\theta}{g}\bigg)sen\theta\\ &- \frac{1}{2}g\bigg(\frac{2v_0sen\theta}{g}\bigg)^2\Bigg)\bold{j}\\ &= \frac{2v_0^2 sen\theta cos\theta}{g}\bold{i}\\ &= \frac{v_0^2sen2\theta}{g}\bold{i} \end{aligned}$$Por lo tanto, la expresión para el alcance o rango de un proyectil disparado en un ángulo $\theta$ es
$$R = \frac{v_0^2sen2\theta}{g}\bold{i}$$La única variable en esta expresión es $\theta$. Para maximizar la distancia recorrida, toma la derivada del coeficiente de $\bold{i}$ con respecto a $\theta$ y hazlo igual a cero:
$$\begin{aligned} \frac{d}{d\theta}\bigg(\frac{v_0^2 sen2\theta}{g}\bigg) &= 0\\ \frac{2v_0^2cos2\theta}{g} &= 0\\ \theta &= 45^o \end{aligned}$$Este valor de $\theta$ es el valor positivo más pequeño que hace que la derivada sea igual a cero. Por lo tanto, en ausencia de resistencia al aire, el mejor ángulo para disparar un proyectil (para maximizar el alcance) está en un ángulo de $45^o$. La distancia que viaja viene dada por
$$\bold{s}\bigg(\frac{2v_0sen45}{g} \bigg) = \frac{v_0^2sen90}{g}\bold{i} = \frac{v_0^2}{g}\bold{j}$$Por lo tanto, el rango para un ángulo de $45^o$ es $v_0^2/g$.
A principios del siglo XVII, Johannes Kepler pudo utilizar los datos sorprendentemente precisos de su mentor Tycho Brahe, para formular sus tres leyes de movimiento planetario, ahora conocidas como las leyes de movimiento planetario de Kepler. Estas leyes también se aplican a otros objetos en el sistema solar en órbita alrededor del Sol, como los cometas (por ejemplo, el cometa Halley) y los asteroides. Las variaciones de estas leyes se aplican a los satélites en órbita alrededor de la Tierra.
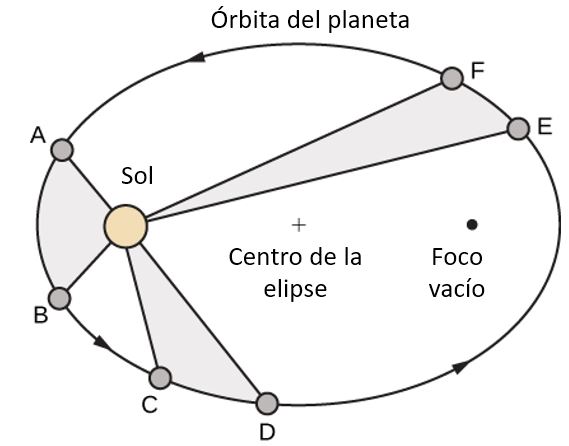
Figura 3.18. La primera y segunda ley de Kepler se muestran aquí. El Sol está ubicado en un foco de la órbita elíptica de cualquier planeta. Además, las áreas sombreadas son todas iguales, suponiendo que la cantidad de tiempo medida a medida que el planeta se mueve es la misma para cada región.
La tercera ley de Kepler es especialmente útil cuando se usan unidades apropiadas. En particular, $1\;\text{ unidad astronómica }\;$ se define como la distancia promedio de la Tierra al Sol, y ahora se reconoce que es $149,597,870,700\; mo$ aproximadamente $93,000,000\;\text{ millas}$. Por lo tanto, escribimos $1 A.U. = 93,000,000\;\text{ mi}$. Dado que el tiempo que tarda la Tierra en orbitar al Sol es de 1 año, utilizamos los años terrestres por unidades de tiempo. Luego, sustituyendo 1 año por el período de la Tierra y 1 A.U. para la distancia promedio al Sol, la tercera ley de Kepler se puede escribir como
$$T_p^2 = D_p^3$$para cualquier planeta en el sistema solar, donde $T_P$ es el período de ese planeta medido en años terrestres y $D_P$ es la distancia promedio de ese planeta al Sol medido en unidades astronómicas. Por lo tanto, si conocemos la distancia promedio de un planeta al Sol (en unidades astronómicas), podemos calcular la duración de su año (en años terrestres) y viceversa.
Las leyes de Kepler fueron formuladas en base a observaciones de Brahe; sin embargo, no se probaron formalmente hasta que Sir Isaac Newton pudo aplicar el cálculo. Además, Newton pudo generalizar la tercera ley de Kepler a otros sistemas orbitales, como una luna que orbita alrededor de un planeta. La tercera ley original de Kepler solo se aplica a los objetos que orbitan alrededor del Sol.
Probemos ahora la primera ley de Kepler usando el cálculo de funciones con valores vectoriales. Primero necesitamos un sistema de coordenadas.
Coloquemos el Sol en el origen del sistema de coordenadas y dejemos que la función de valor vectorial $\bold{r}(t)$ represente la ubicación de un planeta en función del tiempo. Newton probó la ley de Kepler usando su segunda ley de movimiento y su ley de gravitación universal. La segunda ley de movimiento de Newton se puede escribir como $\bold{F} = m\bold{a}$, donde $\bold{F}$ representa la fuerza neta que actúa en el planeta. Su ley de gravitación universal se puede escribir en la forma $\bold{F} = −\frac{GmM}{\|r\|^2}\cdot\frac{r}{\|r\|}$, lo que indica que la fuerza resultante de la atracción gravitacional del Sol apunta hacia el Sol y tiene una magnitud $\frac{GmM}{\|r\|^2}$ (Figura 3.19).
Figura 3.19. La fuerza gravitacional entre la Tierra y el Sol es igual a la masa de la tierra multiplicada por su aceleración.
Al establecer estas dos fuerzas iguales entre sí, y utilizando el hecho de que $\bold{a}(t) = \bold{v^{\prime}}(t)$, obtenemos
$$m\bold{v^{\prime}}(t) = −\frac{GmM}{\|r\|^2}\cdot\frac{r}{\|r\|}$$que puede reescribirse como
$$\frac{d\bold{v}}{dt} = −\frac{GmM}{\|r\|^3}\bold{r}$$Esta ecuación muestra que los vectores $\frac{d\bold{v}}{dt}$ y $\bold{r}$ son paralelos entre sí, por lo que $\frac{d\bold{v}}{dt}\times\bold{r} = 0$. A continuación, diferenciemos $\bold{r}\times\bold{v}$ con respecto al tiempo:
$$\frac{d}{dt}\bold{r}\times\bold{v} = \frac{d\bold{r}}{dt}\times\bold{v} + \bold{r}\times\frac{d\bold{v}}{dt} = \bold{v}\times\bold{v} = 0$$Esto demuestra que $\bold{r}\times\bold{v}$ es un vector constante, que llamamos $\bold{C}$. Dado que $\bold{r}$ y $\bold{v}$ son perpendiculares a $\bold{C}$ para todos los valores de $t$, deben estar en un plano perpendicular a $\bold{C}$. Por lo tanto, el movimiento del planeta se encuentra en un plano.
A continuación calculamos la expresión $d\bold{v}/dt\times\bold{C}$:
$$\frac{d\bold{v}}{dt}\times\bold{C} = −\frac{GmM}{\|r\|^3}\bold{r}\times (\bold{r}\times\bold{v}) = −\frac{GmM}{\|r\|^3}[(\bold{r}\cdot\bold{v})\bold{r}-(\bold{r}\cdot\bold{r})\bold{v}]\tag{$3.26$}$$Esto demuestra que $\bold{r}\times\bold{v}$ es un vector constante, que llamamos $\bold{C}$. Dado que $\bold{r}$ y $\bold{v}$ son perpendiculares a $\bold{C}$ para todos los valores de $t$, deben estar en un plano perpendicular a $\bold{C}$. Por lo tanto, el movimiento del planeta se encuentra en un plano.
A continuación calculamos la expresión $d\bold{v}/ dt\times \bold{C}$:
$$\frac{d}{dt}(\bold{r}\cdot\bold{r}) = \frac{d\bold{r}}{dt}\cdot\bold{r} + \bold{r}\cdot\frac{d\bold{r}}{dt} = 2\bold{r}\cdot\frac{d\bold{r}}{dt} = 2\bold{r}\cdot\bold{v} \tag{$3.27$}$$Como $\bold{r}\cdot\bold{r} = \|\bold{r}\|^2$, también tenemos
Combinando las ecuaciones 3.27 y 3.28, obtenemos
$$\begin{aligned} 2\bold{r}\cdot\bold{v} &= 2\|\bold{r}\|\frac{d}{dt}\|\bold{r}\|\\ \bold{r}\cdot\bold{v} &= \|\bold{r}\|\frac{d}{dt}\|\bold{r}\| \end{aligned}$$Sustituyendo lo anterior en la ecuación 3.26 nos da
$$\begin{aligned} \frac{d\bold{v}}{dt} \times\bold{C} &= -\frac{GM}{\|\bold{r}\|^3}[(\bold{r}\cdot\bold{v})\bold{r} - (\bold{r}\cdot\bold{r})\bold{v}]\\ &= -\frac{GM}{\|\bold{r}\|^3}\bigg[\|\bold{r}\|(\frac{d}{dt}\|\bold{r}\|)\bold{r} - \|\bold{r}\|^2\bold{v}\bigg]\\ &= -GM\bigg[\frac{1}{\|\bold{r}\|^2}(\frac{d}{dt}\|\bold{r}\|)\bold{r} - \frac{1}{\|\bold{r}\|}\bold{v}\bigg]\\ &= GM\bigg[\frac{\bold{v}}{\|\bold{r}\|} - \frac{r}{\|\bold{r}\|^2}(\frac{d}{dt}\|\bold{r}\|) \bigg] \end{aligned}\tag{$3.29$}$$Sin embargo,
$$\begin{aligned} \frac{d}{dt}\frac{\bold{r}}{\|\bold{r}\|} &= \frac{\frac{d}{dt}(\bold{r})\|\bold{r}\| - \bold{r}\frac{d}{dt}\|\bold{r}\|}{\|\bold{r}\|^2}\\ &= \frac{\frac{d\bold{r}}{dt}}{\|\bold{r}\|} - \frac{\bold{r}}{\|\bold{r}\|^2}\frac{d}{dt}\|\bold{r}\|\\ &= \frac{\bold{v}}{\|\bold{r}\|} - \frac{\bold{r}}{\|\bold{r}\|^2}\frac{d}{dt}\|\bold{r}\| \end{aligned}$$Por lo tanto, la ecuación 3.29 se convierte en
$$\frac{d\bold{v}}{dt}\times\bold{C} = GM\bigg(\frac{d}{dt}\frac{\bold{r}}{\|\bold{r}\|}\bigg)$$Como $\bold{C}$ es un vector constante, podemos integrar ambos lados y obtener
$$\bold{v}\times\bold{C} = GM\frac{\bold{r}}{\|\bold{r}\|} + \bold{D},$$donde $\bold{D}$ es un vector constante. Nuestro objetivo es resolver para $|\bold{r}\|$. Comencemos calculando $\bold{r}\cdot(\bold{v}\times\bold{C})$:
$$\begin{aligned} \bold{r}\cdot(\bold{v}\times\bold{C}) &= \bold{r}\cdot\bigg(GM\frac{\|\bold{r}\|^2}{\|\bold{r}\|}+\bold{D}\bigg)\\ &= GM\frac{\|\bold{r}\|^2}{\|\bold{r}\|} + \bold{r}\cdot\bold{D} = GM\|\bold{r}\|+\bold{r}\cdot\bold{D} \end{aligned}$$Sin embargo, $\bold{r}\cdot(\bold{v}\times\bold{C}) = (\bold{r}\times\bold{v})\cdot\bold{C}$, entonces
$$\bold{r}\cdot(\bold{v}\times\bold{C}) = GM\|\bold{r}\|+\bold{r}\cdot\bold{D}$$Como $\bold{r}\times\bold{v} = \bold{C}$, tenemos
$$\|\bold{C}\|^2 = GM\|\bold{r}\|+\bold{r}\cdot\bold{D}$$Observa que $\bold{r}\cdot\bold{D} = \|\bold{r}\|\|\bold{D}\|cos\theta$, donde $\theta$ es el ángulo entre $\bold{r}$ y $\bold{D}$. Por lo tanto,
$$\|\bold{C}\|^2 = GM\|\bold{r}\|+\|\bold{r}\|\|\bold{D}\|cos\theta$$Resolviendo para $\|\bold{r}\|$
$$\|\bold{r}\|= \frac{\|\bold{C}\|^2}{GM+\|\bold{D}\|cos\theta} = \frac{\|\bold{C}\|^2}{GM}\bigg(\frac{1}{1+ecos\theta}\bigg),$$donde $e = \|\bold{D}\|/GM$. Esta es la ecuación polar de una cónica con un foco en el origen, que configuramos para ser el Sol. Es una hipérbola si $e\gt 1$, una parábola si $e = 1$, o una elipse si $e \lt 1$. Como los planetas tienen órbitas cerradas, la única posibilidad es una elipse. Sin embargo, en este punto debe mencionarse que los cometas hiperbólicos existen. Estos son objetos que simplemente pasan a través del sistema solar a velocidades demasiado grandes para quedar atrapados en una órbita alrededor del Sol. A medida que pasan lo suficientemente cerca del Sol, el campo gravitacional del Sol desvía la trayectoria lo suficiente como para que el camino se vuelva hiperbólico.
 |
Uso de la tercera ley de Kepler para órbitas no heliocéntricas |
La tercera ley de Kepler del movimiento planetario puede modificarse para el caso de un objeto en órbita alrededor de un objeto que no sea el Sol, como la Luna alrededor de la Tierra. En este caso, la tercera ley de Kepler se convierte en
$$P^2 = \frac{4\pi^2a^3}{G(m+M)}\tag{$3.30$}$$donde $m$ es la masa de la Luna y $M$ es la masa de la Tierra, $a$ representa la longitud del eje mayor de la órbita elíptica y $P$ representa el período.
Dado que la masa de la Luna es $7.35 \times 10^{22}\;kg$, la masa de la Tierra es $5.97\times 10^{24}\;kg, G = 6.67 \times 10^{−11}\;m^3/kg\cdot seg^2$, y el período de la luna es $27.3$ días, encontremos la longitud del Eje mayor de la órbita de la Luna alrededor de la Tierra.

La siguiente escena interactiva hace parte de la unidad didáctica El Sistema planetario: Trayectorias elípticas. Primera ley de Kepler, del proyecto Un100, diseñada por José Luis Abreu. En esta escena se muestra una órbita elíptica en el espacio 3D y los parámetros keperianos que la definen, los cuales puedes modificar y observar cómo se modifica la órbita.
Si haces clic sobre uno de los parámetros (en el nombre), aparecerá una descripción del mismo. En este enlace puedes explorar otra unidad didáctica con la segunda Ley de Kepler.
 |
Introducción del capítulo: el cometa Halley |

Ahora volvemos al primer apartado, que analiza el movimiento del cometa Halley alrededor del Sol. La primera ley de Kepler establece que el cometa Halley sigue un camino elíptico alrededor del Sol, con el Sol como foco de la elipse. El período del cometa Halley es de aproximadamente $76,1$ años, dependiendo de qué tan cerca pase de Júpiter y Saturno a medida que pasa a través del sistema solar exterior. Usemos $T = 76.1$ años. ¿Cuál es la distancia promedio del cometa Halley del Sol?

Terminamos este capítulo, con el siguiente proyecto estudiantil.
¿Qué tan rápido puede viajar un auto de carrera a través de un giro circular sin derrapar y golpear la pared? La respuesta podría depender de varios factores:
En este proyecto investigamos esta pregunta para los autos de las carreras NASCAR en el Bristol Motor Speedway en Tennessee. Antes de considerar esta pista en particular, usamos funciones con valores vectoriales para desarrollar las matemáticas y la física necesarias para responder preguntas como esta.
Un carro de masa $m$ se mueve con velocidad angular constante $\omega$ alrededor de una curva circular de radio $R$ (Figura 3.20). La curva está inclinada en un ángulo $\theta$. Si la altura del automóvil desde el suelo es $h$, entonces la posición del automóvil en el tiempo $t$ viene dada por la función $\bold{r}(t) = \lang Rcos(\omega t), Rsen (\omega t), h\rang$.
Figura 3.20. Vistas de un auto de carreras moviéndose por una pista.
Figura 3.21. El automóvil tiene tres fuerzas que actúan sobre él: la gravedad (denotada por $mg$), la fuerza de fricción $\bold{f}$ y la fuerza ejercida por la carretera $\bold{N}$.

Figura 3.22. En el Bristol Motor Speedway, Bristol, Tennessee (a), las curvas tienen un radio interior de aproximadamente $211$ pies y un ancho de $40$ pies (b) (crédito: parte (a) foto de Raniel Díaz, Flickr)
El coeficiente de fricción para un neumático normal en condiciones secas es aproximadamente $0.7$. Por lo tanto, suponemos que el coeficiente para un neumático NASCAR en condiciones secas es de aproximadamente $0,98$.
Antes de responder las siguientes preguntas, ten en cuenta que es más fácil hacer cálculos en términos de pies y segundos, y luego convertir las respuestas a millas por hora como paso final.

155. Dado $\bold{r}(t) = (3t^2−2)\bold{i} + (2t − sen (t))\bold{j}$, encuentra la velocidad de una partícula que se mueve a lo largo de esta curva (Solución).
156. Dado $\bold{r}(t) = (3t^2−2)\bold{i} + (2t − sen (t))\bold{j}$, encuentra el vector de aceleración de una partícula que se mueve a lo largo de la curva en el ejercicio anterior.
 Dadas las siguientes funciones de posición, encuentra la velocidad, aceleración y rapidez en términos del parámetro $t$.
Dadas las siguientes funciones de posición, encuentra la velocidad, aceleración y rapidez en términos del parámetro $t$.
157. $\bold{r}(t) = \lang 3cost, 3sent, t^2\rang$ (Solución) 158. $\bold{r}(t) = e^{−t}\bold{i} + t^2\bold{j} + tant\bold{k}$ 159. $\bold{r}(t) = 2cost\bold{j} + 3sent\bold{k}$ (Solución). El gráfico se muestra a continuación:
 Encuentra la velocidad, aceleración y rapidez de una partícula con la función de posición dada.
Encuentra la velocidad, aceleración y rapidez de una partícula con la función de posición dada.
160. $\bold{r}(t) =\lang t^2−1, t\rang$
161. $\bold{r}(t) = \lang e^t, e^{−t}\rang$ (Solución)
162. $\bold{r}(t) = \lang sent, t, cost\rang$. El gráfico se muestra aquí:
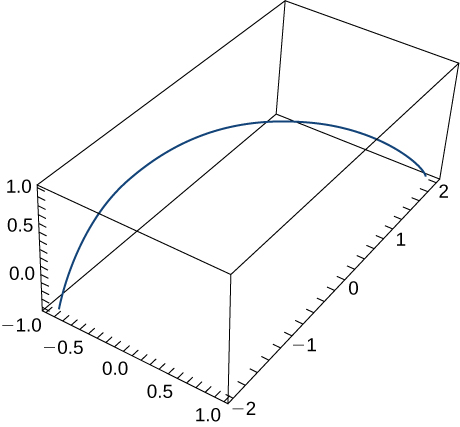 163. La función de posición de un objeto viene dada por $\bold{r}(t) = \lang t^2,5t, t^2−16t\rang$. ¿A qué hora es la velocidad mínima? (Solución)
164. Sea $\bold{r}(t) = rcosh (\omega t)\bold{i} + rsenh (\omega t)\bold{j}$. Encuentra los vectores de velocidad y aceleración y demuestra que la aceleración es proporcional a $\bold{r}(t)$.
163. La función de posición de un objeto viene dada por $\bold{r}(t) = \lang t^2,5t, t^2−16t\rang$. ¿A qué hora es la velocidad mínima? (Solución)
164. Sea $\bold{r}(t) = rcosh (\omega t)\bold{i} + rsenh (\omega t)\bold{j}$. Encuentra los vectores de velocidad y aceleración y demuestra que la aceleración es proporcional a $\bold{r}(t)$.
 Considera el movimiento de un punto en la circunferencia de un círculo rodante. A medida que el círculo rueda, genera el cicloide $\bold{r}(t) = (\omega t − sen (\omega t))\bold{i} + (1 − cos (\omega t))\bold{j}$, donde $\omega$ es la velocidad angular del círculo:
Considera el movimiento de un punto en la circunferencia de un círculo rodante. A medida que el círculo rueda, genera el cicloide $\bold{r}(t) = (\omega t − sen (\omega t))\bold{i} + (1 − cos (\omega t))\bold{j}$, donde $\omega$ es la velocidad angular del círculo:
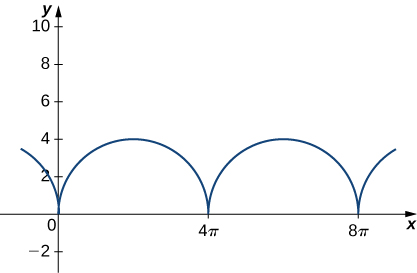
165. Encuentra las ecuaciones para la velocidad, aceleración y rapidez de la partícula en cualquier momento. (Solución)
 Un ala delta está en espiral hacia arriba como resultado del aire que sube rápidamente en una trayectoria que tiene el vector de posición $\bold{r}(t) = (3cost)\bold{i} + (3sent)\bold{j} + t^2\bold{k}$. La ruta es similar a la de una hélice, aunque no es una hélice. El gráfico se muestra aquí:
Un ala delta está en espiral hacia arriba como resultado del aire que sube rápidamente en una trayectoria que tiene el vector de posición $\bold{r}(t) = (3cost)\bold{i} + (3sent)\bold{j} + t^2\bold{k}$. La ruta es similar a la de una hélice, aunque no es una hélice. El gráfico se muestra aquí:
Encuentra las siguientes cantidades:
166. Los vectores de velocidad y aceleración. 167. La velocidad del planeador en cualquier momento (Solución). 168. Los tiempos, si los hay, en los que la aceleración del planeador es ortogonal a su velocidad.
 Dado que $\bold{r}(t) = \lang e^{−5t}sent, e^{−5t}cost, 4e^{−5t}\rang$ es el vector de posición de una partícula en movimiento, encuentra las siguientes cantidades:
Dado que $\bold{r}(t) = \lang e^{−5t}sent, e^{−5t}cost, 4e^{−5t}\rang$ es el vector de posición de una partícula en movimiento, encuentra las siguientes cantidades:
169. La velocidad de la partícula (Solución). 170. La rapidez de la partícula. 171. La aceleración de la partícula (Solución). 172. Encuentra la velocidad máxima de un punto en la circunferencia de un neumático de automóvil con un radio de $1$ pie cuando el automóvil viaja a $55$ mph.
 Se dispara un proyectil en el aire desde el nivel del suelo con una velocidad inicial de $500\; m/seg$ en un ángulo de $60^o$ con la horizontal. El gráfico se muestra aquí:
Se dispara un proyectil en el aire desde el nivel del suelo con una velocidad inicial de $500\; m/seg$ en un ángulo de $60^o$ con la horizontal. El gráfico se muestra aquí:
173. ¿A qué hora alcanza el proyectil la altura máxima? (Solución) 174. ¿Cuál es la altura máxima aproximada del proyectil? 175. ¿A qué hora se alcanza el alcance máximo del proyectil? (Solución) 176. ¿Cuál es el rango máximo? 177. ¿Cuál es el tiempo total de vuelo del proyectil? (Solución)
 Se dispara un proyectil a una altura de $1.5\; m$ sobre el suelo con una velocidad inicial de $100\; m/seg$ y en un ángulo de $30^o$ sobre la horizontal. Usa esta información para responder las siguientes preguntas:
Se dispara un proyectil a una altura de $1.5\; m$ sobre el suelo con una velocidad inicial de $100\; m/seg$ y en un ángulo de $30^o$ sobre la horizontal. Usa esta información para responder las siguientes preguntas:
178. Determina la altura máxima del proyectil. 179. Determina el alcance del proyectil. (Solución) 180. Una pelota de golf es golpeada en dirección horizontal desde el borde superior de un edificio de $100\; pies$ de altura. ¿Qué tan rápido debe lanzarse la pelota para aterrizar a $450\; pies$ de distancia? 181. Se dispara un proyectil desde el nivel del suelo en un ángulo de $8^o$ con la horizontal. El proyectil debe tener un alcance de $50\; m$. Encuentra la velocidad mínima necesaria para lograr este rango. (Solución) 182. Demuestra que un objeto que se mueve en línea recta a una velocidad constante tiene una aceleración de cero. 183. La aceleración de un objeto viene dada por $\bold{a}(t) = t\bold{j} + t\bold{k}$. La velocidad en $t = 1\; seg$ es $v(1) = 5\bold{j}$ y la posición del objeto en $t = 1\; seg$ es $r(1) = 0\bold{i} + 0\bold{j} + 0\bold{k}$. Encuentra la posición del objeto en cualquier momento. (Solución) 184. Encuentra $\bold{r}(t)$ dado que $\bold{a}(t) = - 32\bold{j}, v(0) = 600\sqrt{3}\bold{i} + 600\bold{j}$, y $r (0) = 0$.
185. Encuentra las componentes tangenciales y normales de la aceleración para $\bold{r}(t) = acos (\omega t)\bold{i} + bsen (\omega t)\bold{j}$ en $t = 0$ (Solución). 186. Dado $\bold{r}(t) = t^2\bold{i} + 2t\bold{j}$ y $t = 1$, encuentra las componentes tangencial y normal de la aceleración.
 Para cada uno de los siguientes problemas, encuentra los componentes tangencial y normal de la aceleración.
Para cada uno de los siguientes problemas, encuentra los componentes tangencial y normal de la aceleración.
187. $\bold{r}(t) = \lang e^t cost, e^tsent, e^t\rang$ (ver gráfico) (Solución):
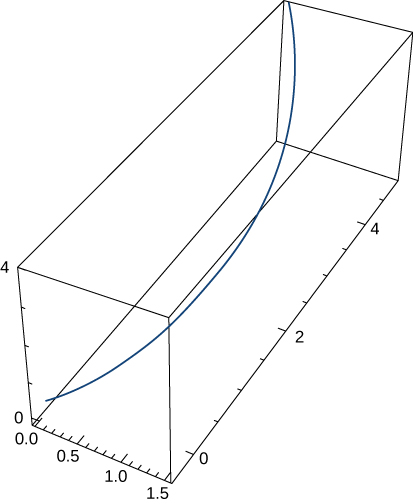
188. $\bold{r}(t) = \lang cos (2t), sen (2t), 1\rang$ 189. $\bold{r} = \bigg\lang 2t, t^2, \frac{t^3}{3}\bigg\rang$ (Solución) 190. $\bold{r} = \bigg\lang \frac{2}{3} (1 + t)^{3/2}, \frac{2}{3}(1 − t)^{3/2},\sqrt{2}t\bigg\rang$ 191. $\bold{r} = \lang 6t, 3t^2,2t^3\rang$ (Solución) 192. $\bold{r} = t^2\bold{i} + t^2\bold{j} + t^3\bold{k}$ 193. $\bold{r} = 3cos (2\pi t)\bold{i} + 3sen (2\pi t)\bold{j}$ (Solución)
194. Encuentra la función de valor vectorial de posición $\bold{r}$, dado que $\bold{a}(t) = \bold{i} + e^t\bold{j}, v(0) = 2\bold{j}$ y $r (0) = 2\bold{i}$. 195. La fuerza sobre una partícula viene dada por $\bold{f}(t) = (cost)\bold{i} + (sent)\bold{j}$. La partícula se encuentra en el punto $(c, 0)$ en $t = 0$. La velocidad inicial de la partícula viene dada por $v(0) = v_0\bold{j}$. Encuentra el camino de la partícula de masa $m$ (Recuerda, $\bold{F} = m\cdot\bold{a}$) (Solución). 196. Un automóvil que pesa $2700\; lb$ gira en un camino plano mientras viaja a $56\; pies / seg$. Si el radio de giro es de $70\; pies$, ¿cuál es la fuerza de fricción requerida para evitar que el auto patine? 197. Usando las leyes de Kepler, se puede demostrar que $v_0 = \frac{2GM}{r_0}$ es la velocidad mínima necesaria cuando $\theta = 0$ para que un objeto escape de la fuerza central resultante de la masa $M$. Usa este resultado para encontrar el velocidad mínima cuando $\theta = 0$ para que una cápsula espacial escape del tirón gravitacional de la Tierra si la sonda está a una altitud de $300\; km$ sobre la superficie de la Tierra (Solución). 198. Encuentra el tiempo en años que le toma al planeta enano Plutón hacer una órbita alrededor del Sol dado que $a = 39.5\; A.U.$
 Supón que la función de posición para un objeto en tres dimensiones viene dada por la ecuación $\bold{r}(t) = tcos(t)\bold{i} + tsen (t)\bold{j} + 3t\bold{k}$.
Supón que la función de posición para un objeto en tres dimensiones viene dada por la ecuación $\bold{r}(t) = tcos(t)\bold{i} + tsen (t)\bold{j} + 3t\bold{k}$.
199. Demuestra que la partícula se mueve en un cono circular. 200. Encuentra el ángulo entre los vectores de velocidad y aceleración cuando $t = 1.5$. 201. Encuentra los componentes tangencial y normal de la aceleración cuando $t = 1.5$ (Solución).

Figura 4.1. Los estadounidenses usan (y pierden) millones de pelotas de golf al año, lo que mantiene a los fabricantes de pelotas de golf en el negocio. En este capítulo, estudiaremos los elementos que nos acercan a un modelo de ganancias y a los métodos para calcular los niveles óptimos de producción (ver parte 2 de este libro) para una empresa típica de fabricación de pelotas de golf (crédito: modificación del trabajo de oatsy40, Flickr)
En las aplicaciones de las derivadas, estudiaste cómo determinar el máximo y el mínimo de una función de una variable durante un intervalo cerrado. Esta función puede representar la temperatura durante un intervalo de tiempo determinado, la posición de un automóvil en función del tiempo o la altitud de un avión a reacción mientras viaja de Medellín a Madrid.
En cada uno de estos ejemplos, la función tiene una variable independiente.
Supongamos, sin embargo, que tenemos una cantidad que depende de más de una variable. Por ejemplo, la temperatura puede depender de la ubicación y la hora del día, o el modelo de ganancias de una empresa puede depender de la cantidad de unidades vendidas y la cantidad de dinero gastado en publicidad.
Cuando se trata de una función de más de una variable independiente, surgen naturalmente varias preguntas. Por ejemplo, ¿cómo calculamos los límites de las funciones de más de una variable? La definición de derivada que usamos antes implicaba un límite. ¿La nueva definición de derivada también implica límites? ¿Se aplican las reglas de diferenciación en este contexto? ¿Podemos encontrar extremos relativos de funciones usando derivadas? Todas estas preguntas se responden en este capítulo.
Nuestro primer paso es explicar qué es una función de más de una variable, comenzando con las funciones de dos variables independientes. Este paso incluye identificar el dominio y el rango de tales funciones y aprender a graficarlas. También examinaremos formas de relacionar las gráficas de funciones en tres dimensiones con gráficas de funciones planas más familiares.
La definición de una función de dos variables es muy similar a la definición de una función de una variable.
La principal diferencia es que, en lugar de asignar valores de una variable a valores de otra variable, asignamos pares de variables ordenadas a otra variable.
Figura 4.2. El dominio de una función de dos variables consiste en pares ordenados $(x, y)$.
Determinar el dominio de una función de dos variables implica tener en cuenta las restricciones de dominio que puedan existir. Vamos a ver.
 |
Dominios y rangos para funciones de dos variables |
Encuentra el dominio y el rango de cada una de las siguientes funciones:

Supongamos que deseamos graficar la función $z = (x, y)$. Esta función tiene dos variables independientes ($x$ e $y$) y una variable dependiente ($z$). Cuando graficamos una función $y = f (x)$ de una variable, usamos el plano cartesiano. Podemos graficar cualquier par ordenado $(x, y)$ en el plano, y cada punto en el plano tiene un par ordenado $(x, y)$ asociado. Con una función de dos variables, cada par ordenado $(x, y)$ en el dominio de la función se asigna a un número real $z$. Por lo tanto, la gráfica de la función $f$ consiste en triples ordenados $(x, y, z)$. La gráfica de una función $z = (x, y)$ de dos variables se llama superficie.
Para comprender completamente el concepto de trazar un conjunto de triples ordenados para obtener una superficie en un espacio tridimensional, imagina el sistema de coordenadas $(x, y)$ tendido en plano.
 |
Gráficas de funciones de dos variables |
Crea un gráfico de cada una de las siguientes funciones:

En la siguiente página, presentamos dos escenas interactivas que muestran las dos gráficas del ejercicio anterior. En la primera escena, puedes modificar el valor del radio del hemisferio. La escena del paraboloide es tomada del libro Curvas y superficies paramétricas, de Navarro y Rivera (2018), en la cual es posible evidenciar la revolución de la superficie, al reducir el valor del parámtero $t$.
Recuerda que con clic izquierdo sostenido puedes rotar la gráfica 3D. Se recomienda ampliar la escena (clic en la esquina superior derecha de la escena).
 |
Tuercas y tornillos |
Una función de beneficio para un fabricante de hardware viene dada por $$f (x, y) = 16− (x − 3)^2− (y − 2)^2,$$ donde $x$ es el número de tuercas vendidas por mes (medido en miles) e $y$ representa el número de tornillos vendidos por mes (medido en miles). La ganancia se mide en miles de dólares. Dibuja un gráfico de esta función.

Si los excursionistas caminan por senderos escarpados, podrían usar un mapa topográfico que muestre cuán abruptamente cambian los senderos. Un mapa topográfico contiene líneas curvas llamadas curvas de nivel. Cada línea de contorno corresponde a los puntos en el mapa que tienen la misma elevación (figura 4.7). Una curva de nivel de una función de dos variables $f (x, y)$ es completamente análoga a una línea de contorno en un mapa topográfico.

Figura 4.7. (a) Un mapa topográfico de Devil’s Tower, Wyoming. Las líneas que están juntas indican un terreno muy empinado. (b) Una foto en perspectiva de la Torre del Diablo muestra cuán empinados son sus lados. Observa que la parte superior de la torre tiene la misma forma que el centro del mapa topográfico.
Volviendo a la función $g (x, y) = \sqrt{9 − x^2 − y^2}$, podemos determinar las curvas de nivel de esta función. El rango de $g$ es el intervalo cerrado $[0,3]$. Primero, elegimos cualquier número en este intervalo cerrado, por ejemplo, $c = 2$. La curva de nivel correspondiente a $c = 2$ se describe mediante la ecuación
Para simplificar, eleva al cuadrado ambos lados de esta ecuación:
$$9 − x^2 − y^2 = 4$$ $$x^2 + y^2 = 5$$Esta ecuación describe un círculo centrado en el origen con radio $\sqrt{5}$. El uso de valores de $c$ entre $0$ y $3$ produce otros círculos también centrados en el origen. Si $c = 3$, entonces el círculo tiene radio $0$, por lo que consiste únicamente en el origen. La figura 4.8 es un gráfico de las curvas de nivel de esta función correspondientes a $c = 0,1,2 y 3$. Observa que en la derivación anterior puede ser posible que hayamos introducido soluciones adicionales al cuadrar ambos lados. Este no es el caso aquí porque el rango de la función de raíz cuadrada no es negativo.
Figura 4.8. Curvas de nivel de la función $g (x, y) = \sqrt{9 − x2 − y2}$, usando $c = 0,1,2,$ y $3$ ($c = 3$ corresponde al origen).
Un gráfico de las diversas curvas de nivel de una función se denomina mapa de contorno.
 |
Hacer un mapa de contorno |
Dada la función $f (x, y) = \sqrt{8 + 8x − 4y − 4x^2 − y^2}$, encuentra la curva de nivel correspondiente a $c = 0$. Luego crea un mapa de contorno para esta función. ¿Cuáles son el dominio y el rango de $f$

Otra herramienta útil para comprender el gráfico de una función de dos variables se llama traza vertical. Las curvas de nivel siempre se grafican en el plano $xy$, pero como su nombre lo indica, las trazas verticales se grafican en los planos $xz$ o $yz$.
 |
Encontrar trazas verticales |
Encuentra las trazas verticales para la función$ f (x, y) = senxcosy$ correspondiente a $x = −\frac{\pi}{4},0,$ y $\frac{\pi}{4}$, e $y = −\frac{\pi}{4},0,$ y $\frac{\pi}{4}$.

Las funciones de dos variables pueden producir algunas superficies de aspecto llamativo. La siguiente figura muestra dos ejemplos.
Figura 4.12. Ejemplos de superficies que representan funciones de dos variables: (a) una combinación de una función de potencia y una función seno y (b) una combinación de funciones trigonométricas, exponenciales y logarítmicas.
Puedes interactuar con la siguiente escena interactiva, diseñada por Dr. Doug Davis en GeoGebra, en la que presentamos, inicialmente, la función $f(x,y) = senxcosy$
Puedes cambiar la función en el cuadro de texto. Observa que aparece información adicional, que aún no hemos trabajado; no obstante, puedes explorar las trazas para diferentes valores de $x = a$ e $y = b$, además del mapa de contorno. Practica con las funciones de la figura 4.12.
Lo más común son las funciones de dos variables; no obstante, demos una mirada a funciones como:
$$f(x,y,z)=x^2−2xy+y^2+3yz−z^2+4x−2y+3x−6\\ \text{(una función polinomial de tres variables)}$$y
$$g(x,y,t)=(x^2−4xy+y^2)sent−(3x+5y)cost.$$En la primera función, $(x, y, z)$ representa un punto en el espacio, y la función $f$ asigna cada punto en el espacio a una cuarta cantidad, como la temperatura o la velocidad del viento. En la segunda función, $(x, y)$ puede representar un punto en el plano, y $t$ puede representar el tiempo. La función podría asignar un punto en el plano a una tercera cantidad (por ejemplo, presión) en un momento dado $t$. El método para encontrar el dominio de una función de más de dos variables es análogo al método para funciones de una o dos variables.
 |
Dominio para funciones de tres variables |
Encuentra el dominio de cada una de las siguientes funciones:

Las funciones de dos variables tienen curvas de nivel, que se muestran como curvas en el plano $xy$. Sin embargo, cuando la función tiene tres variables, las curvas se convierten en superficies, por lo que podemos definir superficies de nivel para funciones de tres variables.
 |
Encontrar una superficie de nivel |
Encuentre la superficie de nivel para la función $f (x, y, z) = 4x^2 + 9y^2 − z^2$ correspondiente a $c = 1$.

La siguiente escena interactiva del hiperboloide es tomada del libro Curvas y superficies paramétricas, de Navarro y Rivera (2018), en la cual puedes variar algunos parámetros, entre ellos, el valor de $c$.

 Para los siguientes ejercicios, evalúa cada función en los valores indicados.
Para los siguientes ejercicios, evalúa cada función en los valores indicados.
1. $W (x, y) = 4x^2 + y^2$. Encuentra $W (2, −1), W (−3,6)$. (Solución). 2. $W (x, y) = 4x^2 + y^2$. Encuentra $W (2 + h, 3 + h)$. 3. El volumen de un cilindro circular derecho se calcula mediante una función de dos variables, $V (x, y) = \pi x^2y$, donde $x$ es el radio del cilindro circular derecho e $y$ representa la altura del cilindro. Evalúa $V (2,5)$ y explica lo que esto significa (Solución). 4. Un tanque de oxígeno está construido con un cilindro derecho de altura y radio $x$ con dos hemisferios de radio $x$ montados en la parte superior e inferior del cilindro. Expresa el volumen del tanque en función de dos variables, $x$ e $y$, encuentra $V (10,2)$ y explica lo que esto significa.
 Para los siguientes ejercicios, encuentra el dominio de la función.
Para los siguientes ejercicios, encuentra el dominio de la función.
5. $V(x,y)=4x^2+y^2$ (Solución) 6. $f(x,y)=\sqrt{x^2+y^2−4}$ 7. $f(x,y)=4ln(y^2−x)$ (Solución) 8. $g(x,y)=\sqrt{16−4x^2−y^2}$ 9. $z(x,y)=y^2−x^2$ (Solución) 10. $f(x,y)=\frac{y+2}{x^2}$
 Para los siguientes ejercicios, encuentra el rango.
Para los siguientes ejercicios, encuentra el rango.
11. $g(x,y)=\sqrt{16−4x^2−y^2}$ (Solución) 12. $V(x,y)=4x^2+y^2$ 13. $z=y^2−x^2$ (Solución)
 Para los siguientes ejercicios, encuentra las curvas de nivel de cada función en el valor indicado de $c$ para visualizar la función dada.
Para los siguientes ejercicios, encuentra las curvas de nivel de cada función en el valor indicado de $c$ para visualizar la función dada.
14. $z(x,y)=y^2−x^2, c=1$ 15. $z(x,y)=y^2−x^2, c=4$ (Solución) 16. $g(x,y)=x^2+y^2;c=4,c=9$ 17. $g(x,y)=4−x−y;c=0,4$ (Solución) 18. $f(x,y)=xy;c=1;c=−1$ 19. $h(x,y)=2x−y;c=0,−2,2$ (Solución) 20. $f(x,y)=x^2−y;c=1,2$ 21. $g(x,y)=\frac{x}{x+y};c=−1,0,2$ (Solución) 22. $g(x,y)=x^3−y;c=−1,0,2$ 23. $g(x,y)=e^{xy};c=12,3$ (Solución) 24. $f(x,y)=x^2;c=4,9$ 25. $f(x,y)=xy−x;c=−2,0,2$ (Solución) 26. $h(x,y)=ln(x^2+y^2);c=−1,0,1$ 27. $g(x,y)=ln(\frac{y}{x^2});c=−2,0,2$ (Solución) 28. $z=f(x,y)=\sqrt{x^2+y^2}, c=3$ 29. $f(x,y)=\frac{y+2}{x^2}, c= \text{cualquier constante}$ (Solución)
 Para los siguientes ejercicios, encuentra las trazas verticales de las funciones en los valores indicados de $x$ e $y$, y dibuja las trazas.
Para los siguientes ejercicios, encuentra las trazas verticales de las funciones en los valores indicados de $x$ e $y$, y dibuja las trazas.
30. $z=4−x−y;x=2$ 31. $f(x,y)=3x+y^3,x=1$ (Solución) 32. $z=cos\sqrt{x^2+y^2}, x=1$
 Encuentra el dominio de las siguientes funciones.
Encuentra el dominio de las siguientes funciones.
33. $z=\sqrt{100−4x^2−25y^2}$ (Solución) 34. $z=ln(x−y^2)$ 35. $f(x,y,z)=\frac{1}{\sqrt{36−4x^2−9y^2−z^2}}$ (Solución) 36. $f(x,y,z)=\sqrt{49−x^2−y^2−z^2}$ 37. $f(x,y,z)=\sqrt[3]{16−x^2−y^2−z^2}$ (Solución) 38. $f(x,y)=cos\sqrt{x^2+y^2}$
 Para los siguientes ejercicios, traza una gráfica de la función.
Para los siguientes ejercicios, traza una gráfica de la función.
39. $z = f (x, y) = \sqrt{x^2 + y^2}$ (Solución) 40. $z = x^2 + y^2$ 41. Usa la tecnología para graficar $z = x^2y$ (Solución).
 Dibuja lo siguiente encontrando las curvas de nivel. Verifica el gráfico usando tecnología.
Dibuja lo siguiente encontrando las curvas de nivel. Verifica el gráfico usando tecnología.
42. $f(x,y)=\sqrt{4−x^2−y^2}$
43. $f(x,y)=2−\sqrt{x^2+y^2}$ (Solución). 44. $z=1+e^{−x^2−y^2}$ 45. $z=cos\sqrt{x^2+y^2}$ (Solución). 46. $z=y^2−x^2$ 47. Describe las líneas de contorno para varios valores de $c$ para $z = x^2 + y^2−2x − 2y$ (Solución).
 Encuentra la superficie de nivel para las funciones de tres variables y descríbela.
Encuentra la superficie de nivel para las funciones de tres variables y descríbela.
48. $w(x,y,z)=x−2y+z,c=4$ 49. $w(x,y,z)=x^2+y^2+z^2,c=9$ (Solución). 50. $w(x,y,z)=x^2+y^2−z^2,c=−4$ 51. $w(x,y,z)=x^2+y^2−z^2,c=4$ (Solución). 52. $w(x,y,z)=9x^2−4y^2+36z^2,c=0$
 Para los siguientes ejercicios, encuentra una ecuación de la curva de nivel de $f$ que contenga el punto $P$.
Para los siguientes ejercicios, encuentra una ecuación de la curva de nivel de $f$ que contenga el punto $P$.
53. $f (x, y) = 1−4x^2 − y^2, P (0,1)$ (Solución) 54. $g (x, y) = y^2arctanx, P (1,2)$ 55. $g (x, y) = e^{xy} (x^2 + y^2), P (1,0)$ (Solución) 56. La fuerza $E$ de un campo eléctrico en el punto $(x, y, z)$ resultante de un cable cargado infinitamente largo que se extiende a lo largo del eje $y$ está dado por $E (x, y, z) = k /\sqrt{x^2 + y^2}$, donde $k$ es una constante positiva. Para simplificar, deja $k = 1$ y encuentra las ecuaciones de las superficies de nivel para $E = 10$ y $E = 100$.
57. Una placa delgada de hierro se encuentra en el plano $xy$. La temperatura $T$ en grados Celsius en un punto $P (x, y)$ es inversamente proporcional al cuadrado de su distancia desde el origen. Expresa $T$ en función de $x$ e $y$ (Solución). 58. Consulta el problema anterior. Usando la función de temperatura que se encuentra allí, determina la constante de proporcionalidad si la temperatura en el punto $P (1,2)$ es de $50^oC$. Usa esta constante para determinar la temperatura en el punto $Q (3,4)$.
59. Consulta el problema anterior. Encuentra las curvas de nivel para $T = 40^oC$ y $T = 100^oC$, y describe lo que representan las curvas de nivel (Solución).
Ahora hemos examinado funciones de más de una variable y hemos visto cómo representarlas gráficamente. En esta sección, veremos cómo tomar el límite de una función de más de una variable y lo que significa que una función de más de una variable sea continua en un punto de su dominio. Resulta que estos conceptos tienen aspectos que simplemente no ocurren con funciones de una variable.
Recuerda la definición de un límite de una función de una variable:
Sea f (x) definida para todo $x \cancel{=} a$ en un intervalo abierto que contenga a. Sea L un número real. Luego
$$\lim\limits_{x \to a} f(x)=L$$si para cada $\epsilon \gt 0$, existe un $\delta\gt 0$, de modo que si $0 \lt| x − a | \lt \delta$ para todo $x$ en el dominio de $f$, entonces
$$|f(x)−L|\lt \epsilon$$Antes de que podamos adaptar esta definición para definir un límite de una función de dos variables, primero debemos ver cómo extender la idea de un intervalo abierto en una variable a un intervalo abierto en dos variables.
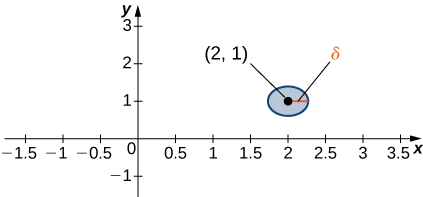
Figura 4.14. Un disco $\delta$ centrado alrededor del punto (2,1).
La idea de un disco $\delta$ aparece en la definición del límite de una función de dos variables.
Si $\delta$ es pequeño, entonces todos los puntos $(x, y)$ en el disco $\delta$ están cerca de $(a, b)$.
Esto es completamente análogo a que $x$ esté cerca de $a$ en la definición de un límite de una función de una variable. En una dimensión, expresamos esta restricción como
$$a-\delta\lt x \lt a+\delta$$En más de una dimensión, usamos un disco $\delta$.
Probar que existe un límite usando la definición de un límite de una función de dos variables puede ser un desafío. En su lugar, usamos el siguiente teorema, que nos da atajos para encontrar límites.
Figura 4.15. El límite de una función que involucra dos variables requiere que $f (x, y)$ esté dentro un $\epsilon$ de $L$ siempre que $(x, y)$ esté dentro de un $\delta$ de $(a, b)$. Cuanto menor es el valor de $\epsilon$, menor es el valor de $\delta$.
Las pruebas de estas propiedades son similares a las de los límites de las funciones de una variable.
 |
Encontrar el límite de una función de dos variables |
Encuentra cada uno de los siguientes límites:

Dado que estamos tomando el límite de una función de dos variables, el punto $(a, b)$ está en $\Reals^2$, y es posible acercarse a este punto desde un número infinito de direcciones. A veces, al calcular un límite, la respuesta varía según el camino que se tome hacia $(a, b)$. Si este es el caso, entonces el límite no existe. En otras palabras, el límite debe ser único, independientemente de la ruta tomada.
 |
Límites que no existen |
Demuestra que ninguno de los siguientes límites existe:

La función de la primera parte del ejercicio la hemos representado en la escena interactiva de la siguiente página. Rota la escena para que verifiques lo enunciado en la solución; por ejemplo, para $y=0$ (eje $x$) observa que la función permanece fija en cero.
Para estudiar la continuidad y la diferenciabilidad de una función de dos o más variables, primero necesitamos aprender alguna nueva terminología.
Figura 4.17. En el conjunto $S$ que se muestra, $(−1,1)$ es un punto interior y $(2,3)$ es un punto de frontera.
Un ejemplo de un conjunto abierto es un disco $\delta$. Si incluimos el límite del disco, se convierte en un conjunto cerrado. Un conjunto que contiene algunos, pero no todos, sus puntos de frontera no está abierto ni cerrado. Por ejemplo, si incluimos la mitad del límite de un disco $\delta$ pero no la otra mitad, entonces el conjunto no está abierto ni cerrado.
La definición de un límite de una función de dos variables requiere que el disco $\delta$ esté contenido dentro del dominio de la función. Sin embargo, si deseamos encontrar el límite de una función en un punto límite del dominio, el disco $\delta$ no está contenido dentro del dominio. Por definición, algunos de los puntos del disco $\delta$ están dentro del dominio y otros están fuera. Por lo tanto, solo necesitamos considerar los puntos que están dentro del disco $\delta$ y el dominio de la función. Esto lleva a la definición del límite de una función en un punto de frontera.
 |
Límite de una función en un punto de frontera |
Demuestra que $\lim\limits_{(x,y) \to (4,3)}\sqrt{25-x^2-y^2}=0$

Observa la siguiente escena interactiva, que muestra la función del ejercicio y el punto $(4,3)$ en la frontera.
Hemos definido la continuidad de una función de una variable basada en el límite de una función de una variable. En particular, son necesarias tres condiciones para que $f (x)$ sea continua en el punto $x = a$:
Estas tres condiciones son también necesarias para la continuidad de una función de dos variables.
 |
Demostrando la continuidad para una función de dos variables |
Demuestra que la función $f (x, y) = \sqrt{3x + 2y}{x + y + 1}$ es continua en el punto $(5, −3)$.

La continuidad de una función de cualquier número de variables también se puede definir en términos de delta y épsilon. Una función de dos variables es continua en un punto $(x_0, y_0)$ en su dominio si para cada $\epsilon\gt 0$ existe un $\delta\gt 0$ tal que, siempre que $\sqrt{(x − x_0)^2+ (y − y_0)^2} \lt \delta$ es cierto, $| f (x, y) −f (a, b) | \lt\epsilon$.
Esta definición se puede combinar con la definición formal (es decir, la definición épsilon-delta) de continuidad de una función de una variable para probar los siguientes teoremas:
Figura 4.20. La composición de dos funciones continuas es continua.
Ahora usemos los teoremas anteriores para mostrar la continuidad de las funciones en los siguientes ejercicios.
 |
Más ejercicios de continuidad de una función de dos variables |
Demuestra que las funciones $f (x, y) = 4x^3y^2$ y $g (x, y) = cos (4x^3y^2)$ son continuas en todas partes.

El límite de una función de tres o más variables ocurre fácilmente en las aplicaciones. Por ejemplo, supongamos que tenemos una función $f (x, y, z)$ que da la temperatura en una ubicación física $(x, y, z)$ en tres dimensiones. O tal vez una función $g (x, y, z, t)$ puede indicar la presión del aire en una ubicación $(x, y, z)$ en el tiempo $t$. ¿Cómo podemos tomar un límite en un punto en $\Reals^3$? ¿Qué significa ser continuo en un punto en cuatro dimensiones?
Las respuestas a estas preguntas se basan en extender el concepto de un disco $\delta$ en más de dos dimensiones. Entonces, las ideas del límite de una función de tres o más variables y la continuidad de una función de tres o más variables son muy similares a las definiciones dadas anteriormente para una función de dos variables.
Para mostrar que existe un límite de una función de tres variables en un punto $(x_0, y_0, z_0)$, es suficiente mostrar que para cualquier punto en una bola $\delta$ centrada en $(x_0, y_0, z_0)$, el valor de la función en ese punto está arbitrariamente cerca de un valor fijo (el valor límite). Todas las leyes de límites para funciones de dos variables también se aplican a funciones de más de dos variables.
 |
Encontrar el límite de una función de tres variables |
Encuentra $\lim\limits_{(x,y,z)\to (4,1,-3)}\frac{x^2y-3z}{2x+5y-z}$


 Para los siguientes ejercicios, encuentre el límite de la función.
Para los siguientes ejercicios, encuentre el límite de la función.
60. $\lim\limits_{(x,y) \to (1,2)}x$. 61. $\lim\limits_{(x,y) \to (1,2)}\frac{5x^2y}{x^2+y^2}$ (Solución). 62. Demuestra que el límite $\lim\limits_{(x,y) \to (1,2)}\frac{5x^2y}{x^2+y^2}$ existe y es el mismo a lo largo de las rutas: eje $y$ y eje $x$, y a lo largo de $y = x$.
 Para los siguientes ejercicios, evalúa los límites en los valores indicados de $x$ y $y$. Si el límite no existe, indícalo y explica por qué el límite no existe.
Para los siguientes ejercicios, evalúa los límites en los valores indicados de $x$ y $y$. Si el límite no existe, indícalo y explica por qué el límite no existe.
63. $\lim\limits_{(x,y) \to (0,0)}\frac{4x^2+10y^2+4}{4x^2-10y^2+6}$ (Solución) 64. $\lim\limits_{(x,y) \to (11,13)}\sqrt{\frac{1}{xy}}$
65. $\lim\limits_{(x,y) \to (0,1)}\frac{y^2senx}{x}$ (Solución) 66. $\lim\limits_{(x,y) \to (0,0)}sen\big(\frac{x^8+y^7}{x-y+10}\bigg)$ 67. $\lim\limits_{(x,y) \to (\pi/4,1)}\frac{ytanx}{y+1}$ (Solución) 68. $\lim\limits_{(x,y) \to (0,\pi/4)}\frac{secx+2}{3x-tany}$ 69. $\lim\limits_{(x,y) \to (2,5)}\bigg(\frac{1}{x}-\frac{5}{y}\bigg)$ (Solución) 70. $\lim\limits_{(x,y) \to (4,4)}xlny$ 71. $\lim\limits_{(x,y) \to (4,4)}e^{-x^2-y^2}$ (Solución) 72. $\lim\limits_{(x,y) \to (0,0)}\sqrt{9-x^2-y^2}$ 73. $\lim\limits_{(x,y) \to (1,2)}(x^2y^3−x^3y^2+3x+2y)$ (Solución) 74. $\lim\limits_{(x,y) \to (\pi,\pi)}xsen\bigg(\frac{x+y}{4}\bigg)$ 75. $\lim\limits_{(x,y) \to (0,0)}\frac{xy+1}{x^2+y^2+1}$ (Solución) 76. $\lim\limits_{(x,y) \to (0,0)}\frac{x^2+y^2}{\sqrt{x^2+y^2+1}-1}$ 77. $\lim\limits_{(x,y) \to (0,0)}ln\big(x^2+y^2\big)$ (Solución)
 Para los siguientes ejercicios, completa la declaración.
Para los siguientes ejercicios, completa la declaración.
78. Un punto $(x_0, y_0)$ en una región plana $R$ es un punto interior de $R$, si _________________. 79. Un punto $(x_0, y_0)$ en una región plana, $R$ se denomina punto de frontera de $R$, si ___________ (Solución).
 Para los siguientes ejercicios, usa técnicas algebraicas para evaluar el límite.
Para los siguientes ejercicios, usa técnicas algebraicas para evaluar el límite.
80. $\lim\limits_{(x,y) \to (2,1)}\frac{x-y-1}{\sqrt{x-y}-1}$ 81. $\lim\limits_{(x,y) \to (0,0)}\frac{x^4-4^y4}{x^2-2y^2}$ (Solución) 82. $\lim\limits_{(x,y) \to (0,0)}\frac{x^3-y^3}{x-y}$ 83. $\lim\limits_{(x,y) \to (0,0)}\frac{x^2-xy}{\sqrt{}x-sqrt{y}}$ (Solución)
 Para los siguientes ejercicios, evalúa los límites de las funciones de tres variables.
Para los siguientes ejercicios, evalúa los límites de las funciones de tres variables.
84. $\lim\limits_{(x,y,z) \to (1,2,3)}\frac{xz^2-y^2z}{xyz-1}$ 85. $\lim\limits_{(x,y,z) \to (0,0,0)}\frac{x^2-y^2-z^2}{x^2+y^2-z^2}$ (Solución)
 Para los siguientes ejercicios, evalúa el límite de la función determinando el valor al que se acerca la función a lo largo de las rutas indicadas. Si el límite no existe, explica por qué no.
Para los siguientes ejercicios, evalúa el límite de la función determinando el valor al que se acerca la función a lo largo de las rutas indicadas. Si el límite no existe, explica por qué no.
86. $\lim\limits_{(x,y) \to (0,0)}\frac{xy+y^3}{x^2+y^2}$ a. A lo largo del eje $x (y = 0)$ b. A lo largo del eje $y (x = 0)$ c. A lo largo del camino $y = 2x$ 87. Evalúa $\lim\limits_{(x,y) \to (0,0)}\frac{xy+y^3}{x^2+y^2}$, usando los resultados del ejercicio anterior (Solución).
88. $\lim\limits_{(x,y) \to (0,0)}\frac{x^2y}{x^4+y^2}$ a. A lo largo del eje $x (y = 0)$ b. A lo largo del eje $y (x = 0)$ c. A lo largo del camino $y = x^2$ 89. Evalúa $\lim\limits_{(x,y) \to (0,0)}\frac{x^2y}{x^4+y^2}$, usando los resultados del ejercicio anterior (Solución).
 Discute la continuidad de las siguientes funciones. Encuentra la región más grande en el plano $xy$ en el que las siguientes funciones son continuas.
Discute la continuidad de las siguientes funciones. Encuentra la región más grande en el plano $xy$ en el que las siguientes funciones son continuas.
90. $f(x,y)=sen(xy)$ 91. $f(x,y)=ln(x+y)$ (Solución) 92. $f(x,y)=e^{3xy}$ 93. $f(x,y)=\frac{1}{xy}$ (Solución)
 Para los siguientes ejercicios, determina la región en la que la función es continua. Explica tu respuesta.
Para los siguientes ejercicios, determina la región en la que la función es continua. Explica tu respuesta.
94. $f(x,y) = \frac{x^2y}{x^2+y^2}$ 95. $f(x,y) = \begin{cases} \frac{x^2y}{x^2+y^2} &\text{si } (x,y)\cancel{=} (0,0) \\ 0 &\text{si } (x,y)=(0,0) \end{cases}$ (Sugerencia: demuestra que la función se aproxima a diferentes valores a lo largo de dos rutas diferentes) (Solución).
96. $f(x,y) = \frac{sen(x^2+y^2)}{x^2+y^2}$
97. Determina si $g (x, y) = \frac{x^2 − y^2}{x^2 + y^2}$ es continua en $(0,0)$ (Solución). 98. Crea un diagrama utilizando un software de gráficos para determinar dónde no existe el límite. Determina la región del plano de coordenadas en el que $f (x, y) = \frac{1}{x^2 − y}$ es continua. 99. Determina la región del plano $xy$ en la que la función compuesta $g (x, y) = arctan \big(\frac{xy^2}{x + y}\big)$ es continua. Usa la tecnología para respaldar tu conclusión (Solución). 100. Determina la región del plano $xy$ en la que $f (x, y) = ln (x^2 + y^2−1)$ es continua. Usa la tecnología para respaldar tu conclusión (Sugerencia: ¡elige el rango de valores para $x$ e $y$ con cuidado!) 101. ¿En qué puntos del espacio es $g (x, y, z) = x^2 + y^2−2z^2$ continua? (Solución) 102. ¿En qué puntos del espacio es $g (x, y, z) = \frac{1}{x^2 + z^2−1}$ continua? 103. Demuestra que $\lim\limits_{(x, y) \to (0,0)}\frac{1}{x^2 + y^2}$ no existe en $(0,0)$ al trazar el gráfico de la función (Solución). 104. [T] Evalúa $\lim\limits_{(x, y) \to (0,0} \frac{−xy^2}{x^2 + y^4}$ trazando la función usando un CAS. Determina analíticamente el límite a lo largo de la ruta $x = y^2$. 105. [T] (Solución) a. Usa un CAS para dibujar un mapa de contorno de $z = \sqrt{9 − x^2 − y^2 }$ b. ¿Cuál es el nombre de la forma geométrica de las curvas de nivel? c. Da la ecuación general de las curvas de nivel. d. ¿Cuál es el valor máximo de z? e. ¿Cuál es el dominio de la función? f. ¿Cuál es el rango de la función?
106. Verdadero o Falso: Si evaluamos $\lim\limits_{(x, y)\to (0,0)} f (x)$ a lo largo de varias rutas y cada vez que el límite es $1$, podemos concluir que $\lim\limits_{(x, y)\to (0,0)} f (x) = 1$.
107. Usa coordenadas polares para encontrar $\lim\limits_{(x, y) \to (0,0)} \frac{sen\sqrt{x^2 + y^2}}{\sqrt{x^2 + y^2}}$. También puedes usar la regla de L’Hôpital (Solución). 108. Usa coordenadas polares para encontrar $\lim\limits_{(x, y) \to (0,0)} cos (x^2 + y^2)$ 109. Discute la continuidad de $f (g (x, y))$ donde $f (t) = 1 / t$ y $g (x, y) = 2x − 5y$ (Solución). 110. Dado $f (x, y) = x^2−4y$, encuentra $\lim\limits_{h \to 0}\frac{f (x + h, y) −f (x, y)}{h}$. 111. Dado $f (x, y) = x^2−4y$, encuentra $\lim\limits_{h \to 0}\frac{f (1 + h, y) −f (1, y)}{h}$ (Solución)
Ahora que hemos examinado los límites y la continuidad de las funciones de dos variables, podemos proceder a estudiar las derivadas. Encontrar derivadas de funciones de dos variables es el concepto clave en este capítulo, con tantas aplicaciones en matemáticas, ciencias e ingeniería como la diferenciación de funciones de una sola variable. Sin embargo, ya hemos visto que los límites y la continuidad de las funciones multivariables tienen nuevos problemas y requieren una nueva terminología e ideas para abordarlos. Esto lleva a la diferenciación también.
Al estudiar las derivadas de funciones de una variable, encontramos que una interpretación de la derivada es una tasa de cambio instantánea de $y$ como una función de $x$. La notación de Leibniz para la derivada es $dy / dx$, lo que implica que $y$ es la variable dependiente y $x$ es la variable independiente.
Para una función $z = f (x, y)$ de dos variables, $x$ e $y$ son las variables independientes y $z$ es la variable dependiente. Esto plantea dos preguntas de inmediato: ¿Cómo adaptamos la notación de Leibniz para las funciones de dos variables? Además, ¿qué es una interpretación de la derivada? La respuesta se encuentra en derivadas parciales.
Esta definición ya muestra dos diferencias. Primero, la notación cambia, en el sentido de que todavía usamos una versión de la notación de Leibniz, pero la $d$ en la notación original se reemplaza con el símbolo $\partial$. (Esta "$d$" redondeada generalmente se llama "parcial", por lo que $\partial f / \partial x$ se dice que es "parcial de $f$ con respecto a $x$".) Esta es la primera pista de que estamos tratando con derivadas parciales.
En segundo lugar, ahora tenemos dos derivadas diferentes que podemos tomar, ya que hay dos variables independientes diferentes. Dependiendo de la variable que elijamos, podemos obtener diferentes derivadas parciales por completo, y a menudo lo hacemos.
 |
Cálculo de derivadas parciales a partir de la definición |
Usa la definición de la derivada parcial como límite para calcular $\partial f / \partial x$ y $\partial f / \partial y$ para la función $$f (x, y) = x^2−3xy + 2y^2−4x + 5y − 12$$.

La idea a tener en cuenta al calcular derivadas parciales es tratar todas las variables independientes, distintas de la variable con respecto a la cual nos estamos diferenciando, como constantes. Luego procede a diferenciar como con una función de una sola variable. Para ver por qué esto es cierto, primero arregla y y define $g (x) = f (x, y)$ en función de x. Luego
$$g^{\prime}(x) = \lim\limits_{h \to 0}\frac{g (x + h) −g (x)}{h} = \lim\limits_{h \to 0}\frac{f (x + h, y) −f (x, y)}{h} = \frac{\partial f}{\partial x}$$Lo mismo es cierto para calcular la derivada parcial de $f$ con respecto a $y$. Esta vez, arregla $x$ y define $h (y) = f (x, y)$ en función de $y$. Luego
Se aplican todas las reglas de diferenciación que ya conocemos.
¿Cómo podemos interpretar estas derivadas parciales? Recuerda que la gráfica de una función de dos variables es una superficie en $\Reals^3$. Si eliminamos el límite de la definición de la derivada parcial con respecto a $x$, el cociente de diferencia permanece:
$$\frac{f(x+h,y)−f(x,y)h}{h}$$Esto se parece al cociente de la diferencia para la derivada de una función de una variable, excepto por la presencia de la variable $y$. La figura 4.21 ilustra una superficie descrita por una función arbitraria $z = f (x, y)$.
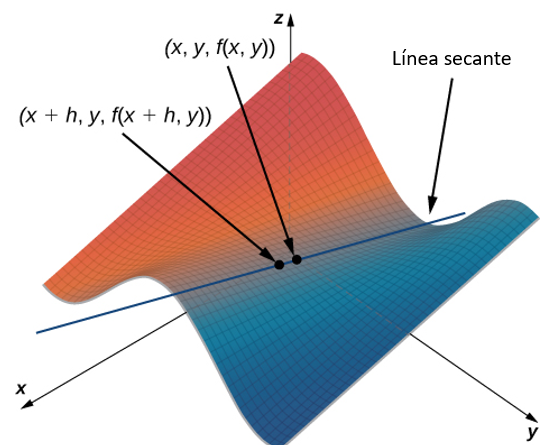
Figura 4.21. Recta secante que pasa por los puntos $(x, y, f (x, y)) $ y $(x + h, y, f (x + h, y))$.
En la figura 4.21, el valor de $h$ es positivo. Si graficamos $f (x, y)$ y $f (x + h, y)$ para un punto arbitrario $(x, y)$, entonces la pendiente de la recta secante que pasa por estos dos puntos viene dada por
$$\frac{f (x + h, y) −f (x, y)}{h}$$Esta recta es paralela al eje $x$. Por lo tanto, la pendiente de la recta secante representa una tasa de cambio promedio de la función $f$ a medida que viajamos paralelos al eje $x$. Cuando $h$ se aproxima a cero, la pendiente de la recta secante se aproxima a la pendiente de la recta tangente.
Si elegimos cambiar $y$ en lugar de $x$ por el mismo valor incremental $h$, entonces la recta secante es paralela al eje $y$, al igual que la recta tangente. Por lo tanto, $\partial f /\partial x$ representa la pendiente de la recta tangente que pasa por el punto $(x, y, f (x, y))$ paralela al eje $x$ y $\partial f /\partial y$ representa la pendiente de la recta tangente que pasa a través del punto $(x, y, f (x, y))$ paralelo al eje $y$. Si deseamos encontrar la pendiente de una recta tangente que pasa por el mismo punto en cualquier otra dirección, entonces necesitamos lo que se llama derivadas direccionales, que discutiremos en un próximo apartado.
En la siguiente escena interactiva, diseñada por Tim Brzezinski en GeoGebra, puedes observar e interactuar con una ilustración gráfica de las derivadas parciales.
Amplía la escena para una mejor interacción. En ella puedes cambiar la función; por ejemplo, $f(x,y) = sen(x)cos(y)$ y observar tanto el plano tangente como las rectas tangentes en un punto dado, el cual también puedes modificar.
Ahora volvemos a la idea de los mapas de contorno, que presentamos en Funciones de varias variables. Podemos usar un mapa de contorno para estimar derivadas parciales de una función $g (x, y)$.
 |
Derivadas parciales en un mapa de contorno |
Usa un mapa de contorno para estimar $\partial g /\partial x $ en el punto $(\sqrt{5}, 0) $para la función $g (x, y) = \sqrt{9 − x^2 − y^2 }$.

Supongamos que tenemos una función de tres variables, como $w = f (x, y, z)$. Podemos calcular derivadas parciales de $w $ con respecto a cualquiera de las variables independientes, susando las definiciones para funciones de dos variables.
Podemos calcular una derivada parcial de una función de tres variables usando la misma idea que usamos para una función de dos variables.
Por ejemplo, si tenemos una función $f$ de $x, y$, y $z$, y deseamos calcular $\partial f /\partial x$, tratamos las otras dos variables independientes como si fueran constantes, luego las diferenciamos con respecto a $x$.
 |
Cálculo de derivadas parciales para una función de tres variables |
Usa la definición de límite de derivadas parciales para calcular $\frac{\partial f}{\partial x}$ para la función $$f(x,y,z)=x^2−3xy+2y^2−4xz+5yz^2−12x+4y−3z$$ Luego, encuentra $\frac{\partial f}{\partial y}$ y $\frac{\partial f}{\partial z}$ estableciendo las otras dos variables constantes y diferenciando en consecuencia.

 |
Cálculo de derivadas parciales para una función de tres variables |
Calcula las tres derivadas parciales de las siguientes funciones. a. $f(x,y,z)=\frac{x^2y−4xz+y^2}{x-3yz}$ b. $g(x,y,z) = sen(x^2y−z)+cos(x^2−yz)$
Luego, encuentra $\frac{\partial f}{\partial y}$ y $\frac{\partial f}{\partial z}$ estableciendo las otras dos variables constantes y diferenciando en consecuencia.
Considera la función
$$f (x, y) = 2x^3−4xy^2 + 5y^3−6xy + 5x − 4y + 12$$Sus derivadas parciales son
$$\frac{\partial f}{\partial x} = 6x^2−4y^2−6y + 5\text{ y }\frac{\partial f}{\partial y} = −8xy + 15y^2−6x − 4$$Cada una de estas derivadas parciales es una función de dos variables, por lo que podemos calcular derivadas parciales de estas funciones. Al igual que con las derivadas de funciones de una sola variable, podemos llamar a estas derivadas de segundo orden, derivadas de tercer orden, etc. En general, se denominan derivadas parciales de orden superior. Hay cuatro derivadas parciales de segundo orden para cualquier función (siempre que existan):
$$\frac{\partial^2 f}{\partial x^2} = \frac{\partial}{\partial x}\Bigg[\frac{\partial f}{\partial x}\Bigg], \frac{\partial^2 f}{\partial x\partial y} = \frac{\partial}{\partial x}\Bigg[\frac{\partial f}{\partial y}\Bigg], \frac{\partial^2 f}{\partial y\partial x} = \frac{\partial}{\partial y}\Bigg[\frac{\partial f}{\partial x}\Bigg], \frac{\partial^2 f}{\partial y^2} = \frac{\partial}{\partial y}\Bigg[\frac{\partial f}{\partial y}\Bigg]$$Una notación alternativa para cada una es $f_{xx}, f_{yx}, f_{xy}$ y $f_{yy}$, respectivamente. Las derivadas parciales de orden superior calculadas con respecto a diferentes variables, como $f_{xy}$ y $f_{yx}$, se denominan comúnmente derivadas parciales mixtas.
 |
Cálculo de segundas derivadas parciales |
Calcular las las cuatro segundas derivadas parciales de de la función $f (x, y) = xe^{−3y} + sen(2x − 5y)$.

En este punto, deberíamos notar que bajo ciertas condiciones $\frac{\partial^2 f}{\partial x\partial y} = \frac{\partial^2 f}{\partial y\partial x}$. De hecho, es una consecuencia directa del siguiente teorema.
El teorema de Clairaut garantiza que, siempre que las derivadas mixtas de segundo orden sean continuas, el orden en el que elegimos diferenciar las funciones (es decir, qué variable va primero, luego la segunda, etc.) no importa. También puede extenderse a derivadas de orden superior. La prueba del teorema de Clairaut se puede encontrar en los libros de cálculo más avanzados.
Se pueden calcular otras dos derivadas parciales de segundo orden para cualquier función $f (x, y)$.
La derivada parcial $f_{xx}$ es igual a la derivada parcial de $f_x$ con respecto a $x$, y $f_{yy}$ igual a la derivada parcial de $f_y$ con respecto a $y$.
En el curso de ecuaciones diferenciales, estudiaste ecuaciones diferenciales en las que la función desconocida tenía una variable independiente. Una ecuación diferencial parcial es una ecuación que involucra una función desconocida de más de una variable independiente y una o más de sus derivadas parciales. Ejemplos de ecuaciones diferenciales parciales son
$$u_t=c^2(u_{xx}+u_{yy})\tag{$4.17$}$$(ecuación de calor en dos dimensiones)
$$u_{tt=}c^2(u_{xx}+u_{yy})\tag{$4.18$}$$(ecuación de onda en dos dimensiones)
$$u_{xx=}+u_{yy}=0\tag{$4.19$}$$(La ecuación de Laplace en dos dimensiones)
En las dos primeras ecuaciones, la función desconocida $u$ tiene tres variables independientes: $t, x$ e $y$, y $c$ es una constante arbitraria. Las variables independientes $x$ e $y$ se consideran variables espaciales, y la variable $t$ representa el tiempo. En la ecuación de Laplace, la función desconocida $u$ tiene dos variables independientes $x$ e $y$.
 |
Una solución a la ecuación de onda |
Comprueba esto $$u (x, y, t) = 5sen (3\pi x) sen (4\pi y) cos (10\pi t)$$ es una solución a la ecuación de onda $$u_{tt} = 4 (u_{xx} + u_{yy})\tag{$4.20$}$$

Dado que la solución a la ecuación del calor bidimensional es una función de tres variables, no es fácil crear una representación visual de la solución. Podemos graficar la solución para valores fijos de $t$, lo que equivale a instantáneas de las distribuciones de calor en tiempos fijos. Estas instantáneas muestran cómo se distribuye el calor sobre una superficie bidimensional a medida que pasa el tiempo. El gráfico de la solución anterior en el tiempo $t = 0 $ aparece en la siguiente figura. A medida que pasa el tiempo, los extremos se nivelan, acercándose a cero a medida que $t$ se acerca al infinito.
Si consideramos la ecuación de calor en una dimensión, entonces es posible graficar la solución con el tiempo. La ecuación de calor en una dimensión se convierte en
$$u_t=c^2u_{xx}$$donde $c^2$ representa la difusividad térmica del material en cuestión.
Figura 4.21.
Una solución de esta ecuación diferencial se puede escribir en la forma
$$u_m(x,t)= e^{−\pi^2m^2c^2t}sen(m\pi x)$$donde $m$ es cualquier número entero positivo. Un gráfico de esta solución que usa $m = 1$ aparece en la Figura 4.24, donde la distribución de temperatura inicial sobre un cable de longitud $1$ está dada por $u (x, 0) = sen\pi x$. Observa que a medida que pasa el tiempo, el cable se enfría. Esto se ve porque, de izquierda a derecha, la temperatura más alta (que ocurre en el medio del cable) disminuye y cambia de color de rojo a azul.
Figura 4.24. Gráfico de una solución de la ecuación de calor en una dimensión a lo largo del tiempo.
Lord Kelvin y la era de la tierra
A finales de 1800, los científicos del nuevo campo de la geología llegaron a la conclusión de que la Tierra debe tener "millones y millones" de años. Casi al mismo tiempo, Charles Darwin había publicado su tratado sobre la evolución.

Figura 4.25. (a) William Thomson (Lord Kelvin), 1824-1907, fue un físico e ingeniero eléctrico británico; (b) Kelvin utilizó la ecuación de difusión de calor para estimar la edad de la Tierra (crédito: modificación del trabajo de la NASA).
El punto de vista de Darwin era que la evolución necesitaba muchos millones de años para tener lugar, e hizo una audaz afirmación de que los campos "Weald chalk", donde se encontraron fósiles importantes, fueron el resultado de 300 millones de años de erosión.
En ese momento, el físico eminente William Thomson (Lord Kelvin) usó una ecuación diferencial parcial importante, conocida como la ecuación de difusión de calor, para estimar la edad de la Tierra al determinar cuánto tiempo le tomaría a la Tierra enfriarse de la roca fundida a lo que teníamos en ese momento. Su conclusión fue un rango de 20 a 400 millones de años, pero muy probablemente unos 50 millones de años. Durante muchas décadas, las proclamaciones de este ícono irrefutable de la ciencia no le sentaron bien a los geólogos ni a Darwin.
Kelvin hizo suposiciones razonables basadas en lo que se sabía en su tiempo, pero también hizo varias suposiciones que resultaron estar equivocadas. Una suposición incorrecta era que la Tierra es sólida y que, por lo tanto, el enfriamiento fue solo por conducción, lo que justifica el uso de la ecuación de difusión. Pero el error más grave fue perdonable: la omisión del hecho de que la Tierra contiene elementos radiactivos que continuamente suministran calor debajo del manto de la Tierra. El descubrimiento de la radiactividad llegó cerca del final de la vida de Kelvin y reconoció que su cálculo tendría que modificarse.
Kelvin usó el modelo unidimensional simple aplicado solo a la capa externa de la Tierra, y dedujo la edad de los gráficos y el gradiente de temperatura más o menos conocido cerca de la superficie de la Tierra. Echemos un vistazo a una versión más apropiada de la ecuación de difusión en coordenadas radiales, que tiene la forma
$$\frac{\partial T}{\partial t} = K\bigg[\frac{\partial^2 T}{\partial r^2} +\frac{2}{r} \frac{\partial T}{\partial r} \bigg]\tag{$4.23$}$$Aquí, $T (r, t)$ es la temperatura en función de $r$ (medido desde el centro de la Tierra) y el tiempo $t$. $K$ es la conductividad térmica, para roca fundida, en este caso. El método estándar para resolver una ecuación diferencial parcial de este tipo es mediante la separación de variables, donde expresamos la solución como el producto de funciones que contienen cada variable por separado. En este caso, escribiríamos la temperatura como
$$T(r,t)=R(r)f(t)$$Observa cómo los valores de $\alpha n$ provienen de la condición de frontera aplicada en la parte b. El término $\frac{−1^{n − 1}}{n}$ es la constante $A_n$ para cada término de la serie, determinada a partir de la aplicación del método de Fourier.
Dejando $\beta = \pi R_E$, examina los primeros términos de esta solución que se muestran aquí y observa cómo $\lambda^2$ en el exponencial hace que los términos más altos disminuyan rápidamente a medida que pasa el tiempo:
$$T(r,t) = \frac{T_0R_E}{\pi r}\bigg(e^{-K\beta^2 r}(sen \beta r) + \frac{1}{2}e^{-4K\beta^2 r} (sen 2\beta r)+ \frac{1}{3}e^{-9K\beta^2 r}(sen 3\beta r)\\ -\frac{1}{4}e^{-16K\beta^2 r}(sen 4\beta r) +\frac{1}{5}e^{-25K\beta^2 r}(sen 5\beta r)\bigg)...$$Cerca del tiempo $t = 0$, se necesitan muchos términos de la solución para la precisión. Insertando valores para la conductividad $K$ y $\beta = \pi / R_E$ para un tiempo cercano a solo miles de años, solo los primeros términos hacen una contribución significativa. Kelvin solo necesitaba mirar la solución cerca de la superficie de la Tierra (Figura 4.26) y, después de un largo tiempo, determinar qué tiempo produjo el gradiente de temperatura estimado conocido durante su era (aumento $1^o F$ por cada $50 pies$). Simplemente eligió un rango de veces con un gradiente cercano a este valor. En la figura 4.26, las soluciones se trazan y escalan, con la temperatura de la superficie de $300 K$ añadida. Ten en cuenta que el centro de la Tierra sería relativamente frío. En ese momento, se pensaba que la Tierra debía ser sólida.
El 20 de mayo de 1990, el físico Ernest Rutherford habló en la Royal Institution para anunciar un cálculo revisado que incluía la contribución de la radiactividad como fuente de calor de la Tierra. En las propias palabras de Rutherford:
Entré en la habitación, que estaba medio oscura, y actualmente vi a Lord Kelvin en la audiencia, y me di cuenta de que estaba en
Figura 4.26. Temperatura versus distancia radial desde el centro de la Tierra. (a) Los resultados de Kelvin, trazados a escala. (b) Un primer plano de los resultados a una profundidad de $4.0 mi$ debajo de la superficie de la Tierra.
problemas en la última parte de mi discurso sobre la edad de la Tierra, donde mis puntos de vista estaban en conflicto con el suyo. Para mi alivio, Kelvin se quedó profundamente dormido, pero cuando llegué al punto importante, vi al viejo pájaro sentarse, abrir un ojo y lanzarme una mirada huraña. Entonces llegó una inspiración repentina, y dije que Lord Kelvin había limitado la edad de la Tierra, siempre que no se descubriera una nueva fuente [de calor]. Esa expresión profética se refería a lo que ahora estamos considerando esta noche, ¡radio! ¡Mirad! El viejo muchacho sonrió sobre mí.
Rutherford calculó una edad para la Tierra de unos $500$ millones de años. El valor aceptado hoy de la edad de la Tierra es de unos $4.600$ millones de años.

 Para los siguientes ejercicios, calcula la derivada parcial utilizando solo las definiciones de límite.
Para los siguientes ejercicios, calcula la derivada parcial utilizando solo las definiciones de límite.
112. $\frac{\partial z}{\partial x}$ para $z=x^2−3xy+y^2$ 113. $\frac{\partial z}{\partial y}$ para $z=x^2−3xy+y^2$ (Solución).
 Para los siguientes ejercicios, calcula el signo de la derivada parcial usando la gráfica de la superficie.
Para los siguientes ejercicios, calcula el signo de la derivada parcial usando la gráfica de la superficie.
114. $f_x(1,1)$ 115. $f_x(−1,1)$ (Solución) 116. $f_y(1,1)$ 117. $f_x(0,0)$ (Solución)
 Para los siguientes ejercicios, calcula las derivadas parciales.
Para los siguientes ejercicios, calcula las derivadas parciales.
118. $\frac{\partial z}{\partial x}$ para $z = sen (3x) cos (3y)$ 119. $\frac{\partial z}{\partial y}$ para $z = srn (3x) cos (3y)$ (Solución) 120. $\frac{\partial z}{\partial x}$ y $\frac{\partial z}{\partial y}$ para $z = x^8e^{3y}$ 121. $\frac{\partial z}{\partial x}$ y $\frac{\partial z}{\partial y}$ para $z = ln (x^6 + y^4)$ (Solución) 122. Encuentra $f_y (x, y)$ para $f (x, y) = e^{xy}cos (x) sen (y)$ 123. Sea $z = e^{xy}$. Encuentra $\frac{\partial z}{\partial x}$ y $\frac{\partial z}{\partial y}$ (Solución) 124. Sea $z = ln (\frac{x}{y})$. Encuentra $\frac{\partial z}{\partial x}$ y $\frac{\partial z}{\partial y}$ 125. Sea $z = tan (2x − y)$. Encuentra $\frac{\partial z}{\partial x}$ y $\frac{\partial z}{\partial y}$ (Solución). 126. Sea $z = senh (2x + 3y)$. Encuentra $\frac{\partial z}{\partial x}$ y $\frac{\partial z}{\partial y}$ 127. Sea $f (x, y) = arctan (\frac{y}{x})$. Evalúa $f_x (2, −2)$ y $f_y (2, −2)$ (Solución) 128. Sea $f (x, y) = \frac{xy}{x − y}$. Encuentra $f_x (2, −2)$ y $f_y (2, −2)$
 Evaluar las derivadas parciales en el punto P (0,1).
Evaluar las derivadas parciales en el punto P (0,1).
129. Encuentra $\frac{\partial z}{\partial x}$ en $(0,1)$ para $z = e^{−x}cos (y)$ (Solución) 130. Dado $f (x, y, z) = x^3yz^2$, encuentra $\frac{\partial^ z}{\partial x \partial y}$ y $f_z (1,1,1)$ 131. Dado $f (x, y, z) = 2sen (x + y)$, encuentra $f_x (0, \frac{\pi}{2}, −4)$, $f_y (0, \frac{\pi}{2}, −4)$ y $f_z (0, \frac{\pi}{2}, −4)$ (Solución) 132. El área de un paralelogramo con longitudes de lados adyacentes que son $a$ y $b$, y en el que el ángulo entre estos dos lados es $\theta$, viene dada por la función $A (a, b, \theta) = basen (\theta)$. Encuentra la tasa de cambio del área del paralelogramo con respecto a lo siguiente:
133. Expresa el volumen de un cilindro circular derecho en función de dos variables:
134. Calcula $\frac{\partial w}{\partial z}$ para $w = zsen (xy^2 + 2z)$.
 Encuentra las derivadas parciales de orden superior indicadas.
Encuentra las derivadas parciales de orden superior indicadas.
135. $f_{xy}$ para $z = ln (x − y)$ (Solución) 136. $f_{yx}$ para $z = ln (x − y)$ 137. Sea $z = x^2 + 3xy + 2y^2$. Encuentra $\frac{\partial^2 z}{\partial x^2}$ y $\frac{\partial^2 z}{\partial y^2}$ (Solución). 138. Dado $z = e^xtany$, encuentra $\frac{\partial^2 z}{\partial x \partial y}$ y $\frac{\partial^2 z}{\partial y \partial x}$. 139. Dado $f (x, y, z) = xyz$, encuentra $f_{xyy}, f_{yxy}$ y $f_{yyx}$ (Solución). 140. Dado $f (x, y, z) = e^{− 2x}sen (z^2y)$, demuestra que $f_{xyy} = f_{yxy}$. 141. Demuestra que $z = 12 (e^y − e^{−y}) senx$ es una solución de la ecuación diferencial $\frac{\partial^2 z}{\partial x^2} + \frac{\partial^2 z}{\partial y^2} = 0$ (Solución). 142. Encuentra $f_{xx} (x, y)$ para $f (x, y) = \frac{4x^2}{y} + \frac{y2}{2x}$.
143. Sea $f (x, y, z) = x^2y^3z − 3xy^2z^3 + 5x^2z − y^3z$. Encuentra a $f_{xyz}$ (Solución). 144. Sea $F (x, y, z) = x^3yz^2−2x^2yz + 3xz − 2y^3z$. Encuentra la derivada parcial $F_{xyz}$ 145. Dado $f (x, y) = x^2 + x − 3xy + y^3−5$, encuentra todos los puntos en los que $f_x = f_y = 0$ simultáneamente (Solución). 146. Dado $f (x, y) = 2x^2 + 2xy + y^2 + 2x − 3$, encuentra todos los puntos en los que $\frac{\partial f}{\partial x} = 0$ y $\frac{\partial f}{\partial y} = 0$ simultáneamente. 147. Dado $f (x, y) = y^3−3yx^2−3y^2−3x^2 + 1$, encuentra todos los puntos en $f $en los que $f_x = f_y = 0$ simultáneamente (Solución). 148. Dado $f (x, y) = 15x^3−3xy + 15y^3$, encuentra todos los puntos en los que $f_x (x, y) = f_y (x, y) = 0$ simultáneamente. 149. Demuestra que $z = e^xseny$ satisface la ecuación $\frac{\partial^2 z}{\partial x^2} + \frac{\partial^2 z}{\partial y^2}$ = 0 (Solución). 150. Demuestra que $f (x, y) = ln (x^2 + y^2)$ resuelve la ecuación de Laplace $\frac{\partial^2 z}{\partial x^2} + \frac{\partial^2 z}{\partial y^2} = 0$. 151. Demuestra que $z = e^{−t}cos (\frac{x}{c})$ satisface la ecuación de calor $\frac{\partial z}{\partial t} = −e^{−t}cos (\frac{x}{c})$ (Solución). 152. Encuentra $\lim\limits_{\Delta x \to 0}\frac{f (x + \Delta x) −f (x, y)}{\Delta x}$ para $f (x, y) = - 7x − 2xy + 7y$. 153. Encuentra $\lim\limits_{\Delta y \to 0}\frac{f (x + \Delta y) −f (x, y)}{\Delta y}$ para $f (x, y) = - 7x − 2xy + 7y$ (Solución). 154. Encuentra $\lim\limits_{\Delta x \to 0}\frac{f (x + \Delta x) −f (x, y)}{\Delta x}$ para $f (x, y) = x^2y^2 + xy + y$ 155. Encuentra $\lim\limits_{\Delta y \to 0}\frac{f (x + \Delta y) −f (x, y)}{\Delta y}$ para $f (x, y) = sen (xy)$ (Solución).
156. La función $P (T, V) = \frac{nRT}{V}$ da la presión en un punto de un gas en función de la temperatura $T$ y el volumen $V$. Las letras $n$ y $R$ son constantes. Encuentra $\frac{\partial P}{\partial V}$ y $\frac{\partial P}{\partial T}$, y explica qué representan estas cantidades. 157. La ecuación para el flujo de calor en el plano $xy$ es $\frac{\partial f}{\partial t} = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}$. Demuestra que $f (x, y, t) = e^{−2t}senxseny$ es una solución. 158. La ecuación de onda básica es $f_{tt} = f_{xx}$. Verifica que $f (x, t) = sen (x + t)$ y $f (x, t) = sen (x − t)$ son soluciones. 159. La ley de los cosenos puede considerarse como una función de tres variables. Sea $x, y$, y $\theta$ dos lados de cualquier triángulo donde el ángulo $\theta$ es el ángulo incluido entre los dos lados. Entonces, $F (x, y, \theta) = x^2 + y^2−2xycos\theta$ da el cuadrado del tercer lado del triángulo. Encuentra $\frac{\partial F}{\partial \theta}$ y $\frac{\partial F}{\partial x}$ cuando $x = 2, y = 3$ y $\theta = \frac{\pi}{6}$ (Solución). 160. Supongamos que los lados de un rectángulo cambian con respecto al tiempo. El primer lado está cambiando a una velocidad de $2\; pulgadas/ seg$ mientras que el segundo lado está cambiando a una velocidad de $4\; pulgadas / seg$. ¿Qué tan rápido cambia la diagonal del rectángulo cuando el primer lado mide $16\; pulgadas$ y el segundo lado mide $20\; pulgadas$? (Redondea a tres decimales). 161. Una función de producción de Cobb-Douglas es $f (x, y) = 200x^{0.7}y^{0.3}$, donde $x$ y $y$ representa la cantidad de trabajo y capital disponible. Sea $x = 500$ e $y = 1000$. Encuentre $\frac{\partial f}{\partial x}$ y $\frac{\partial f}{\partial y}$ en estos valores, que representan la productividad marginal del trabajo y el capital, respectivamente (Solución). 162. El índice de temperatura aparente es una medida de cómo se siente la temperatura, y se basa en dos variables: $h$, que es la humedad relativa, y $t$, que es la temperatura del aire.
$A = 0.885t − 22.4h + 1.20th − 0.544$. Encuentra $\frac{\partial A}{\partial t}$ y $\frac{\partial A}{\partial h}$ cuando $t = 20^o F$ y $h = 0.90$.
Consideramos el problema de encontrar el plano tangente a una superficie, que es análogo a encontrar la ecuación de una recta tangente a una curva $y=f(x)$. La pendiente de la recta tangente en el punto $x = a$ es dada por $m = f'(a)$; ¿Cuál es la pendiente de un plano tangente?
Intuitivamente, parece claro que, en un plano, solo una recta puede ser tangente a una curva en un punto. Sin embargo, en el espacio tridimensional, muchas rectas pueden ser tangentes a un punto dado. Si estas rectas se encuentran en el mismo plano, determinan el plano tangente en ese punto. Un plano tangente en un punto regular contiene todas las rectas tangentes a ese punto. Una forma más intuitiva de pensar en un plano tangente es asumir que la superficie es lisa en ese punto (sin esquinas). Luego, una recta tangente a la superficie en ese punto en cualquier dirección no tiene cambios abruptos en la pendiente porque la dirección cambia suavemente.
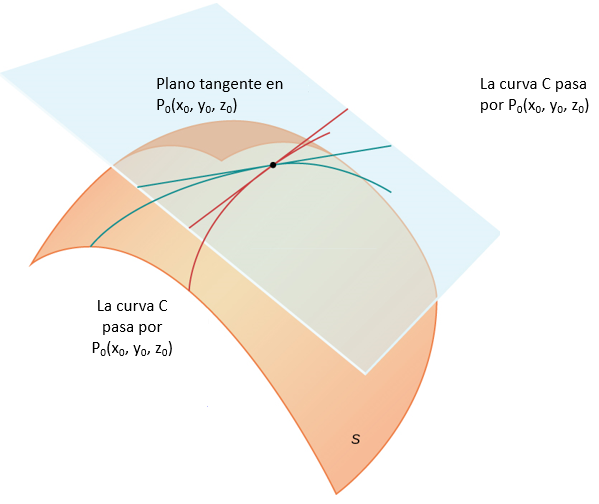
Figura 4.27. El plano tangente a una superficie $S$ en un punto $P_0$ contiene todas las rectas tangentes a curvas en $S$ que pasan por $P_0$.
Para que exista un plano tangente a una superficie en un punto de esa superficie, es suficiente que la función que define la superficie sea diferenciable en ese punto, definida más adelante en este apartado. Definimos el término plano tangente aquí y luego exploramos la idea intuitivamente.
Para ver por qué esta fórmula es correcta, primero encontremos dos rectas tangentes a la superficie $S$. La ecuación de la recta tangente a la curva que está representada por la intersección de $S$ con la traza vertical dada por $x = X_0$ es $z = f(x_ 0, y_00) + f_y(X_0, y_0)(y - y_0)$ . Del mismo modo, la ecuación de la recta tangente a la curva que está representada por la intersección de $S$ con la traza vertical dada por $y = y_0$ es $z= f(Xx_0, y_0) + f_x(x_0, y_0)(x - x_0)$ . Un vector paralelo a la primera recta tangente es $\bold{a} = \bold{j} + f_y(x_0, y_0)\bold{k}$; un vector paralelo a la segunda recta tangente es $\bold{b} = \bold{i} + f_x(x_0, y_0)\bold{k}$ . Podemos tomar el producto cruz de estos dos vectores:
$$\begin{aligned} \bold{a \times b} &= (\bold{j} + f_y(x_0, y_0)\bold{k})\times (\bold{i} + f_x(x_0, y_0)\bold{k}\\ &= \begin{vmatrix} \bold{i} & \bold{j} & \bold{k}\\ 0 & 1 & f_y(x_0, y_0)\\ 1 & 0 & f_x(x_0, y_0) \end{vmatrix}\\ &= f_x(x_0, y_0)\bold{i} + f_y(x_0, y_0)\bold{j} − \bold{k} \end{aligned}$$Este vector es perpendicular a ambas rectas y, por lo tanto, perpendicular al plano tangente. Podemos usar este vector como un vector normal para el plano tangente, junto con el punto $P_0 = (x_0, y_0, f(x_0, y_0))$ en la ecuación para un plano:
Resolviendo esta ecuación para $z$ da la ecuación 4.24.
 |
Encontrar un plano tangente |
Encuentra la ecuación del plano tangente a la superficie definida por la función $f(x , y) = 2x^2 - 3xy + 8y^2 + 2x - 4y + 4$ en el punto $(2 , −1)$

 |
Encontrar otro plano tangente |
Encuentra la ecuación del plano tangente a la superficie definida por la función $f(x, y) = sen(2x)cos(3y)$ en el punto $(\pi/3, \pi/4)$.

Un plano tangente a una superficie no siempre existe en cada punto de la superficie. Considera la función:
$$f(x, y) = \begin{cases} \frac{xy}{\sqrt{x^2+y^2}}\;\;(x, y)\cancel{=}(0, 0) \\ 0\;\;(x, y)=(0, 0) \end{cases}$$El gráfico de esta función es:
Figura 4.29. Gráfico de una función que no tiene un plano tangente en el origen.
Si algún $x = 0$ o $y = 0$, entonces $f(x, y)=0$, luego el valor de la función no cambia ni en el eje $x$ ni en el eje $y$ . Por lo tanto, $f_x(x, 0) = f_y(0, y) = 0$, así como $x$ o $y$ cercanos a cero, estas derivadas parciales permanecen iguales a cero. Sustituyéndolos en la ecuación 4.24 da $z = 0$ como la ecuación de la recta tangente.
Puedes interactuar con la gráfica, diseñada en DescartesJS, a continuación:
Sin embargo, si nos acercamos al origen desde una dirección diferente, obtenemos una historia diferente. Por ejemplo, supongamos que nos acercamos al origen a lo largo de la recta $y = x$. Si ponemos $y = x$ en la función original, se convierte en
$$f(x, x) = \frac{x(x)}{\sqrt{x^2+(x)^2}} = \frac{x^2}{\sqrt{2x^2}} = \frac{|x|}{\sqrt{2}}$$ Cuando $x \gt 0$, la pendiente de esta curva es igual a $\sqrt{2}/2$; cuando $x \lt 0$, la pendiente de esta curva es igual a $−\sqrt{2}/2$.Esto presenta un problema. En la definición de plano tangente, suponemos que todas las rectas tangentes a través del punto $P$ (en este caso, el origen) se encontraba en el mismo plano. Claramente, este no es el caso aquí. Cuando estudiamos funciones diferenciables, veremos que esta función no es diferenciable en el origen.
Recordemos a partir de aproximaciones lineales y diferenciales que la fórmula para la aproximación lineal de una función $f(x)$ en el punto $x = a$ está dada por:
$$y \approx f(a) + f'(a)(x − a)$$El diagrama para la aproximación lineal de una función de una variable aparece en el siguiente gráfico.
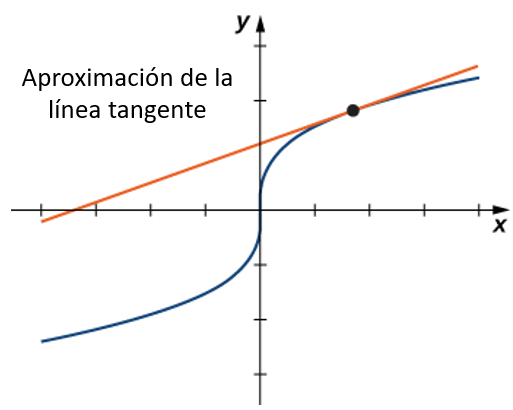
Figura 4.30. Aproximación lineal de una función en una variable.
La recta tangente se puede utilizar como una aproximación a la función $f(x)$ para valores de $x$ razonablemente cerca de $x = a$. Cuando se trabaja con una función de dos variables, la recta tangente se reemplaza por un plano tangente, pero la idea de aproximación es muy parecida.
Observa que esta ecuación también representa el plano tangente a la superficie definida por $z = f(x, y)$ en el punto $(x_0, y_0)$. La idea detrás del uso de una aproximación lineal es que, si hay un punto $(x_0, y_0)$ en el cual el valor preciso de $f(x, y)$ es conocido, entonces por valores de $(x, y)$ razonablemente cerca de $(x_0, y_0)$, la aproximación lineal (es decir, el plano tangente) produce un valor que también es razonablemente cercano al valor exacto de $f(x, y)$ (Figura 4.31). Además, el plano que se usa para encontrar la aproximación lineal es también el plano tangente a la superficie en el punto $(x_0, y_0)$.

Figura 4.31. Uso de un plano tangente para la aproximación lineal en un punto.
 |
Usando una aproximación de plano tangente |
Dada la función $f(x, y) = \sqrt{41 - 4x^2 - y^2}$, aproxima $f( 2.1, 2.9 )$ utilizando el punto $(2, 3)$ para $(x_0, y_0)$. ¿Cuál es el valor aproximado de $f( 2.1, 2.9 )$ a cuatro decimales?

Cuando trabajas con una función $y = f(x)$ de una variable, se dice que la función es diferenciable en un punto $x = a$ si $f′(a)$ existe. Además, si una función de una variable es diferenciable en un punto, el gráfico es "suave" en ese punto (es decir, no existen esquinas) y una recta tangente está bien definida en ese punto.
La idea detrás de la diferenciabilidad de una función de dos variables está relacionada con la idea de suavidad en ese punto. En este caso, se considera que una superficie es lisa en el punto $P$ si existe un plano tangente a la superficie en ese punto. Si una función es diferenciable en un punto, entonces existe un plano tangente a la superficie en ese punto. Recordemos la fórmula para un plano tangente en un punto $(x_0, y_0)$ está dado por
$$z = f(x_0, y_0) + f_x(x_0, y_0)(x − x_0) + f_y(x_0, y_0)(y − y_0)$$Para que exista un plano tangente en el punto $(x_0, y_0)$, las derivadas parciales deben por lo tanto existir en ese punto. Sin embargo, esta no es una condición suficiente para la suavidad, como se ilustra en la Figura 4.29. En ese caso, las derivadas parciales existían en el origen, pero la función también tenía una esquina en el gráfico en el origen.
El último término en la ecuación 4.26 se conoce como el término de error y representa la proximidad del plano tangente a la superficie en un pequeño vecindario (disco $\delta$) del punto $P$. Para que la función $f$ sea diferenciable en $P$, la función debe ser suave, es decir, la gráfica de $f$ debe estar cerca del plano tangente para los puntos cercanos a $P$.
 |
Demostrando la diferenciabilidad |
Demuestra que la función $f (x, y) = 2x^2−4y$ es diferenciable en el punto $(2, −3)$.

La función $f(x, y) = \begin{cases} \frac{xy}{\sqrt{x^2+y^2}}\;\;(x, y) \cancel{=} (0, 0) \\ 0\;\;(x, y)=(0, 0) \end{cases}$ no es diferenciable en el origen. Podemos ver esto calculando las derivadas parciales. Esta función apareció anteriormente en la sección, donde mostramos que $f_x(0, 0) = f_y(0, 0) = 0$. Sustituyendo esta información en la Ecuación 4.26 y usando $x_0 = 0$ e $y_0 = 0$, obtenemos
Calculando el límite:
$$\begin{aligned} \lim\limits_{(x, y) \to (x_0, y_0)}\frac{E(x, y)}{\sqrt{(x - x_0)^2 + (y - y_0)^2}} &= \lim\limits_{(x, y) \to (0, 0)}\frac{\frac{xy}{\sqrt{x^2 + y^2}}}{\sqrt{x^2 + y^2}}\\ &= \lim\limits_{(x, y) \to (0, 0)}\frac{xy}{x^2 + y^2} \end{aligned}$$Dependiendo de la ruta tomada hacia el origen, este límite toma diferentes valores. Por lo tanto, el límite no existe y la función $f$ no es diferenciable en el origen como se muestra en la siguiente figura.
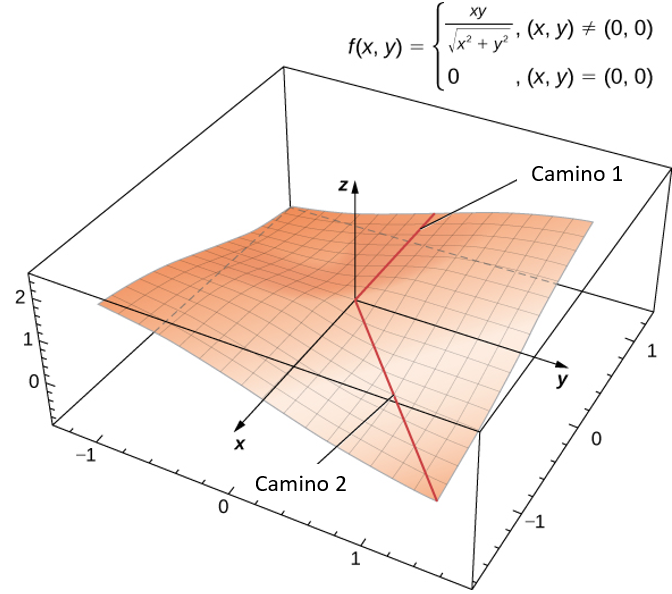
Figura 4.32. Esta función $f(x, y)$ no es diferenciable en el origen.
La diferenciabilidad y la continuidad para funciones de dos o más variables están conectadas, lo mismo que para funciones de una variable. De hecho, con algunos ajustes de notación, el teorema básico es el mismo.
La diferenciabilidad implica que la continuidad muestra que si una función es diferenciable en un punto, entonces es continua allí. Sin embargo, si una función es continua en un punto, entonces no es necesariamente diferenciable en ese punto. Por ejemplo,
$$f(x, y) = \begin{cases} \frac{xy}{\sqrt{x^2+y^2}}\;\;(x, y) \cancel{=} (0, 0) \\ 0\;\;(x, y)=(0, 0) \end{cases}$$es continua en el origen, pero no es diferenciable en el origen. Esta observación también es similar a la situación en el cálculo de una sola variable.
La continuidad de las primeras derivadas parciales implica diferenciabilidad, explora aún más la conexión entre continuidad y diferenciabilidad en un punto. Este teorema dice que si la función y sus derivadas parciales son continuas en un punto, la función es diferenciable.
Recordemos que anteriormente mostramos que la función
$$f(x, y) = \begin{cases} \frac{xy}{\sqrt{x^2+y^2}}\;\;(x, y) \cancel{=} (0, 0) \\ 0\;\;(x, y)=(0, 0) \end{cases}$$no era diferenciable en el origen. Calculemos las derivadas parciales $f_x$ y $f_y$:
$$\frac{\partial f}{\partial x} = \frac{y^3}{(x^2+y^2)^{3/2}}\;\;y\;\; \frac{\partial f}{\partial y} = \frac{x^3}{(x^2+y^2)^{3/2}}$$La contraposición del teorema anterior establece que si una función no es diferenciable, entonces al menos una de las hipótesis debe ser falsa. Exploremos la condición que $f_x(0, 0)$ debe ser continua. Para que esto sea cierto, debe ser cierto que $\lim\limits_{(x, y) \to (0, 0)}f_x(0, 0) = f_x(0, 0)$:
$$\lim\limits_{(x, y) \to (0, 0)}f_x(0, 0) = \lim\limits_{(x, y) \to (0, 0)}\frac{y^3}{(x^2+y^2)^{3/2}}$$Sea x = ky. Luego
$$\begin{aligned} \lim\limits_{(x, y) \to (0, 0)}\frac{y^3}{(x^2+y^2)^{3/2}} &= \lim\limits_{y \to 0}\frac{y^3}{\bigg((ky)^2+y^2\bigg)^{3/2}}\\ &= \lim\limits_{y \to 0}\frac{y^3}{(k^2y^2+y^2)^{3/2}}\\ &= \lim\limits_{y \to 0}\frac{y^3}{|y|^3(k^2+1)^{3/2}}\\ &= \frac{1}{(k^2+1)^{3/2}}\lim\limits_{y \to 0}\frac{|y|}{y} \end{aligned}$$Si $y\gt 0$, entonces esta expresión es igual a $1/(k^2 + 1)^{3/2}$; si $y\lt 0$, entonces es igual a $-\bigg(1/(k^2 + 1)^{3/2}\bigg)$. En cualquier caso, el valor depende de $k$, por lo que el límite no existe.
En el apartado "Aproximaciones lineales y diferenciales", primero estudiamos el concepto de diferenciales. El diferencial de $y$, escrito $dy$, se define como $f^′(x)dx$. El diferencial se usa para aproximar $\Delta y = f(x + \Delta x) − f(x)$, donde $\Delta x = dx$. Extendiendo esta idea a la aproximación lineal de una función de dos variables en el punto $(x_0, y_0)$ se obtiene la fórmula para el diferencial total para una función de dos variables.
El diferencial $dz$, también llamado diferencial total de $z = f(x, y)$ en $(x_0, y_0)$, se define como
$$dz = f_x(x_0,y_0)dx + f_y(x_0,y_0)dy \tag{$4.27$}$$Observa que el símbolo $\partial$ no se usa para denotar el diferencial total; más bien, $d$ aparece delante de $z$. Ahora, definamos $\Delta z = f(x + \Delta x, y + \Delta y) − f(x, y)$. Usamos $dz$ para aproximar $\Delta z$, entonces
$$\Delta z \approx dz = f_x(x_0, y_0)dx + f_y(x_0, y_0)dy$$Por lo tanto, el diferencial se usa para aproximar el cambio en la función $z = f(x_0, y_0)$ en el punto $(x_0, y_0)$ para valores dados de $\Delta x$ y $\Delta y$. Como $\Delta z = f(x + \Delta x, \Delta y + \Delta y) − f(x, y)$, esto se puede usar para aproximar $f(x + \Delta x, y + \Delta y)$:
$$\begin{aligned} f(x + \Delta x, \Delta y + \Delta y) &= f(x,y) + \Delta z\\ &\approx f(x, y) + f_x(x_0, y_0)\Delta x + f_y(x_0, y_0)\Delta y \end{aligned}$$Observa la siguiente figura:
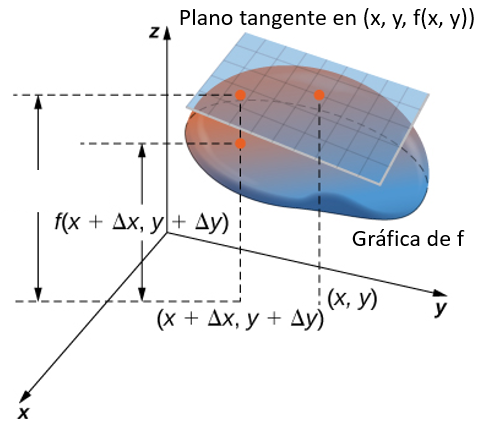
Figura 4.33. La aproximación lineal se calcula mediante la fórmula $f(x + \Delta x, y + \Delta y) \approx f(x, y) + f_x(x_0, y_0)\Delta x + f_y(x_0, y_0)\Delta y$.
Una aplicación de esta idea es determinar la propagación de errores. Por ejemplo, si estamos fabricando un dispositivo y estamos fuera de cierta cantidad al medirla, el diferencial se puede usar para estimar el error en el volumen total del dispositivo.
 |
Aproximación por diferenciales |
Encuentra el diferencial $dz$ de la función $f(x, y) = 3x^2−2xy + y^2$ y úsalo para aproximar $\Delta z$ en el punto $(2, −3)$. Usa $\Delta x = 0.1$ y $\Delta y = −0.05$. ¿Cuál es el valor exacto de $\Delta z$?

Todos los resultados anteriores para la diferenciabilidad de las funciones de dos variables se pueden generalizar a funciones de tres variables. Primero, la definición:
Si una función de tres variables es diferenciable en un punto $(x_0, y_0, z_0)$, entonces es continua allí. Además, la continuidad de las primeras derivadas parciales en ese punto garantiza la diferenciabilidad.

 Para los siguientes ejercicios, encuentra un vector normal unitario de la superficie en el punto indicado.
Para los siguientes ejercicios, encuentra un vector normal unitario de la superficie en el punto indicado.
163. $f(x, y) = x^3, (2, −1, 8)$ (Solución) 164. $ln\bigg(\frac{x}{y - z}\bigg) = 0$ cuando $x = y = 1$.
 Para los siguientes ejercicios, como una revisión útil de las técnicas utilizadas en esta sección, encuentra un vector normal y un vector tangente en el punto $P$.
Para los siguientes ejercicios, como una revisión útil de las técnicas utilizadas en esta sección, encuentra un vector normal y un vector tangente en el punto $P$.
165. $x^2 + xy + y^2=3, P(−1, −1)$ (Solución) 166. $(x^2 + y^2)^2 = 9(x^2 − y^2), P(\sqrt{2}, 1)$ 167. $xy^2 − 2x^2 + y + 5x = 6, P(4, 2)$ (Solución) 168. $2x^3 − x^2y^2 = 3x − y − 7, P(1, −2)$ 169. $ze^{x^2−y^2} − 3 =0, P(2, 2, 3)$ (Solución)
 Para los siguientes ejercicios, encuentra la ecuación para el plano tangente a la superficie en el punto indicado (Insinuación: Resuelve $z$ en términos de $x$ e $y$)
Para los siguientes ejercicios, encuentra la ecuación para el plano tangente a la superficie en el punto indicado (Insinuación: Resuelve $z$ en términos de $x$ e $y$)
170. $−8x − 3y − 7z = −19, P(1, −1, 2)$ 171. $z = −9x^2 − 3y^2, P(2, 1, −39)$ (Solución) 172. $x^2 + 10xyz + y^2 + 8z^2 = 0, P(−1, −1, −1)$
173. $z = ln(10x^2 + 2y^2 + 1), P(0, 0, 0)$ (Solución) 174. $z = e^{7x^2 + 4y^2}, P(0, 0, 1)$ 175. $xy + yz + zx = 11, P(1, 2, 3)$ (Solución) 176. $x^2 + 4y^2 = z^2, P(3, 2, 5)$ 177. $x^3 + y^3 = 3xyz, P(1, 2, \frac32)$ (Solución) 178. $z = axy, P(1, \frac{1}{a}, 1)$ 179. $z = sen x + sen y + sen(x + y), P(0, 0, 0)$ (Solución) 180. $h(x, y) = ln \sqrt{x^2 + y^2}, P(3, 4)$ 181. $z=x^2 − 2xy + y^2, P(1, 2, 1)$ (Solución)
 Para los siguientes ejercicios, encuentra las ecuaciones paramétricas para la recta normal a la superficie en el punto indicado. (Recuerda que para encontrar la ecuación de una recta en el espacio, necesitas un punto en la recta, $P_0 (x_0, y_0, z_0)$ y un vector $\bold{n} = \lang a, b, c\rang$ que es paralelo a la recta. Luego la ecuación de la recta es $x − x_0 = at, y − y_0 = bt, z − z_0 = ct$).
Para los siguientes ejercicios, encuentra las ecuaciones paramétricas para la recta normal a la superficie en el punto indicado. (Recuerda que para encontrar la ecuación de una recta en el espacio, necesitas un punto en la recta, $P_0 (x_0, y_0, z_0)$ y un vector $\bold{n} = \lang a, b, c\rang$ que es paralelo a la recta. Luego la ecuación de la recta es $x − x_0 = at, y − y_0 = bt, z − z_0 = ct$).
182. $−3x + 9y + 4z = −4, P(1,−1,2)$ 183. $z = 5x^2 − 2y^2, P(2, 1, 18)$ (Solución) 184. $x^2 − 8xyz + y^2 + 6z^2 = 0, P(1, 1, 1)$ 185. $z = ln(3x^2 + 7y^2 + 1), P(0, 0, 0)$ (Solución) 186. $z = e^{4x^2 + 6y^2}, P(0, 0, 1)$ 187. $z = x^2 − 2xy + y^2, P(1, 2, 1)$ (Solución)
 Para los siguientes ejercicios, observa la siguiente imagen:
Para los siguientes ejercicios, observa la siguiente imagen:
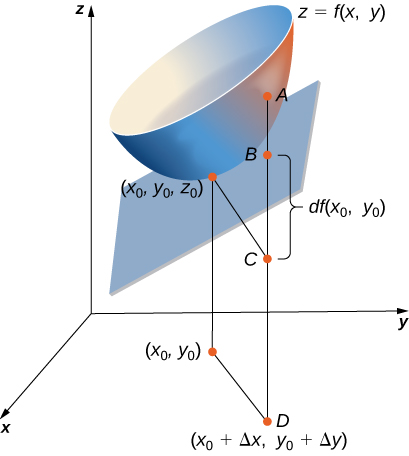
188. ¿La longitud del segmento de recta $AC$ es igual a qué expresión matemática? 189. ¿La longitud del segmento de recta $BC$ es igual a qué expresión matemática? (Solución) 190. Usando la figura, explica qué representa la longitud del segmento de recta $AB$.
 Para los siguientes ejercicios, completa cada tarea.
Para los siguientes ejercicios, completa cada tarea.
191. Demuestra que $f(x, y) = e^{xy}x$ es diferenciable en el punto $(1,0)$ (Solución).
192. Encuentra el diferencial total de la función $w = e^{y}cos(x) + z^2$. 193. Demuestra que $f(x, y) = x^2 + 3y$ es diferenciable en cada punto. En otras palabras, demuestra que $\Delta z = f(x + \Delta x, y + \Delta y) − f(x, y) = f_x\Delta x + f_y\Delta y + \epsilon_1\Delta x + \epsilon_2\Delta y$, donde $\epsilon_1$ y $\epsilon_2$ se aproximan a cero cuando $(\Delta x, \Delta y)$ se acerca $(0, 0)$ (Solución). 194. Encuentra el diferencial total de la función $z = \frac{xy}{y + x}$ donde $x$ cambia de $10$ a $10.5$ e $y$ cambia de $15$ a $13$. 195. Sea $z = f(x, y) = xe^y$. Calcula $\Delta z$ de $P(1, 2)$ a $Q(1.05, 2.1)$ y luego encuentra el cambio aproximado en $z$ del punto $P$ al punto $Q$. Recuerda que $\Delta z = f(x + \Delta x, y + \Delta y) − f(x, y)$, y $dz$ y $\Delta z$ son aproximadamente iguales (Solución). 196. El volumen de un cilindro circular derecho viene dado por $V(r, h) = \pi r^2h$. Encuentra el diferencial $dV$. Interpreta la fórmula geométricamente. 197. Ver el problema anterior. Utiliza diferenciales para estimar el volumen de aluminio en una lata de aluminio cerrada con un diámetro de $8.0 cm$ y una altura de $12 cm$ si el aluminio tiene un espesor de $0.04 cm$ (Solución). 198. Usa el diferencial $dz$ para aproximar el cambio en $z = \sqrt{4 − x^2 − y^2}$ a medida que $(x, y)$ se mueve de $(1,1)$ a $(1.01, 0.97)$. Compara esta aproximación con el cambio real en la función. 199. Sea $z = f (x, y) = x^2 + 3xy − y^2$. Encuentra el cambio exacto en la función y el cambio aproximado en la función a medida que $x$ cambia de $2.00$ a $2.05$ e $y$ cambia de $3.00$ a $2.96$ (Solución). 200. La aceleración centrípeta de una partícula que se mueve en un círculo viene dada por a $(r, v) = \frac{v^2}{r}$, donde $v$ es la velocidad y $r$ es el radio del círculo. Aproxima el porcentaje de error máximo al medir la aceleración resultante de errores del $3%$ en $v$ y del $2%$ en $r$
(Recuerda que el error porcentual es la relación de la cantidad de error sobre la cantidad original. Entonces, en este caso, el error porcentual en $a$ viene dado por $\frac{da}{a}$). 201. El radio $r$ y la altura $h$ de un cilindro circular derecho se miden con posibles errores del $4%$ y $5%$, respectivamente. Aproxima el error porcentual máximo posible al medir el volumen (recuerda que el error porcentual es la relación de la cantidad de error sobre la cantidad original. Entonces, en este caso, el error porcentual en $V$ viene dado por $\frac{dV}{V}$) (Solución). 202. El radio base y la altura de un cono circular derecho se miden como $10\; pulg$ y $25\; pulg$, respectivamente, con un posible error en la medición de hasta $0.1\; pulg$ cada una. Usa diferenciales para estimar el error máximo en el volumen calculado del cono. 203. La resistencia eléctrica $R$ producida por el cableado de las resistencias $R_1$ y $R_2$ en paralelo se puede calcular a partir de la fórmula $\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}$. Si $R_1$ y $R_2$ se miden en $7\Omega$ y $6\Omega$, respectivamente, y si estas mediciones son precisas dentro de $0.05\Omega$, calcula el error máximo posible en el cálculo de $R$ (El símbolo $\Omega$ representa un ohm, la unidad de resistencia eléctrica) (Solución). 204. El área de una elipse con ejes de longitud $2a$ y $2b$ viene dada por la fórmula $A = \pi ab$. Aproxima el porcentaje de cambio en el área cuando $a$ aumenta en un $2%$ y $b$ aumenta en un $1,5%$. 205. El período $T$ de un péndulo simple con pequeñas oscilaciones se calcula a partir de la fórmula $T = 2\pi \sqrt{\frac{L}{g}}$, donde $L$ es la longitud del péndulo y $g$ es la aceleración resultante de la gravedad. Supón que $L$ y $g$ tienen errores de, como máximo, $0.5%$ y $0.1%$, respectivamente. Utiliza diferenciales para aproximar el error porcentual máximo en el valor calculado de $T$ (Solución).
206. La potencia eléctrica $P$ viene dada por $P = \frac{V^2}{R}$, donde $V$ es el voltaje y $R$ es la resistencia. Aproxima el error porcentual máximo al calcular la potencia si se aplican $120\; V$ a una resistencia de $2000\Omega$ y los posibles errores porcentuales en la medición de $V$ y $R$ son $3%$ y $4%$, respectivamente.
 Para los siguientes ejercicios, encuentra la aproximación lineal de cada función en el punto indicado.
Para los siguientes ejercicios, encuentra la aproximación lineal de cada función en el punto indicado.
207. $f(x, y) = x\sqrt{y}, P (1,4)$ (Solución) 208. $f(x, y) = e^xcosy; P (0, 0)$ 209. $f(x, y) = arctan (x + 2y), P (1,0)$ (Solución) 210. $f(x, y) = \sqrt{20 − x^2 − 7y^2}, P (2, 1)$ 211. $f(x, y, z) = \sqrt{x^2 + y^2 + z^2}, P (3, 2, 6)$ (Solución) 212. [T] Encuentra la ecuación del plano tangente a la superficie $f(x, y) = x^2 + y^2$ en el punto $(1, 2, 5)$, y grafica la superficie y el plano tangente en el punto. 213. [T] Encuentra la ecuación para el plano tangente a la superficie en el punto indicado, y grafica la superficie y el plano tangente: $z = ln(10x^2 + 2y^2 + 1), P (0, 0, 0)$ (Solución). 214. [T] Encuentra la ecuación del plano tangente a la superficie $z = f(x, y) = sen (x + y^2)$ en el punto $(\frac{\pi}{4},0,2\sqrt{2})$, y grafica la superficie y el plano tangente.