Solución

A partir de las ecuaciones simétricas de la recta, sabemos que el vector v=⟨4,2,1⟩\bold{v} = \lang 4,2,1\rang es un vector direccional para la recta. Al establecer las ecuaciones simétricas de la recta igual a cero, vemos que el punto P(3,−1,3)P (3, -1,3) se encuentra en la recta. Luego,

PM→=⟨1−3,1−(−1),3−3⟩=⟨−2,2,0⟩\overrightarrow{PM} =\lang 1−3,1−(−1),3−3\rang = \lang −2,2,0\rang

Para calcular la distancia, necesitamos encontrar PM→×v\overrightarrow{PM}\times\bold{v}:

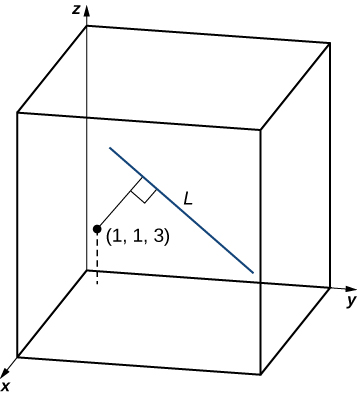
PM→×v=∣ijk−220421∣=(2−0)i−(−2−0)j+(−4−8)k=2i+2j−12k\begin{aligned} \overrightarrow{PM}\times\bold{v} &= \begin{vmatrix} \bold{i} & \bold{j} & \bold{k}\\-2 & 2 & 0\\4 & 2 & 1\end{vmatrix}\\ &= (2−0)\bold{i}−(−2−0)\bold{j}+(−4−8)\bold{k}\\ &= 2\bold{i}+2\bold{j}−12\bold{k} \end{aligned}

Por lo tanto, la distancia entre el punto y la recta es (Figura 2.66)

d=∥PM→×v∥∥v∥=22+22+12242+22+12=23821\begin{aligned} \bold{d} &= \frac{\bigg\|\overrightarrow{PM} \times \bold{v}\bigg\|}{\|\bold{v}\|}\\ &= \frac{\sqrt{2^2+2^2+12^2}}{\sqrt{4^2+2^2+1^2}}\\ &= \frac{2\sqrt{38}}{\sqrt{21}} \end{aligned}

Figura 2.66. El punto (1,1,3)(1,1,3) está aproximadamente a 2.72.7 unidades de la recta con ecuaciones simétricas x−34=y+12=z−3\frac{x − 3}{4} = \frac{y + 1}{2} = z − 3.